Πρόλογος
Το βιβλίο αυτό απευθύνεται σε φοιτητές Μαθηματικών Τμημάτων και κατά κύριο μέρος στηρίζεται στις διαλέξεις μας στο προπτυχιακό μάθημα «Θεωρία Galois» που επί σειρά ετών διδάσκoυμε στο Τμήμα Μαθηματικών της Σχολής Θετικών Επιστημών του Αριστοτελείου Πανεπιστημίου Θεσσαλονίκης.
Η Θεωρία Galois αρχικά αναφέρεται στην επίλυση αλγεβρικών, δηλ. πολυωνυμικών, εξισώσεων. Η επίλυση αλγεβρικών εξισώσεων απασχόλησε τους ανθρώπους περίπου από το 1700 π. Χ. σε διάφορες μορφές διατυπωμένες ανάλογα με το επίπεδο γνώσεων της εποχής. Φυσικά το πρώτο ερώτημα που διατυπώθηκε ήταν πώς μπορεί να λυθεί μία τέτοια εξίσωση και με την πάροδο των αιώνων οι μαθηματικοί αναρωτήθηκαν αν επιλύονται πάντα αυτές οι εξισώσεις. Την τελική απάντηση για την επιλυσιμότητα των αλγεβρικών εξισώσεων έδωσε ο Evariste Galois (1811-1832) στην ηλικία των 21 ετών στηριζόμενος στη μεγαλοφυΐα του και στο γιγάντιο σχετικό επιστημονικό έργο που είχε προηγηθεί της ζωής του.
Στο βιβλίο αναπτύσσουμε τη θεωρία που έλαβε το όνομά της από τον Galois. Σκοπός μας δεν είναι να δώσουμε τεχνικές επίλυσης διαφόρων συγκεκριμένων περιπτώσεων. Σκοπός μας είναι να αναπτύξουμε μία εξαιρετική μαθηματική θεωρία που αναπτύχθηκε από τον 17ο αιώνα και μετά και οδηγεί σε απαντήσεις ερωτημάτων που διατυπώθηκαν από τους Βαβυλώνιους και τους Αρχαίους Έλληνες και απαντήθηκαν τον 19ο αιώνα. Δεν θα μας απασχολήσει η ιστορική παρουσίαση των επιστημονικών γεγονότων κεντρικά, ούτε θα παρουσιάσουμε τη Θεωρία Galois όπως αυτή παρουσιάστηκε από τον Galois και αμέσως μετά όπως αυτή διατυπώθηκε από τους μαθηματικούς του 19-ου αιώνα. Παρουσιάζουμε τη θεωρία αυτή με τη σύγχρονη θεώρηση της Άλγεβρας, ώστε ο αναγνώστης να εξοικειωθεί με τις εκπληκτικές ιδέες του νεαρού Galois, αλλά να μπορεί επίσης να παρακολουθήσει την εξέλιξη αυτής της θεωρίας και να κατευθύνει τους προβληματισμούς του σε σωστές διαδρομές σύγχρονwν επιτευγμάτων.
Το βιβλίο αποτελείται από οκτώ Κεφάλαια. Στο Κεφάλαιο 1 παρουσιάζονται τα κύρια θέματα που θα αναπτυχθούν στο κείμενο αυτό. Ακόμη, δίνονται οι απαιτούμενες έννοιες από τη θεωρία πολυωνύμων και τη θεωρία σωμάτων για την μελέτη της θεωρίας Galois. Στο Κεφάλαιο 2 περιέχεται h θεωρία επεκτάσεων σωμάτων και ιδιαίτερα των αλγεβρικών επεκτάσεων. Επίσης δίνεται η έννοια της ομάδας Galois μίας επέκτασης. Στο Κεφάλαιο 3 μελετώνται οι επεκτάσεις Galois και αποδεικνύεται το θεμελιώδες θεώρημα της θεωρίας Galois. Η θεωρία που αναπτύχθηκε στο Κεφάλαια 3 εφαρμόζεται στις επεκτάσεις πεπερασμένων σωμάτων και αυτό είναι το αντικείμενο του κεφαλαίου 4. Στο Κεφάλαιο 5 συνεχίζεται η εφαρμογή της θεωρίας των επεκτάσεων Galois στη μελέτη των ριζών της μονάδας και των κυκλοτομικών επεκτάσεων. Στο Κεφάλαιο 5 αντιμετωπίζεται το ερώτημα πότε μπορεί να επιλυθεί μία αλγεβρική εξίσωση. Λέγοντας να επιλυθεί μία αλγεβρική εξίσωση εννοούμε να μπορούμε να βρούμε έναν τύπο που να παρέχει τις λύσεις της εξίσωσης, όπως αυτό συμβαίνει όταν το πολυώνυμο είναι δευτέρου βαθμού και έχουμε τον γνωστό τύπο από τις σχολικές μας γνώσεις. Στο Κεφάλαιο αυτό αποδεικνύεται το Θεώρημα του Galois που δίνει μία ικανή και αναγκαία συνθήκη ώστε να είναι επιλύσιμη με ριζικά μία αλγεβρική εξίσωση, απαντώντας σε ένα ερώτημα πολλών αιώνων και αποτελεί ένα από τα σημαντικότερα θεωρήματα των μαθηματικών. Ως εφαρμογή του θεωρήματος του Galois αντιμετωπίζονται τα τρία κλασικά προβλήματα κατασκευασιμότητας με κανόνα και διαβήτη που διατύπωσαν oι αρχαίοι έλληνες καθώς και προβλήματα κατασκευασιμότητας κανονικών πολυγώνων. Τέλος στο Κεφάλαιο αυτό αποδεικνύεται το θεμελιώδες θεώρημα της Άλγεβρας κυρίως ως εφαρμογή του θεμελιώδους θεωρήματος της θεωρίας Galois. Στο Κεφάλαιο 7 εξετάζονται βαθύτερα οι αλγεβρικές επεκτάσεις και μελετώνται οι αλγεβρικά κλειστές επεκτάσεις. Η Θεωρία Galois είναι μία θεωρία που αναδεικνύει μία εξαιρετική σχέση μεταξύ της θεωρίας σωμάτων και της θεωρίας ομάδων. Βέβαια καθώς η μεγάλη επινόηση του Galois ήταν να εξετάσει τον ρόλο των μεταθέσεων των ριζών πολυωνύμων στην επιλυσιμότητα των πολυωνυμικών εξισώσεων, η ομάδα μεταθέσεων των αντικειμένων ήταν η μόνη ομάδα που απασχόλησε τους μαθηματικούς τον 19ο αιώνα. Στο Κεφάλαιο 8 αποδεικνύεται ότι υπάρχει πολυώνυμο του οποίου η ομάδα Galois είναι η . Αυτό σημαίνει, ως συνέπεια του Θεμελιώδους Θεωρήματος της Θεωρίας Galois, ότι κάθε πεπερασμένη ομάδα είναι ομάδα Galois κάποιας επέκτασης σωμάτων. Στο υπόλοιπο του 8-ου κεφαλαίου σχολιάζουμε το καίριο ερώτημα που δημιουργείται: αν είναι μία πεπερασμένη ομάδα υπάρχει επέκταση του σώματος των ρητών αριθμών με ομάδα Galois την Το ερώτημα αυτό δεν έχει απαντηθεί ακόμη και αποτελεί το λεγόμενο «Αντίστροφο Πρόβλημα της Θεωρίαc Galois».
Κάθε Κεφάλαιο του βιβλίου περιέχει πληθώρα παραδειγμάτων και στο τέλος κάθε κεφαλαίου υπάρχει ένα εδάφιο ασκήσεων. Μετά το 8-ο Κεφάλαιο παρατίθεται το Παράρτημα στο οποίο έχουν συμπεριληφθεί όλες οι προαπαιτούμενες γνώσεις της θεωρίας ομάδων, της θεωρίας δακτυλίων και της θεωρίας πολυωνύμων για την ανάπτυξη της μελέτης μας, ώστε το κείμενο να είναι πιο ολοκληρωμένο για το απρόσκοπτο διάβασμα. Δίνονται αναφορές που καθοδηγούν τον αναγνώστη σε άλλα συγγράμματα για τις προαπαιτούμενες γνώσεις, που συνήθως οι φοιτητές έχουν από άλλα μαθήματα άλγεβρας. Επίσης στο τέλος κάθε κεφαλαίου υπάρχει εκτενής βιβλιογραφία. Μέσα στο κείμενο οι αναφορές των θεωρημάτων, προτάσεων, πορισμάτων, παραδειγμάτων και ασκήσεων γίνεται με το αύξοντα αριθμό της θέσης του στο κείμενο. Π. χ. το Θεώρημα 3.5.3 είναι με αύξοντα αριθμό 3 στο εδάφιο 5 του κεφαλαίου 3. Το Παράδειγμα 1.2.7.1 είναι το παράδειγμα με αύξοντα αριθμό 1 στα Παραδείγματα με αριθμό 1.2.7. Ανάλογα αναφέρονται και οι ασκήσεις. Το Παράρτημα έχει πέντε εδάφια: Ι, ΙΙ, ΙΙΙ, ΙV, V έτσι το Θεώρημα Ι. 15 είναι το θεώρημα με αύξοντα αριθμό 15 στο εδάφιο Ι του Παραρτήματος. Το τέλος κάθε απόδειξης επισημαίνεται με το σύμβολο .
Όπως κάθε επιστημονικό αντικείμενο έτσι και αυτό κατακτάται με μελέτη και επιμονή. Η σελίδα-σελίδα κατανόηση του κειμένου είναι απαραίτητη για τη συνέχεια της μελέτης και ο έλεγχος της γνώσης γίνεται με την επίλυση των ασκήσεων. Αυτή η διαδικασία είναι εγγύηση για το αποτέλεσμα που επιδιώκει ο συνετός αναγνώστης. Τα παραδείγματα που παραθέτουμε καθώς και οι υποδείξεις των λύσεων έχουν στόχο να καταστήσουν τη διαδρομή μελέτης πι ο κατανοητή και, ελπίζουμε, απολαυστική. Θα είμαστε υπερήφανες αν καταφέρναμε συνεχώς και περισσότεροι αναγνώστες του βιβλίου αυτού να μπορέσουν να γευθούν την ηδονή της κατάκτησης και επεξεργασίας αυτής της καθόλου εύκολης αλλά σημαντικής γνώσης των μαθηματικών. Για μας η καθοδήγηση των δασκάλων μας σε όλη την πορεία μας φώτισε τις προσπάθειές μας. Οι φοιτητές μας, αγόρια και κορίτσια, με την αγάπη τους για τα μαθηματικά, την περιέργεια για την απάντηση στο ερώτημα, την έντονη προσπάθεια για την εύρεσή της, ο ενθουσιασμός και η υπερηφάνειά τους για την κατάκτηση της όλης γνώσης ήταν ο λόγος που αποφασίσαμε να συμπεριλάβουμε σε αυτό το κείμενο την εμπειρία μας από την μακρόχρονη διδασκαλία του αντικειμένου αυτού.
Μερικές συμβουλές για τον αναγνώστη αυτού του βιβλίου τις θεωρούμε απαραίτητες. Ο αναγνώστης που δεν είναι εξοικειωμένος με τη Θεωρία Ομάδων και τη Θεωρία Δακτυλίων οφείλει να ξεκινήσει τη μελέτη του από το Παράρτημα και να μελετήσει τα τέσσερα πρώτα εδάφια, δηλ. τα εδάφια I-IV. Στο εδάφιο V του Παραρτήματος, για πληρότητα, δίδονται οι ρίζες του γενικού πολυωνύμου τρίτου και η μελέτη του εδαφίου αυτού είναι ανεξάρτητη των υπολοίπων.
Στο εδάφιο με τίτλο «Υποδείξεις λύσεων επιλεγμένων ασκήσεων» δίνεται υπόδειξη λύσης των ασκήσεων που παρουσιάζουν μεγαλύτερη δυσκολία, ή δίνεται το αποτέλεσμα κάποιων εξ αυτών.
Σε όλο το κείμενο, μετά την εμφάνιση κάποιου επιστημονικού όρους για πρώτη φορά, η οποία επισημαίνεται με έντονους τυπογραφικού χαρακτήρες, ακολουθεί ο ίδιος όρος στην Αγγλική γλώσσα. Στο εδάφιο με τίτλο «Ευρετήρια» παραθέτουμε τα ευρετήρια των συμβολισμών και των μαθηματικών όρων και επώνυμων Θεωρημάτων και Λημμάτων που αναφέρονται στο κείμενο στην Ελληνική και Αγγλική γλώσσα και σημειώνουμε τη σελίδα στην οποία βρίσκονται. Με το ευρετήριο της Αγγλικής ορολογίας ο αναγνώστης μπορεί εύκολα να αναζητήσεις αντίστοιχα θέματα στην Αγγλική βιβλιογραφία, εφόσον το επιθυμεί.
Το παρακάτω διάγραμμα δηλώνει τη σχέση εξάρτησης μεταξύ των κεφαλαίων του βιβλίου, εκτός του Παραρτήματος.
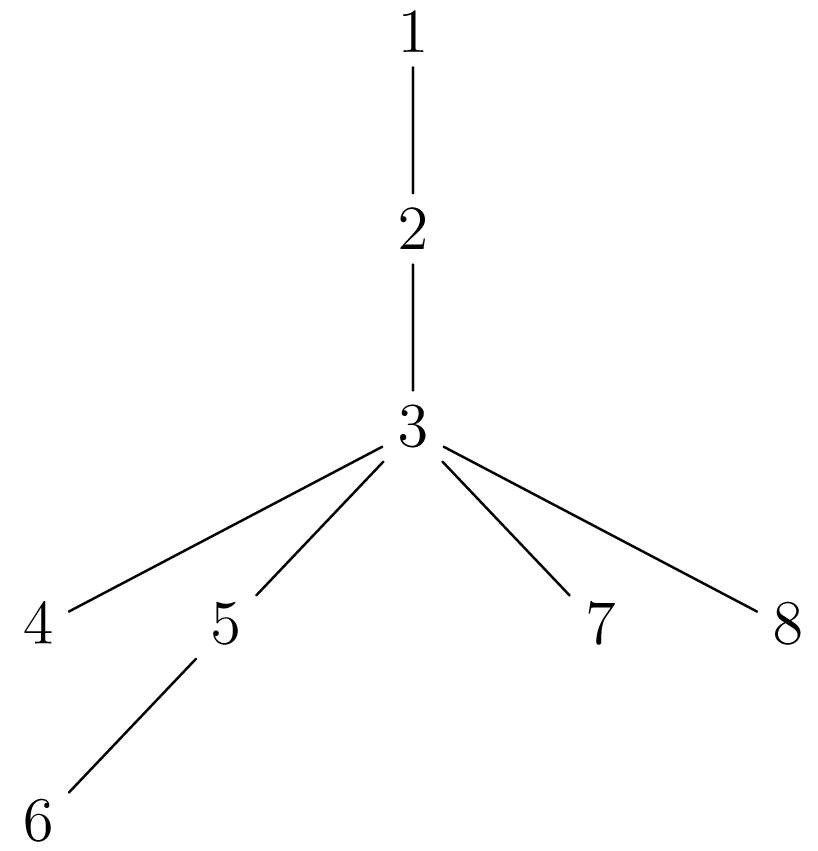
Για παράδειγμα, το Κεφάλαιο 4 μπορεί να διαβαστεί ανεξάρτητα των Κεφαλαίων 5 και 6 κ.ο.κ. Το βιβλίο αυτό γράφτηκε στα πλαίσια του έργου Κάλλιπος. Ευχαριστούμε θερμά τον κριτικό αναγνώστη του βιβλίου, Καθηγητή του Τμήματος Μαθηματικών του Εθνικού Καποδιστριακού Πανεπιστήμιου Αθηνών κ. Αριστείδη Κοντογεώργη για τις χρήσιμες παρατηρήσεις του, τον κ. Ιωάννη Καρύδη για τη μετατροπή του συγγράμματος σε μερφή HTML5 και την κ. Μαρία-Ιωάννα Χριστοφορίδου για την επιμέλεια το εξώφυλλου.