Θεωρία Galois

Κεφάλαιο 7Απλές επεκτάσεις και Αλγεβρικές Θήκες

Στο κεφάλαιο αυτό εξετάζουμε τις απλές επεκτάσεις σωμάτων και τις συγκρίνουμε με τις επεκτάσεις Galois. Eπίσης εξετάζουμε τις αλγεβρικά κλειστές επεκτάσεις και τις συγκρίνουμε με το σώμα των μιγαδικών αριθμών.

7.1 Απλές επεκτάσεις

Στην ενότητα αυτή θα εξετάσουμε ποιες επεκτάσεις σωμάτων είναι απλές. Έστω $F$ ένα πεπερασμένο σώμα με $\operatorname{char}F=p$ και $Ε/F$ μία επέκταση του Galois. Aφού $[Ε:F]<\infty$ , έπεται ότι το $Ε$ είναι πεπερασμένο σώμα. Σύμφωνα με το Πόρισμα 4.2.4 υπάρχει $a\in E$ , τέτοιο ώστε $Ε=\operatorname{GF}(p)(a)$ . Αφού

Ε=\operatorname{GF}(p)(a)\subseteq F(a)\subseteq E,

συμπεραίνουμε ότι $E=F(a)$ . Δείξαμε λοιπόν ότι κάθε επέκταση του Galois $Ε/F$ είναι απλή επέκταση, όταν $\operatorname{char}F=p$ και $|E|<\infty$ . Θα δούμε ότι το αντίστοιχο ισχύει για επεκτάσεις Galois $Ε/F$ , όταν η χαρακτηριστική του $F$ είναι μηδέν.

Θεώρημα 7.1.1.

Έστω ότι $Ε/F$ είναι επέκταση του Galois με $\operatorname{char}F=0$ . Τότε υπάρχει $a\in E$ έτσι ώστε $E=F(a)$ .

Απόδειξη.

An το $E=F$ , το συμπέρασμα είναι προφανές. Έστω, λοιπόν, ότι $Ε\neq F$ . Αφού $[Ε:F]<\infty$ , σύμφωνα με την άσκηση 2.4.10, υπάρχουν $b_{1},\ldots,b_{n}$ έτσι ώστε $E=F(b_{1},\ldots,b_{n})$ . Με απλή επαγωγή στο $n$ , βλέπουμε ότι αρκεί να αποδείξουμε ότι $Ε$ είναι απλή επέκταση του $F$ στην περίπτωση που το $E=F(b,c)$ και το $c\notin F(b)$ , δηλ. όταν

F(b)\subsetneqq F(b,c)=E.

(7.1.1.1)

Σύμφωνα με την άσκηση 3.7.12, τα πολυώνυμα $\operatorname{irr}_{(F,b)}(x)$ και $\operatorname{irr}_{(F,c)}(x)$ αναλύονται σε γινόμενα γραμμικών παραγόντων στο $E[x]$ . Αφού $\operatorname{char}F=0$ , τα ανάγωγα πολυώνυμα του $F[x]$ είναι διαχωρίσιμα. Έστω $b_{1},\ldots,b_{n}\in E$ οι ρίζες του $\operatorname{irr}_{(F,b)}(x)$ στο $Ε$ , παίρνοντας ως $b_{1}$ το $b$ , και όπου $n=\deg\operatorname{irr}_{(F,b)}(x)$ . Αντίστοιχα, έστω και $c_{1},\ldots,c_{μ}\in E$ οι ρίζες του $\operatorname{irr}_{(F,c)}(x)$ στο $Ε$ με $c_{1}=c$ , όπου $m=\deg\operatorname{irr}_{(F,c)}(x)$ . Στη συνέχεια, θεωρούμε το παρακάτω (πεπερασμένο) υποσύνολο του $E$ :

\Big\{\frac{b_{i}-b}{c-c_{j}}:\ 1<i\leq n,1<j\leq m\Big\}\subset E\ .

Αφού Το $F$ είναι άπειρο, υπάρχει κάποιο στοιχείο του $F$ , διάφορο του μηδενός, που να μην ανήκει στο παραπάνω σύνολο, έστω $d$ . Έτσι,

d\neq\ \frac{b_{i}-b}{c-c_{j}},\textrm{ άρα }d(c-c_{j})\neq b_{i}-b\textrm{ κα% ι επομένως }(b+dc)\neq(b_{i}+dc_{j}),

(7.1.1.2)

όπου $1<i\leq n$ και $1<j\leq m$ . Έστω τώρα Το στοιχείο $a=b+dc$ . Το $a$ ανήκει βέβαια στο $E$ . Aν $a\in F$ τότε

c=\frac{a-b}{d}\in F(b),

άτοπο, αφού είμαστε στην περίπτωση της (7.1.1.1). Επομένως $a\notin F$ . Επίσης, από την σχέση (7.1.1.2) προκύπτει ότι, για $1<i\leq n$ και $1<j\leq m$ ,

a\neq b_{ι}+dc_{j}\ .

(7.1.1.3)

Θα δείξουμε ότι $F(a)=Ε$ . Έστω

h(x)=\operatorname{irr}_{(F,b)}(a-dx)\in F(a)[x].

Παρατηρούμε ότι το $c$ είναι κοινή ρίζα των $h(x)$ και $\operatorname{irr}_{(F,c)}(x)$ , ενώ δεν υπάρχει άλλη κοινή ρίζα αυτών των πολυωνύμων. Πράγματι,

h(c)=\operatorname{irr}_{(F,b)}(a-dc)=\operatorname{irr}_{(F,b)}(b)=0.

Αν, τώρα, $c_{j}$ ήταν ρίζα του $h(x)$ , για κάποιο $j\neq 1$ , τότε $\operatorname{irr}_{(F,b)}(a-dc_{j})=0$ και επομένως $a-dc_{j}$ πρέπει να είναι ένα από τα $b_{i}$ , όπου $i=1,\ldots,n$ . Αν $a-dc_{j}=b_{1}$ , τότε αφού $a=b_{1}+dc_{1}$ , έχουμε ότι

b_{1}+dc_{1}-dcj=b_{1}\Rightarrow c=c_{j},

άτοπο, αφού οι ρίζες $c_{1},\ldots,c_{m}$ του $\operatorname{irr}_{(F,c)}(x)$ είναι διακεκριμένες και $j\neq 1$ . An $a-dc_{j}=b_{i}$ , για $i\neq 1$ , οδηγούμαστε πάλι σε άτοπο, από τη σχέση (7.1.1.3). Άρα το $c$ είναι η μόνη κοινή ρίζα των $h(x)$ και $\operatorname{irr}_{(F,c)}(x)$ .

Έστω $q(x)\in F(a)[x]$ o μέγιστος κοινός διαιρέτης των $h(x)$ και $\operatorname{irr}_{(F,c)}(x)$ στον δακτύλιο $F(a)[x]$ . Ο μέγιστος κοινός διαιρέτης υπολογίζεται σύμφωνα με τον Ευκλείδειο αλγόριθμο. Έτσι, το $q(x)$ είναι μέγιστος κοινός διαιρέτης των $h(x)$ και $\operatorname{irr}_{(F,c)}(x)(x)$ στον δακτύλιο $E[x]$ , βλ. Θεώρημα III.3. Αφού το $c$ είναι η μόνη κοινή ρίζα στο $Ε$ των $h(x)$ και $\operatorname{irr}_{(F,c)}(x)$ στον $Ε$ και γνωρίζουμε πλήρως την ανάλυση των δύο αυτών πολυωνύμων σε γραμμικούς παράγοντες στον $E[x]$ , συμπεραίνουμε ότι

q(x)=x-c.

Όμως, το $q(x)\in F(a)[x]$ και άρα $c\in F(a)$ . Επίσης, αφού $b=a-dc$ συμπεραίνουμε ότι $b\in F(a)$ και επομένως

F(a)\subset F(b,c)\subset F(a).

δηλ. $F(a)=F(b,c)$ και η επέκταση $F(b,c)$ είναι απλή. ∎

Σημειώνουμε ότι αν $F=\operatorname{GF}(p)(x^{p},y^{p})$ και $Ε=\operatorname{GF}(p)(x,y)$ τότε η επέκταση $E/F$ είναι πεπερασμένη. Όμως το $E$ δεν είναι απλή επέκταση του $F$ , (βλ. άσκηση 7.3.3).

7.2 Αλγεβρικά κλειστές επεκτάσεις

Στην Ενότητα 6.3 αποδείξαμε ότι το ${\mathbb{C}}$ είναι αλγεβρικά κλειστό και ότι είναι το μικρότερο σώμα με αυτήν την ιδιότητα που περιέχει το ${\mathbb{R}}$ . Σε αυτήν την ενότητα θα γενικεύσουμε τα παραπάνω για τυχαία σώματα.

Ορισμός 7.2.1.

Έστω $E/F$ επέκταση σωμάτων. Η αλγεβρική θήκη (algebraic closure) του $F$ στο $Ε$ συμβολίζεται με $\overline{F}_{E}$ και είναι το σύνολο

\overline{F}_{E}=\{a\in E:\ a\textrm{ είναι αλγεβρικό πάνω από το }F\}.

Πρόταση 7.2.2.

Έστω $E/F$ επέκταση σωμάτων. Τότε η αλγεβρική θήκη $\overline{F}_{E}$ είναι σώμα.

Απόδειξη.

Αν $a,b\in\overline{F}_{E}$ , τότε από το Πόρισμα 2.2.14 προκύπτει ότι $F(a,b)/F$ είναι αλγεβρική επέκταση. Επομένως κάθε στοιχείο του $F(a,b)$ ανήκει στην $\overline{F}_{E}$ . ’Aρα $a-b$ και $a/b$ ανήκουν στην $\overline{F}_{E}$ και επομένως $\overline{F}_{E}$ είναι σώμα. ∎

Παραδείγματα 7.2.3.

1.

Έστω $Ε={\mathbb{Q}}(\sqrt{2})$ . Η αλγεβρική θήκη $\overline{{\mathbb{Q}}}_{E}$ είναι το το σώμα $E$ , αφού κάθε στοιχείο του $Ε$ είναι αλγεβρικό πάνω από το ${\mathbb{Q}}$ , βλ. Πόρισμα 2.2.14.
2.

Αν $E/F$ είναι αλγεβρική επέκταση, τότε $\overline{F}_{E}=Ε$ .
3.

H επέκταση $\overline{{\mathbb{Q}}}_{\mathbb{R}}/{\mathbb{Q}}$ είναι άπειρη και αριθμήσιμη (countable), δηλ. υπάρχει μία αριθμήσιμη βάση του σώματος $\overline{{\mathbb{Q}}}_{\mathbb{R}}$ πάνω από το ${\mathbb{Q}}$ , βλ. άσκηση 7.3.5.

Ορισμός 7.2.4.

Ένα σώμα $F$ λέγεται αλγεβρικά κλειστό (algebraic closure) αν $\overline{F}_{E}=F$ , για κάθε σώμα $Ε$ που περιέχει το $F$ .

Είναι φανερό ότι ένα σώμα $F$ είναι αλγεβρικά κλειστό αν και μόνο αν κάθε μη σταθερό πολυώνυμο στο $F[x]$ έχει σώμα ανάλυσης το $F$ . Βέβαια, για να δείξει κανείς ότι ένα σώμα είναι αλγεβρικά κλειστό, αρκεί να δείξει ότι κάθε μη σταθερό πολυώνυμο στο $F[x]$ , έχει τουλάχιστον μία ρίζα στο $F$ .

Παραδείγματα 7.2.5.

1.

${\mathbb{Q}}$ και ${\mathbb{R}}$ δεν είναι αλγεβρικά κλειστά σώματα.
2.

Το Θεμελιώδες Θεώρημα της Άλγεβρας λέει ότι το ${\mathbb{C}}$ είναι αλγεβρικά κλειστό.
3.

Έστω $F$ ένα πεπερασμένο σώμα. Το $F$ δεν είναι αλγεβρικά κλειστό, (άσκηση 7.3.5).

Το επόμενο συμπέρασμα γενικεύει το Θεώρημα 2.2.10.

Θεώρημα 7.2.6.

Έστω $F$ σώμα και έστω $p_{1}(x),\ldots,p_{n}(x)\in F[x]$ . Τότε υπάρχει επέκταση $Ε/F$ , τέτοια ώστε $[Ε:F]<\infty$ και κάθε ένα από τα πολυώνυμα $p_{1}(x),\ldots,p_{n}(x)$ να αναλύεται σε γινόμενο γραμμικών παραγόντων στο $Ε$ .

Απόδειξη.

Θα εφαρμόσουμε επαγωγή στο $n$ . Aν $n=1$ τότε, είμαστε στην περίπτωση του Θεωρήματος 2.2.10. Υποθέτουμε τώρα, ότι η πρόταση είναι αληθής για $n-1$ πολυώνυμα. Έστω, λοιπόν, $Ε^{\prime}/F$ μία επέκταση σωμάτων έτσι ώστε $[Ε^{\prime}:F]<\infty$ και κάθε ένα από τα $p_{2}(x),\ldots,p_{n}(x)$ να αναλύεται σε γινόμενο γραμμικών παραγόντων στο $Ε^{\prime}$ . Αφού $F\subset E^{\prime}$ , θεωρούμε το $p_{1}(x)$ ως πολυώνυμο του $E^{\prime}[x]$ . Από το Θεώρημα 2.2.10, υπάρχει σώμα ανάλυσης $Ε$ του $p_{1}(x)$ πάνω από το $E^{\prime}$ και $[E:E^{\prime}]<\infty$ . Επομένως, από την Πρόταση 2.2.12, έπεται ότι

[Ε:F]=[Ε:Ε^{\prime}]\;[Ε^{\prime}:F]<\infty

και το $Ε$ έχει τις επιθυμητές ιδιότητες της πρότασης. ∎

Το επόμενο παράδειγμα θα βοηθήσει να γίνει κατανοητή η κατασκευή της απόδειξης του Θεωρήματος 7.2.8.

Παράδειγμα 7.2.7.

Έστω $f_{1}(x)=x^{2}-2$ και $f_{2}(x)=x^{3}-5$ πολυώνυμα στον ${\mathbb{Q}}[x]$ . Περνάμε τώρα στον δακτύλιο πολυωνύμων με τρεις ανεξάρτητες μεταβλητές, $R={\mathbb{Q}}[X_{1},X_{2},X_{3}]$ . Στη συνέχεια, θεωρούμε τα πολυώνυμα $f_{1}(X_{1})$ και $f_{2}(X_{2})$ του $R$ . Έστω $Ι$ το παρακάτω ιδεώδες του $R$

Ι=\langle X_{1}^{2}+2,X_{2}^{3}-5\rangle.

Για παράδειγμα, το πολυώνυμο

g(X_{1},X_{2},X_{3})=(X_{1}X_{3})f_{1}(X_{1})+(X_{1}+2)f_{2}(X_{2})

ανήκει στο $I$ . Επίσης, το $g(\sqrt{2},\sqrt[3]{5},X_{3})$ είναι το μηδενικό πολυώνυμο στο ${\mathbb{Q}}(\sqrt{2},\sqrt[3]{5})[x]$ , αφού

g(\sqrt{2},\sqrt[3]{5},X_{3})=(\sqrt{2}X_{3})f_{1}(\sqrt{2})+(\sqrt{2}+2)f_{2}% (\sqrt[3]{5})=(\sqrt{2}X_{3})0+(\sqrt{2}+2)0=0.

Θεώρημα 7.2.8.

Έστω $F$ σώμα. Υπάρχει επέκταση $L/F$ , τέτοια ώστε κάθε μη σταθερό πολυώνυμο να έχει μία ρίζα στο $L$ .

Απόδειξη.

Έστω

S=\{f:\ f\in F[x],\ \deg f\geq 1\}.

Σε κάθε στοιχείο $f$ του $S$ αντιστοιχούμε μία ανεξάρτητη μεταβλητή $X_{f}$ . Θεωρούμε $R$ , τον πολυωνυμικό δακτύλιο στις (άπειρες) μεταβλητές $\{X_{f}\}_{f\in S}$ και $I$ το ιδεώδες που παράγεται από τα πολυώνυμα $f(X_{f})$ στον $R$ . An $g\in I$ τότε

g=r_{1}f_{1}(X_{f_{1}})+\cdots+r_{n}f_{n}(X_{f_{n}})\textrm{ για κάποιο }n\in{% \mathbb{N}},{f_{i}}\in S\textrm{ kai }r_{i}\in R.

(7.2.8.1)

Χρησιμοποιώντας το Θεώρημα 7.2.6, μπορεί να δείξει κανείς ότι το $Ι$ είναι γνήσιο ιδεώδες του $R$ . Πράγματι, θα υποθέσουμε ότι $I=R$ και θα καταλήξουμε σε άτοπο. Έστω, λοιπόν, ότι $I=R$ , δηλ. ότι $1\in I$ . Τότε το $1$ έχει μία έκφραση της μορφής (7.2.8.1). ’ρα

1=r_{1}f_{1}(X_{f_{1}})+\cdots+r_{n}f_{n}(X_{f_{n}})\textrm{ για κάποιο }n\in{% \mathbb{N}},{f_{i}}\in S\textrm{ kai }r_{i}\in R.

(7.2.8.2)

Από το Θεώρημα 7.2.6, υπάρχει μία επέκταση $E$ του $F$ τέτοια ώστε κάθε ένα από τα $f_{i}(x)\in F[x]$ να έχει από μία ρίζα, έστω $a_{i}\in E$ , για $i=1,\ldots,n$ . Στην έκφραση (7.2.8.2), αντικαθιστούμε τις τιμές $a_{1},\ldots,a_{n}$ για τις μεταβλητές $X_{f_{1}},\ldots,X_{f_{n}}$ και $0$ για κάθε μεταβλητή $X_{f}$ , αν $f\neq f_{1},\ldots,f_{n}$ . Με την αντικατάσταση αυτή προκύπτει ότι $0=1$ . Καταλήξαμε σε άτοπο, γιατί υποθέσαμε ότι $I=R$ . Επομένως $Ι$ είναι γνήσιο ιδεώδες του $R$ και σύμφωνα με την Πρόταση II.9, υπάρχει μέγιστο ιδεώδες $M$ του $R$ που να περιέχει το $I$ . Έστω το σώμα $L=R/M$ . Τότε

F:\ \rightarrow L,\quad c\mapsto c+M

είναι εμφύτευση του $F$ στο $L$ . Έστω τώρα $f(x)$ μη σταθερό πολυώνυμο στο $F[x]$ . Τότε

f(X_{f}+M)=f(X_{f})+M=M,

δηλ. 0, αφού $f(X_{f})$ ανήκει στο $I$ και επομένως $X_{f}+M$ είναι ρίζα του $f(x)$ στο $Λ$ .

∎

H κύρια ιδέα της απόδειξης του επόμενου Θεωρήματος είναι η διαδοχική εφαρμογή του Θεωρήματος 7.2.8. Με αυτόν τον τρόπο κατασκευάζεται μία αλυσίδα σωμάτων

F=L_{0}\hookrightarrow L_{1}\hookrightarrow L_{2}\cdots

(7.2.8.3)

τέτοια ώστε, για κάθε $i\geq 0$ , ο ομομορφισμός $\phi_{i,i+1}:\ L_{i}\rightarrow L_{i+1}$ να είναι εμφύτευση σωμάτων και κάθε πολυώνυμο του $L_{i}[x]$ να έχει μία ρίζα στο $L_{i+1}$ . Παρατηρούμε ότι, παίρνοντας τις διαδοχικές συνθέσεις των εμφυτεύσεων, βρίσκουμε εμφυτεύσεις $\phi_{i,j}:\ L_{i}\rightarrow L_{j}$ , για κάθε $i\leq j$ , όπου βέβαια $\phi_{i,i}:\ L_{i}\rightarrow L_{i}$ είναι ο ταυτικός αυτομορφισμός του $L_{i}$ . Η μαθηματική κατασκευή του ευθέως ορίου (direct limit) των $L_{i}$ , $\underrightarrow{\lim}L_{i}$ , δίνει ένα σώμα $E=\underrightarrow{\lim}L_{i}$ μαζί με ένα σύστημα εμφυτεύσεων $\phi_{i}:\ L_{i}\rightarrow E$ , έτσι ώστε το διάγραμμα του σχήματος (7.1) να είναι αντιμεταθετικό (commutative), δηλ. $\phi_{i}=\phi_{j}\circ\phi_{i,j}$ .

Σχήμα 7.1: Ευθύ όριο επεκτάσεων σωμάτων.

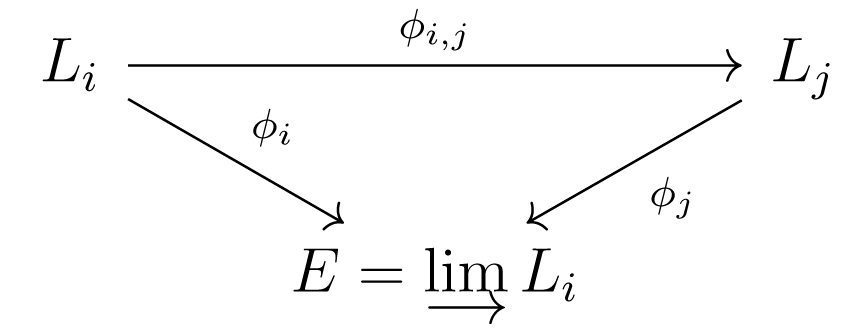
Χωρίς να μπούμε στις λεπτομέρειες της κατασκευής, σημειώνουμε ότι αν στην αλυσίδα (7.2.8.3), οι εμφυτεύσεις είναι εγκλεισμοί, an δηλ. για $i\geq 0$ , $L_{i}\subset L_{i+1}$ , τότε

E=\underrightarrow{\lim}L_{i}=\bigcup_{i}L_{i}.

Γενικότερα, μπορούμε να σκεφτούμε το ευθύ όριο των $L_{i}$ , ως την ένωση των $L_{i}$ , όπου όμως για κάθε $j\geq i$ , ταυτίζουμε τα στοιχεία των $L_{i}$ με τις εικόνες τους στα $L_{j}$ . Έτσι, αν για κάποιο λόγο, η διαδοχική εφαρμογή του Θεωρήματος 7.2.8, μας οδηγεί σε ένα σημείο σταθερότητας $m$ , όπου για κάθε $i\geq m$ , το $L_{i}=L_{m}$ , όπως δείχνουμε στη παρακάτω αλυσίδα,

F=L_{0}\hookrightarrow L_{1}\hookrightarrow L_{2}\cdots\hookrightarrow L_{m}% \hookrightarrow L_{m}

τότε $\underrightarrow{\lim}L_{i}=L_{m}$ . Θα αγνοήσουμε, για τις ανάγκες αυτού του κειμένου, τις περαιτέρω τεχνικότητες της κατασκευής και θα εστιάσουμε στη παρακάτω παρατήρηση: κάθε στοιχείο του $E$ , προκύπτει από κάποια εμφύτευση $\phi_{i}:\ L_{i}\rightarrow Ε$ . Έτσι για οποιαδήποτε πεπερασμένη συλλογή στοιχείων του $E$ μπορούμε να επιλέξουμε κατάλληλο μεγάλο δείκτη $n$ και να θεωρήσουμε ότι όλα τα στοιχεία αυτής της συλλογής προέρχονται από εμφύτευση στοιχείων του $L_{n}$ .

Θα δείξουμε τώρα ότι κάθε μη σταθερό πολυώνυμο στο $E$ έχει μία ρίζα στο $E$ . Έστω, λοιπόν, $p(x)=\sum a_{i}x^{i}\in E[x]$ , $\deg p(x)\geq 1$ και $n$ φυσικός αριθμός, έτσι ώστε $p(x)=\sum\phi_{n}(b_{i})x^{i}$ , όπου $b_{i}\in L_{n}$ . Θεωρούμε το πολυώνυμο

q(x)=\sum b_{i}x^{i}\in L_{n}[x].

Παρατηρούμε ότι $\deg q(x)\geq 1$ . Από το βήμα κατασκευής της αλυσίδας (7.2.8.3), το $q(x)$ έχει μία ρίζα, έστω $a$ , στο $L_{n+1}[x]$ . επομένως,

\sum\phi_{n,n+1}(b_{i})a^{i}=0\ .

Σύμφωνα με το αντιμεταθετικό διάγραμμα του Σχήματος (7.1), προκύπτει ότι:

\sum a_{i}\phi_{n+1}(a)^{i}=\sum\phi_{n+1}(\phi_{n,n+1}(b_{i}))\;\phi_{n+1}(a^% {i})=\phi_{n+1}(\sum\phi_{n,n+1}(b_{i})a^{i})=0

και επομένως $\phi_{n+1}(a)$ είναι ρίζα του $p(x)$ . Αποδείξαμε λοιπόν το παρακάτω συμπέρασμα:

Θεώρημα 7.2.9.

Έστω $F$ σώμα. Υπάρχει αλγεβρικά κλειστό σώμα $Ε$ , τέτοιο ώστε Το $F$ να εμφυτεύεται στο $Ε$ .

Αφού το ${\mathbb{C}}$ είναι αλγεβρικά πάνω από το ${\mathbb{R}}$ και το ${\mathbb{C}}$ είναι αλγεβρικά κλειστό, είναι φανερό ότι το ${\mathbb{C}}=\overline{R}_{{\mathbb{C}}}$ . Το ${\mathbb{C}}$ είναι το μικρότερο αλγεβρικά κλειστό σώμα που περιέχει το ${\mathbb{R}}$ .

Ορισμός 7.2.10.

Έστω $L/F$ επέκταση σωμάτων. Το $Ε$ λέγεται αλγεβρική θήκη (algebraic cover) του $F$ αν το $L$ είναι αλγεβρικά κλειστό και εάν η επέκταση του $L/F$ είναι αλγεβρική.

Όπως είδαμε προηγουμένως, το ${\mathbb{C}}$ είναι η αλγεβρική θήκη του ${\mathbb{R}}$ . Το επόμενο θεώρημα αφορά την ύπαρξη αλγεβρικών θηκών.

Θεώρημα 7.2.11.

Έστω $F$ σώμα. Υπάρχει επέκταση $E/F$ έτσι ώστε το $Ε$ να είναι η αλγεβρική θήκη του $F$ .

Απόδειξη.

Aπό το Θεώρημα 7.2.9, υπάρχει επέκταση $E/F$ έτσι ώστε Το $E$ να είναι αλγεβρικά κλειστό. Θεωρούμε την αλγεβρική θήκη $L$ του $F$ sΤο $E$ , δηλ. $L=\overline{F}_{E}$ . Για να δείξουμε ότι $\overline{L}=L$ , πρέπει να δείξουμε ότι Το $L$ είναι αλγεβρικά κλειστό σώμα. Έστω $p(x)\in L[x]$ . Τότε Το $p(x)\in E[x]$ και αφού το $Ε$ είναι αλγεβρικά κλειστό, υπάρχει κάποια ρίζα $a$ του $p(x)$ στο $Ε$ . Επομένως η επέκταση $L(a)/L$ είναι αλγεβρική. Αφού η επέκταση $L/F$ είναι επίσης αλγεβρική, συμπεραίνουμε ότι $L(a)/F$ είναι αλγεβρική, βλ. Πρόταση 2.2.15. ’ρα $a$ είναι αλγεβρικό πάνω από το $F$ και επομένως ανήκει στην αλγεβρική θήκη του $F$ στο $Ε$ . Συνεπώς $a\in L$ και Το $L$ είναι αλγεβρικά κλειστό. ∎

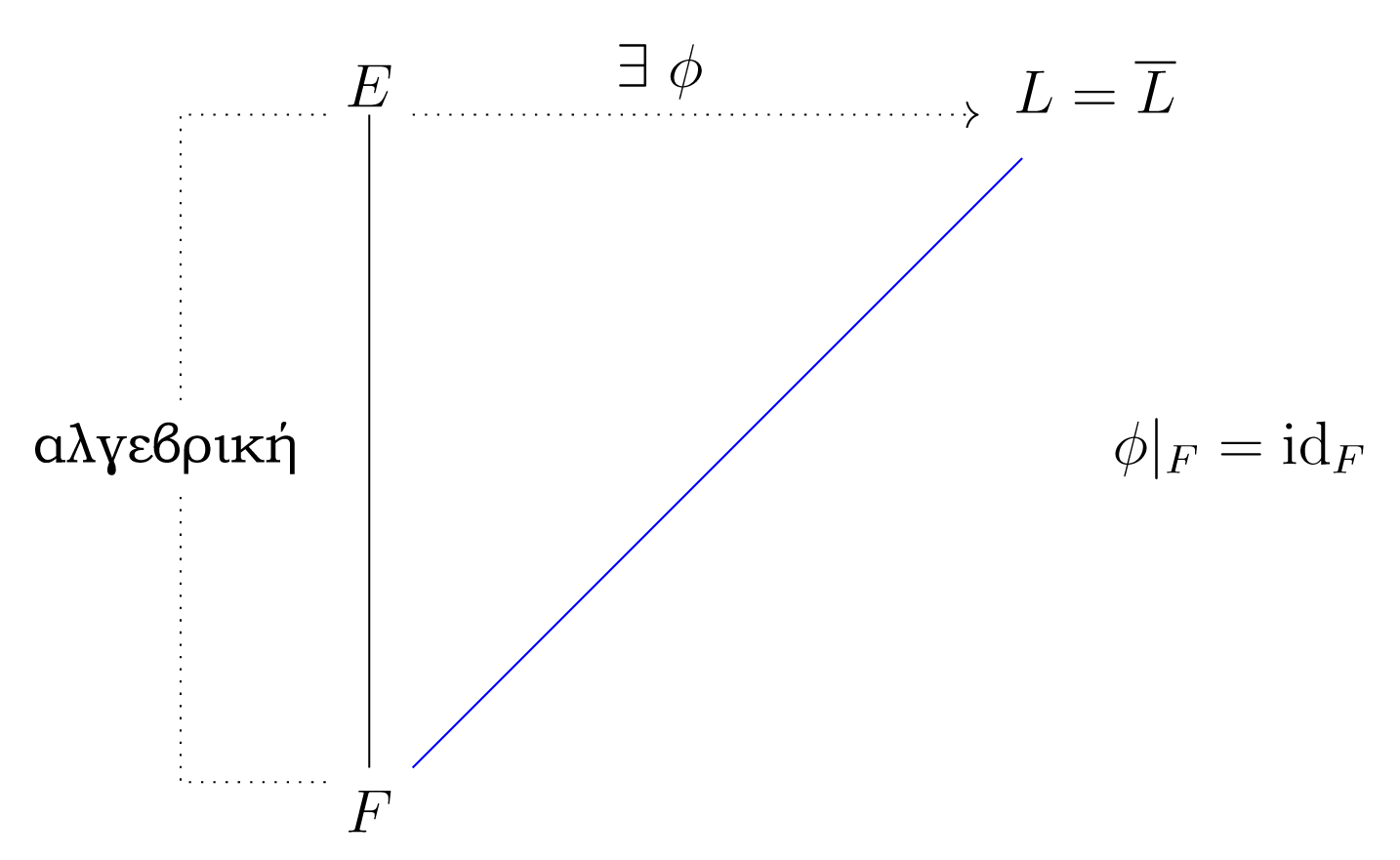
Είναι η αλγεβρική θήκη μοναδική με προσέγγιση $F$ -ισομορφίας; Η απάντηση είναι θετική, όπως μπορεί να δείξει κανείς χρησιμοποιώντας το Λήμμα του Zorn. Πρώτα, όμως, είναι χρήσιμο να δείξoυmε ότι, αν h $E/F$ είναι αλγεβρική επέκταση σωμάτων και $L/Φ$ ένα μία επέκταση σωμάτων, όπου $L=\overline{L}$ , τότε υπάρχει $F$ -εμφύτευση $\phi:E\rightarrow L$ , όπου $\phi(c)=c$ , για κάθε $c\in F$ .

Σχήμα 7.2: $F$ -εμφύτευση αλγεβρικής επέκτασης σε αλγεβρικά κλειστό σώμα

Η συνήθης τεχνική, για την απόδειξη της $F$ -εμφύτευσης, είναι να θεωρήσει κανείς το μη κενό μερικά διατεταγμένο σύνολο $\Omega$ , με στοιχεία ζεύγη $(K,\psi)$ , όπου $K$ είναι ενδιάμεσο σώμα της επέκτασης $E/F$ και $\psi:K\rightarrow L$ μία $Φ$ -εμφύτευση. Το σύνολο $\Omega$ είναι όντως μη κενό, αφού περιέχει το ζεύγος $(F,i)$ , όπου $i$ είναι η εμφύτευση του $F$ στο $L$ . Η σχέση διάταξης στο $\Omega$ συγκρίνει ταυτόχρονα και τις δύο ενότητες του ζεύγους:

(K_{1},\psi_{1})\leq(K_{2},\psi_{2})\textrm{ αν }Κ_{1}\subset K_{2},\textrm{ % kai }\psi_{2}|_{K_{1}}=\psi_{1}.

Στη συνέχεια ελέγχουμε ότι κάθε αλυσίδα στο $\Omega$ έχει άνω φράγμα, και συμπεραίνει ότι το $\Omega$ έχει μέγιστο στοιχείο, από το Λήμμα του Zorn. Τέλος, δείχνουμε ότι το μέγιστο στοιχείο του $\Omega$ είναι της μορφής $(E,\phi)$ . Εφαρμόζοντας τα παραπάνω, όταν Το $E$ και Το $L$ είναι αλγεβρικές θήκες του $F$ , προκύπτουν $F$ -ισομορφισμοί $\phi:E\rightarrow L$ και $\psi:L\rightarrow E$ . Έτσι οδηγoύμαστε στο συμπέρασμα της μοναδικότητας της αλγεβρικής θήκης. Ο αναγνώστης καλείται να συμπληρώσει τις λεπτομέρειες της απόδειξης.

Θεώρημα 7.2.12.

Η αλγεβρική θήκη ενός σώματος $F$ είναι μοναδική με προσέγγιση $F$ -ισομορφίας, δηλ. αν $Ε_{1}$ και $E_{2}$ είναι δύο αλγεβρικές θήκες του $F$ τότε υπάρχει $\phi:E_{1}\rightarrow E_{2}$ , τέτοια ώστε $\phi(c)=c$ , για κάθε $c\in F$ .

Ως τελευταία παρατήρηση, ας αναφέρουμε έναν ακόμη συλλογισμό εξηγώντας το γιατί δεν τον χρησιμοποιήσαμε για να επιχειρηματολογήσουμε για την ύπαρξη της αλγεβρικής θήκης του $F$ : έστω $S$ η συλλογή

S=\{K:\ F/K\textrm{ αλγεβρική επέκταση του }F\},

με σχέση διάταξης τον εγκλεισμό συνόλων. Τότε, η $S$ περιέχει το $F$ και κάθε αλυσίδα στην $S$

K_{1}\leq K_{2}\leq\cdots

έχει άνω φράγμα στο $S$ το σύνολο

\bigcup_{i}K_{i}.

Αποδεικνύεται ότι h $K/F$ είναι αλγεβρική επέκταση σωμάτων. Από το Λήμμα του Zorn, προκύπτει ότι η $S$ έχει μέγιστο στοιχείο $E$ . Στη συνέχεια μπορεί να apodeiqje’i ότι το $Ε$ είναι αλγεβρικά κλειστό και άρα είναι η αλγεβρική θήκη του $F$ . L’hmma του Zorn

Είναι, όμως, η συλλογή $S$ όπως έχει οριστεί (και για να μπορούμε να εφαρμόσουμε το Λήμμα του Zorn) σύνολο, ή επισέρχονται τα παράδοξα της Θεωρίας Συνόλων; Ξεφεύγει από τους στόχους του συγγράμματος αυτό το ερώτημα. Ο ενδιαφερόμενος αναγνώστης μπορεί να μελετήσει περαιτέρω το θέμα. Για μία σχετική ιδέα αναφέρουμε και την άσκηση 7.3.4.

7.3 Ασκήσεις

1.

Nα αποδείξετε ότι κάθε αλγεβρικά κλειστό σώμα $F$ είναι τέλειο.
2.

Να δείξετε ότι ${\mathbb{Q}}(\sqrt[3]{2},\sqrt{5},\sqrt{7})$ είναι απλή επέκταση πάνω από το ${\mathbb{Q}}$ .
3.

Nα δείξετε ότι αν $F=\operatorname{GF}(p)(x^{p},y^{p})$ και $Ε=\operatorname{GF}(p)(x,y)$ τότε η επέκταση $E/F$ είναι πεπερασμένη. Όμως, $E$ δεν είναι απλή επέκταση του $F$ .
4.

Να αποδείξετε ότι η επέκταση $\overline{{\mathbb{Q}}}_{\mathbb{R}}/{\mathbb{Q}}$ είναι άπειρη και αριθμήσιμη, δηλ. υπάρχει μία αριθμήσιμη βάση του σώματος $\overline{{\mathbb{Q}}}_{\mathbb{R}}$ πάνω από το ${\mathbb{Q}}$ .
5.

Έστω $F$ ένα πεπερασμένο σώμα. Να αποδείξετε ότι το $F$ δεν είναι αλγεβρικά κλειστό.
6.

Να αποδείξετε ότι η ομάδα $\operatorname{Gal}({\mathbb{C}}/{\mathbb{Q}})$ είναι άπειρη. (Σημειώστε και την εκφώνηση της άσκησης 2.4.25.)

Βιβλιογραφία Κεφαλαίου 7

1.

Dummit, D.S., Foote, R.M. Abstract Algebra. J. Wiley and Sons, Inc, 2004.
2.

Lang, S. Algebra. Springer, 2002.
3.

Rotman, J. Θεωρία Galois. Leader Books, 2000.