Θεωρία Galois

Κεφάλαιο 1Βασικές Έννοιες

Στο Κεφάλαιο αυτό δίνουμε τις απαραίτητες προκαταρτικές γνώσεις από τη θεωρία πολυωνύμων και τη θεωρία σωμάτων που απαιτούνται για τα επόμενα κύρια κεφάλαια. Στο Εδάφιο 1.1 παρουσιάζουμε τα βασικά θέματα που πρόκειται να αναπτυχθούν εκτενώς στα κείμενο αυτό. Ο αναγνώστης μπορεί να συμβουλευτεί τα συγγράμματα της προτεινόμενης βιβλιογραφίας για αποδείξεις θεωρημάτων που παραλείπονται.

1.1 Εισαγωγικά

Στο εδάφιο αυτό θα περιγράψουμε τα τρία βασικά θέματα που θα μας απασχολήσουν σε αυτό το κείμενο:

•

το Θεμελιώδες Θεώρημα της Άλγεβρας,
•

την εύρεση ριζών πολυωνυμικών εξισώσεων και
•

την κατασκευασιμότητα κανονικών πολυγώνων με κανόνα και διαβήτη.

1.1.1 Το Θεμελιώδες Θεώρημα της Άλγεβρας

Το Θεμελιώδες Θεώρημα της Άλγεβρας (Fundamental Theorem of Algebra) είναι από τα σημαντικότερα θεωρήματα στα μαθηματικά.

Θεμελιώδες Θεώρημα της Άλγεβρας Αν $f(x)\in\mathbb{C}[x]$ και $\deg f(x)>0$ , τότε υπάρχει $a\in\mathbb{C}$ έτσι ώστε $f(a)=0$ . Δηλαδή κάθε μη σταθερό πολυώνυμο με συντελεστές από το σύνολο των μιγαδικών αριθμών έχει τουλάχιστον μία ρίζα στο $\mathbb{C}$ .
Είναι αξιοσημείωτο να τονίσουμε ότι το Θεμελιώδες Θεώρημα της Άλγεβρας βεβαιώνει την ύπαρξη ρίζας του $f(x)$ , δεν κατασκευάζει, όμως, τη ρίζα αυτή. Παρατηρούμε ότι αν $f(x)\in\mathbb{C}[x]$ και $f(a)=0$ , τότε υπάρχει $q(x)\in\mathbb{C}[x]$ έτσι ώστε $f(x)=(x-a)q(x)$ . Μπορεί λοιπόν να αποδειχθεί με απλή επαγωγή στον βαθμό του πολυωνύμου $f(x)$ , ότι αν $f(x)\in\mathbb{C}[x]$ και $n=\deg f(x)>0$ , τότε το $f(x)$ έχει $n$ ρίζες στο $\mathbb{C}$ . Λέμε ότι το σώμα $\mathbb{C}$ είναι αλγεβρικά κλειστό εξαιτίας αυτής της ιδιότητας. Η ιδιότητα αυτή έχει ως συνέπεια ότι κάθε πολυώνυμο του $\mathbb{C}[x]$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο $\mathbb{C}[x]$ . Από το Θεμελιώδες Θεώρημα της Άλγεβρας προκύπτει ακόμα ότι τα μόνα ανάγωγα πολυώνυμα του $\mathbb{C}[x]$ είναι τα πολυώνυμα βαθμού 1. Αφού τα πολυώνυμα του $\mathbb{R}[x]$ ανήκουν και στον $\mathbb{C}[x]$ , τα μη μηδενικά πολυώνυμα με πραγματικούς συντελεστές έχουν τόσες μιγαδικές ρίζες όσος είναι ο βαθμός τους, μετρώντας τις ρίζες σύμφωνα με την πολλαπλότητά τους. Όμως σε αντίθεση με το $\mathbb{C}$ , το σώμα $\mathbb{R}$ δεν είναι αλγεβρικά κλειστό. Για παράδειγμα το πολυώνυμο $x^{2}+1\in\mathbb{R}[x]$ δεν έχει ούτε μία ρίζα στον $\mathbb{R}$ .

Η πρώτη απόδειξη του Θεμελιώδους Θεωρήματος της Άλγεβρας αποδίδεται στον Gauss Το 1799. H απόδειξη αυτή χρησιμοποιεί ιδέες από τη τοπολογία και έχει κάποια κενά. Η πρώτη πλήρης απόδειξη οφείλεται στον Argand το 1814, ενώ στη συνέχεια ο Gauss έδωσε τουλάχιστον άλλες δύο πλήρεις διαφορετικές αποδείξεις. Έως σήμερα έχουν δοθεί πάνω από 200 αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας που χρησιμοποιούν και σε κάποιες περιπτώσεις συνδυάζουν μεθόδους από τη μαθηματική ανάλυση, την τοπολογία, την άλγεβρα, τη θεωρία αριθμών, ακόμα και από τη θεωρία πιθανοτήτων.

Στο Κεφάλαιο 6 θα δώσουμε μία αλγεβρική απόδειξη του Θεμελιώδους Θεωρήματος της Άλγεβρας χρησιμοποιώντας τις βασικές ιδέες της Θεωρίας Galois. Για κάποια ιστορικά στοιχεία σχετικά με την απόδειξη του Θεμελιώδους Θεωρήματος της Άλγεβρας παραπέμπουμε σε πολυμεσικές διαλέξεις του ψηφιακού μαθήματος (open courses) Ιστορία των Μαθηματικών του Τμήματος Μαθηματικών, Α.Π.Θ. και συγκεκριμένα στη διάλεξη της Ενότητας t7.3. Για τον Gauss και την προσφορά του στα μαθηματικά παραπέμπουμε ειδικότερα στη διάλεξη της Ενότητας t8.2 καθώς και στον [5, Κεφ. 15].

1.1.2 Τύποι για τις ρίζες πολυωνύμων

Έως τον 19 αιώνα, ο όρος Άλγεβρα αναφερόταν στην επίλυση πολυωνυμικών εξισώσεων, δηλαδή εξισώσεων της μορφής $f(x)=0$ , όπου $f(x)$ είναι ένα πολυώνυμο με συντελεστές από ένα σώμα. Όπως είδαμε προηγουμένως το Θεμελιώδες Θεώρημα της Άλγεβρας εγγυάται την ύπαρξη ριζών του $f(x)$ , δεν δίνει όμως πληροφορίες για τον υπολογισμό αυτών των ριζών.

Τον 16ο αιώνα Ιταλοί Μαθηματικοί (dal Ferro, Cardano, Tartaglia, Ferrari) βρήκαν τύπους για την εύρεση ριζών πολυωνύμων βαθμού 3 και 4. Σημειώνουμε ότι στη διατύπωση αυτών των τύπων εμφανίζονται η πρόσθεση και αφαίρεση, ο πολλαπλασιασμός και η διαίρεση αριθμών, καθώς και η εξαγωγή ριζικών με χρήση των συντελεστών των πολυωνύμων. Για παράδειγμα ο τύπος για την εύρεση μίας ρίζας του πολυωνύμου $x^{3}+mx-n$ , όπου $m, n$ είναι ακέραιοι αριθμοί, είναι ο ακόλουθος:

\sqrt[3]{\frac{n}{2}+\sqrt{\left(\frac{n}{2}\right)^{2}+\left(\frac{m}{3}% \right)^{3}}}-\sqrt[3]{-\frac{n}{2}+\sqrt{\left(\frac{n}{2}\right)^{2}+\left(% \frac{m}{3}\right)^{3}}}.

(1.1.2.1)

Οι τύποι γίνονται πιο πολύπλοκοι για πολυώνυμα τέταρτου βαθμού. Η αναλυτική περιγραφή των ριζών πολυωνύμων τρίτου και τέταρτου βαθμού δίνεται στο Παράρτημα V. Εάν οι ρίζες ενός πολυωνύμου περιγράφονται με τύπους τέτοιας μορφής, λέμε ότι το πολυώνυμο επιλύεται με ριζικά.

Οι τύποι αυτοί ανάγκασαν τους μαθηματικούς της εποχής να αποδεχτούν το μυστήριο της άλγεβρας των φανταστικών αριθμών. Αν και οι τύποι των ριζών των τριτοβάθμιων και τεταρτοβάθμιων πολυωνύμων διατυπώθηκαν αρχικά για πολυώνυμα με ρητούς συντελεστές, οι τύποι αυτοί ισχύουν και για πολυώνυμα με συντελεστές από το $\mathbb{C}$ . Μετά την επίλυση με ριζικά του τεταρτοβάθμιου πολυωνύμου η προσπάθεια επικεντρώθηκε στην εύρεση αντίστοιχου τύπου για τις ρίζες των πολυωνύμων πέμπτου βαθμού. Ο πρώτος, που ισχυρίστηκε γραπτά ότι δεν υπάρχει τέτοιος τύπος, ήταν ο Ιταλός μαθηματικός Ruffini σε μία εργασία του το 1799. Εκεί ο Ruffini εισήγαγε για πρώτη φορά την έννοια της ομάδας των μεταθέσεων. Ο Lagrange το 1771 είχε ορίσει τις μεταθέσεις στοιχείων, δεν είχε όμως αναγνωρίσει μία ιδιαίτερη δομή στο σύνολο των μεταθέσεων. Η εργασία του Ruffini είχε κάποια μικρά κενά και δεν αναγνωρίστηκε εκείνη την εποχή από την Μαθηματική κοινότητα, ούτε και οι μετέπειτα προσπάθειες του, όπου διόρθωνε ο ίδιος τα κενά, δημοσιεύοντας τις εργασίες του με δικά του έξοδα. Το 1824 ο Abel έδωσε μία ολοκληρωμένη απόδειξη της μη επιλυσιμότητας του γενικού πολυωνύμου πέμπτου βαθμού, χρησιμοποιώντας και αυτός τις μεταθέσεις των ριζών του πολυωνύμου. Σήμερα στο αντίστοιχο θεώρημα αποδίδουμε και τα δύο ονόματα κατά αλφαβητική σειρά των επιθέτων των συγγραφέων, όπως είθισται στις μαθηματικές εργασίες.

Θεώρημα των Abel-Ruffini. Δεν υπάρχει τύπος με ριζικά που να επιλύει όλα τα πολυώνυμα βαθμού 5 με πραγματικούς συντελεστές.
Σίγουρα, όμως, υπάρχουν πολυώνυμα βαθμού 5 που είναι επιλύσιμα με ριζικά. Για παράδειγμα ας θεωρήσουμε το πολυώνυμο $f(x)=x^{5}-2\in\mathbb{C}[x]$ . Mία ρίζα του $f(x)$ είναι ο πραγματικός αριθμός $b$ , που δίνεται από τον τύπο $b=\sqrt[5]{2}$ . Διαιρώντας το $f(x)$ με το $x-b$ , προκύπτει ότι υπάρχει πολυώνυμο $q(x)\in\mathbb{R}[x]$ έτσι ώστε $f(x)=(x-b)q(x)$ . Ο βαθμός του $q(x)$ είναι $4$ και επομένως το πολυώνυμο $q(x)$ είναι επιλύσιμο με ριζικά (αφού όλα τα πολυώνυμα βαθμού τρία ή τέσσερα είναι επιλύσιμα με ριζικά). Οι ρίζες, όμως, του $q(x)$ είναι και ρίζες του $f(x)$ . Έτσι το $f(x)$ είναι και αυτό επιλύσιμο με ριζικά όπως ισχυριστήκαμε. Τίθεται λοιπόν το εύλογο ερώτημα: ποια πολυώνυμα είναι τελικά επιλύσιμα με ριζικά;

Ο πρώτος που αντιλήφθηκε ότι η δυνατότητα προσδιορισμού των ριζών ενός πολυωνύμου $f(x)$ με τύπο συνδέεται με τη δομή της ομάδας των μεταθέσεων των ριζών του $f(x)$ είναι ο Galois, το 1831. Ο Galois χρησιμοποίησε μία υποομάδα της ομάδας των μεταθέσεων των ριζών του πολυωνύμου $f(x)$ , η οποία σήμερα λέγεται ομάδα του Galois. Στο Κεφάλαιο 3 θα αποδείξουμε το ακόλουθο θεώρημα που αναφέρεται στην επιλυσιμότητα με ριζικά.

Θεώρημα του Galois. Τα πολυώνυμα, των οποίων οι ρίζες εκφράζονται από κάποιον τύπο που εμπεριέχει πρόσθεση, αφαίρεση, πολλαπλασιασμό, διαίρεση και εξαγωγή ριζικών των συντελεστών, είναι ακριβώς εκείνα για τα οποία η αντίστοιχη ομάδα του Galois είναι επιλύσιμη.

Η έννοια της επιλυσιμότητας μίας ομάδας προέρχεται, όπως θα δούμε στο Κεφάλαιο 6, από τη Θεωρία Ομάδων. Για να αποδείξουμε το παραπάνω θεώρημα θα χρειαστούμε το Θεμελιώδες Θεώρημα της Θεωρίας Galois, που περιγράφουμε εδώ χωρίς μαθηματική αυστηρότητα στη σύγχρονη έκδοσή του:

Θεμελιώδες Θεώρημα της Θεωρίας Galois. Έστω $F$ σώμα και $f(x)\in F[x]$ . Έστω $Ε$ το μικρότερο σώμα που περιέχει το $F$ και όλες τις ρίζες του $f(x)$ . Υπάρχει μία πλήρης αντιστοιχία ανάμεσα στα υποσώματα του $Ε$ που περιέχουν το $F$ και στις υποομάδες της ομάδας Galois του $f(x)$ .

Παραλείψαμε σκόπιμα κάποιες συνθήκες στο παραπάνω θεώρημα για να κάνουμε κατανοητή τη βασική ιδέα. Για παράδειγμα, το θεώρημα ισχύει για τα διαχωρίσιμα πολυώνυμα. Ένα άλλο σημείο, όπου θα επιμείνουμε αργότερα, είναι η έννοια του μικρότερου σώματος που περιέχει το σώμα στο οποίο ανήκουν οι συντελεστές του πολυωνύμου, αλλά και οι ρίζες του, καθώς και η συνεπαγόμενη ερώτηση για το πόσα τέτοια διαφορετικά σώματα υπάρχουν. Θα χρειαστεί, λοιπόν, να μελετήσουμε ιδιότητες σωμάτων και να καταλάβουμε τις δομές τους. Θα τα μελετήσουμε όλα αυτά στα επόμενα εδάφια αυτού του κειμένου. Για την ιστορία που οδήγησε στην ανακάλυψη της θεωρημάτων των Abel-Ruffini και Galois παραπέμπουμε στο [5, Ενότητες 9.3, 15.2, 15.3] και στις πολυμεσικές διαλέξεις του ψηφιακού μαθήματος Ιστορία των Μαθηματικών του Τμήματος Μαθηματικών, Α.Π.Θ. και συγκεκριμένα στις διαλέξεις των Ενοτήτων 9.2 και 9.3.

1.1.3 Κατασκευές με κανόνα και διαβήτη.

Ως κατασκευές με κανόνα και διαβήτη εννοούμε τις γεωμετρικές κατασκευές για τις οποίες επιτρέπεται μόνο η χρήση του κανόνα και του διαβήτη. Ο κανόνας είναι ένα γεωμετρικό εργαλείο με μία πλευρά. Με τον κανόνα μπορούμε να χαράξουμε ένα ευθύγραμμο τμήμα με άκρα δύο προσδιορισμένα σημεία. Δεχόμαστε ότι μπορούμε να επεκτείνουμε το ευθύγραμμο τμήμα με τον κανόνα και προς τις δύο κατευθύνσεις απεριόριστα. Ο κανόνας, όμως, δεν φέρει υποδιαιρέσεις και δεν μπορεί από μόνος του να καθορίσει αποστάσεις. Ο διαβήτης είναι το γεωμετρικό εργαλείο με το οποίο μπορούμε να χαράξουμε την περιφέρεια ενός κύκλου του οποίου γνωρίζουμε το κέντρο και την ακτίνα. Στο κέντρο του κύκλου τοποθετούμε το άκρο του ενός σκέλους του διαβήτη, ενώ η ακτίνα προσδιορίζεται από το άνοιγμα των άκρων των σκελών του διαβήτη.

Για να μπορέσουμε να προχωρήσουμε σε μία γεωμετρική κατασκευή θα πρέπει να μπορούμε να κατασκευάσουμε σημεία, δηλ. να προσδιορίσουμε τη θέση τους πάντα και μόνο με κανόνα και διαβήτη και να συνδέουμε τα σημεία που μας ενδιαφέρουν με ευθείες γραμμές με τη χρήση του κανόνα. Θα εξετάσουμε πώς μπορούμε να κατασκευάσουμε σημεία στο επίπεδο. Όμως, πρώτα ας παρατηρήσουμε ότι αν ήδη έχουμε κατασκευάσει κάποια σημεία, τα νέα σημεία που μπορούμε να κατασευάσουμε από αυτά προκύπτουν με τον κανόνα και τον διαβήτη με έναν από τους ακόλουθους τρεις τρόπους:

•

ως τομή δύο ευθύγραμμων τμημάτων,
•

ως τομή ενός ευθυγράμμου τμήματος και της περιφέρειας ενός κύκλου,
•

ως τομή των περιφερειών δύο κύκλων.

Θα ξεκινήσουμε με δύο αρχικά σημεία στο επίπεδο. Λέμε ότι μία απόσταση είναι κατασκευάσιμη (constructible) αν προκύπτει ως απόσταση ανάμεσα σε δύο κατασκευάσιμα σημεία. Συμφωνούμε η απόσταση ανάμεσα στα δύο αρχικά σημεία να είναι ίση με τη μονάδα μέτρησης, που συμβολίζουμε με 1, και χαράζουμε την ευθεία που διέρχεται από τα δύο αρχικά σημεία με τη χρήση του κανόνα. Στη συνέχεια ταυτίζουμε την ευθεία αυτή με την ευθεία των πραγματικών αριθμών και ορίζουμε τα αρχικά σημεία με 0 και 1, με το 1 στα δεξιά του 0. Θα προσπαθήσουμε να βρούμε όλα τα σημεία επί της πραγματικής ευθείας που είναι κατασκευάσιμα και τις αντίστοιχες κατασκευάσιμες αποστάσεις. Ξεκινούμε με την κατασκευή των ακεραίων αριθμών. Με κέντρο το σημείο 1 και ακτίνα το μήκος της μονάδας χαράσσουμε μία περιφέρεια κύκλου η οποία τέμνει την ευθεία σε ένα σημείο δεξιά του σημείου 1. Το σημείο αυτό είναι το 2. Συνεχίζοντας με αυτό το τρόπο, κατασκευάζουμε όλους τους φυσικούς αριθμούς. Επαναλαμβάνοντας τη διαδικασία αριστερά του σημείου 0 κατασκευάζουμε με κανόνα και διαβήτη τους αριθμούς $-1,-2$ , κ.ο.κ. Έχουμε κατασκευάσει έτσι όλους τους ακέραιους αριθμούς. Παρατηρούμε επίσης ότι, αν $a, b$ είναι κατασκευάσιμοι πραγματικοί αριθμοί επί της ευθείας που αρχικά χαράξαμε, μπορούμε με τον διαβήτη να κατασκευάσουμε τον αριθμό $a\pm b$ .

Πριν προχωρήσουμε στην κατασκευή των ρητών αριθμών ας θυμηθούμε, ότι με κανόνα και διαβήτη είναι δυνατές οι επόμενες κατασκευές στο επίπεδο, (βλ. Άσκηση 1.5.1):

•

να χαράξουμε κάθετη ευθεία σε δοθείσα ευθεία που να περνάει από συγκεκριμένο σημείο επί της αρχικής ευθείας,
•

να μεσοκάθετη σε δοθέν ευθύγραμμο τμήμα,
•

να χαράξουμε ευθεία παράλληλη σε δοθείσα ευθεία που να περνάει από συγκεκριμένο σημείο εκτός της δοθείσης ευθείας,
•

να χαράξουμε τη διχοτόμο δοθείσης γωνίας στο επίπεδο.

Για να κατασκευάσουμε τους αριθμούς $a,b,a^{-1}$ , όπου $a, b$ φυσικοί αριθμοί, χρησιμοποιούμε το Θεώρημα του Θαλή για τα όμοια τρίγωνα. Χαράσσουμε την κάθετη στο σημείο $O$ της αρχικής ευθείας. Στην οριζόντια ευθεία με τον διαβήτη ορίζουμε το σημείο $Β$ έτσι ώστε το τμήμα $O Β$ να έχει μήκος ίσο με 1, το σημείο $C$ έτσι ώστε το τμήμα $O C$ να έχει μήκος $a$ και στην κατακόρυφη ευθεία ορίζουμε το σημείο $D$ έτσι ώστε το τμήμα $O D$ να έχει μήκος $b$ , (βλ. Σχήμα 1.1). Ενώνουμε τα σημεία $B D$ με μία ευθεία χρησιμοποιώντας τον κανόνα και από το σημείο $C$ φέρουμε παράλληλο προς την ευθεία που διέρχεται από τα σημεία $B$ και $D$ . Έστω $Ε$ το σημείο τομής αυτής της παραλλήλου με την αρχική ευθεία.

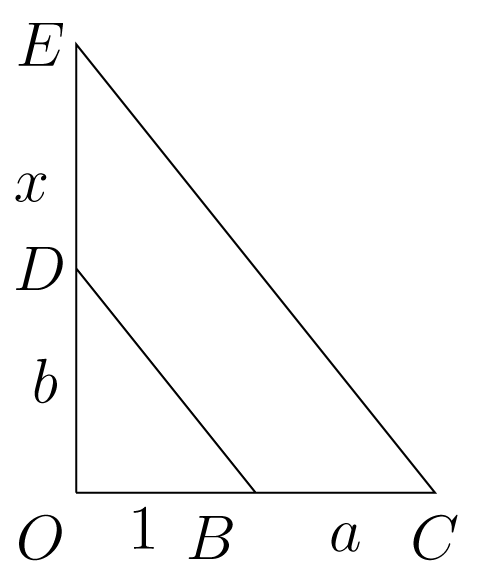
Αν $x$ είναι το μήκος του τμήματος $O E$ , τότε, από το Θεώρημα του Θαλή, προκύπτει ότι:

\frac{1}{b}=\frac{a}{x}\Rightarrow x=ab\ .

Όμοια, σύμφωνα με το Σχήμα 1.2, κατασκευάζουμε το κλάσμα $\displaystyle{\frac{a}{b}}$ από τους αριθμούς $a, b$ , όταν $b\neq 0$ .

Σχήμα 1.2: $y=\displaystyle{\frac{a}{b}}$

Η διαδικασία που ακολουθήσαμε μπορεί να εφαρμόζεται κάθε φορά που οι αριθμοί $a, b$ είναι κατασκευάσιμοι θετικοί αριθμοί. Αφού ο αρνητικός αριθμός ενός κατασκευάσιμου αριθμού είναι κατασκευάσιμος, αντιλαμβανόμαστε ότι το σύνολο των κατασκευάσιμων αριθμών είναι σώμα: το άθροισμα, η διαφορά, το γινόμενο και το κλάσμα (όπου η διαίρεση επιτρέπεται) κατασκευάσιμων αριθμών είναι κατασκευάσιμος αριθμός. Έστω $F$ το σώμα των κατασκευάσιμων αριθμών. Από τα παραπάνω έπεται ότι το $F$ περιέχει τους ρητούς. Σύμφωνα με την άσκηση 1.5.2, αν ο $a\geq 0$ είναι κατασκευάσιμος αριθμός, τότε ο $\sqrt{a}$ είναι κατασκευάσιμος αριθμός. Αφού, λοιπόν, ο $2$ είναι κατασκευάσιμος αριθμός, έπεται ότι ο $\sqrt{2}\in F$ . Ως γνωστό ο $\sqrt{2}$ δεν είναι ρητός. Έτσι βλέπουμε ότι το σώμα $F$ εκτός από τους ρητούς περιέχει και άλλους πραγματικούς αριθμούς.

Παρατηρούμε, επίσης, ότι μπορούμε να κατασκευάσουμε στο επίπεδο ένα σύστημα καρτεσιανών συντεταγμένων: o ένας άξονας είναι η αρχική ευθεία, ο δεύτερος άξονας είναι η κάθετος στο σημείο $O$ , ενώ στο σημείο $O$ δίνουμε τις συντεταγμένες $(0,0)$ . Διαπιστώνουμε ότι μπορούμε να κατασκευάσουμε σημεία στο επίπεδο ανάγοντας αυτές τις κατασκευές στις συντεταγμένες των σημείων. Συμπεραίνουμε ότι όλα τα σημεία του συνόλου $\{(a,b):\ a^{2},b^{2}\in\mathbb{Q}\}$ είναι κατασκευάσιμα.

Τα θέματα της κατασκευασιμότητας με κανόνα και διαβήτη απασχόλησαν τους αρχαίους Έλληνες που θρησκευτικές επιταγές και η αναζήτηση της μαθηματικής καθαρότητας απαιτούσαν τη χρήση μόνο κανόνα και διαβήτη. Έτσι γρήγορα οδηγήθηκαν στην ανάγκη επίλυσης των προβλημάτων:

•

Μπορούμε να κατασκευάσουμε την τριχοτόμηση μίας γωνίας;
•

Μπορούμε να κατασκευάσουμε κύβο με διπλάσιο όγκο ενός άλλου κύβου;
•

Μπορούμε να τετραγωνίσουμε τον κύκλο;
•

Ποια κανονικά πολύγωνα είναι κατασκευάσιμα;
•

Ποιες αποστάσεις είναι κατασκευάσιμες;

Αυτά τα θέματα κατασκευασιμότητας με κανόνα και διαβήτη θα εξετάσουμε στο Κεφάλαιο 6 ως εφαρμογές της Θεωρίας Galois. Για ιστορικά στοιχεία σχετικά με τα άλυτα γεωμετρικά προβλήματα της αρχαιότητας παραπέμπουμε στην πολυμεσική διάλεξη 2.3 του ψηφιακού μαθήματος Ιστορία των Μαθηματικών του Τμήματος Μαθηματικών, Α.Π.Θ. Για τις μίνι-εφαρμογές (applets) των γεωμετρικών κατασκευών παραπέμπουμε στο 9.

1.2 Βασικές ιδιότητες των πολυωνύμων

Στο εδάφιο αυτό θα εξετάσουμε τις βασικές ιδιότητες των πολυωνύμων με συντελεστές από μία ακέραια περιοχή $R$ ή από ένα σώμα $F$ . Συχνά θα μας ενδιαφέρουν πολυώνυμα πάνω από το $\mathbb{Z}$ και το $\mathbb{Q}$ . Ο αναγνώστης καλείται να ανατρέξει στις Ενότητες II, III του Παραρτήματος για τους βασικούς ορισμούς. Εδώ θα αναφέρουμε τις έννοιες και τα συμπεράσματα που απαιτούνται για την ανάπτυξη της Θεωρίας Galois. Τις σχετικές αποδείξεις ο αναγνώστης μπορεί να τις αναζητήσει στα [3, Κεφάλαια 4, 6] και [2, Κεφάλαιο 9] καθώς και στο [7].

Έστω ότι $F$ είναι σώμα και $F[x]$ ο δακτύλιος των πολυωνύμων με συντελεστές από το $F$ . Ο δακτύλιος $F[x]$ είναι ένας $F$ -διανυσματικός χώρος άπειρης διάστασης, αφού τα στοιχεία $\{x^{i}:\ i\in\mathbb{N}\}$ αποτελούν μία $F$ -βάση του $F[x]$ . Σημειώνουμε, λοιπόν, ότι ${\rm dim}_{F}F[x]=\infty$ . Θυμίζουμε επίσης ότι ένα πολυώνυμο λέγεται κανονικό ή μονικό αν ο συντελεστής της μεγιστοβάθμιας δύναμης του $x$ είναι ίσος με 1. Έτσι το πολυώνυμο $x^{2}-1\in\mathbb{Q}[x]$ είναι κανονικό, ενώ το πολυώνυμο $2x-1$ δεν είναι. Το επόμενο θεώρημα χαρακτηρίζει τον δακτύλιο πολυωνύμων $F[x]$ πάνω από σώμα $F$ , βλ. Παράρτημα, Θεώρημα III.3.

Θεώρημα 1.2.1.

i.

Έστω ότι $F$ είναι σώμα και έστω $f(x),g(x)\in F[x]$ , $g(x)\neq 0$ . Τότε υπάρχουν μοναδικά πολυώνυμα $q(x),r(x)\in F[x]$ τέτοια ώστε $f(x)=g(x)q(x)+r(x)$ με $\deg r(x)<\deg g(x)$ ή $r(x)=0$ .
ii.

Έστω $F$ ένα σώμα. Τότε ο δακτύλιος $F[x]$ είναι περιοχή κυρίων ιδεωδών (Π.Κ.Ι.).

Το πρώτο σκέλος του προηγουμένου θεωρήματος δηλώνει ότι ισχύει ο Ευκλείδειος αλγόριθμος στον $F[x]$ . Από το δεύτερο σκέλος προκύπτει ότι αν $Ι$ είναι ιδεώδες του $F[x]$ , τότε υπάρχει ένα πολυώνυμο $f(x)\in F[x]$ ώστε:

I=\langle f(x)\rangle=\{f(x)g(x):\ g(x)\in F[x]\}.

Το πολυώνυμο $f(x)$ καλείται γεννήτορας του ιδεώδους $Ι$ και δεν ορίζεται μοναδικά για το $Ι$ , αφού $\langle f(x)\rangle=\langle uf(x)\rangle$ , για κάθε αντιστρέψιμο στοιχείο $u\in F[x]$ , δηλ. για κάθε $u\in F^{*}$ . Για αυτόν τον λόγο επιλέγουμε συνήθως ως γεννήτορα του $Ι$ ένα κανονικό πολυώνυμο του $F[x]$ , τον οποίο καλούμε κανονικό γεννήτορα του $Ι$ . Πράγματι,

a_{0}+\cdots+a_{n}x^{n}\neq 0\ \Leftrightarrow\ a_{n}\neq 0

και σε αυτήν την περίπτωση

\langle a_{0}+\cdots a_{n}x^{n}\rangle=\langle a_{n}^{-1}(a_{0}+\cdots a_{n}x^% {n})\rangle=\langle a_{0}a_{n}^{-1}+\cdots a_{n-1}a_{n}^{-1}x^{n-1}+x^{n}\rangle.

Έτσι προκύπτει ότι ο κανονικός γεννήτορας ενός μη μηδενικού ιδεώδους του $F[x]$ ορίζεται μοναδικά και προσδιορίζεται από την ιδιότητα ότι είναι το μοναδικό κανονικό πολυώνυμο ελάχιστου βαθμού που ανήκει στο ιδεώδες.

Ο δακτύλιος $F[x]$ ως Π.Κ.Ι. είναι Π.Μ.Α. Έτσι τα ανάγωγα στοιχεία του $F[x]$ είναι τα πρώτα στοιχεία του. Αυτό σημαίνει ότι αν Το $f(x)$ είναι ανάγωγο, τότε κάθε φορά που το $f(x)$ διαιρεί το γινόμενο δύο πολυωνύμων πρέπει να διαιρεί αναγκαστικά το ένα από τα δύο. Από τον ορισμό της Π.Μ.Α. προκύπτει ότι κάθε πολυώνυμο $f(x)\neq 0$ του $F[x]$ αναλύεται μοναδικά ως γινόμενο

f(x)=up_{1}^{t_{1}}(x)\cdots p_{s}^{t_{s}}(x),

όπου $u\in F^{*}$ και τα $p_{i}(x)$ , $1\leq i\leq s$ , είναι κανονικά ανάγωγα πολυώνυμα.

Όπως στην αριθμητική του $\mathbb{Z}$ , έτσι και σε κάθε Π.Μ.Α. σημαντικό ρόλο παίζουν ο μέγιστος κοινός διαιρέτης (ΜΚΔ) και το ελάχιστο κοινό πολλαπλάσιο (ΕΚΠ) πεπερασμένου πλήθους στοιχείων του $F[x]$ . Έστω $f_{1}(x),\ldots,f_{s}(x)$ στοιχεία (πολυώνυμα) του $F[x]$ . Τότε υπάρχουν τα πολυώνυμα

\text{ΜΚΔ}\left(f_{1}(x),\ldots,f_{s}(x)\right),\ \text{ΕΚΠ}\left(f_{1}(x),% \ldots,f_{s}(x)\right)

και αυτά ορίζονται μοναδικά με προσέγγιση ενός αντιστρέψιμου στοιχείου του $F[x]$ . Αν $h(x)=\operatorname{\textrm{ΜΚΔ}}\left(f_{1}(x),\ldots,f_{s}(x)\right)$ , τότε από το Παράρτημα, Θεώρημα II.11, προκύπτει ότι υπάρχουν πολυώνυμα $q_{1}(x),\ldots,q_{s}(x)$ του $F[x]$ , ώστε

h(x)=f_{1}(x)q_{1}(x)+\cdots+f_{s}(x)q_{s}(x)

και επομένως ισχύει η παρακάτω ισότητα για τα ιδεώδη:

\langle h(x)\rangle=\langle f_{1}(x),\ldots,f_{s}(x)\rangle,

δηλ. το κύριο ιδεώδες με γεννήτορα το $h(x)$ είναι το ιδεώδες του $F[x]$ που παράγεται από τα στοιχεία $f_{1}(x),\ldots,f_{s}(x)$ .

Ιδιαίτερα, αν δύο πολυώνυμα $f_{1}(x)$ και $f_{2}(x)$ του $F[x]$ είναι πρώτα μεταξύ τους, δηλ. an $\operatorname{\textrm{ΜΚΔ}}(f_{1}(x),f_{2}(x))=1$ , τότε

\langle f_{1}(x),f_{2}(x)\rangle=F[x]\;.

Το παραπάνω γενικεύεται για $s$ πολυώνυμα $f_{1}(x),\ldots,f_{s}(x)\in F[x]$ όταν γνωρίζουμε ότι ΜΚΔ $(f_{1}(x),\ldots,$ $f_{s}(x))=1$ . Σε αυτή τη περίπτωση

\langle f_{1}(x),\ldots,f_{s}(x)\rangle=F[x]\;.

Λόγω της μοναδικής παραγοντοποίησης κάθε πολυωνύμου $f(x)\in F[x]$ σε γινόμενο αναγώγων πολυωνύμων καταλαβαίνουμε ότι τα ανάγωγα πολυώνυμα και, για πρακτικούς λόγους, τα κανονικά ανάγωγα πολυώνυμα παίζουν σημαντικό ρόλο στη μελέτη μας. Καταρχήν αν $p(x)\in F[x]$ είναι ανάγωγο, τότε το ιδεώδες $\langle p(x)\rangle$ είναι μέγιστο, βλ. Παράρτημα, Θεώρημα III.3, αλλά και αντίστροφα κάθε μέγιστο ιδεώδες του $F[x]$ έχει γεννήτορα ένα ανάγωγο πολυώνυμο του $F[x]$ .

Ο έλεγχος για το αν ένα δοθέν πολυώνυμο είναι ανάγωγο δεν είναι εύκολη διαδικασία και δεν υπάρχει αλγόριθμος που να μας οδηγεί σε ένα τέτοιο συμπέρασμα. Υπάρχουν, όμως, κάποια κριτήρια με τα οποία θα ασχοληθούμε αργότερα για τον έλεγχο της αναγωγιμότητας ενός πολυωνύμου που δεν δίνουν, όμως, πάντα ικανές και αναγκαίες συνθήκες.

Οι ρίζες ενός πολυωνύμου συνδέονται με την παραγοντοποίησή του, όπως προκύπτει από το επόμενο συμπέρασμα με απλή εφαρμογή της Ευκλείδειας διαίρεσης.

Πρόταση 1.2.2.

Έστω $f(x)\in F[x]$ . Το $a\in F$ είναι ρίζα του $f(x)$ αν και μόνο αν το $x-a$ διαιρεί το $f(x)$ στον $F[x]$ .

Απόδειξη.

Σύμφωνα με τον Ευκλείδειο αλγόριθμο $f(x)=(x-a)q(x)+r(x)$ , όπου $\deg r(x)<1$ , και συνεπώς $r(x)=r\in F$ . Άρα το $x-a$ διαιρεί το $f(x)$ αν και μόνο αν το υπόλοιπο $r=0$ . Αυτό, όμως, συμβαίνει αν και μόνο αν $f(a)=0$ , δηλαδή αν $a$ είναι ρίζα του $f(x)$ . ∎

Εφαρμόζοντας διαδοχικά την παραπάνω Πρόταση προκύπτει το επόμενο Πόρισμα.

Πόρισμα 1.2.3.

Aν $f(x)\in F[x]$ και $a_{1},\ldots,a_{n}\in F$ είναι διακεκριμένες ρίζες του $f(x)$ τότε

f(x)=(x-a_{1})\cdots(x-a_{n})p(x),\textrm{ όπου }p(x)\in F[x].

Ειδικότερα αν $n=\deg f(x)$ και $a_{1},\ldots,a_{n}\in F$ είναι διακεκριμένες ρίζες του $f(x)$ t’ote

f(x)=c(x-a_{1})\cdots(x-a_{n}),\textrm{ όπου }c\in F.

’Estw ότι $\phi:\ F\rightarrow L$ είναι εμφύτευση σωμάτων και

\tilde{\phi}:\ F[x]\rightarrow L[x]:\ \sum c_{i}x^{i}\mapsto\sum\phi(c_{i})x^{i}

είναι ο αντίστοιχος ομομορφισμός ανάμεσα στους δακτυλίους πολυωνύμων. Συμβολίζουμε με $\tilde{f}(x)$ την εικόνα του $f(x)$ στον $L[x]$ . Είναι εύκολο να δούμε ότι αν $a$ είναι ρίζα του $f(x)$ τότε $\phi(a)$ είναι ρίζα του $\tilde{f}(x)$ . Πράγματι:

\tilde{f}(\phi(a))=\sum\phi(c_{i})\phi(a)^{i}=\sum\phi(c_{i}a^{i})=\phi(\sum c% _{i}a^{i})=\phi(f(a))=\phi(0)=0.

Έτσι από το Πόρισμα 1.2.3 προκύπτει το επόμενο συμπέρασμα με τον παραπάνω συμβολισμό.

Πόρισμα 1.2.4.

Έστω ότι $a_{1},\ldots,a_{n}\in F$ είναι διακεκριμένες ρίζες του $f(x)$ , όπου $n=\deg f(x)$ , $\phi:\ F\rightarrow L$ εμφύτευση σωμάτων και έστω ότι $\phi(a_{1}),\ldots,\phi(a_{n})$ είναι ρίζες ενός πολυωνύμου $g(x)\in L[x]$ . Τότε

g(x)=\tilde{f}(x)p(x),\textrm{ 'opou }p(x)\in L[x].

Παραθέτουμε αμέσως δύο παραδείγματα πολυωνύμων τα οποία αναλύουμε σε γινόμενο παραγόντων για να εφαρμόσουμε κάποιες γνωστές μεθόδους, αλλά και για να αντιληφθούμε τα ερωτήματα που ανακύπτουν από αυτές τις προσπάθειες.

Παράδειγμα 1.2.5.

Θα αναλύσουμε το πολυώνυμο $f(x)=x^{3}-2$ σε γινόμενο αναγώγων παραγόντων ως πολυώνυμο του $\mathbb{Q}[x]$ , του $\mathbb{R}[x]$ και του $\mathbb{C}[x]$ . Ξεκινούμε βρίσκοντας τις ρίζες του $f(x)$ στο σώμα $\mathbb{C}$ . Παρατηρούμε ότι to $b=\sqrt[3]{2}$ είναι μία ρίζα του $f(x)$ (είναι μάλιστα η ρίζα που προκύπτει από τον τύπο 1.1.2.1 αντικαθιστώντας $m=0$ , $n=2$ ). Επομένως το πολυώνυμο $x-b\in\mathbb{R}[x]$ διαιρεί το πολυώνυμο $x^{3}-2$ . Σύμφωνα με τον Ευκλείδειο αλγόριθμο διαίρεσης δύο πολυωνύμων βρίσκουμε ότι:

f(x)=x^{3}-2=(x-\sqrt[3]{2})(x^{2}+\sqrt[3]{2}\ x+\sqrt[3]{4}),

δηλαδή

f(x)=(x-b)(x^{2}+b\ x+b^{2}).

Θέτουμε $p(x)=x^{2}+b\ x+b^{2}$ και χρησιμοποιώντας τον τύπο που δίνει τις ρίζες ενός δευτεροβάθμιου πολυωνύμου, βρίσκουμε ότι οι άλλες δύο ρίζες του $x^{3}-2$ είναι:

\sqrt[3]{2}\left(-\frac{1}{2}\pm\frac{i\sqrt{3}}{2}\right).

Θέτουμε τώρα

\omega=-\frac{1}{2}+\frac{i\sqrt{3}}{2}=\cos\left(\frac{2\pi}{3}\right)+i\sin% \left(\frac{2\pi}{3}\right).

Παρατηρούμε ότι

\omega=e^{2\pi i/3},\ \omega^{2}=-\frac{1}{2}-\frac{i\sqrt{3}}{2},\omega^{3}=e% ^{2\pi i}=1.

Άρα μπορούμε να γράψουμε τις 3 ρίζες του $x^{3}-2$ στο $\mathbb{C}$ ως εξής: $b$ , $\omega b$ και $\omega^{2}b$ . Επίσης σημειώνουμε τα παρακάτω:

i.

Καμία από τις ρίζες του $f(x)$ δεν ανήκει στο $\mathbb{Q}$ . Αυτό σημαίνει ότι δεν υπάρχει πολυώνυμο βαθμού 1 στο $\mathbb{Q}[x]$ που να διαιρεί το $f(x)$ . Κατά συνέπεια, το $f(x)$ δεν μπορεί να γραφεί ως γινόμενο δύο πολυωνύμων βαθμού (και των δύο) μικρότερου του 3. Άρα το $f(x)$ είναι ανάγωγο στον $\mathbb{Q}[x]$ .
ii.

Αφού Το $b\in\mathbb{R}$ όπως και οι συντελεστές του $q(x)$ , έπεται ότι $x-b,q(x)\in\mathbb{R}[x]$ και άρα στον $\mathbb{R}[x]$ ισχύει ότι $f(x)=(x-b)q(x)$ . Επομένως το $f(x)$ δεν είναι ανάγωγο στον $\mathbb{R}[x]$ . Το πολυώνυμο $q(x)$ έχει βαθμό 2, ενώ οι ρίζες του δεν ανήκουν στον $\mathbb{R}$ . Όπως και προηγουμένως, από την ανάλυση των βαθμών προκύπτει ότι το $q(x)$ είναι ανάγωγο στον $\mathbb{R}[x]$ . Έπεται επομένως ότι στον δακτύλιο $\mathbb{R}[x]$ η ανάλυση του $f(x)$ σε ανάγωγους παράγοντες είναι το γινόμενο $f(x)=(x-b)q(x)$ .
iii.

Κάθε πολυώνυμο βαθμού 1 είναι ανάγωγο. Έτσι η ανάλυση του $f(x)$ σε ανάγωγους παράγοντες στο $\mathbb{C}[x]$ είναι $f(x)=(x-b)(x-\omega b)(x-\omega^{2}b)$ .

Σημειώνουμε τα παρακάτω δύο συμπεράσματα. Το πρώτο προκύπτει από την ανάλυση των βαθμών. Το δεύτερο είναι επίσης άμεσο.

Πρόταση 1.2.6.

Έστω $f(x)\in F[x]$ , όπου $F$ σώμα.

i.

Αν $\deg f(x)$ είναι 2 ή 3, τότε το $f(x)$ είναι ανάγωγο αν και μόνο αν το $f(x)$ δεν έχει ρίζες στο $F$ .
ii.

Έστω ότι $F\subset E$ , όπου $E$ σώμα. Αν το $f(x)$ είναι ανάγωγο στο $E[x]$ , τότε το $f(x)$ είναι ανάγωγο στο $F[x]$ .

Παράδειγμα 1.2.7.

Εξετάζουμε τώρα το πολυώνυμο $f(x)=x^{3}-1$ . Το πολυώνυμο αυτό δεν είναι ανάγωγο στον $\mathbb{Q}[x]$ , αφού $f(1)=0$ και

x^{3}-1=(x-1)(x^{2}+x+1).

(1.2.7.1)

Έστω $\Phi_{3}(x)=x^{2}+x+1$ . Υπολογίσαμε τις ρίζες του $\Phi_{3}(x)$ στο προηγούμενο παράδειγμα: είναι οι συζυγείς μιγαδικοί αριθμοί $\omega$ και $\omega^{2}$ , όπου $\omega=e^{2\pi i/3}$ . Στο Σχήμα 1.3 δίνεται η γραφική παράσταση των ριζών $\omega$ , $\omega^{2}$ και $\omega^{3}=1$ του πολυωνύμου $x^{3}-1$ στο μιγαδικό επίπεδο.

Οι τρεις λοιπόν ρίζες της μονάδας, δηλαδή οι ρίζες του πολυωνύμου $x^{3}-1$ , είναι oi $\omega$ , $\omega^{2}$ και $\omega^{3}=1$ , όπου $\omega=e^{2\pi i/3}$ . Εύκολα επιβεβαιώνουμε ότι

(x-\omega)(x-\omega^{2})=x^{2}+x+1.

Επομένως

1.

$\omega^{2}+\omega+1=0$ και $(\omega^{2})^{2}+\omega^{2}+1=0$ .
2.

$\omega\cdot\omega^{2}=1$ .

Από την Πρόταση 1.2.6 και αφού οι ρίζες του $\Phi_{3}(x)$ δεν είναι πραγματικοί αριθμοί, έπεται ότι το πολυώνυμο $\Phi_{3}(x)$ είναι ανάγωγο στον $\mathbb{R}[x]$ και στον $\mathbb{Q}[x]$ . Βέβαια, το $\Phi_{3}(x)$ δεν είναι ανάγωγο στον $\mathbb{C}[x]$ . Έτσι η ανάλυση του $x^{3}-1$ σε γινόμενο ανάγωγων πολυωνύμων στους δακτυλίους $\mathbb{R}[x]$ και $\mathbb{Q}[x]$ είναι η ανάλυση της σχέσης (1.2.7.1), δηλ.

x^{3}-1=(x-1)(x^{2}+x+1),

ενώ η ανάλυση του $x^{3}-1$ σε γινόμενο ανάγωγων πολυωνύμων στον ${\mathbb{C}}[x]$ είναι

x^{3}-1=(x-1)(x-\omega)(x-\omega^{2}).

Πριν προχωρήσουμε στο πολυώνυμο $x^{n}-1$ , σημειώνουμε τη θέση των ριζών του πολυωνύμου $x^{3}-2$ στο μιγαδικό επίπεδο, βλ. Παράδειγμα 1.2.5.

Οι επόμενες παρατηρήσεις αφορούν το πολυώνυμο $x^{n}-1$ και τις ρίζες του στον ${\mathbb{C}}$ . An

\omega=e^{2\pi i/n}=\cos\left(\frac{2\pi}{n}\right)+i\sin\left(\frac{2\pi}{n}% \right),

τότε ισχύουν τα εξής:
i) $x^{n}-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+x+1)$ ,
ii) οι ρίζες του $x^{n-1}+x^{n-2}+\cdots+x+1$ στο $\mathbb{C}$ είναι οι $\omega$ , $\omega^{2}$ , …, $\omega^{n-1}$ , που μαζί με την μονάδα είναι οι $n$ - ρίζες της μονάδας,
iii) $(\omega^{k})^{n-1}+(\omega^{k})^{n-2}\cdots+(\omega^{k})+1=0$ , για $k=1,\ldots,n-1$ .
Οι $n$ -ρίζες της μονάδας στο μιγαδικό επίπεδο, βρίσκονται επί του μοναδιαίου κύκλου σε γωνίες που αντιστοιχούν σε πολλαπλάσια του $2\pi/n$ . Είδαμε, στο Σχήμα 1.3, τη γραφική αναπαράσταση των $3$ -ριζών της μονάδας. Ως δεύτερο παράδειγμα, οι $5$ -ρίζες της μονάδας απεικονίζονται στο Σχήμα 1.5.

Στο επόμενο εδάφιο θα δούμε ότι όταν $p$ είναι πρώτος φυσικός αριθμός, το πολυώνυμο $x^{p-1}+x^{p-2}+\cdots+x+1$ είναι ανάγωγο πολυώνυμο του δακτυλίου $\mathbb{Q}[x]$ και συμβολίζεται με $\Phi_{p}(x)$ . Έτσι στον $\mathbb{Q}[x]$ ισχύει ότι

x^{5}-1=(x-1)\Phi_{5}(x)

είναι η ανάλυση του $x^{5}-1$ σε γινόμενο ανάγωγων παραγόντων. Εάν ο $n$ δεν είναι πρώτος, τότε $x^{n-1}+x^{n-2}+\cdots+x+1$ δεν είναι ανάγωγο πολυώνυμο του $\mathbb{Q}[x]$ . Για παράδειγμα όταν $n=4$ , τότε $x^{3}+x^{2}+x+1=(x+1)(x^{2}+1)$ και

x^{4}-1=(x-1)(x+1)(x^{2}+i)\

είναι η ανάλυση του $x^{4}-1$ σε γινόμενο ανάγωγων πολυωνύμων στον $\mathbb{R}[x]$ αλλά και στον $\mathbb{Q}[x]$ . Παρατηρούμε ότι $\omega=e^{2\pi i/4}=e^{\pi i/2}=i$ είναι ρίζα του ανάγωγου πολυωνύμου $x^{2}+1$ , που βέβαια είναι παράγοντας του $x^{3}+x^{2}+x+1$ . Τονίζουμε ότι από τη γραφική παράσταση των ριζών της μονάδας, όταν ο $n$ είναι περιττός φυσικός αριθμός, προκύπτει ότι Το $x^{n-1}+x^{n-2}+\cdots+x+1$ δεν έχει πραγματικές ρίζες, άρα δεν έχει ανάγωγο παράγοντα βαθμού ένα στον $\mathbb{Q}[x]$ και στον ${\mathbb{R}}[x]$ . Περισσότερα στοιχεία για αυτά τα πολυώνυμα θα δούμε στο Εδάφιο 5.

Ας θεωρήσουμε γενικότερα ένα ανάγωγο πολυώνυμο $p(x)\in F[x]$ . Όπως είδαμε το ιδεώδες $\langle p(x)\rangle$ είναι μέγιστο και o δακτύλιος $F[x]/\langle p(x)\rangle$ είναι σώμα. Αντίστροφα παρατηρούμε ότι τα πρώτα ιδεώδη $Ι$ του $F[x]$ είναι ακριβώς εκείνα για τα οποία ο δακτύλιος πηλίκο $F[x]/I$ είναι ακέραια περιοχή. Κάθε πρώτο ιδεώδες $I\neq 0$ του $F[x]$ έχει γεννήτορα ένα πρώτο στοιχείο $p(x)$ του $F[x]$ . Όμως, το $p(x)$ είναι ανάγωγο στον $F[x]$ . Επομένως κάθε πρώτο μη μηδενικό ιδεώδες του $F[x]$ είναι μέγιστο και έχει γεννήτορα ένα ανάγωγο πολυώνυμο.

Για το ανάγωγο πολυώνυμο $p(x)$ του $F[x]$ η απεικόνιση

\phi:\ F\rightarrow F[x]/\langle p(x)\rangle,\ c\mapsto c+\langle p(x)\rangle

(1.2.7.2)

είναι ένας μονομορφισμός σωμάτων, (βλ. άσκηση 1.5.14). Επομένως το σώμα $F$ εμφυτεύεται στο σώμα $F[x]/\langle p(x)\rangle$ και το $F[x]/\langle p(x)\rangle$ είναι επέκταση του $F$ μέσω αυτής της εμφύτευσης. Με αυτό εννοούμε ότι Το $F[x]/\langle p(x)\rangle$ είναι επέκταση του σώματος $\phi(F)$ . Θα διευκρινίσουμε τα παραπάνω με δύο παραδείγματα.

Παραδείγματα 1.2.8.

1.

Το ιδεώδες $Ι=\langle x^{2}+1\rangle$ είναι μέγιστο στον $\mathbb{R}[x]$ . Το σώμα $\mathbb{R}[x]/Ι$ είναι επέκταση του $\mathbb{R}$ μέσω της εμφύτευσης:

$\phi:\ \mathbb{R}\rightarrow\mathbb{R}[x]/Ι,\ \phi(r)=r+I.$

Τα στοιχεία του $\mathbb{R}[x]/Ι$ είναι της μορφής $f(x)+I$ . Σύμφωνα, όμως, με τον Ευκλείδειο αλγόριθμο διαίρεσης:

$f(x)=(x^{2}+1)q(x)+r(x),\textrm{ όπου }r(x)\in\mathbb{R}[x],\deg r(x)\leq 1\$

και επομένως $f(x)+I=r(x)+I$ . Άρα τα στοιχεία του $\mathbb{R}[x]/I$ είναι της μορφής $a+bx+I$ , $a,b\in\mathbb{R}$ . Παρατηρούμε επίσης ότι το $Ι$ είναι ο πυρήνας του επιμορφισμού δακτυλίων

${\mathbb{R}}[x]\rightarrow{\mathbb{C}},\ f(x)\mapsto f(i).$

Άρα η συνάρτηση

$\psi:\ \mathbb{R}[x]/I\rightarrow\mathbb{C},\ f(x)+I\mapsto f(i)$

είναι ισομορφισμός σωμάτων και μάλιστα παρατηρούμε ότι

$\psi(a+bx+I)=a+bi.$

Έτσι h sun’arthsh

$\psi\circ\phi:\ \mathbb{R}\rightarrow\mathbb{C},\ \ \ \psi\circ\phi\;(r)=\psi(% r+I)=r$

είναι εμφύτευση του $\mathbb{R}$ στο $\mathbb{C}$ .
2.

Έστω τώρα το ιδεώδες $Ι=\langle x^{2}-3\rangle$ του ${\mathbb{Q}}[x]$ . Ο δακτύλιος $Ε=\mathbb{Q}[x]/Ι$ είναι σώμα, αφού το πολυώνυμο $x^{2}-3$ είναι ανάγωγο στον $\mathbb{Q}[x]$ . Τα στοιχεία του $Ε$ είναι της μορφής $f(x)+I$ , όπου $f(x)\in\mathbb{Q}[x]$ . Σύμφωνα με τον Ευκλείδειο αλγόριθμο διαίρεσης, ισχύει

$f(x)=(x^{2}-3)q(x)+r(x),$

όπου $r(x)\in\mathbb{Q}[x]$ , $\deg r(x)\leq 1$ . Επομένως

$E=\{ax+b+I:\ a,b\in{\mathbb{Q}}\}.$

Το σώμα $Ε$ είναι επέκταση του $\mathbb{Q}$ μέσω της εμφύτευσης $c\mapsto c+I$ . Στη συνέχεια θα δούμε πώς υπολογίζουμε το αντίστροφo στοιχείou του $Ε^{*}$ . Θα ξεκινήσουμε με το αντίστροφο του $x^{2}+I$ στον $Ε$ . Αφού $x^{2}+I=3+I$ έπεται ότι

$\frac{1}{3}(x^{2}+I)=\frac{1}{3}x^{2}+I=1+I\Rightarrow(x+I)\left(\frac{1}{3}x+% I\right)=1+I,$

άρα

$(x+I)^{-1}=\frac{1}{3}x+I.$

Στη γενική περίπτωση, παρατηρούμε ότι αν $r(x),f(x),g(x)\in{\mathbb{Q}}(x)$ έτσι ώστε

$f(x)r(x)+g(x)(x^{2}-3)=1,\textrm{ τότε }f(x)r(x)+Ι=1+I$ (1.2.8.1)

και άρα

$(r(x)+I)^{-1}=f(x)+I.$

Αν για δοθέν $r(x)$ ισχύει ότι $r(x)+I\neq I$ , τότε τα πολυώνυμα $f(x),g(x)\in{\mathbb{Q}}(x)$ της σχέσης (1.2.8.1) υπάρχουν, σύμφωνα με το Θεώρημα II.11 του Παραρτήματος. Θα εφαρμόσουμε τα παραπάνω για να υπολογίσουμε το $(r(x)+I)^{-1}$ , όπου $r(x)=x+2$ . Σύμφωνα με τον Ευκλείδειο αλγόριθμο διαίρεσης του $x^{2}-3$ με το $x-2$ βρίσκουμε ότι:

$x^{2}-3=(x-2)(x+2)+1\ \Rightarrow\ (2-x)(x+2)+(x^{2}-3)=1\$

και άρα

$(x+2+I)^{-1}=-x+2+I.$

Τα πολυώνυμα στα δύο προηγούμενα παραδείγματα δεν είχαν ρίζες στο σώμα ορισμού τους. Η επόμενη πρόταση δείχνει ότι σε κάθε περίπτωση ο αριθμός ριζών ενός πολυωνύμου με συντελεστές από ένα σώμα δεν μπορεί να υπερβαίνει τον βαθμό του.

Πρόταση 1.2.9.

Έστω $f(x)\in F[x]$ , όπου $F$ σώμα και $\deg f(x)=n<\infty$ . Τότε το $f(x)$ έχει το πολύ $n$ ρίζες στο $F$ .

Απόδειξη.

Αν $f(x)$ έχει $s$ ρίζες, έστω $a_{1},\ldots,a_{s}$ , τότε εφαρμόζοντας διαδοχικά την Πρόταση 1.2.2 έπεται ότι $f(x)=(x-a_{1})\cdots(x-a_{s})g(x)$ , για κάποιο πολυώνυμο $g(x)\in F[x]$ . Συγκρίνοντας τους βαθμούς των πολυωνύμων των δύο μελών προκύπτει ότι $s\leq n$ . ∎

Ο παρακάτω ορισμός αφορά την περίπτωση που το πολυώνυμο $f(x)\in F[x]$ , βαθμού $n$ , έχει ακριβώς $n$ ρίζες (μετρημένες με τη πολλαπλότητά τους) στο $F$ .

Ορισμός 1.2.10.

Λέμε ότι το $f(x)\in F[x]$ , όπου $F$ σώμα, με $\deg f(x)=n$ αναλύεται σε γινόμενο γραμμικών παραγόντων (splits) στον $F[x]$ αν

f(x)=c(x-a_{1})\cdots(x-a_{n}),

όπου $c,a_{1},\ldots,a_{n}\in F$ .

1.3 Ανάγωγα πολυώνυμα

Έστω ότι $F$ είναι σώμα. Στην Πρόταση 1.2.6 δώσαμε ένα κριτήριο για πολυώνυμα βαθμού $\leq 3$ ώστε να είναι ανάγωγα. Παρακάτω θυμίζουμε κάποια χρήσιμα κριτήρια κυρίως για πολυώνυμα στο $\mathbb{Q}[x]$ ώστε να είναι ανάγωγα. Για τις αποδείξεις που παραλείπουμε, ο αναγνώστης μπορεί να συμβουλευτεί τα [3, Ενότητες 4.6, 6.1] και [2, Ενότητες 9.4, 9.5]. Ξεκινάμε με το Κριτήριο του Gauss. Το θεώρημα αυτό αφορά πρωταρχικά (primitive) πολυώνυμα, δηλ. πολυώνυμα του $\mathbb{Z}[x]$ της μορφής $a_{n}x^{n}+\cdots+a_{0}$ με την ιδιότητα $\operatorname{\textrm{ΜΚΔ}}(a_{0},\ldots,a_{n})=1$ .

Κριτήριο του Gauss

Θεώρημα 1.3.1 (Κριτήριο του Gauss).

Έστω ότι $f(x)=a_{n}x^{n}+\cdots+a_{0}\in\mathbb{Z}[x]$ είναι πρωταρχικό πολυώνυμο και έστω ότι $\deg f(x)>0$ . Τότε to $f(x)$ είναι ανάγωγο στον $\mathbb{Z}[x]$ αν και μόνο αν Το $f(x)$ είναι ανάγωγο στον $\mathbb{Q}[x]$ .

Η επόμενη πρόταση είναι χρήσιμη για την εύρεση ριζών ενός πολυωνύμου με ακέραιους συντελεστές.

Πρόταση 1.3.2.

Έστω ότι $f(x)=a_{n}x^{n}+\cdots+a_{0}\in\mathbb{Z}[x]$ , $\deg f(x)=n$ .

\textrm{ An }\frac{r}{s}\in\mathbb{Q},\ \operatorname{\textrm{ΜΚΔ}}(r,s)=1% \textrm{ kai }f(\frac{r}{s})=0,\textrm{ τότε }r|a_{0}\textrm{ kai }s|a_{n}.

Ιδιαίτερα, αν το $f(x)$ είναι κανονικό πολυώνυμο και $f(a)\neq 0$ , για όλους τους ακέραιους $a$ που διαιρούν το $a_{0}$ , τότε το $f(x)$ δεν έχει ρίζες στο $\mathbb{Q}$ .

Σημειώνουμε επίσης την παρακάτω πρόταση, συνέπεια του κριτηρίου του Gauss.

Πρόταση 1.3.3.

Έστω $f(x)\in{\mathbb{Z}}[x]$ κανονικό πολυώνυμο. Η ανάλυση

f(x)=f_{1}(x)\cdots f_{s}(x)

σε γινόμενο αναγώγων παραγόντων στο ${\mathbb{Z}}[x]$ είναι επίσης η ανάλυση του $f(x)$ σε γινόμενο αναγώγων παραγόντων στο ${\mathbb{Q}}[x]$ .

Παραδείγματα 1.3.4.

1.

Έστω Το κανονικό πολυώνυμο $f(x)=x^{3}-3x-1$ . Οι μόνοι ακέραιοι διαιρέτες του σταθερού όρου είναι οι $\pm 1$ . Αφού $f(\pm 1)\neq 0$ , σύμφωνα με την Πρόταση 1.3.2, έπεται ότι Το $f(x)$ δεν έχει ρίζες στο $\mathbb{Q}[x]$ . Αφού $\deg f(x)=3$ , έπεται ότι Το $f(x)$ είναι ανάγωγο στον $\mathbb{Q}[x]$ , σύμφωνα με την Πρόταση 1.2.6.
2.

Έστω $n\in{\mathbb{Z}}$ έτσι ώστε $\sqrt{n}\notin{\mathbb{Q}}$ . Για παράδειγμα έστω $n$ πρώτος φυσικός αριθμός. Το πολυώνυμο $x^{2}-n$ δεν έχει ρίζα στο $\mathbb{Q}[x]$ , σύμφωνα με την Πρόταση 1.3.2, και κατά συνέπεια είναι ανάγωγο στον $\mathbb{Q}[x]$ , σύμφωνα με την Πρόταση 1.2.6. Αντίστοιχα συμπεράσματα έχουμε για το πολυώνυμο $x^{3}-n$ όταν $\sqrt[3]{n}\notin{\mathbb{Q}}$ .

Το επόμενο θεώρημα είναι γνωστό ως Κριτήριο του Eisenstein.

Θεώρημα 1.3.5 (Κριτήριο του Eisenstein).

Έστω ότι το $f(x)=a_{n}x^{n}+\cdots+a_{0}\in\mathbb{Z}[x]$ και $p\in\mathbb{Z}$ φυσικός πρώτος αριθμός. Αν ο $p$ διαιρεί τους συντελεστές $a_{i}$ , για $i=0,\ldots,n-1$ , δεν διαιρεί, όμως, τον $a_{n}$ , ενώ ο $p^{2}$ δεν διαιρεί τον $a_{0}$ , τότε το πολυώνυμο $f(x)$ είναι ανάγωγο στον $\mathbb{Q}[x]$ .

Θα εφαρμόσουμε το Κριτήριο του Eisenstein στο επόμενο παράδειγμα:

Παράδειγμα 1.3.6.

Έστω το πολυώνυμο

f(x)=\displaystyle\frac{2}{9}x^{5}+\displaystyle\frac{5}{3}x^{4}+x^{3}+% \displaystyle\frac{1}{3}\in\mathbb{Q}[x].

Παρατηρούμε ότι $f(x)$ είναι ανάγωγο στο $\mathbb{Q}[x]$ αν και μόνο αν

9f(x)=2x^{5}+15x^{4}+9x^{3}+3

είναι ανάγωγο στον $\mathbb{Q}[x]$ . Το κριτήριο του Eisenstein (για $p=3$ ) ισχύει για το πολυώνυμο $9f(x)$ και επομένως το $9f(x)$ είναι ανάγωγο στο $\mathbb{Q}[x]$ . Κατά συνέπεια το πολυώνυμο $f(x)$ είναι ανάγωγο στον $\mathbb{Q}[x]$ .

Σημειώνουμε επίσης την επόμενη πρόταση.

Πρόταση 1.3.7.

Έστω $F$ σώμα και $f(x)\in F[x]$ . Το πολυώνυμο $f(x)$ είναι ανάγωγο στο $F[x]$ αν και μόνο αν $g(x)=f(ax+b)$ είναι ανάγωγο στο $F[x]$ , όπου $a,b\in F$ και $a\neq 0$ . Το πολυώνυμο $f(x)$ είναι ανάγωγο στον $F[x]$ αν και μόνο αν $cf(x)$ είναι ανάγωγο στον $F[x]$ , όπου $c\in F^{*}$ .

H πρόταση αυτή μπορεί να χρησιμοποιηθεί όταν το κριτήριο του Eisenstein δεν εφαρμόζεται άμεσα.

Παράδειγμα 1.3.8.

Έστω $p$ πρώτος φυσικός αριθμός. Θα δείξουμε ότι το πολυώνυμο $\Phi_{p}(x)=x^{p-1}+x^{p-2}+\cdots+x+1\in\mathbb{Q}[x]$ είναι ανάγωγο, εφαρμόζοντας το κριτήριο του Eisenstein στο $\Phi_{p}(x+1)$ για τον πρώτο $p$ . Πράγματι

\Phi_{p}(x)(x-1)=x^{p}-1,

άρα

\Phi_{p}(x+1)\big((x-1)+1\big)=(x+1)^{p}-1\Rightarrow\Phi_{p}(x+1)x=(x+1)^{p}-1.

Επομένως

\Phi_{p}(x+1)=\frac{(x+1)^{p}-1}{x}=\frac{x^{p}+{p\choose 1}x^{p-1}+{p\choose 2% }x^{p-2}+\cdots+{p\choose p-1}x+1-1}{x}

=x^{p-1}+{p\choose 1}x^{p-2}+\cdots+{p\choose p-1}=x^{p-1}+px^{p-2}+\cdots+p.

Αφού o $p$ είναι πρώτος, έπεται ότι $p|{p\choose n}$ , για $n=1,\ldots,p-1$ . Το κριτήριο του Eisenstein (για τον $p$ ) αποδεικνύει ότι το πολυώνυμο $\Phi_{p}(x+1)$ είναι ανάγωγο στον $\mathbb{Q}[x]$ . Έτσι σύμφωνα με την Πρόταση 1.3.2 το πολυώνυμο $\Phi_{p}(x)$ είναι ανάγωγο στον $\mathbb{Q}[x]$ .

Το επόμενο κριτήριο ανάγει το πρόβλημα της αναγωγιμότητας του $f(x)\in\mathbb{Z}[x]$ σε αντίστοιχο πρόβλημα στον δακτύλιο $\mathbb{Z}_{p}[x]$ , όπου $p$ πρώτος φυσικός αριθμός. Θεωρούμε τον φυσικό ομομορφισμό

\psi:\ \mathbb{Z}\rightarrow\mathbb{Z}_{p},\ a\mapsto\hbox{\vbox{\hrule height% 0.3pt\kern 2.15pt\hbox{\kern-1.0pt$a$\kern-1.0pt}}}\equiv a\operatorname{mod}p.

O $\psi$ επεκτείνεται στον ομομορφισμό δακτυλίων

\Psi:\ \mathbb{Z}[x]\rightarrow\mathbb{Z}_{p}[x],\ a_{0}+a_{1}x+\cdots+a_{n}x^% {n}\mapsto\hbox{\vbox{\hrule height 0.3pt\kern 2.15pt\hbox{\kern-1.0pt$a_{0}$% \kern-1.0pt}}}+\hbox{\vbox{\hrule height 0.3pt\kern 2.15pt\hbox{\kern-1.0pt$a_% {1}$\kern-1.0pt}}}x+\cdots+\hbox{\vbox{\hrule height 0.3pt\kern 2.15pt\hbox{% \kern-1.0pt$a_{n}$\kern-1.0pt}}}x^{n}.

Παρατηρούμε ότι ο βαθμός του $\Psi(f(x))$ είναι ίσος με τον βαθμό του $f(x)$ αν και μόνο αν o συντελεστής του μεγιστοβάθμιου όρου του $f(x)$ δε διαιρείται από το $p$ .

Πρόταση 1.3.9.

Έστω $f(x)\in\mathbb{Z}[x]$ , $p$ πρώτος φυσικός αριθμός, έτσι ώστε $\deg f(x)$ να ισούται με τον $\deg\Psi(f(x))$ . Αν Το $\Psi(f(x))$ είναι ανάγωγο στο $\mathbb{Z}_{p}[x]$ , τότε Το $f(x)$ είναι ανάγωγο στον δακτύλιο ${\mathbb{Q}}[x]$ .

Το πλεονέκτημα αυτού του κριτηρίου βρίσκεται στο γεγονός ότι ο δακτύλιος $\mathbb{Z}_{p}$ είναι πεπερασμένο σώμα και επομένως η εύρεση παραγόντων αλλά και ριζών του $\Psi(f(x))$ είναι ευκολότερη εργασία. Για τα πολυώνυμα στο επόμενο παράδειγμα θα γράφουμε για λόγους απλότητας και συντομίας $m$ για να εννοούμε τον ακέραιο $m$ όταν είμαστε στον δακτύλιο ${\mathbb{Q}}[x]$ αλλά και το στοιχείο $m$ όταν είμαστε στον δακτύλιο $\mathbb{Z}_{p}[x]$ .

Παραδείγματα 1.3.10.

1.

Σύμφωνα με την Πρόταση 1.2.6, tα πολυώνυμα $x^{2}+x+1$ , $x^{3}+x+1$ και $x^{3}+x^{2}+1$ είναι ανάγωγα στον $\mathbb{Z}_{2}[x]$ , αφού δεν έχουν ρίζες στο $\mathbb{Z}_{2}$ . Σύμφωνα με το Παράδειγμα 1.3.8 ta πολυώνυμα $x^{2}+x+1$ , $x^{3}+x+1$ και $x^{3}+x^{2}+1$ είναι ανάγωγα στον $\mathbb{Q}[x]$ .
2.

Το πολυώνυμο $x^{2}+1$ δεν είναι ανάγωγο στο $\mathbb{Z}_{2}[x]$ , αφού $x^{2}+1=(x+1)^{2}$ στον $\mathbb{Z}_{2}[x]$ . Είναι, όμως, ανάγωγο στο $\mathbb{Z}[x]$ . Το αντίστροφο, λοιπόν, της Πρότασης 1.3.9 δεν ισχύει.
3.

Εξετάζοντας όλα τα πολυώνυμα βαθμού $2$ και $3$ στον ${\mathbb{Z}}_{2}[x]$ (υπάρχουν 12 τέτοια πολυώνυμα) και σύμφωνα με την Πρόταση 1.2.6, προκύπτει ότι τα ανάγωγα πολυώνυμα βαθμού $\leq 3$ του $\mathbb{Z}_{2}[x]$ είναι τα

$x,\ x+1,\ x^{2}+x+1,\ x^{3}+x^{2}+1,$

εφόσον είναι τα μόνα πολυώνυμα βαθμού $\leq 3$ που δεν έχουν ρίζες στο ${\mathbb{Z}}_{2}$ .

Υπάρχουν $2^{4}$ πολυώνυμα βαθμού $4$ στον ${\mathbb{Z}}_{2}[x]$ . Θα δείξουμε ότι το $x^{4}+x+1$ είναι ανάγωγο στον ${\mathbb{Z}}_{2}[x]$ . Αφού ο ${\mathbb{Z}}_{2}[x]$ είναι Π.Κ.Ι. συμπεραίνουμε ότι αν $x^{4}+x+1$ δεν ήταν ανάγωγο, τότε θα είχε έναν ανάγωγο παράγοντα βαθμού $1$ ή $2$ . Αφού όμως $x^{4}+x+1$ δεν έχει ρίζες στο ${\mathbb{Z}}_{2}$ έπεται ότι $x^{4}+x+1$ δεν έχει ανάγωγο παράγοντα βαθμού 1. Μένει να εξετάσουμε αν το $x^{4}+x+1$ διαιρείται από το $x^{2}+x+1$ στον ${\mathbb{Z}}_{2}[x]$ . Σύμφωνα με τον Ευκλείδειο Αλγόριθμο Διαίρεσης προκύπτει ότι:

$x^{4}+x+1=(x^{2}+x+1)(x^{2}+x)+1$

και άρα το $x^{4}+x+1$ δεν έχει ανάγωγο παράγοντα στο ${\mathbb{Z}}_{2}[x]$ βαθμού $2$ . Από τα παραπάνω βλέπουμε ότι to $x^{4}+x+1$ είναι ανάγωγο στον ${\mathbb{Z}}_{2}[x]$ . Σύμφωνα με την Πρόταση 1.3.9 το πολυώνυμο $x^{4}+x+1$ είναι ανάγωγο στον ${\mathbb{Q}}[x]$ . Συμπεραίνουμε επίσης ότι το πολυώνυμο $x^{4}+11x-1$ είναι και αυτό ανάγωγο στον ${\mathbb{Q}}[x]$ , αφού στον ${\mathbb{Z}}_{2}[x]$ μας δίνει και αυτό το ίδιο πολυώνυμο $x^{4}+x+1$ .
4.

Το πολυώνυμο $f(x)=x^{4}-10x+1\in\mathbb{Z}[x]$ δεν είναι ανάγωγο στον $\mathbb{Z}_{p}[x]$ για $p<17$ , είναι, όμως, ανάγωγο στον $\mathbb{Z}_{17}[x]$ και άρα είναι ανάγωγο στον $\mathbb{Q}[x]$ .

Απομονώνουμε μία παρατήρηση που χρησιμοποιήσαμε στο παραπάνω παράδειγμα.

Παρατήρηση 1.3.11.

Έστω $F$ σώμα και $f(x)\in F[x]$ . Αφού o $F[x]$ είναι Π.Κ.Ι., το πολυώνυμο $f(x)$ είναι ανάγωγο στον $F[x]$ αν και μόνο αν το $f(x)$ δεν έχει ανάγωγο παράγοντα βαθμού μικρότερου ή ίσου του ημίσεως του $\deg f(x)$ .

H παρατήρηση αυτή είναι ιδιαίτερα χρήσιμη, όταν το σώμα $F$ είναι πεπερασμένο και το σύνολο των ανάγωγων πολυωνύμων σε κάθε βαθμό είναι πεπερασμένο.

1.4 Σώμα Ανάλυσης ενός πολυωνύμου

Έστω ότι το $F$ είναι σώμα. Στο εδάφιο αυτό εξετάζουμε τις ρίζες ενός πολυωνύμου $f(x)\in F[x]$ σε σχέση με επεκτάσεις του σώματος $F$ . Στόχος μας είναι να αναζητήσουμε μία επέκταση $E$ του $F$ έτσι ώστε το πολυώνυμο $f(x)$ , όταν το θεωρούμε ως πολυώνυμο του $E[x]$ , να έχει όλες του τις ρίζες στο $Ε$ , δηλ. να αναλύεται σε γινόμενο γραμμικών παραγόντων στον $E[x]$ . Το Θεμελιώδες Θεώρημα της Άλγεβρας διαβεβαιώνει ότι αν $F={\mathbb{Q}}$ , τότε το σώμα ${\mathbb{C}}$ περιέχει όλες τις ρίζες του $f(x)$ . Τι συμβαίνει, όταν το $F$ είναι τυχαίο σώμα; Σε κάθε περίπτωση, πώς μπορούμε να εντοπίσουμε το μικρότερο σώμα που περιέχει όλες τις ρίζες του $f(x)$ ; Αυτό θα επιτευχθεί στο επόμενο κεφάλαιο.

Παραδείγματα 1.4.1.

1.

Το πολυώνυμο $x^{2}+1\in{\mathbb{R}}[x]$ αναλύεται σε γινόμενο γραμμικών παραγόντων στον $\mathbb{C}[x]$ ως $x^{2}+1=(x-i)(x+i)$ . Είναι φανερό ότι δεν υπάρχει σώμα $F$ έτσι ώστε ${\mathbb{R}}\subsetneqq F\subsetneqq{\mathbb{C}}$ που να περιέχει τις ρίζες $\pm i$ . Πράγματι, αν ${\mathbb{R}}\subset F$ και $i\in F$ , τότε $a+bi\in F$ , για $a,b\in{\mathbb{R}}$ , και άρα $F={\mathbb{C}}$ .
2.

Έστω τώρα το σώμα $Ε=\mathbb{R}[y]/I$ , όπου $Ι$ το ιδεώδες $\langle y^{2}+1\rangle$ του ${\mathbb{R}}[y]$ . Είδαμε στο Παράδειγμα 1.2.8.1 ότι $E\cong{\mathbb{C}}$ . Θα θεωρήσουμε στη συνέχεια τον δακτύλιο $E[x]$ . Θα δούμε ότι to πολυώνυμο $f(x)=x^{2}+1\in E[x]$ αναλύεται σε γινόμενο γραμμικών παραγόντων στον $E[x]$ . Σημειώνουμε ότι το μοναδιαίο στοιχείο του $E$ είναι το $1+Ι$ . Όπου χρειάζεται, χρησιμοποιούμε δείκτες για να τονίσουμε το σώμα στο οποίο ανήκουν τα στοιχεία μας. Έτσι $1_{E}=1_{\mathbb{R}}+Ι$ και δίνοντας αυτήν την έμφαση γράφουμε $f(x)=x^{2}+1_{E}$ . Έστω $a=y+Ι$ . Αφού

$-y^{2}+Ι=1_{\mathbb{R}}+Ι=1_{Ε},$

έχουμε ότι

$\displaystyle(x-a)(x+a)=(x-(y+Ι))(x+(y+Ι))=(x-y+Ι)(x+y+Ι)=\\ \displaystyle=x^{2}-y^{2}+Ι=x^{2}+1_{Ε}=f(x).$

Από τα παραπάνω έπεται ότι ta $\pm a$ είναι οι δύο ρίζες του $f(x)$ στο $Ε$ , δηλ. το $f(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο $E[x]$ .
3.

Έστω $Ε=\mathbb{Q}[y]/Ι$ , όπου $Ι=\langle y^{2}-3\rangle$ . Αφού το $y^{2}-3$ είναι ανάγωγο στον ${\mathbb{Q}}[y]$ , ο δακτύλιος $E$ είναι σώμα. Έστω $b=y+Ι$ . Όπως στο προηγούμενο παράδειγμα ο αναγνώστης καλείται να δείξει ότι στον $E[x]$ το πολυώνυμο $x^{2}-3\in E[x]$ αναλύεται σε γινόμενο γραμμικών παραγόντων:

$x^{2}-3=(x-b)(x+b).$

Σημειώνουμε ότι έχουμε ταυτίσει τα στοιχεία του ${\mathbb{Q}}$ με την εμφύτευσή τους στο $E$ . Έτσι ο σταθερός όρος του $f(x)$ είναι, στην πραγματικότητα, το στοιχείο $3+I$ του $Ε$ .

Έστω $F$ ένα σώμα, $p(y)$ ένα ανάγωγο πολυώνυμο του $F[y]$ , $Ι=\langle p(y)\rangle$ και $E$ το σώμα $F[y]/Ι$ . H εμφύτευση (1.2.7.2) $F\rightarrow E$ , $c\mapsto{c+Ι}$ , μετατρέπει το σώμα $E$ σε $F$ διανυσματικό χώρο, όπου

c\cdot(f(x)+I):=cf(x)+I.

Το Θεώρημα 1.4.2 γενικεύει τα προηγούμενα παραδείγματα.

Θεώρημα 1.4.2.

Έστω $F$ ένα σώμα και $p(x)$ ένα ανάγωγο πολυώνυμο του $F[x]$ . Τότε το $p(x)$ έχει μία ρίζα στο $F[y]/\langle p(y)\rangle$ .

Απόδειξη.

Έστω ότι $Ι=\langle p(y)\rangle$ και $Ε=F[y]/Ι$ . Παρατηρούμε ότι Το $y+Ι\in E$ είναι ρίζα του ${p}(x)$ . Πράγματι έστω ότι $p(x)=a_{0}+a_{1}x+\cdots+a_{n}x^{n}\in F[x]$ . Τότε

{p}(y+Ι)=a_{0}(1+Ι)+a_{1}(y+Ι)+\cdots+a_{n}(y+Ι)^{n}

=(a_{0}+Ι)+(a_{1}y+Ι)+\cdots+(a_{n}y^{n}+I)=p(y)+I=I.

∎

Το επόμενο θεώρημα είναι γνωστό ως Θεώρημα του Kronecker.

Θεώρημα 1.4.3 (Kronecker).

Έστω $f(x)\in F[x]$ , όπου το $F$ είναι σώμα. Υπάρχει μία επέκταση σωμάτων $L/F$ έτσι ώστε το $f(x)$ να αναλύεται σε γραμμικούς παράγοντες στο $L[x]$ .

Απόδειξη.

H απόδειξη γίνεται επαγωγικά ως προς τον βαθμό του $f(x)$ . Αν $\deg f(x)=1$ τότε $L=F$ . Έστω ότι $\deg f(x)>1$ και $f(x)=g(x)p(x)$ , όπου τα $p(x),g(x)\in F[x]$ και το $p(x)$ είναι ανάγωγο πολυώνυμο. Αν το $p(x)$ είναι βαθμού 1 τότε το $f(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων σε ένα σώμα $L$ , αρκεί το $g(x)$ να αναλύεται σε γινόμενο γραμμικών παραγόντων στον $L$ . Όμως, τέτοιο σώμα υπάρχει από την υπόθεση της μαθηματικής επαγωγής, αφού $\deg g(x)=\deg f(x)-1<\deg f(x)$ .

Τέλος αν $\deg p(x)>1$ , τότε, από το Θεώρημα 1.4.2, υπάρχει μία επέκταση $Μ/\ F$ στην οποία το $p(x)$ έχει μία ρίζα, έστω $a\in M$ . ’ρα $p(x)=(x-a)h(x)\in M[x]$ και $f(x)=(x-a)h(x)g(x)\in M[x]$ . Όμως, $\deg h(x)g(x)<\deg f(x)$ . Επομένως υπάρχει ένα σώμα $L$ επέκταση του $Μ$ τέτοιο ώστε το $h(x)g(x)$ να αναλύεται σε γινόμενο γραμμικών παραγόντων. Κατά συνέπεια το $f(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο σώμα $L$ που είναι επέκταση του $F$ . ∎

Έστω $f(x)\in F[x]$ , όπου $F$ είναι ένα σώμα, και έστω $L/F$ μία επέκταση του $F$ τέτοια ώστε το $f(x)$ να αναλύεται σε γραμμικούς παράγοντες στο $L[x]$ . Αν $\deg f(x)=n$ , τότε στο σώμα $L$ το $f(x)$ έχει την ανάλυση

f(x)=c(x-a_{1})^{s_{1}}\cdots(x-a_{t})^{s_{t}},

όπου $c\in F$ , $a_{i}\in L$ και $a_{i}\neq a_{J}$ , για $1\leq i,j\leq t$ . Οι ρίζες του $f(x)$ στο $L$ είναι τα στοιχεία $a_{1},\dots,a_{s}$ του $L$ . Είναι φανερό ότι το πλήθος των ριζών του $f(x)$ είναι ακριβώς $n$ και $n=s_{1}+\cdots+s_{t}$ , συγκρίνοντας τους βαθμούς των πολυωνύμων των δύο μερών. Οι φυσικοί αριθμοί $s_{1},\ldots,s_{t}$ είναι οι πολλαπλότητες (multiplicities) των ριζών $a_{1},\ldots,a_{t}$ αντίστοιχα. Η Πρόταση 1.4.5 που ακολουθεί είναι χρήσιμη προκειμένου να δούμε αν το $f(x)$ έχει πολλαπλές ρίζες. Χρειαζόμαστε, όμως, πρώτα τον επόμενο ορισμό.

Ορισμός 1.4.4.

Έστω $F$ ένα σώμα και $f(x)=c_{n}x^{n}+\cdots+c_{1}x+c_{o}\in F[x]$ . Παράγωγος (derivative) του $f(x)$ λέγεται το πολυώνυμο

c_{1}+2c_{2}+\cdots+nc_{n}x^{n-1}

και συμβολίζεται με $f^{\prime}(x)$ .

Δώσαμε παραπάνω τον ορισμό της παραγώγου ενός πολυωνύμου και δεν τον θεωρήσαμε δεδομένο από τη Μαθηματική Ανάλυση, διότι ένα πολυώνυμο είναι τυπική σειρά και όχι συνάρτηση, βλ. την Ενότητα ΙΙΙ του Παραρτήματος. Είναι χρήσιμο να σημειώσουμε ότι το πολυώνυμο $f^{\prime}(x)$ έχει τις ιδιότητες της παραγώγου από τη Μαθηματική Ανάλυση. Έτσι,

(f(x)g(x))^{\prime}=f^{\prime}(x)g(x)+f(x)g^{\prime}(x).

Πρόταση 1.4.5.

Έστω $f(x)=c_{0}+c_{1}x+\cdots+c_{n}x^{n}\in F[x]$ , όπου $F$ είναι ένα σώμα, και έστω $L/F$ μία επέκταση του $F$ όπου Το $f(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων. Το πολυώνυμο $f(x)$ έχει πολλαπλές ρίζες στο $L$ αν και μόνο αν $\operatorname{\textrm{ΜΚΔ}}(f(x),f^{\prime}(x))\neq 1$ .

Απόδειξη.

Έστω ότι τα πολυώνυμα $q(x),r(x)$ του $F(x)$ είναι τέτοια ώστε, σύμφωνα με τον Ευκλείδειο αλγόριθμο στον $F(x)$ , να ισχύει ότι

f(x)=f^{\prime}(x)q(x)+r(x),\ \deg r(x)<\deg f^{\prime}(x)\textrm{ ή }r(x)=0.

(1.4.5.1)

Αφού $F[x]\subset L[x]$ , έπεται ότι $q(x),r(x)\in L(x)$ . Επομένως η σχέση 1.4.5.1 ισχύει στον δακτύλιο $L[x]$ και τα πολυώνυμα $q(x),r(x)$ είναι ακριβώς το πηλίκο και το υπόλοιπο που προβλέπει ο Ευκλείδειος αλγόριθμος από τη διαίρεση του $f(x)$ με το $f^{\prime}(x)$ στον $L[x]$ . Παρατηρούμε ότι ο υπολογισμός του $\operatorname{\textrm{ΜΚΔ}}\left(f(x),f^{\prime}(x)\right)$ προκύπτει με τη χρήση του Ευκλείδιου αλγόριθμου. Έτσι οι $\operatorname{\textrm{ΜΚΔ}}\left(f(x),f^{\prime}(x)\right)$ στα σώμαtα $F$ και $L$ ταυτίζονται. Έστω τώρα ότι

f(x)=c(x-a_{1})^{s_{1}}\cdots(x-a_{t})^{s_{t}}\in L[x].

Παρατηρούμε ότι αν $s_{i}>1$ , για κάποιο $i\in\{1,\ldots,t\}$ , τότε το $x-a_{i}$ διαιρεί το $f(x)$ και το $f^{\prime}(x)$ και επομένως,

\operatorname{\textrm{ΜΚΔ}}\left(f(x),f^{\prime}(x)\right)\neq 1.

Το αντίστροφο προκύπτει ανάλογα. ∎

Έστω ότι το $g (x) \in F [x]$ είναι ανάγωγο και έστω ότι το $g (x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στην επέκταση $L / F$ . Λέμε ότι το $g (x)$ είναι διαχωρίσιμο όταν οι ρίζες του $g (x)$ στο $L$ είναι απλές. Γενικότερα, λέμε ότι το $g (x) \in F [x]$ είναι διαχωρίσιμο (separable), όταν κάθε ανάγωγος παράγοντας του $g (x)$ έχει απλές ρίζες. Έτσι για παράδειγμα, τα πολυώνυμα $x^{2} + 3$ , $(x - 1)^{2}$ είναι διαχωρίσιμα στο $Q [x]$ . Όπως είδαμε παραπάνω, το ανάγωγο πολυώνυμο $g(x)$ είναι διαχωρίσιμο αν και μόνο αν ο $\operatorname{\textrm{ΜΚΔ}}\left(g(x),g^{\prime}(x)\right)=1$ . Όμως, αν οι ρίζες του $f(x)$ είναι απλές σε κάποια επέκταση του $F$ παρατηρούμε ότι τότε θα είναι απλές πάνω από κάθε επέκταση του $F$ .

Πόρισμα 1.4.6.

Έστω $F$ ένα σώμα, $g(x)\in F[x]$ ένα ανάγωγο πολυώνυμο και έστω ότι το $g(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στον $L[x]$ , όπου $L/F$ μία επέκταση του $F$ . Αν το $F$ έχει χαρακτηριστική 0, τότε το $g(x)$ είναι διαχωρίσιμο.

Απόδειξη.

Αφού η χαρακτηριστική του $F$ είναι $0$ , έπεται ότι $g^{\prime}(x)\neq 0$ . Σύμφωνα με την υπόθεση, το πολυώνυμο $g(x)$ είναι ανάγωγο στον $F[x]$ και άρα οι μόνοι διαιρέτες του $g(x)$ στο $F[x]$ είναι τα σταθερά μη μηδενικά πολυώνυμα και το ίδιο το $g(x)$ . Αφού ο $\operatorname{\textrm{ΜΚΔ}}\left(g(x),g^{\prime}(x)\right)$ διαιρεί το πολυώνυμο $g(x)$ και $\deg g^{\prime}(x)=\deg g(x)-1$ έπεται ότι $\operatorname{\textrm{ΜΚΔ}}\left(g(x),g^{\prime}(x)\right)=1$ Έτσι σύμφωνα με την Πρόταση 1.4.5, όλες οι ρίζες του $g(x)$ είναι απλές. ∎

Αν το $F$ έχει χαρακτηριστική $p$ , όπου $p$ είναι πρώτος φυσικός αριθμός, τότε πρέπει να είμαστε πιο προσεκτικοί. Παρατηρούμε ότι $g^{\prime}(x)=0$ όταν ακριβώς Το $g(x)$ είναι της μορφής

r_{0}+r_{1}x^{p}+\cdots+r_{n}x^{np},\ r_{i}\in F.

Στην περίπτωση αυτή έχουμε ότι ο $\operatorname{\textrm{ΜΚΔ}}\left(g(x),g^{\prime}(x)\right)=g(x)$ . Έτσι καταλήγουμε στην παρακάτω πρόταση:

Πόρισμα 1.4.7.

Έστω $F$ ένα σώμα τέτοιο ώστε $\operatorname{char}F=p$ , $g(x)\in F[x]$ ένα πολυώνυμο και έστω ότι το $g(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων sΤο $L[x]$ , όπου $L/F$ μία επέκταση του $F$ . Το πολυώνυμο $g(x)$ δεν είναι διαχωρίσιμο αν και μόνο αν $g(x)$ είναι της μορφής

g(x)=r_{0}+r_{1}x^{p}+\cdots+r_{n}x^{np}.

Στα επόμενα παραδείγματα θα αντιμετωπίσουμε τέτοιες περιπτώσεις.

Παραδείγματα 1.4.8.

1.

Έστω $f(x)=x^{2}+1\in\mathbb{Z}_{2}[x]$ . Τότε $f^{\prime}(x)=0$ και $f(x)=(x+1)^{2}$ έχει ρίζα το 1 με πολλαπλότητα 2. Βέβαια, το πολυώνυμο $f(x)$ δεν είναι ανάγωγο στον ${\mathbb{Z}}_{2}[x]$ .
2.

Έστω $f(x)=x^{p}+x+a\in\mathbb{Z}_{p}[x]$ , όπου $p$ πρώτος, και έστω ότι Το $f(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στον $L[x]$ , όπου $L$ μία επέκταση του ${\mathbb{Z}}_{p}$ . Αφού $f^{\prime}(x)=1$ , έπεται ότι οι ρίζες του $f(x)$ στο $L$ είναι απλές.
3.

Έστω $F=\mathbb{Z}_{2}(t)$ το σώμα κλασμάτων του ${\mathbb{Z}}_{2}[x]$ . Έτσι

${\mathbb{Z}}_{2}(t)=\left\{\frac{a(t)}{b(t)}:\ a(t),b(t)\in\mathbb{Z}_{2}[t],b% (t)\neq 0\right\}.$

Το σώμα $F$ έχει χαρακτηριστική 2. Αφού το πολυώνυμο $f(x)=x^{2}-t$ δεν έχει ρίζες στο $F$ , βλ. Άσκηση 1.5.15, έπεται ότι το $f(x)$ είναι ανάγωγο στο $F[x]$ . Αφού $f^{\prime}(x)=0$ , έπεται ότι $\operatorname{\textrm{ΜΚΔ}}\left(f(x),f^{\prime}(x)\right)=f(x)$ και άρα το $f(x)$ δεν είναι διαχωρίσιμο.

Έστω $F$ ένα σώμα και $f(x)\in F[x]$ . Μας ενδιαφέρουν οι μικρότερες επεκτάσεις $L/\ F$ με αυτήν την ιδιότητα για ένα συγκεκριμένο πολυώνυμο.

Ορισμός 1.4.9.

Έστω $F$ ένα σώμα, $f(x)\in F[x]$ ένα πολυώνυμο και έστω $L/F$ μία επέκταση έτσι ώστε $f(x)$ να αναλύεται σε γραμμικούς παράγοντες του $L[x]$ . Εάν δεν υπάρχει ενδιάμεση επέκταση $F\subsetneqq Ε\subsetneqq L$ τέτοια ώστε το $f(x)$ να αναλύεται σε γραμμικούς παράγοντες στο $F[x]$ , τότε το $L$ λέγεται σώμα ανάλυσης (splitting field) του $f(x)$ πάνω από το $F$ .

Στο επόμενο κεφάλαιο θα δούμε πως κατασκευάζουμε σώματα ανάλυσης πολυωνύμων, βλ. Θεώρημα 2.2.10.

Παραδείγματα 1.4.10.

a)

Το σώμα $\mathbb{C}$ δεν είναι σώμα ανάλυσης του $x^{2}-2$ πάνω από το $\mathbb{Q}$ , αφού $x^{2}-2=(x-\sqrt{2})(x+\sqrt{2})$ αναλύεται σε γραμμικούς παράγοντες στο $\mathbb{R}[x]$ .
b)

Το σώμα ${\mathbb{R}}$ είναι σώμα ανάλυσης του $x^{2}-2$ πάνω από το $\mathbb{R}$ , αφού $x^{2}-2=(x-\sqrt{2})(x+\sqrt{2})$ αναλύεται σε γραμμικούς παράγοντες στο $\mathbb{R}[x]$ .

1.5 Ασκήσεις

1.

Να δείξετε ότι με κανόνα και διαβήτη είναι δυνατές οι επόμενες κατασκευές στο επίπεδο:
α) να χαράξουμε κάθετη ευθεία σε δοθείσα ευθεία που να περνάει από συγκεκριμένο σημείο επί της αρχικής ευθείας,
β) να χαράξουμε μεσοκάθετη σε δοθέν ευθύγραμμο τμήμα,
γ) να χαράξουμε ευθεία παράλληλη σε δοθείσα ευθεία που να περνάει από συγκεκριμένο σημείο εκτός της δοθείσης ευθείας,
δ) να χαράξουμε τη διχοτόμο δοθείσης γωνίας στο επίπεδο.
2.

Να αποδείξετε ότι αν $a$ κατασκευάσιμος, τότε $\sqrt{a}$ είναι κατασκευάσιμος.
3.

Να αποδείξετε ότι μία γωνία $\theta$ είναι κατασκευάσιμη αν και μόνο αν ο αριθμός $\cos(\theta)$ είναι κατασκευάσιμος. Στη συνέχεια να δείξετε ότι το $\cos(\theta)$ είναι κατασκευάσιμος αριθμός αν και μόνο αν $\sin(\theta)$ είναι κατασκευάσιμος αριθμός.
4.

Έστω $n$ φυσικός αριθμός. Να αποδείξετε ότι το κανονικό $n$ -γωνo είναι κατασκευάσιμo αν και μόνο αν η γωνία $2\pi i/n$ είναι κατασκευάσιμη και ισοδύναμα αν και μόνο αν το σημείο $(\cos(2\pi i/p),\sin(2\pi i/p))$ είναι κατασκευάσιμο.
5.
Να εξετάσετε αν τα παρακάτω πολυώνυμα του $\mathbb{Q}[x]$ είναι ανάγωγα:
- –
  
  $x^{9}+4x+6$ ,
- –
  
  $x+1$ ,
- –
  
  $x^{4}+4$ ,
- –
  
  $8x^{3}-6x-1$ ,
- –
  
  $x^{4}+1$ ,
- –
  
  $x^{7}+7x+14$ ,
- –
  
  $(4/3)x^{5}+(6/5)x^{2}+2$ ,
- –
  
  $x^{5}-10x+2$ ,
6.

Να βρείτε όλα τα ανάγωγα πολυώνυμα βαθμού $4$ στο ${\mathbb{Z}}_{2}[x]$ .
7.

Εξετάζοντας ανάγωγους παράγοντες βαθμού ένα, δύο και τρία να δείξετε ότι $x^{6}+x^{3}+1$ είναι ανάγωγο στο ${\mathbb{Z}}_{2}[x]$ . Να συμπεράνετε ότι $25x^{6}-x^{3}+19$ είναι ανάγωγο στο ${\mathbb{Q}}[x]$ .
8.
Να εξετάσετε αν τα παρακάτω πολυώνυμα είναι ανάγωγα:
- –
  
  $x^{4}+4\in Z_{3}[x]$ ,
- –
  
  $x^{4}+4\in Z_{13}[x]$ ,
- –
  
  $x^{2}+3\in Z_{7}[x]$ .
9.

Να αποδείξετε ότι $\mathbb{Q}(\sqrt{2})=\{a+b\sqrt{2}:a,b\in{\mathbb{Q}}\}$ είναι σώμα. Nα δείξετε ότι το πολυώνυμο $x^{2}-5$ δεν έχει ρίζες στο $\mathbb{Q}(\sqrt{2})$ και άρα είναι ανάγωγο πολυώνυμο tou $\mathbb{Q}(\sqrt{2})[x]$ .
10.

Να βρείτε ανάγωγο πολυώνυμο βαθμού 12 πάνω από το $\mathbb{Q}$ .
11.

Να βρείτε ανάγωγο πολυώνυμο βαθμού 12 πάνω από το $\mathbb{Ζ}_{3}$ .
12.

Να βρείτε τους ανάγωγους παράγοντες του $x^{7}+x^{6}+\cdots+x+1$ και του $x^{8}+x^{7}+\cdots+1$ στους $\mathbb{Q}[x]$ , $\mathbb{R}[x]$ και $\mathbb{C}[x]$ .
13.

Να αποδείξετε ότι $\mathbb{Q}[x]/I$ είναι σώμα, όπου $I=\langle x^{4}+x^{3}+x^{2}+x+1\rangle$ . Στη συνέχεια να βρείτε τον αντίστροφο του $2x^{5}+3+I$ .
14.

Έστω $p(x)$ ανάγωγο πολυώνυμο του $K[x]$ . Να αποδείξετε ότι η απεικόνιση

$\phi:\ K\rightarrow K[x]/\langle p(x)\rangle,\ c\mapsto c+\langle p(x)\rangle$

είναι ένας μονομορφισμός σωμάτων
15.

Έστω $K=\mathbb{Z}_{2}(t)$ . Nα δείξετε ότι το πολυώνυμο $f(x)=x^{2}-t\in K[x]$ είναι ανάγωγο. Να βρείτε ένα σώμα ανάλυσης $L/K$ για το πολυώνυμο $f(x)$ και να δείξετε ότι το $f(x)$ έχει μία διπλή ρίζα.
16.

Έστω $Ε, F$ δύο σώματα και έστω $\sigma:E\rightarrow F$ ισομορφισμός σωμάτων. Να δείξετε ότι ο $\sigma$ επεκτείνεται σε έναν ισομορφισμό $\widehat{\sigma}$ των δακτυλίων $E[x]$ και $F[x]$ , ως εξής:

$\widehat{\sigma}:E[x]\rightarrow F[x],\ \sum a_{i}x^{i}\mapsto\sigma(a_{i})x^{% i}\ .$

Στη συνέχεια να δείξετε ότι αν Το $E$ είναι σώμα ανάλυσης του $f(x)\in E[x]$ , τότε Το $F$ είναι σώμα ανάλυσης του $\widehat{\sigma}(f(x))\in F[x]$ . Τέλος να δείξετε ότι αν το $g(x)\in E[x]$ είναι διαχωρίσιμο, τότε το $\widehat{\sigma}(g(x))$ είναι διαχωρίσιμο.
17.

Έστω $p(x),g(x)\in F[x]$ έτσι ώστε to $p(x)$ να είναι ανάγωγο και Το $g(x)$ να είναι διαχωρίσιμο. Αν τα $p(x)$ και $g(x)$ έχουν κοινές ρίζες σε ένα σώμα ανάλυσης του $p(x)$ , να δείξετε ότι το $p(x)$ είναι διαχωρίσιμο και ’ότι το $p(x)|g(x)$ .
18.

Στον τύπο των Ιταλών μαθηματικών για τη ρίζα του τριτοβάθμιου πολυωνύμου, σε ορισμένες περιπτώσεις, εμφανίζεται η τετραγωνική ρίζα ενός αρνητικού ρητού αριθμού και γενικότερα η έκφραση

$\sqrt[3]{a+bi}+\sqrt[3]{a-bi}\ ,$ (1.5.0.1)

όπου $a,b\in{\mathbb{R}}$ . Με υπολογισμούς που έκανε ο Bombelli, σε κάποιες συγκεκριμένες περιπτώσεις, προκύπτει ότι η ρίζα του παραπάνω τύπου είναι πραγματικός αριθμός. Να εντοπίσετε γραφικά στο μιγαδικό επίπεδο τις τρεις ρίζες του μιγαδικού αριθμού $\sqrt[3]{a+bi}$ και στη συνέχεια τις τρεις ρίζες του $\sqrt[3]{a-bi}$ . Να δείξετε ότι με κατάλληλη επιλογή ρίζας για κάθε έναν από τους δύο προσθετέους στην έκφραση 1.5.0.1, το άθροισμα είναι πραγματικός αριθμός.

Βιβλιογραφία Κεφαλαίου 1

1.

Βάρσος, Δ., Δεριζιώτης, Δ., Μαλιάκας, Μ., Ταλλέλη Ο., Εμμανουήλ, Ι., Μελάς, Α. Μια Εισαγωγή στην Άλγεβρα. EKPA, Εκδ. Σοφία, 2012.
2.

Dummit, D.S., Foote, R.M. Abstract Algebra. J. Wiley and Sons, INc, 2004.
3.

Fraleigh, J. Εισαγωγή στην Άλγεβρα. Πανεπιστημιακές εκδόσεις Κρήτης, 2011.
4.

Hungerford,T. Algebra. Springer, 1974.
5.

Katz, V. Ιστορία των Μαθηματικών, Μία εισαγωγή. Πανεπιστημιακές Εκδόσεις Κρήτης, 2013.
6.

Λάκκης, Κ. Άλγεβρα. Θεσσαλονίκη, 1980.
7.

Lang, S. Algebra. Springer, 2002.
8.

Menini, C. Van Oystaeyen, F. Abstract Algebra. Marcel Dekker, 2004.
9.

Page, John D. Constructions From Math Open Reference http://www.mathopenref.com/tocs/constructionstoc.html
10.

Πουλάκης, Δ. Άλγεβρα. Ζήτη, 2015.
11.

Stewart, I. Galois Theory. Champan and Hall, 1973.