Θεωρία Galois

Κεφάλαιο 3 Θεμελιώδες Θεώρημα της Θεωρίας Galois

Στο κεφάλαιο αυτό εξετάζουμε λεπτομερέστερα τις oμάδες Galois και μελετάμε τις επεκτάσεις ισομορφισμών σωμάτων. Στη συνέχεια ορίζουμε τις επεκτάσεις Galois σωμάτων και αποδεικνύουμε το θεμελιώδες θεώρημα της θεωρίας Galois.

3.1 Μεταθέσεις και ομάδα Galois

Στο Παράδειγμα 2.3.6 υπολογίσαμε την ομάδα Galois $\operatorname{Gal}(E/{\mathbb{Q}})$ του σώματος ανάλυσης $E$ του πολυωνύμου $f(x)=x^{3}-2$ πάνω από το ${\mathbb{Q}}$ και είδαμε ότι είναι ισόμορφη με την $S_{3}$ . Tο βασικό θεώρημα αυτής της παραγράφου, συνδέει τα στοιχεία της $\operatorname{Gal}(E/F)$ και τις μεταθέσεις των ριζών του $f(x)\in F[x]$ , όταν το $E$ είναι το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ . Έτσι αντιλαμβανόμαστε την αξία αυτού του ισομορφισμού.

Θεώρημα 3.1.1.

Έστω $f(x)\in F[x]$ διαχωρίσιμο και ανάγωγο, $\deg f(x)=n$ και έστω $E$ σώμα ανάλυσης του $f(x)$ . Τότε η ομάδα $\operatorname{Gal}(E/F)$ εμφυτεύεται στην ομάδα των μεταθέσεων $S_{n}$ .

Απόδειξη.

Έστω $X=\{b_{1},\ldots,b_{n}\}$ το σύνολο των ριζών του $f(x)$ . Τότε $Ε=F(b_{1},\ldots,b_{n})$ . Τα στοιχεία του $S_{X}$ είναι αμφιμονότιμες και επί συναρτήσεις του $X$ στον εαυτό του και $S_{X}\cong S_{n}$ . Αν $G=\operatorname{Gal}(E/F)$ και $\sigma\in G$ , τότε θεωρούμε τη συνάρτηση $\theta_{\sigma}:X\rightarrow X,\ \theta_{\sigma}(b_{i})=\sigma(b_{i})\ i=1,% \ldots,n$ . Είναι εύκολο να δείξει κανείς ότι $\theta_{\sigma}\in S_{X}$ , δηλαδή ότι $\theta(b_{i})=\theta(b_{j})\Leftrightarrow b_{i}=b_{j}$ . Έτσι οδηγούμαστε στον επόμενο ορισμό:

\phi_{G}:G\rightarrow S_{X},\quad\sigma\mapsto\theta_{\sigma}.

Ο αναγνώστης μπορεί εύκονα να επιβεβαιώσει ότι

•

$\phi_{G}(\sigma\,\tau)=\phi_{G}(\sigma)\,\phi_{G}(\tau)$ , για $\sigma,\tau\in G$ και
•

$\phi_{G}$ είναι αμφιμονότιμη, δηλ. $\phi_{G}(\sigma)=\phi_{G}(\tau)\Leftrightarrow\sigma=\tau$ , για $\sigma,\tau\in G$ .

Επομένως η συνάρτηση $\phi$ είναι μονομορφισμός ομάδων. ∎

Στα επόμενα παραδείγματα θα μελετήσουμε την εμφύτευση του Θεωρήματος 3.1.1.

Παραδείγματα 3.1.2.

1.

Έστω $f(x)=x^{3}-2\in{\mathbb{Q}}[x]$ , $\omega=e^{2\pi i/3}$ , $b=\sqrt[3]{2}$ και $E=\mathbb{Q}(b,\omega b)$ . Όπως είδαμε στο παράδειγμα 2.3.6, Το σώμα $E$ είναι το σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ και η ομάδα $G=\operatorname{Gal}(E/{\mathbb{Q}})$ καθορίζεται από τον παρακάτω πίνακα:

$\begin{matrix}b&\vline&b&\omega b&\omega^{2}b&b&\omega b&\omega^{2}b\cr\hline% \omega&\vline&\omega&\omega&\omega&\omega^{2}&\omega^{2}&\omega^{2}\cr\hline&% \vline&\operatorname{id}_{E}&\sigma&\sigma^{2}&\tau&\sigma\tau&\tau\sigma\end{matrix}$

Η ομάδα $G$ είναι ισόμορφη με την $S_{3}$ και οι εικόνες των στοιχείων της $G$ σύμφωνα με τον ισομορφισμό $\phi_{G}$ είναι:

$\operatorname{id}_{E}\mapsto\begin{pmatrix}b&\omega b&\omega^{2}b\cr b&\omega b% &\omega^{2}b\end{pmatrix},\ \sigma\mapsto\begin{pmatrix}b&\omega b&\omega^{2}b% \cr\omega b&\omega^{2}b&b\end{pmatrix},\ \sigma^{2}\mapsto\begin{pmatrix}b&% \omega b&\omega^{2}b\cr\omega^{2}b&b&\omega b\end{pmatrix}\ ,$

$\tau\mapsto\begin{pmatrix}b&\omega b&\omega^{2}b\cr b&\omega^{2}b&\omega b\end% {pmatrix},\ \sigma\tau\mapsto\begin{pmatrix}b&\omega b&\omega^{2}b\cr\omega b&% b&\omega^{2}b\end{pmatrix},\ \tau\sigma\mapsto\begin{pmatrix}b&\omega b&\omega% ^{2}b\cr\omega^{2}b&\omega b&b\end{pmatrix}.$

Το σχήμα 3.1, αντιστοιχεί την ομάδα $G$ με τις συμμετρίες του ισόπλευρου τριγώνου.

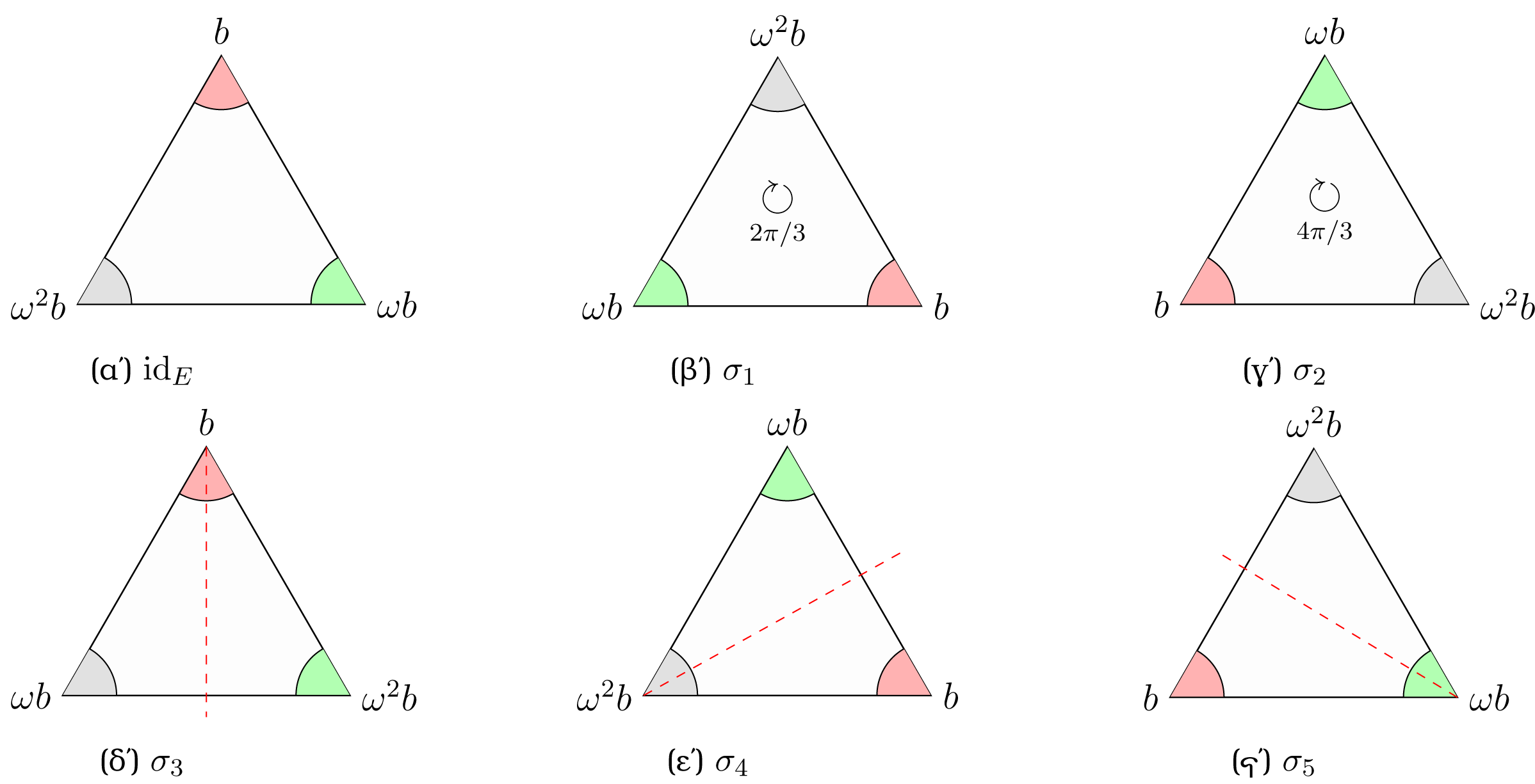
Σχήμα 3.1: Συμμετρίες του ισόπλευρου τριγώνου και η ομάδα $\operatorname{Gal}({\mathbb{Q}}(\omega,b)/{\mathbb{Q}})$
2.

Έστω $f(x)=(x^{2}-2)(x^{2}-3)\in{\mathbb{Q}}[x]$ . Το $E={\mathbb{Q}}(\sqrt{2},\sqrt{3})$ είναι σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ . Στο Παράδειγμα 2.3.5.7 είδαμε ότι $\operatorname{Gal}(E/{\mathbb{Q}})\cong{\mathbb{Z}}_{2}\times{\mathbb{Z}}_{2}$ και ότι τα στοιχεία της $G$ καθορίζονται από τον παρακάτω πίνακα:

$\begin{matrix}\sqrt{2}&\vline&\sqrt{2}&\sqrt{2}&-\sqrt{2}&-\sqrt{2}\cr\hline% \sqrt{3}&\vline&\sqrt{3}&-\sqrt{3}&\sqrt{3}&-\sqrt{3}\cr\hline&\vline&% \operatorname{id}_{E}&\sigma_{1}&\sigma_{2}&\sigma_{1}\sigma_{2}&\end{matrix}$

Αν διατάξουμε τις ρίζες του $f(x)$ ως το σύνολο $\{\sqrt{2},\sqrt{3},-\sqrt{2},-\sqrt{3}\}$ , τότε οι εικόνες των $\sigma_{1}$ , $\sigma_{2}$ και $\sigma_{3}=\sigma_{1}\sigma_{2}$ στην $S_{4}$ σύμφωνα με τον ισομορφισμό $\phi_{G}$ του Θεωρήματος 3.1.1 αντιστοιχούν στις μεταθέσεις $(2\;4)$ , $(1\;3)$ και $(1\;3)(2\;4)$ αντίστροφα. Το σχήμα 3.2, αντιστοιχεί την ομάδα $G$ με κάποιες από τις γεωμετρικές συμμετρίες του τετραγώνου. Τοποθετώντας τις ρίζες του $f(x)$ ως κορυφές ενός τετραγώνου, παρατηρούμε ότι οι $\sigma_{1}$ και $\sigma_{2}$ αντιστοιχoύν σε αντικατοπτρισμούς ως προς τις διαγωνίους, ενώ ο $\sigma_{1}\sigma_{2}$ αντιστοιχεί στη περιστροφή κατά γωνία $\pi$ .

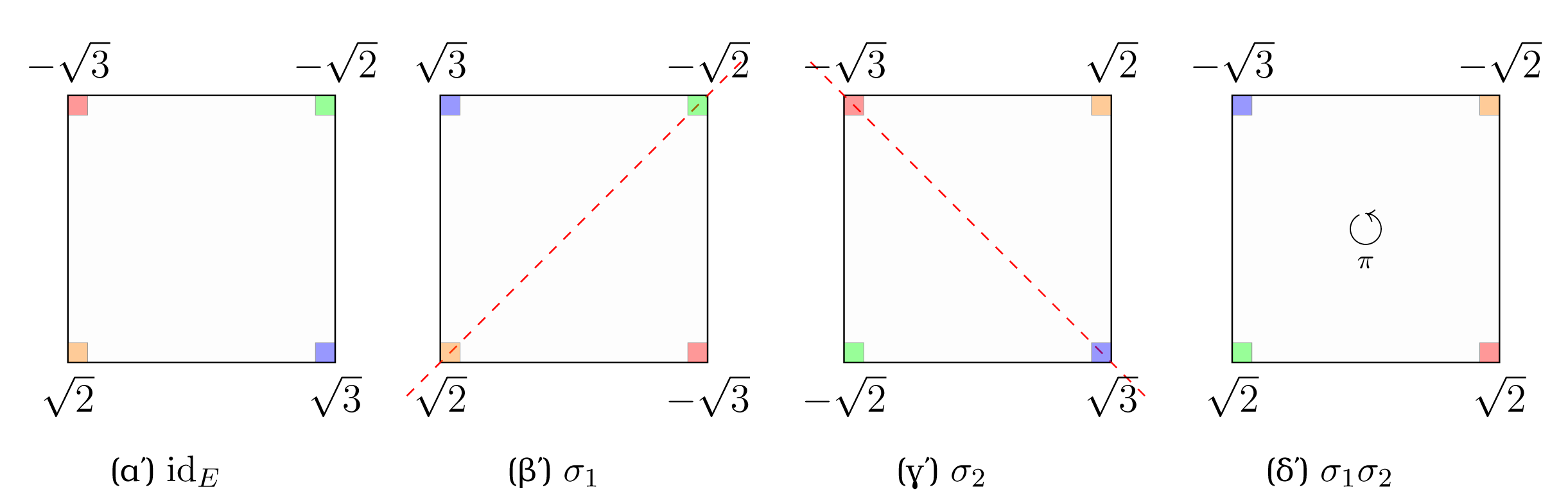
Σχήμα 3.2: Συμμετρίες και η ομάδα $\operatorname{Gal}({\mathbb{Q}}(\sqrt{2},\sqrt{3})/{\mathbb{Q}})$
3.

Έστω $f(x)=x^{4}-2$ . Αν $b=\sqrt[4]{2}$ , oι ρίζες του $f(x)$ στο $\mathbb{C}$ είναι $\pm b$ , $\pm bi$ και $Ε=\mathbb{Q}(2^{1/4},i)$ είναι σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ . Θα δείξουμε ότι η ομάδα $G=\operatorname{Gal}(E/\mathbb{Q})$ είναι ισόμορφη με την ομάδα των συμμετριών του τετραγώνου. Πράγματι η $G$ έχει το πολύ 8 στοιχεία, αφού αν $\sigma\in G$ , τότε

$\sigma(b)=\begin{cases}b\cr-b\cr ib\cr-ib\end{cases},\ \sigma(i)=\begin{cases}% i\cr-i\end{cases}.$

Έστω $F={\mathbb{Q}}(i)$ . Από το Θεώρημα 2.3.3, αφού το $i b$ είναι ρίζα του $\operatorname{irr}_{(F,b)}=x^{4}-2$ και $E=F(b)$ , υπάρχει αυτομορφισμός $\sigma\in G$ έτσι ώστε

$\sigma:\ b\mapsto ib,i\mapsto i.$

Ομοίως βλέπουμε ότι υπάρχει $\tau\in G$ έτσι ώστε

$\tau:\ b\mapsto b,i\mapsto-i.$

Οι συνθέσεις των $\sigma$ και $\tau$ δίνουν έξι νέα στοιχεία της ομάδας $G$ . Άρα η ομάδα $G$ έχει όντως ακριβώς οκτώ στοιχεία. Αναλυτικά τα στοιχεία της $G$ καθορίζονται από τον πίνακα:

Οι αυτομορφισμοί $\sigma$ και $\tau$ αντιστοιχoύν στις μεταθέσεις

$\begin{pmatrix}b&-b&ib&-ib\cr ib&-ib&-b&b\end{pmatrix}\text{ και }\begin{% pmatrix}b&-b&ib&-ib\cr b&-b&-ib&ib\ .\end{pmatrix}$

Τοποθετώντας τις ρίζες του $f(x)$ ως κορυφές ενός τετραγώνου όπως στο παραπάνω σχήμα, παρατηρούμε ότι ο $\sigma$ αντιστοιχεί σε αριστερόστροφη περιστροφή με γωνία

$\frac{2\pi}{4}=\frac{\pi}{2},$

ενώ ο $\tau$ αντιστοιχεί σton αντικατοπτρισμό ως προς τη διαγώνιο που περνάει από τις κορυφές $b,-b$ .

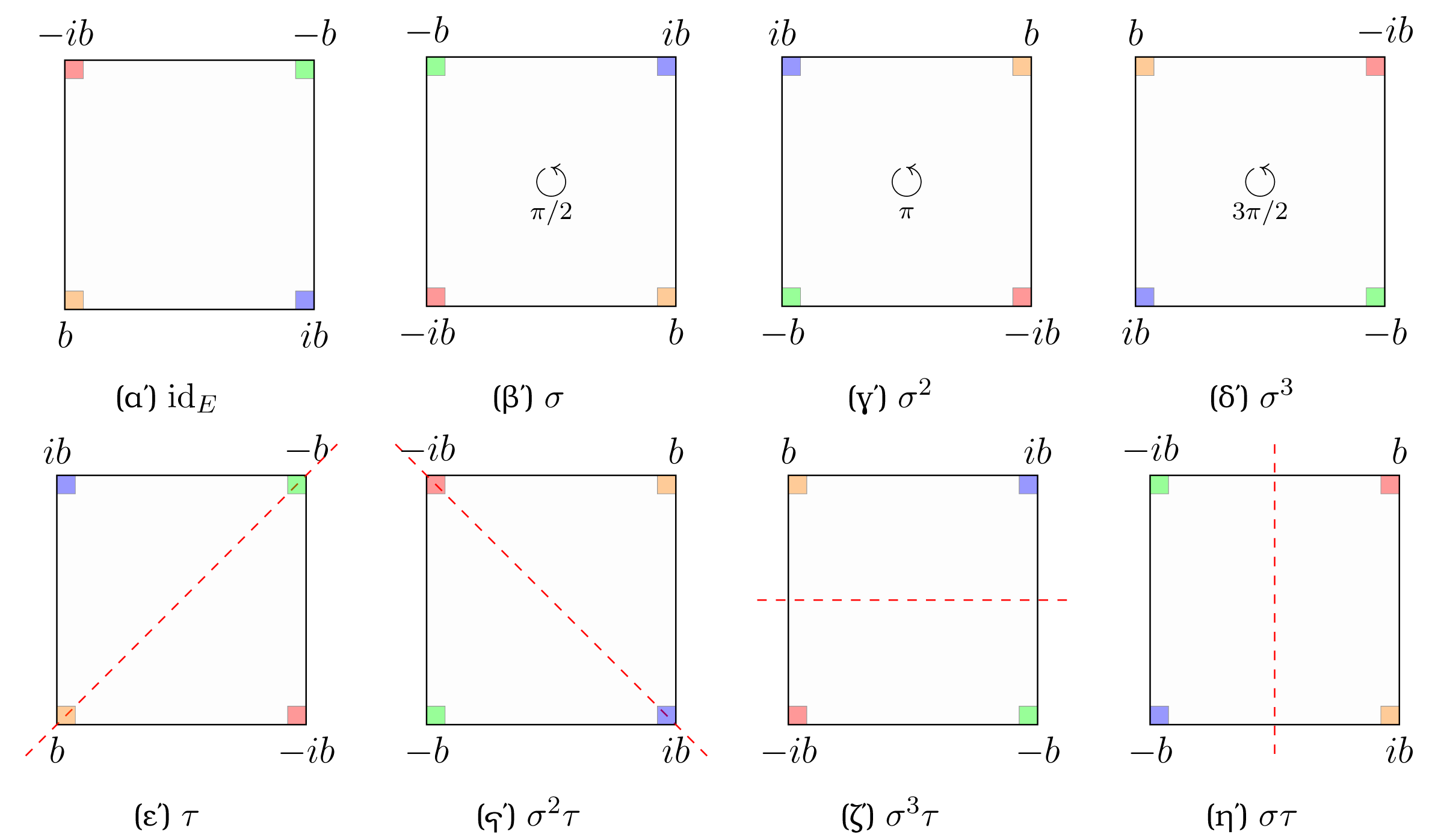
Σχήμα 3.3: Συμμετρίες του τετραγώνου και η ομάδα $\operatorname{Gal}({\mathbb{Q}}(i,b)/{\mathbb{Q}})$

Από τα παραδείγματα που έχουμε δει ως τώρα αλλά και το Θεώρημα 3.1.1 δημιουργούνται εύλογα ερωτήματα:

•

Ποιες ομάδες εμφανίζονται ως ομάδες Galois επεκτάσεων πάνω από σώματα;
•

Αν $E$ είναι το σώμα ανάλυσης του $f(x)$ πάνω από το $K$ , pότε ισχύει ο ισομορφισμός $\operatorname{Gal}(E/K)\cong S_{n}$ ;

Θα απαντήσουμε σε αυτά τα ερωτήματα κατά τη διάρκεια του συγγράμματος. Παραπέμπουμε τον αναγνώστη στην Ενότητα 8.2 για μία τελική απάντηση.

3.2 Τάξη της ομάδας Galois

Έστω $Ε, F$ δύο σώματα και έστω $\sigma:E\rightarrow F$ ισομορφισμός σωμάτων. Σύμφωνα με την άσκηση 1.5.16, ο $\sigma$ επεκτείνεται σε έναν ισομορφισμό $\widehat{\sigma}$ των δακτυλίων πολυωνύμων $E[x]$ και $F[x]$ ως εξής:

\widehat{\sigma}:E[x]\rightarrow F[x],\ \sum a_{i}x^{i}\mapsto\sigma(a_{i})x^{% i}.

Αυτός ο ισομορφισμός θα χρησιμοποιηθεί στο επόμενο θεώρημα. Θυμίζουμε ότι ένα ανάγωγο πολυώνυμο $f(x)$ με συντελεστές από ένα σώμα $F$ είναι διαχωρίσιμο αν και μόνο αν οι ρίζες του $f(x)$ , σε κάποιο σώμα ανάλυσης του $f(x)$ πάνω από το $F$ , είναι απλές ή ισοδύναμα αν και μόνο αν $\operatorname{\textrm{ΜΚΔ}}(f(x),f^{\prime}(x))=1$ .

Θεώρημα 3.2.1.

Έστω $\sigma:F\smash{\mathop{\;\longrightarrow\;}\limits}F^{\prime}$ ισομορφισμός σωμάτων και $E/F$ και $E^{\prime}/F^{\prime}$ επεκτάσεις σωμάτων έτσι ώστε Το $E$ να είναι ένα σώμα ανάλυσης του $f(x)\in F[x]$ πάνω από το $F$ και $E^{\prime}$ να είναι το σώμα ανάλυσης του $\widehat{\sigma}(f(x))$ πάνω από το $F^{\prime}$ . Τότε υπάρχει ${\tilde{\sigma}}:E\smash{\mathop{\;\longrightarrow\;}\limits}Ε^{\prime}$ έτσι ώστε $\tilde{\sigma}{|_{F}}=\sigma$ . Αν το $f(x)$ είναι διαχωρίσιμο, τότε υπάρχουν ακριβώς $[E:F]$ τέτοιες επεκτάσεις.

Απόδειξη.

Σχήμα 3.4: Επέκταση του ισομορφισμού $s$ σε σώματα ανάλυσης.

Η απόδειξη θα γίνει με επαγωγή στον βαθμό $[E:F]$ . Έστω ότι $[E:F]=1$ . Επομένως $E=F$ , δηλ. οι ρίζες του $f(x)$ ανήκουν στο $F$ και Το $f(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο $F[x]$ . Επομένως, το $\tilde{\sigma}(f(x))$ αναλύεται σε γινόμενο γραμμικών παραγόντων στον $F^{\prime}[x]$ , (βλ. άσκηση 1.5.16), και άρα $F=F^{\prime}$ . Έτσι $\sigma={\tilde{\sigma}}$ .

Θα υποθέσουμε τώρα ότι η πρόταση ισχύει όταν ο βαθμός της επέκτασης $[E:F]$ είναι μικρότερος του $n$ . Έστω ότι $[E:F]=n>1$ . Τότε $Ε\neq F$ και μία από τις ρίζες του $f(x)$ , έστω $b$ , δεν ανήκει στο $F$ . Άρα $F(b)\neq F$ και επομένως $[F(b):F]>1$ . Από τη σχέση

[Ε:F]=[E:F(b)][F(b):F],

προκύπτει ότι $[E:F(b)]<n$ . Θεωρούμε στη συνέχεια το πολυώνυμο $g(x)=\operatorname{irr}_{(F,b)}(x)\in F[x]$ . Σημειώνουμε ότι Το $g(x)$ διαιρεί το $f(x)$ (βλ. την παρατήρηση μετά το Θεώρημα 2.2.12) και αντίστοιχα το $\widehat{\sigma}(g(x))$ διαιρεί το $\widehat{\sigma}(f(x))$ . Έστω $b^{\prime}$ τυχαία ρίζα του $\widehat{\sigma}(g(x))$ στο $E^{\prime}$ . Σύμφωνα με το Θεώρημα 2.3.4 υπάρχει ισομορφισμός

\sigma^{\prime}:\ F(b)\rightarrow F^{\prime}(b^{\prime}),\quad\sigma^{\prime}|% _{F}=\sigma.

Σημειώνουμε ότι αφού Το $Ε$ είναι σώμα ανάλυσης του $f(x)$ πάνω από το $F$ και Το $E$ περιέχει το $F(b)$ , έπεται ότι Το $Ε$ είναι σώμα ανάλυσης του $f(x)$ πάνω από το $F(b)$ . Αντίστοιχα, Το $E^{\prime}$ είναι σώμα ανάλυσης του $\widehat{\sigma}(g(x))$ πάνω από το $F^{\prime}(b^{\prime})$ . Από την υπόθεση της επαγωγής έπεται ότι υπάρχει $\tilde{\sigma}:\ E\smash{\mathop{\;\longrightarrow\;}\limits}E^{\prime}$ που επεκτείνει τον $\sigma^{\prime}$ , δηλ. $\tilde{\sigma}|_{F(b)}=\sigma^{\prime}$ . Επομένως

\tilde{\sigma}{|_{F}}=(\tilde{\sigma}|_{F(b)})|_{Ε_{1}}=\sigma^{\prime}|_{Ε_{1% }}=\sigma.

Σχήμα 3.5: Ενδιάμεσο βήμα στην απόδειξη της ύπαρξης $\tilde{\sigma}$ .

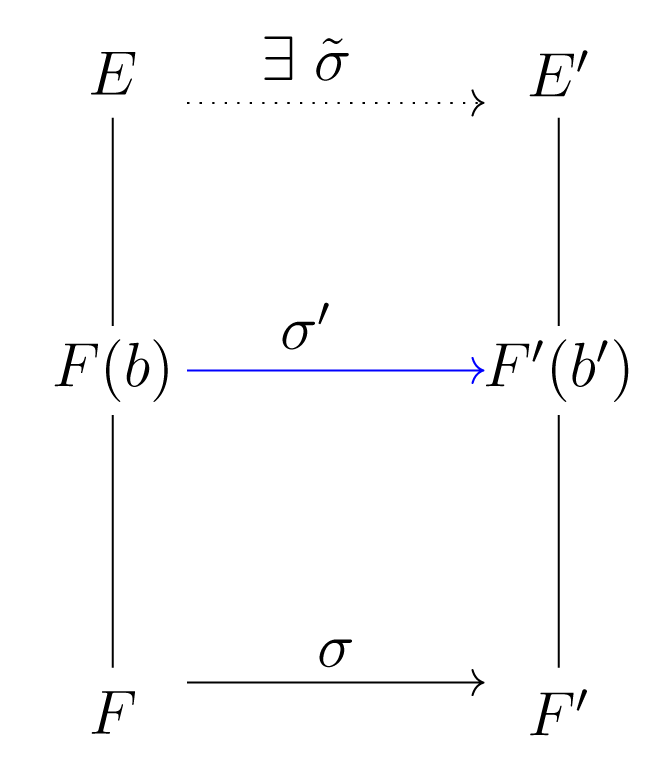
Έστω, τώρα, ότι το $f(x)$ είναι διαχωρίσιμο. Αφού το πολυώνυμο $g(x)=\operatorname{irr}_{(F,b)}(x)$ διαιρεί το $f(x)$ , έπεται ότι οι ρίζες του $g(x)$ στο $Ε$ είναι απλές και ότι το $g(x)$ είναι και αυτό διαχωρίσιμο. Από την υπόθεση της επαγωγής για τον ισομορφισμό $\sigma^{\prime}:\ F(b)\rightarrow F^{\prime}(b^{\prime})$ που προκύπτει για κάθε ρίζα $b^{\prime}$ του $\tilde{\sigma}(g(x))$ , συμπεραίνουμε ότι υπάρχουν $[E:F(b)]$ ισομορφισμοί $\tilde{\sigma}:\ E\rightarrow Ε^{\prime}$ έτσι ώστε $\tilde{\sigma}|_{F(b)}=\sigma^{\prime}$ . Μένει, λοιπόν, να μετρήσουμε τις διαφορετικές ρίζες $b^{\prime}$ του $\widehat{\sigma}(g(x))$ . Σύμφωνα με την άσκηση 1.5.16, το ανάγωγο πολυώνυμο $\widehat{\sigma}(g(x))$ είναι διαχωρίσιμο. Επομένως ο αριθμός των διαφορετικών ριζών του $\widehat{\sigma}(g(x))$ είναι ίσος με τον βαθμό του πολυωνύμου $\widehat{\sigma}(g(x))$ και

\deg(\widehat{\sigma}(g(x)))=\deg(g(x))=[F(b):F].

Άρα συνολικά έχουμε

\left[E:F(b)\right]\;\left[F(b):F\right]

πλήθους επιλογές, δηλ. υπάρχουν $[E:F]$ επεκτάσεις του $\sigma$ . ∎

Ως άμεσο πόρισμα του Θεωρήματος 3.2.1 προκύπτει ότι το σώμα ανάλυσης ενός πολυωνύμου είναι μοναδικό με προσέγγιση ισομορφίας.

Πόρισμα 3.2.2.

Έστω $F$ ένα σώμα, $f(x)\in F[x]$ και $E,E^{\prime}$ δύο σώματα ανάλυσης του $f(x)$ πάνω από το $F$ . Τότε υπάρχει $F$ -ισομορφισμός $\phi:E\smash{\mathop{\;\longrightarrow\;}\limits}E^{\prime}$ και επομένως το σώμα ανάλυσης του $f(x)\in F[x]$ είναι μοναδικό με προσέγγιση $F$ -ισομορφίας.

Απόδειξη.

Αφού $\widehat{\operatorname{id}}_{F}(f(x))=f(x)$ , οι υποθέσεις του Θεωρήματος 3.2.1 ικανοποιούνται, με $F^{\prime}=F$ και $\sigma=\operatorname{id}_{F}$ και υπάρχει επέκταση $\phi:E\smash{\mathop{\;\longrightarrow\;}\limits}E^{\prime}$ έτσι ώστε $\phi|_{F}=\operatorname{id}_{F}$ , δηλ. ο $\phi$ είναι $F$ -ισομορφισμός.

Σχήμα 3.6: Το σώμα ανάλυσης είναι μοναδικό με προσέγγιση ισομορφίας.

∎

Αφού το σώμα ανάλυσης ενός πολυωνύμου είναι μοναδικό με προσέγγιση ισομορφίας μπορούμε να δώσουμε τον παρακάτω ορισμό.

Ορισμός 3.2.3.

Έστω $F$ σώμα και $f(x)\in F[x]$ . Η ομάδα Galois του $f(x)$ είναι η ομάδα $\operatorname{Gal}(E/F)$ , όπου $E$ είναι Το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ .

Η επόμενη πρόταση υπολογίζει την τάξη της ομάδας Galois.

Πόρισμα 3.2.4.

Έστω $f(x)\in F[x]$ διαχωρίσιμο πολυώνυμο και $Ε$ ένα σώμα ανάλυσης του $f(x)$ . Τότε $|\operatorname{Gal}(E/F)|=[E:F]$ .

Απόδειξη.

Eφαρμόζουμε το Θεώρημα 3.2.1 στον ταυτοτικό ισομορφισμό $\operatorname{id}_{F}:\ F\smash{\mathop{\;\longrightarrow\;}\limits}F$ με $E=E^{\prime}$ . ∎

Παραδείγματα 3.2.5.

1.

Έστω $Ε=\mathbb{Q}(\sqrt{2},\sqrt{3},\sqrt{5})$ . Τότε Το $Ε$ είναι σώμα ανάλυσης του διαχωρίσιμου πολυωνύμου $f(x)=(x^{2}-2)(x^{2}-3)(x^{2}-5)$ πάνω από το ${\mathbb{Q}}$ . Αφού $[Ε:\mathbb{Q}]=8$ (βλ. άσκηση 2.4.8) έπεται ότι $|\operatorname{Gal}(E/\mathbb{Q})|=8$ . Τα στοιχεία της $\operatorname{Gal}(E/\mathbb{Q})$ καθορίζονται από τις παρακάτω εικόνες:

$\sqrt{2}\mapsto\pm\sqrt{2},\ \sqrt{3}\mapsto\pm\sqrt{3},\ \sqrt{5}\mapsto\pm% \sqrt{5}.$

Εύκολα ο αναγνώστης μπορεί να διαπιστώσει ότι η ομάδα $\operatorname{Gal}(E/\mathbb{Q})$ είναι αντιμεταθετική και ότι κάθε στοιχείο της έχει τάξη 2, άρα

$\operatorname{Gal}(E/\mathbb{Q})\cong\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times% \mathbb{Z}_{2}.$
2.

Έστω $b=2^{1/3}$ , $\omega=e^{2\pi i/3}$ και $E$ Το σώμα ανάλυσης του $x^{3}-b$ πάνω από το ${\mathbb{Q}}$ . Η $\operatorname{Gal}(E/{\mathbb{Q}})\cong S_{3}$ , βλ. Παράδειγμα 2.3.6. Στη συνέχεια θα υπολογίσουμε την ομάδα $\operatorname{Gal}(E/F)$ όπου $F=\mathbb{Q}(\omega)$ .

Το σώμα $Ε$ είναι σώμα ανάλυσης του διαχωρίσιμου πολυωνύμου $x^{3}-2$ πάνω από το $F$ . Έτσι Το σύνολο $\{1,b,b^{2}\}$ είναι μία $F$ -βάση του $E$ και $[E:F]=3$ . Σύμφωνα με το Πόρισμα 3.2.4, $|\operatorname{Gal}(E/F)|=3$ και επομένως $\operatorname{Gal}(E/F)\cong{\mathbb{Z}}_{3}$ . Αφού τα στοιχεία $\operatorname{id}_{E}$ , $\sigma$ , $\sigma^{2}$ της $\operatorname{Gal}(E/{\mathbb{Q}})$ αφήνουν σταθερά τα στοιχεία του σώματος $F$ (βλ. Παράδειγμα 2.3.6) ο αναγνώστης μπορεί να διαπιστώσει ότι $\operatorname{Gal}(E/F)=\{\operatorname{id}_{E},\sigma,\sigma^{2}\}\cong{% \mathbb{Z}}_{3}$ . Παρατηρούμε ότι $\operatorname{Gal}(E/F)$ είναι υποομάδα της $\operatorname{Gal}(E/{\mathbb{Q}})$ και μάλιστα $\operatorname{Gal}(E/F)\lhd\operatorname{Gal}(E/{\mathbb{Q}})$ , αφού $|\operatorname{Gal}(E/{\mathbb{Q}})|=6$ και $|\operatorname{Gal}(E/F)|=3$ , βλ. Παρατήρηση I.13.

Στο επόμενο παράδειγμα δείχνουμε ότι υπάρχει $f(x)\in{\mathbb{Q}}[x]$ με σώμα ανάλυσης $Ε$ πάνω από το ${\mathbb{Q}}$ έτσι ώστε $\operatorname{Gal}(E/{\mathbb{Q}})\cong S_{5}$ . Για την απόδειξη θα χρειαστούμε δύο θεωρήματα από τη Θεωρία Ομάδων, το Θεώρημα του Cauchy (Θεώρημα I.25) και το Θεώρημα I.35.

Παράδειγμα 3.2.6.

Έστω $f(x)=x^{5}-4x+2$ , $E$ το σώμα ανάλυσης του $f(x)$ πάνω από το $\mathbb{Q}$ και $G=\operatorname{Gal}(E/\mathbb{Q})$ . Το πολυώνυμο $f(x)$ είναι ανάγωγο σύμφωνα με το κριτήριο του Eisenstein, για $p=2$ , και διαχωρίσιμο, αφού το $\mathbb{Q}$ έχει χαρακτηριστική 0. Επομένως το $f(x)$ έχει 5 διαφορετικές ρίζες. Σχεδιάζουμε το γράφημα του $f(x)$ στο πραγματικό επίπεδο με τη βοήθεια των παραγώγων $f^{\prime}(x)=5x^{4}-4$ και $f^{\prime\prime}(x)=20x^{3}$ .

Σχήμα 3.7: Το γράφημα του $x^{5}-4x+2$ .

Παρατηρούμε ότι το $f(x)$ συναντά τον άξονα των $x$ ακριβώς 3 φορές. Άρα Το $f(x)$ έχει τρεις πραγματικές ρίζες, έστω $a_{1},a_{2},a_{3}$ , και δύο μιγαδικές, έστω $a_{4},a_{5}$ . Γνωρίζουμε ότι $a_{4}$ , $a_{5}$ , (Πόρισμα 2.2.5), είναι συζυγείς μιγαδικοί αριθμοί, δηλ. $a_{4}=a+bi$ και $a_{5}=a-bi$ , για $a,b\in{\mathbb{R}}$ .

Έτσι $E=\mathbb{Q}(a_{1},\ldots,a_{5})$ . Αφού $\operatorname{irr}_{(Q,a_{1})}(x)=f(x)$ , συμπεραίνουμε ότι

|G|=[E:\mathbb{Q}]=[E:\mathbb{Q}(a_{1})]\;[\mathbb{Q}(a_{1}):Q]=5\;[E:\mathbb{% Q}(a_{1})]

και σύμφωνα με το Θεώρημα του Cauchy, η $G$ περιέχει ένα στοιχείο που έχει τάξη 5.

Θα δείξουμε τώρα ότι η $G$ περιέχει μία αντιμετάθεση. Πράγματι, έστω

\sigma:\ {\mathbb{C}}\smash{\mathop{\;\longrightarrow\;}\limits}{\mathbb{C}},% \quad c+di\mapsto c-di.

(3.2.6.1)

Ο $\sigma$ είναι ${\mathbb{Q}}$ -αυτομορφισμός του ${\mathbb{C}}$ , δηλ. $\sigma|_{\mathbb{Q}}=\operatorname{id}_{\mathbb{Q}}$ . Θα δείξουμε ότι $\sigma|_{E}$ ανήκει στην $\operatorname{Gal}(E/{\mathbb{Q}})$ , δηλ. ότι $\sigma|_{E}$ είναι αυτομορφισμός του $E$ . Πρέπει, λοιπόν, να δείξουμε ότι $\sigma|_{E}(Ε)\subset E$ . Όμως, $E=\mathbb{Q}(a_{1},\ldots,a_{5})$ και $\sigma(a_{i})=a_{i}$ , για $ι=1,2,3$ , ενώ $\sigma(a_{4})=a_{5}$ . Άρα $\sigma|_{E}\in\operatorname{Gal}(E/{\mathbb{Q}})$ και μάλιστα $\sigma|_{E}$ ως αντιμετάθεση δύο ριζών του $f(x)$ έχει τάξη 2.

Αφού, λοιπόν, η ομάδα $G$ περιέχει ένα στοιχείο που έχει τάξη 5 και μία αντιμετάθεση, σύμφωνα με το Θεώρημα I.35, έπεται ότι η ομάδα $G$ είναι ισόμορφη με την $S_{5}$ .

Έστω $E_{1}=\mathbb{Q}(a_{1},a_{2},a_{3})$ . Σύμφωνα με την άσκηση 2.4.13, το πολυώνυμο $\operatorname{irr}_{(E_{1},a_{4})}(x)$ έχει βαθμό δύο, όσος είναι ο βαθμός του $\operatorname{irr}_{({\mathbb{R}},a_{4})}(x)$ . Επομένως $\operatorname{irr}_{(E_{1},a_{4})}(x)=\operatorname{irr}_{({\mathbb{R}},a_{4})% }(x)$ (βλ. άσκηση 2.4.12). Άρα $|\operatorname{Gal}(E/E_{1})|=2$ και σύμφωνα με το Παράδειγμα 2.2.2.5

\operatorname{irr}_{(Ε_{1},a_{4})}(x)=x^{2}-2ax+(a^{2}+b^{2})\in E_{1}[x].

επομένως $a,b^{2}\in E_{1}$ και

E=E_{1}(a_{4})=E_{1}(a+bi)=E_{1}(bi).

Σημειώνουμε ότι αφού οι δύο ρίζες του $x^{2}+b\in E_{1}[x]$ είναι οι $\pm bi$ , σύμφωνα με το Θεώρημα 2.3.3, υπάρχει $\tau\in\operatorname{Gal}(E/E_{1})$ , έτσι ώστε $\tau(bi)=-bi$ . Είναι εύκολο να δει κανείς ότι $\tau=\sigma|_{E}$ , όπου $\sigma$ είναι ο αυτομορφισμός της εξίσωσης (3.2.6.1).

3.3 Ενδιάμεσα σώματα και υποομάδες της ομάδας Galois

Στην ενότητα αυτή θα εξετάσουμε λεπτομερέστερα τη σχέση ανάμεσα στα ενδιάμεσα σώματα της επέκτασης $E/F$ και στις υποοομάδες της $G=\operatorname{Gal}(E/F)$ . Είναι εύκολο να δούμε ότι σε κάθε ενδιάμεσο σώμα της $E/F$ αντιστοιχεί μία υποομάδα της $G$ .

Πρόταση 3.3.1.

Έστω $Β$ ενδιάμεσο σώμα της επέκτασης $E/F$ . Τότε $\operatorname{Gal}(E/B)$ είναι υποομάδα της $\operatorname{Gal}(E/F)$ .

Απόδειξη.

Αν $\sigma\in\operatorname{Gal}(E/B)$ , τότε $\sigma(b)=b$ , για κάθε $b\in B$ , και άρα $\sigma(c)=c$ , για κάθε $c\in F$ . Επομένως $\sigma\in\operatorname{Gal}(E/F)$ . ∎

Το επόμενο θεώρημα εξετάζει πότε η υποομάδα $\operatorname{Gal}(E/B)$ της $G$ είναι κανονική.

Θεώρημα 3.3.2.

Έστω $f(x)\in F[x]$ και $Ε$ το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ . Αν το $Β$ είναι ενδιάμεσο σώμα της επέκτασης $E/F$ και είναι σώμα ανάλυσης του $g(x)\in F[x]$ πάνω από το $F$ , τότε $\operatorname{Gal}(E/B)$ είναι κανονική υποομάδα της $\operatorname{Gal}(E/F)$ και

\operatorname{Gal}(E/F)/\operatorname{Gal}(E/B)\cong\operatorname{Gal}(B/F).

Απόδειξη.

Αφού Το $B$ είναι το σώμα ανάλυσης του $g(x)$ πάνω από το $F$ , έπεται ότι $B=F(b_{1},\ldots,b_{n})$ , όπου $b_{i}$ είναι οι ρίζες του $g(x)$ , για $i=1,\ldots,n$ . Έστω $\sigma\in\operatorname{Gal}(E/F)$ . Θα αποδείξουμε ότι

\phi:\ \operatorname{Gal}(E/F)\smash{\mathop{\;\longrightarrow\;}\limits}% \operatorname{Gal}(B/F),\quad\sigma\mapsto\sigma|_{B}

είναι συνάρτηση, δηλ. ότι $\sigma|_{B}:\ B\smash{\mathop{\;\longrightarrow\;}\limits}B\in\operatorname{% Gal}(B/F)$ . Αφού o $\sigma$ είναι ομομορφισμός δακτυλίων, αρκεί νa δείξουμε ότι $\sigma(B)\subset B$ . Όμως, τα στοιχεία του $B$ είναι πολυωνυμικοί συνδυασμοί των $b_{1},\ldots,b_{n}$ . Έτσι, αρκεί να δείξουμε ότι $\sigma(b_{i})\in B$ , για $1\leq i,j\leq n$ . Αυτό, όμως, προκύπτει εύκολα, αφού $\sigma(b_{i})=b_{j}$ , για $1\leq i,j\leq n$ , σύμφωνα με τη Πρόταση 2.3.2. Είναι εύκολο να δει κανείς ότι η συνάρτηση $\phi$ είναι ομομορφισμός ομάδων:

\phi(\sigma_{1}\sigma_{2})=(\sigma_{1}\sigma_{2})|_{B}=(\sigma_{1}|_{B})(% \sigma_{2}|_{B})=\phi(\sigma_{1})\phi(s_{2}).

Σύμφωνα με το Πρώτο Θεώρημα Ισομορφίας Ομάδων έπεται ότι $\ker\phi$ είναι κανονική υποομάδα της $\operatorname{Gal}(E/F)$ και ότι

\operatorname{Gal}(E/F)/\ker\phi\cong{\rm Im}\phi.

Στη συνέχεια θα δείξουμε ότι $\ker\phi=\operatorname{Gal}(E/B)$ . Πράγματι,

\ker\phi=\{\sigma\in\operatorname{Gal}(E/F):\ \phi(\sigma)=\operatorname{id}_{% B}\}=\{\sigma\in\operatorname{Gal}(E/F):\ \sigma|_{B}=\operatorname{id}_{B}\}=% \operatorname{Gal}(E/B).

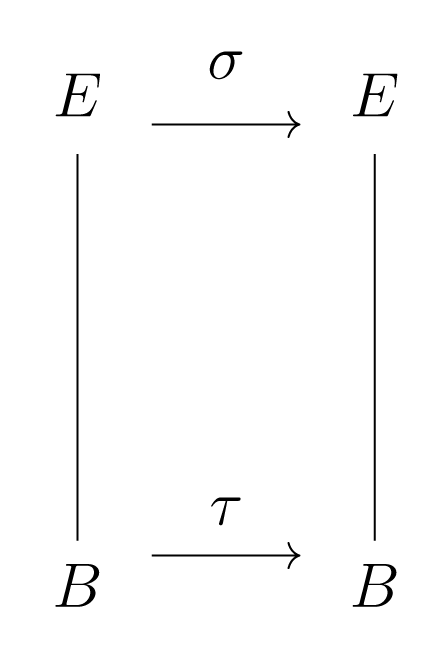
Τέλος, θα δείξουμε ότι Το $\phi$ είναι επιμορφισμός. Έστω ότι $\tau\in\operatorname{Gal}(B/F)$ . Αφού το $E$ είναι σώμα ανάλυσης του $f(x)$ πάνω από το $F$ , έπεται ότι το $E$ είναι σώμα ανάλυσης του $f(x)$ πάνω από το $Β$ . Eφαρμόζουμε το Θεώρημα 3.2.1 για τον ισομορφισμό $\tau:B\rightarrow B$ . Επομένως, υπάρχει $\sigma:\ B\smash{\mathop{\;\longrightarrow\;}\limits}B$ έτσι ώστε $\sigma|_{B}=\tau$ .

Σχήμα 3.8: $\sigma\in\operatorname{Gal}(E/F)$ , τέτοιο ώστε $\sigma|_{B}=\tau$ .

Αφού $\tau\in\operatorname{Gal}(B/F)$ , έπεται ότι $\tau(c)=c$ , για κάθε $c\in F$ . Επομένως, για $c\in F$ , έχουμε ότι $\sigma(c)=\sigma|_{B}(c)=\tau(c)=c$ και $\sigma\in\operatorname{Gal}(E/F)$ . ∎

Σημειώνουμε ότι στο παραπάνω θεώρημα, η υπόθεση ότι Το $Ε$ είναι το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ , χρησιμοποιήθηκε μόνο για να μπορέσουμε να εφαρμόσουμε ο Θεώρημα 3.2.1 και να δείξουμε ότι o $\phi$ είναι επιμορφισμός.

Παράδειγμα 3.3.3.

Έστω $G=\operatorname{Gal}({\mathbb{Q}}(\omega,b)/\mathbb{Q})$ , όπου $b=2^{1/3}$ , $\omega=e^{2\pi i/3}$ , και έστω $F=\mathbb{Q}(\omega)$ , όπως στο Παράδειγμα 3.2.5. Αφού Το $F$ είναι σώμα ανάλυσης του $x^{3}-1\in{\mathbb{Q}}[x]$ ,

G/\operatorname{Gal}(E/F)\;\cong\;\operatorname{Gal}(\mathbb{Q}(\omega)/% \mathbb{Q})\;\cong\;\mathbb{Z}_{2}.

Έστω $Ε/F$ μία επέκταση σωμάτων. Αν $Η<\operatorname{Gal}(E/F)$ , το σώμα των σταθερών στοιχείων της $H$ (field of constants of $H$ in $E$ ) συμβολίζεται ως ${E^{H}}$ και είναι το σύνολο

E^{H}=\{a\in E:\ \sigma(a)=a,\ \forall\sigma\in H\}.

σώμα των σταθερών στοιχείων ${E^{H}}$ field of constants Ο αναγνώστης καλείται να διαπιστώσει ότι Το $E^{H}$ είναι πράγματι σώμα και να αποδείξει τη παρακάτω σημαντική πρόταση, (βλ. άσκηση 3.7.1).

Πρόταση 3.3.4.

Έστω $Ε/F$ επέκταση σωμάτων και $H_{1},H_{2}<\operatorname{Gal}(E/F)$ . Αν $H_{1}<H_{2}$ , τότε $Ε^{Η_{2}}\subset E^{H_{1}}$ .

Στα επόμενα παραδείγματα θα υπολογίσουμε κάποια ενδιάμεσα σώματα.

Παραδείγματα 3.3.5.

1.

Έστω $Ε=\mathbb{Q}(i)$ και $G=\operatorname{Gal}(E/\mathbb{Q})$ . Τότε $G=\{id_{E},\sigma_{1}\}$ , όπου $\sigma_{1}(a+bi)=a-bi$ . Αν $a+bi\in E^{G}$ τότε $b=0$ . Επομένως $Ε^{G}\cong\mathbb{Q}$ .
2.

Έστω $Ε=\mathbb{Q}(2^{1/3})$ , $G=\operatorname{Gal}(E/\mathbb{Q})$ . Τότε $G=\{id_{E}\}$ (βλ. Παράδειγμα 2.3.5.6). Επομένως $Ε^{G}\cong E$ .
3.

Έστω $Ε=\mathbb{Q}(\omega,b)$ , όπου $\omega=e^{2\pi i/3}$ , $b=2^{1/3}$ και έστω $G=\operatorname{Gal}(E/\mathbb{Q})$ . Στο Παράδειγμα 2.3.6 υπολογίσαμε τα στοιχεία της $G$ . Έστω $\sigma\in G$ ο αυτομορφισμός του $Ε$ , ο οποίος καθορίζεται από τις εικόνες $\sigma(b)=\omega b$ και $\sigma(\omega)=\omega$ και $Η=\langle\sigma\rangle<G$ . Θα δείξουμε ότι $Ε^{H}=\mathbb{Q}(\omega)$ . Πράγματι, είναι φανερό ότι $\mathbb{Q}(\omega)\subseteq Ε^{H}\subset E$ . Αφού $[E:\mathbb{Q}(\omega)]=3$ , δεν υπάρχει ενδιάμεσο σώμα $Β$ έτσι ώστε $\mathbb{Q}(\omega)\subsetneq Β\subsetneq E$ (βλ. Πόρισμα 2.2.16) και άρα $Ε^{H}=\mathbb{Q}(\omega)$ . Θα επιβεβαιώσουμε αυτό το συμπέρασμα με αναλυτικούς υπολογισμούς. Για να το δείξουμε αυτό, θα χρησιμοποιήσουμε το ανάγωγο πολυώνυμο του $\omega$ πάνω από το ${\mathbb{Q}}$ . Παρατηρούμε, λοιπόν, ότι $\omega^{2}=-1-\omega$ , αφού $\operatorname{irr}_{{\mathbb{Q}},\omega}=x^{2}+x+1$ . Στη συνέχεια, θεωρούμε τη $\mathbb{Q}$ -βάση $\{1,\omega,b,b\omega,b^{2},b^{2}\omega\}$ του $Ε$ και υπολογίζουμε τις εικόνες των στοιχείων της, όπως φαίνεται στον παρακάτω πίνακα:

$\begin{array}[]{rl }\sigma(1)=&1\\ \sigma(\omega)=&\omega\\ \sigma(b)=&b\omega\\ \sigma(b\omega)=&b\omega^{2}=-b-b\omega\\ \sigma(b^{2})=&b^{2}\omega^{2}=-b^{2}-b^{2}\omega\\ \sigma(b^{2}\omega)=&b^{2}\omega^{3}=b^{2}\end{array}$

Έστω

$a=a_{0}+a_{1}\omega+a_{2}b+a_{3}b\omega+a_{4}b^{2}+a_{5}b^{2}\omega\in E,\ a_{% i}\in\mathbb{Q}\ .$

Tότε

$\sigma(a)=a_{0}+a_{1}\omega-a_{3}b+(a_{2}-a_{3})b\omega+(a_{5}-a_{4})b^{2}-a_{% 4}b^{2}.$

Επομένως, Το $a\in E^{H}$ , δηλ. $a=\sigma(a)$ αν και μόνο αν $a_{2}=-a_{3}$ , $a_{3}=a_{2}-a_{3}$ , $a_{5}=a_{5}-a_{4}$ και $a_{5}=-a_{4}$ . Λύνοντας αυτές τις εξισώσεις για $a_{2},\ldots,a_{5}$ , προκύπτει ότι η μόνη λύση είναι η μηδενική. Άρα

$Ε^{H}=\{a_{0}+a_{1}\omega:\ a_{i}\in\mathbb{Q}\}=\mathbb{Q}(\omega).$

Έστω $Ε/F$ μία επέκταση σωμάτων. Στην επόμενη ενότητα θα δούμε ότι $Ε^{\operatorname{Gal}(E/F)}=F$ αν και μόνο αν to $E$ είναι σώμα ανάλυσης ενός διαχωρίσιμου πολυωνύμου $f(x)\in F[x]$ .

3.4 Ιδιότητες της ομάδας Galois

Στο εδάφιο αυτό θα ορίσουμε τις επεκτάσεις Galois, θα εξετάσουμε βασικές ιδιότητές τους και θα αποδείξουμε ικανές και αναγκαίες συνθήκες για να είναι μία επέκταση σωμάτων επέκταση Galois. Έτσι θα ετοιμάσουμε το έδαφος για την απόδειξη του Θεμελιώδους Θεωρήματος της Θεωρίας Galois που είναι το αντικείμενο του επόμενου εδαφίου.

Ορισμός 3.4.1.

H επέκταση $E/F$ λέγεται επέκταση του Galois (Galois extension) αν το $Ε$ είναι σώμα ανάλυσης ενός διαχωρίσιμου πολυωνύμου $f(x)\in F[x]$ .

Είναι φανερό ότι αν $E/F$ είναι μία επέκταση του Galois και $Β$ είναι ενδιάμεσο σώμα τότε $E/B$ είναι επέκταση του Galois. Η πράξη της ομάδας Galois είναι βέβαια η σύνθεση των $F$ -αυτομορφισμών. Αν θεωρήσουμε γραμμικούς συνδυασμούς των $F$ -αυτομορφισμών με συντελεστές από το $E$ , το αποτέλεσμα δεν είναι πια κατανάγκην $F$ -αυτομορφισμός. Παρόλα αυτά, δεν είναι δύσκολο να δει κανείς ότι ένας τέτοιος γραμμικός συνδυασμός, δίνει έναν ομομορφισμό της προσθετικής ομάδας του $E$ . Αναλυτικά, αν $\sigma_{1},\ldots,\sigma_{n}\in\operatorname{Gal}(E/F)$ και $y_{1},\ldots,y_{n}\in E$ , τότε $\sum y_{i}\sigma_{i}$ ορίζεται ως εξής:

\sum y_{i}\sigma_{i}:\ Ε\smash{\mathop{\;\longrightarrow\;}\limits}E,\quad b% \mapsto\sum y_{i}\sigma_{i}(b).

Είναι φανερό ότι Το $\sum y_{i}\sigma_{i}$ , για κατάλληλα $y_{i}$ , έχει μη μηδενικό πυρήνα. Για ένα απλό παράδειγμα, ας θεωρήσουμε τους ${\mathbb{Q}}$ -αυτομορφισμούς $\sigma$ και $\sigma^{2}$ του Παραδείγματος 2.3.6. Τότε $(\sigma-\sigma^{2})\;(\omega)=\sigma(\omega)-\sigma^{2}(\omega)=0$ και είναι φανερό ότι $\sigma-\sigma^{2}$ δεν είναι η μηδενική συνάρτηση στο $Ε$ , αφού $(\sigma-\sigma^{2})\;(b)=(w-w^{2})b\neq 0$ . Είναι γενικά δυνατόν να βρούμε κάποιον (μη μηδενικό) γραμμικό συνδυασμό $\sum y_{i}\sigma_{i}$ των στοιχείων της $G$ που να είναι η μηδενική συνάρτηση στο $Ε$ ; Σε αυτό το ερώτημα απαντά η επόμενη πρόταση.

Λήμμα 3.4.2.

Έστω $E/F$ πεπερασμένη επέκταση, $\{\sigma_{1},\ldots,\sigma_{n}\}$ διακεκριμένα στοιχεία της $\operatorname{Gal}(E/F)$ και $y_{1},\ldots,y_{n}\in E$ . An $y_{1}\sigma_{1}+\cdots+y_{n}\sigma_{n}:\ E\smash{\mathop{\;\longrightarrow\;}% \limits}E$ είναι η μηδενική συνάρτηση, δηλ. an

\sum_{i=1}^{n}y_{i}\sigma_{i}(b)=0,\quad\forall\;b\in E,

τότε $y_{i}=0,\textrm{ για }i=1,\ldots,n$ .

Απόδειξη.

Έστω ότι υπάρχουν $y_{1},\ldots,y_{n}\in E$ όχι όλα μηδέν έτσι ώστε

y_{1}\sigma_{1}(b)+\cdots+y_{n}\sigma_{n}(b)=0,\quad\forall\;b\in E.

(3.4.2.1)

Χωρίς περιορισμό της γενικότητας μπορούμε να υποθέσουμε ότι $y_{n}\neq 0$ . Αφού $\sigma_{n}\neq\sigma_{1}$ , υπάρχει $c\in E$ έτσι ώστε $\sigma_{n}(c)\neq\sigma_{1}(c)$ . Είναι φανερό ότι $c\in E\setminus E^{G}$ και ότι, αφού $c\neq 0$ , $\sigma_{1}(c)\sigma_{n}(c)\neq 0$ .

Αντικαθιστούμε στη σχέση (3.4.2.1) το στοιχείο $b c$ στη θέση του $b$ . Έστω ότι $\sigma_{i}(c)=c_{i}$ . Επομένως,

y_{1}c_{1}\sigma_{1}(b)+\cdots+y_{n}c_{n}\sigma_{n}(b)=0.

(3.4.2.2)

Πολλαπλασιάζοντας τη σχέση (3.4.2.1) με $c_{1}$ και αφαιρώντας από τη σχέση (3.4.2.2) βρίσκουμε ότι

y_{2}{(c_{2}-c_{1})}\sigma_{2}(b)+\cdots+y_{n}(c_{n}-c_{1})\sigma_{n}(b)=0.

(3.4.2.3)

Παρατηρούμε ότι ο συντελεστής του $\sigma_{n}(b)$ στη σχέση (3.4.2.3) είναι και πάλι διάφορος του μηδενός. Άρα υπάρχει $(z_{2},\ldots,z_{n})$ , όπου $z_{n}\neq 0$ , έτσι ώστε

\forall\ b\in E:\ z_{2}\sigma_{2}(b)+\cdots+z_{n}\sigma_{n}(b)=0.

Επαναλαμβάνουμε αυτή τη διαδικασία άλλες $n-2$ φορές. Καταλήγουμε στο συμπέρασμα ότι υπάρχει μη μηδενικό $t\in E$ έτσι ώστε $t\sigma_{n}(b)=0$ , $\forall\;b\in E$ . Άρα $\forall\ b\in E$ , $\sigma_{n}(b)=0$ . Αυτό, όμως, είναι αδύνατοn, αφού $\sigma_{n}$ είναι αυτομορφισμός του $E$ . Καταλήξαμε σε άτοπο, γιατί υποθέσαμε ότι υπάρχουν $y_{1},\ldots,y_{n}\in E$ , όχι όλα μηδέν, έτσι ώστε $y_{1}\sigma_{1}+\cdots+y_{n}\sigma_{n}$ να είναι η μηδενική συνάρτηση στο $E$ . Άρα αυτό είναι αδύνατον. ∎

Εξαιτίας της ιδιότητας του Λήμματος 3.4.2 λέμε ότι τα στοιχεία της $\operatorname{Gal}(E/F)$ είναι γραμμικά ανεξάρτητα (linearly indenpendent) πάνω από το σώμα $E$ . Μία σημαντική συνέπεια είναι το παρακάτω Θεώρημα, γνωστό ως το Λήμμα του Artin.

Θεώρημα 3.4.3 (Artin).

Έστω $Ε/F$ πεπερασμένη επέκταση. Τότε $[E:E^{G}]\geq n$ , όπου $n$ είναι η τάξη της ομάδας $\operatorname{Gal}(E/F)$ .

Απόδειξη.

Έστω ότι $[E:E^{G}]=m<n$ και ότι $\{a_{1},\ldots,a_{μ}\}$ είναι μία $E^{G}$ -βάση του $Ε$ . Κάθε στοιχείο $b\in E$ γράφεται ως $E^{G}$ -γραμμικός συνδυασμός:

b=c_{1}a_{1}+\cdots+c_{m}a_{m}=\sum c_{i}a_{i},\ c_{i}\in E^{G}.

Αν $\sigma\in G$ , τότε $\sigma(c_{i})=c_{i}$ , για $i=1,\ldots,m$ , και άρα $\sigma\in G$ είναι μία $E^{G}$ -γραμμική συνάρτηση:

\sigma(b)=\sigma(\sum c_{i}a_{i})=\sum c_{1}\sigma(a_{i}).

Θεωρούμε το ομογενές σύστημα με $m$ εξισώσεις και $n$ αγνώστους στο $Ε$ :

\begin{array}[]{cc}\sigma_{1}(a_{1})x_{1}+\cdots+\sigma_{n}(a_{1})x_{n}&=0\cr% \vdots\cr\sigma_{1}(a_{m})x_{1}+\cdots+\sigma_{n}(a_{m})x_{n}&=0.\end{array}

Αφού $m<n$ , το σύστημα έχει μία μη μηδενική λύση στο $E$ , έστω $(y_{1},\ldots,y_{n})\neq 0$ μία τέτοια λύση. Δηλαδή, για $i=1,\ldots,m$ , ισχύει ότι

y_{1}\sigma_{1}(a_{i})+\cdots+y_{n}\sigma_{n}(a_{i})=0.

(3.4.3.1)

Αφού η σχέση (3.4.3.1) ισχύει για κάθε στοιχείο της $E^{G}$ -βάσης του $E$ , είναι εύκολο να δείξουμε ότι ισχύει για κάθε $b\in E$ . Πράγματι, έστω ότι $b=\sum c_{i}\,a_{i}$ με $c_{i}\in E^{G}$ , για $i=1,\ldots,m$ . Θα δείξουμε ότι

y_{1}\sigma_{1}(b)+\cdots+y_{n}\sigma_{n}(b)=0.

(3.4.3.2)

Παρατηρούμε ότι αν $c\in E^{G}$ , τότε

c\,\sigma_{j}(a_{i})=\sigma_{j}(c)\sigma_{i}(a_{i})=\sigma_{j}(c\,a_{i}),\quad 1% \leq j\leq n.

Πολλαπλασιάζοντας την εξίσωση (3.4.3.1) με $c_{t}$ , για $t=1,\ldots,m$ , προκύπτοuν οι παρακάτω $m$ ισότητες:

\begin{array}[]{cc}y_{1}\sigma_{1}(c_{1}a_{i})+\cdots+y_{n}\sigma_{n}(c_{1}a_{% i})&=0\\ \vdots\\ y_{1}\sigma_{1}(c_{m}a_{i})+\cdots+y_{n}\sigma_{n}(c_{m}a_{i})&=0.\end{array}

Προσθέτοντας τις παραπάνω σχέσεις, έπεται ότι

y_{1}\sigma_{1}(c_{1}a_{1}+\cdots+c_{m}a_{m})+\cdots+y_{n}\sigma_{n}(c_{1}a_{1% }+\cdots+c_{m}a_{m})=0,

δηλ. η σχέση (3.4.3.2). Από το Λήμμα 3.4.2, αυτό είναι άτοπο. Καταλήξαμε σε άτοπο γιατί υποθέσαμε ότι $m<n$ . Άρα $m\geq n$ . ∎

Θα αποδείξουμε, τώρα, ότι το σταθερό σώμα της ομάδας $\operatorname{Gal}(E/F)$ είναι το $F$ .

Θεώρημα 3.4.4.

Έστω $Ε/F$ επέκταση του Galois. Τότε $E^{\operatorname{Gal}(E/F)}=F$ .

Απόδειξη.

Σύμφωνα με το Πόρισμα 3.2.4, $|\operatorname{Gal}(E/F)|=[E:F]$ . Έστω $G=\operatorname{Gal}(E/F)$ και $n=|\operatorname{Gal}(E/F)|$ . Αφού

[Ε:F]=[E:E^{G}]\;[E^{G}:F],

Για να δείξουμε ότι $E^{G}=F$ , αρκεί να δείξουμε ότι $[E^{G}:F]=1$ ή ισοδύναμα ότι $[E:E^{G}]=n$ . Σύμφωνα με το Θεώρημα 3.4.3 $m\geq n$ . επομένως $[E:E^{G}]=n$ και $Ε^{G}=F$ . ∎

Σημειώνουμε μία εξαιρετικά σημαντική ιδιότητα εκείνων των πεπερασμένων επεκτάσεων $E/F$ , για τις οποίες $E^{\operatorname{Gal}(E/F)}=F$ .

Θεώρημα 3.4.5.

Έστω $E/F$ μία πεπερασμένη επέκταση έτσι ώστε $E^{\operatorname{Gal}(E/F)}=F$ . Κάθε ανάγωγο πολυώνυμο $p(x)\in F[x]$ που έχει μία ρίζα στο $Ε$ είναι διαχωρίσιμο και έχει όλες τις ρίζες του στο $Ε$ .

Απόδειξη.

Έστω $G=\operatorname{Gal}(E/F)$ και έστω $b\in Ε$ ρίζα του ανάγωγου πολυωνύμου $p(x)\in F[x]$ . Θα δείξουμε ότι το $p(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο $E[x]$ και ότι οι ρίζες του $p(x)$ είναι απλές. Έστω ότι το σύνολο $X=\{\sigma(b):\;\sigma\in G\}$ των συζυγών του $b$ είναι $X=\{b_{1},\ldots,b_{n}\}$ , δηλ. $b_{1},\ldots,b_{n}$ είναι οι διακεκριμένες εικόνες του $b$ μέσω των στοιχείων της $G$ . Σύμφωνα με τη Πρόταση 2.3.2 τα στοιχεία του $X$ είναι ρίζες του $p(x)$ . Θεωρούμε το πολυώνυμο

\displaystyle g(x)=(x-b_{1})\cdots(x-b_{n})=x^{n}-(b_{1}+\cdots+b_{n})x^{n-1}+% \\ \displaystyle(b_{1}b_{2}+\cdots+b_{n-1}b_{n})x^{n-2}+\cdots+(-1)^{n}b_{1}% \cdots b_{n}=\sum c_{j}x^{j}\in E[x]

Θα δείξουμε ότι $g(x)=p(x)$ . Πράγματι, για $j=0,\ldots,n-1$ , οι συντελεστές $c_{j}$ του $x^{j}$ είναι εκφράσεις συμμετρικές ως προς τα $b_{1},\ldots,b_{n}$ . Επομένως, αν $\sigma\in G$ , τότε $\sigma(c_{j})=c_{j}$ . Άρα $c_{j}\in E^{G}$ . Αφού $E^{G}=F$ , έπεται ότι $g(x)\in F[x]$ . Αφού όλες οι ρίζες του $g(x)$ είναι διακεκριμένες και είναι ρίζες του $p(x)$ έπεται ότι το $g(x)$ διαιρεί το $p(x)$ στον δακτύλιο $F[x]$ , βλ. άσκηση 1.5.17. Επομένως $g(x)=p(x)$ , δηλ. το $p(x)$ είναι διαχωρίσιμο και αναλύεται σε γινόμενο γραμμικών παραγόντων στο $Ε[x]$ . ∎

Θα δείξουμε, τώρα, ότι ισχύει το αντίστροφο του Θεωρήματος 3.4.4.

Θεώρημα 3.4.6.

Έστω $E/F$ μία πεπερασμένη επέκταση σωμάτων και $G=\operatorname{Gal}(E/F)$ . An Κάθε ανάγωγο πολυώνυμο $p(x)\in F[x]$ που έχει μία ρίζα στο $Ε$ είναι διαχωρίσιμο και έχει όλες τις ρίζες του στο $Ε$ , τότε η επέκταση $E/F$ είναι επέκταση του Galois.

Απόδειξη.

Υποθέτουμε ότι $[E:F]>1$ και επιλέγουμε ένα στοιχείο $a_{1}\in E\setminus F$ . Το $a_{1}$ είναι αλγεβρικό πάνω από το $F$ , αφού η επέκταση $E/F$ είναι πεπερασμένη. Έστω $p_{1}(x)=\operatorname{irr}_{(F,a_{1})}(x)$ . Από την υπόθεση, το $p_{1}(x)$ είναι διαχωρίσιμο και έχει όλες τις ρίζες του στο $E$ . Επισυνάπτουμε στο $F$ τις ρίζες του $p_{1}(x)$ και θεωρούμε $E_{1}$ το σώμα ανάλυσης του $p_{1}(x)$ . Αν $E_{1}=E$ , τότε $E/F$ είναι επέκταση του Galois. Διαφορετικά, υπάρχει $a_{2}\in E\setminus E_{1}$ . Έστω $p_{2}(x)=\operatorname{irr}_{(F,a_{2})}(x)$ . Επισυνάπτοντας στο $E_{1}$ τις ρίζες του $p_{2}(x)$ παίρνουμε το $E_{2}$ , που είναι σώμα ανάλυσης του $p_{1}(x)p_{2}(x)\in F[x]$ . Συνεχίζουμε με αυτόν τον τρόπο μέχρις ότου βρούμε ένα σώμα $E_{m}=E$ . Αυτό θα συμβεί μετά από πεπερασμένου πλήθους βήματα γιατί η επέκταση $E/F$ είναι πεπερασμένη. ∎

Στο παρακάτω θεώρημα συγκεντρώνουμε τις ικανές και αναγκαίες συνθήκες ώστε μία επέκταση σωμάτων $Ε/F$ να είναι επέκταση του Galois αξιοποιώντας τα προηγούμενα συμπεράσματα αυτού του εδαφίου.

Θεώρημα 3.4.7.

Έστω $E/F$ μία πεπερασμένη επέκταση σωμάτων και $G=\operatorname{Gal}(E/F)$ . Οι επόμενες συνθήκες είναι ισοδύναμες:

i.

Η επέκταση $E/F$ είναι επέκταση του Galois.
ii.

$F=E^{G}=\{a\in E:\sigma(a)=a,\forall\ \sigma\in G\}$ .
iii.

Κάθε ανάγωγο πολυώνυμο $p(x)\in F[x]$ που έχει μία ρίζα στο $Ε$ είναι διαχωρίσιμο και έχει όλες τις ρίζες του στο $Ε$ .

Απόδειξη.

H συνεπαγωγή (i $\Rightarrow$ ii) είναι το Θεώρημα 3.4.4. H συνεπαγωγή (ii $\Rightarrow$ iii) είναι το Θεώρημα 3.4.5. Τέλος, η συνεπαγωγή (iiι $\Rightarrow$ i) είναι το Θεώρημα 3.4.6. ∎

Πριν ολοκληρώσουμε τα προκαταρτικά της απόδειξης του Θεμελιώδους Θεωρήματος της Θεωρίας Galois ας μελετήσουμε λίγο προσεκτικότερα την απόδειξη του Θεωρήματος 3.4.3. Πού ακριβώς χρησιμοποιήσαμε ότι το σύνολο $G = G a l (E / F)$ έχει την αλγεβρική δομή ομάδας; Παρατηρούμε, λοιπόν, ότι η δομή της ομάδας δεν έπαιξε κανέναν ρόλο στην απόδειξη. Παρόλα αυτά, η εκφώνηση του θεωρήματος αναφερόταν στην $G$ και στο σταθερό σώμα $Ε^{G}$ . Είναι, όμως, αναγκαίο να περιοριστούμε σε σταθερά σώματα υποομάδων της ομάδας Galois; Μπορούμε να γενικεύσουμε τον ορισμό του σταθερού σώματος $Ε^{X}$ , όπου $X$ τυχαίο υποσύνολο της $G$ ; Πράγματι, παρατηρούμε ότι το σύνολο $Ε^{X} = {a \in E : σ (a) = a, \forall σ \in X}$ είναι ενδιάμεσο σώμα της επέκτασης $Ε / F$ για κάθε υποσύνολο $X$ της $G$ . Επομένως προκύπτει η παρακάτω γενική μορφή του Λήμματος του Artin.

Θεώρημα 3.4.8.

Έστω $Ε / F$ πεπερασμένη επέκταση και $X \subset G a l (E / F)$ . Τότε $[E : E^{X}] \geq | X |$ .

Στην περίπτωση που το $X$ είναι υποομάδα της $G a l (E / F)$ μπορούμε να αποδείξουμε ότι ισχύει ισότητα στο παραπάνω θεώρημα.

Θεώρημα 3.4.9.

Έστω $Ε / F$ πεπερασμένη επέκταση και $H \leq G a l (E / F)$ . Τότε $[E : E^{H}] = | H |$ .

Απόδειξη.

Έστω ότι $H = {σ_{1}, \dots, σ_{n}}$ . Θα αποδείξουμε ότι οποιαδήποτε $n + 1$ στοιχεία του $Ε$ είναι γραμμικά εξαρτημένα πάνω από το σώμα $E^{H}$ . Έστω ${a_{1}, \dots, a_{n + 1}}$ $ ένα $Ε^{Η}$ -γραμμικά ανεξάρτητο υποσύνολο του $E$ . Θεωρούμε το ομογενές σύστημα με $n$ εξισώσεις και $n + 1$ αγνώστους στο $E$ :

\begin{array}{cc} σ_{1} (a_{1}) x_{1} + \dots + σ_{1} (a_{n + 1}) x_{n + 1} & = 0 \\ ⋮ \\ σ_{n} (a_{1}) x_{1} + \dots + σ_{n} (a_{n + 1}) x_{n + 1} & = 0 . \end{array}

(3.4.9.1)

Έστω

(c_{1}, \dots, c_{n}, c_{n + 1})

μία μη μηδενική λύση. Χωρίς βλάβη της γενικότητας μπορούμε να θεωρήσουμε ότι

c_{n + 1} \neq 0

και κατά συνέπεια (διαιρώντας με το

c_{n + 1}

) ότι

r = (r_{1}, \dots, r_{n}, r_{n + 1})

είναι λύση του παραπάνω συστήματος, με

r_{n + 1} = 1

. Επομένως

\sum_{j = 1}^{n + 1} σ_{i} (a_{j}) r_{j} = 0, i = 1, \dots, n .

(3.4.9.2)

Το 1 ανήκει, βέβαια, στο

E^{H}

. Όμως, υπάρχει κάποιο

r_{t}

, για

t = 1, \dots, n

, έτσι ώστε

r_{t} \notin E^{H}

. Διαφορετικά,

σ_{1} (r_{j}) = r_{j}

, για

j = 1, \dots, n + 1

, και καταλήγουμε σε άτοπο εξαιτίας της γραμμικής ανεξαρτησίας του

{a_{1}, \dots, a_{n + 1}}

πάνω από το

Ε^{Η}

\sum_{i = 1}^{n + 1} σ_{1} (a_{j}) r_{j} = 0 \Rightarrow \sum_{i = 1}^{n + 1} σ_{1} (a_{j}) σ_{1} (r_{j}) = 0 \Rightarrow \sum_{i = 1}^{n + 1} σ_{1} (a_{j} r_{j}) = 0 \Rightarrow \sum_{i = 1}^{n + 1} a_{j} r_{j} = 0.

Έστω ότι το στοιχείο

σ \in H

είναι αυτό που μετακινεί το

r_{t}

, δηλ.~

σ (r_{t}) \neq r_{t}

. Από το σύστημα (3.4.9.2) προκύπτει, λοιπόν, ότι:

σ (\sum_{j = 1}^{n + 1} σ_{i} (a_{j}) r_{j}) = 0, i = 1, \dots, n,

δηλ.

\sum_{j = 1}^{n + 1} σ σ_{i} (a_{j}) σ (r_{j}) = 0, i = 1, \dots, n .

(3.4.9.3)

Όμως, η

Η

είναι ομάδα και επομένως

{σ σ_{1}, \dots, σ σ_{n}} = {σ_{1}, \dots, σ_{n}} .

Άρα, σύμφωνα με τη σχέση 3.4.9.3,

r^{'} = (σ (r_{1}), \dots, σ (r_{n}), 1)

είναι επίσης λύση του συστήματος (3.4.9.1). Επομένως και η διαφορά

r - r^{'} = (r_{1} - σ (r_{1}), \dots, r_{n} - σ (r_{n}), 0)

είναι λύση του συστήματος (3.4.9.1) και μάλιστα μη μηδενική, αφού

r_{t} - σ (r_{t}) \neq 0

. Συνεχίζοντας καταυτόν τον τρόπο καταλήγουμε σε μία μη μηδενική λύση του συστήματος (3.4.9.1) με μία μόνο μη μηδενική συντεταγμένη. Αυτό όμως οδηγεί σε άτοπο, αφού αν

c \neq 0

και

σ_{i} (a_{t}) c = 0

, τότε

α_{t} = 0

και δεν μπορεί να είναι μέρος κανενός γραμμικά ανεξάρτητου συνόλου πάνω από το

Ε^{Η}

. Αποδείξαμε λοιπόν ότι οποιαδήποτε

n + 1

στοιχεία του

Ε

είναι γραμμικά εξαρτημένα πάνω από το σώμα

E^{H}

$. Άρα

[E : E^{H}] \leq n

και από το Θεώρημα 3.4.8 προκύπτει ότι

[E : E^{H}] = n

, δηλ.~

[E : E^{H}] = | Η |

.∎

3.5 Θεμελιώδες Θεώρημα Θεωρίας Galois

Στο εδάφιο αυτό όπως προαναγγείλαμε θα αποδείξουμε το Θεμελιώδες Θεώρημα της Θεωρίας Galois. Έστω $Ε/F$ μία επέκταση Galois και έστω $\mathcal{A}$ το σύνολο των ενδιάμεσων σωμάτων της επέκτασης $E/F$ και $\mathcal{D}$ Το σύνολο των υποομάδων της $\operatorname{Gal}(E/F)$ . Το Θεμελιώδες Θεώρημα της Θεωρίας Galois αφορά την αντιστοιχία ανάμεσα στα στοιχεία toυ $\mathcal{A}$ και του $\mathcal{D}$ .

Θεώρημα 3.5.1 (Θεμελιώδες Θεώρημα της Θεωρίας Galois).

Έστω $Ε/F$ μία επέκταση του Galois $G=\operatorname{Gal}(E/F)$ . Τότε υπάρχει μία αμφιμονότιμη και επί συνάρτηση $f$ μεταξύ των στοιχείων του συνόλου $\mathcal{A}$ των ενδιάμεσων σωμάτων της επέκτασης $E/F$ και των στοιχείων του συνόλου $\mathcal{D}$ των υποομάδων της $G$ :

f:\ \mathcal{A}\smash{\mathop{\;\longrightarrow\;}\limits}\mathcal{D},\quad% \quad B\mapsto\operatorname{Gal}(E/B).

Αντίστροφα, αν $H$ είναι υποομάδα της $G$ τότε η αντιστοιχία

\phi:\mathcal{D}\smash{\mathop{\;\longrightarrow\;}\limits}\mathcal{A},\quad% \quad H\mapsto E^{H}

έχει τις εξής ιδιότητες:

i.

$[B:F]=[G:\operatorname{Gal}(E/B)]$ και $[G:H]=[E^{H}:F]$
ii.

$E^{\operatorname{Gal}(E/B)}=B$ και $\operatorname{Gal}(E/E^{H})=H$
iii.

$B/F$ είναι επέκταση Galois αν και μόνο αν $\operatorname{Gal}(E/B)\unlhd G$ .

Απόδειξη.

Είναι φανερό ότι οι $f$ και $\phi$ είναι συναρτήσεις. Θα αποδείξουμε πρώτα το (ii). Η $E/F$ είναι επέκταση του Galois, οπότε η $E/Β$ είναι επέκταση του Galois. Από το Θεώρημα 3.4.7 , έπεται ότι $E^{\operatorname{Gal}(E/B)}=B$ . Άρα

\operatorname{Gal}(E/B_{1})=\operatorname{Gal}(E/B_{2})\Rightarrow E^{% \operatorname{Gal}(E/B_{1})}=E^{\operatorname{Gal}(E/B_{2})}\Rightarrow B_{1}=% B_{2}

και η $f$ είναι αμφιμονότιμη.

Έστω τώρα $Η\leq G$ και $Η^{\prime}=\operatorname{Gal}(E/E^{H})=\{\sigma\in G:\ \sigma|_{E^{H}}=% \operatorname{id}_{Ε^{H}}\}$ . Είναι φανερό ότι $Η\subseteq Η^{\prime}$ και άρα

|H|\leq|H^{\prime}|.

(3.5.1.1)

Επίσης, αφού η $E/E^{H}$ είναι επέκταση του Galois, από το Θεώρημα 3.4.4 , προκύπτει ότι

Ε^{\operatorname{Gal}(E/E^{H})}=E^{H}.

Από το Πόρισμα 3.2.4, έπεται ότι

|Η^{\prime}|=[Ε:Ε^{H}].

(3.5.1.2)

Σύμφωνα με το Θεώρημα 3.4.9,

[Ε:Ε^{H}]\geq|H|.

(3.5.1.3)

Άρα $|Η|=|Η^{\prime}|$ και $\operatorname{Gal}(E/E^{H})=H$ . Επομένως

Ε^{Η_{1}}=Ε^{Η_{2}}\Rightarrow\operatorname{Gal}(E/E^{H_{1}})=\operatorname{% Gal}(E/E^{H_{2}})\Rightarrow Η_{1}=Η_{2}

και η $\phi$ είναι αμφιμονότιμη. Είναι φανερό ότι oi $f$ και $\phi$ είναι αντίστροφες συναρτήσεις, άρα είναι επί.

Στη συνέχεια αποδεικνύουμε το (i). Αφού οι $f$ και $\phi$ είναι αντίστροφες συναρτήσεις, αρκεί να αποδείξουμε τη μία από τις δύο ισότητες. Έστω $Β$ ενδιάμεσο σώμα και $H=\operatorname{Gal}(E/B)$ . Αφού $Ε/Β$ είναι επέκταση του Galois, $[E:B]=|H|$ (Πόρισμα 3.2.4). Από τη σχέση

[E:F]=[E:B]\;[B:F]

προκύπτει ότι

|G|=|H|\;[B:F],

άρα, σύμφωνα με το Θεώρημα του Lagrange, (Θεώρημα I.10)

[B:F]=[G:H]\;\Rightarrow\;[B:F]=[G:\operatorname{Gal}(E/B)].

Επομένως, για κάθε υποομάδα $H$ της $G$ ισχύει

[G:H]=[E^{H}:F].

Τέλος, για το (iii), παρατηρούμε ότι αν $B/F$ είναι επέκταση του Galois τότε $\operatorname{Gal}(E/B)\unlhd G$ , από το Θεώρημα 3.3.2. Για την αντίστροφη κατεύθυνση, ας υποθέσουμε ότι $Η\unlhd G$ , όπου $H=\operatorname{Gal}(E/B)$ . Αυτό σημαίνει ότι αν $\sigma\in G$ και $\tau\in H$ , τότε $\sigma\tau^{\prime}=\tau\sigma$ , για κάποιο $\tau^{\prime}\in H$ (βλ. Ορισμό I.11). Για κάθε $a\in G$ , έχουμε $\sigma\tau^{\prime}(a)=\tau\sigma(a)$ . An $a\in E^{H}$ , δηλ. αν $a\in B$ , τότε $\tau(a)=a$ , άρα $\sigma(a)=\tau\sigma(a)$ . Επομένως $\sigma(a)\in E^{H}$ , για κάθε $\sigma\in G$ και για κάθε $a\in E^{H}$ , δηλ. $\sigma(B)\subseteq B$ . Θα αποδείξουμε ότι η επέκταση $Β/F$ είναι επέκταση του Galois εφαρμόζοντας το Θεώρημα 3.4.7. Έστω $p(x)\in F[x]$ ένα ανάγωγο πολυώνυμο που έχει μία ρίζα $b\in B$ . Θα αποδείξουμε ότι όλες οι ρίζες του $p(x)$ ανήκουν στο $Β$ . Ας υποθέσουμε ότι υπάρχει μία ρίζα $\gamma$ του $p(x)$ και $\gamma\notin B$ . Βέβαια όλες οι ρίζες του $p(x)$ ανήκουν στο σώμα $Ε$ , γιατί το $p(x)$ έχει μία ρίζα στο $E$ (Θεώρημα 3.4.7). Θεωρούμε τον $F$ -ισομορφισμό του Θεωρήματος 2.3.3:

F(b)\smash{\mathop{\;\longrightarrow\;}\limits}F(\gamma),\quad b\mapsto\gamma,

και ο οποίος επεκτείνεται σε έναν $F$ -αυτομορφισμό ${\sigma}$ του $E$ , (Θεώρημα 3.2.1). Άρα $\sigma\in G$ . Όμως $\sigma(B)\nsubseteq B$ , αφού $\sigma(b)=\gamma\notin B$ . Αυτό είναι άτοπο, γιατί όπως είδαμε $\sigma(B)\subseteq B$ , για κάθε $\sigma\in G$ . Άρα όλες οι ρίζες του $p(x)$ ανήκουν στο $Β$ και h επέκταση $B/F$ είναι επέκταση του Galois σύμφωνα με το Θεώρημα 3.4.7. ∎

Σημειώνουμε το παρακάτω πόρισμα του Θεμελιώδους Θεωρήματος της Θεωρίας Galois.

Πόρισμα 3.5.2.

Έστω $Ε/F$ μία επέκταση Galois. Η επέκταση έχει πεπερασμένο αριθμό ενδιάμεσων σωμάτων.

Απόδειξη.

Η ομάδα $\operatorname{Gal}(E/F)$ είναι πεπερασμένη και έχει πεπερασμένο αριθμό υποομάδων. Επομένως, σύμφωνα με το Θεμελιώδες Θεώρημα της Θεωρίας Galois υπάρχουν πεπερασμένου πλήθους ενδιάμεσα σώματα. ∎

Αν $Κ$ , $L$ είναι σώματα, τότε με $Κ L$ συμβολίζουμε το μικρότερο σώμα που περιέχει το $Κ$ και το $L$ . Tο παρακάτω θεώρημα αναφέρεται και ως θεώρημα του παραλληλογράμμου για τις επεκτάσεις του Galois.

Θεώρημα 3.5.3.

Έστω ότι $Ε/F$ είναι επέκταση σωμάτων, $L, K$ ενδιάμεσα υποσώματα της επέκτασης τέτοια ώστε $L/F$ να είναι επέκταση του Galois. Τότε oi $KL/K$ και $L/\,L\cap K$ είναι επεκτάσεις του Galois και $\operatorname{Gal}(KL/K)$ είναι ισόμορφη με την $\operatorname{Gal}\left(L/(L\cap K)\right)$ .

Σχηματικά, το θεώρημα συνδέει τις παράλληλες πλευρές του εσωτερικού παραλληλογράμμου του σχήματος 3.9.

Απόδειξη.

Αφού $L/F$ είναι επέκταση του Galois και $F\subset L\cap K$ , η επέκταση $L/(L\cap K)$ είναι επέκταση του Galois. άρα το $L$ είναι σώμα ανάλυσης ενός διαχωρίσιμου πολυώνυμου $g(x)\in(L\cap K)[x]$ . Τότε, όμως, $g(x)\in K[x]$ και το $K L$ είναι σώμα ανάλυσης του $g(x)$ . άρα η $KL/K$ είναι επίσης επέκταση του Galois. Αν τώρα, o $\sigma\in\operatorname{Gal}(KL/K)$ τότε, ο περιορισμός του $\sigma$ στο σώμα $L$ κρατά σταθερά τα στοιχεία του $(L\cap K)\subset K$ και επομένως, $\sigma|_{L}\in\operatorname{Gal}\left(L/(L\cap K)\right)$ . Έστω, λοιπόν, η συνάρτηση $\phi$ όπου

\phi:\ \operatorname{Gal}(KL/K)\rightarrow\operatorname{Gal}\left(L/(L\cap K)% \right),\ \sigma\mapsto\sigma|_{L}.

Είναι φανερό ότι η $\phi$ είναι μονομορφισμός ομάδων. Θα αποδείξουμε ότι η $\phi$ είναι και επιμορφισμός. Για να το πετύχουμε αυτό, θέτουμε $H={\rm Im}\phi$ . Θα δείξουμε ότι $L^{H}=L\cap K$ και ο ισχυρισμός μας θα προκύψει από το Θεμελιώδες Θεώρημα της Θεωρίας Galois.

Ο εγκλεισμός $(L\cap K)\subset L^{H}$ είναι προφανής, αφού $(L\cap K)\subset K$ και τα στοιχεία της $Η$ είναι της μορφής $\sigma|_{L}$ , όπου $\sigma\in\operatorname{Gal}(KL/K)$ . Για την αντίστροφη κατεύθυνση, αν $a\in L^{H}$ τότε $a\in L$ και $\sigma|_{L}(a)=a$ , για κάθε $\sigma\in\operatorname{Gal}(KL/K)$ . Επομένως το $a\in KL$ και $\sigma(a)=a$ , για κάθε $\sigma\in\operatorname{Gal}(KL/K)$ , δηλ. $α\in(KL)^{\operatorname{Gal}(KL/K)}$ . Όμως, σύμφωνα με το Θεμελιώδες Θεώρημα της Θεωρίας Galois, $(KL)^{\operatorname{Gal}(KL/K)}=Κ$ και άρα $a\in(L\cap K)$ . Άρα $L^{H}\subset(L\cap K)$ και τελικά $H={\rm Im}\phi=\operatorname{Gal}\left(L/(L\cap K)\right)$ . ∎

3.6 Υπολογισμοί και Παραδείγματα

Έστω $f(x)\in F[x]$ ένα κανονικό, διαχωρίσιμο πολυώνυμο βαθμού $n$ , $E$ Το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ και $X=\{\alpha_{1},\ldots,\alpha_{n}\}\subset E$ το σύνολο των ριζών του $f(x)$ . Με ${\Delta}$ συμβολίζουμε το στοιχείο

{\Delta}=\prod_{i<j}(\alpha_{i}-a_{j})\in E.

Aπό το Θεώρημα 2.3.3 προκύπτει ότι αν $\sigma\in\operatorname{Gal}(E/F)$ , τότε $\sigma({\Delta})=\pm{\Delta}$ και $\sigma({\Delta}^{2})={\Delta}^{2}$ . Επομένως ${\Delta}^{2}\in E^{G}$ . Αφού $E/F$ είναι επέκταση του Galois, από το Θεώρημα 3.4.7 προκύπτει ότι

{\Delta}^{2}\in F.

Eίναι φανερό ότι το ${\Delta}^{2}$ δεν εξαρτάται από την αρίθμηση των ριζών του $f(x)$ . Η διακρίνουσα (discriminant) του $f(x)$ , συμβολίζεται συνήθως με ${D}$ και είναι το στοιχείο

D={\Delta}^{2}.

Παρατηρούμε ότι όταν $\operatorname{char}F=2$ , τότε $-\Delta=\Delta$ , συνεπώς $\sigma({\Delta})={\Delta}$ , για κάθε $\sigma\in\operatorname{Gal}(E/F)$ , άρα $\Delta\in F$ . Στη περίπτωση που $\operatorname{char}F\neq 2$ και $\Delta\notin F$ , τότε προκύπτει ένα αξιοσημείωτο συμπέρασμα για την ομάδα $\operatorname{Gal}(E/F)$ . Πράγματι, παρατηρούμε ότι

\operatorname{irr}_{(F,\Delta)}(x)=x^{2}-D.

Επομένως, από το Θεώρημα 2.2.3 και το Θεμελιώδες Θεώρημα της Θεωρίας Galois (Θεώρημα 3.5.1), έπεται ότι

2=[F(\Delta):F]=[G:\operatorname{Gal}(E/F(\Delta))].

(3.6.0.1)

Αποδείξαμε λοιπόν το εξής:

Πρόταση 3.6.1.

Έστω $f(x)\in F[x]$ ένα κανονικό, διαχωρίσιμο πολυώνυμο βαθμού $n$ και $E$ Το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ . Aν $\Delta\notin F$ , τότε η ομάδα Galois του $f(x)$ έχει μία κανονική υποομάδα με δείκτη $2$ .

Θα εφαρμόσουμε τα παραπάνω όταν $\deg f(x)=3$ .

Πρόταση 3.6.2.

Έστω $f(x)\in F[x]$ ένα κανονικό, ανάγωγο, διαχωρίσιμο πολυώνυμο βαθμού $3$ και $Ε$ το σώμα ανάλυσης του $f(x)$ . Αν $\Delta\notin F$ τότε $\operatorname{Gal}(E/F)\cong S_{3}$ .

Απόδειξη.

H ομάδα $\operatorname{Gal}(E/F)$ εμφυτεύτεται στην $S_{3}$ . Αφού $\deg f(x)$ διαιρεί την τάξη της $\operatorname{Gal}(E/F)$ , έπεται ότι η τάξη της $\operatorname{Gal}(E/F)$ είναι τρία ή έξι. Αν $\Delta\notin F$ τότε, από την Πρόταση 3.6.1, το 2 διαιρεί την τάξη της ομάδας $|\operatorname{Gal}(E/F)|$ και άρα $\operatorname{Gal}(E/F)\cong S_{3}$ . ∎

Στην άσκηση 3.7.5 ο αναγνώστης καλείται να διαπιστώσει ότι αν $\operatorname{char}F\neq 2$ και $\Delta\in F$ για ένα ανάγωγο και διαχωρίσιμο πολυώνυμο βαθμού $3$ , τότε $\operatorname{Gal}(E/F)\cong Α_{3}$ .

Παράδειγμα 3.6.3.

Έστω $f(x)=x^{3}-3x-1\in{\mathbb{Q}}[x]$ . Το $f(x)$ είναι ανάγωγο στο ${\mathbb{Q}}[x]$ , αφού μπορεί να αποδειχθεί ότι δεν έχει ρίζες στο ${\mathbb{Q}}$ (βλ. Πρόταση 1.3.2). Έστω $E$ το σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ . Μπορεί να δείξει κανείς ότι $\Delta\in\mathbb{Q}$ , βλ. τον τύπο στο Παράρτημα V. Επομένως $\operatorname{Gal}(E/\mathbb{Q})\cong A_{3}$ .

Στα επόμενα παραδείγματα θα υπολογίσουμε τις ομάδες Galois πάνω από το ${\mathbb{Q}}$ , για πολυώνυμα βαθμού $4$ . Θα καταλήξουμε σε ενδιαφέροντα συμπεράσματα χρησιμοποιώντας τους τύπους της Ενότητας V του Παραρτήματος. Σημειώνουμε την επόμενη παρατήρηση.

Παρατηρήσεις 3.6.4.

i.

Έστω $f(x)=x^{4}+ax+b$ . Τότε η διακρίνουσα του $f(x)$ είναι ίση με $-27a^{4}+256b^{3}$ .
ii.

Έστω $f(x)=x^{4}+ax^{2}+b$ . Τότε η διακρίνουσα του $f(x)$ είναι ίση με $16(α^{2}-4b)^{2}$ .
iii.

Έστω $f(x)\in{\mathbb{Q}}[x]$ , κανονικό πολυώνυμο και $\deg f(x)=4$ , $E$ το σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ και $\alpha_{1},\ldots,\alpha_{4}$ οι ρίζες του $f(x)$ . Τότε οι ρίζες της κυβικής επιλύουσας (Παράρτημα V) είναι ίσες με

$\alpha_{1}\alpha_{2}+\alpha_{3}\alpha_{4},\alpha_{1}\alpha_{3}+\alpha_{2}% \alpha_{4},\alpha_{1}\alpha_{4}+\alpha_{2}\alpha_{3}$

και ανήκουν στο $E$ . Άρα, το σώμα ανάλυσης της κυβικής επιλύουσας είναι ενδιάμεσο σώμα της επέκτασης $E/{\mathbb{Q}}$ .

Όταν to $f(x)$ είναι ανάγωγο, τότε η ομάδα Galois $G$ του $f(x)$ εμφυτεύεται στην $S_{4}$ . Σύμφωνα με το Θεώρημα 3.2.1 η $G$ έχει μία ενδιαφέρουσα ιδιότητα: για κάθε ζεύγος ριζών $b,\gamma$ του $f(x)$ , υπάρχει $\sigma\in G$ , έτσι ώστε $\sigma(β)=\gamma$ . Αυτό περιορίζει τις υποομάδες της $S_{4}$ που θα μπορούσαν να είναι ομάδες Galois ανάγωγων πολυωνύμων βαθμού 4.

Στην άσκηση 3.7.6, ο αναγνώστης καλείται να συμπληρώσει τις λεπτομέρεις του επόμενου παραδείγματος.

Παράδειγμα 3.6.5.

Έστω $f(x)=x^{4}+2x+2\in{\mathbb{Q}}[x]$ , $E$ το σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ και $G=\operatorname{Gal}(E/{\mathbb{Q}})$ . Tο $f(x)$ είναι ανάγωγο, από το κριτήριο του Eisenstein. Η κυβική επιλύουσα του $f(x)$ είναι το πολυώνυμο $g(x)=x^{3}-8x-4$ , το οποίο είναι και αυτό ανάγωγο. Έστω $Β$ το σώμα ανάλυσης του $g(x)$ . Αφού η διακρίνουσα $D$ του $g(x)$ δεν είναι τετράγωνο ρητού αριθμού, έπεται ότι $\operatorname{Gal}(B/{\mathbb{Q}})\cong S_{3}$ (Πρόταση 3.6.2) και επομένως το $6$ διαιρεί την τάξη της $G$ . Αφού η $S_{4}$ έχει τάξη $24$ και η $G$ εμφυτεύεται στην $S_{4}$ , η $G$ είναι ισόμορφη είτε με την $A_{4}$ είτε με την $S_{4}$ . Όμως, η διακρίνουσα του $f(x)$ δεν είναι τετράγωνο ρητού αριθμού. Επομένως η $G$ περιέχει μία μη άρτια αντιμετάθεση. Συνεπώς, η $G\cong S_{4}$ .

Στο επόμενο παράδειγμα θα υπολογίσουμε αναλυτικά τα ενδιάμεσα σώματα της επέκτασης $E/{\mathbb{Q}}$ , όπου $E$ είναι το σώμα ανάλυσης του $f(x)=x^{4}-2$ πάνω από το ${\mathbb{Q}}$ .

Παράδειγμα 3.6.6.

Έστω $f(x)=x^{4}-2\in\mathbb{Q}$ , $E=\mathbb{Q}(b,i)$ , όπου $b=2^{1/4}$ , και έστω $G=\operatorname{Gal}(E/\mathbb{Q})$ . στο Παράδειγμα 3.1.2, είδαμε ότι $G\cong D_{8}$ και ότι τα στοιχεία της $G$ καθορίζονται από τον παρακάτω πίνακα, όπου η τελευταία γραμμή υπολογίζει την τάξη του ισομορφισμού, ως στοιχείου της $G$ .

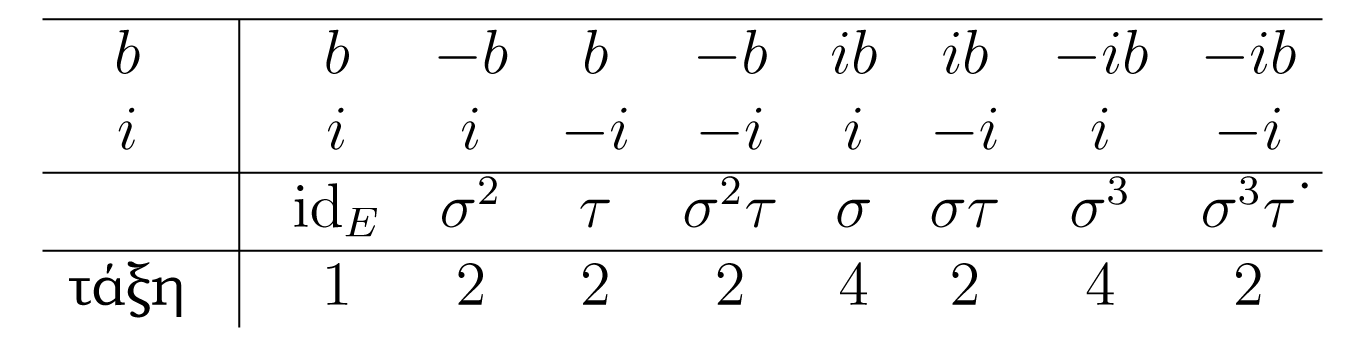
Οι γνήσιες μη τετριμμένες υποομάδες της $G$ τάξης 4 είναι οι:

Η_{1}=\langle\sigma\rangle=\{\operatorname{id}_{E},\sigma,\sigma^{2},\sigma^{3% }\},\quad H_{2}=\{\operatorname{id}_{E},\sigma^{2},\tau,\sigma^{2}\tau\}\quad H% _{3}=\{\operatorname{id}_{E},\tau,\sigma\tau,\sigma^{3}\tau\},

ενώ κάθε ένα από τα στοιχεία της $G$ με τάξη 2 παράγει μία αντίστοιχη υποομάδα τάξης 2. Έτσι Το διάγραμμα των υποομάδων της $G$ είναι:

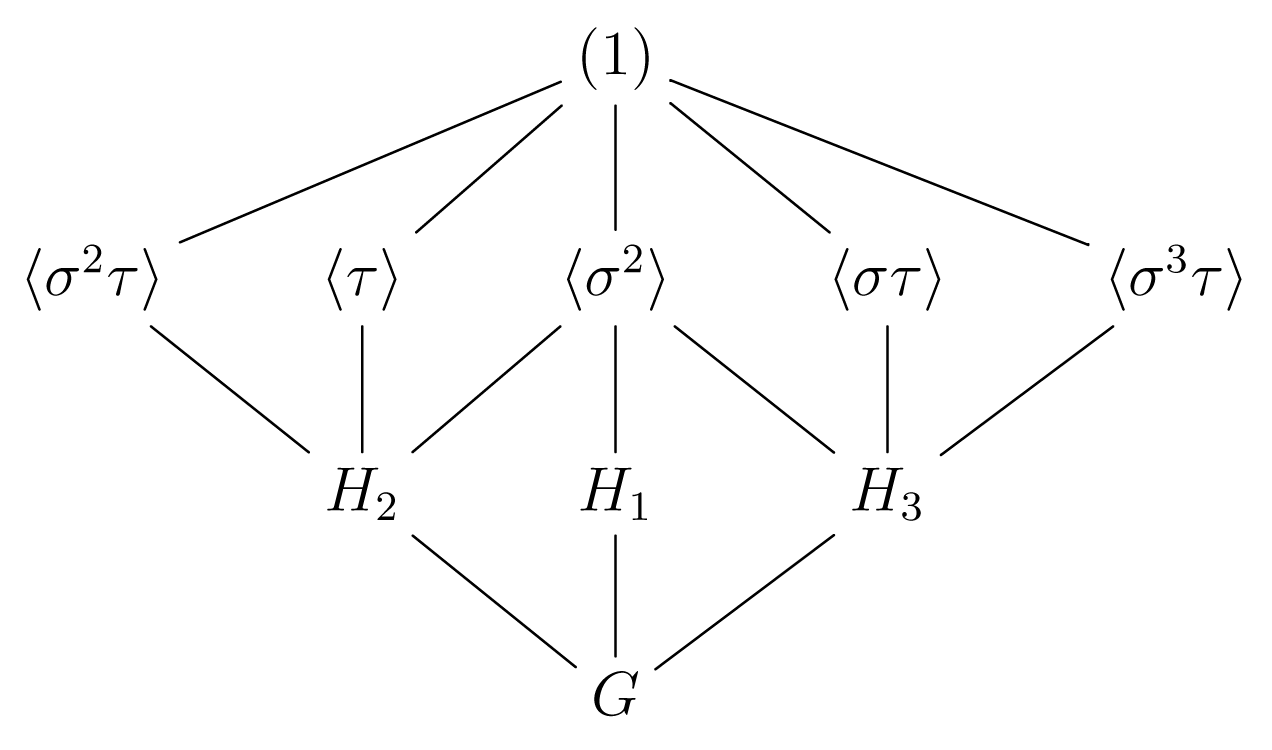
Από τις υποομάδες της $G$ που έχουν τάξη 2, μόνον η $\langle\tau\rangle$ είναι κανονική, όπως εύκολα ελέγχει κανείς. Σε αντιδιαστολή, κάθε μία από τις υποοομάδες της $G$ τάξης 4 είναι κανονική. Θα υπολογίσουμε τα ενδιάμεσα σώματα σύμφωνα με το Θεμελιώδες Θεώρημα της Θεωρίας Galois. Θα ξεκινήσουμε με την ομάδα $\langle\sigma\tau\rangle$ . Μία βάση του $Ε$ ως προς το $\mathbb{Q}$ είναι το σύνολο $\{1,b,b^{2},b^{3},i,ib,ib^{2},ib^{3}\}$ , και ένα τυχαίο στοιχείο $y$ του $Ε$ είναι ένας γραμμικός συνδυασμός

y=a_{0}+a_{1}b+a_{2}b^{2}+a_{3}b^{3}+a_{4}i+a_{5}ib+a_{6}ib^{2}+a_{7}ib^{3},

όπου $a_{i}\in\mathbb{Q}$ . Επομένως

\sigma\tau(y)=a_{0}+a_{1}ib-a_{2}b^{2}-ia_{3}b^{3}-a_{4}i+a_{5}b+a_{6}ib^{2}-a% _{7}b^{3}

Επομένως

\sigma\tau(y)=y\Leftrightarrow a_{1}=a_{5},a_{2}=0,a_{3}=-a_{7},a_{4}=0,

και

\sigma\tau(y)=y\Leftrightarrow y=a_{0}+a_{1}b(1+i)+a_{3}b^{3}(1-i)+a_{6}ib^{2}.

Άρα

Ε^{\langle\sigma\tau\rangle}=\mathbb{Q}(b(1+i),b^{3}(1-i),ib^{2}).

Αφού $(b(1+i))^{2}=2ib^{2}$ , $(b(1+i))^{3}=-2b^{3}(1-i)$ , έπεται ότι

Ε^{\langle\sigma\tau\rangle}=\mathbb{Q}(b(1+i)).

Στη συνέχεια θα βρούμε το σώμα $Ε^{\langle\sigma^{2}\rangle}$ . Αφού $[G:\langle\sigma^{2}\rangle]=4$ , από το Θεμελιώδες Θεώρημα της Θεωρίας Galois συμπεραίνουμε ότι $[Ε^{\langle\sigma^{2}\rangle}:{\mathbb{Q}}]=4$ . Αφού

\sigma^{2}(i)=i\textrm{ και }\sigma^{2}(b^{2})=\sigma^{2}(b)\sigma^{2}(b)=(-b)^{2}=b^{2},

έπεται ότι

\mathbb{Q}(b^{2},i)\subset E^{\langle\sigma^{2}\rangle}.

Αν $\mathbb{Q}(b^{2},i)\neq E^{\langle\sigma^{2}\rangle}$ τότε

[\mathbb{Q}(b^{2},i):{\mathbb{Q}}]<4=[E^{\langle\sigma^{2}\rangle}:{\mathbb{Q}% }].

Όμως, από τους εγκλεισμούς

\mathbb{Q}\subsetneq\mathbb{Q}(i)\subsetneq\mathbb{Q}(i,b^{2})\subsetneq Ε,

έπεται ότι $[\mathbb{Q}(i,b^{2}):\mathbb{Q}]=4$ . Άρα $E^{\langle\sigma^{2}\rangle}=\mathbb{Q}(i,b^{2})$ . Με αυτές τις τεχνικές βρίσκουμε και τα υπόλοιπα ενδιάμεσα σώματα του $Ε$ .

Έτσι στο διάγραμμα του σχήματος 3.10, αντιστοιχεί το παρακάτω διάγραμμα των ενδιάμεσων σωμάτων, αν στη θέση της υποομάδας $H$ της $G$ τοποθετήσουμε το σταθερό σώμα $E^{H}$ . Σημειώνουμε ότι οι εγκλεισμοί αντιστρέφονται.

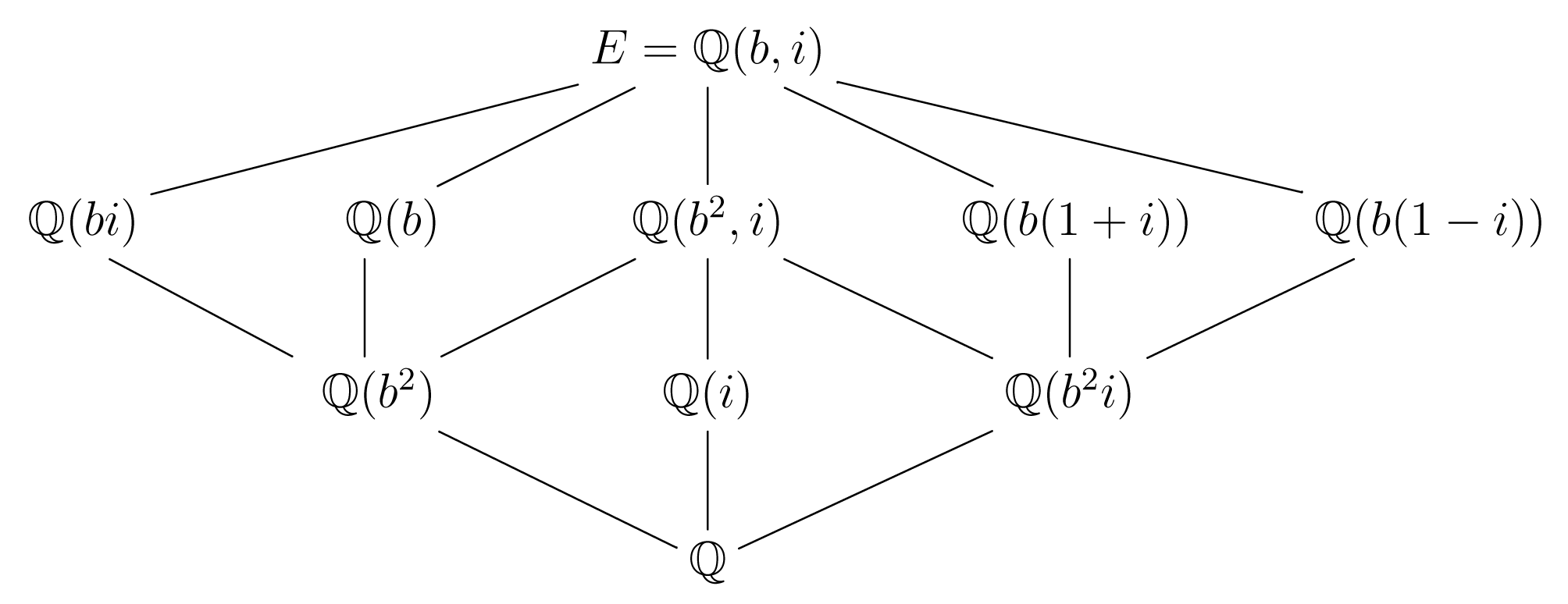
Σχήμα 3.11: Eνδιάμεσα σώματα της $E/{\mathbb{Q}}$ .

Τέλος παρατηρούμε ότι στις κανονικές υποοομάδες της $G$ αντιστοιχούν τα παρακάτω ενδιάμεσα σώματα, όλα επεκτάσεις Galois πάνω από το ${\mathbb{Q}}$ :

•

$\mathbb{Q}(b^{2})$ είναι το σώμα ανάλυσης του $x^{2}-b$ πάνω από το $\mathbb{Q}$ .
•

$\mathbb{Q}(i)$ είναι το σώμα ανάλυσης του $x^{2}+1$ πάνω από το $\mathbb{Q}$ .
•

$\mathbb{Q}(b^{2}i)$ είναι το σώμα ανάλυσης του $x^{2}+2$ πάνω από το $\mathbb{Q}$ .
•

$\mathbb{Q}(b^{2},i)$ είναι το σώμα ανάλυσης του $(x^{2}-b)(x^{2}+1)$ πάνω από το $\mathbb{Q}$ .

3.7 Ασκήσεις

1.

Έστω $Ε/F$ επέκταση σωμάτων, $G=\operatorname{Gal}(E/F)$ και $Η<G$ . Na αποδείξετε ότι $E^{H}$ είναι ενδιάμεσο σώμα της $E/F$ , δηλ. $F\subset E^{H}\subset E$ . Αν $H_{1}<H_{2}<G$ , τότε να αποδείξετε ότι $Ε^{Η_{2}}\subset E^{H_{1}}$ .
2.
Για κάθε μία από τις παρακάτω περιπτώσεις να δώσετε ένα παράδειγμα επεκτάσεων $\mathbb{Q}\subsetneqq B\subsetneqq E$ ή να εξηγήσετε γιατί είναι αδύνατον να συμβεί:
- –
  
  $Ε/Β$ επέκταση του Galois, $B/{\mathbb{Q}}$ επέκταση του Galois και $E/{\mathbb{Q}}$ δεν είναι επέκταση του Galois,
- –
  
  $Ε/B$ δεν είναι επέκταση του Galois, $B/{\mathbb{Q}}$ επέκταση του Galois και $E/{\mathbb{Q}}$ επέκταση του Galois,
- –
  
  $Ε/B$ επέκταση Galois, $B/{\mathbb{Q}}$ δεν είναι επέκταση Galois και $E/{\mathbb{Q}}$ είναι επέκταση του Galois.
3.
Έστω $f(x)$ το πολυώνυμο $f(x)=x^{4}-4\in\mathbb{Q}[x]$ , $E$ το σώμα ανάλυσης του $f(x)$ πάνω από το $\mathbb{Q}$ και $G=\operatorname{Gal}(E/\mathbb{Q})$ .
- –
  
  Να υπολογίσετε το $Ε$ .
- –
  
  Να γράψετε τα στοιχεία της $G$ ως στοιχεία του $S_{4}$ .
- –
  
  Να αποδείξετε ότι $G\cong\mathbb{Z}_{2}\times\mathbb{Z}_{2}$ .
- –
  
  Για τα υποσώματα $B_{1}=\mathbb{Q}(i\sqrt{2}),\ B_{2}=\mathbb{Q}(i),\ B_{3}=\mathbb{Q}(\sqrt{2})$ του $Ε$ , να βρείτε τις υποομάδες $\operatorname{Gal}(E/B_{1})$ $\operatorname{Gal}(E/B_{2})$ $\operatorname{Gal}(E/B_{3})$ της $G$ .
- –
  
  Έστω $a=\sqrt{2}+i$ . Να υπολογίσετε την εικόνα του $a$ για κάθε έναν από τους αυτομορφισμούς του $Ε$ . Να αποδείξετε ότι $Ε=\mathbb{Q}(a)$ .
- –
  
  Να γράψετε το στοιχείο $a^{-1}$ ως γραμμικό συνδυασμό δυνάμεων του $a$ .
4.
Έστω $Ε=\mathbb{Q}(\sqrt{3},\sqrt{5})$ .
- –
  
  Να αποδείξετε ότι $Ε/{\mathbb{Q}}$ είναι επέκταση του Galois, να υπολογίσετε τον βαθμό $[E:\mathbb{Q}]$ , και να βρείτε μία ${\mathbb{Q}}$ -βάση του $Ε$ .
- –
  
  Να περιγράψετε τα στοιχεία της ομάδας $G=\operatorname{Gal}(E/\mathbb{Q})$ .
- –
  
  Να βρείτε όλα τα ενδιάμεσα σώματα $Β$ του $E$ πάνω από το $\mathbb{Q}$ και να υπολογίσετε τις ομάδες $\operatorname{Gal}(B/\mathbb{Q})$ και $\operatorname{Gal}(E/B)$ .
- –
  
  Να βρείτε ανάγωγο πολυώνυμο $f(x)$ έτσι ώστε $Ε$ να είναι σώμα ανάλυσης του $f(x)$ πάνω από το $\mathbb{Q}$ .
5.

Έστω $f(x)\in F[x]$ ανάγωγο, διαχωρίσιμο πολυώνυμο βαθμού $3$ , $\operatorname{char}F\neq 2$ , και $Ε$ το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ . Aν $\Delta\in F$ να αποδείξετε ότι $\operatorname{Gal}(E/F)\cong Α_{3}$ .
6.

Να συμπληρώσετε τις λεπτομέρειες του Παραδείγματος 3.6.5 και να αποδείξετε ότι η ομάδα Galois του $f(x)=x^{4}+2x+2\in{\mathbb{Q}}[x]$ είναι ισόμορφη με την $S_{4}$ . Να παρατηρήσετε κάτι ενδιαφέρον σχετικά με τις διακρίνουσες.
7.

Να αποδείξετε ότι η ομάδα Galois του $f(x)=x^{4}-8x+12\in{\mathbb{Q}}[x]$ είναι ισόμορφη με την $Α_{4}$ .
8.

Να αποδείξετε ότι η ομάδα Galois του $f(x)=x^{4}+5x+5\in{\mathbb{Q}}[x]$ είναι κυκλική τάξης 4.
9.
Έστω $E=\mathbb{Q}(\omega,\sqrt[5]{3})$ και $G=\operatorname{Gal}(E/\mathbb{Q})$ , όπου $\omega=e^{2\pi i/5}$ .
- –
  
  Να βρείτε πολυώνυμο $f(x)\in\mathbb{Q}[x]$ έτσι ώστε $Ε$ να είναι το σώμα ανάλυσης του $f(x)$ και να υπολογίσετε τον βαθμό $[E:\mathbb{Q}]$ .
- –
  
  Να αποδείξετε ότι η $G$ εμφυτεύεται στην $S_{5}$ και ότι $G\ncong S_{5}$ .
- –
  
  Να βρείτε τα στοιχεία της $G_{1}=\operatorname{Gal}(E/\mathbb{Q}(\sqrt[5]{3}))$ . Να υπολογίσετε Το $\sigma(a)$ , όπου $a$ τυχαίο στοιχείο της $Ε$ και $\sigma\in G_{1}$ , $\sigma\neq id_{E}$ , (για ένα μόνο τέτοιο στοιχείο). Nα δείξετε ότι η $G_{1}$ είναι κυκλική ομάδα.
- –
  
  Να βρείτε τα στοιχεία της $G_{2}=\operatorname{Gal}(E/\mathbb{Q}(\omega))$ . Nα δείξετε ότι η $G_{2}$ είναι κυκλική ομάδα. Να υπολογίσετε Το $\sigma(a)$ , όπου $a$ τυχαίο στοιχείο της $Ε$ και $\sigma\in G_{2}$ , $\sigma\neq id_{E}$ (για ένα μόνο τέτοιο στοιχείο).
- –
  
  Να βρείτε δύο στοιχεία της ομάδας $G=\operatorname{Gal}(E/\mathbb{Q})$ που δεν αντιμετατίθενται.
10.
Έστω $E=\mathbb{Q}(\omega)$ , όπου $\omega=e^{2\pi i/5}$ .
- –
  
  Να δείξετε ότι $E/{\mathbb{Q}}$ είναι επέκταση Galois και να βρείτε τον βαθμό $[E:\mathbb{Q}]$ .
- –
  
  Έστω $G=\operatorname{Gal}(E/\mathbb{Q})$ . Να αποδείξετε ότι η $G$ είναι κυκλική ομάδα.
- –
  
  Να βρείτε όλα τα ενδιάμεσα σώματα του $E$ .
11.

Έστω $Ε/F$ μία επέκταση Galois, $a\in E$ , $G=\operatorname{Gal}(E/F)$ . Nα αποδείξετε ότι $N(a)\in F$ , όπου

$N(a)=\prod_{\sigma\in G}\sigma(a).$
12.

Έστω $Ε/F$ μία επέκταση Galois και έστω $a\in E$ . Να αποδείξετε ότι $\operatorname{irr}_{(F,a)}(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο $Ε[x]$ .
13.

Αν $L/F$ επέκταση του Galois και $L\subset E$ , να αποδείξετε ότι $L(a)/F(a)$ είναι επέκταση του Galois, όπου $a\in E$ .

Βιβλιογραφία Κεφαλαίου 3

1.

Bastida, J. R. Field Extensions and Galois Theory, Vol. 22. Addison-Wesley, 2007.
2.

Bewersdorff, J. Galois Theory for Beginners, A Historical Perspective. AMS, 2006.
3.

Conrad, K. Galois groups of cubics and quartics. Expository Papers, http://www.math.uconn.edu/~kconrad/blurbs/galoistheory/cubicquartic.pdf.
4.

Dummit, D.S., Foote, R.M. Abstract Algebra. J. Wiley and Sons, INc, 2004.
5.

Edwards, H.M. Galois Theory. Springer, 1984.
6.

Escofier, J.P. Galois Theory. Springer, 2001.
7.

Fox, D. Galois Theory. John Wiley & Sons, 2012.
8.

Fraleigh, J. Εισαγωγή στην Άλγεβρα. Πανεπιστημιακές εκδόσεις Κρήτης, 2011.
9.

Gaal, L. Classical Galois Theory with Examples. Chelsea, 1988.
10.

Hadlock, C. R. Field Theory and its Classical Problems. ΜΑΑ, 2000.
11.

Menini, C. Van Oystaeyen, F. Abstract Algebra. Marcel Dekker, 2004.
12.

Milne, J.S. Fields and Galois Theory. www.jmilne.org, 2014.
13.

Rotman, J. Θεωρία Galois. Leader Books, 2000.
14.

Stewart, I. Galois Theory. Champan and Hall, 1973.
15.

Swallow, J. Exploratory Galois Theory. Cambridge University Press, 2004.
16.

Tignol, J.P. Galois Theory of Algebraic Equations. World Scientific, 2011.