Θεωρία Galois

Κεφάλαιο 6Eφαρμογές

Στο Κεφάλαιο αυτό θα χρησιμοποιήσουμε τα εργαλεία της Θεωρίας Galois, για να απαντήσουμε σε ερωτήματα που θέσαμε στην αρχή του συγγράμματος. Έτσι, δοθέντος ενός πολυωνύμου, θα βρούμε ικανή και αναγκαία συνθήκη για να υπάρχει ακριβής τύπος για τις ρίζες του πολυωνύμου, δηλ. Το Θεώρημα του Galois. Θα βρούμε επίσης ικανή και αναγκαία συνθήκη για να είναι κατασκευάσιμο κάποιο σημείο του πραγματικού επιπέδου. Τέλος, θα δώσουμε μία, κατά βάση αλγεβρική, απόδειξη του Θεμελιώδους Θεωρήματος της λΑλγεβρας.

6.1 Επιλυσιμότητα με ριζικά

Στην Ενότητα 1.1.2 δώσαμε μία ιστορική αναφορά για την εύρεση των ριζών ενός πολυωνύμου με συντελεστές από το ${\mathbb{Q}}$ . Είδαμε ότι υπάρχουν τύποι για την εύρεση ριζών όλων των πολυωνύμων του $\mathbb{Q}[x]$ με βαθμό $\leq 4$ . Είδαμε επίσης, ότι υπάρχουν πολυώνυμα βαθμού μεγαλύτερου του $4$ που επιλύονται με ριζικά και οι ρίζες τους προκύπτουν από συνδυασμό πράξεων, όπως η πρόσθεση, ο πολλαπλασιασμός αλλά και εξαγωγή ριζικών στοιχείων του ${\mathbb{Q}}$ . Στο εδάφιο αυτό θα αποδείξουμε το σημαντικό Θεώρημα του Galois, όπου δίνεται μία ικανή και αναγκαία συνθήκη για να είναι ένα πολυώνυμο επιλύσιμο με ριζικά.

Θα ξεκινήσουμε με τον ακριβή ορισμό της έκφρασης «επιλύεται με ριζικά», όπως προκύπτει από την μελέτη των αλγεβρικών επεκτάσεων σωμάτων που έχουμε αναπτύξει.

Ορισμός 6.1.1.

Έστω $F\subset{\mathbb{C}}$ ένα σώμα και $a$ ένα στοιχείο του ${\mathbb{C}}$ αλγεβρικό πάνω από το $F$ . Θα λέμε ότι το στοιχείο $α$ εκφράζεται με ριζικά (expressed with radicals) αν ανήκει σε ένα σώμα $Ε$ τέτοιο ώστε να υπάρχει μία ακολουθία σωμάτων

F=F_{0}\subset F_{1}\subset\cdots F_{i}\subset F_{i+1}\subset\cdots\subset F_{% s}=E,

(6.1.1.1)

για κάποιον φυσικό αριθμό $s$ , όπου

F_{i+1}=F_{i}\left(\sqrt[n_{i}]{a_{i}}\right),

για κάποιο $a_{i}\in F_{i}$ και $n_{i}$ φυσικό αριθμό, $0\leq i\leq{s-1}$ . Me $\sqrt[n_{i}]{a_{i}}$ συμβολίζουμε μία ρίζα του πολυωνύμου

x^{n_{i}}-a_{i}\in F_{i}[x].

H ακολουθία (6.1.1.1) λέγεται ριζική ακολουθία (radical sequence) σωμάτων ριζική ακολουθία και η επέκταση $E/F$ λέγεται ριζική επέκταση (radical extension). Ένα πολυώνυμο $f(x)\in F[x]$ λέγεται επιλύσιμο με ριζικά (resolved by radicals) πάνω από το $F$ αν κάθε ρίζα του εκφράζεται με ριζικά, δηλ. αν υπάρχει μία ριζική επέκταση που περιέχει το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ .

Παραδείγματα 6.1.2.

1.

Aν $\omega$ είναι μία $n$ -ρίζα της μονάδας, τότε το $\omega$ εκφράζεται με ριζικά πάνω από το ${\mathbb{Q}}$ , ως ρίζα του πολυωνύμου $x^{n}-1\in{\mathbb{Q}}[x]$ , σύμφωνα με την ριζική ακολουθία σωμάτων ${\mathbb{Q}}\subsetneq{\mathbb{Q}}(\omega)$ .
2.
Έστω $a=1+\sqrt{2}+\sqrt{1+\sqrt{2}}$ και $b={1+\sqrt{2}}$ . Θεωρούμε την ακολουθία

${\mathbb{Q}}\subsetneq{\mathbb{Q}}\left(\sqrt{2}\right)\subsetneq F_{1}(\sqrt{% b}).$

Η ακολουθία αυτή είναι ριζική. Πράγματι, έστω $F_{1}={\mathbb{Q}}\left(\sqrt{2}\right)$ και $F_{2}=F_{1}(\sqrt{b})$ . Τότε
- –
  
  Το $\sqrt{2}$ είναι ρίζα του $x^{2}-2\in{\mathbb{Q}}[x]$ ,
- –
  
  Το $\sqrt{b}$ είναι ρίζα του $x^{2}-(1+\sqrt{2})\in F_{1}[x]$ ,
- –
  
  Το $a\in F_{2}$ .
Επομένως, το $a$ εκφράζεται με ριζικά πάνω από το ${\mathbb{Q}}$ . Ο αναγνώστης καλείται να αποδείξει ότι h $F_{2}/F_{1}$ είναι γνήσια επέκταση του $F_{1}$ , (βλ. άσκηση 6.4.1).
3.

Έστω $F\subset{\mathbb{C}}$ ένα σώμα που περιέχει όλες τις $n$ -ρίζες της μονάδας, δηλ. τις ρίζες του $x^{n}-1\in F[x]$ . An $a\in F$ , τότε το πολυώνυμο $f(x)=x^{n}-a\in F[x]$ είναι επιλύσιμο με ριζικά, με ριζική ακολουθία την

$F\subset F\left(\sqrt[n]{a}\right).$
4.

Η επέκταση ${\mathbb{Q}}\subset{\mathbb{Q}}\left(\sqrt[3]{2}\right)$ είναι ριζική, αλλά όχι επέκταση του Galois.
5.
Έστω $f(x)=x^{3}+q(x)+r\in\mathbb{Q}[x]$ . Οι ρίζες του $f(x)$ δίνονται από τους τύπους $y+z,\omega y+\omega_{3}^{2}z,\omega^{2}y+\omega z$ , όπου

$\omega=e^{2\pi i/3}\ ,$

$y=\left(\frac{1}{2}\left(-r+\sqrt{r^{2}+\frac{4q^{3}}{27}}\right)\right)^{% \frac{1}{3}}$

και

$z=\left(\frac{1}{2}\left(-r-\sqrt{r^{2}+\frac{4q^{3}}{27}}\right)\right)^{% \frac{1}{3}},$

(βλ. Ενότητα V του Παραρτήματος). Παρατηρούμε ότι οι ρίζες του $f(x)$ εκφράζονται με την βοήθεια των πράξεων της πρόσθεσης και του πολλαπλασιασμού και με την εξαγωγή ριζών δευτέρου και τρίτου βαθμού. Το σώμα $L=\mathbb{Q}(y+z,\omega y+\omega^{2}z,\omega^{2}y+\omega z)$ είναι σώμα ανάλυσης του $f(x)$ . Θέτουμε $b={r^{2}+{4q^{3}}/{27}}$ και θεωρούμε τα στοιχεία

$\alpha_{1}=e^{2\pi i/6},\ \alpha_{2}=\sqrt{b},\ \alpha_{3}=y,\ a_{4}=z$

και τα αντίστοιχα σώματα

$Β_{1}={\mathbb{Q}}(\alpha_{1}),\ B_{2}=B_{1}(\alpha_{2}),\ B_{3}=B_{2}(\alpha_% {3}),\ B_{4}=B_{3}(\alpha_{4}).$

Είναι φανερό ότι $L\subset B_{4}$ αφού $w=\alpha_{1}^{2}\in B_{4}$ και όλες οι ρίζες του $f(x)$ ανήκουν στο $B_{4}$ . Η ακολουθία

${\mathbb{Q}}\subsetneq Β_{1}\subset Β_{2}\subset Β_{3}\subset Β_{4}$ (6.1.2.1)

είναι ριζική αφού

$b\in B_{1},\ \ \alpha_{3}^{3}=\frac{-r+\alpha_{2}}{2}\in B_{2},\ \ \alpha_{4}^% {3}=\frac{-r-\alpha_{2}}{2}\in B_{4}$

και
- –
  
  $\alpha_{1}$ είναι ρίζα του $x^{12}-1\in{\mathbb{Q}}[x]$ ,
- –
  
  $\alpha_{2}$ είναι ρίζα του $x^{2}-b\in B_{1}[x]$ ,
- –
  
  $\alpha_{3}$ είναι ρίζα του $x^{3}-\alpha_{3}^{3}\in B_{2}[x]$ ,
- –
  
  $\alpha_{4}$ είναι ρίζα του $x^{3}-\alpha_{4}^{3}\in B_{3}[x]$ .
επομένως, το πολυώνυμο $f(x)$ επιλύεται με ριζικά. Σημειώνουμε ότι αφού $\omega\in B_{1}$ , οι 3 ρίζες του $x^{3}-\alpha_{3}^{3}$ , δηλ. οι $a_{3},\omega a_{3}$ , $\omega^{2}a_{3}$ ανήκουν στο $Β_{3}$ . Επομένως Το $B_{3}$ είναι Το σώμα ανάλυσης του πολυωνύμου $x^{3}-\alpha_{3}^{3}\in B_{2}[x]$ .

Το επόμενο θεώρημα οφείλεται στον Galois και δίνει ικανή και αναγκαία συνθήκη για να είναι το πολυώνυμο $f(x)$ είναι επιλύσιμο με ριζικά. Παραπέμπουμε στο Παράρτημα I για τους σχετικούς ορισμούς και τα αναγκαία θεωρήματα από τη Θεωρία Ομάδων.

Θεώρημα 6.1.3 (Θεώρημα του Galois).

Έστω $F\subset{\mathbb{C}}$ ένα σώμα, $f(x)\in F[x]$ με σώμα ανάλυσης το $L \subset C$ . Tο πολυώνυμο $f(x)$ είναι επιλύσιμο με ριζικά πάνω από το ${\mathbb{Q}}$ αν και μόνο αν η ομάδα $\operatorname{Gal}(L/F)$ είναι επιλύσιμη.

Απόδειξη.

Έστω $G=\operatorname{Gal}(L/F)$ και έστω ότι το πολυώνυμο $f(x)\in F[x]$ είναι επιλύσιμο με ριζικά. Τότε υπάρχει μία ριζική επέκταση $E/F$ , τέτοια ώστε το σώμα ανάλυσης $L$ του $f(x)$ να περιέχεται στο $Ε$ . Εφόσον η επέκταση $E/F$ είναι ριζική, υπάρχει μία ριζική ακολουθία

F=F_{0}\subset F_{1}\subset\cdots\subset F_{s}=E,

(6.1.3.1)

για κάποιον φυσικό αριθμό $s$ , όπου για $1\leq i\leq{s}$ , $F_{i}=F_{i-1}(\sqrt[n_{i}]{a_{i}})$ , τα $a_{i}\in F_{i-1}$ και οι $n_{i}$ είναι φυσικοί αριθμοί. Όμως, η επέκταση $F_{s} / F$ μπορεί να μην είναι επέκταση του Galois και δεν μπορούμε να εφαρμόσουμε άμεσα τα εργαλεία της Θεωρίας Galois. Έστω λοιπόν

n = Ε Κ Π (n_{1}, \dots, n_{s}), ω = e^{2 π i / n}, F_{i}^{'} = F_{i} (ω), για 0 \leq i \leq s .

Τότε η ακολουθία

F\subsetneq F_{0}^{\prime}\subset F_{1}^{\prime}\cdots\subset F_{s}^{\prime}.

(6.1.3.2)

είναι ριζική, αφού $F_{i}^{'} = F_{i - 1}^{'} (\sqrt[n_{i}]{a_{i}})$ και $a_{i} \in F_{i - 1}^{'}$ , για $1 \leq i \leq s$ . Επιπλέον, αφού $ω$ είναι ρίζα τou $x^{n} - 1 \in F [x]$ , έπεται ότι η επέκταση $F_{i}^{'} / F_{i - 1}^{'}$ είναι επέκταση του Galois, ως σώμα ανάλυσης του πολυωνύμου

x^{n_{i}} - a_{i} \in F_{i - 1}^{'} [x] .

Παρατηρούμε, επίσης, ότι σύμφωνα με το Θεώρημα 5.1.4, η ομάδα

G a l (F_{0}^{'} / F) = G a l (F (ω) / F)

είναι αβελιανή και άρα επιλύσιμη. Έστω, τώρα, ότι $Κ \subset F_{s}^{'}$ είναι το σώμα ανάλυσης του $f (x) (x^{n} - 1) \in F [x]$ . Αφού $ω \in K$ και $F_{0}^{'} = F (ω)$ , έπεται ότι $F_{0}^{'} \subset K$ , ενώ είναι φανερό ότι $L \subset Κ$ . Η παρακάτω εικόνα απεικονίζει την κατάσταση:

Παρατηρούμε ότι, για να δείξουμε ότι η ομάδα $G = G a l (L / F)$ είναι επιλύσιμη, αρκεί να δείξουμε ότι η ομάδα $G a l (K / F_{0}^{'})$ είναι επιλύσιμη. Πράγματι, έστω ότι η κανονική υποομάδα $G a l (K / F_{0}^{'})$ της $G a l (K / F)$ είναι επιλύσιμη ομάδα. Όπως είδαμε παραπάνω, η ομάδα πηλίκο (βλ. Θεώρημα 3.3.2):

G a l (K / F) / G a l (K / F_{0}^{'}) ≅ G a l (F_{0}^{'} / F)

είναι επιλύσιμη. Επομένως, σύμφωνα με το Θεώρημα Ι.29.ii, η ομάδα $G a l (K / F)$ είναι επιλύσιμη. Όμως, η ομάδα $G a l (L / F)$ είναι ομάδα πηλίκο της $G a l (K / F)$ :

G a l (K / F) / G a l (K / L) ≅ G a l (L / F) .

Συνεπώς, σύμφωνα με το Θεώρημα Ι.29.ii, η ομάδα $G a l (L / F)$ είναι επιλύσιμη.

Στη συνέχεια, θα αποδείξουμε ότι η ομάδα $G a l (K / F_{0}^{'})$ είναι επιλύσιμη. Θα χρησιμοποιήσουμε επαγωγή στο $s$ , το μήκος της ριζικής ακολουθίας

F_{0}^{'} \subset F_{1}^{'} \dots \subset F_{s}^{'} .

Έστω ότι $s = 1$ . Τότε η $F_{1}^{'} / F_{0}^{'}$ είναι επέκταση Galois, αφού το $F_{1}^{'}$ είναι το σώμα ανάλυσης του διαχωρίσιμου πολυωνύμου $x^{n_{1}} - a_{1} \in F_{0}^{'} [x]$ . Σύμφωνα με το Θεώρημα 5.3.6, η ομάδα $G a l (F_{1}^{'} / F_{0}^{'})$ είναι κυκλική και άρα επιλύσιμη. Επομένως, η ομάδα $G a l (K / F_{0}^{'})$ είναι επιλύσιμη, ως ομάδα πηλίκο της $G a l (F_{1}^{'} / F_{0}^{'})$ .

Έστω τώρα ότι $s > 1$ . Θεωρούμε $Κ^{'} \subset F_{s}^{'}$ το σώμα ανάλυσης του διαχωρίσιμου πολυωνύμου $g (x) = f (x) (x^{n_{1}} - a_{1}) \in F_{0}^{'} [x]$ . Παρατηρούμε ότι $F_{1}^{'} \subset K^{'}$ και ότι η επέκταση $Κ^{'} / F_{1}^{'}$ είναι επέκταση του Galois. Eστιάζουμε, λοιπόν, στην επέκταση του Galois $Κ^{'} / F_{1}^{'}$ και στο πολυώνυμο $g (x) \in F_{1}^{'} [x]$ . Το $g (x)$ επιλύεται με ριζικά, όπως είναι φανερό από τη ριζική ακολουθία

F_{1}^{'} \subset F_{2}^{'} \dots \subset F_{s}^{'} .

(6.1.3.3)

Σύμφωνα με την υπόθεση της επαγωγής, η ομάδα $G a l (K^{'} / F_{1}^{'})$ είναι επιλύσιμη ομάδα. Από το παρακάτω διάγραμμα:

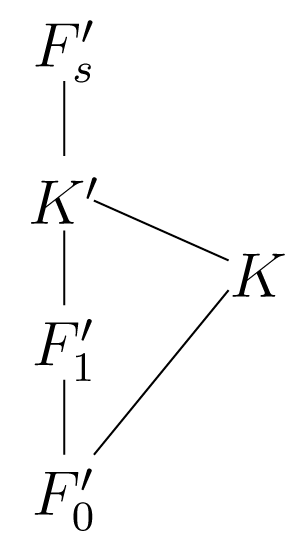
συμπεραίνουμε, όπως και προηγουμένως, ότι η $G a l (K^{'} / F_{0}^{'})$ είναι επιλύσιμη ομάδα με ομάδα πηλίκο την ομάδα $G a l (K / F_{0}^{'})$ . Άρα η $G a l (K / F_{0}^{'})$ είναι επιλύσιμη ομάδα. Επομένως, αποδείξαμε ότι αν το πολυώνυμο $f (x) \in F [x]$ είναι επιλύσιμο με ριζικά πάνω από το $F$ , τότε η ομάδα $G a l (L / F)$ είναι επιλύσιμη.

Αντίστροφα, ας υποθέσουμε ότι η $G=\operatorname{Gal}(L/F)$ είναι επιλύσιμη. Θεωρούμε μία πρωταρχική $m$ -ρίζα της μονάδας $\omega$ , όπου $m=|G|$ . Παρατηρούμε ότι, αφού $F\subset L$ , το μικρότερο σώμα που περιέχει τα σώματα $L$ και $F(\omega)$ ταυτόχρονα, δηλ. το $LF(\omega)$ , είναι το σώμα $L(\omega)$ . Έτσι, έχουμε το διάγραμμα σωμάτων που απεικονίζεται στο Σχήμα 6.1.

Σχήμα 6.1: Διάγραμμα υποσωμάτων του $L(\omega)$

Η επέκταση $L(\omega)/L$ είναι επέκταση του Galois, αφού είναι σώμα ανάλυσης του διαχωρισίμου πολυωνύμου $x^{m}-1\in L[x]$ . Επίσης, $L(\omega)/F(\omega)$ είναι επέκταση του Galois, αφού είναι σώμα ανάλυσης του $f(x)\in F(\omega)$ , βλ. άσκηση 3.7.13. Σύμφωνα με το Θεώρημα 3.5.3, έπεται ότι

\operatorname{Gal}\left(L(\omega)/F(\omega)\right)\cong\operatorname{Gal}\left% (L/(F(\omega)\cap L)\right).

Έστω $Η=\operatorname{Gal}\left(L(\omega)/F(\omega)\right)$ . O παραπάνω ισομορφισμός δείχνει ότι η $Η$ είναι ισόμορφη με υποομάδα της $G$ . Επειδή η ομάδα $G$ είναι επιλύσιμη, έπεται ότι και η $Η$ είναι επιλύσιμη και υπάρχει μία κανονική σειρά από υποομάδες της $Η$ , με κυκλικούς παράγοντες τάξης πρώτου αριθμού (Θεώρημα I.29):

H=Η_{0}\mathrel{\rhd}Η_{1}\cdots\mathrel{\rhd}Η_{r}=\{e\},

όπου $|Η_{i}/H_{i+1}|=p_{i}$ , για κάποιον πρώτο φυσικό αριθμό $p_{i}$ , $0\leq i\leq r$ . Παρατηρούμε ότι ο $p_{i}$ διαιρεί την τάξη της $H$ , για $0\leq i\leq r$ , όπως μπορεί εύκολα να αποδειχθεί με επαγωγή στο $r$ και με το Θεώρημα του Lagrange. Επομένως, ο $p_{i}$ διαιρεί την τάξη της $G$ , δηλ. $p_{i}|m$ , για $0\leq i\leq r$ . Στη συνέχεια, θεωρούμε το σώμα

E_{i}=L(\omega)^{H_{i}},\ 0\leq i\leq r.

Αφού $H_{i}$ είναι υποομάδα της $\operatorname{Gal}\left(L(\omega)/F(\omega)\right)$ , το σώμα $Ε_{i}$ είναι ενδιάμεσο σώμα της επέκτασης $L(\omega)/F(\omega)$ και έτσι προκύπτει η παρακάτω ακολουθία σωμάτων

F(\omega)=E_{0}\subset E_{1}\subset\cdots\subset E_{r}=L(\omega).

(6.1.3.4)

Παρατηρούμε ότι, για $1\leq i\leq r$ , η επέκταση $E_{i}/E_{i-1}$ είναι κυκλική, αφού σύμφωνα με το Θεμελιώδες Θεώρημα της Θεωρίας Galois

\operatorname{Gal}(E_{i}/E_{i-1})\cong H_{i-1}/H_{i}\textrm{ και άρα }[E_{i}:E% _{i-1}]=p_{i}.

Αφού $\omega$ είναι πρωταρχική $m$ -ρίζα της μονάδας και ανήκει σε κάθε $E_{i}$ και $p_{i}\;|\;m$ , για $0\leq i\leq r$ , είναι φανερό ότι Το $E_{i}$ περιέχει όλες τις $p_{i}$ -ρίζες της μονάδας. Επομένως από το Θεώρημα 5.3.6 προκύπτει ότι, για $0\leq i\leq r$ , υπάρχει $a_{i}\in E_{i-1}$ , τέτοιο ώστε

E_{i}=E_{i-1}\left(\sqrt[p_{i}]{a_{i}}\right).

’ρα η ακολουθία σωμάτων

F\subset F(\omega)=E_{0}\subset E_{1}\subset\cdots\subset E_{r}=L(\omega)

είναι μία ριζική ακολουθία, δηλ. η $L(\omega)/F$ είναι μία ριζική επέκταση, η οποία περιέχει το σώμα ανάλυσης $L$ του $f(x)\in F[x]$ . Άρα το $f(x)$ είναι επιλύσιμο με ριζικά. ∎

Παραδείγματα 6.1.4.

Έστω $f(x)=x^{5}-4x+2\in{\mathbb{Q}}[x]$ και έστω $Ε$ το σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ . Στο Παράδειγμα 3.2.6 αποδείξαμε ότι $\operatorname{Gal}(E/{\mathbb{Q}})\cong S_{5}$ . Αφού η $G$ δεν είναι επιλύσιμη (βλ. Θεώρημα I.35) το $f(x)$ δεν είναι επιλύσιμο με ριζικά.

Στι [6, 4.5] αναφέρεαι ένας αλγόριθμος επίλυσης ενός πολωνύμου επιλύσιμου με ριζικά. Επίσης, στο [6,4.9] δίνεται η μέθοδος του Lagrange για τον υπολογισμό της ομάδας του Galois ενός ανάγωγου πολυώνυμου χωρίς τον υπολογισμό των ριζών του πολυώνυμου και με τη χρήση της επιλύουσας του Lagrange.

6.2 Κατασκευάσιμοι αριθμοί και πολύγωνα

Στην Ενότητα 1.1.3, εισάγαμε το θέμα των κατασκευών με κανόνα και διαβήτη. Ένα σημείο του επιπέδου είναι κατασκευάσιμο (constructible) αν προκύπτει ως σημείο τομής κατασκευάσιμων ευθειών και κύκλων. Θυμίζουμε ότι για να είναι μία ευθεία κατασκευάσιμη, είναι αναγκαίο να έχουν προσδιοριστεί δύο κατασκευάσιμα σημεία επί της ευθείας, ενώ για να είναι ένας κύκλος κατασκευάσιμος, είναι αναγκαίο το κέντρο και η ακτίνα του κύκλου να είναι κατασκευάσιμα. Αν ταυτίσουμε την αρχική κατασκευάσιμη ευθεία με την ευθεία των πραγματικών αριθμών, το ζήτημα που τίθεται είναι ο προσδιορισμός των πραγματικών αριθμών που είναι κατασκευάσιμοι. Στην ενότητα 1.1.3, είδαμε ότι αν $F$ είναι το σύνολο των κατασκευάσιμων αριθμών, τότε το $F$ είναι υπόσωμα του $\mathbb{R}$ . Αυτόματα, λοιπόν, το $F$ περιέχει ως πρώτο σώμα τους ρητούς. Είδαμε επίσης ότι αν $a\in\mathbb{R}$ και $a^{2}\in\mathbb{Q}$ , τότε $a\in F$ . Έτσι είναι φανερό ότι

{\mathbb{Q}}\subsetneq F\subset{\mathbb{R}}

και ότι ο βαθμός $[F:{\mathbb{Q}}]=\infty$ , βλ. άσκηση 6.4.4. Ποιοι πραγματικοί αριθμοί είναι, λοιπόν, κατασκευάσιμοι; Η κατασκευή κατασκευάσιμων σημείων γίνεται με τη χρήση εργαλείων με αναφορά στο επίπεδο (τον κανόνα και τον διαβήτη). Για να μπορέσουμε να απαντήσουμε στο παραπάνω ερώτημα, θα εισάγουμε την έννοια του πλέγματος του $K$ (lattice of $K$ ), δηλ. το σύνολο $Κ\times K$ , για κάθε ενδιάμεσο σώμα της επέκτασης $F/{\mathbb{Q}}$ . Γεωμετρικά, για κάθε τέτοιο σώμα $K$ , τοποθετούμε το πλέγμα του $Κ$ εντός του ${\mathbb{R}}^{2}$ . Έτσι, αν το $k\in K$ , το στοιχείο $(k,0)$ εμφανίζεται με κόκκινο στο σχήμα 6.2.

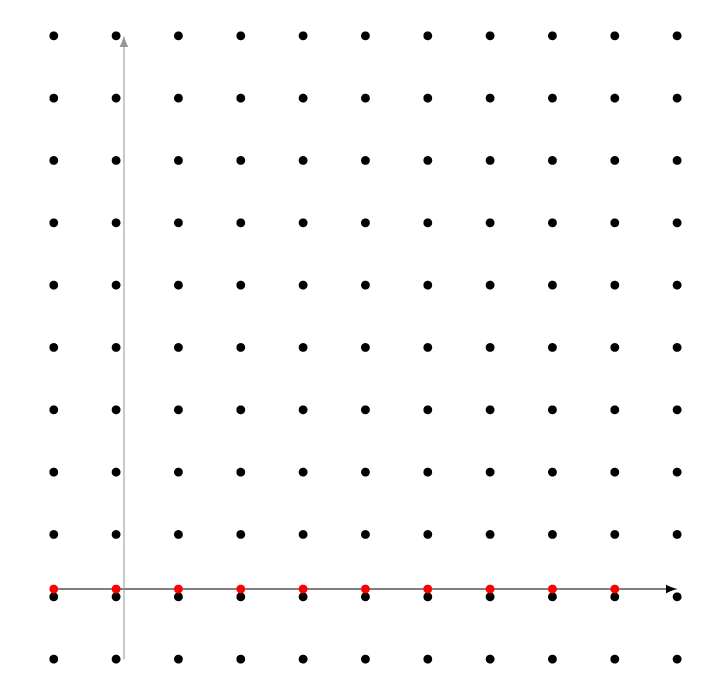
Σχήμα 6.2: Το πλέγμα του $\color{red}\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{1}{0}{0}% \pgfsys@color@rgb@fill{1}{0}{0}K$ στο ${\mathbb{R}}^{2}$ .

Σημειώνουμε ότι τα στοιχεία του $Κ$ είναι κατασκευάσιμοι αριθμοί. Είναι εύκολο να συμπεράνει κανείς ότι τα σημεία του πλέγματος του $Κ$ είναι κατασκευάσιμα. Θα λέμε ότι μία ευθεία είναι κατασκευάσιμη εντός του $K$ αν περνά από δύο σημεία του πλέγματος του $Κ$ . Θα λέμε ότι ένας κύκλος είναι κατασκευάσιμος εντός του $K$ αν το κέντρο του είναι στο πλέγμα του $Κ$ και η ακτίνα του είναι στο $Κ$ . Θα λέμε ότι ένα σημείο κατασκευάζεται από το $Κ$ σε ένα βήμα, αν το σημείο προκύπτει ως σημείο τομής είτε δύο ευθειών κατασκευάσιμες εντός του $Κ$ , είτε μίας ευθείας και ενός κύκλου κατασκευάσιμων εντός του $Κ$ , είτε δύο κύκλων κατασκευάσιμων εντός του $Κ$ . Αφήνουμε την απόδειξη των προτάσεων της επόμενης παρατήρησης ως εύκολη άσκηση για τον αναγνώστη, βλ. άσκηση 6.4.5.

Παρατήρηση 6.2.1.

Έστω ότι $Κ$ είναι ενδιάμεσο σώμα της επέκτασης $F/{\mathbb{Q}}$ , όπου $F$ το υπόσωμα των κατασκευάσιμων αριθμών στο ${\mathbb{R}}$ .

i)

Aν $c\in F$ , τότε τα στοιχεία του $Κ(c)$ είναι και αυτά στο $F$ .
ii)

Αν $l$ είναι μία κατασκευάσιμη ευθεία εντός του $Κ$ , τότε η εξίσωση της ευθείας είναι της μορφής $ax+by+c=0$ , όπου $a,b,c\in K$ .
iii)

Αν $C$ είναι ένας κύκλος κατασκευάσιμος εντός του $K$ , τότε η εξίσωση του $C$ είναι της μορφής $x^{2}+y^{2}+ax+by+c=0$ όπου $a,b,c\in K$ .

Έστω, λοιπόν, ότι $K$ είναι ενδιάμεσο σώμα της επέκτασης $F/{\mathbb{Q}}$ , όπου $F$ το υπόσωμα των κατασκευάσιμων αριθμών στο ${\mathbb{R}}$ . Είναι φανερό ότι η τομή δύο ευθειών με συντελεστές από το $Κ$ θα δώσει σημείο που ήδη βρίσκεται στο πλέγμα του $Κ$ . Επίσης είναι εύκολο να δει κανείς ότι το πρόβλημα εύρεσης σημείου τομής δύο κύκλων ανάγεται στο πρόβλημα εύρεσης τομής ενός κύκλου και μίας ευθείας, βλ. άσκηση 6.4.6. Έτσι, για να βρούμε σημεία κατασκευάσιμα από το $Κ$ εκτός του πλέγματος του $Κ$ αρκεί να επικεντρωθούμε σε σημεία τομής μίας ευθείας και ενός κύκλου με συντελεστές από το $Κ$ .

Λήμμα 6.2.2.

Έστω $Κ$ υπόσωμα του ${\mathbb{R}}$ . Αν $l:\ ax+by+c=0$ είναι μία ευθεία στο ${\mathbb{R}}^{2}$ , όπου $a,b,c\in K$ και $C:\ x^{2}+y^{2}+dx+ey+f=0$ είναι ένας κύκλος στο ${\mathbb{R}}^{2}$ , όπου $d,e,f\in K$ , έτσι ώστε $l, C$ να έχουν σημεία τομής στο ${\mathbb{R}}^{2}$ , τότε υπάρχει $q\in\mathbb{R}$ τέτοιος ώστε τα σημεία τομής των $l$ και $C$ να ανήκουν στο πλέγμα του $K(q)$ .

Απόδειξη.

Έστω ότι $a\neq 0$ . Λύνοντας την εξίσωση της $l$ ως προς το $a$ και αντικαθιστώντας στην εξίσωση του $C$ προκύπτει μία εξίσωση δευτέρου βαθμού ως προς το $y$ με συντελεστές από το $Κ$ . Η τετραγωνική ρίζα της διακρίνουσας είναι το ζητούμενο $q$ . Σημειώνουμε, ότι αφού $l, C$ τέμνονται, η διακρίνουσα είναι θετική και $q\in{\mathbb{R}}$ . Αν $a=0$ , κάνουμε το αντίστοιχο λύνοντας ως προς $y$ . ∎

Είναι φανερό ότι αν ένα σημείο στο επίπεδο είναι κατασκευάσιμο, τότε το σημείο τομής της ευθείας που περνά από αυτό το σημείο και είναι κάθετη στη πραγματική ευθεία είναι κατασκευάσιμο, βλ. άσκηση 1.5.1. Διαδοχική, λοιπόν, εφαρμογή του παραπάνω Λήμματος οδηγεί στο εξής συμπέρασμα:

Θεώρημα 6.2.3.

Το $c\in\mathbb{R}$ είναι κατασκευάσιμο αν και μόνο αν υπάρχει μία ακολουθία σωμάτων

\mathbb{Q}=Κ_{0}\subset K_{1}\cdots\subset K_{t}

έτσι ώστε $c\in K_{t}$ και $[K_{i+1}:K_{i}]=2$ , $i=1,\ldots,t-1$ .

Απόδειξη.

Οι παρατηρήσεις πριν την εκφώνηση του Θεωρήματος 6.2.3, δείχνουν ότι η συνθήκη είναι αναγκαία. Για την αντίστροφη κατεύθυνση, θα δείξουμε ότι αν $K$ είναι ενδιάμεσο σώμα της επέκτασης $F/{\mathbb{Q}}$ , όπου $F$ το υπόσωμα των κατασκευάσιμων αριθμών στο ${\mathbb{R}}$ και $L/K$ είναι μία επέκταση με $[L:K]=2$ , τότε $L\subset F$ . Πράγματι, έστω $a$ ένα στοιχείο του $L$ που δεν ανήκει στο $K$ . Tότε $K(a)=L$ και $\deg\operatorname{irr}_{(K,a)}(x)=2$ . Έστω ότι

f(x)=\operatorname{irr}_{(K,a)}(x)=x^{2}+bx+c.

Οι ρίζες του $f(x)$ , και επομένως και το $α$ , προκύπτουν από τον τύπο

\frac{-b\pm\sqrt{b^{2}-4ac}}{2}.

(6.2.3.1)

Αφού $b^{2}-4c\in K$ , έπεται ότι $\sqrt{b^{2}-4c}\in F$ (βλ. άσκηση 1.5.2). Αφού το $F$ είναι σώμα, από τον τύπο (6.2.3.1) συμπεραίνουμε ότι $a\in F$ . Αποδείξαμε, λοιπόν, ότι αν $K$ είναι ενδιάμεσο σώμα της επέκτασης $F/{\mathbb{Q}}$ , όπου $F$ το υπόσωμα των κατασκευάσιμων αριθμών στο ${\mathbb{R}}$ και $L/K$ είναι μία επέκταση με $[L:K]=2$ , τότε $L\subset F$ . Έστω, λοιπόν, ότι υπάρχει μία ακολουθία σωμάτων

\mathbb{Q}=Κ_{0}\subset K_{1}\cdots\subset K_{t}

έτσι ώστε $c\in K_{t}$ και $[K_{i+1}:K_{i}]=2$ , $i=1,\ldots,t-1$ . Εφαρμόζοντας διαδοχικά το προηγούμενο βήμα προκύπτει ότι το $c$ είναι κατασκευάσιμο. ∎

Tο παρακάτω συμπέρασμα προκύπτει άμεσα από το Θεώρημα 6.2.3.

Πόρισμα 6.2.4.

Αν το $c\in{\mathbb{R}}$ είναι κατασκευάσιμο, τότε το $c$ είναι αλγεβρικό στοιχείο πάνω από το $\mathbb{Q}$ και $\deg\operatorname{irr}_{(\mathbb{Q},c)}(x)=2^{n}$ , για $n\in{\mathbb{N}}_{\geq 0}$ .

Απόδειξη.

Έστω ότι το $c$ είναι κατασκευάσιμο και έστω $K_{0},\ldots,K_{t}$ , όπως στο Θεώρημα 6.2.3. Αφού $[K_{t}:\mathbb{Q}]=2^{t}$ , έπεται ότι ο βαθμός $[\mathbb{Q}(c):\mathbb{Q}]$ διαιρεί το $2^{t}$ . Επομένως, αφού $\deg\operatorname{irr}_{\mathbb{Q},c}(x)=[\mathbb{Q}(c):\mathbb{Q}]$ , έπεται ότι ο βαθμός του ανάγωγου πολυωνύμου του $c$ πάνω από το ${\mathbb{Q}}$ είναι μία δύναμη του 2. ∎

Παράδειγμα 6.2.5.

Το $a=\sqrt[3]{5}$ δεν είναι κατασκευάσιμο, αφού $\operatorname{irr}_{({\mathbb{Q}},a)}(x)=x^{3}-5$ .

Σημειώνουμε, ότι η συνθήκη του Πορίσματος 6.2.4 είναι αναγκαία αλλά δεν είναι ικανή για να είναι Το $c\in{\mathbb{R}}$ κατασκευάσιμο. Έτσι, το Πόρισμα 6.2.4 δεν είναι ισοδύναμο με το Θεώρημα 6.2.3. Σύμφωνα με την άσκηση 6.4.7, για να είναι το $c$ κατασκευάσιμο, είναι απαραίτητο ο βαθμός της επέκτασης $L/{\mathbb{Q}}$ πάνω από το ${\mathbb{Q}}$ να είναι δύναμη του $2$ , όπου $L$ το σώμα ανάλυσης του ανάγωγου πολυωνύμου του $c$ πάνω από το ${\mathbb{Q}}$ .

Παράδειγμα 6.2.6.

Έστω $f(x)=x^{4}+2x-2\in{\mathbb{Q}}[x]$ . Το $f(x)$ είναι ανάγωγο πάνω από το ${\mathbb{Q}}$ και δεν είναι δύσκολο να δει κανείς ότι το $f(x)$ έχει τουλάχιστον δύο πραγματικές ρίζες. Έστω $b$ μία πραγματική ρίζα του $f(x)$ στο σώμα ανάλυσης $L$ του $f(x)$ πάνω από το ${\mathbb{Q}}$ . Mπορεί να δείξει κανείς, ότι το $3$ διαιρεί την ομάδα $\operatorname{Gal}(L/Q)$ και επομένως, σύμφωνα με την άσκηση 6.4.7, το $b$ δεν είναι κατασκευάσιμο, (βλ. άσκηση 6.4.8).

Στη συνέχεια θα δώσουμε απαντήσεις στα άλυτα γεωμετρικά προβλήματα της αρχαιότητας.

Πόρισμα 6.2.7.

Mία γωνία $60^{\circ}$ δεν μπορεί να τριχοτομηθεί με κανόνα και διαβήτη.

Απόδειξη.

Έστω ότι ήταν δυνατόν να τριχοτομηθεί η γωνία των $60^{\circ}$ . Τότε θα ήταν δυνατόν να κατασκευασθεί ένα ορθογώνιο τρίγωνο με γωνίες $20^{\circ}$ και $70^{\circ}$ . Επομένως θα ήταν δυνατόν να κατασκευασθεί και ο πραγματικός αριθμός $\cos(20)$ ως πηλίκο δύο κατασκευάσιμων αριθμών, βλ. άσκηση 1.5.3. Έστω $a=\cos(20)$ . Aπό τους τριγωνομετρικούς τύπους γνωρίζουμε ότι

\cos(3\theta)=4\cos^{3}(\theta)-3\cos(\theta).

Αφού $\cos(60^{\circ})=1/2$ , συμπεραίνουμε ότι Το $a$ είναι ρίζα του πολυωνύμου $8x^{3}-6x-1$ . Το πολυώνυμο αυτό δεν έχει ρίζες στο $\mathbb{Q}$ και είναι ανάγωγο στο $\mathbb{Q}[x]$ . Επομένως,

\operatorname{irr}_{({\mathbb{Q}},a)}(x)=x^{3}-\frac{3}{4}x-\frac{1}{8},

και $[\mathbb{Q}(a)):\mathbb{Q}]=3$ . Επομένως Το $\cos(20^{\circ})$ δεν είναι κατασκευάσιμος αριθμός και ότι η γωνία $60^{\circ}$ δεν μπορεί να τριχοτομηθεί με κανόνα και διαβήτη. ∎

Πόρισμα 6.2.8.

Δεν είναι δυνατόν να διπλασιασθεί ένας κύβος με κανόνα και διαβήτη.

Απόδειξη.

Έστω κύβος με πλευρά 1. Ο νέος κύβος (διπλάσιο σε όγκο) έχει πλευρά μήκους $a=\sqrt[3]{2}$ . Το ανάγωγο πολυώνυμο του $a$ είναι $x^{3}-2$ και $[{\mathbb{Q}}(a):{\mathbb{Q}}]=3$ . Άρα Το $a$ δεν είναι κατασκευάσιμος αριθμός και ο κύβος δεν μπορεί να διπλασιαστεί με κανόνα και διαβήτη.∎

Πόρισμα 6.2.9.

Δεν είναι δυνατόν να τετραγωνίσουμε τον κύκλο.

Απόδειξη.

Έστω κύκλος με ακτίνα 1. Εάν ήταν δυνατό να κατασκευάσουμε ένα τετράγωνο με εμβαδό $\pi$ , τότε η ακμή του τετραγώνου θα είχε μήκος $\sqrt{\pi}$ . Όμως, o $\pi$ και κατά συνέπεια και ο $\sqrt{\pi}$ δεν είναι αλγεβρικοί αριθμοί πάνω από το ${\mathbb{Q}}$ . Επομένως o $\sqrt{\pi}$ δεν είναι κατασκευάσιμος και είναι αδύνατον να τετραγωνίσουμε τον κύκλο με κανόνα και διαβήτη. ∎

Θα εξετάσουμε τώρα ποιά κανονικά $p$ -γωνα είναι κατασκευάσιμα, όταν $p$ είναι περιττός πρώτος αριθμός. Παρατηρούμε ότι ένα κανονικό $n$ -γωνο είναι κατασκευάσιμο αν και μόνο αν η γωνία $2\pi i/n$ είναι κατασκευάσιμη (άσκηση 1.5.4). Έστω $\omega=2^{\pi i/n}$ . Το σώμα $L={\mathbb{Q}}(\omega)$ είναι σώμα ανάλυσης του διαχωρίσιμου πολυωνύμου $x^{n}-1$ . Επομένως, από την άσκηση 6.4.10 προκύπτει το επόμενο συμπέρασμα.

Πρόταση 6.2.10.

Το κανονικό $n$ -γωνο είναι κατασκευάσιμο αν και μόνο αν $[{\mathbb{Q}}(\omega):{\mathbb{Q}}]=2^{s}$ , όπου $\omega=2^{\pi i/n}$ .

Το επόμενο θεώρημα φέρει το όνομα του Gauss.

Θεώρημα 6.2.11 (Gauss).

Αν $p$ είναι περιττός πρώτος, τότε το κανονικό $p$ -γωνο είναι κατασκευάσιμο αν και μόνο αν

p=2^{2^{m}}+1,\ m\in\mathbb{N}.

Απόδειξη.

Έστω $p$ περιττός πρώτος, $\omega=e^{2\pi i/p}$ και έστω ότι το κανονικό $p$ -γωνο είναι κατασκευάσιμο. Τότε σύμφωνα με την Πρόταση 6.2.10, ο βαθμός $[\mathbb{Q}(\omega):\mathbb{Q}]$ είναι δύναμη του 2. Αφού

\operatorname{irr}_{(\mathbb{Q},\omega)}=x^{p-1}+\cdots+x+1,

έπεται ότι $p-1=2^{s}$ , για κάποιο $s\in{\mathbb{N}}_{\geq 0}$ . Θα πρέπει τότε και το $s$ να είναι δύναμη του 2. Πράγματι, αν υπάρχει περιττός αριθμός $k$ τέτοιος ώστε $s=κ\lambda$ , τότε ο αριθμός

p=2^{s}+1=(2^{\lambda})^{k}+1

έχει ως παράγοντα το $2^{\lambda}+1$ , αδύνατον αφού $p$ πρώτος. Άρα $p-1={2^{2}}^{m}$ , για κάποιο $m\geq 0$ .

Για την αντίστροφη κατεύθυνση έστω ότι

p={2^{2}}^{m}+1,\ m\in\mathbb{N}.

επομένως

|\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})|=p-1={2^{2}}^{m},

και σύμφωνα με την Πρόταση 6.2.10, το κανονικό $π$ -γωνο είναι κατασκευάσιμο. ∎

Οι πρώτοι αριθμοί της μορφής ${2^{2}}^{m}+1$ λέγονται πρώτοι αριθμοί του Fermat (Fermat’s prime). Αναφέρουμε χωρίς απόδειξη το θεώρημα που αφορά την περίπτωση του κανονικού $n$ -γώνου. Για την απόδειξη παραπέμπουμε στο [5, Theorem 1.1.6].

Θεώρημα 6.2.12 (Θεώρημα των Gauss-Wantzel).

Ένα κανονικό $n$ -γωνο είναι κατασκευάσιμο αν και μόνο αν

n=2^{s}p_{1}\cdots p_{r},

για κάποιον φυσικό $s$ , όπου $p_{1},\ldots,p_{r}$ είναι διακεκριμένοι πρώτοι αριθμοί του Fermat.

6.3 Θεμελιώδες Θεώρημα της Άλγεβρας

Στην Eνότητα 1.1.1, παρουσιάσαμε κάποια ιστορικά στοιχεία για το Θεμελιώδες Θεώρημα της Άλγεβρας. Το Θεμελιώδες Θεώρημα της Άλγεβρας, εγγυάται ότι κάθε πολυώνυμο με μιγαδικούς συντελεστές έχει μία ρίζα στο ${\mathbb{C}}$ . Ειδικότερα, από το Θεμελιώδες Θεώρημα της Άλγεβρας προκύπτει ότι αν $f(x)\in{\mathbb{R}}[x]$ , τότε $f(x)$ έχει μία ρίζα στο ${\mathbb{C}}$ και κατά συνέπεια το σώμα ανάλυσης του πολυωνύμου εμφυτεύεται στο ${\mathbb{C}}$ . Ισοδύναμα, όπως θα δούμε κατά τη διάρκεια της απόδειξης του Θεμελιώδους Θεωρήματος της Άλγεβρας, η ύπαρξη μιγαδικής ρίζας για πολυώνυμa με πραγματικούς συντελεστές, συνεπάγεται την ύπαρξη μιγαδικής ρίζας για πολυώνυμa με μιγαδικούς συντελεστές.

Η απόδειξη που δίνουμε σε αυτήν την ενότητα για το Θεμελιώδες Θεώρημα της Άλγεβρας έχει κυρίως αλγεβρικό χαρακτήρα. Βέβαια, ο μαθηματικός ορισμός του συνόλου των πραγματικών αριθμών χρησιμοποιεί τη γλώσσα της Μαθηματικής Ανάλυσης για την έννοια της πληρότητας. Έτσι ένα θεώρημα, που θεμελιωδώς αφορά το ${\mathbb{R}}$ , είναι αδύνατον να μην χρησιμοποιεί με κάποιο τρόπο αναλυτικά εργαλεία. Η απόδειξη που δίνουμε χρησιμοποιεί από την Μαθηματική Ανάλυση το Θεώρημα της Μέσης Τιμής (J.M.T) (Mean Value Theorem) για πολυώνυμα με πραγματικούς συντελεστές. O κύριος όμως κορμός της παρούσας σύντομης (σχετικά) απόδειξης του Θεμελιώδους Θεωρήματος της Άλγεβρας, στηρίζεται στην αντιστοιχία, ανάμεσα στις υποομάδες μία ομάδας Galois και τα ενδιάμεσα σώματα και χρειάζεται από τη Θεωρία Ομάδων, το Θεώρημα I.24. Για πληρότητα της παρουσίασης, υπενθυμίζουμε το βασικό Θεώρημα της Mέσης Tιμής, που βασίζεται στην πληρότητα του συνόλου των πραγματικών αριθμών και στην έννοια της συνέχειας.

Θεώρημα Μέσης Τιμής (Θ.Μ.Τ.)Έστω $f(x)\in\mathbb{R}[x]$ . Eάν υπάρχουν $a,b\in\mathbb{R}$ έτσι ώστε $f(a)>0$ και $f(b)<0$ , τότε υπάρχει $c\in\mathbb{R}$ έτσι ώστε $f(c)=0$ .

Σημειώνουμε τις παρακάτω συνέπειες του Θ.Μ.Τ.:

Πρόταση 6.3.1.

Έστω $a\in\mathbb{R}^{+}$ . Τότε υπάρχει $r\in\mathbb{R}^{+}$ έτσι ώστε $r^{2}=a$ .

Απόδειξη.

Έστω $f(x)=x^{2}-a\in\mathbb{R}[x]$ . Τότε $f(1+a)=1+a^{2}+a$ , άρα $f(1+a)>0$ . Aκόμη $f(0)=-a<0$ . Από το Θ.Μ.Τ. έπεται ότι υπάρχει $c$ έτσι ώστε $f(c)=0$ . Παρατηρούμε ότι οι ρίζες του $f(x)$ είναι οι $\pm c$ . Έτσι επιλέγουμε για $r$ τη θετική ρίζα του $f(x)$ . ∎

Συμβολίζουμε τον θετικό πραγματικό αριθμό $r$ της προηγούμενης πρότασης me $\sqrt{a}$ . Στη συνέχεια θεωρούμε τους μιγαδικούς αριθμούς. Oi μόνες παραδοχές που κάνουμε για τα στοιχεία του ${\mathbb{C}}$ είναι ότι

{\mathbb{C}}=\{a+bi:\ a,b\in{\mathbb{R}},\;i^{2}=-1\}

και ότι κάθε μιγαδικός αριθμός $z\in\mathbb{C}$ μπορεί να γραφεί στη μορφή $re^{i\theta}$ όπου $r\in\mathbb{R}^{+}$ . Δεν γνωρίζουμε a priori ότι ο μιγαδικός $z$ έχει τετραγωνική ρίζα στο ${\mathbb{C}}$ , δηλ. ότι υπάρχει κάποιο $w\in{\mathbb{C}}$ , τέτοιο ώστε $w^{2}={\mathbb{C}}$ . Αυτό, λοιπόν, διευκρινίζεται με την επόμενη πρόταση.

Πρόταση 6.3.2.

Έστω $z\in C$ . Τότε υπάρχει $w\in{\mathbb{C}}$ , τέτοιο ώστε $w^{2}\in{\mathbb{C}}$ .

Απόδειξη.

Έστω ότι $z=re^{i\theta}$ , όπου $r\in\mathbb{R}^{+}$ . Σύμφωνα με την Πρόταση 6.3.1, υπάρχει $\sqrt{r}\in\mathbb{R}^{+}$ και άρα $w=\sqrt{r}e^{i\theta/2}\in\mathbb{C}$ και $w^{2}=z$ . ∎

Συμβολίζουμε με $\sqrt{z}$ το $w$ της προηγούμενης πρότασης. Το επόμενο αποτέλεσμα αφορά την ύπαρξη ριζών (στο ${\mathbb{C}}$ ) για πολυώνυμα του ${\mathbb{C}}[x]$ δευτέρου βαθμού.

Πρόταση 6.3.3.

Έστω $f(x)=z_{1}x^{2}+z_{2}x+z_{3}\in\mathbb{C}[x]$ , $\deg f(x)=2$ . Υπάρχει $\alpha\in\mathbb{C}$ , τέτοιο ώστε $f(\alpha)=0$ . Επομένως, δεν υπάρχει ανάγωγο πολυώνυμο στο ${\mathbb{C}}[x]$ βαθμού 2.

Απόδειξη.

Θα χρησιμοποιήσουμε τον γνωστό τύπο της δευτεροβάθμιας εξίσωσης. Από τηn Πρόταση 6.3.2 υπάρχει μιγαδικός αριθμός $\sqrt{z_{2}^{2}-4z_{1}z_{3}}$ . Εύκολα επιβεβαιώνει κανείς ότι οι μιγαδικοί αριθμοί

\frac{-z_{2}\pm\sqrt{z_{2}^{2}-4z_{1}z_{3}}}{2z_{1}},

είναι ρίζες του $f(x)$ . ∎

Πρόταση 6.3.4.

Το σώμα $\mathbb{C}$ δεν έχει επέκταση βαθμού $2$ .

Απόδειξη.

Έστω $[E:\mathbb{C}]=2$ . Τότε υπάρχει $a\in E\setminus\mathbb{C}$ και αναγκαστικά $E=\mathbb{C}(a)$ . Επομένως $\deg\operatorname{irr}_{\mathbb{C},a}(x)=2$ . Προκύπτει άτοπο από την Πρόταση 6.3.3. ∎

Πρόταση 6.3.5.

Έστω $f(x)\in\mathbb{R}[x]$ ανάγωγο κανονικόπολυώνυμο. Τότε $\deg f(x)=2k$ .

Απόδειξη.

Αρκεί να αποδείξουμε ότι αν $f(x)\in{\mathbb{R}}[x]$ και $\deg f(x)$ είναι περιττός ακέραιος, τότε το $f(x)$ έχει τουλάχιστον μία ρίζα στον $\mathbb{R}$ . Έστω, λοιπόν, ότι

f(x)=a_{0}+a_{1}x+\cdots+x^{n}\in{\mathbb{R}}[x],\textrm{ όπου }n=2k+1.

Θέτουμε

t=1+\sum_{i=0}^{i=n-1}|a_{i}|>0.

Τότε

t-1=\sum_{i=0}^{i=n-1}|a_{i}|,\textrm{ άρα }|a_{i}|\leq t-1,\ \textrm{ για }i=% 0,\ldots,n-1.

Επομένως,

\displaystyle|a_{0}+\cdots+a_{n-1}t^{n-1}|\leq|a_{0}|+\cdots+|a_{n-1}|\;t^{n-1% }\leq(t-1)+\cdots+(t-1)t^{n-1}=\\ \displaystyle=(t-1)(1+t+\cdots+t^{n-1})=t^{n}-1<t^{n}.

Δηλαδή

\left|\sum_{i=0}^{n-1}a_{i}t^{i}\right|<t^{n},\textrm{ άρα }-t^{n}<a_{0}+a_{1}% t+\cdots+a_{n-1}t^{n-1}<t^{n}.

Επομένως,

0<(a_{0}+a_{1}t+\cdots+a_{n-1}t^{n-1})+t^{n}=f(t).

Παρατηρούμε επίσης ότι

\left|\sum_{i=0}^{n-1}a_{i}(-t)^{i}\right|\leq|a_{0}|t+|a_{1}|t+\cdots+|a_{n-1% }|t^{n-1}

και με τους ίδιους συλλογισμούς όπως προηγουμένως, οδηγούμαστε στις ανισότητες

-t^{n}\leq a_{0}-a_{1}t+\cdots-a_{n-2}t^{n-2}+a_{n-1}t^{n-1}\leq t^{n}.

Αφού $n=2k+1$ , έπεται ότι $(-t)^{n}=(-1)t^{n}$ και άρα

f(-t)=a_{0}-a_{1}t+\cdots-a_{n-2}t^{n-2}+a_{n-1}t^{n-1}-t^{n}<0.

Δείξαμε ότι an $n=2k+1$ , τότε $f(t)>0$ , ενώ $f(-t)<0$ . Σύμφωνα με το Θ.Μ.Τ. το $f(x)$ έχει μία πραγματική ρίζα. ∎

Πρόταση 6.3.6.

Έστω $L/\mathbb{R}$ μία πεπερασμένη επέκταση σωμάτων έτσι ώστε ${\mathbb{R}}\neq L$ . Τότε $[L:\mathbb{R}]=2ν$

Απόδειξη.

Έστω $a\in L$ , αλλά όχι στον $\mathbb{R}$ . Από την Πρόταση 6.3.5, ο βαθμός του $\operatorname{irr}_{(\mathbb{R},a)}(x)$ πρέπει να είναι άρτιος. Επομένως

[L:\mathbb{R}]=[L:\mathbb{R}(a)][\mathbb{R}(a):\mathbb{R}]

είναι άρτιος. ∎

Δίνουμε έμφαση στα συμπεράσματα των Προτάσεων 6.3.4, 6.3.6. Έχουμε δείξει ως τώρα ότι δεν υπάρχει επέκταση $L$ του ${\mathbb{C}}$ έτσι ώστε $[L:\mathbb{C}]=2$ , ενώ έχουμε επίσης δείξει ότι κάθε πεπερασμένη επέκταση του $\mathbb{R}$ πρέπει να είναι άρτιου βαθμού. Είμαστε έτοιμοι για την απόδειξη του κυρίου θεωρήματος αυτής της ενότητας.

Θεώρημα 6.3.7 (Θεμελιώδες Θεώρημα της Άλγεβρας).

Κάθε μη σταθερό πολυώνυμο του $\mathbb{C}[x]$ έχει μία μιγαδική ρίζα.

Απόδειξη.

Έστω $f(x)=\sum a_{i}x^{i}\in\mathbb{C}[x]$ . Με $\overline{f(x)}$ συμβολίζουμε το πολυώνυμο $\sum\overline{a_{i}}x^{i}$ , όπου $\overline{a}$ είναι ο συζυγής του $a\in{\mathbb{C}}$ . Παρατηρούμε ότι

\overline{f(x)\overline{f(x)}}=f(x)\overline{f(x)}

και άρα $f(x)\overline{f(x)}\in\mathbb{R}[x]$ . Ακόμη παρατηρούμε ότι

f(z)=0\Leftrightarrow\overline{f(\overline{z})}=0\ .

Άρα Το $f(x)$ έχει μιγαδική ρίζα αν και μόνο αν $f(x)\overline{f(x)}\in\mathbb{R}[x]$ έχει μιγαδική ρίζα. Aρκεί, λοιπόν, να αποδείξουμε ότι το θεώρημα ισχύει για πολυώνυμα με πραγματικούς συντελεστές. Αφού κάθε πολυώνυμo γράφεται μοναδικά ως γινόμενο αναγώγων, αρκεί να αποδείξουμε το θεώρημα για ανάγωγα πολυώνυμα του $\mathbb{R}[x]$ .

Έστω, λοιπόν, $p(x)\in\mathbb{R}[x]$ ανάγωγο πολυώνυμο. Θα θεωρήσουμε το πολυώνυμο

q(x)=(x^{2}+1)p(x)\in{\mathbb{C}}[x].

Έστω $L$ Το σώμα ανάλυσης του $q(x)$ πάνω από το $\mathbb{C}$ (Θεώρημα 2.2.10). Θα δείξουμε ότι $L=\mathbb{C}$ και άρα το πολυώνυμο $q(x)$ και κατά συνέπεια το $p(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο $\mathbb{C}[x]$ . Για να επιτύχουμε το στόχο μας, θα μελετήσουμε το βαθμό της επέκτασης $[L:{\mathbb{C}}]$ , επιζητώντας να δείξουμε ότι είναι ίσος με $1$ . Θα χρησιμοποιήσουμε το Θεμελιώδες Θεώρημα της Θεωρίας Galois, μελετώντας την ομάδα $\operatorname{Gal}(L/\mathbb{R})$ καθώς και την υποομάδα $\operatorname{Gal}(L/\mathbb{C})$ . Πρώτα θα δείξουμε ότι η ομάδα $\operatorname{Gal}(L/\mathbb{R})$ έχει τάξη μία δύναμη του 2 και στη συνέχεια θα δείξουμε ότι $\operatorname{Gal}(L/\mathbb{C})$ είναι η τετριμμένη υποομάδα της $\operatorname{Gal}(L/\mathbb{R})$ .

Αφού to $L$ έχει χαρακτηριστική 0, το πολυώνυμο $q(x)$ είναι διαχωρίσιμο και το $L$ είναι επέκταση Galois πάνω από το $\mathbb{C}$ και το $\mathbb{R}$ . Έστω $G=\operatorname{Gal}(L/\mathbb{R})$ και έστω ότι $|G|=2^{m}k$ , όπου $(2,k)=1$ . Σύμφωνα με το Θεώρημα I.24 υπάρχει μία υποομάδα $H$ της $G$ έτσι ώστε $|Η|=2^{m}$ και άρα $[G:H]=k$ . Σύμφωνα με το Θεμελιώδες Θεώρημα της Θεωρίας Galois έπεται ότι $[L^{H}:\mathbb{R}]=k$ , ενώ $(2,k)=1$ . Αν το $k$ δεν είναι $1$ , αν δηλ. $L^{H}\neq k$ , τότε οδηγούμαστε σε άτοπο, από την Πρόταση 6.3.6. Επομένως $k=1$ , $L^{H}={\mathbb{R}}$ και $G=H$ , ενώ $|G|=2^{m}$ .

Κάθε υποομάδα της $G$ , λοιπόν, έχει τάξη μία δύναμη του $2$ . Έστω

V=\operatorname{Gal}(L/\mathbb{C})<G.

Τότε $|V|=2^{n}$ , για κάποιο $n\geq 0$ . Αν $n>0$ , τότε από το Θεώρημα I.24 η ομάδα $V$ έχει μία υποομάδα $J$ έτσι ώστε $|J|=2^{n-1}$ . Επομένως $[V:J]=2$ . Σύμφωνα πάλι με το Θεμελιώδες Θεώρημα της Θεωρίας Galois, έπεται ότι $[L^{J}:\mathbb{C}]=2$ . Αυτό, όμως, είναι άτοπο από την Πρόταση 6.3.4. Άρα $n=0$ , δηλ. $|V|=|\operatorname{Gal}(L/\mathbb{C})|=1$ . Επομένως $[L:\mathbb{C}]=1$ , $L=\mathbb{C}$ και το σώμα ανάλυσης του $q(x)$ πάνω από το $\mathbb{C}$ είναι το ${\mathbb{C}}$ . άρα κάθε πολυώνυμο $f(x)\in{\mathbb{C}}[x]$ έχει μία ρίζα στο ${\mathbb{C}}$ . ∎

6.4 Ασκήσεις

1.

Έστω $b=1+\sqrt{2}$ , $F_{1}={\mathbb{Q}}\left(\sqrt{2}\right)$ και $F_{2}=F_{1}(\sqrt{b})$ . Να εξετάσετε αν $F_{2}/F_{1}$ είναι γνήσια επέκταση του $F_{1}$ και να βρείτε τον βαθμό $[F_{2}:F_{1}]$ . Να εξετάσετε αν h $F_{2}/{\mathbb{Q}}$ είναι επέκταση του Galois. Στη συνέχεια να βρείτε τον βαθμό $[F_{2}:{\mathbb{Q}}]$ και να περιγράψετε την ομάδα $\operatorname{Gal}(F_{2}/{\mathbb{Q}})$ .
2.

Να βρείτε μία ριζική επέκταση που να περιέχει το σώμα ανάλυσης του $x^{4}-2$ .
3.

Έστω $f(x)=x^{4}+2x^{2}+2x+2$ . Να βρείτε μία ριζική επέκταση που να περιέχει το σώμα ανάλυσης του $f(x)$ .
4.

Να αποδείξετε ότι αν $F$ είναι το σώμα των κατασκευάσιμων αριθμών, τότε $F/{\mathbb{Q}}$ είναι άπειρη επέκταση.
5.
Έστω ότι Το $Κ$ είναι ενδιάμεσο σώμα της επέκτασης $F/{\mathbb{Q}}$ , όπου $F$ το υπόσωμα των κατασκευάσιμων αριθμών στο ${\mathbb{R}}$ . Να αποδείξετε ότι
1. i)
  
  Aν $c\in F$ , τότε τα στοιχεία του $Κ(c)$ είναι και αυτά στο $F$ .
2. ii)
  
  Αν $l$ είναι μία ευθεία κατασκευάσιμη ευθεία εντός του $Κ$ , τότε η εξίσωση της ευθείας είναι της μορφής $ax+by+c=0$ , όπου $a,b,c\in K$ .
3. iii)
  
  Αν $C$ είναι ένας κύκλος, κατασκευάσιμος εντός του $K$ , τότε η εξίσωση του $C$ είναι της μορφής $x^{2}+y^{2}+ax+by+c=0$ , όπου $a,b,c\in K$ .
6.

Να αποδείξετε ότι το πρόβλημα εύρεσης σημείου τομής δύο κύκλων ανάγεται στο πρόβλημα εύρεσης τομής ενός κύκλου και μίας ευθείας.
7.

Έστω $c\in{\mathbb{R}}$ αλγεβρικό πάνω από το ${\mathbb{Q}}$ , $f(x)=\operatorname{irr}_{({\mathbb{Q}},c)}(x)$ και έστω $L$ το σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ . Να αποδείξετε ότι αν $[L:{\mathbb{Q}}]=2^{n}$ , για κάποιον φυσικό αριθμό $n$ , τότε κάθε στοιχείο του $L$ είναι κατασκευάσιμο.
8.

Έστω $f(x)=x^{4}+2x-2\in{\mathbb{Q}}[x]$ . Να αποδείξετε ότι το $f(x)$ είναι ανάγωγο και ότι έχει τουλάχιστον μία πραγματική ρίζα $b$ . Στη συνέχεια, αν $L$ είναι το σώμα ανάλυσης του $f(x)$ πάνω από το ${\mathbb{Q}}$ να δείξετε ότι το $3$ διαιρεί την ομάδα $\operatorname{Gal}(L/Q)$ . Να συμπεράνετε ότι το $b$ δεν είναι κατασκευάσιμο.
9.

Να αποδείξετε ότι το σημείο $(\cos(2\pi/5),\sin(2\pi/5))$ είναι κατασκευάσιμο.
10.

Να αποδείξετε ότι το σημείο $(a,b)\in{\mathbb{R}}^{2}$ είναι κατασκευάσιμο αν και μόνο αν το $z=a+bi$ περιέχεται σε μία επέκταση Galois $L/{\mathbb{Q}}$ τέτοια ώστε η ομάδα $\operatorname{Gal}(L/{\mathbb{Q}})$ να έχει τάξη κάποια δύναμη του $2$ .

Βιβλιογραφία Κεφαλαίου 6

1.

Alekseev, V. B. Abel’s Theorem in Problems and Solutions, (based on the lectures of Prof. V.I. Arnold). Kluwer Academic Publishers, 2004.
2.

Bastida, J. R. Field Extensions and Galois Theory, Vol. 22. Addison-Wesley, 2007.
3.

Edwards, H. M. Galois Theory. Springer, 1984.
4.

Escofier, J. P. Galois Theory. Springer, 2001.
5.

Fox, D. Galois Theory. John Wiley & Sons, 2012.
6.

Gaal, L. Classical Galois Theory with Examples. Chelsea, 1988.
7.

Hadlock, C. R. Field Theory and its Classical Problems. ΜΑΑ, 2000.
8.

Milne, J. S. Fields and Galois Theory. www.jmilne.org, 2014.
9.

Rotman, J. Θεωρία Galois. Leader Books, 2000.
10.

Stewart, I. Galois Theory. Champan and Hall, 1973.
11.

Swallow, J. Exploratory Galois Theory. Cambridge University Press, 2004.
12.

Tignol, J. P. Galois Theory of Algebraic Equations. World Scientific, 2011.