Θεωρία Galois

Κεφάλαιο 5Κυκλοτομικά πολυώνυμα

Σε αυτό το κεφάλαιο εφαρμόζουμε τη θεωρία Galois, όπως αυτή αναπτύχθηκε στο Kεφάλαιο 3, για τα πολυώνυμα $x^{n}-1$ και $x^{n}-a$ . Eπίσης εξετάζουμε τις κυκλοτομικές, τις κυκλικές και τις αβελιανές επεκτάσεις σωμάτων.

5.1 Ρίζες της μονάδας

Έστω $F$ σώμα χαρακτηριστικής $p$ , για κάποιον πρώτο αριθμό $p$ . Αν $n=p^{t}k$ , όπου $(k,p)=1$ , τότε

x^{n}-1=x^{kp^{t}}-1=(x^{k})^{p^{t}}-1=(x^{k}-1)^{p^{t}},

(βλ. την απόδειξη της Παρατήρησης 4.3.4). Άρα, οι $n$ -ρίζες της μονάδας είναι ακριβώς οι $k$ -ρίζες της μονάδας. Έτσι, θα ασχοληθούμε με τις παρακάτω περιπτώσεις:

•

η χαρακτηριστική του $F$ είναι μηδέν, $\operatorname{char}F=0$ ,
•

$\operatorname{char}F=p$ και ο $p$ δεν διαιρεί τον $n$ .

Και στις δύο περιπτώσεις, το πολυώνυμο $x^{n}-1$ είναι διαχωρίσιμο και μπορούμε να εφαρμόσουμε τα εργαλεία της Θεωρίας Galois.

Έστω, λοιπόν, $Ε$ Το σώμα ανάλυσης του πολωνύμου $f(x)=x^{n}-1\in F[x]$ , όπου $F$ και $n$ είναι όπως θέσαμε παραπάνω. Το σύνολο των $n$ -ριζών της μονάδας είναι υποομάδα της πολλαπλασιαστικής ομάδας του $E^{*}$ και θα το καλούμε ομάδα των n-ριζών της μονάδας (group of the $n$ th roots of unity) πάνω από το σώμα F. Σύμφωνα με το Θεώρημα 4.2.3, η υποομάδα αυτή είναι κυκλική. Ένα παράγον στοιχείο αυτής της ομάδας καλείται n-πρωταρχική ρίζα της μονάδας ( $n$ th primitive root of unity) πάνω από το $F$ .

Παράδειγμα 5.1.1.

Tο στοιχείο $e^{2\pi i/n}$ είναι πρωταρχική $n$ -ρίζα της μονάδας πάνω από το $\mathbb{Q}$ .

Η επόμενη πρόταση συγκεντρώνει μερικές ιδιότητες των $n$ -ριζών της μονάδας που μας είναι γνωστές από τις κυκλικές ομάδες.

Πρόταση 5.1.2.

Έστω $F$ ένα σώμα και έστω ότι $\omega\in E$ , όπου $\omega$ είναι μία πρωταρχική $n$ -ρίζα της μονάδας πάνω από το $F$ και $n$ είναι φυσικόs αριθμός. Τότε:

i)

Oι πρωταρχικές $n$ -ρίζες της μονάδας πάνω από το $F$ είναι πλήθους $\phi(n)$ , όπου $\phi$ είναι η συνάρτηση του Euler.
ii)

Έστω $d|n$ . Τότε κάθε $d$ -ρίζα της μονάδας είναι επίσης $n$ -ρίζα. H $\omega^{n/d}$ είναι μία $d$ -πρωταρχική ρίζα της μονάδας πάνω από το $F$ .

Απόδειξη.

Η υπόθεση ότι το $E$ περιέχει την $\omega$ σημαίνει ότι Το $E$ περιέχει όλες τις δυνάμεις του $\omega$ άρα και όλες τις ρίζες του $x^{n}-1\in F[x]$ . Το i) είναι άμεση συνέπεια του Θεωρήματος I.8. για το ii), παρατηρούμε ότι σύμφωνα με την Πρόταση I.7.iv, έχουμε ότι $\operatorname{ord}\left(\omega^{n/d}\right)=d$ και άρα $\omega^{n/d}$ παράγει την κυκλική ομάδα των $d$ -ριζών της μονάδας. ∎

Παραδείγματα 5.1.3.

1.

Έστω $p$ πρώτος. Oi πρωταρχικές $(p-1)$ -ρίζες της μονάδας πάνω από το $\mathbb{Q}$ είναι οι

$\omega^{2\pi i/p},\;\omega^{4\pi i/p},\;\cdots,\omega^{2(p-1)\pi i/p}.$
2.

Θα υπολογίσουμε τις πρωταρχικές $8$ -ρίζες της μονάδας πάνω από το ${\mathbb{Q}}$ . Αφού $\phi(8)=4$ , υπάρχουν 4 τέτοιες ρίζες. Είναι οι

$\omega^{\pi i/4},\;\omega^{3\pi i/4},\;\omega^{5\pi i/4},\;\omega^{7\pi i/4}.$
3.

Έστω $E$ πεπερασμένο σώμα, έτσι ώστε $|Ε|=2^{4}$ . Σύμφωνα με το Θεώρημα 4.2.6, το $E^{*}$ είναι κυκλική ομάδα. Όπως είδαμε στο Παράδειγμα 4.1.3.3, υπάρχει $a\in E$ έτσι ώστε $\operatorname{ord}(a)=15$ . Άρα το $Ε={\mathbb{Z}}_{2}(a)$ είναι σώμα ανάλυσης του $x^{15}-1$ πάνω από το ${\mathbb{Z}}_{2}$ και ότι το $a$ είναι πρωταρχική $15$ -ρίζα της μονάδας πάνω από το ${\mathbb{Z}}_{2}$ . Υπάρχουν $\phi(15)$ , δηλ. οκτώ, πρωταρχικές $15$ -ρίζες της μονάδας πάνω από το ${\mathbb{Z}}_{2}$ . Είναι οι

$a,\;a^{2},\;a^{4},\;a^{7},\;a^{8},\;a^{11},\;a^{13},\;a^{17}.$

Σημειώνουμε ότι $\deg\operatorname{irr}_{({\mathbb{Z}}_{2},a)}(x)=4$ , αφού

$4=[E:{\mathbb{Z}}_{2}]=\deg\operatorname{irr}_{({\mathbb{Z}}_{2},a)}(x).$
4.

Έστω τώρα $d=5$ . Θα μελετήσουμε το πολυώνυμο $f(x)=x^{5}-1$ πάνω από το ${\mathbb{Z}}_{2}$ . Έστω $a$ το πρωταρχικό στοιχείο του $E$ του προηγούμενου παραδείγματος. Σύμφωνα με την Πρόταση 5.1.2, το στοιχείο $a^{3}$ είναι μία $5$ -πρωταρχική ρίζα της μονάδας πάνω από το ${\mathbb{Z}}_{2}$ . Οι $5$ -ρίζες της μονάδας είναι

$1,\;a^{3},\;a^{6},\;a^{9},\;a^{12}.$

Το σώμα ανάλυσης $L={\mathbb{Z}}_{2}(a^{3})$ του $f(x)$ πάνω από το ${\mathbb{Z}}_{2}$ είναι υπόσωμα του $Ε={\mathbb{Z}}_{2}(a)$ και έχει τουλάχιστον 5 στοιχεία. Παρατηρούμε ότι Το $f(x)$ πάνω από το ${\mathbb{Z}}_{2}$ αναλύεται ως γινόμενο ανάγωγων πολυωνύμων ως εξής:

$x^{5}-1=(x^{5}-1)(x^{4}+x^{3}+x^{2}+x+1).$

Επομένως $\operatorname{irr}_{({\mathbb{Z}}_{2},a^{3})}(x)=x^{4}+x^{3}+x^{2}+x+1$ και έχει βαθμό 4. Συμπεραίνουμε ότι $[L:{\mathbb{Z}}_{2}(a^{3})]=4$ και επομένως $L=E$ . Τέλος, σημειώνουμε ότι η ανάλυση σε γινόμενο ανάγωγων πολυωνύμων του $x^{15}-1$ πάνω από το ${\mathbb{Z}}_{2}$ έχει ως εξής:

$x^{15}-1=(x-1)(x^{2}+x+1)(x^{4}+x+1)(x^{4}+x^{3}+1)(x^{4}+x^{3}+\cdots+1).$

Έστω $E$ σώμα ανάλυσης του $x^{n}-1$ πάνω από το σώμα $F$ . Ένα πρώτο αποτέλεσμα για την ομάδα $\operatorname{Gal}(E/F)$ δίνεται στο Θεώρημα 5.1.4, στη περίπτωση που $\operatorname{char}F\nmid n$ . Για την περίπτωση που το σώμα $F$ είναι το σώμα των ρητών, τότε όπως θα δούμε, η απάντηση δίνεται από το Πόρισμα 5.1.5 και το Θεώρημα 5.2.9.

Θεώρημα 5.1.4.

Έστω $F$ ένα σώμα έτσι ώστε $\operatorname{char}F\nmid p$ , $f(x)=x^{n}-1\in F[x]$ και $E$ Το σώμα ανάλυσης του $f(x)$ . Η ομάδα $\operatorname{Gal}(E/F)$ είναι ισόμορφη με μία υποομάδα της $\mathbb{Z}_{n}^{\sharp}$ και ο βαθμός της επέκτασης $[E:F]$ διαιρεί τον $\phi(n)$ .

Απόδειξη.

Έστω $G=\operatorname{Gal}(L/F)$ , $\omega$ μία πρωταρχική $n$ -ρίζα της μονάδας στο $L$ . Τότε το $E=F(\omega)$ . Έστω $\sigma\in G$ . Αφού το σύνολο των $n$ -ριζών της μονάδας στο $E$ είναι η κυκλική ομάδα $\langle\omega\rangle$ , έπεται ότι $\sigma(\omega)=\omega^{i}$ , για κάποιο $i\in\{1,\ldots,n\}$ . Επομένως, ο περιορισμός του $\sigma$ στην υποομάδα $\langle\omega\rangle$ του $Ε^{*}$ είναι αυτομορφισμός της $\langle\omega\rangle$ . Επίσης,

\tau=\sigma|_{\langle\omega\rangle}:\ \langle\omega\rangle\longrightarrow% \langle\omega\rangle,\quad\omega\mapsto\omega^{i}

είναι ισομορφισμός ομάδων, αφού είναι μονομορφισμός πεπερασμένης ομάδας. Επομένως το $\omega^{i}$ είναι και αυτό παράγον στοιχείο της $\langle\omega\rangle$ . Σύμφωνα με την Πρόταση I.7, ο μέγιστος κοινός διαιρέτης $(i,n)$ είναι $1$ . Θεωρούμε τώρα την απεικόνιση

\psi:\ G\rightarrow\mathbb{Z}_{n}^{\sharp},\quad\sigma\mapsto\bar{i},\textrm{ % όπου }\sigma(\omega)=\omega^{i}.

Είναι εύκολο να αποδειχθεί ότι η $\psi$ είναι ομομορφισμός ομάδων. Ακόμη

\ker\psi=\{\sigma\in G:\ \bar{i}=\bar{1}\}=\{\sigma\in G:\ \sigma(\omega)=% \omega\}=\{\operatorname{id}_{L}\}

και η $\psi$ είναι μονομορφισμός. ∎

Έστω τώρα $p$ ένας πρώτος αριθμός. Το σώμα ανάλυσης του $x^{p}-1$ πάνω από το ${\mathbb{Q}}$ είναι το ${\mathbb{Q}}(\omega)$ , όπου $\omega=e^{2\pi i/p}$ . Από το Θεώρημα 5.1.4 προκύπτει το παρακάτω Πόρισμα.

Πόρισμα 5.1.5.

Έστω $Ε={\mathbb{Q}}(\omega)$ , όπου $\omega=e^{2\pi i/p}$ , για κάποιον πρώτο φυσικό αριθμό $p$ . Τότε

\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})\cong\mathbb{Z}_{p}^{*},

και

\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})=\langle\sigma\rangle,\textrm% { όπου }\sigma:\omega\mapsto\omega^{2}.

Απόδειξη.

Σύμφωνα με το Παράδειγμα 1.3.8 το πολυώνυμο

\Phi_{p}(x)=x^{p-1}+\cdots+x+1

είναι ανάγωγο. Αφού $x^{p}-1=(x-1)\Phi_{p}(x)=0$ και $\omega^{p}-1=0$ , έπεται ότι το $\omega$ είναι ρίζα του $\Phi_{p}(x)$ . Επομένως $\operatorname{irr}_{(\mathbb{Q},\omega)}(x)=\Phi_{p}(x)$ και $\deg\operatorname{irr}_{(\mathbb{Q},\omega)}(x)=p-1$ . Άρα

|\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})|=p-1.

Σύμφωνα με το Θεώρημα 5.1.4, η ομάδα $\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})$ είναι ισόμορφη με υποομάδα της $\mathbb{Z}_{p}^{*}$ . Επίσης, αφού $|\mathbb{Z}_{p}^{*}|=p-1$ , έπεται ότι

\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})\cong\mathbb{Z}_{p}^{*}\ .

Τέλος, αφού η ομάδα $\mathbb{Z}_{p}^{*}$ είναι κυκλική, έπεται ότι και η ομάδα $\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})$ είναι κυκλική και

\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})=\langle\sigma\rangle,\textrm% { όπου }\sigma:\omega\mapsto\omega^{2}.

∎

Παραδείγματα 5.1.6.

1.

Έστω $\omega=e^{2\pi i/8}=e^{\pi i/4}$ , η πρωταρχική $8$ -ρίζα της μονάδας. Τότε $\operatorname{irr}_{(\mathbb{Q},\omega)}(x)=x^{4}+1$ και

$|\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})|=4.$

Σύμφωνα με το Θεώρημα 5.1.4 η ομάδα $\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})$ είναι ισόμορφη με υποομάδα της $\mathbb{Z}_{8}^{\sharp}$ . Αφού $|\mathbb{Z}_{8}^{\sharp}|=4$ , έπεται ότι $\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})\cong\mathbb{Z}_{8}^{\sharp},$ που δεν είναι κυκλική, βλ. Παράδειγμα 4.2.6.1. Άρα $\operatorname{Gal}(\mathbb{Q}(\omega)/\mathbb{Q})$ είναι ισόμορφη με την ομάδα του Klein.
2.

Ο μονομορφισμός του Θεωρήματος 5.1.4 δεν είναι πάντα επιμορφισμός. Για παράδειγμα, έστω $Ε={\mathbb{Z}}_{2}(a)$ το σώμα ανάλυσης του $x^{15}-1$ πάνω από το ${\mathbb{Z}}_{2}$ , όπως στο Παράδειγμα 5.1.3.3. Η ομάδα $\mathbb{Z}_{15}^{\sharp}$ έχει 8 στοιχεία. Αφού $|Ε|=16$ και $[E:{\mathbb{Z}}_{2}]=4$ , η ομάδα $\operatorname{Gal}(E/{\mathbb{Z}}_{2})$ έχει τάξη 4 και μάλιστα $\operatorname{Gal}(E/{\mathbb{Z}}_{2})\cong{\mathbb{Z}}_{4}$ , σύμφωνα με το Θεώρημα 4.2.10.

5.2 Κυκλοτομικά πολυώνυμα

Σε αυτό το εδάφιο θα ασχοληθούμε με την ανάλυση του πολυωνύμου $x^{n}-1$ σε γινόμενο ανάγωγων παραγόντων στο ${\mathbb{Q}}[x]$ . Ας συμβολίsουμε με $U_{n}$ το σύνολο των πρωταρχικών $n$ -ριζών της μονάδας. Από την Πρόταση 5.1.2 έχουμε ότι $|U_{n}|=\phi(n)$ , όπου $\phi$ είναι η συνάρτηση του Euler. Το πολυώνυμο

\Phi_{n}(x)=\prod_{\omega\in U_{n}}(x-\omega)\in{\mathbb{C}}[x]

(5.2.0.1)

λέγεται n-κυκλοτομικό πολυώνυμο ( $n$ -cyclotomic polynomial). πολυώνυμο!κυκλοτομικό polynomial!cyclotomic $\Phi_{n}(x)$

Παράδειγμα 5.2.1.

Oi $3$ -ρίζες της μονάδας είναι οι $1$ , $\omega$ , $\omega^{2}$ , όπου $\omega=e^{2\pi i/3}$ . Από αυτές οι $\omega$ και $\omega^{2}$ έχουν τάξη 3 και είναι πρωταρχικές $3$ -ρίζες της μονάδας. Άρα

\Phi_{3}(x)=(x-\omega)(x-\omega^{2})=\frac{x^{3}-1}{x-1}=x^{2}+x+1.

Στο Παράδειγμα 5.2.3.2 βλέπουμε ότι, όταν o $n$ είναι πρώτος, τότε ο τύπος της (5.2.0.1) δίνει το κυκλοτομικό πολυώνυμο όπως το είδαμε στο Παράδειγμα 1.2.7. Η ορολογία κυκλοτομικό πολυώνυμο οφείλεται στην ιδιότητα που έχουν οι $n$ -ρίζες της μονάδας να διαιρούν τον κύκλο σε $n$ πλήθους ίσα τόξα όπως φαίνεται στο Σχήμα 5.1.

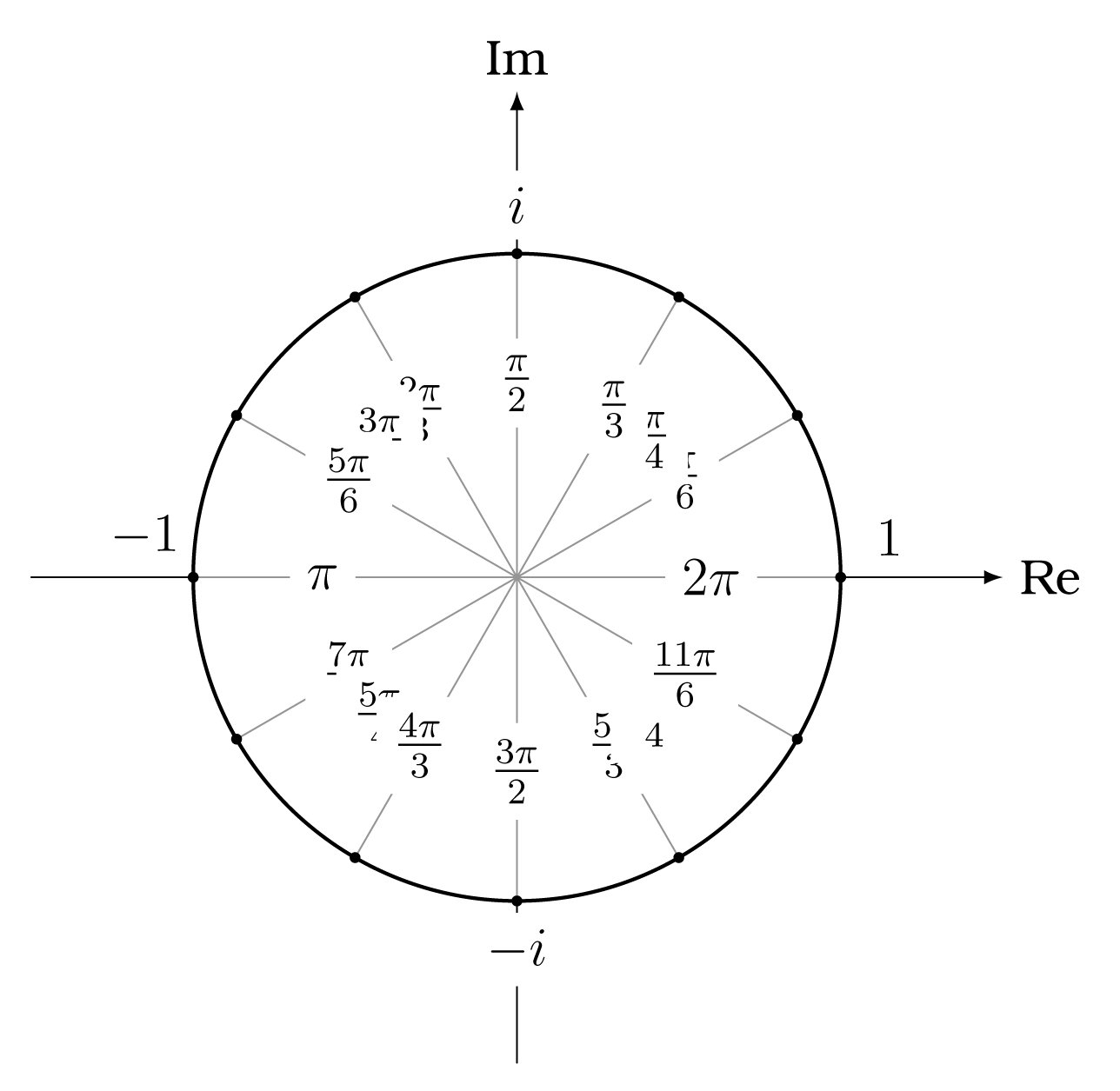
Πρόταση 5.2.2.

Έστω $n>0$ ένας φυσικός αριθμός. Τότε

x^{n}-1=\prod_{d\;|\;n}\Phi_{d}(x).

Απόδειξη.

Έστω $G$ η κυκλική ομάδα των $n$ -ριζών της μονάδας στο σώμα των μιγαδικών αριθμών. Τα στοιχεία που παράγουν την υποομάδα της $G$ τάξης $d$ , όπου $d|n$ , είναι οι πρωταρχικές $d$ -ρίζες της μονάδας και αποτελούν το σύνολο $U_{d}$ . Σύμφωνα με τον τύπο 4.2.0.1 έχουμε ότι

G=\bigcup_{d\;|\;n}U_{d}.

Αφού

x^{n}-1=\prod_{a\in G}(x-a)

και

\Phi_{d}(x)=\prod_{a\in U_{d}}(x-a),

έπεται ότι

x^{n}-1=\prod_{d\;|\;n}\Phi_{d}(x).

∎

Παραδείγματα 5.2.3.

1.
Υπολογίζουμε το κυκλοτομικό πολυώνυμο $\Phi_{n}(x)$ για κάποιες μικρές τιμές του θετικού ακεραίου $n>0$ . Με $\omega$ συμβολίζουμε κάθε φορά μία πρωταρχική $n$ -ρίζα της μονάδας.
- –
  
  $\Phi_{1}(x)=x-1$ .
- –
  
  $\Phi_{2}(x)=x+1$ . Πράγματι
  
  $\Phi_{2}(x)=\frac{x^{2}-1}{x-1}=x+1.$
- –
  
  Όπως είδαμε στο Παράδειγμα 5.2.1, $\Phi_{3}(x)=x^{2}+x+1$ .
- –
  
  $\Phi_{4}(x)=x^{2}+1$ . Πράγματι
  
  $\Phi_{4}(x)=\prod_{(t,4)=1}(x-\omega^{t})=(x-\omega)(x-\omega^{3}).$
  
  Παρατηρούμε επίσης ότι
  
  $\Phi_{1}(x)\Phi_{2}(x)\Phi_{4}(x)=x^{4}-1.$
  
  Εναλλακτικά, λοιπόν, θα μπορούσαμε να υπολογίσουμε το πολυώνυμο $\Phi_{4}(x)$ ως το πηλίκο
  
  $\Phi_{4}(x)=\frac{x^{4}-1}{\Phi_{1}(x)\Phi_{2}(x)}=\frac{x^{4}-1}{x^{2}-1}=x^{% 2}+1.$
- –
  
  $\Phi_{5}(x)=x^{4}+x^{3}+x^{2}+x+1$ .
- –
  
  $\Phi_{6}(x)=x^{2}-x+1$ .
2.

Όταν $p$ είναι πρώτος φυσικός αριθμός, τότε $U_{p}=\{\omega,\ldots,\omega^{p-1}\}$ . Επομένως

$x^{p}-1=(x-1)\Phi_{p}(x)\;\Rightarrow\;\Phi_{p}(x)=x^{p-1}+\cdots+x+1.$

Οι επόμενες προτάσεις δίνουν σημαντικές πληροφορίες για τα κυκλοτομικά πολυώνυμα.

Πρόταση 5.2.4.

$\Phi_{n}(x)\in{\mathbb{Z}}[x]$ , για κάθε φυσικό αριθμό $n$ .

Απόδειξη.

Θα αποδείξουμε την πρόταση επαγωγικά ως προς το $n$ . Για $n=1$ , η πρόταση ισχύει αφού $\Phi_{1}(x)=x-1$ . Έστω ότι η πρόταση ισχύει για $1\leq k\leq n$ , δηλ. $\Phi_{k}(x)\in{\mathbb{Z}}[x]$ για $1\leq k\leq n$ . Θα αποδείξουμε την πρόταση για τον $n$ . Παρατηρούμε ότι

x^{n}-1=\prod_{d\;|\;n}\Phi_{d}(x)=\Phi_{n}(x)\prod_{\substack{d\;|\;n\\ d<n}}\Phi_{d}(x).

(5.2.4.1)

Όμως, το πολυώνυμο $\prod_{\substack{d|n\\ d<n}}\Phi_{d}(x)$ έχει ακέραιους συντελεστές από την υπόθεση της μαθηματικής επαγωγής. Επομένως, από τη σχέση 5.2.4.1, συμπεραίνουμε ότι Το $\prod_{\substack{d\;|\;n\\ d<n}}\Phi_{d}(x)$ διαιρεί το $x^{n}-1$ στον ${\mathbb{Z}}[x]$ και επομένως $\Phi_{n}(x)\in{\mathbb{Z}}[x]$ .

∎

Έστω $n$ ένας θετικός ακέραιος, $\omega$ μία πρωταρχική ρίζα της μονάδας και $f(x)=\operatorname{irr}_{({\mathbb{Q}},\omega)}(x)$ . Αφού $\omega$ είναι ρίζα του $x^{n}-1$ , έπεται ότι

x^{n}-1=f(x)g(x),

για κάποιο $g(x)\in{\mathbb{Q}}[x]$ . Επομένως, σύμφωνα με την Πρόταση 1.3.3, το $f(x)$ ανήκει στους ανάγωγους παράγοντες του $x^{n}-1$ στο ${\mathbb{Z}}[x]$ και κατά συνέπεια το $g(x)\in{\mathbb{Z}}[x]$ .

Πρόταση 5.2.5.

Έστω $n$ ένας θετικός ακέραιος, $\omega$ μία πρωταρχική $n$ -ρίζα της μονάδας και $f(x)=\operatorname{irr}_{({\mathbb{Q}},\omega)}(x)$ . Tότε το $\omega^{p}$ είναι επίσης ρίζα του $f(x)$ , για κάθε πρώτο $p\nmid n$ .

Απόδειξη.

Σύμφωνα με τις παρατηρήσεις πριν από την πρόταση, βλέπουμε ότι

x^{n}-1=f(x)g(x),

για κάποιο πολυώνυμο $g(x)\in{\mathbb{Z}}[x]$ . Ας υποθέσουμε ότι $f(\omega^{p})\neq 0$ , για κάποιο πρώτο $p\hskip-4.0pt\not|\hskip 2.0ptn$ . Σημειώνουμε ότι το $g(x)$ είναι κανονικό πολυώνυμο, αφού τα $x^{n}-1$ και $f(x)$ είναι κανονικά πολυώνυμα στο ${\mathbb{Z}}[x]$ . Επίσης, σημειώνουμε ότι το $\omega^{p}$ είναι και αυτό πρωταρχική $n$ -ρίζα της μονάδας. Επομένως

f(\omega^{p})g(\omega^{p})={(\omega^{p})^{n}}-1=0.

Αφού $f(\omega^{p})\neq 0$ , έπεται ότι $g(\omega^{p})=0$ και άρα το $\omega$ είναι ρίζα του $g(x^{p})$ . Όμως, $f(x)=\operatorname{irr}_{({\mathbb{Q}},\omega)}(x)$ και άρα

g(x^{p})=f(x)h(x),

για κάποιο $h(x)\in{\mathbb{Q}}[x]$ . Παρατηρούμε ότι $h(x)\in{\mathbb{Z}}[x]$ , σύμφωνα με την Πρόταση 1.3.3. Θεωρούμε τώρα τον ομομορφισμό δακτυλίων της Πρότασης 1.3.9:

\Psi:\ \mathbb{Z}[x]\rightarrow\mathbb{Z}_{p}[x],\ a_{0}+a_{1}x+\cdots+a_{n}x^% {n}\mapsto\bar{a}_{0}+\bar{a}_{1}x+\cdots+\bar{a}_{n}x^{n}\ .

Στον ${\mathbb{Z}}_{p}[x]$ ισχύει ότι

x^{n}-\bar{1}=\Psi\left(f(x)\right)\Psi\left(g(x)\right)

και

\Psi\left(g(x^{p})\right)=\Psi\left(f(x)\right)\Psi\left(h(x)\right).

(5.2.5.1)

Όμως, σύμφωνα με την Πρόταση III.4,

\Psi\left(g(x^{p})\right)=\Psi\left(g(x)\right)^{p}

και επομένως

\Psi\left(g(x)\right)^{p}=\Psi\left(f(x)\right)\Psi\left(h(x)\right).

Αφού $Ψ (f (x))$ διαιρεί το $Ψ {(g (x))}^{p}$ , κάθε ανάγωγος παράγοντας του $Ψ (f (x))$ διαιρεί το $Ψ (g (x))$ και άρα $Μ Κ Δ (Ψ (f (x)), Ψ (g (x))) \neq 1.$ Έστω, λοιπόν, $q (x) \in Z_{p} [x]$ ο μέγιστος κοινός διαιρέτης των $Ψ (f (x))$ και $Ψ (g (x))$ . Τότε $\deg q (x) \geq 1$ και από τη σχέση (5.2.5.1), το $q (x)^{2}$ διαιρεί το $x^{n} - 1$ . Επομένως το πολυώνυμο $x^{n} - 1$ του $ℤ_{p} [x]$ έχει πολλαπλές ρίζες. Αυτό, όμως, είναι άτοπο αφού η παράγωγος του $x^{n} - 1$ είναι $n x^{n - 1} \neq 0$ και $Μ Κ Δ (x^{n} - 1, n x^{n - 1}) = 1$ (Πρόταση 1.4.5). Καταλήξαμε σε άτοπο γιατί υποθέσαμε ότι $f (ω^{p}) \neq 0$ . Επομένως $f(\omega^{p})=0$ για κάθε $p$ πρώτο, $p\hskip-4.0pt\not|\hskip 2.0ptn$ . ∎

Στα Παραδείγματα 5.2.3 είδαμε ότι, για $n\leq 6$ και όταν $n$ είναι πρώτος, το πολυώνυμο $\Phi_{n}(x)$ είναι ανάγωγο. Το επόμενο θεώρημα, δείχνει, ότι αυτή είναι ιδιότητα του $\Phi_{n}(x)$ , για κάθε φυσικό αριθμό $n$ .

Θεώρημα 5.2.6.

Έστω $n$ ένας θετικός ακέραιος. Το κυκλοτομικό πολυώνυμο $\Phi_{n}(x)$ είναι ανάγωγο στον ${\mathbb{Q}}[x]$ .

Απόδειξη.

Έστω $\omega$ πρωταρχική $n$ -ρίζα της μονάδας και $f(x)=\operatorname{irr}_{({\mathbb{Q}},\omega)}(x)$ . Το σύνολο $U_{n}$ περιγράφεται ως εξής: $U_{n} = {ω^{s} : (s, n) = 1} .$ Έστω λοιπόν $ω^{s}$ άλλη πρωταρχική ρίζα. Τότε $s = p_{1} \dots p_{t}$ , όπου $p_{i}$ είναι πρώτοι φυσικοί αριθμοί με την ιδιότητα $p_{i} ∤ n$ , $1 \leq i \leq t$ . Παρατηρούμε ότι ${ω^{p_{1}}, ω^{p_{1} p_{2}} = {(ω^{p_{1}})}^{p_{2}}, \dots, ω^{p_{1} \dots p_{s - 1}}, ω^{s}} \subset U_{n} .$ Εφαρμόζοντας διαδοχικά την Πρόταση 5.2.5 για τa στοιχεία

\omega^{p_{1}},\;\omega^{p_{1}p_{2}}=\left(\omega^{p_{1}}\right)^{p_{2}},\;% \ldots,\;\omega^{s}=\left(\omega^{p_{1}\cdots p_{s-1}}\right)^{p_{s}}

προκύπτει ότι $f(\omega^{s})=0$ . Επομένως όλες οι πρωταρχικές $n$ -ρίζες της μονάδας έχουν το ίδιο ανάγωγο πολυώνυμο πάνω από το ${\mathbb{Q}}[x]$ και επομένως το $f(x)$ διαιρεί το $\Phi_{n}(x)$ . Όμως, τα δύο πολυώνυμα $f(x)$ , $\Phi_{n}(x)$ έχουν τον ίδιο βαθμό. Τέλος, αφού τα $f(x),\Phi_{n}(x)$ είναι κανονικά πολυώνυμα έπεται ότι $f(x)=\Phi_{n}(x)$ . Άρα Το $\Phi_{n}(x)$ είναι ανάγωγο στον ${\mathbb{Q}}[x]$ . ∎

Ως άμεση συνέπεια της Πρότασης 5.2.2 και του Θεωρήματος 5.2.6, έχουμε το παρακάτω πόρισμα.

Πόρισμα 5.2.7.

Η ανάλυση του $x^{n}-1$ σε γινόμενο ανάγωγων πολυωνύμων στον ${\mathbb{Q}}[x]$ είναι:

x^{n}-1=\prod_{d\;|\;n}\Phi_{d}(x).

Ένα σώμα ανάλυσης $L$ του $x^{n}-1\in K[x]$ , όπου $Κ$ είναι ένα σώμα με $\operatorname{char}K=0$ και $n$ ένας θετικός ακέραιος, λέγεται κυκλοτομικό σώμα τάξης $n$ (cyclotomic field of order $n$ ) πάνω από το $Κ$ . Από το Θεώρημα 5.1.4, η ομάδα $\operatorname{Gal}(L/K)$ είναι αβελιανή, ως υποομάδα της ${\mathbb{Z}}_{n}^{\sharp}$ . Τέτοιες επεκτάσεις λέγονται αβελιανές επεκτάσεις (abelian extensions).

Στην Αλγεβρική Θεωρία Αριθμών, όπου μελετώνται πεπερασμένες επεκτάσεις πάνω από το ${\mathbb{Q}}$ , οι αβελιανές επεκτάσεις παίζουν σημαντικό ρόλο. Έτσι είναι εξαιρετικά ενδιαφέρον το ερώτημα, σχετικά με το αντίστροφο του Θεωρήματος 5.1.4 πάνω από το ${\mathbb{Q}}$ . Κάθε πεπερασμένη επέκταση του Galois $L/{\mathbb{Q}}$ για την οποία η $\operatorname{Gal}(L/{\mathbb{Q}})$ είναι αβελιανή, δηλ. η $L/{\mathbb{Q}}$ είναι αβελιανή επέκταση, περιέχεται σε ένα κυκλοτομικό σώμα πάνω από το ${\mathbb{Q}}$ ;

Το ερώτημα αυτό απαντήθηκε θετικά από τους Kronecker (1853) και Weber (1886). Το συμπέρασμά τους αποτελεί ένα από τα βαθύτερα θεωρήματα της Αλγεβρικής Θεωρίας Αριθμών (βλ. [5]).

Θεώρημα 5.2.8 (Kronecker - Weber).

Αν $L/{\mathbb{Q}}$ είναι μία πεπερασμένη αβελιανή επέκταση, τότε υπάρχει μία ρίζα της μονάδας $\omega$ , τέτοια ώστε $L\subset{\mathbb{Q}}(\omega)$ .

Η επόμενη πρόταση γενικεύει το Παράδειγμα 5.1.3.2 και το Πόρισμα 5.1.5.

Θεώρημα 5.2.9.

Έστω $n>0$ ένας φυσικός αριθμός και έστω $Ε$ ένα κυκλοτομικό σώμα τάξης $n$ πάνω από το ${\mathbb{Q}}$ . Τότε $[E:{\mathbb{Q}}]=\phi(n)$ και $\operatorname{Gal}(E/{\mathbb{Q}})\cong{\mathbb{Z}}_{n}^{\sharp}$ .

Απόδειξη.

Η επέκταση $Ε/{\mathbb{Q}}$ είναι σώμα ανάλυσης του $x^{n}-1$ πάνω από το ${\mathbb{Q}}$ και είναι επέκταση του Galois, αφού το $x^{n}-1\in{\mathbb{Q}}[x]$ είναι διαχωρίσιμο. Από το Θεώρημα 5.1.4, η $\operatorname{Gal}(E/{\mathbb{Q}})$ εμφυτεύεται στη ${\mathbb{Z}}_{n}^{\sharp}$ . Αν $\omega$ είναι μία πρωταρχική ρίζα της μονάδας, τότε $Ε={\mathbb{Q}}(\omega)$ και

[{\mathbb{Q}}(\omega):{\mathbb{Q}}]=\deg\Phi_{n}(x)=\phi(n),

όπου $\phi$ είναι η συνάρτηση του Euler, αφού $\Phi_{n}(x)=\operatorname{irr}_{({\mathbb{Q}},\omega)}(x)$ , (bλ. Θεώρημα 5.2.6). Αφού η τάξη της ${\mathbb{Z}}_{n}^{\sharp}$ είναι ίση με $\phi(n)$ , συμπεραίνουμε ότι $\operatorname{Gal}(E/{\mathbb{Q}})\cong{\mathbb{Z}}_{n}^{\sharp}$ . ∎

5.3 Το πολυώνυμο $x^{n}-a$

Έστω $n$ ένας φυσικός ακέραιος και $F$ ένα σώμα, έτσι ώστε $\operatorname{char}F\nmid n$ . Έστω επίσης ότι το $F$ περιέχει το $\omega$ , μία πρωταρχική $n$ -ρίζα της μονάδας, και έστω το $α$ ένα στοιχείο του $F$ . Στην ενότητα αυτή θα εξετάσουμε το πολυώνυμο $f(x)=x^{n}-a\in F[x]$ και την ομάδα $G=\operatorname{Gal}(L/F)$ , όπου $L$ ένα σώμα ανάλυσης του $f(x)$ πάνω από το $F$ .

Παρατηρούμε ότι αν $b$ είναι μία ρίζα του $f(x)$ , τότε οι ρίζες του $f(x)$ είναι οι

b,b\omega,\cdots,b\omega^{n-1}.

Επομένως $L=F(b)$ . Αν $\sigma$ είναι ένα στοιχείο της $G$ , τότε $\sigma(b)=b\omega^{i}$ , για κάποιο $i$ , αφού το $\sigma(b)$ πρέπει να είναι ρίζα του $f(x)$ . Έτσι το $\sigma$ προσδιορίζεται από τον εκθέτη $i$ . Θεωρούμε την αντιστοιχία

\psi:\ G\rightarrow\mathbb{Z}_{n},\quad\sigma\mapsto\bar{i}\ .

Παρατηρούμε ότι αν

\sigma,\tau\in G\ \psi(\sigma)=\psi(\tau)\Rightarrow\sigma(b)=\tau(b)% \Rightarrow\sigma=\tau,

δηλαδή η $\psi$ είναι αμφιμονότιμη συνάρτηση. Είναι δε φανερό ότι η $\psi$ είναι oμομορφισμός ομάδων. Άρα η $G$ εμφυτεύεται στη $\mathbb{Z}_{n}$ .

Έστω, τώρα, ότι Το $f(x)$ είναι ανάγωγο στο $F[x]$ . Τότε το $f(x)$ είναι το $\operatorname{irr}_{(F,b)}(x))$ και είναι διαχωρίσιμο, άρα $L/F$ είναι επέκταση του Galois. Επομένως $|G|=[L:F]=\deg f(x)=n$ . Άρα h $G$ είναι ισόμορφη με την $\mathbb{Z}_{n}$ . Αντίστροφα αν η $G$ είναι ισόμορφη με την $\mathbb{Z}_{n}$ και $\psi$ είναι επιμορφισμός, τότε η πρώτη παρατήρηση που κάνουμε είναι ότι όλες οι ρίζες του $f(x)$ είναι διακεκριμένες. Θα δείξουμε ότι $f(x)$ είναι ανάγωγο. Έστω, λοιπόν, ότι

f(x)=g(x)h(x),\quad g(x),h(x)\in F[x],\quad(g(x),h(x))=1.

Χωρίς περιορισμό της γενικότητας έστω ότι $g(b)=0$ και $h(b\omega^{i})=0$ , για κάποιο $i$ . Αφού η $\psi$ είναι επιμορφισμός, έπεται ότι υπάρχει $\sigma\in G$ έτσι ώστε $\sigma(b)=b\omega^{i}$ . Αφού $g(b)=0$ , έπεται ότι $\operatorname{irr}_{(F,b)}(x)$ διαιρεί το $g(x)$ ενώ αντίστοιχα $\operatorname{irr}_{(F,\sigma(b))}(x)$ διαιρεί το $h(x)$ . Σύμφωνα με την Πρόταση 2.3.2 προκύπτει ότι

\operatorname{irr}_{(F,\sigma(b))}(x)=\operatorname{irr}_{(F,b)}(x).

Άρα το $\operatorname{irr}_{(F,b)}(x)$ διαιρεί τον μέγιστο κοινό διαιρέτη $(g(x),h(x))$ , το οποίο είναι αδύνατον. Αποδείξαμε, λοιπόν, ότι:

Θεώρημα 5.3.1.

Αν το σώμα $F$ περιέχει μία πρωταρχική $n$ -ρίζα της μονάδας και $Ε$ είναι σώμα ανάλυσης του $f(x)=x^{n}-a\in F[x]$ τότε η $\operatorname{Gal}(Ε/F)$ εμφυτεύεται στην $(\mathbb{Z}_{n},+)$ . H $\operatorname{Gal}(Ε/F)$ είναι ισόμορφη με την $\mathbb{Z}_{n}$ αν και μόνο αν το $f(x)$ είναι ανάγωγο, δηλ. αν και μόνο αν $[E:F]=n$ .

Το θεώρημα αυτό μας οδηγεί στο επόμενο συμπέρασμα:

Πόρισμα 5.3.2.

Έστω $p$ πρώτος φυσικός αριθμός, $F$ ένα σώμα που περιέχει μία $p$ -ρίζα της μονάδας και $a\in F$ . Αν Το $x^{p}-a$ δεν είναι ανάγωγο στο $F[x]$ , τότε το $x^{p}-a$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο $F[x]$ .

Απόδειξη.

Έστω $L$ σώμα ανάλυσης του $x^{p}-a$ . Είδαμε ότι η ομάδα $\operatorname{Gal}(L/F)$ εμφυτεύεται στο $\mathbb{Z}_{p}$ . Άρα υπάρχουν ακριβώς δύο περιπτώσεις. Η πρώτη είναι $\operatorname{Gal}(L/F)\cong\{\operatorname{id}_{L}\}$ και η δεύτερη είναι $\operatorname{Gal}(L/F)\cong\mathbb{Z}_{p}$ . Παρατηρούμε ότι στη πρώτη περίπτωση

L^{\operatorname{Gal}(L/F)}=L.

Όμως $L/{\mathbb{Z}}_{p}$ είναι επέκταση του Galois και σύμφωνα με το Θεμελιώδες Θεώρημα της Θεωρίας Galois,

L^{\operatorname{Gal}(L/F)}=F.

Επομένως, αν $\operatorname{Gal}(L/F)\cong\{\operatorname{id}_{L}\}$ τότε $L=F$ και επομένως Το $x^{p}-a$ δεν είναι ανάγωγο στο $F[x]$ και αναλύεται σε γινόμενο γραμμικών παραγόντων στο $F[x]$ . Σύμφωνα με το Θώρημα 5.3.1 η δεύτερη περίπτωση ισχύει ακριβώς όταν το $x^{p}-a$ είναι ανάγωγο. ∎

Παράδειγμα 5.3.3.

Έστω $Ε$ , υπόσωμα του ${\mathbb{C}}$ , έτσι ώστε $Ε$ να είναι το σώμα ανάλυσης του $f(x)=x^{p}-2\in{\mathbb{Q}}[x]$ , όπου $p$ είναι πρώτος φυσικός αριθμός. Σημειώνουμε ότι $E/{\mathbb{Q}}$ είναι επέκταση του Galois. Το $f(x)\in{\mathbb{Q}}[x]$ είναι ανάγωγο σύμφωνα με το κριτήριο του Eisenstein και $\operatorname{irr}_{({\mathbb{Q}},\sqrt[p]{2})}(x)=x^{p}-2$ . Σημειώνουμε ότι $E/{\mathbb{Q}}$ είναι επέκταση του Galois. Οι ρίζες του $f(x)$ στο $Ε$ είναι:

\sqrt[p]{2},\;\sqrt[p]{2}\omega,\ldots\;,\sqrt[p]{2}\omega^{p-1},

όπου $\omega$ είναι μία πρωταρχική $p$ -ρίζα της μονάδας. Άρα

Ε={\mathbb{Q}}(\omega,\sqrt[p]{2}).

Από το ακόλουθο διάγραμμα των επεκτάσεων

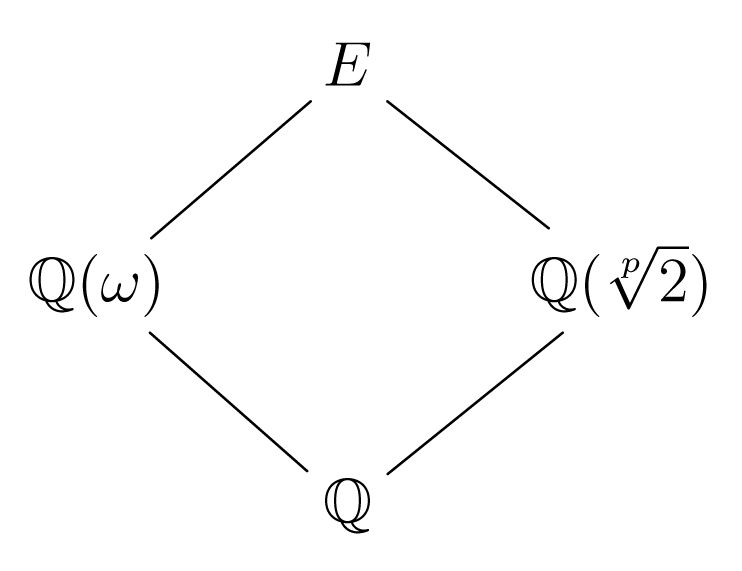
Σχήμα 5.2: Σώμα ανάλυσης του $x^{p}-2$ και υποσώματα.

παρατηρούμε ότι

[{\mathbb{Q}}(\omega):{\mathbb{Q}}]=\deg\Phi(p)=\phi(p)=p-1

και ότι

[{\mathbb{Q}}(\sqrt[p]{2}):{\mathbb{Q}}]=\deg\operatorname{irr}_{({\mathbb{Q}}% ,\sqrt[p]{2})}(x)=p.

Άρα οι φυσικοί αριθμοί $p-1$ και $p$ διαιρούν τον $[E:{\mathbb{Q}}]$ και αφού $(p,p-1)=1$ , έπεται ότι Το γινόμενο $p(p-1)$ διαιρεί τον $[E:{\mathbb{Q}}]$ και επομένως $[Ε:{\mathbb{Q}}]\geq p(p-1)$ . Επίσης,

[Ε:{\mathbb{Q}}]=[E:{\mathbb{Q}}(\omega)][{\mathbb{Q}}(\omega):{\mathbb{Q}}]

και

[E:{\mathbb{Q}}(\omega)]=[{\mathbb{Q}}(\omega),\sqrt[p]{2}):{\mathbb{Q}}(% \omega)]\leq p,

αφού $\sqrt[]{2}$ είναι ρίζα του $x^{p}-2\in{\mathbb{Q}}[\omega]$ . Από τις ανισότητες

p(p-1)\;\leq\;[Ε:{\mathbb{Q}}]\;\leq\;p\,[{\mathbb{Q}}(\omega):{\mathbb{Q}}]=p% (p-1),

έπεται ότι

[Ε:{\mathbb{Q}}]=p(p-1)

και ότι $[E:{\mathbb{Q}}(\omega)]=p$ . Άρα το $f(x)$ είναι ανάγωγο πάνω από το ${\mathbb{Q}}(\omega)$ . Από το Θεώρημα 5.3.1 προκύπτει ότι

\operatorname{Gal}\left(E/{\mathbb{Q}}(\omega)\right)\cong{\mathbb{Z}}_{p},

ενώ από το Πόρισμα 5.1.5 προκύπτει ότι

\operatorname{Gal}\left({\mathbb{Q}}(\omega):{\mathbb{Q}}\right)\cong{\mathbb{% Z}}_{p}^{*}.

Η επέκταση ${\mathbb{Q}}(\omega)/{\mathbb{Q}}$ είναι επέκταση του Galois και επομένως

\operatorname{Gal}\left(E/{\mathbb{Q}}(\omega)\right)\lhd\operatorname{Gal}(E/% {\mathbb{Q}}).

Έστω $\sigma$ , $\tau$ , τα στοιχεία της $\operatorname{Gal}(E/{\mathbb{Q}})$ , όπως αυτά καθορίζονται από τη δράση τους στα στοιχεία $\sqrt[p]{2}$ και $\omega$ του $E$ :

\begin{matrix}\sigma:&&\sqrt[p]{2}\mapsto\sqrt[p]{2}\omega,&&\omega\mapsto% \omega\cr\tau:&&\sqrt[p]{2}\mapsto\sqrt[p]{2},&&\omega\mapsto\omega^{2}.\end{matrix}

Εύκολα επιβεβαιώνει κανείς ότι $\sigma\tau\neq\tau\sigma$ και άρα η ομάδα $\operatorname{Gal}(E/{\mathbb{Q}})$ δεν είναι αβελιανή.

Ορισμός 5.3.4.

Μία επέκταση σωμάτων $E/F$ λέγεται κυκλική (cyclic) αν $E/F$ είναι επέκταση του Galois και an η ομάδα $\operatorname{Gal}(E/F)$ είναι κυκλική.

Παραδείγματα 5.3.5.

1.

Έστω $Ε={\mathbb{Q}}(\omega)$ , όπου $\omega=e^{2\pi i/p}$ , για κάποιον πρώτο φυσικό αριθμό $p$ . Σύμφωνα με το Πόρισμα 5.1.5, η επέκταση $E/{\mathbb{Q}}$ είναι κυκλική.
2.

Έστω $\omega=e^{\pi i/4}$ και $E={\mathbb{Q}}(\omega)$ . H κυκλοτομική επέκταση $E/{\mathbb{Q}}$ δεν είναι κυκλική, βλ. Παράδειγμα 5.1.6.1.

Το επόμενο θεώρημα χαρακτηρίζει τις κυκλικές επεκτάσεις. Αν $a\in{\mathbb{C}}$ , με $\sqrt[n]{α}$ συμβολίζουμε μία οποιαδήποτε ρίζα του πολυωνύμου $x^{n}-a$ στο ${\mathbb{C}}$ .

Θεώρημα 5.3.6.

Έστω $F\subset{\mathbb{C}}$ ένα σώμα που περιέχει όλες τις $n$ -ρίζες της μονάδας πάνω από το ${\mathbb{Q}}$ . Μία επέκταση $E/F$ είναι κυκλική βαθμού $n$ αν και μόνο αν $E=F\left(\sqrt[n]{a}\right)$ , για κάποιο $a\in F$ .

Απόδειξη.

Έστω ότι $E=F\left(\sqrt[n]{a}\right)$ , για κάποιο $a\in F$ . Τότε η επέκταση $E/F$ είναι κυκλική σύμφωνα με το Θεώρημα 5.3.1, αφού κάθε υποομάδα κυκλικής ομάδας είναι κυκλική.

Αντίστροφα, έστω ότι η επέκταση $E/F$ είναι κυκλική βαθμού $n$ και έστω ότι το $\sigma$ παράγει την $\operatorname{Gal}(E/F)$ , δηλ.

\operatorname{Gal}(E/F)=\langle\sigma\rangle=\{\operatorname{id}_{E},\sigma,% \ldots,\sigma^{n-1}\}.

Έστω $\omega$ μία πρωταρχική $n$ -ρίζα της μονάδας. Τα στοιχεία της ομάδας $\operatorname{Gal}(E/F)$ είναι γραμμικά ανεξάρτητα πάνω από το σώμα $Ε$ , βλ. Θεώρημα 3.4.2. Επομένως, ο γραμμικός συνδυασμός

h=\operatorname{id}_{E}+\omega\sigma+\cdots+\omega^{n-1}\sigma^{n-1}:\ \ E\longrightarrow E

δεν είναι η μηδενική συνάρτηση στο $E$ και υπάρχει ένα στοιχείο $b\in E$ τέτοιο ώστε $h(b)\neq 0$ . Έστω $\gamma=h(b)$ . Τότε

\gamma=b+\sigma(b)\omega+\cdots+\sigma^{n-1}(b)\omega^{n-1}.

(5.3.6.1)

και θεωρούμε την επέκταση $F(\gamma)/F$ . Έτσι

F\subset F(\gamma)\subset E.

Παρατηρούμε ότι, αφού ο βαθμός της επέκτασης $E/F$ είναι $n$ , (δηλ. $[E:F]=n$ ), ο βαθμός της επέκτασης $F(\gamma)/F$ διαιρεί το $n$ και άρα $[F(\gamma):F]\leq n$ . Θα αποδείξουμε ότι

[F(\gamma):F]=n\textrm{ και }F(\gamma)=E.

Πράγματι,

\begin{split}\displaystyle\sigma(\gamma)&\displaystyle=\sigma(b)+\sigma^{2}(b)% \omega+\cdots+\sigma^{n-1}(b)\omega^{n-2}+b\omega^{n-1}=\omega^{n-1}\gamma\\ \displaystyle\sigma^{2}(\gamma)&\displaystyle=\omega^{n-1}\sigma(\gamma)=% \omega^{n-1}\omega^{n-1}\sigma(\gamma)=\omega^{n-2}\gamma\\ \displaystyle\vdots&\\ \displaystyle\sigma^{n-1}(\gamma)&\displaystyle=\omega\gamma.\end{split}

Άρα τα στοιχεία $\gamma$ , $\sigma(\gamma),\ldots,\sigma^{n-1}(\gamma)$ είναι όλα διακεκριμένα. Σύμφωνα με την άσκηση 2.4.19, έπεται ότι $\deg\operatorname{irr}_{(F,\gamma)}(x)\geq n$ και επομένως $\deg\operatorname{irr}_{(F,\gamma)}(x)=n$ . Άρα

n=\deg\operatorname{irr}_{(F,\gamma)}(x)=[F(\gamma):F]\ \Rightarrow E=F(\gamma).

Μένει να δείξουμε ότι υπάρχει στοιχείο $a$ στο $F$ έτσι ώστε Το $\gamma$ na είναι ρίζα του πολυωνύμου $x^{n}-a\in F[x]$ . Πράγματι, θέτουμε $a=\gamma^{n}$ . Θα αποδείξουμε ότι $a\in F$ . Παρατηρούμε ότι γia $0\leq i\leq n-1$ ,

\sigma^{i}(a)=\sigma^{i}(\gamma^{n})=\left(\sigma^{i}(\gamma)\right)^{n}=\left% (\omega^{n-i}\gamma\right)^{n}=\gamma^{n}=a.

Άρα $a\in E^{\operatorname{Gal}(E/F)}$ . Όμως h $E/F$ είναι επέκταση του Galois και σύμφωνα με το Θεμελιώδες Θεώρημα της Θεωρίας Galois, $E^{\operatorname{Gal}(E/F)}=F$ . Άρα το $a\in F$ και το $\gamma$ είναι ρίζec του $x^{n}-a\in F[x]$ . Με άλλα λόγια, $E=F\left(\sqrt[n]{a}\right)$ και αποδείχτηκε το αντίστροφο. ∎

Το στοιχείο $\gamma$ λέγεται επιλύουσα του Lagrange (Lagrange’s resolvent) για τα στοιχεία $b$ , $\omega$ και $\sigma$ .

5.4 Ασκήσεις

1.

Να υπλολογήσετε τα $\Phi_{8}(x)$ και $\Phi_{9}(x)$ .
2.

Να εξετάσετε αν το $x^{(p-1)p}+x^{(p-2)^{p}}+\cdots+x^{2p}+x^{p}+1$ είναι ανάγωγο όταν o $p$ είναι πρώτος φυσικός αριθμός.
3. Έστω ένα σώμα με char ⁡ F = 0 , a ∈ F και E το σώμα ανάλυσης του πολυωνύμου x n - a , όπου n είναι φυσικός αριθμός. Αν ω είναι μια πρωταρχική n -ρίζα της μονάδας, να αποδείξετε ότι
1. (a)
  
  η επέκταση $F(\omega)/F$ είναι επέκταση του Galois.
2. (b) η σειρά $\operatorname{Gal}(E/E)\unlhd\operatorname{Gal}(E/F(\omega))\unlhd% \operatorname{Gal}(E/F)$ είναι επιλύσιμη.
4.

Έστω $E$ το σώμα ανάλυσης του $x^{5}-1$ πάνω από το ${\mathbb{Z}}_{2}$ . Να βρείτε όλα τα ενδιάμεσα υποσώματα.
5.

Έστω $E$ το σώμα ανάλυσης του $x^{5}-1$ πάνω από το ${\mathbb{Q}}$ . Να βρείτε όλα τα ενδιάμεσα υποσώματα.
6.

Να αποδείξετε ότι για $p$ πρώτο, $p>2$ ,

$\Phi_{2p}(x)=x^{p-1}-x^{p-2}+\cdots-x+1.$
7.

Έστω $Ε$ το κυκλοτομικό σώμα τάξης $12$ πάνω από το ${\mathbb{Q}}$ . Να βεθούν όλα τα ενδιάμεσα σώματα.
8.

Έστω $n>2$ ένας θετικός ακέραιος και $\omega$ μία πρωταρχική $n$ -ρίζα της μονάδας πάνω από το ${\mathbb{Q}}$ . Να αποδείξετε ότι

$[{\mathbb{Q}}\left(\omega+\omega^{-1}\right):{\mathbb{Q}}]=\frac{\phi(n)}{2}.$

Βιβλιογραφία Κεφαλαίου 5

1.

Bastida, J. R. Field Extensions and Galois Theory, Vol. 22. Addison-Wesley, 2007.
2.

Gaal, L. Classical Galois Theory with Examples. Chelsea, 1988.
3.

Hadlock, C. R. Field Theory and its Classical Problems. ΜΑΑ, 2000.
4.

Milne, J. S. Fields and Galois Theory. www.jmilne.org, 2014.
5.

Ribenhoim, P. Algebraic Numbers. Wiley-Interscience, New York, 1972.
6.

Rotman, J. Θεωρία Galois. Leader Books, 2000.
7.

Stewart, I. Galois Theory. Champan and Hall, 1973.
8.

Tignol, J. P. Galois Theory of Algebraic Equations. World Scientific, 2011.

Κεφάλαιο 5Κυκλοτομικά πολυώνυμα

5.1 Ρίζες της μονάδας

Παράδειγμα 5.1.1.

Πρόταση 5.1.2.

Απόδειξη.

Παραδείγματα 5.1.3.

Θεώρημα 5.1.4.

Απόδειξη.

Πόρισμα 5.1.5.

Απόδειξη.

Παραδείγματα 5.1.6.

5.2 Κυκλοτομικά πολυώνυμα

Παράδειγμα 5.2.1.

Πρόταση 5.2.2.

Απόδειξη.

Παραδείγματα 5.2.3.

Πρόταση 5.2.4.

Απόδειξη.

Πρόταση 5.2.5.

Απόδειξη.

Θεώρημα 5.2.6.

Απόδειξη.

Πόρισμα 5.2.7.

Θεώρημα 5.2.8 (Kronecker - Weber).

Θεώρημα 5.2.9.

Απόδειξη.

5.3 Το πολυώνυμο xn-a

Θεώρημα 5.3.1.

Πόρισμα 5.3.2.

Απόδειξη.

Παράδειγμα 5.3.3.

Ορισμός 5.3.4.

Παραδείγματα 5.3.5.

Θεώρημα 5.3.6.

Απόδειξη.

5.4 Ασκήσεις

Βιβλιογραφία Κεφαλαίου 5

5.3 Το πολυώνυμο $x^{n}-a$