Θεωρία Galois

Κεφάλαιο 4Πεπερασμένα σώματα

Στο κεφάλαιο αυτό εφαρμόζουμε τη Θεωρία Galois, όπως αυτή αναπτύχθηκε στα δύο προηγούμενα κεφάλαια, στην περίπτωση των πεπερασμένων σωμάτων.

4.1 Βασικές Έννοιες

Έστω $F$ ένα πεπερασμένο σώμα, δηλ. $|F|<\infty$ . Τότε η χαρακτηριστική του $F$ είναι κάποιος πρώτος αριθμός $p$ και έτσι το σώμα ${\mathbb{Z}}_{p}$ εμφυτεύεται στο $F$ , βλ. Ενότητα IV του Παραρτήματος. Επομένως προκειμένου να εξετάσουμε τα πεπερασμένα σώματα αρκεί να εξετάσουμε πεπερασμένες επεκτάσεις σωμάτων $F/{\mathbb{Z}}_{p}$ .

Έστω, λοιπόν, ότι $[F:\mathbb{Z}_{p}]=n$ , για κάποιον φυσικό αριθμό $n$ . Τότε το σώμα $F$ είναι $\mathbb{Z}_{p}$ -διανυσματικός χώρος διάστασης $n$ , $|F|=p^{n}$ , και $\operatorname{char}F=p$ , βλ. Πρόταση IV.5. Η πολλαπλασιαστική ομάδα $(F^{*},\cdot)$ του σώματος $F$ , όπου $F^{*}=F-\{0\}$ έχει $p^{n}-1$ στοιχεία. Ως συνέπεια του Θεωρήματος του Lagrange για τις πεπερασμένες ομάδες (βλ. Θεώρημα I.10), γνωρίζουμε ότι κάθε στοιχείο μίας ομάδας υψούμενο στην τάξη της ομάδας ισούται με το μοναδιαίο στοιχείο της ομάδας. Επομένως, για κάθε $a\in F^{*},$ ισχύει

a^{p^{n}-1}=1\Rightarrow a^{p^{n}}=a\Rightarrow a^{p^{n}}-a=0,

δηλαδή το $a$ είναι ρίζα του πολυωνύμου

f(x)=x^{p^{n}}-x\in\mathbb{Z}_{p}[x].

Το 0 είναι και αυτό ρίζα του $f(x)$ . Ισχύει, λοιπόν, η παρακάτω πρόταση:

Πρόταση 4.1.1.

Έστω $F$ πεπερασμένο σώμα και $|F|=p^{n}$ όπου $p$ πρώτος φυσικός αριθμός. Κάθε στοιχείο του $F$ είναι ρίζα του πολυωνύμου $f(x)=x^{p^{n}}-x$ και το $F$ είναι σώμα ανάλυσης του $f(x)$ , δηλ.

x^{p^{n}}-x=\prod_{a\in F}(x-a).

Θα αποδείξουμε τώρα ότι, για κάθε φυσικό αριθμό $n>1$ και για κάθε πρώτο φυσικό πρώτο αριθμό $p$ , υπάρχει ένα σώμα $F$ με $p^{n}$ στοιχεία. Η χαρακτηριστική του $F$ είναι βέβαια $p$ . Έστω $f(x)=x^{p^{n}}-x\in\mathbb{Z}_{p}[x]$ . Αφού $f^{\prime}(x)=-1\neq 0$ , έπεται ότι Το $f(x)$ είναι διαχωρίσιμο (Πρόταση 1.4.5). Από το Θεώρημα του Kronecker (Θεώρημα 1.4.3) υπάρχει μία επέκταση $L$ του $\mathbb{Z}_{p}$ που είναι σώμα ανάλυσης του $f(x)=x^{p^{n}}-x$ . Θεωρούμε, λοιπόν, το σύνολο των ριζών $M$ του $f(x)$ στο $L$ , δηλαδή

Μ=\{a\in L:a^{p^{n}}=a\}.

Θα δείξουμε ότι το $M$ είναι υπόσωμα του $L$ . Έστω $a,b\in M$ . Αφού

p\;|\;{p^{n}\choose i}\textrm{ για }1\leq i\leq p^{n}-1,

από την Πρόταση II.7 προκύπτει ότι

(a-b)^{p^{n}}=a^{p^{n}}-b^{p^{n}}=a-b\Rightarrow a-b\in M.

Ακόμη, αν $a,b\in M$ , $b\neq 0$ τότε

(ab^{-1})^{p^{n}}=a^{p^{n}}(b^{p^{n}})^{-1}=ab^{-1}\Rightarrow ab^{-1}\in M.

Άρα όντως Το $Μ$ είναι υπόσωμα του $L$ . Το πλήθος των στοιχείων του $M$ είναι το πλήθος των διακεκριμένων ριζών του $f(x)$ που είναι ακριβώς $p^{n}$ , αφού Το $f(x)$ είναι διαχωρίσιμο. Άρα Το $Μ$ είναι το ζητούμενο σώμα. Το $Μ$ ως σώμα ανάλυσης του διαχωρίσιμου πωλυωνύμου $f(x)\in{\mathbb{Z}}_{p}[x]$ είναι επέκταση του Galois πάνω από το ${\mathbb{Z}}_{p}$ . Ακόμη το $Μ$ είναι μοναδικό με προσέγγιση ισομορφίας, ως σώμα ανάλυσης του $f(x)$ (βλ. Πόρισμα 3.2.2). Τα παραπάνω, λοιπόν, αποδεικνύουν το επόμενο θεώρημα:

Θεώρημα 4.1.2.

Για κάθε πρώτο αριθμό $p$ και για κάθε φυσικό αριθμό $n>1$ υπάρχει μοναδικό πεπερασμένο σώμα $F$ με $p^{n}$ στοιχεία. H επέκταση $F/{\mathbb{Z}}_{p}$ είναι επέκταση Galois βαθμού $n$ .

Το σώμα με $p^{n}$ στοιχεία, όπως αναφέρεται στο Θεώρημα 4.1.2, λέγεται σώμα Galois με ${p^{n}}$ στοιχεία (Galois field with $p^{n}$ elements) και συνήθως συμβολίζεται ως ${\operatorname{GF}(p^{n})}$ . Ως συνήθως, η πολλαπλασιαστική ομάδα του $\operatorname{GF}(p^{n})$ συμβολίζεται ως $\operatorname{GF}(p^{n})^{*}$ . Όταν $n=1$ , $\operatorname{GF}(p)\cong{\mathbb{Z}}_{p}$ και χρησιμοποιούμε ελεύθερα και τους δύο συμβολισμούς.

Παραδείγματα 4.1.3.

1.

Θα κατασκευάσουμε ένα σώμα με 4 στοιχεία, δηλ. το $\operatorname{GF}(2^{2})$ . Είναι φανερό ότι η χαρακτηριστική του $\operatorname{GF}(2^{2})$ είναι 2 και ότι το $\operatorname{GF}(2^{2})$ είναι επέκταση του $\mathbb{Z}_{2}$ βαθμού 2. Έστω ακόμη ότι $\operatorname{GF}(2^{2})=\{0,1,a,b\}$ . Παρατηρούμε ότι το στοιχείο $a+1\in\operatorname{GF}(2^{2})$ και ότι $a+1=b$ . Πράγματι αν $a+1=a$ τότε $1=0$ , αδύνατον. Αν $a+1=1$ τότε $a=0$ αδύνατον. Αν $a+1=0$ τότε $a=-1$ , άρα $α=1$ , αδύνατον επίσης. Ο παρακάτω πίνακας αποτυπώνει τα αποτελέσματα των πράξεων στην προσθετική ομάδα $(\operatorname{GF}(2^{2}),+)$ :

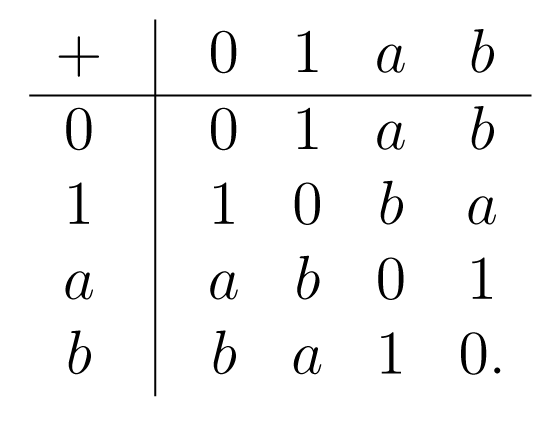
Η πολλαπλασιαστική ομάδα $(\operatorname{GF}(2^{2})^{*},\cdot)$ του $\operatorname{GF}(2^{2})$ έχει τρία στοιχεία, άρα είναι κυκλική και παράγεται είτε από το $a$ είτε από το $b$ . Έτσι $\operatorname{GF}(2^{2})^{*}=\{1,a,a^{2}=b\}$ . Έτσι, για τον πολλαπλασιασμό στην $(\operatorname{GF}(2^{2})^{*},\cdot)$ έχουμε τον παρακάτω πίνακα:

Παρατηρούμε ακόμη ότι αφού $a^{2}=b$ και $1=-1$ στο ${\mathbb{Z}}_{2}$ , τότε

$a^{2}=a+1\Rightarrow a^{2}-a-1=0\Rightarrow a^{2}+a+1=0.$

Δηλαδή το $a$ είναι ρίζα του πολυωνύμου $x^{2}+x+1\in\mathbb{Z}_{2}[x]$ . Όμως, Το $x^{2}+x+1$ είναι ανάγωγο, αφού δεν έχει ρίζα στο ${\mathbb{Z}}_{2}$ . Άρα $\operatorname{GF}(2^{2})=\mathbb{Z}_{2}(a)$ και $\operatorname{irr}_{(\mathbb{Z}_{2},a)}(x)=x^{2}+x+1$ . Οι ρίζες του $x^{2}+x+1$ sΤο $\operatorname{GF}(2^{2})$ είναι $a$ , $a^{2}=a+1$ .
2.
Έστω $\operatorname{GF}(2^{3})$ το σώμα με 8 στοιχεία που κατασκευάζεται σύμφωνα με το Θεώρημα 4.1.2. Θα μελετήσουμε τη δομή του $\operatorname{GF}(2^{3})$ . Παρατηρούμε καταρχήν ότι η πολλαπλασιαστική ομάδα $(\operatorname{GF}(2^{3})^{*},\cdot)$ του $\operatorname{GF}(2^{3})$ έχει 7 στοιχεία. Αφού Το 7 είναι πρώτος, η ομάδα $\operatorname{GF}(2^{3})^{*}$ είναι κυκλική (Θεώρημα I.14) και μάλιστα κάθε στοιχείο $1\neq b\in\operatorname{GF}(2^{3})^{*}$ παράγει την $\operatorname{GF}(2^{3})^{*}$ (Πρόταση I.8). Επομένως αν $0,1\neq b\in\operatorname{GF}(2^{3})$ , τότε κάθε μη μηδενικό στοιχείο του $\operatorname{GF}(2^{3})$ προκύπτει ως κάποια δύναμη του $b$ και επομένως $\operatorname{GF}(2^{3})=Z_{2}(b)$ , $0,1\neq b\in\operatorname{GF}(2^{3})$ . Παρατηρούμε, επίσης, ότι $[\operatorname{GF}(2^{3}):\mathbb{Z}_{2}]=3$ , βλ. Πρόταση IV.5. Σύμφωνα με το Θεώρημα 4.1.2, Το $\operatorname{GF}(2^{3})$ είναι το σώμα ανάλυσης του πολυωνύμου $x^{8}-x$ πάνω από το ${\mathbb{Z}}_{2}$ . Παρατηρούμε ότι $x$ και $x+1$ είναι δύο ανάγωγοι παράγοντες του $x^{8}-x$ . Με υπολογισμούς βρίσκουμε ότι το $x^{2}+x+1$ δεν διαιρεί το $x^{8}-x$ , ενώ τα πολυώνυμα $x^{3}+x^{2}+1$ , $x^{3}+x+1$ το διαιρούν. Έτσι η ανάλυση του $x^{8}-x$ σε γινόμενο ανάγωγων πολυωνύμων στο $\mathbb{Z}_{2}[x]$ είναι:

$x^{8}-x=x^{8}+x=x(x+1)(x^{3}+x^{2}+1)(x^{3}+x+1),$

Έστω $a\in\operatorname{GF}(2^{3})$ ρίζα του $x^{3}+x^{2}+1$ . Δηλαδή $\operatorname{irr}_{(\mathbb{Z}_{2},a)}(x)=x^{3}+x^{2}+1$ . Αφού $[{\mathbb{Z}}_{2}(a):{\mathbb{Z}}_{2}]=3$ , έπεται ότι $\mathbb{Z}_{2}(a)=\operatorname{GF}(2^{3})$ . Τα στοιχεία $1,a,a^{2}$ είναι μια $\mathbb{Z}_{2}$ -βάση του $\operatorname{GF}(2^{3})$ . Αυτό σημαίνει ότι

$\operatorname{GF}(2^{3})=\{c_{0}+c_{1}a+c_{2}a^{2}:c_{i}\in\mathbb{Z}_{2},0% \leq i\leq 2\}$

$=\{0,1,a,1+a,a^{2},1+a^{2},a+a^{2},1+a+a^{2}\}.$

Συγκεκριμένα αφού $\operatorname{irr}_{(\mathbb{Z}_{2},a)}(x)=x^{3}+x^{2}+1$ έπεται ότι
- –
  
  $a^{3}=a^{2}+1$ ,
- –
  
  $a^{4}=aa^{3}=a^{2}+a+1$ ,
- –
  
  $a^{5}=a^{2}a^{3}=a+1$ ,
- –
  
  $a^{6}=aa^{5}=a^{2}+a$ ,
- –
  
  $a^{7}=1$ .
Οι ρίζες του $x^{3}+x^{2}+1$ είναι οι $a,a^{2},α^{4}$ , ενώ οι ρίζες του $x^{3}+x+1$ είναι οι $a^{3},a^{5},a^{6}$ . Η αντίστοιχη ανάλυση μπορεί να γίνει και για $a\in\operatorname{GF}(2^{3})$ που είναι ρίζα του $x^{3}+x+1$ και αφήνεται για τον αναγνώστη. Επίσης ο αναγνώστης μπορεί να υπολογίσει τους πίνακες για τις πράξεις στις ομάδες $(\operatorname{GF}(2^{3}),+)$ και $(\operatorname{GF}(2^{3})^{*},\cdot)$ .
3.
Έστω τώρα $\operatorname{GF}(2^{4})$ το σώμα με 16 στοιχεία που κατασκευάζεται σύμφωνα με το Θεώρημα 4.1.2. Θα δείξουμε ότι υπάρχει $a\in\operatorname{GF}(2^{4})$ έτσι ώστε $\operatorname{GF}(2^{4})={\mathbb{Z}}_{2}(a)$ . Πράγματι, αρκεί να δείξουμε ότι υπάρχει ένα στοιχείο $a\in\operatorname{GF}(2^{4})^{*}$ έτσι ώστε η τάξη του $a$ στην πολλαπλασιαστική ομάδα $\operatorname{GF}(2^{4})^{*}$ να είναι 15. Θα προσπαθήσουμε, λοιπόν, να μετρήσουμε τον αριθμό των στοιχείων του $\operatorname{GF}(2^{4})^{*}$ με τάξη μικρότερη του 15. Σύμφωνα με το Θεώρημα του Lagrange, τα στοιχεία αυτά του $\operatorname{GF}(2^{4})^{*}$ θα έχουν τάξη 5, 3 ή 1. Αφού, όμως,
- –
  
  τα στοιχεία με τάξη 5 είναι ρίζες του πολυωνύμου $x^{5}-1$ ,
- –
  
  ένα πολυώνυμο βαθμού $n$ πάνω από το σώμα $F$ έχει το πολύ $n$ ρίζες και
- –
  
  το 1 είναι ρίζα του $x^{5}-1$ και $1$ έχει τάξη 1,
έπεται ότι υπάρχουν το πολύ 4 στοιχεία με τάξη 5 στο $\operatorname{GF}(2^{4})^{*}$ . Αντίστοιχα υπάρχουν το πολύ 2 στοιχεία του $F^{*}$ με τάξη 3. Υπάρχει βέβαια ακριβώς ένα στοιχείο με τάξη 1. Δηλαδή υπάρχουν το πολύ 7 στοιχεία στο $\operatorname{GF}(2^{4})^{*}$ με τάξη μικρότερη του 15. Επομένως υπάρχουν τουλάχιστον $15-7=8$ στοιχεία στο $\operatorname{GF}(2^{4})^{*}$ με τάξη 15. Έστω $a$ ένα τέτοιο στοιχείο. Άρα $\operatorname{GF}(2^{4})^{*}=\langle a\rangle$ και συνεπώς $\operatorname{GF}(2^{4})={\mathbb{Z}}_{2}(a)$ .
Παρατηρούμε επίσης ότι γενικότερα για κάθε κυκλική ομάδα $G=\langle a\rangle$ me $|G|=15$ ισχύουν τα εξής (βλ. Προτάσεις I.7 και I.8:
- –
  
  $1\leq n\leq 14$ και $(n,15)=1$ , τότε Το $a^{n}$ έχει και αυτό τάξη $15$ . Δηλαδή υπάρχουν $\phi(15)=8$ στοιχεία με τάξη $15$ που προκύπτουν ως δυνάμεις του $a$ , όπου $\phi$ είναι η συνάρτηση του Euler.
- –
  
  αν $1\leq n\leq 14$ και $(n,15)=3$ , τότε $a^{n}$ έχει τάξη $5$ . Υπάρχουν $\phi(5)=4$ πλήθους τέτοιοι αριθμοί και $\langle a^{3}\rangle=\langle a^{6}\rangle=\langle a^{9}\rangle=\langle a^{12}\rangle$ . Πράγματι, αφού $15=5\cdot 3$ , αν ξεκινήσουμε με $n=3$ , αρκεί στη συνέχεια να θεωρήσουμε τα πολλαπλάσια $3κ$ , όπου $1\leq k\leq 5$ , $(k,5)=1$ .
- –
  
  αν $1\leq n\leq 14$ και $(n,15)=5$ , τότε Το $a^{n}$ έχει τάξη $3$ . Υπάρχουν $2$ τέτοιοι αριθμοί $n$ : $n=5$ , $n=10$ . Δηλαδή $2=\phi(3)$ . Είναι επίσης φανερό ότι $\langle a^{5}\rangle=\langle a^{10}\rangle$ .
Άρα ισχύει η παρακάτω σχέση:

$15=\phi(15)+\phi(5)+\phi(3)+\phi(1).$

4.2 Πρωταρχικά στοιχεία

Στην ενότητα αυτή θα γενικεύσουμε τις παρατηρήσεις που έγιναν στα προηγούμενα παραδείγματα. Έστω $\phi:\mathbb{N}\rightarrow\mathbb{N}$ , η γνωστή συνάρτηση του Euler (βλ. Παράδειγμα I.2.3), όπου $\phi(n)=|\mathbb{Z}_{n}^{\sharp}|$ . Όταν $C$ είναι μία κυκλική ομάδα, συμβολίζουμε με ${g(C)}$ το σύνολο των στοιχείων που παράγουν τη $C$ . Έτσι, όταν $|C|=m$ τότε $|g(C)|=\phi(m)$ (βλ. Πρόταση I.8). Έστω $G$ μία τυχαία ομάδα και $C_{1}$ , $C_{2}$ δύο κυκλικές υποομάδες της $G$ . Αν $C_{1}\neq C_{2}$ τότε $g(C_{1})\cap g(C_{2})=\emptyset$ . Είναι φανερό ότι ισχύει

G=\bigcup_{C}g(C),

(4.2.0.1)

όπου Το $C$ διατρέχει όλες τις κυκλικές υποομάδες της $G$ .

Θα εφαρμόσουμε την παραπάνω σχέση στην περίπτωση που η ομάδα $G$ είναι κυκλική τάξης $n$ . Μετρώντας τα στοιχεία στα σύνολα που εμφανίζονται και στα δύο σκέλη της σχέση (4.2.0.1) βρίσκουμε ότι

n=\sum_{C}|g(C)|,

(4.2.0.2)

όπου το $C$ διατρέχει όλες τις υποομάδες της $G$ . Αφού, για κάθε $d$ που διαιρεί το $n$ , υπάρχει ακριβώς μία (κυκλική) ομάδα $C$ έτσι ώστε $|C|=d$ (βλ. Θεώρημα I.14) και $|g(C)|=\phi(d)$ προκύπτει το εξής συμπέρασμα:

Πρόταση 4.2.1.

Έστω $n>1$ φυσικός αριθμός. Τότε

n=\sum_{d\ {|}\ n}\phi(d)

Παρατηρούμε ότι στη γενική περίπτωση μίας ομάδας $G$ πληθυκότητας $n$ είναι πιθανόν, να υπάρχουν παραπάνω από μία κυκλικές ομάδες τάξης $d$ , όπου Το $d$ διαιρεί το $n$ , ή και καμία. Παρακάτω αποδεικνύουμε το αντίστροφο του Θεωρήματος I.8.ii, χρησιμοποιώντας τις σχέσεις 4.2.0.1 και 4.2.1.

Θεώρημα 4.2.2.

Μία ομάδα $G$ τάξης $n<\infty$ είναι κυκλική αν και μόνο αν, για κάθε διαιρέτη $d$ του $n$ , υπάρχει το πολύ μία κυκλική υποομάδα τάξης $d$ .

Απόδειξη.

Αν η $G$ είναι κυκλική τότε το συμπέρασμα προκύπτει από το Θεώρημα I.8.ii. Υποθέτουμε αντίστροφα ότι, για κάθε διαιρέτη $d$ του $n$ , υπάρχει το πολύ μία κυκλική υποομάδα τάξης $d$ . Άρα όλα τα στοιχεία που έχουν τάξη $d$ (αν υπάρχουν), παράγουν την ίδια υποομάδα και έτσι στη σχέση (4.2.0.2) μπορούμε ισοδύναμα να προσθέσουμε τους διαιρέτες του $n$ . Επίσης, αν υπάρχει κυκλική υποομάδα $C$ της $G$ τάξης $d$ , τότε όπως είδαμε $|g(C)|=\phi(d)$ . Άρα

n=\sum_{d|n,\atop|C|=d}\phi(d),

όπου $C$ είναι κυκλική ομάδα (αν υπάρχει). Εάν, λοιπόν, για κάποιο $d$ δεν υπάρχει κάποια κυκλική υποομάδα τάξης $d$ , ο όρος $\phi(d)$ δε θα εμφανίζεται στο παραπάνω άθροισμα. Όμως, από τη Πρόταση 4.2.1, προκύπτει ότι αναγκαστικά, για κάθε $d$ διαιρέτη του $n$ , υπάρχει ακριβώς μία κυκλική υποομάδα της $G$ τάξης $d$ . Αυτό συμβαίνει και για $d=n$ , δηλαδή η $G$ είναι κυκλική. ∎

Oδηγούμαστε, λοιπόν, στο επόμενο θεώρημα.

Θεώρημα 4.2.3.

Κάθε πεπερασμένη υποομάδα της πολλαπλασιαστικής ομάδας ενός σώματος $F$ είναι κυκλική.

Απόδειξη.

Έστω $G$ μία υποομάδα της $(F^{*},\cdot)$ τάξης $n$ και $d|n$ . Αν $C$ είναι μία κυκλική υποομάδα της $G$ τάξης $d$ , τότε από το θεώρημα του Lagrange $c^{d}=1,\forall\ c\in C$ . Αν υπήρχε και δεύτερη κυκλική υποομάδα της $G$ τάξης $d$ , τότε θα υπήρχαν τουλάχιστον $d+1$ στοιχεία $x$ της $G$ που ικανοποιούν την εξίσωση $x^{d}=1$ . Όμως, το πολυώνυμο $x^{d}-1$ έχει το πολύ $d$ ρίζες σε ένα σώμα. Άρα υπάρχει το πολύ μία κυκλική υποομάδα της $G$ τάξης $d$ , για κάθε $d$ διαιρέτη του $n$ . Από το Θεώρημα 4.2.2 προκύπτει ότι η $G$ είναι κυκλική. ∎

Πόρισμα 4.2.4.

Αν $\operatorname{GF}(p^{n})$ είναι ένα πεπερασμένο σώμα τότε η $(\operatorname{GF}(p^{n})^{*},\cdot)$ είναι κυκλική ομάδα και $\operatorname{GF}(p^{n})=\operatorname{GF}(p)(a)$ , για κάποιον πρώτο $p$ και για κάποιο στοιχείο $a$ .

Ειδικότερα, για $p$ πρώτο φυσικό αριθμό, ισχύει η παρακάτω πρόταση.

Πρόταση 4.2.5.

Έστω $p$ πρώτος. Η πολλαπλασιαστική ομάδα $\operatorname{GF}(p)^{*}$ είναι κυκλική.

Παρατηρούμε ότι h Πρόταση 4.2.5 δεν είναι αληθής για τυχαίο $n$ , όπως δείχνουν τα επόμενα παραδείγματα.

Παραδείγματα 4.2.6.

1.

Η ομάδα $\mathbb{Z}_{8}^{\sharp}$ έχει $\phi(8)=4$ πλήθους στοιχεία και $\mathbb{Z}_{8}^{\sharp}=\{\bar{1},\overline{3},\bar{5},\bar{7}\}$ . Αφού η τάξη των $\bar{3}$ , $\bar{5}$ , $\bar{7}$ είναι ίση με 2, η ομάδα $\mathbb{Z}_{8}^{\sharp}$ δεν είναι κυκλική. Επομένως, η $\mathbb{Z}_{8}^{\sharp}$ είναι ισόμορφη με την ομάδα του Klein.
2.

Η ομάδα $\mathbb{Z}_{9}^{\sharp}$ έχει $\phi(9)=6$ πλήθους στοιχεία και $\mathbb{Z}_{8}^{\sharp}=\{\bar{1},\bar{2},\bar{4},\bar{5},\bar{7},\bar{8}\}$ . Είναι εύκολο να υπολογίσουμε ότι η $\operatorname{ord}(\bar{2})=6$ . Επομένως η $\mathbb{Z}_{9}^{\sharp}$ είναι κυκλική.

Ένα στοιχείο $a\in\operatorname{GF}(p^{n})^{*}$ λέγεται πρωταρχικό (primitive) αν

(\operatorname{GF}(p^{n})^{*},\cdot)=\langle a\rangle.

Σημειώνουμε ότι αν $a\in\operatorname{GF}(p^{n})^{*}$ είναι πρωταρχικό τότε

\operatorname{GF}(p^{n})=\operatorname{GF}(p)(a).

Όπως θα δούμε στα επόμενα παραδείγματα, δεν ισχύει το αντίστροφο. Έτσι, είναι δυνατόν να ισχύει ότι $\operatorname{GF}(p^{n})=\operatorname{GF}(p)(a)$ και $α$ να μην είναι πρωταρχικό. Στη γενική περίπτωση δεν είναι γνωστή μία μέθοδος προσδιορισμού πρωταρχικών στοιχείων. Στα παρακάτω παραδείγματα ταυτίζουμε τον φυσικό αριθμό $m$ με την εικόνα του $\bar{m}$ στον ${\mathbb{Z}}_{p}\cong\operatorname{GF}(p)$ και στην επέκταση $\operatorname{GF}(p^{n})$ του $\operatorname{GF}(p)$ .

Παραδείγματα 4.2.7.

1.

Στο σώμα $\operatorname{GF}(11)\cong{\mathbb{Z}}_{11}$ , το ${2}$ είναι πρωταρχικό. Πράγματι, η τάξη του ${2}$ στο $\mathbb{Z}_{11}^{*}$ πρέπει να διαιρεί το 10 σύμφωνα με το Θεώρημα του Lagrange. Απλοί υπολογισμοί, δείχνουν ότι

${2^{2}}={4}\neq{1},\textrm{ ενώ }{2^{5}}={32}={-1}\neq{1}.$

Επομένως $\operatorname{ord}\left({2}\right)=10$ και ${\mathbb{Z}}_{11}=\langle{2}\rangle$ .
2.
Το πολυώνυμο $f(x)=x^{2}-2$ είναι ανάγωγο πάνω από το $\mathbb{Z}_{5}$ , αφού δεν έχει ρίζες στο $\mathbb{Z}_{5}$ . Έστω $F$ Το σώμα ανάλυσης του $f(x)$ πάνω από το $\mathbb{Z}_{5}$ . Αν $a\in F$ είναι μία ρίζα του $f(x)$ τότε η άλλη ρίζα του $f(x)$ είναι το $-a$ . Συνεπώς $F=\mathbb{Z}_{5}(a)$ και $|F|=25$ . Επομένως $F\cong\operatorname{GF}(5^{2})$ . Τα στοιχεία του $F$ είναι της μορφής $k+la$ , όπου $k,l\in\mathbb{Z}_{5}$ . Παρατηρούμε ότι το $a$ δεν είναι πρωταρχικό, αφού $a^{2}=2$ . Υπολογίζοντας διαδοχικά τις δυνάμεις του $b=2+a$ διαπιστώνουμε ότι το $b$ είναι πρωταρχικό. Πράγματι, οι δυνατές τάξεις του $b$ είναι οι διαιρέτες του $24$ . Bλέπουμε ότι:
- –
  
  $b^{2}=2+4a+a^{2}=4+4a+2=6+4a=1+4a$ .
- –
  
  $b^{3}=(2+a)(1+4a)=2+9a+4a^{2}=4a$ .
- –
  
  $b^{4}=3+3a$ .
- –
  
  $b^{6}=(b^{3})^{2}=2$ .
- –
  
  $b^{8}=2+3a$ .
- –
  
  $b^{12}=(b^{6})^{2}=4$ .
Άρα, η τάξη του $b$ στην $(F^{*},\cdot)$ είναι 24, το $b$ είναι πρωταρχικό και επομένως $F=\mathbb{Z}_{5}(b)$ .

Σημειώνουμε την παρακάτω χρήσιμη πρόταση.

Πρόταση 4.2.8.

Έστω $a$ πρωταρχικό στοιχείο του $\operatorname{GF}(p^{n})$ . Τότε το $a$ είναι ρίζα ενός αναγώγου πολυωνύμου βαθμού $n$ πάνω από το $\operatorname{GF}(p)$ .

Απόδειξη.

Έστω $f(x)=\operatorname{irr}_{(\mathbb{Z}_{p},a)}(x)$ . Από το Πόρισμα 4.2.4 $\operatorname{GF}(p^{n})=\operatorname{GF}(p)(a)$ έπεται ότι $\operatorname{GF}(p^{n})=\operatorname{GF}(p)(a)$ . Αφού $[\operatorname{GF}(p^{n}):\operatorname{GF}(p)]=n$ , από το Θεώρημα 2.2.3 προκύπτει ότι $\deg f(x)=n$ . ∎

Ως άμεση συνέπεια του Πορίσματος 4.2.4 και της Πρότασης 4.2.8, συμπεραίνουμε την ύπαρξη ανάγωγων πολυωνύμων στο $\operatorname{GF}(p)[x]$ .

Πόρισμα 4.2.9.

Για κάθε φυσικό αριθμό $n>1$ , υπάρχει ανάγωγο πολυώνυμο $f(x)\in\operatorname{GF}(p)[x]$ βαθμού $n$ .

Στη συνέχεια εξετάζουμε την ομάδα Galois $\operatorname{Gal}\left(\operatorname{GF}(p^{n})/\operatorname{GF}(p)\right)$ .

Θεώρημα 4.2.10.

Έστω $n>1$ φυσικός αριθμός. Τότε

\operatorname{Gal}\left(\operatorname{GF}(p^{n})/\operatorname{GF}(p)\right)% \cong\mathbb{Z}_{n}.

Απόδειξη.

Σύμφωνα με το Πόρισμα 4.2.4, υπάρχει $a\in\operatorname{GF}(p^{n})$ πρωταρχικό. Έστω $f(x)=\operatorname{irr}_{(\mathbb{Z}_{p},a)}(x)$ και $G=\operatorname{Gal}\left(\operatorname{GF}(p^{n})/\operatorname{GF}(p)\right)$ . Από το Θεώρημα 4.1.2, η επέκταση $\operatorname{GF}(p^{n})/\operatorname{GF}(p)$ είναι επέκταση του Galois. Αφού το $a$ είναι πρωταρχικό στοιχείο του $\operatorname{GF}(p^{n})$ , έπεται ότι $\operatorname{GF}(p^{n})=\operatorname{GF}(p)(a)$ . Κάθε ρίζα του $f(x)$ είναι επίσης ρίζα του διαχωρίσιμου πολυωνύμου $x^{p^{n}}-x\in\operatorname{GF}(p)[x]$ , άρα το $f(x)$ είναι επίσης διαχωρίσιμο. Επομένως, από το Πόρισμα 3.2.4 έπεται ότι

|G|=[\operatorname{GF}(p^{n}):\operatorname{GF}(p)]=n.

Στη συνέχεια θα δείξουμε ότι η ομάδα $G$ είναι κυκλική προσδιορίζοντας έναν από τους γεννήτορες της $G$ . H συνάρτηση

\sigma:\ \operatorname{GF}(p^{n})\rightarrow\operatorname{GF}(p^{n}),\quad b% \mapsto b^{p},\;b\in\operatorname{GF}(p^{n}),

είναι αυτομορφισμός του $\operatorname{GF}(p^{n})$ , (βλ. άσκηση 4.4.5), και διατηρεί τα στοιχεία του $\operatorname{GF}(p)$ σταθερά. Πράγματι, αφού η πολλαπλαστιακή ομάδα $(\operatorname{GF}(p)^{*},\cdot)$ έχει $p-1$ στοιχεία, έπεται ότι $\forall c\in\operatorname{GF}(p)^{*}$ , $c^{p-1}=1$ και άρα $c^{p}=c$ , $\forall c\in\operatorname{GF}(p)^{*}$ . Άρα τα στοιχεία του $\operatorname{GF}(p)^{*}$ απεικονίζονται στον εαυτό τους. Εύκολα μπορεί να ελεγχθεί ότι η $\sigma$ είναι ομομορφισμός δακτυλίων και ότι ο πυρήνας της είναι τετριμμένος. Aναγκαστικά αφού το σώμα $\operatorname{GF}(p)^{*}$ είναι πεπερασμένο ο μονομορφισμός $\sigma$ είναι και επιμορφισμός, δηλαδή αυτομορφισμός του $\operatorname{GF}(p)^{*}$ . Συμπεραίνουμε, λοιπόν, ότι $\sigma\in G$ . Ακόμα τα στοιχεία $\sigma,\sigma^{2},\ldots,\sigma^{n}$ είναι διακεκριμένα στοιχεία της $G$ . Διαφορετικά, για κάποιο $i<n$ , θα είχαμε ότι $\sigma^{i}=\operatorname{id}_{\operatorname{GF}(p^{n})}$ και ότι, για κάθε $b\in\operatorname{GF}(p^{n})$ , θα ίσχυε ότι

\sigma^{i}(b)=b\Rightarrow b^{p^{i}}=b\Rightarrow{b^{p^{i}}}-b=0.

Δηλαδή, για κάθε $b\in\operatorname{GF}(p^{n})$ , το $b$ θα ήταν ρίζα του πωλυωνύμου $x^{p^{i}}-x$ . Όμως $|\operatorname{GF}(p^{n})|=p^{n}$ , ενώ $\deg(x^{p^{i}}-x)=p^{i}<p^{n}$ που είναι αδύνατον. Άρα

G=\langle\sigma\rangle.

Επομένως η $G$ είναι κυκλική τάξης $n$ , άρα είναι ισόμορφη με την $(\mathbb{Z}_{n},+)$ . ∎

Είδαμε ότι όταν $p$ είναι πρώτος φυσικός αριθμός, τότε ο $\operatorname{GF}(p)$ -αυτομορφισμός του $\operatorname{GF}(p^{n})$

\sigma:\operatorname{GF}(p^{n})\rightarrow\operatorname{GF}(p^{n}),\quad b% \mapsto b^{p},

παράγει την ομάδα $\operatorname{Gal}\left(\operatorname{GF}(p^{n})/\operatorname{GF}(p)\right)$ . Ο αυτομορφισμός αυτός λέγεται αυτομορφισμός του Frobenius (Frobenius automorphism). Όταν $n=1$ , τότε ο αυτομορφισμός του Frobenius για το σώμα $\operatorname{GF}(p)$ είναι ακριβώς o ταυτοτικός. Το σώμα $\operatorname{GF}(p^{n})$ είναι τέλειο. Γενικότερα, ένα σώμα $F$ λέγεται τέλειο (perfect) αν είναι χαρακτηριστικής μηδέν ή αν έχει χαρακτηριστική $p$ και η συνάρτηση του Frobenius

f:F\rightarrow F,\quad a\mapsto a^{p}

είναι αυτομορφισμός. Η εικόνα της συνάρτησης του Frobenius συμβολίζεται με ${F^{p}}$ , δηλ.

F^{p}=\{a^{p}:\ a\in F\}.

Είναι φανερό ότι το $F^{p}$ είναι ένα υπόσωμα του $F$ (βλ. άσκηση 4.4.6) και αποτελείται από τα στοιχεία $\beta\in F$ για τα οποία $\sqrt[p]{\beta}\in F$ .

Παράδειγμα 4.2.11.

Το σώμα κλασμάτων $F={\mathbb{Z}}_{p}(x)$ του πολυωνυμικού δακτυλίου μίας μεταβλητής με συντελεστές από το σώμα ${\mathbb{Z}}_{p}$ είναι άπειρο και έχει χαρακτηριστική $p$ . Tο σώμα $F$ δεν είναι τέλειο. Πράγματι, έστω $f$ η συνάρτηση του Frobenius. Η $f$ είναι μονομορφισμός. Όμως η $f$ δεν είναι επιμορφισμός, αφού το στοιχείο $x\notin{\rm Im}f$ , δηλ. δεν υπάρχουν πολυώνυμα $f(x)$ , $g(x)\in{\mathbb{Z}}_{p}[x]$ έτσι ώστε

\left(\frac{f(x)}{g(x)}\right)^{p}=x.

(συγκρίνετε τους βαθμούς των πολυωνύμων $xg(x)^{p}$ , $f(x)^{p}$ , για να oδηγηθείτε σε άτοπο).

4.3 Eνδιάμεσα υποσώματα

Στην ενότητα αυτή θα υπολογίσουμε τα ενδιάμεσα υποσώματα $Ε$ του $\operatorname{GF}(p^{n})$ , για $n\geq 1$ , όπου

\operatorname{GF}(p)\subset E\subset\operatorname{GF}(p^{n}).

Παρατηρούμε καταρχήν ότι o βαθμός της επέκτασης $E/\operatorname{GF}(p)$ , δηλ. ο $[E:\operatorname{GF}(p)]$ διαιρεί το $n$ αφού

n=[\operatorname{GF}(p^{n}):\operatorname{GF}(p)]=[\operatorname{GF}(p^{n}):E]% \,[E:\operatorname{GF}(p)].

Από το Θεμελιώδες Θεώρημα της Θεωρίας Galois γνωρίζουμε ότι σε κάθε υποομάδα της $\operatorname{Gal}\left(\operatorname{GF}(p^{n})/\operatorname{GF}(p)\right)$ αντιστοιχεί ακριβώς ένα ενδιάμεσο υποσώμα του $\operatorname{GF}(p^{n})$ . Από το Θεώρημα I.14 που περιγράφει όλες τις υποομάδες της κυκλικής ομάδας ${\mathbb{Z}}_{n}$ , οδηγούμαστε στο παρακάτω συμπέρασμα.

Θεώρημα 4.3.1.

Έστω $n\geq 1$ ένας φυσικός αριθμός. Για κάθε $m|n$ υπάρχει μοναδικό υπόσωμα $E$ του $\operatorname{GF}(p^{n})$ τέτοιο ώστε $|E|=p^{m}$ . Αντίστροφα κάθε υπόσωμα $Ε$ του $\operatorname{GF}(p^{n})$ έχει $p^{m}$ στοιχεία, για κάποιο $m|n$ .

Στο παρακάτω παράδειγμα υπολογίζουμε τα υποσώματα του $\operatorname{GF}(p^{12})$ .

Παράδειγμα 4.3.2.

Το διάγραμμα των υποσωμάτων του $\operatorname{GF}(p^{12})$ φαίνεται στο Σχήμα 4.1:

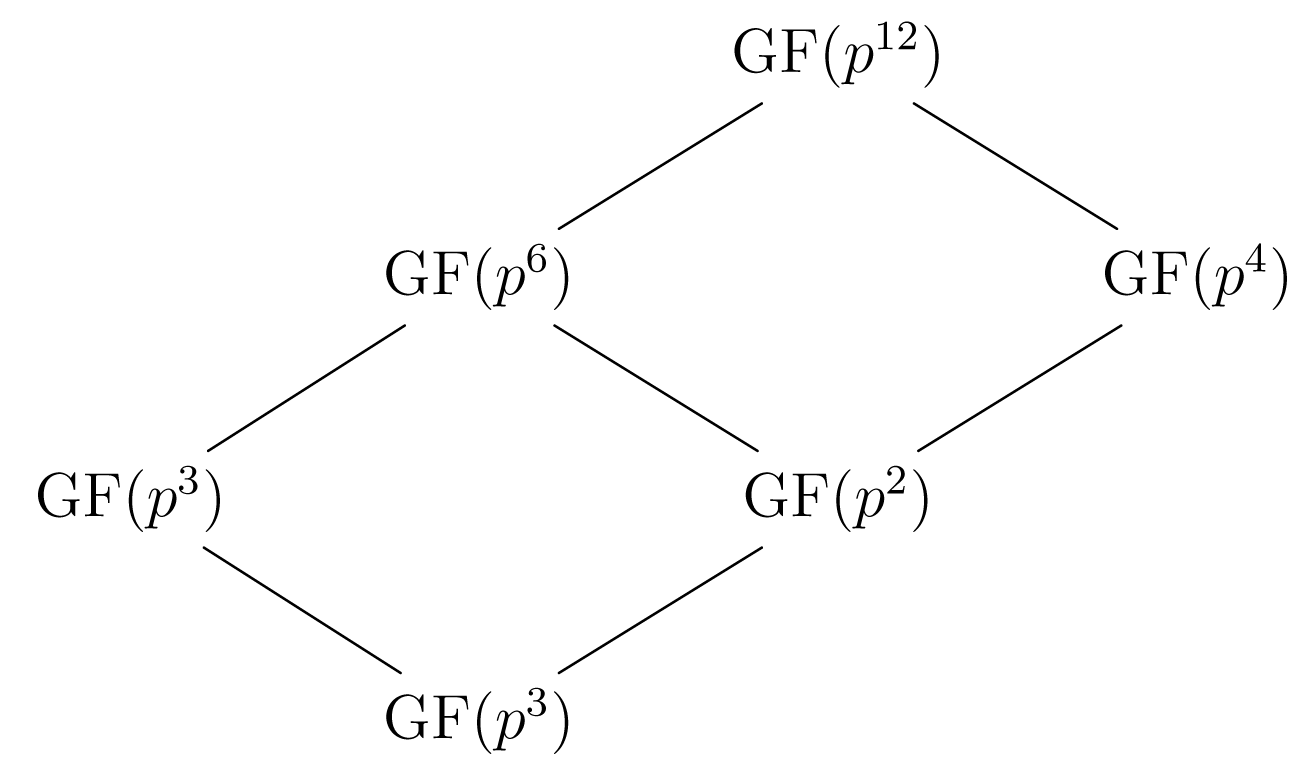
Σχήμα 4.1: Τα υποσώματα του $\operatorname{GF}(p^{12})$

Έστω $\sigma\in\operatorname{Gal}\left(\operatorname{GF}(p^{n})/\operatorname{GF}(p)\right)$ ο αυτομορφισμός του Frobenius. Στο Θεώρημα 4.2.10 αποδείξαμε ότι το $\sigma$ έχει τάξη $n$ και ότι

\operatorname{Gal}\left(\operatorname{GF}(p^{n})/\operatorname{GF}(p)\right)=% \langle\sigma\rangle.

Έστω $a$ πρωταρχικό στοιχείο του $\operatorname{GF}(p^{n})$ . Από την Πρόταση 2.3.2 προκύπτει ότι τα συζυγή στοιχεία του $a$ στην $\operatorname{GF}(p^{n})/\operatorname{GF}(p)$ , δηλ. τα στοιχεία $\sigma^{i}(a)$ , για $i=0,\ldots,n-1$ είναι ρίζες του $\operatorname{irr}_{(\operatorname{GF}(p),a)}(x)$ . Αφού

\deg\operatorname{irr}_{(\operatorname{GF}(p),a)}(x)=[\operatorname{GF}(p^{n})% :\operatorname{GF}(p)]=n,

από την άσκηση 2.4.19 προκύπτει ότι τα στοιχεία αυτά είναι διακεκριμένα. Απομονώνουμε, λοιπόν, τη χρήσιμη αυτή παρατήρηση.

Πρόταση 4.3.3.

Aν $a$ είναι ένα πρωταρχικό στοιχείο του σώματος $\operatorname{GF}(p^{n})$ , τότε οι ρίζες του $\operatorname{irr}_{(\operatorname{GF}(p),a)}(x)$ είναι οι

a,\;a^{p},\;a^{p^{2}},\;\cdots\;,a^{p^{n-1}}.

Θα γενικεύσουμε αυτή τη πρότaση παρακάτω. Πρώτα, όμως, έχουμε την επόμενη παρατήρηση.

Παρατήρηση 4.3.4.

Έστω $q=p^{n}$ και $f(x)\in\operatorname{GF}(q)[x]$ . Τότε $f(x^{q})=f(x)^{q}$ . Έτσι αν $a$ είναι ρίζα του $f(x)$ , τότε το $a^{q^{τ}}$ είναι επίσης ρίζα του $f(x)$ , για κάθε φυσικό αριθμό $t$ .

Απόδειξη.

Έστω ότι

f(x)=\sum_{i=0}^{s}c_{i}x^{i}\in\operatorname{GF}(q)[x],\textrm{ 'opou }c_{i}% \in\operatorname{GF}(q).

Θα αποδείξουμε ότι $f(x^{q})=f(x)^{q}$ . Καταρχήν, πριν υπολογήσουμε τη δύναμη $f(x)^{q}$ , παρατηρούμε ότι $c^{q}=c$ , για κάθε $c\in\operatorname{GF}(q)$ . Πράγματι, αυτό είναι προφανές όταν $c=0$ , ενώ όταν $c\in\operatorname{GF}(q)^{*}$ , τότε $c^{q-1}=1$ από το Θεώρημα του Lagrange και άρα $c^{q}=c$ . Στη συνέχεια, θα αποδείξουμε ότι

\left(\sum_{i=0}^{s}c_{i}x^{i}\right)^{q}=\sum_{i=0}^{s}c_{i}^{q}x^{iq}.

Με απλή μαθηματική επαγωγή αρκεί να αποδείξουμε αναλυτικά την παραπάνω πρόταση στην περίπτωση δύο προσθετέων. Αρκεί, λοιπόν, να αποδείξουμε ότι

(f_{1}+f_{2})^{q}=f_{1}^{q}+f_{2}^{q},\textrm{ gia }f_{1},f_{2}\in% \operatorname{GF}(q)[x].

Αφού η ακέραι περιοχή $\operatorname{GF}(q)[x]$ έχει χαρακτηριστική τον πρώτο αριθμό $p$ και o $p$ διαιρεί τον διωνυμικό συντελεστή ${p\choose i}$ , για $i=1,\ldots,p-1$ , από την ανάπτυξη του διώνυμου, βλέπουμε ότι

(f_{1}+f_{2})^{p}=x_{1}^{p}+x_{2}^{p},\textrm{ για }f_{1},f_{2}\in% \operatorname{GF}(q)[x].

Έτσι

(f_{1}+f_{2})^{p^{2}}=\left((f_{1}+f_{2})^{p}\right)^{p}=f_{1}^{p^{2}}+f_{2}^{% p^{2}}.

Επαναλαμβάνοντας προκύπτει ότι

(f_{1}+f_{2})^{q}=f_{1}^{q}+f_{2}^{q},\textrm{ gia }f_{1},f_{2}\in% \operatorname{GF}(q)[x].

Επομένως

f(x)^{q}=(\sum_{i=0}^{s}c_{i}x^{i})^{q}=\sum_{i=0}^{s}c_{i}^{q}x^{iq}=\sum_{i=% 0}^{s}c_{i}(x^{q})^{i}=f(x^{q}).

Έτσι, αν $a$ είναι ρίζα του $f(x)$ και $f(a)=0$ , τότε

0=f(a)^{q}=f(a^{q}),

δηλ. $a^{q}$ είναι επίσης ρίζα του $f(x)$ . Επαναλαμβάνοντας, έχουμε ότι αν $a$ είναι ρίζα του $f(x)$ τότε $a^{q^{t}}$ είναι ρίζα του $f(x)$ για κάθε φυσικό αριθμό $t$ . ∎

Όταν το πολυώνυμο $f(x)\in\operatorname{GF}(q)[x]$ είναι ανάγωγο, τότε μπορούμε να πούμε κάτι περισσότερο.

Πρόταση 4.3.5.

Έστω $n\geq 1$ φυσικός αριθμός, $p$ ένας πρώτος φυσικός αριθμός, $q=p^{n}$ και $f(x)\in\operatorname{GF}(q)[x]$ ένα ανάγωγο πολυώνυμο βαθμού $s$ .

i)

για έναν φυσικό αριθμό $t$ , o $s$ διαιρεί τον $t$ αν και μόνο αν το $f(x)$ διαιρεί το πολυώνυμο $x^{q^{t}}-x$ .
ii)

Το $f(x)$ έχει μία ρίζα $a\in\operatorname{GF}(q^{s})$ και όλες οι ρίζες του $f(x)$ στο $\operatorname{GF}(q^{s})$ είναι οι: $a,a^{q},\ldots,a^{q^{s-1}}$ .

Απόδειξη.

i) Έστω $α\in E$ μία ρίζα του $f(x)$ , όπου $E$ είναι το σώμα ανάλυσης του $f(x)$ . Από το Θεώρημα 2.2.3, έχουμε την ισότητα

\deg f(x)=s=[\operatorname{GF}(q)(a):\operatorname{GF}(q)]

και επομένως $\operatorname{GF}(q)(a)$ είναι πεπερασμένο σώμα με $q^{s}$ στοιχεία. Σύμφωνα με το Θεώρημα 4.1.2 συμπεραίνουμε ότι to $\operatorname{GF}(q)(a)$ ταυτίζεται με το $\operatorname{GF}(q^{s})$ με προσέγγιση ισομορφίας. Αν τώρα το $f(x)$ διαιρεί το πολυώνυμο $x^{q^{t}}-x$ , τότε αφού το $\operatorname{GF}(q^{t})$ είναι το σώμα ανάλυσης του $x^{q^{t}}-x$ , ισχύει ο εγκλεισμός

\operatorname{GF}(q)(a)\subseteq Ε\subseteq\operatorname{GF}(q^{t}).

Έτσι,

\operatorname{GF}(q)\subseteq\operatorname{GF}(q)(a)\subseteq\operatorname{GF}% (q^{t})

και

[\operatorname{GF}(q^{t}):\operatorname{GF}(q)]=[\operatorname{GF}(q^{t}):% \operatorname{GF}(q)(a)]\;[\operatorname{GF}(q)(a):\operatorname{GF}(q)].

Επομένως

t=[\operatorname{GF}(q^{t}):\operatorname{GF}(q)(a)]\,s

και $s|t$ .

Αντίστροφα, αν $s|t$ τότε $\operatorname{GF}(q^{s})\subseteq\operatorname{GF}(q^{t})$ και επομένως κάθε ρίζα του $f(x)$ εμφυτεύεται στο $\operatorname{GF}(q^{t})$ . Αφού τα στοιχεία του $\operatorname{GF}(q^{t})$ είναι οι ρίζες του $x^{q^{t}}-x$ (βλ. Πρόταση 4.1.1), συμπεραίνουμε ότι Το $f(x)$ διαιρεί το $x^{q^{t}}-x$ (βλ. Πόρισμα 1.2.4).

ii) Έστω $a$ μία ρίζα του $f(x)$ σε ένα σώμα ανάλυσης $E$ . Όπως είδαμε στην απόδειξη του i), $\operatorname{GF}(q)(a)=\operatorname{GF}(q^{s})$ . Έστω $Η=\operatorname{Gal}\left(\operatorname{GF}(q^{s})/\operatorname{GF}(q)\right)$ και $G=\operatorname{Gal}\left(\operatorname{GF}(q^{s})/\operatorname{GF}(p)\right)$ . Αφού το $f(x)$ είναι ανάγωγο, από το Θεώρημα 2.2.3, έπεται ότι $|H|=s$ . Από το Θεμελιώδες Θεώρημα της Θεωρίας Galois έχουμε ότι $Η\leq G$ . Επίσης, αφού $q^{s}=(p^{n})^{s}=p^{ns}$ , σύμφωνα με το Θεώρημα 4.2.10, η ομάδα $G$ είναι κυκλική, τάξης $n s$ και παράγεται από τον $\sigma$ , τον αυτομορφισμό του Frobenius. Έτσι, σύμφωνα με το Θεώρημα I.14, η υποομάδα $Η$ της $G$ παράγεται από τον αυτομορφισμό $\sigma^{\frac{ns}{s}}=\sigma^{n}$ . Παρατηρούμε ότι

\sigma^{n}:\ \operatorname{GF}(q^{s})\rightarrow\operatorname{GF}(q^{s}),\quad a% \mapsto a^{q}.

Σύμφωνα με την άσκηση 2.4.19, τα στοιχεία

a,a^{q},\ldots,a^{q^{s-1}}

είναι διακεκριμένα. Από την Πρόταση 2.3.2 (ή την Παρατήρηση 4.3.4) τα στοιχεία αυτά είναι ρίζες του $f(x)$ . ∎

Aπό την απόδειξη της Πρότασης 4.3.5, προκύπτει το παρακάτω συμπέρασμα.

Παρατήρηση 4.3.6.

Έστω $q=p^{n}$ και $f(x)\in\operatorname{GF}(q)[x]$ ανάγωγο. Τότε το $f(x)$ είναι διαχωρίσιμο.

Απόδειξη.

Έστω $\deg f(x)=s$ . Τότε σύμφωνα με την Πρόταση 4.3.5

f(x)\;|\;(x^{q^{s}}-x).

Το $x^{q^{s}}-x\in\operatorname{GF}(q)[x]$ είναι διαχωρίσιμο, άρα και το $f(x)$ . ∎

Σημειώνουμε ότι η ιδιότητα αυτή, δηλ. ότι κάθε ανάγωγο πολυώνυμο είναι και διαχωρίσιμο, χαρακτηρίζει τα τέλεια σώματα, βλ. άσκηση 4.4.8.

Παράδειγμα 4.3.7.

Έστω $F$ σώμα με χαρακτηριστική $p\neq 0$ και $a\in F$ . Θα αποδείξουμε ότι το πολυώνυμο $x^{p^{n}}-a\in F[x]$ , όπου $n>1$ είναι ένας φυσικός αριθμός, είναι ανάγωγο αν και μόνο αν $a\notin F^{p}$ . Πράγματι, αν $a\in F^{p}$ , δηλ. $b^{p}=a$ , για κάποιο $b\in F$ , τότε

x^{p^{n}}-a=x^{p^{n}}-b^{p}=(x^{p^{n-1}})\,^{p}-b^{p}=(x^{p^{n-1}}-b)\,^{p}.

Αντίστροφα, έστω ότι $x^{p^{n}}-a$ δεν είναι ανάγωγο. Τότε υπάρχει $g(x)\in F[x]$ κανονικό, ανάγωγο και τέτοιο ώστε

g(x)\,|\,(x^{p^{n}}-a).

Από το Θεώρημα του Kronecker (Θεώρημα 1.4.3) υπάρχει μία επέκταση $K/F$ , όπου το $g(x)$ έχει μία ρίζα, έστω $\beta$ . Αυτό σημαίνει ότι

g(b)=0\Rightarrow b^{p^{n}}-a=0\Rightarrow\beta^{p^{n}}=a.

Άρα, στον δακτύλιο $K[x]$ ισχύει ότι

x^{p^{n}}-a=x^{p^{n}}-\beta^{p^{n}}=\left(x-\beta\right)^{p^{n}}

και

g(x)\,|\,(x-\beta)^{p^{n}}.

Αφού ο δακτύλιος $K[x]$ είναι Π.Μ.Α. έπεται ότι η ανάλυση του $g(x)$ σε ανάγωγους παράγοντες στον $K[x]$ είναι της μορφής

g(x)=(x-\beta)^{s},\textrm{ όπου }s=\deg g(x).

Επομένως, στον $F[x]$ ισχύει ότι

g(x)=x^{s}-\beta x^{s-1}+\cdots+(-1)^{s}\beta^{s}.

Άρα $\beta^{s}\in F$ και μάλιστα $1\leq s<p^{n}$ . Έστω $p^{t}=\operatorname{\textrm{ΜΚΔ}}(s,p^{n})$ . Τότε $t<n$ και

p^{t}=ks+lp^{n}\textrm{ για }k,l\in{\mathbb{Z}}.

Επομένως, για το $\beta^{p^{t}}\in F$ ισχύει:

\beta^{p^{t}}=\beta^{ks}\beta^{lp^{n}}=(b^{s})^{k}(b^{p^{n}})^{l}=(b^{s})^{k}a% ^{l}.

Συνεπώς

\beta^{p^{n-1}}=(\beta^{p^{t}})^{p^{n-1-t}}\in F.

Τότε, όμως,

a=\beta^{p^{n}}=(\beta^{p^{n-1}})^{p}\in F^{p}.

Αποδείξαμε, λοιπόν, το επόμενο συμπέρασμα:

Πρόταση 4.3.8.

$x^{p^{n}}-a\in F[x]$ είναι ανάγωγο αν και μόνο αν $a\notin F^{p}$ .

4.4 Ασκήσεις

1.
Έστω $Ε=\operatorname{GF}(8)$ .
- –
  
  Να υπολογίσετε τους πίνακες για τις πράξεις στις ομάδες $(E,+)$ και $(E^{*},\cdot)$ .
- –
  
  Να βρείτε ένα πρωταρχικό στοιχείο του $E$ .
- –
  
  Να δείξετε ότι $Ε$ είναι τέλειο, δείχνοντας αναλυτικά ότι $E=E^{2}$ .
2.
Έστω $f(x)=x^{3}+x^{2}+2x\in{\mathbb{Z}}_{5}[x]$ .
- –
  
  Να βρείτε ένα σώμα ανάλυσης $E$ του $f(x)$ .
- –
  
  Να περιγράψετε τα στοιχεία του $E$ .
- –
  
  Να βρείτε ένα στοιχείο $a$ έτσι ώστε $E=\mathbb{Z}_{5}(a)$ .
3.

Να δείξετε ότι υπάρχει ανάγωγο πολυώνυμο βαθμού 6 πάνω από το $\mathbb{Ζ}_{5}$ .
4.

Να υπολογίσετε τα υποσώματα $\operatorname{GF}(p)\subset E\subset\operatorname{GF}(p^{36})$ .
5.

Να αποδείξετε ότι αν $F$ είναι σώμα χαρακτηριστικής $p\neq 0$ , τότε η συνάρτηση του Frobenius, $f:\ F\rightarrow F$ , $b\mapsto b^{p}$ είναι αυτομορφισμός του $F$ .
6.

Να αποδείξετε ότι αν $F$ είναι σώμα χαρακτηριστικής $p\neq 0$ , τότε $F^{p}$ είναι υπόσωμα του $F$ .
7.

Έστω $p$ ένας πρώτος φυσικός αριθμός και $F$ ένα σώμα με $\operatorname{char}F=p$ . Δίνεται Το πολυώνυμο $f(x)=x^{p}-x-a\in F[x]$ . Αν το $f(x)$ έχει μία ρίζα, έστω $\beta$ , στο $F$ , να αποδείξετε ότι οι ρίζες του $f(x)$ είναι οι $\beta,\beta+1,\ldots,\beta+(p-1)\in F$ . Να αποδείξετε ότι Το $f(x)$ είναι ανάγωγο στο $F[x]$ ή Το $f(x)$ αναλύεται σε γινόμενο γραμμικών παραγόντων στο $F[x]$ .
8.

Να αποδείξετε ότι ένα σώμα $F$ είναι τέλειο αν και μόνον αν κάθε ανάγωγο πολυώνυμο του $F[x]$ είναι διαχωρίσιμο.

Βιβλιογραφία Κεφαλαίου 4

1.

Bastida, J. R. Field Extensions and Galois Theory, Vol. 22. Addison-Wesley, 2007.
2.

Dummit, D.S., Foote, R.M. Abstract Algebra. J. Wiley and Sons, INc, 2004.
3.

Escofier, J.P. Galois Theory. Springer, 2001.
4.

Fox, D. Galois Theory. John Wiley & Sons, 2012.
5.

Lidl, R., Niederreiter, H. Finite Fields. Cambridge University Press, New York 1994.
6.

Milne, J.S. Fields and Galois Theory. www.jmilne.org, 2014.
7.

Rotman, J. Θεωρία Galois. Leader Books, 2000.
8.

Stewart, I. Galois Theory. Champan and Hall, 1973.