Θεωρία Galois

Κεφάλαιο 2Σώματα και βαθμοί επεκτάσεων

Στο κεφάλαιο αυτό μελετούμε τις επεκτάσεις σωμάτων. Ιδιαίτερα σημαντικό εργαλείο για τη μελέτη μας αυτή είναι τα πολυώνυμα, έτσι θα εφαρμόσουμε το περιεχόμενο του Κεφαλαίου 1. Έστω $E/F$ μία επέκταση σωμάτων. Το σώμα $E$ έχει την πρόσθετη δομή του $F$ -διανυσματικού χώρου, με τη πράξη του εξωτερικού πολλαπλασιασμού να είναι ο συνήθης πολλαπλασιασμός: $F\times E\rightarrow E$ , $(c,a)\mapsto ca$ . Θα χρησιμοποιήσουμε αυτή τη δομή για να καταλάβουμε καλύτερα το $E$ .

2.1 Αλγεβρικά στοιχεία πάνω από ένα σώμα.

Όταν $E/F$ είναι επέκταση σωμάτων και $f(x)\in F[x]$ , τότε το $f(x)$ είναι στοιχείο και του δακτυλίου $E[x]$ . Βέβαια, το πολυώνυμο $f(x)\in F[x]$ μπορεί να είναι ανάγωγο στο $F[x]$ , αλλά να μην είναι ανάγωγο στο $E[x]$ .

Ορισμός 2.1.1.

Έστω $E/F$ επέκταση σωμάτων και $a\in E$ . Το $a$ λέγεται αλγεβρικό (algebraic) πάνω από το $F$ aν υπάρχει $f(x)\in F[x]$ , έτσι ώστε $f(x)\neq 0$ και $f(a)=0$ . Αν το $α$ δεν είναι αλγεβρικό πάνω από το $F$ , τότε το $a$ λέγεται υπερβατικό (transcendental) πάνω από το $F$ .

Παραδείγματα 2.1.2.

1.

Αν $a\in E$ , τότε το $a$ είναι αλγεβρικό πάνω από το $E$ , αφού είναι ρίζα του $f(x)=x-a\in E[x]$ .
2.

Το $a=\sqrt{3}\in\mathbb{R}$ είναι αλγεβρικό πάνω από το $\mathbb{Q}$ , αφού $a$ είναι ρίζα του $f(x)=x^{2}-3\in\mathbb{Q}[x]$ .
3.

Έστω $Ι$ το ιδεώδες $(y^{2}-3)$ του ${\mathbb{Q}}[y]$ , $E=\mathbb{Q}[y]/I$ και $b=y+i$ . Τότε το $b$ είναι ρίζα του πολυωνύμου $x^{2}-3\in{\mathbb{Q}}[x]$ , βλ. Παράδειγμα 1.4.1.3, και άρα το $b$ είναι αλγεβρικό πάνω από το $\mathbb{Q}$ .
4.

Έστω $f(x)\in F[x]$ ένα ανάγωγο πολυώνυμο, $Ι=(f(x))$ και $E=F[x]/I$ . Το στοιχείο $x+I\in E$ είναι αλγεβρικό πάνω από το $F$ , βλ. Θεώρημα 1.4.2.
5.

Έστω ότι $E$ είναι ενδιάμεσο σώμα της επέκτασης $L/F$ και ότι το $a\in L$ είναι αλγεβρικό πάνω από το $F$ . Υπάρχει, λοιπόν, $0\neq f(x)\in F[x]$ έτσι ώστε $f(a)=0$ . Αφού το $f(x)\in E[x]$ , συμπεραίνουμε ότι το $a$ είναι αλγεβρικό πάνω από το $Ε$ .
6.

Το στοιχείο $i\in\mathbb{C}$ είναι αλγεβρικό πάνω από τα σώματα $\mathbb{R}$ και $\mathbb{Q}$ .
7.

Έστω $z=a+bi\in\mathbb{C}$ , $a,b\in\mathbb{R}$ . Τότε $z-a=bi$ και $z^{2}-2az+a^{2}=-b^{2}$ . Άρα το $z$ είναι ρίζα του πολυωνύμου $x^{2}-2ax+(a^{2}+b^{2})\in\mathbb{R}[x]$ . Επομένως κάθε στοιχείο του $\mathbb{C}$ είναι αλγεβρικό πάνω από το $\mathbb{R}$ . Παρατηρούμε ότι η άλλη ρίζα του πολυωνύμου $x^{2}-2ax+(a^{2}+b^{2})$ είναι ο συζυγής του $z$ , δηλ. $\bar{z}=a-bi$ . επομένως όταν $z\notin{\mathbb{R}}$ , τότε το πολυώνυμο $x^{2}-2ax+(a^{2}+b^{2})=x^{2}-2{\rm Re}\,z+z\bar{z}$ είναι ανάγωγο, βλ. Πρόταση 1.2.6.
8.

Τα στοιχεία $a=\sqrt{2}$ και $b=\sqrt{3}\in\mathbb{R}$ είναι αλγεβρικά πάνω από το $\mathbb{Q}$ , αφού είναι ρίζες αντίστοιχα των πολυωνύμων $x^{2}-2$ και $x^{2}-3\in\mathbb{Q}[x]$ . Το γινόμενο $a\cdot b=\sqrt{6}$ είναι αλγεβρικό πάνω από το $\mathbb{Q}$ , αφού είναι ρίζα του πολυωνύμου $x^{2}-6\in\mathbb{Q}[x]$ .
9.

Το άθροισμα $a+b=\sqrt{2}+\sqrt{3}$ είναι αλγεβρικό πάνω από το $\mathbb{Q}$ . Πράγματι έστω $c=a+b=\sqrt{2}+\sqrt{3}$ . Τότε $c^{2}=5+2\sqrt{6}$ , οπότε $c^{2}-5=2\sqrt{6}$ . Άρα $(c^{2}-5)^{2}=24$ και $c^{4}-10c+1=0$ . Επομένως το $c$ είναι ρίζα του πολυωνύμου $f(x)=x^{4}-10x+1$ . Στην επόμενη ενότητα, Παράδειγμα 2.2.13, θα δούμε ότι Το $f(x)$ είναι ανάγωγο στο $\mathbb{Q}[x]$ χρησιμοποιώντας τις διαστάσεις κατάλληλων διανυσματικών χώρων.
10.

Το $\pi\in\mathbb{R}$ είναι υπερβατικό πάνω από το $\mathbb{Q}$ . H απόδειξη της υπερβατικότητας ενός στοιχείου συνήθως είναι ιδιαίτερα δύσκολη. Η απόδειξη για τον αριθμό $\pi$ δόθηκε από τον Lindemann το 1882 και στηρίζεται στο ότι ο αριθμός $e$ είναι επίσης υπερβατικός πάνω από το $\mathbb{Q}$ , όπως έδειξε ο Hermite το 1873, ενώ $e^{i\pi}=-1$ (βλ. [3, Section1.7] και [5]).
11.

Έστω $Ε=F(x)$ το σώμα κλασμάτων του δακτυλίου $F[x]$ . Τότε το $x\in Ε$ είναι υπερβατικό πάνω από το $F$ , (βλ. άσκηση 2.4.1).

Έστω $E/F$ μία επέκταση σωμάτων και $a\in E$ . Για να καταλάβουμε αν το $a$ είναι αλγεβρικό ή υπερβατικό πάνω από το $F$ , θα μελετήσουμε τον μικρότερο δακτύλιο που περιέχει το $F$ και το $a$ .

Ορισμός 2.1.3.

Έστω $E/F$ επέκταση σωμάτων και $a\in E$ . Ορίζουμε ${F[a]}$ και ${F(a)}$ να είναι τα παρακάτω υποσύνολα του $E$ :

F[a]=\{f(a):f(x)\in F[x]\},

F(a)=\left\{\;\frac{f(a)}{g(a)}:g(a)\neq 0,f(x),g(x)\in F[x]\right\}.

Έστω $E/F$ επέκταση σωμάτων και $a\in E$ . Είναι εύκολο να αποδείξουμε ότι το σύνολο $F[a]$ είναι υποδακτύλιος του $E$ , άρα το $F[a]$ είναι ακέραια περιοχή και το $F(a)$ είναι το σώμα κλασμάτων του $F[a]$ . Το σώμα $F(a)$ λέγεται απλή (simple) επέκταση του $F$ .

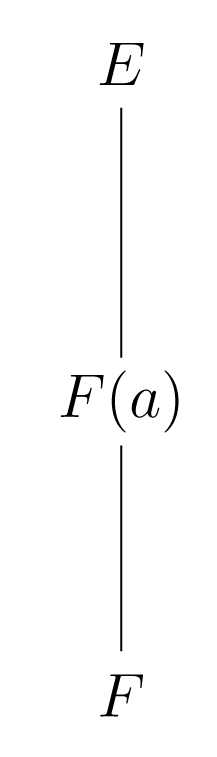
Παρατηρούμε ότι το $F(a)$ είναι το ελάχιστο υπόσωμα του $E$ που περιέχει το $F$ και το $a$ . Επομένως για να δείξουμε ότι η $E/F(a)$ είναι επέκταση σωμάτων, αρκεί να δείξουμε ότι η $Ε/F$ είναι επέκταση σωμάτων και ότι το $a\in E$ . Τέλος, παρατηρούμε ότι αν $F[a]$ είναι σώμα, τότε $F[a]=F(a)$ .

Παραδείγματα 2.1.4.

1.

Έστω $Φ$ σώμα. Αν $a\in F$ , τότε $F[α]=F(α)=F$ .
2.

Αφού $i^{2l}=\pm 1$ ενώ $i^{2l+1}=\pm i$ , για $l\in\mathbb{N}$ , έπεται ότι, για τυχαίο $f(x)\in\mathbb{R}[x]$ , ισχύει $f(i)=a+bi$ , όπου $a,b\in\mathbb{R}$ . Άρα

$\mathbb{R}[i]=\{a+bi:\ a,b\in\mathbb{R}\}=\mathbb{C}\textrm{ και επομένως }% \mathbb{R}[i]=\mathbb{R}(i).$

Μία $\mathbb{R}$ -βάση του $\mathbb{R}(i)$ είναι το σύνολο $\{1,i\}$ και ${\rm dim}_{\mathbb{R}}\mathbb{R}(i)=2$ .
3.

Έστω ότι $\gamma\in{\mathbb{C}}$ και $\gamma\notin{\mathbb{R}}$ . Τότε $\gamma=a+bi\in{\mathbb{C}}$ , όπου $a,b\in{\mathbb{R}}$ και $b\neq 0$ . Έστω $f(x)=x/b\in{\mathbb{R}}[x]$ . Τότε

$i=\frac{a+bi}{b}=f(\gamma)\textrm{ και επομένως }i\in{\mathbb{R}}[\gamma]% \textrm{ και }{\mathbb{R}}[i]\subseteq{\mathbb{R}}[\gamma]\subseteq{\mathbb{C}}.$

Αφού ${\mathbb{C}}={\mathbb{R}}[i]$ , προκύπτει ότι ${\mathbb{R}}[\gamma]={\mathbb{C}}$ και άρα ${\mathbb{R}}[\gamma]={\mathbb{R}}(\gamma)$ και κάθε $\gamma\in{\mathbb{C}}$ είναι αλγεβρικό πάνω από το ${\mathbb{R}}$ .
4.

Αφού ${\sqrt{3}}^{2l}=3^{l}$ και ${\sqrt{3}}^{2l+1}=3^{l}\sqrt{3}$ , για $l\in\mathbb{N}$ , έπεται ότι

$\mathbb{Q}[\sqrt{3}]=\{a+b\sqrt{3}:\ a,b\in\mathbb{Q}\}.$

Παρατηρούμε ότι αν κάποιο από τα $a,b\in\mathbb{Q}$ είναι διάφορο του μηδενός, τότε $0\neq a^{2}-3b^{2}\in\mathbb{Q}$ και θέτοντας $c=a^{2}-3b^{2}$ βλέπουμε ότι:

$\frac{1}{a+b\sqrt{3}}=\frac{a-b\sqrt{3}}{a^{2}-3b^{2}}\ =\frac{a}{c}-\frac{b}{% c}\sqrt{3}\ \in\mathbb{Q}[\sqrt{3}].$

Άρα $\mathbb{Q}(\sqrt{3})\subset\mathbb{Q}[\sqrt{3}]$ και $\mathbb{Q}[\sqrt{3}]=\mathbb{Q}(\sqrt{3})$ . Mία $\mathbb{Q}$ -βάση του $\mathbb{Q}(\sqrt{3})$ είναι το σύνολο $\{1,\sqrt{3}\}$ και ${\rm dim}_{\mathbb{Q}}\mathbb{Q}(\sqrt{3})=2$ .
5.

Θα μελετήσουμε τον δακτύλιο $\mathbb{Q}[\sqrt[3]{2}]$ . Έστω ότι $m\in\mathbb{N}$ . Εκφράζουμε το $m=3l+k$ , όπου $k,l\in\mathbb{N}$ και $l\leq 2$ . Αφού

$(\sqrt[3]{2})^{m}=(\sqrt[3]{2})^{3l+k}=2^{l}(\sqrt[3]{2})^{k},$

έπεται ότι, για τυχαίο $f(x)=\sum c_{i}x^{i}\in\mathbb{Q}[x]$ , ισχύει

$f(\sqrt[3]{2})=a_{0}+a_{1}\sqrt[3]{2}+a_{2}{\sqrt[3]{2}}^{2}:\quad a_{i}\in% \mathbb{Q}.$

Άρα $\mathbb{Q}[\sqrt[3]{2}]=\left\{{a_{0}+a_{1}\sqrt[3]{2}+a_{2}\sqrt[3]{4}:\ a_{i% }\in\mathbb{Q}}\right\}$ . Το σύνολο $\left\{1,\sqrt[3]{2},\sqrt[3]{4}\right\}$ παράγει το $\mathbb{Q}[\sqrt[3]{2}]$ ως $\mathbb{Q}$ -διανυσματικό χώρο και άρα ${\rm dim}_{\mathbb{Q}}\mathbb{Q}[\sqrt[3]{2}]\leq 3$ . Στην επόμενη ενότητα θα δούμε ότι ${\rm dim}_{\mathbb{Q}}\mathbb{Q}[\sqrt[3]{2}]=3$ .
6.

Έστω $Ε_{1}=\mathbb{Q}[\sqrt{2}]$ , $E_{2}=\mathbb{Q}[\sqrt{2}+\sqrt{3}]$ . Θα δείξουμε ότι $E_{1}\subsetneqq E_{2}$ . Πράγματι

$-\sqrt{2}+\sqrt{3}=\frac{1}{\sqrt{2}+\sqrt{3}}\in E_{2}$

και

$\sqrt{2}=\frac{(\sqrt{2}+\sqrt{3})-(-\sqrt{2}+\sqrt{3})}{2}\in E_{2}.$

Άρα $Ε_{1}\subset E_{2}$ . Για να δείξουμε ότι $E_{2}\neq E_{1}$ , αρκεί να δείξουμε ότι $\sqrt{2}+\sqrt{3}\notin E_{1}$ . Θα υποθέσουμε ότι $\sqrt{2}+\sqrt{3}\in E_{1}$ και θα καταλήξουμε σε άτοπο. Έστω, λοιπόν, ότι $\sqrt{2}+\sqrt{3}\in E_{1}$ . Τότε

$\sqrt{3}=(\sqrt{2}+\sqrt{3})-(\sqrt{2})\in E_{1}.$

Αφού μία $\mathbb{Q}$ -βάση του $Ε_{1}$ είναι το σύνολο $\{1,\sqrt{2}\}$ ενώ $\sqrt{3}\notin{\mathbb{Q}}$ , έπεται ότι

$\sqrt{3}=a+b\sqrt{2},\ a,b\in\mathbb{Q}\textrm{ και }b\neq 0.$ (2.1.4.1)

Αν $a=0$ , τότε

$\sqrt{3}=b\sqrt{2}\Rightarrow 3=b^{2}2,$

άτοπο, αφού $2\nmid 3$ . Επομένως $ab\neq 0$ στην έκφραση (2.1.4.1) και υψώνοντας στο τετράγωνο

$3=a^{2}+2b^{2}+2ab\sqrt{2}\Rightarrow\sqrt{2}=\frac{3-(a^{2}+2b^{2})}{2ab},$

άτοπο, αφού $\sqrt{2}\notin\mathbb{Q}$ .
7.

Έστω $p$ πρώτος, $\omega=e^{2\pi i/p}$ και $k\in\mathbb{N}$ έτσι, ώστε $\operatorname{\textrm{ΜΚΔ}}(k,p)=1$ . Θα δείξουμε ότι $\mathbb{Q}[\omega]=\mathbb{Q}[\omega^{k}]$ . Ο εγκλεισμός $\mathbb{Q}[\omega^{k}]\subset\mathbb{Q}[\omega]$ είναι εμφανής, αφού $\omega^{k}\in\mathbb{Q}[\omega]$ . Για τον αντίστροφο εγκλεισμό παρατηρούμε ότι υπάρχουν $r,t\in\mathbb{Z}$ έτσι, ώστε $rp+tk=1$ . Επομένως

$\omega=\omega^{rp+tk}=\omega^{rp}\ \omega^{tk}={\omega^{k}}^{t}\in\mathbb{Q}[% \omega^{k}].$

Έστω $E/F$ επέκταση σωμάτων και $a\in E$ . Eύκολα μπορεί να ελεγχθεί ότι η συνάρτηση

\phi:F[x]\rightarrow F[a],\quad\phi(h(x))=h(a)

(2.1.4.2)

είναι επιμορφισμός δακτυλίων (βλ. Πρόταση III.5). Παρατηρούμε ότι $\phi(c)=c$ , όταν $c\in F$ , ενώ $\phi(x)=a$ . Έχουμε ακόμα ότι $\ker\phi=\{f(x)\in F[x]:\ f(a)=0\}$ . Σύμφωνα με το Πρώτο Θεώρημα Ισομορφίας Δακτυλίων, προκύπτει ότι $F[x]/\ker\phi\cong\operatorname{Im}\phi=F[a]$ . Εφόσον το $F[a]$ είναι ακεραία περιοχή, έπεται ότι $\ker\phi$ είναι πρώτο ιδεώδες.

Πρόταση 2.1.5.

Έστω $E/F$ μία επέκταση σωμάτων και έστω ότι $a\in E$ . Tο $a$ είναι αλγεβρικό πάνω από το $F$ αν και μόνο αν $F[a]=F(a)$ . Όταν το $a$ είναι υπερβατικό πάνω από το $F$ , τότε $F[x]\cong F[a]$ και ${\rm dim}_{F}F[a]=\infty$ .

Απόδειξη.

Θεωρούμε τον επιμορφισμό $\phi$ της σχέσης (2.1.4.2). Έστω ότι το $a$ είναι αλγεβρικό πάνω από το $F$ . Τότε υπάρχει $f(x)\in F[x]$ έτσι ώστε $f(a)=0$ και $\ker\phi\neq 0$ . O $\ker\phi$ όπως είδαμε παραπάνω είναι πρώτο ιδεώδες άρα μέγιστο, αφού ο $F[x]$ είναι Π.Κ.Ι. Άρα ο δακτύλιος $F[a]\cong F[x]/\ker\phi$ είναι σώμα. Αφού $F[a]\subset F(a)$ και $F(a)$ είναι το μικρότερο σώμα που περιέχει το $F$ και το $a$ , έπεται ότι $F[a]=F(a)$ .

Αν το $a$ είναι υπερβατικό πάνω από το $F$ , τότε $\ker\phi=0$ και $F[a]\cong F[x]$ . Επομένως ο δακτύλιος $F[a]$ δεν είναι σώμα και ${\rm dim}_{F}F[a]=\infty$ . ∎

Στην επόμενη ενότητα θα υπολογίσουμε τη διάσταση του $F$ -διανυσματικού χώρου $F(a)$ , όταν το $a$ είναι αλγεβρικό. Θα κλείσουμε αυτήν την ενότητα με έναν ακόμη ορισμό.

Ορισμός 2.1.6.

Έστω $E/F$ μία επέκταση σωμάτων. O βαθμός (degree) του $E$ πάνω από το $F$ συμβολίζεται με ${[E:F]}$ και ισούται με τη διάσταση του $E$ ως $F$ -διανυσματικού χώρου.

Παραδείγματα 2.1.7.

1.

Μία βάση του ${\mathbb{C}}$ ως ${\mathbb{R}}$ -διανυσματικού χώρου είναι το σύνολο $\{1,i\}$ και $[\mathbb{C}:\mathbb{R}]=2$ .
2.

Αφού ένα στοιχείο του ${\mathbb{Q}}[\sqrt{3}]$ γράφεται ως $a\cdot 1+b\cdot\sqrt{3}$ , όπου $a,b\in{\mathbb{Q}}\}$ , έπεται ότι μία βάση του ${\mathbb{Q}}[\sqrt{3}]$ ως ${\mathbb{Q}}$ -διανυσματικού χώρου είναι το σύνολο $\{1,\sqrt{3}\}$ . Επομένως $[\mathbb{Q}[\sqrt{3}]:\mathbb{Q}]=2$ .
3.

Παρατηρούμε ότι ${\mathbb{R}}[\sqrt{3}]={\mathbb{R}}$ και επομένως $[\mathbb{R}[\sqrt{3}]:\mathbb{R}]=1$ .
4.

$[\mathbb{Q}[\pi]:{\mathbb{Q}}]=\infty$ .
5.

Το άπειρο σύνολο $\{1,x,x^{2},\ldots\}$ είναι $F$ -βάση του $F[x]$ . Αφού το σώμα $F(x)$ περιέχει ως $F$ -υποχώρο τον δακτύλιο $F[x]$ , έπεται ότι ${\rm dim}_{F}F(x)\geq{\rm dim}_{F}F[x]$ και άρα $[F(x):F]=\infty$ .

Απομονώνουμε τον συλλογισμό του τελευταίου παραδείγματος.

Πρόταση 2.1.8.

Αν $E$ είναι ενδιάμεσο σώμα της επέκτασης $L/F$ και $[E:F]=\infty$ , τότε $[L:F]=\infty$ .

2.2 Αλγεβρικά στοιχεία και διάσταση

Έστω $E/F$ μία επέκταση σωμάτων και $a\in E$ αλγεβρικό πάνω από το $F$ . Στην προηγούμενη ενότητα είδαμε ότι $F[a]=F(a)$ και ότι το σύνολο

I=\{f(x)\in F[x]:\ f(a)=0\}

είναι πρώτο ιδεώδες του $F[x]$ . Επομένως Το $I=\langle g(x)\rangle$ , όπου Το $g(x)$ είναι ανάγωγο πολυώνυμο του $F[x]$ . Άρα, αν $h(x)\in I$ , δηλαδή αν $h(a)=0$ , τότε $h(x)=q(x)g(x)$ και στην περίπτωση που $h(x)\neq 0$ , τότε $\deg h(x)\geq\deg g(x)$ . Επομένως αν $h(x)\in F[x]$ είναι ανάγωγο και $h(a)=0$ , τότε $h(x)=cg(x)$ , όπου $c\in F[x]$ . Οι παραπάνω παρατηρήσεις οδηγούν στον επόμενο ορισμό.

Ορισμός 2.2.1.

Έστω $E/F$ μία επέκταση σωμάτων και $a\in E$ αλγεβρικό πάνω από το $F[x]$ . Το μοναδικό κανονικό ανάγωγο πολυώνυμο του $F[x]$ που έχει το $a$ ως ρίζα, ονομάζεται το ανάγωγο πολυώνυμο (irreducible polynomial) του ${a}$ πάνω από το $F$ και συμβολίζεται με ${\operatorname{irr}}_{(F,a)}(x)$ . Οι ρίζες του $\operatorname{irr}_{(F,a)}(x)$ λέγονται συζυγή στοιχεία (conjugates) του $a$ .

Στα Παραδείγματα 2.2.2 υπολογίζουμε τa ανάγωγα πολυώνυμα σε κάποιες περιπτώσεις.

Παραδείγματα 2.2.2.

1.

Έστω $a\in E$ . Τότε $\operatorname{irr}_{(E,a)}(x)=x-a$ . Αντίστροφα αν $\deg\operatorname{irr}_{(E,a)}(x)=1$ τότε $a\in E$ .
2.

Θεωρούμε την επέκταση ${\mathbb{R}}/{\mathbb{Q}}$ και το στοιχείο $a=\sqrt{3}$ . Αφού $a\notin{\mathbb{Q}}$ , έπεται ότι $\operatorname{irr}_{(E,a)}(x)\geq 2$ . Αφού $\sqrt{3}$ είναι ρίζα του $x^{2}-3$ έπεται ότι $\operatorname{irr}_{(\mathbb{Q},a)}(x)=x^{2}-3$ .
3.

Έστω $p$ πρώτος φυσικός αριθμός και $\omega=e^{2\pi i/p}\in\mathbb{C}$ . Όπως σημειώσαμε μετά το Παράδειγμα 1.2.7, το $\omega$ είναι ρίζα του $\Phi_{p}(x)=x^{p-1}+x^{p-2}+\cdots+1$ . Στο Παράδειγμα 1.3.8 αποδείξαμε ότι $\Phi_{p}(x)$ είναι ανάγωγο πολυώνυμο στο ${\mathbb{Q}}[x]$ . Επομένως $\operatorname{irr}_{(\mathbb{Q},\omega)}(x)=\Phi_{p}(x)=x^{p-1}+x^{p-2}+\cdots+1$ .
4.

Έστω $\omega=e^{2\pi i/8}$ . Όπως και παραπάνω το $\omega$ είναι ρίζα του $x^{7}+x^{6}+\cdots+1$ , αλλά το πολυώνυμο αυτό δεν είναι ανάγωγο. Δεν είναι δύσκολο να δείξει κανείς ότι $\operatorname{irr}_{(\mathbb{Q},\omega)}(x)=x^{4}+1$ , βλ. άσκηση 2.4.5.
5.

Έστω $z=a+bi\in{\mathbb{C}}$ , όπου $b\neq 0$ . Τότε $\operatorname{irr}_{({\mathbb{R}},z)}(x)=x^{2}-2{\rm Re}z+z\bar{z}$ , βλ. Παράδειγμα 2.1.2.7.

Στη συνέχεια εξετάζουμε τη διάσταση του $F(a)$ ως $F$ -διανυσματικού χώρου, όταν το $a$ είναι αλγεβρικό πάνω από το $F$ . Υπενθυμίζουμε ότι $F(α)=F[a]$ , σύμφωνα με την Πρόταση 2.1.5.

Θεώρημα 2.2.3.

Έστω $E/F$ μία επέκταση σωμάτων, $a\in E$ αλγεβρικό πάνω από το $F$ και $\deg\operatorname{irr}_{(F,a)}(x)=n$ . Tο σύνολο $\{1,a,\ldots,a^{n-1}\}$ αποτελεί βάση του $F$ -διανυσματικού χώρου $F(a)$ και $[F(a):F]=n$ .

Απόδειξη.

Θέτουμε $f(x)=\operatorname{irr}_{(F,a)}(x)$ και $Β=\{1,a,\ldots,a^{n-1}\}$ . Έστω $g(a)$ τυχαίο στοιχείο του $F[a]$ , όπου $g(x)\in F[x]$ . Σύμφωνα με τον Ευκλείδειο αλγόριθμο $g(x)=f(x)p(x)+r(x)$ , όπου $p(x),r(x)\in F[x]$ και $t=\deg r(x)<n$ . Δηλαδή

r(x)=c_{t}x^{t}+\cdots+c_{1}x+c_{0}

και $c_{i}\in F$ , για $i=0,\ldots,t$ . Παρατηρούμε ότι

g(a)=f(a)p(a)+r(a)=r(a)=c_{t}a^{t}+\cdots+c_{1}a+c_{0}\cdot 1

και ότι to $g(a)$ είναι $F$ -γραμμικός συνδυασμός στοιχείων του συνόλου $B$ . Θα δείξουμε ότι το σύνολο $Β$ είναι γραμμικά ανεξάρτητο. Έστω $d_{0}\cdot 1+\cdots+d_{n-1}a^{n-1}=0$ , $d_{i}\in F$ , για $i=0,\ldots,n-1$ μία σχέση γραμμικής εξάρτησης των $a^{i}:0\leq i\leq n-1$ . Αν $h(x)=d_{0}+d_{1}x+\cdots+d_{n-1}x^{n-1}$ , τότε $h(a)=0$ και $h(x)\in(f(x))$ . Αν $h(x)\neq 0$ οδηγούμαστε σε άτοπο, αφού $\deg h(x)<\deg f(x)$ . Επομένως $h(x)=0$ και άρα $d_{i}=0$ , για $i=0,\ldots,n-1$ . ∎

H απόδειξη του παρακάτω πορίσματος είναι άμεση:

Πόρισμα 2.2.4.

Έστω $E/F$ επέκταση σωμάτων, $a\in E$ . Τότε το $a$ είναι αλγεβρικό πάνω από το $F$ αν και μόνο αν $[F(a):F]<\infty$ .

Για το επόμενο πόρισμα, θεωρούμε γνωστό το Θεμελιώδες Θεώρημα της Άλγεβρας. Σημειώνουμε ότι η απόδειξη του Θεμελιώδους Θεωρήματος της Άλγεβρας, με τα εργαλεία της Θεωρίας Galois, δίνεται στην Ενότητα 6.3 και είναι ανεξάρτητη του Πορίσματος 2.2.5.

Πόρισμα 2.2.5.

Τα ανάγωγα πολυώνυμα του δακτυλίου $\mathbb{R}[x]$ έχουν βαθμό 1 ή 2. Αν $a\in{\mathbb{C}}$ είναι ρίζα του $f(x)\in{\mathbb{R}}[x]$ , τότε $\overline{a}$ είναι ρίζα του $f(x)$ .

Απόδειξη.

Έστω $f(x)\in\mathbb{R}[x]$ ανάγωγο. Σύμφωνα με το Θεμελιώδες Θεώρημα της Άλγεβρας υπάρχει $a\in{\mathbb{C}}$ , τέτοιο ώστε $f(a)=0$ . Επίσης, αφού $f(x)$ είναι ανάγωγο, έπεται ότι $f(x)=c\operatorname{irr}_{(\mathbb{R},a)}(x)$ , για κάποιο $0\neq c\in\mathbb{R}$ και ότι

\deg f(x)=[\mathbb{R}(a):\mathbb{R}].

Αν, λοιπόν, Το $a$ είναι πραγματικός αριθμός, τότε $\mathbb{R}(a)={\mathbb{R}}$ και $\deg f(x)=1$ . Αν το $a\notin{\mathbb{R}}$ τότε, όπως είδαμε στο Παράδειγμα 2.1.4.2, $f(x)=(x-a)(x-\overline{a})$ , $\mathbb{R}(a)=\mathbb{C}$ και $\deg f(x)=[{\mathbb{C}}:\mathbb{R}]=2$ . ∎

Ιδιαίτερη σημασία έχουν οι επεκτάσεις ενός σώματος $F$ με την ιδιότητα όλα τα στοιχεία τους να είναι αλγεβρικά πάνω από το $F$ .

Ορισμός 2.2.6.

Έστω $E/F$ επέκταση σωμάτων. Το σώμα $E$ λέγεται αλγεβρικό πάνω από το $E$ αν κάθε στοιχείο του $E$ είναι αλγεβρικό πάνω από το $F$ και σε αυτήν την περίπτωση η επέκταση $E/F$ λέγεται αλγεβρική (algebraic extension).

Παράδειγμα 2.2.7.

Το σώμα $\mathbb{C}$ είναι αλγεβρικό πάνω από το $\mathbb{R}$ , βλ. Παράδειγμα 2.1.2.7. Το σώμα $\mathbb{R}$ δεν είναι αλγεβρικό πάνω από το $\mathbb{Q}$ , βλ. Παράδειγμα 2.1.2. 10.

Η παρακάτω πρόταση δίνει ένα κριτήριο για να μπορούμε να αποφασίσουμε αν μία επέκταση $E/F$ είναι αλγεβρική.

Πρόταση 2.2.8.

Έστω $E/F$ μία επέκταση σωμάτων έτσι ώστε $[E:F]<\infty$ . Τότε η επέκταση $E/F$ είναι αλγεβρική.

Απόδειξη.

Έστω ότι $[E:F]=n$ και ότι το $a$ είναι τυχαίο στοιχείο του $E$ . Το σύνολο $\{1,a,\ldots,a^{n}\}$ έχει $n+1$ στοιχεία, επομένως είναι γραμμικά εξαρτημένο. Άρα υπάρχει μία σχέση γραμμικής εξάρτησης $d_{0}\cdot 1+\cdots+d_{n}a^{n}=0$ , όπου $d_{i}\in F$ , για $i=0,\ldots,n$ και τουλάχιστον ένα από αυτά δεν είναι μηδέν. Θεωρούμε το μη μηδενικό πολυώνυμο $g(x)=d_{0}+d_{1}x+\cdots+d_{n}x^{n}\in F[x]$ . Το $a$ είναι ρίζα του $g(x)$ , άρα είναι αλγεβρικό πάνω από το $F$ . ∎

Το αντίστροφο της Πρότασης 2.2.8 δεν ισχύει, βλ. άσκηση 2.4.14

Ορισμός 2.2.9.

Έστω $E/F$ επέκταση σωμάτων, $a_{1},\ldots,a_{n}\in E$ . Ορίζουμε ${F[a_{1},\ldots,a_{n}]}$ να είναι το σύνολο

F[a_{1},\ldots,a_{n}]=\{f(a_{1},\ldots,a_{n}):\ f(x_{1},\ldots,x_{n})\in F[x_{% 1},\ldots,x_{n}]\}.

Αποδεικνύεται εύκολα ότι Το $F[a_{1},\ldots,a_{n}]$ είναι υποδακτύλιος του $E$ και άρα ακέραια περιοχή. Συμβολίζουμε με ${F(a_{1},\ldots,a_{n})}$ το σώμα κλασμάτων του $F[a_{1},\ldots,a_{n}]$ . Είναι φανερό ότι to $F(a_{1},\ldots,a_{n})$ είναι το ελάχιστο υπόσωμα του $E$ που περιέχει το $F$ και τα στοιχεία $a_{1},\ldots,a_{n}$ . Αν $L=F(a_{1},\ldots,a_{n})$ , τότε λέμε ότι ta $a_{1},\ldots,a_{n}$ παράγουν την επέκταση (generate) $E/F$ ή ότι το $L$ προκύπτει από το $F$ με επισύναψη των $a_{1},\ldots,a_{n}$ .

Σημειώνουμε ότι

F[a_{1},\ldots,a_{n}]=F[a_{1},\ldots,a_{n-1}][a_{n}]\textrm{ και }F(a_{1},% \ldots,a_{n})=F(a_{1},\ldots,a_{n-1})(a_{n}).

Θα δούμε, στο Πόρισμα 2.2.14 παρακάτω, ότι όταν ta $a_{1},\ldots,a_{n}\in E$ είναι αλγεβρικά πάνω από το $F$ , τότε $F[a_{1},\ldots,a_{n}]=F(a_{1},\ldots,a_{n})$ .

Θεώρημα 2.2.10.

Έστω $F$ ένα σώμα και $f(x)\in F[x]$ . Τότε υπάρχει επέκταση σωμάτων $L/F$ , τέτοια ώστε $[L:F]<\infty$ και Το $L$ να είναι σώμα ανάλυσης του $f(x)$ πάνω από το $Φ$ .

Απόδειξη.

Από το Θεώρημα 1.4.3, υπάρχει επέκταση $E/F$ , τέτοια ώστε το $f(x)$ να αναλύεται σε γραμμικούς παράγοντες στο $E[x]$ . Έστω ότι

f(x)=\prod_{i=1}^{n}(x-a_{i}),\quad a_{i}\in E

είναι η ανάλυση του $f(x)$ σε γινόμενο γραμμικών παραγόντων στο $E[x]$ , όπου $n=\deg f(x)$ . Θεωρούμε το σώμα $L:=F(a_{1},\ldots,a_{n})$ . Είναι φανερό, ότι το σώμα $L$ είναι σώμα ανάλυσης του $f(x)$ πάνω από το $F$ . ∎

Στην ενότητα 3, θα δούμε ότι an $f(x)\in F[x]$ , τότε το σώμα ανάλυσης του $f(x)$ πάνω από το $F$ είναι μοναδικό με προσέγγιση ισομορφίας, βλ. Πόρισμα 3.2.2.

Παράδειγμα 2.2.11.

Θα αποδείξουμε ότι

\mathbb{Q}[\sqrt{2},\sqrt{3}]=\mathbb{Q}[\sqrt{2}+\sqrt{3}].

Στο Παράδειγμα 2.1.4.6 είδαμε ότι $\sqrt{3}\in\mathbb{Q}[\sqrt{2}+\sqrt{3}]$ και άρα $\mathbb{Q}[\sqrt{2}]\subset\mathbb{Q}[\sqrt{2}+\sqrt{3}]$ . Με τον ίδιο τρόπο προκύπτει ότι $\sqrt{3}\in\mathbb{Q}[\sqrt{2}+\sqrt{3}]$ και άρα $\mathbb{Q}[\sqrt{2}][\sqrt{3}]=\mathbb{Q}[\sqrt{2},\sqrt{3}]\subset\mathbb{Q}[% \sqrt{2}+\sqrt{3}]$ . Για τον αντίστροφο εγκλεισμό παρατηρούμε ότι, αφού το στοιχείο $\sqrt{2}+\sqrt{3}\in\mathbb{Q}[\sqrt{2},\sqrt{3}]$ , έπεται ότι $\mathbb{Q}[\sqrt{2}+\sqrt{3}]\subset\mathbb{Q}[\sqrt{2},\sqrt{3}]$ .

Έστω $E$ ένα ενδιάμεσο σώμα της επέκτασης $L/F$ . Παρατηρούμε ότι το σώμα $L$ έχει τη δομή ενός $E$ -διανυσματικού χώρου όπως και τη δομή ενός $F$ -διανυσματικού χώρου.

Θεώρημα 2.2.12.

Έστω $E$ ένα ενδιάμεσο σώμα της επέκτασης $L/F$ , $[E:F]<\infty$ και $[L:E]<\infty$ . Tότε $[L:F]=[L:E]\;[E:F]$ .

Απόδειξη.

Έστω $\{a_{1},\ldots,a_{n}\}$ μία $E$ -βάση του $L$ και $\{b_{1},\ldots,b_{m}\}$ μία $F$ -βάση του $E$ . Θα δείξουμε ότι το σύνολο $\{a_{i}b_{j}:\ i=1,\ldots,n,j=1,\ldots,m\}$ είναι μία $F$ -βάση του $L$ .

Ξεκινούμε με τη γραμμική ανεξαρτησία. Έστω:

\sum_{i,j}d_{ij}(a_{i}b_{j})=0,\ d_{ij}\in F,i=1,\ldots,n,\ j=1,\ldots,m.

Τότε

\sum_{i}(\sum_{j}d_{ij}b_{j})a_{i}=0,i=1,\ldots,n,\ j=1,\ldots,m.

Αφού $\sum_{j}d_{ij}b_{j}\in L$ , η $E$ -γραμμική ανεξαρτησία των $\{a_{1},\ldots,a_{n}\}$ συνεπάγεται, για $i=1,\ldots,n$ , ότι $\sum_{j}d_{ij}b_{j}=0$ . Για κάθε μία τέτοια εξίσωση, η $F$ -γραμμική ανεξαρτησία των $\{b_{1},\ldots,b_{m}\}$ συνεπάγεται ότι ο συντελεστής $d_{ij}=0$ , για $j=1,\ldots,m$ .

Το τελευταίο κομμάτι της απόδειξης, δηλαδή το ότι τα στοιχεία παράγουν τον $L$ ως $F$ -διανυσματικό χώρο, αφήνεται ως άσκηση, (βλ. άσκηση 2.4.9). ∎

Παρατηρούμε ότι αν $E$ είναι ενδιάμεσο σώμα της επέκτασης $L/F$ και $a\in L$ είναι αλγεβρικό πάνω από το $F$ , τότε το $\operatorname{irr}_{(E,a)}(x)$ διαιρεί το πολυώνυμο $\operatorname{irr}_{(F,a)}(x)$ και $\deg\operatorname{irr}_{(E,a)}(x)\leq\deg\operatorname{irr}_{(F,a)}(x)$ .

Παραδείγματα 2.2.13.

1.

Έστω $Ε=\mathbb{Q}[\sqrt{2}+\sqrt{3}]$ . Από το Παράδειγμα 2.2.11 ισχύει ότι $E={\mathbb{Q}}(\sqrt{2},\sqrt{3})$ . Μία $\mathbb{Q}$ -βάση για το $Ε$ προκύπτει από τις επεκτάσεις $\mathbb{Q}\subset\mathbb{Q}[\sqrt{2}]\subset E$ και είναι ίση με $\{1,\sqrt{2},\sqrt{3},\sqrt{6}\}$ . Στο Παράδειγμα 2.1.2.9 είδαμε ότι το πολυώνυμο $f(x)=x^{4}-10x+1$ μηδενίζεται στο $\sqrt{2}+\sqrt{3}$ . Μπορούμε τώρα να δείξουμε ότι το $f(x)$ είναι ανάγωγο στο $\mathbb{Q}[x]$ . Πράγματι, αφού

$4=[\mathbb{Q}(\sqrt{2}+\sqrt{3}):\mathbb{Q}]=\deg\operatorname{irr}_{(\mathbb{% Q},\sqrt{2}+\sqrt{3})}(x),$

έπεται ότι $\operatorname{irr}_{(\mathbb{Q},\sqrt{2}+\sqrt{3})}(x)=f(x)$ . Έτσι μία άλλη $\mathbb{Q}$ -βάση για το $Ε$ είναι το σύνολο $\{1,\sqrt{2}+\sqrt{3},(\sqrt{2}+\sqrt{3})^{2},(\sqrt{2}+\sqrt{3})^{3}\}$ .
2.

Έστω $b=\sqrt[3]{2}$ και $\omega=e^{2\pi i/3}$ , $L=\mathbb{Q}(b,\omega)$ . Αφού $\operatorname{irr}_{(\mathbb{Q},b)}(x)=x^{3}-2$ , έπεται ότι $[\mathbb{Q}(b):\mathbb{Q}]=3$ και ότι $\{1,b,b^{2}\}$ είναι μία $\mathbb{Q}$ -βάση του $\mathbb{Q}(b)$ . Γνωρίζουμε ότι $\operatorname{irr}_{(\mathbb{Q},\omega)}(x)=x^{2}+x+1$ . Άρα $\operatorname{irr}_{(\mathbb{Q}(b),\omega)}(x)$ διαιρεί το πολυώνυμο $\operatorname{irr}_{(\mathbb{Q},\omega)}(x)$ και έχει βαθμό $\leq 2$ . Όμως, $\omega\notin\mathbb{Q}(b)$ και άρα $\deg\operatorname{irr}_{(\mathbb{Q}(b),\omega)}\geq 2$ . Επομένως

$\operatorname{irr}_{(\mathbb{Q}(b),\omega)}(x)=\operatorname{irr}_{(\mathbb{Q}% ,\omega)}(x)=x^{2}+x+1$

και $\{1,\omega\}$ είναι μία $\mathbb{Q}(b)$ -βάση του $Ε$ . Προκύπτει από την Πρόταση 2.2.12, ότι $[Ε:\mathbb{Q}]=6$ και ότι μία $\mathbb{Q}$ -βάση του $Ε$ είναι το σύνολο $\{1,b,b^{2},\omega,\omega b,\omega b^{2}\}$ .
3.

Έστω $b=\sqrt[5]{2}$ , $\omega=e^{2\pi i/5}$ , $L=\mathbb{Q}(b,\omega)$ . Aφού

$[L:\mathbb{Q}]=[L:\mathbb{Q}(b)][\mathbb{Q}(b):\mathbb{Q}]$ (2.2.13.1)

και $\deg\operatorname{irr}_{(\mathbb{Q},b)}(x)=5$ , έπεται ότι Το $5$ διαιρεί $[L:\mathbb{Q}]$ . Αντίστοιχα, αφού

$[L:\mathbb{Q}]=[L:Q(\omega)][\mathbb{Q}(\omega):\mathbb{Q}]$

και $\deg\operatorname{irr}_{(\mathbb{Q},\omega)}(x)=4$ , έπεται ότι το $4$ διαιρεί τον βαθμό $[L:\mathbb{Q}]$ . Άρα το 20 διαιρεί τον βαθμό $[L:\mathbb{Q}]$ και επομένως $[L:\mathbb{Q}]\geq 20$ . Όμως $[L:\mathbb{Q}(b)]=\deg\operatorname{irr}_{(\mathbb{Q}(b),\omega)}(x)$ και

$\deg\operatorname{irr}_{(\mathbb{Q}(b),\omega)}(x)\leq\deg\operatorname{irr}_{% (\mathbb{Q},\omega)}(x)=4.$

Αντικαθιστώντας στην σχέση (2.2.13.1) προκύπτει ότι $[L:\mathbb{Q}]\leq 20$ . Επομένως $[L:\mathbb{Q}]=20$ και ότι

$\operatorname{irr}_{(\mathbb{Q}(b),\omega)}(x)=x^{4}+x^{3}+x^{2}+x+1$

ενώ

$\operatorname{irr}_{(\mathbb{Q}(\omega),b)}(x)=x^{5}-2.$

Το Θεώρημα 2.2.12 εφαρμόζεται στα παρακάτω πορίσματα:

Πόρισμα 2.2.14.

Έστω $Ε/F$ επέκταση σωμάτων και έστω $a_{1},\ldots,a_{n}\in L$ αλγεβρικά πάνω από το $F$ . Τότε

i)

Ο $[F(a_{1},\ldots,a_{n}):F]<\infty$ .
ii)

Ισχύει ότι $F(a_{1},\ldots,a_{n})=F[a_{1},\ldots,a_{n}]$ .
iii)

Η επέκταση $F(a_{1},\ldots,a_{n})/F$ είναι αλγεβρική.

Απόδειξη.

Για $n=1$ , η πρόταση είναι άμεση συνέπεια του Πορίσματος 2.2.4, της Πρότασης 2.1.5 και της Πρότασης 2.2.8. Υποθέτουμε, λοιπόν, ότι η πρόταση είναι αληθής όταν $n<k$ και θεωρούμε ότι τα στοιχεία $a_{1},\ldots,a_{k}\in Ε$ είναι αλγεβρικά πάνω από το $F$ . Έστω $L=F(a_{1},\ldots,a_{k-1})$ . Σύμφωνα με την υπόθεση της επαγωγής, η επέκταση $L/F$ είναι αλγεβρική, $L=F[a_{1},\ldots,a_{k-1}]$ και $[L:F]<\infty$ . Αφού Το $a_{k}$ είναι αλγεβρικό πάνω από το $F$ , έπεται ότι το $a_{k}$ είναι αλγεβρικό και πάνω από το $L$ . επομένως, από το Πόρισμα 2.2.4, συμπεραίνουμε ότι $[L(a_{k}):E]<\infty$ . Συνεπώς, σύμφωνα με το Θεώρημα 2.2.12, προκύπτει ότι

[L(a_{k}):F]=[L(a_{k}):L][L:F]<\infty.

Τέλος, σύμφωνα με τη παρατήρηση που ακολούθησε τον Ορισμό 2.2.9 και την υπόθεση της επαγωγής, ισχύει ότι

F(a_{1},\ldots,a_{k})=L(a_{1},\ldots,a_{k-1})(a_{k})=L(a_{k})=L[a_{k}]=F[a_{1}% ,\ldots,a_{k}].

∎

Πρόταση 2.2.15.

Έστω ότι οι επεκτάσεις σωμάτων $E/L$ και $L/F$ είναι αλγεβρικές. Τότε η επέκταση $E/F$ είναι αλγεβρική.

Σχήμα 2.2: Αλγεβρικές επεκτάσεις σωμάτων

Απόδειξη.

Έστω $a\in Ε$ . Τότε το $a$ είναι αλγεβρικό πάνω από το $L$ και έστω $f(x)=\operatorname{irr}_{(L,a)}(x)=x^{n}+c_{n-1}x^{n-1}+\cdots+c_{0}\in L[x]$ . Θεωρούμε το σώμα $A=F(c_{0},\cdots,c_{n-1})$ . Αφού το $f(x)\in A[x]$ , Το $a$ είναι αλγεβρικό πάνω από το $A$ . Σύμφωνα με το Πόρισμα 2.2.4, προκύπτει ότι $[A(a):A]<\infty$ . Επίσης, από το Πόρισμα 2.2.14 έπεται ότι $[A:F]<\infty$ και ότι η επέκταση $A/F$ είναι αλγεβρική. Επομένως

[A(a):F]=[A(a):A]\;[A:F]<\infty.

Από το Πόρισμα 2.2.4 έπεται ότι το $a$ είναι αλγεβρικό πάνω από το $F$ . ∎

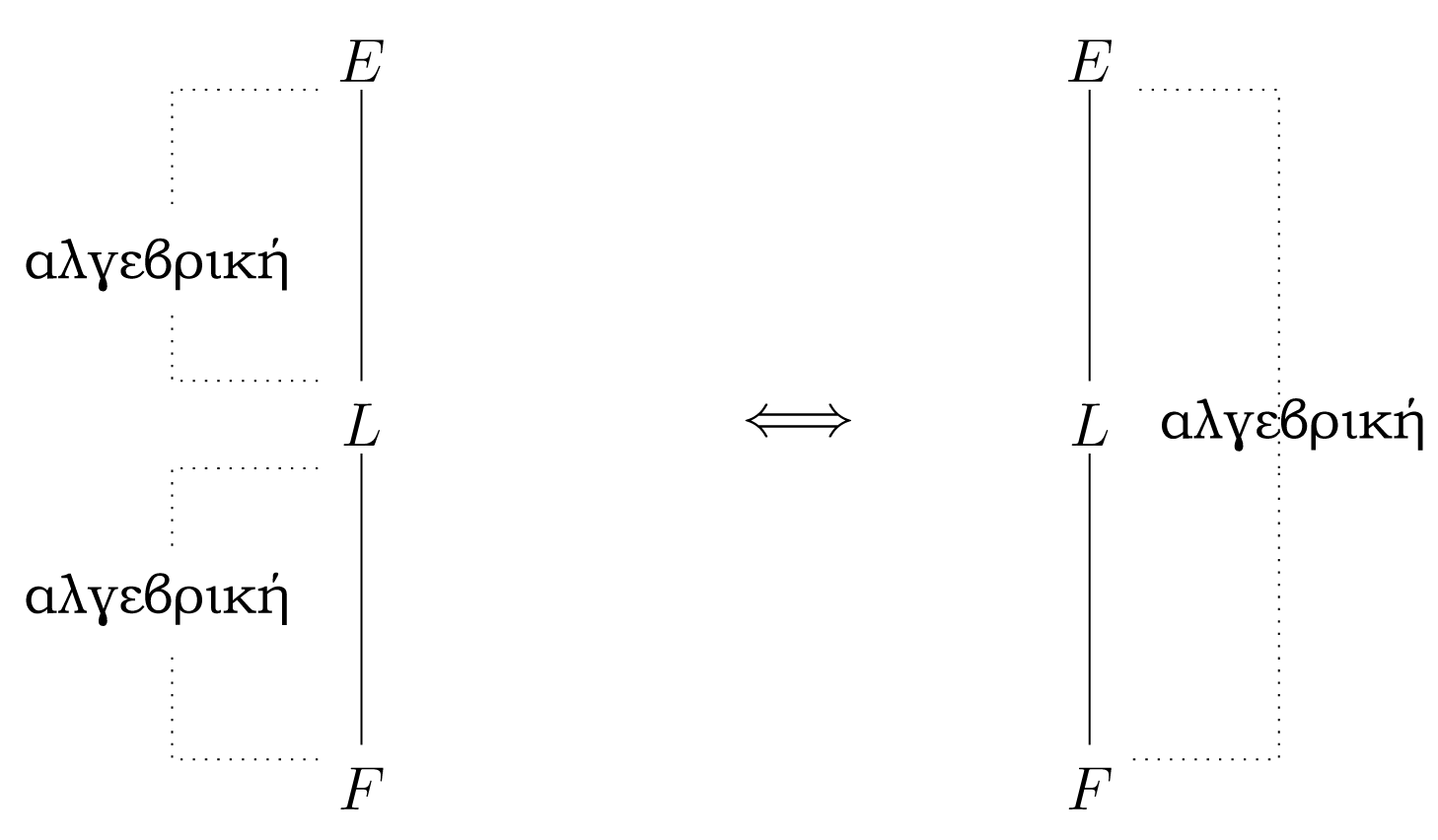
Το Σχήμα 2.2 περιγράφειτο Πόρισμα 2.2.8 και την Πρόταση 2.2.15. H περίπτωση που o βαθμός της επέκτασης $Ε/F$ είναι πρώτος φυσικός αριθμός αντιμετωπίζεται στο επόμενο Πόρισμα.

Πόρισμα 2.2.16.

Έστω $Ε/F$ επέκταση σωμάτων έτσι ώστε $[Ε:F]=p$ , $p$ πρώτος. Τότε Το $Ε$ είναι απλή επέκταση του $F$ και δεν υπάρχει ενδιάμεσο σώμα $L$ έτσι ώστε $F\subsetneq L\subsetneq E$ .

Απόδειξη.

Αφού $[Ε:F]=p$ , έπεται ότι κάθε στοιχείο του $E$ είναι αλγεβρικό πάνω από το $F$ . Έστω $a\in E$ , $a\notin F$ . Tότε το $F\subsetneq F(a)$ και άρα $[F(a):F]\neq 1$ . Σύμφωνα με την Πρόταση 2.2.12, $[F(a):F]$ διαιρεί το $p$ , άρα $[F(a):F]=p$ και κατά συνέπεια $[E:F(a)]=1$ . Επομένως $F(a)=Ε$ . ∎

Παράδειγμα 2.2.17.

Έστω $a=\sqrt[5]{2}\in{\mathbb{R}}$ . Η επέκταση ${\mathbb{Q}}(a)/{\mathbb{Q}}$ έχει βαθμό 5 αφού $\operatorname{irr}_{({\mathbb{Q}},a)}(x)=x^{5}-2$ . Από το προηγούμενο Πόρισμα, συμπεραίνουμε ότι δεν υπάρχει ενδιάμεσο σώμα, ανάμεσα στο ${\mathbb{Q}}$ και στο ${\mathbb{Q}}(a)$ .

2.3 Ομάδα Galois.

Έστω $E/F$ μία επέκταση σωμάτων. Στην ενότητα αυτή θα μελετήσουμε τους $F$ -αυτομορφισμούς του $Ε$ , δηλ. τους ισομορφισμούς $\phi:E\rightarrow E$ έτσι ώστε $\phi(c)=c$ , για κάθε $c\in F$ , βλ. Ενότητα IV του Παραρτήματος.

Ορισμός 2.3.1.

Η ομάδα Galois (Galois group) του $E$ πάνω από το $F$ συμβολίζεται με ${\operatorname{Gal}(E/F)}$ ή ${\operatorname{Aut}_{F}(E)}$ και είναι το σύνολο των αυτομορφισμών του $E$ που διατηρούν σταθερά τα στοιχεία του $F$ :

\operatorname{Gal}(E/F):=\{\phi\in\operatorname{Aut}(E):\ \phi(c)=c,\ \forall c% \in F\}.

Όπως υποννοεί το όνομα, το σύνολο $\operatorname{Gal}(E/K)$ , με πράξη τη σύνθεση συναρτήσεων, είναι υποομάδα της ομάδας $\operatorname{Aut}(E)$ , που αποτελείται από τους αυτομορφισμούς του $E$ . Πράγματι, όπως θα δούμε αμέσως παρακάτω ισχύει ότι

•

η σύνθεση δύο στοιχείων της $\operatorname{Gal}(E/F)$ διατηρεί τα στοιχεία του $F$ σταθερά και επομένως ανήκει στη $\operatorname{Gal}(E/F)$ και
•

το αντίστροφο ενός στοιχείου της $\operatorname{Gal}(E/F)$ διατηρεί τα στοιχεία του $F$ σταθερά και επομένως και αυτό ανήκει στη $\operatorname{Gal}(E/F)$ .

Έστω, λοιπόν, ότι $\phi,\psi\in\operatorname{Gal}(E/F),\ c\in F$ . Τότε

i.

$\phi\circ\psi\ (c)=\phi(\psi(c))=\phi(c)=c$ . Επομένως $\phi\circ\psi\in\operatorname{Gal}(E/F)$ .
ii.

$\phi^{-1}(c)=\phi^{-1}(\phi(c))=(\phi^{-1}\circ\phi)(c)=\operatorname{id}_{F}(% c)=c$ .

Έστω τώρα ότι Το $a\in E$ είναι αλγεβρικό πάνω από το $F$ και έστω ότι $\sigma\in\operatorname{Gal}(E/F)$ . Θα δούμε ότι Το $a$ και Το $\sigma(a)$ έχουν το ίδιο ανάγωγο πολυώνυμο και έτσι αναγκαστικά Το $\sigma(a)$ είναι μία από τις ρίζες του $\operatorname{irr}_{(F,a)}(x)$ , δηλ. Το $\sigma(a)$ είναι συζυγές στοιχείο του $a$ .

Πρόταση 2.3.2.

Έστω $E/F$ μία επέκταση σωμάτων, $a\in E$ αλγεβρικό πάνω από το $F$ και $\sigma\in\operatorname{Gal}(E/F)$ , Τότε $\operatorname{irr}_{(F,a)}(x)=\operatorname{irr}_{\left(F,\sigma(a)\right)}(x)$ .

Απόδειξη.

Έστω $q(x)=\operatorname{irr}_{(F,a)}(x)=\sum c_{i}x^{i}$ . Αφού $q(a)=0$ , έπεται ότι $\sum c_{i}a^{i}=0$ . Επομένως

0=\sigma(\sum c_{i}a^{i})=\sum\sigma(c_{i}a^{i})=\sum\sigma(c_{i})\sigma(a^{i}% )=\sum c_{i}\sigma(a)^{i}=\sum c_{i}b^{i}.

Άρα $q(x)=\operatorname{irr}_{(F,b)}(x)$ . ∎

Για την αντίστροφη κατεύθυνση αυτής της πρότασης έχουμε το εξής Θεώρημα:

Θεώρημα 2.3.3.

Έστω $E/F$ μία επέκταση σωμάτων και $a,b\in E$ αλγεβρικά πάνω από το $F$ τέτοια ώστε $\operatorname{irr}_{(F,a)}(x)$ $=\operatorname{irr}_{(F,b)}(x)$ . Τότε υπάρχει ένας ισομορφισμός σωμάτων $\phi:F(a)\smash{\mathop{\;\longrightarrow\;}\limits}F(b)$ έτσι ώστε $\phi|_{F}=\operatorname{id}_{F}$ και $\phi(a)=b$ .

Απόδειξη.

Θεωρούμε το κύριο ιδεώδες $Ι$ του $Κ[x]$ που παράγεται από το $\operatorname{irr}_{(F,a)}(x)$ . Ο επιμορφισμός

\phi_{1}:F[x]\smash{\mathop{\;\longrightarrow\;}\limits}F[a],\quad\phi_{1}(f(x% ))=f(a)

δίνει τον ισομορφισμό

\bar{\phi_{1}}:F[x]/Ι\smash{\mathop{\;\longrightarrow\;}\limits}F(a),\ \bar{% \phi_{1}}(f(x)+I)=f(a),

σύμφωνα με το Πρώτο Θεώρημα Ισομορφίας Δακτυλίων και την Πρόταση 2.1.5. Συγκεκριμένα $\bar{\phi_{1}}(x+Ι)=a$ , ενώ $\bar{\phi_{1}}(c+Ι)=c$ , για $c\in F$ . Αντίστοιχα έχουμε τον ισομορφισμό

\bar{\phi_{2}}:F[x]/Ι\smash{\mathop{\;\longrightarrow\;}\limits}F(b),\quad\bar% {\phi_{1}}(f(x)+I)=f(b).

Επομένως η σύνθεση

\bar{\phi_{2}}\circ\bar{\phi_{1}}^{-1}:\ F(a)\smash{\mathop{\;\longrightarrow% \;}\limits}F(b)

έχει τις επιθυμητές ιδιότητες. ∎

Είναι εύκολο να δει κανείς ότι αν $\sigma:\ F\smash{\mathop{\;\longrightarrow\;}\limits}F^{\prime}$ είναι ισομορφισμός σωμάτων, τότε η συνάρτηση

\widehat{\sigma}:\ F[x]\smash{\mathop{\;\longrightarrow\;}\limits}F^{\prime}[x% ],\quad\sum a_{i}x^{i}\mapsto\sum\sigma(a_{i})x^{i}

είναι ισομορφισμός, βλ. άσκηση 1.5.16. Σημειώνουμε έτσι την άμεση γενίκευση του Θεωρήματος 2.3.3 και αφήνουμε την απόδειξη ως άσκηση για τον αναγνώστη (άσκηση 2.4.15).

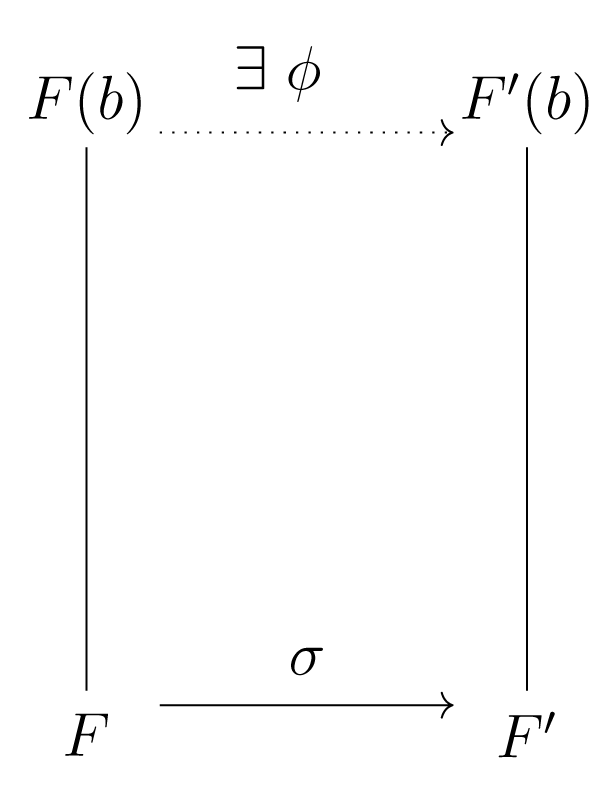
Θεώρημα 2.3.4.

Έστω $E/F$ και $E^{\prime}/F^{\prime}$ επεκτάσεις σωμάτων, $b\in E$ , $b^{\prime}\in E^{\prime}$ αλγεβρικά πάνω από τα $F$ , $F^{\prime}$ αντίστοιχα, και $\sigma:\ F\rightarrow F^{\prime}$ ισομορφισμός έτσι ώστε

\widehat{\sigma}(\operatorname{irr}_{(F,b)}(x))=\operatorname{irr}_{(F^{\prime% },b^{\prime})}(x).

Υπάρχει ένας ισομορφισμός σωμάτων $\phi:F(b)\smash{\mathop{\;\longrightarrow\;}\limits}F^{\prime}(b^{\prime})$ έτσι ώστε $\phi|_{F}=\sigma$ και $\phi(b)=b^{\prime}$ .

Σχήμα 2.3: Επέκταση του ισομορφισμού $\sigma$ .

Στα επόμενα παραδείγματα θα υπολογίσουμε την ομάδα Galois σε διάφορες περιπτώσεις. Παρατηρούμε ότι $\operatorname{id}_{E}$ ανήκει στην ομάδα $G=\operatorname{Aut}_{F}E$ , για κάθε επέκταση σωμάτων $E/F$ .

Παραδείγματα 2.3.5.

Ολοκληρώνουμε αυτήν την ενότητα περιγράφοντας τη μέθοδο που έχουμε ακολουθήσει ως τώρα για την εύρεση της ομάδας $\operatorname{Gal}(E/F)$ στη περίπτωση που ο βαθμός του $E$ πάνω από το $F$ είναι πεπερασμένος. Τα βήματα είναι:

•

Βρίσκουμε μία $F$ -βάση $Β$ του $E$ .
•

Βρίσκουμε ένα σύνολο στοιχείων που παράγουν την επέκταση $E/F$ , ξεκινώντας από τη $Β$ . Η προσπάθειά μας είναι να περιορίσουμε όσο μπορούμε το πλήθος των στοιχείων που παράγουν την επέκταση $E/F$ .
•

Βρίσκουμε τα ανάγωγα πολυώνυμα για τα στοιχεία που αναφέρονται στο προηγούμενο βήμα και τις ρίζες τους στο $E$ .
•

Χρησιμοποιώντας την Πρόταση 2.3.2 βρίσκουμε τις δυνατές εικόνες των στοιχείων που εντοπίσαμε στο δεύτερο βήμα.
•

Βρίσκουμε τα στοιχεία της ομάδας $\operatorname{Gal}(E/F)$ , χρησιμοποιώντας το Θεώρημα 2.3.3.

Στο επόμενο παράδειγμα θα μελετήσουμε το σώμα ανάλυσης του πολυωνύμου $x^{3}-2$ πάνω από το $\mathbb{Q}$ .

Παράδειγμα 2.3.6.

Έστω

b=\sqrt[3]{2},\ \omega=e^{2\pi i/3},\ Ε=\mathbb{Q}(b,\omega b,\omega^{2}b).

Το σώμα $E$ είναι υπόσωμα του ${\mathbb{C}}$ και είναι σώμα ανάλυσης του $x^{3}-2$ πάνω από το ${\mathbb{Q}}$ . Αφού

\omega=\frac{\omega b}{b}\in E,

εύκολα προκύπτει ότι:

E=\mathbb{Q}(b,\omega b)=\mathbb{Q}(b,\omega^{2}b)=\mathbb{Q}(\omega b,\omega^% {2}b)=\mathbb{Q}(b,\omega).

Χρησιμοποιούμε την τελευταία έκφραση $Ε=\mathbb{Q}(b,\omega)$ , κυρίως, γιατί υπάρχουν δύο ανάγωγα (πάνω από το ${\mathbb{Q}}$ ) πολυώνυμα που θα διευκολύνουν τους υπολογισμούς μας, δηλ. τα πολυώνυμα

\operatorname{irr}_{(\mathbb{Q},b)}(x)=x^{3}-2,\ \operatorname{irr}_{(\mathbb{% Q)},\omega}(x)=x^{2}+x+1.

Σύμφωνα με το Θεώρημα 2.2.12, εργαζόμαστε όπως στο Παράδειγμα 2.2.13. Έτσι, προκύπτει ότι μία $\mathbb{Q}$ -βάση για το $Ε$ είναι το σύνολο $\{1,b,b^{2},\omega,\omega b,\omega b^{2}\}$ και ότι $[\;{\mathbb{Q}}(\omega):{\mathbb{Q}}]=6$ .

Έστω $G=\operatorname{Gal}(E/\mathbb{Q})$ και έστω $\sigma\in G$ . Ο αυτομορφισμός $\sigma$ καθορίζεται πλήρως από τις εικόνες $\sigma(b)$ και $\sigma(\omega)$ . Σύμφωνα με την Πρόταση 2.3.2, έχουμε τρεις δυνατές τιμές για την εικόνα $\sigma(b)$ και δύο δυνατές τιμές για την $\sigma(\omega)$ , όσες είναι οι ρίζες των αντίστοιχων αναγώγων πολυωνύμων. Άρα η ομάδα $G$ έχει τάξη το πολύ 6. Θα δείξουμε ότι η ομάδα $G$ έχει τάξη ακριβώς 6.

Πράγματι,

E=\mathbb{Q}(\omega)(b)

και είναι εύκολο να συμπεράνει κανείς ότι

\operatorname{irr}_{(\mathbb{Q}(\omega),b)}(x)=\operatorname{irr}_{(\mathbb{Q}% ,b)}(x)=x^{3}-2.

Σύμφωνα με το Θεώρημα 2.3.3 υπάρχουν τρία διαφορετικά στοιχεία της ομάδας αυτομορφισμών του $Ε$ που διατηρούν σταθερά τα στοιχεία του ${\mathbb{Q}}(\omega)$ , δηλ. απεικονίζουν $c\mapsto c$ , για κάθε $c\in\mathbb{Q}(\omega)$ , και έτσι ώστε Το $b$ να απεικονίζεται σε μία από τις τρεις ρίζες του $x^{3}-2$ :

b\mapsto\begin{cases}\ b\cr\ \omega b\cr\ \omega^{2}b\end{cases}.

Αντίστοιχα, αφού

E=\mathbb{Q}(b)(\omega)

και

\operatorname{irr}_{(\mathbb{Q}(b),\omega)}(x)=\operatorname{irr}_{(\mathbb{Q}% ,\omega)}(x)=x^{2}+x+1,\

υπάρχουν δύο αυτομορφισμοί στην $G$ τέτοιοι ώστε $c\mapsto c$ , $\forall\ c\in\mathbb{Q}(b)$ , ενώ

\omega\mapsto\begin{cases}\ \omega\cr\ \omega^{2}.\end{cases}\

Σημειώνουμε ότι όταν ένας αυτομορφισμός του $Ε$ στέλνει $\omega\mapsto\omega$ και $b\mapsto b$ , τότε $a\mapsto a$ , $\forall\ a\in E$ και είναι ο ταυτοτικός αυτομορφισμός του $Ε$ . Έτσι προς το παρόν έχουμε βρει τέσσερα διαφορετικά στοιχεία της $G$ . Οι συνθέσεις τους μας δίνουν άλλους δύο αυτομορφισμούς. Παρατηρούμε επίσης, ότι αν $\sigma\in G$ είναι ο αυτομορφισμός που στέλνει το $b$ στο $\omega b$ και το $\omega$ στο $\omega$ , τότε ο ομομορφισμός $\sigma^{2}$ δρα ως εξής:

\begin{array}[]{ll}b&\mapsto\omega b\mapsto\omega(\omega b)=\omega^{2}b\\ \omega&\mapsto\omega\mapsto\omega\end{array}

Επομένως η ομάδα $G$ αποτελείται από 6 στοιχεία, όπως φαίνεται από τον παρακάτω πίνακα:

\begin{array}[]{c|ccccccc}b&b&\omega b&\omega^{2}b&b&\omega b&\omega^{2}b\\ \hline\omega&\omega&\omega&\omega&\omega^{2}&\omega^{2}&\omega^{2}\\ \hline&\operatorname{id}_{E}&\sigma&\sigma^{2}&\tau&{\sigma\tau}&\tau\sigma% \end{array}

(2.3.6.1)

H ομάδα $G$ δεν είναι αντιμεταθετική όπως φαίνεται από τον πίνακα (2.3.6.1), αφού $\sigma\tau\neq\tau\sigma$ .

Είδαμε ότι $|G|=6$ . Γνωρίζουμε ότι με προσέγγιση ισομορφίας υπάρχει μόνο μία μη αντιμεταθετική ομάδα με έξι στοιχεία και ότι αυτή είναι η ομάδα $S_{3}$ των μεταθέσεων τριών στοιχείων, βλ. Πρόταση I.23. Άρα

\operatorname{Gal}({\mathbb{Q}}(\omega,b)/{\mathbb{Q}}\cong S_{3}.

Έστω, τώρα, $a\in E$ και ας υπολογίσουμε την εικόνα $\sigma(a)$ . Αφού

a=a_{0}+a_{1}b+a_{2}b^{2}+a_{3}\omega+a_{4}\omega b+a_{5}\omega b^{2},\ % \textrm{ για }a_{i}\in{\mathbb{Q}},\ 1\leq i\leq 5\

και $\sigma(a_{i})=a_{i}$ , $\sigma(b)=\omega b$ , $\sigma(\omega)=\omega$ , έπεται ότι $\sigma(b^{2})=\omega^{2}b^{2}$ , $\sigma(\omega b)=\omega^{2}b$ και $\sigma(\omega b^{2})=\omega^{3}b^{2}=b^{2}$ . Επίσης αφού $\omega$ είναι ρίζα του πολυωνύμου $x^{2}+x+1$ , έπεται ότι $\omega^{2}+\omega+1=0$ , δηλ. $\omega^{2}=-1-\omega$ . Άρα

\sigma_{1}(a)=a_{0}-a_{4}b+(-a_{2}+a_{5})b^{2}+a_{4}\omega+(a_{1}-a_{4})\omega b% -a_{2}\omega b^{2}.

2.4 Ασκήσεις

1.

Έστω $Ε=F(x)$ το σώμα κλασμάτων του δακτυλίου $F[x]$ . Na αποδείξετε ότι το $x\in Ε$ είναι υπερβατικό πάνω από το $F$ .
2.

Να περιγραφούν τα σώματα: $\mathbb{Q}(\sqrt{5},\sqrt{7})$ , $\mathbb{Q}(i\sqrt{11})$ .
3.
Να βρεθεί το πολυώνυμο $\operatorname{irr}_{(\mathbb{Q},a)}(x)$ όταν
- –
  
  $a=\sqrt{7}+1/2$ ,
- –
  
  $a=i\sqrt{3}-1/2$ .
4.

Να γράψετε τον αντίστροφο του $\sqrt[3]{2}^{\ 2}+1$ ως γραμμικό συνδυασμό των δυνάμεων του $\sqrt[3]{2}$ στο σώμα $\mathbb{Q}(\sqrt[3]{2})$ .
5.

Έστω $\omega=e^{2\pi i/8}$ . Να τοποθετήσετε το $\omega$ στον μοναδιαίο κύκλο. Να δείξετε ότι $\operatorname{irr}_{(\mathbb{Q},\omega)}(x)=x^{4}+1$ . Να βρείτε $\operatorname{irr}_{(\mathbb{Q},\omega^{k})}(x)$ για $k=0,\ldots,7$ .
6.
Να βρεθούν οι βαθμοί των επεκτάσεων:
- –
  
  $\mathbb{C}/\ \mathbb{Q}$ ,
- –
  
  $\mathbb{Z}_{5}(x)/\ \mathbb{Z}_{5}$ ,
- –
  
  $\mathbb{R}(\sqrt{5})/\ \mathbb{R}$ ,
- –
  
  $\mathbb{Q}(\sqrt[7]{3})/\ \mathbb{Q}$ .
7.

Να ελέγξετε αν το σώμα $\mathbb{Q}[\sqrt{3}]$ είναι ισόμορφο με το σώμα $\mathbb{Q}[\sqrt{5}]$ .
8.

Έστω $Ε=\mathbb{Q}(\sqrt{2},\sqrt{3},\sqrt{5})$ . Να αποδείξετε ότι $[E:\mathbb{Q}]=8$ .
9.

Έστω $E/F$ , $L/E$ επεκτάσεις σωμάτων και έστω ότι τα $a_{1},\ldots,a_{n}$ παράγουν το σώμα $L$ πάνω από το $E$ , ενώ τα $b_{1},\ldots,b_{m}$ παράγουν το $E$ πάνω από το $F$ . Να αποδείξετε ότι τα $a_{i}b_{j}:\ i=1,\ldots,n,j=1,\ldots,m$ παράγουν το $L$ πάνω από το $F$ .
10.

Αν $[E:F]<\infty$ , για σώματα $F\subset E$ , να δείξετε ότι υπάρχουν $b_{1},\ldots,b_{n}\in E$ έτσι ώστε $E=F(b_{1},\ldots,b_{n})$ .
11.
Έστω ότι τα $a,b\in E$ είναι αλγεβρικά πάνω από το $F$ . Να αποδείξετε τα ακόλουθα
- –
  
  $[F(a+b):F]<\infty$
- –
  
  Το στοιχείο $a+b$ είναι αλγεβρικό υπεράνω του $F$ .
12.

Έστω ότι $Ε$ είναι ενδιάμεσο σώμα της επέκτασης $L/F$ και έστω ότι $a\in E$ . Να αποδείξετε ότι το πολυώνυμο $\operatorname{irr}_{(E,a)}(x)$ διαιρεί το πολυώνυμο $\operatorname{irr}_{(F,a)}(x)$ . Να συμπεράνετε ότι αν $\deg\operatorname{irr}_{(F,a)}(x)=\deg\operatorname{irr}_{(E,a)}(x)$ , τότε $\operatorname{irr}_{(F,a)}(x)=\operatorname{irr}_{(E,a)}(x)$ .
13.

Έστω ότι $Ε$ είναι σώμα ανάλυσης ενός διαχωρίσιμου αναγώγου πολυωνύμου $f(x)\in K[x]$ , βαθμού $n$ , και έστω ότι $a_{1},a_{2},\ldots,a_{n}$ είναι οι ρίζες του $f(x)$ στο $Ε$ . Αν $E_{i}=K(a_{1},\ldots,a_{i})$ να δείξετε ότι $\deg\operatorname{irr}_{(E_{i},a_{i})}(x)\leq n-i+1$ και άρα $[E:E_{i}]\leq(n-i)!$ . Να συμπεράνετε ότι $[E:K]\leq n!$ .
14.

Να θεωρήσετε $\overline{{\mathbb{Q}}}=\{r\in{\mathbb{R}}:\ a\textrm{ αλγεβρικό πάνω από το }% {\mathbb{Q}}\}$ . Να αποδείξετε ότι $\overline{{\mathbb{Q}}}$ είναι υπόσωμα το ${\mathbb{R}}$ και να βρείτε $[\overline{{\mathbb{Q}}}:{\mathbb{Q}}]$ .
15.

Έστω $E/F$ και $E^{\prime}/F^{\prime}$ επεκτάσεις σωμάτων, $b\in E$ , $b^{\prime}\in E^{\prime}$ αλγεβρικά πάνω από ta $F$ , $F^{\prime}$ αντίστοιχα και $\sigma:\ F\rightarrow F^{\prime}$ ισομορφισμός έτσι ώστε

$\widehat{\sigma}(\operatorname{irr}_{(F,b)}(x))=\operatorname{irr}_{(F^{\prime% },b^{\prime})}(x).$

Να αποδείξετε ότι υπάρχει ένας ισομορφισμός σωμάτων $\phi:F[b]\smash{\mathop{\;\longrightarrow\;}\limits}F^{\prime}[b^{\prime}]$ έτσι ώστε $\phi|_{F}=\sigma$ και $\phi(b)=b^{\prime}$ .
16.
- –
  
  Να αποδείξετε ότι $\mathbb{Q}(\sqrt{5}+\sqrt{2})=\mathbb{Q}(\sqrt{5},\sqrt{2})$ .
- –
  
  Να βρείτε το ανάγωγο πολυώνυμο του $\sqrt{5}+\sqrt{2}$ πάνω από το $\mathbb{Q}(\sqrt{2})$ .
- –
  
  Να βρείτε το ανάγωγο πολυώνυμο του $\sqrt{5}+\sqrt{2}$ πάνω από το $\mathbb{Q}(\sqrt{5},\sqrt{2})$ .
- –
  
  Να βρείτε το ανάγωγο πολυώνυμο του $\sqrt{5}+\sqrt{2}$ πάνω από το $\mathbb{Q}$ .
17.

Έστω $[L:K]<\infty$ μία πεπερασμένη επέκταση και $f(x)\in K[x]$ ανάγωγο. Να αποδείξετε ότι αν οι φυσικοί αριθμοί $\deg f(x)>1$ και $[L:K]$ είναι πρώτοι μεταξύ τους, τότε το $f(x)$ δεν έχει ρίζες στο $L$ .
18.
Να υπολογισθεί η ομάδα Galois $\operatorname{Gal}(\mathbb{Q}(a)/\mathbb{Q})$ όταν
- –
  
  $a=\sqrt{5}$ ,
- –
  
  $a=2i$ ,
- –
  
  $a=e^{2\pi i/5}$ ,
- –
  
  $a=\sqrt[3]{-2}$ .
19.

Έστω $E/F$ επέκταση σωμάτων και έστω $e,\sigma_{1},\ldots,\sigma_{n-1}$ διακεκριμένα στοιχεία της ομάδας $\operatorname{Gal}(E/F)$ . Έστω $a\in E$ . Αν τα στοιχεία $a,\sigma_{1}(a),\ldots,\sigma_{n-1}(a)$ είναι διακεκριμένα τότε να δείξετε ότι $\deg\operatorname{irr}_{(F,a)}(x)\geq n$ .
20.

Να βρείτε την τάξη των στοιχείων της ομάδας $\operatorname{Gal}({\mathbb{Q}}(\sqrt{2},\sqrt{3})/\ {\mathbb{Q}})$ .
21.

Να βρείτε την ομάδα $\operatorname{Gal}({\mathbb{Q}}(\sqrt{2},\sqrt{3})/\ {\mathbb{Q}}(\sqrt{2}))$ .
22.

Έστω $\omega=e^{2\pi i/3}$ , $b=\sqrt{5}$ , $Ε={\mathbb{Q}}(\omega,b)$ . Να βρείτε την ομάδα $\operatorname{Gal}(E/{\mathbb{Q}})$ .
23.

Να αποδείξετε το Θεώρημα 2.3.3.
24.

Έστω $F$ σώμα και έστω $Κ$ το πρώτο υπόσωμα του $F$ . Να αποδείξετε ότι $\operatorname{Gal}(F/K)$ είναι υποομάδα της $\operatorname{Aut}(F)$ , δηλ. της ομάδας των αυτομορφισμών του $F$ .
25.

Να αποδείξετε ότι η ομάδα $\operatorname{Gal}({\mathbb{R}}/{\mathbb{Q}})$ είναι η τετριμμένη. (Σημειώστε και την εκφώνηση της άσκησης 7.6.)
26.

Έστω $\omega=e^{2\pi i/11}$ . Να αποδείξετε ότι η ομάδα $\operatorname{Gal}({\mathbb{Q}}(\omega)/{\mathbb{Q}})$ είναι κυκλική και έχει τάξη 10.
27.

Έστω $\omega=e^{2\pi i/12}$ . Να αποδείξετε ότι η ομάδα $\operatorname{Gal}({\mathbb{Q}}(\omega)/{\mathbb{Q}})$ έχει 4 στοιχεία και να ελέγξετε αν είναι κυκλική.
28.
Για κάθε μία από τις παρακάτω προτάσεις να αποφασίσετε αν είναι αληθής ή όχι.
1. (a)
  
  Πεπερασμένες επεκτάσεις σωμάτων ίσου βαθμού είναι ισόμορφες.
2. (b)
  
  Οι άπειρες απλές επεκτάσεις ενός σώματος $F$ είναι ισόμορφες.
3. (c)
  
  Κάθε αλγεβρική επέκταση πάνω από ένα σώμα είναι πεπερασμένη.
4. (d)
  
  Κάθε υπερβατική επέκταση σώματος δεν είναι πεπερασμένη.
5. (e)
  
  Κάθε στοιχείο του ${\mathbb{C}}$ είναι αλγεβρικό πάνω από το ${\mathbb{R}}$ .
6. (f)
  
  Κάθε επέκταση του ${\mathbb{R}}$ είναι πεπερασμένη.
7. (g)
  
  Κάθε επέκταση πεπερασμένου σώματος είναι πεπερασμένη.
8. (h)
  
  Κάθε απλή αλγεβρική επέκταση σωμάτων είναι πεπερασμένη.
9. (i)
  
  Κάθε απλή επέκταση σωμάτων είναι πεπερασμένη.
10. (j)
  
  Κάθε σώμα έχει μη τετριμμένες επεκτάσεις.
11. (k)
  
  Κάθε σώμα έχει μη τετριμμένες αλγεβρικές επεκτάσεις.
12. (l)
  
  Κάθε απλή επέκταση σωμάτων είναι αλγεβρική.
13. (m)
  
  Κάθε επέκταση σωμάτων είναι απλή.
14. (n)
  
  Όλες οι απλές αλγεβρικές επεκτάσεις σωμάτων είναι ισόμορφες.
15. (o)
  
  Όλες οι απλές υπερβατικές επεκτάσεις σώματος είναι ισόμορφες.

Βιβλιογραφία Κεφάλαιου 2

1.

Dummit, D.S., Foote, R.M. Abstract Algebra. J. Wiley and Sons, INc, 2004.
2.

Fraleigh, J. Εισαγωγή στην Άλγεβρα. Πανεπιστημιακές εκδόσεις Κρήτης, 2011.
3.

Hadlock, C. R Field Theory and its Classical Problems. 2000.
4.

Hungerford,T. Algebra. Springer, 1974.
5.

Lang, S. Algebra. Springer, 2002.
6.

Menini, C. Van Oystaeyen, F. Abstract Algebra. Marcel Dekker, 2004.
7.

Rotman, J. Θεωρία Galois. Leader Books, 2000.
8.

Stewart, I. Galois Theory. Champan and Hall, 1973.