Μια Εισαγωγή στη Γραμμική Άλγεβρα για τις Θετικές Επιστήμες

Κεφάλαιο 6Προβολές και Εφαρμογές

Σε αυτό το κεφάλαιο χρησιμοποιώντας την έννοια του εσωτερικού γινομένου ορίζουμε την προβολή ενός διανύσματος του ${\mathbb{R}}^{n}$ πάνω σε έναν διανυσματικό υποχώρο του ${\mathbb{R}}^{n}$ . Στη συνέχεια παρουσιάζουμε διάφορες εφαρμογές που προκύπτουν από τη θεωρία των προβολών και ιδιοδιανυσμάτων.

6.1 Προβολές

Έστω $u,v\in{\mathbb{R}}^{n}$ . H προβολή (projection)του $v$ πάνω στο $u$ είναι ένα διάνυσμα $\operatorname{proj}_{u}(v)$ παράλληλο προς το $u$ τέτοιο ώστε

v=\operatorname{proj}_{\ u}(v)+w,

όπου το $w=v-\operatorname{proj}_{u}(v)$ είναι ορθογώνιο στο $u$ . Πρέπει λοιπόν να ισχύουν οι παρακάτω δύο συνθήκες:

i.

$\operatorname{proj}_{u}v=\lambda u$ , για κάποιο $\lambda\in{\mathbb{R}}$ , και
ii.

$\langle w,u\rangle=0$ .

Παίρνοντας το εσωτερικό γινόμενο $\langle v,u\rangle$ και αφού $v=\lambda u+w$ προκύπτει ότι

\langle v,u\rangle=\langle\lambda u+w,u\rangle=\lambda\langle u,u\rangle+% \langle w,u\rangle=\lambda\langle u,u\rangle,

Άρα

\boxed@math{\;\;\;{\rm proj}_{u}(v)=\frac{\langle v,u\rangle}{\langle u,u% \rangle}\;u\ \hbox{και}\;\displaystyle w=v-\frac{\langle v,u\rangle}{\langle u% ,u\rangle}\;u.}

(6.1.0.1)

Αφού $\langle v,tu\rangle=t\langle v,u\rangle$ και $\langle tu,tu\rangle=t^{2}\langle u,u\rangle$ είναι φανερό ότι

\operatorname{proj}_{tu}{v}=\frac{t\langle v,u\rangle}{t^{2}\langle u,u\rangle% }\;tu=\frac{\langle v,u\rangle}{\langle u,u\rangle}\;u=\operatorname{proj}_{u}% (v),\textrm{gia}t\neq 0.

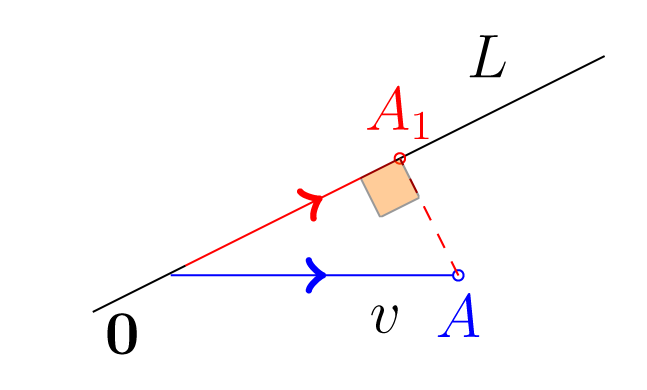
Ορίζουμε την προβολή του $v$ πάνω στην ευθεία $L=\{tu:t\in{\mathbb{R}}\}$ και γράφουμε $\operatorname{proj}_{L}(v)$ να είναι το διάνυσμα $\operatorname{proj}_{u}(v)$ . $\operatorname{proj}_{L}(v)$

Σχήμα 6.1:Προβολή του $v$ στην ευθεία $L$

Αν $v=\vec{OA}$ , τότε από το Πυθαγόρειο Θεώρημα προκύπτει ότι η απόσταση του $A(a_{1},\ldots,a_{n})$ από την ευθεία $L=\{tu:\ t\in{\mathbb{R}}\}$ είναι ίση με το μήκος του $v-\operatorname{proj}_{L}(v)$ . Στο Σχήμα 6.1 απεικονίζεται η προβολή του $v$ στην ευθεία $L$ , δηλ. το διάνυσμα $\vec{OA_{1}}$ . H απόσταση του $A$ από την $L$ είναι το μήκος του $\vec{A_{1}A}$ . Ισχύει ότι

\vec{OA}=\vec{OA_{1}}+\vec{A_{1}A},

όπου $\vec{OA_{1}}$ είναι επίσης $L$ και $\vec{A_{1}A}$ είναι κάθετο επί της $L$ .

Παραδείγματα 6.1.1.

1.

Έστω $v_{1}=(0,1,1)$ , και $v_{2}=(0,2,0)$ . Τότε

${\rm proj}_{v_{1}}(v_{2})=\frac{\langle v_{1},v_{2}\rangle}{\langle v_{1},v_{1% }\rangle}\;v_{1}=\frac{0\cdot 0+1\cdot 2+1\cdot 0}{0\cdot 0+1\cdot 1+1\cdot 1}% \;(0,1,1)=(0,1,1).$
Το διάνυσμα $w=v_{2}-{\rm proj}_{v_{1}}(v_{2})=(0,1,-1)$ είναι ορθογώνιο προς το $v_{1}$
2.

Έστω $u=(1,m)$ .Τότε

$\operatorname{proj}_{u}(e_{1})=\frac{1}{1+m^{2}}(1,m),\ \operatorname{proj}_{u% }(e_{2})=\frac{m}{1+m^{2}}(1,m)\ .$
Έστω $f:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ η συνάρτηση προβολής στην ευθεία $y=mx$ , βλ. Παραδείγματα 4.1.6.6 και 5.1.5.4. Βλέπουμε ότι $f(v)=\operatorname{proj}_{u}(v)$ . Επομένως

$C_{B}(f(e_{1}))=\frac{1}{1+m^{2}}\begin{bmatrix}1\cr m\end{bmatrix},C_{B}(f(e_% {2}))=\frac{m}{1+m^{2}}\begin{bmatrix}1\cr m\end{bmatrix}$
και

$A^{f}_{B,B}=\frac{1}{1+m^{2}}\begin{bmatrix}1&m\cr m&m^{2}\end{bmatrix}\ .$
3.

Έστω $f:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ ο αντικατοπτρισμός ως προς την ευθεία $y=mx$ , βλ. Παράδειγμα 4.1.6.5.

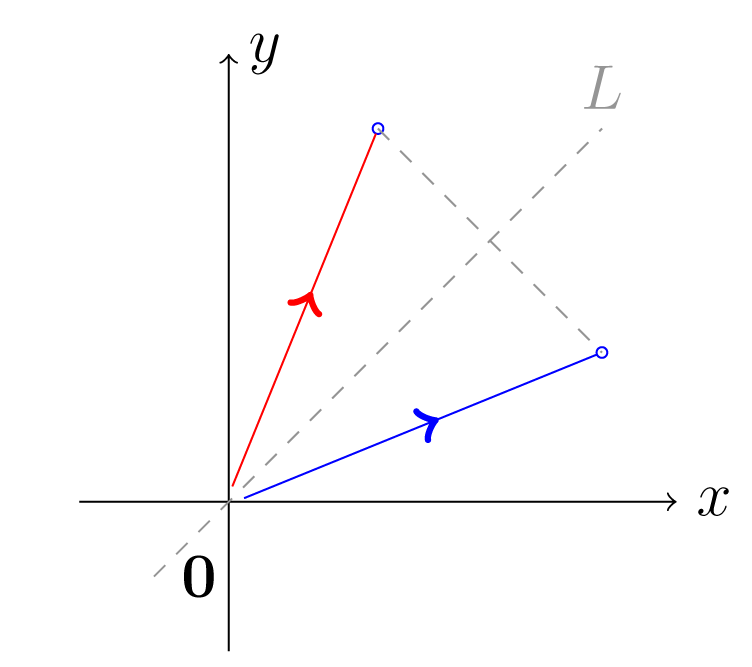
Σχήμα 6.2: Αντικατοπτρισμός ως προς την ευθεία $L$

Έστω $u=(1,m)$ . Αν $v\in{\mathbb{R}}^{2}$ , βλέπουμε ότι αν $w=v-\operatorname{proj}_{u}(v)$ τότε

$f(v)=\operatorname{proj}_{u}(v)-w=\operatorname{proj}_{u}(v)-(v-\operatorname{% proj}_{u}(v))=2\operatorname{proj}_{u}(v)-v\ .$
Άρα

$f(e_{1})=\frac{2}{1+m^{2}}(1,m)-(1,0)=\frac{1}{1+m^{2}}(1-m^{2},2m)$
ενώ

$f(e_{2})=\frac{2m}{1+m^{2}}(1,m)-(0,1)=\frac{1}{1+m^{2}}(2m,m^{2}-1)\ .$
Επομένως, αν $B$ είναι η κανονική βάση του ${\mathbb{R}}^{2}$ , τότε

$A^{f}_{B,B}=\frac{1}{1+m^{2}}\begin{bmatrix}1-m^{2}&2m\cr 2m&m^{2}-1\end{% bmatrix}\ .$

Στη συνέχεια ορίζουμε την ορθογώνια προβολή του $v$ σε έναν υποχώρο του ${\mathbb{R}}^{n}$ , γενικεύοντας την προβολή του $v$ στην ευθεία $L$ . ${\rm proj}_{U}(v)$

Ορισμός 6.1.2 .

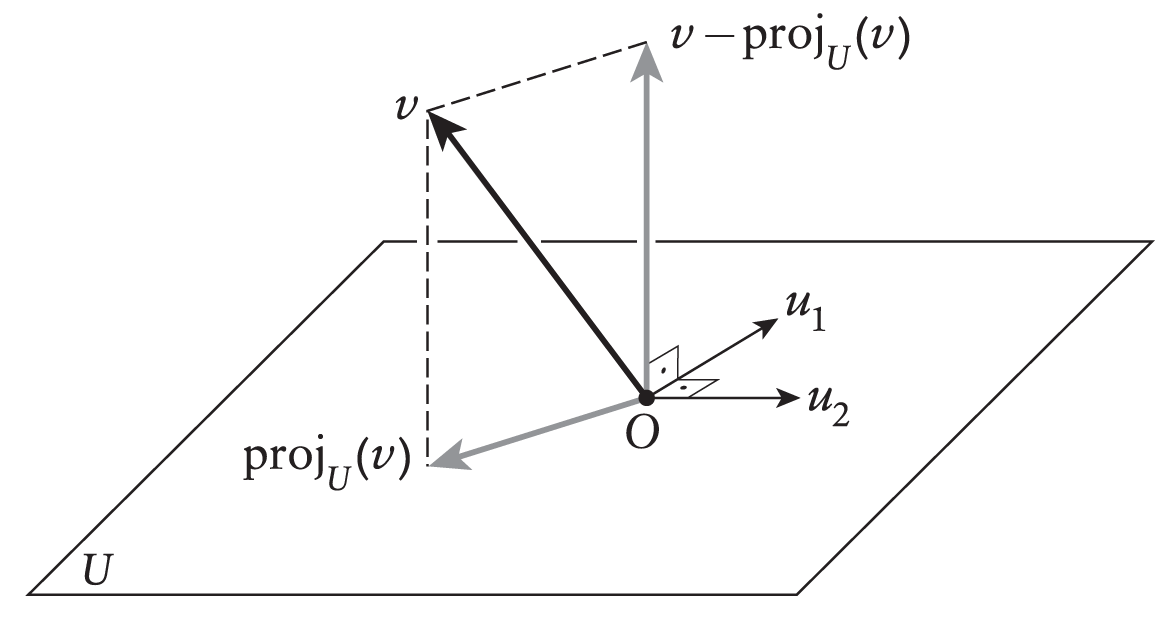
Έστω $U$ διανυσματικός υποχώρος του ${\mathbb{R}}^{m}$ και έστω $v\in{\mathbb{R}}^{m}$ . H ορθογώνια προβολή (orthogonal projection)του $v$ στον $U$ συμβολίζεται με ${\rm proj}_{U}(v)$ , ανήκει στον $U$ και έχει την ιδιότητα $\langle v-{\rm proj}_{U}(v)),u\rangle=0$ , για κάθε $u\in U$ .

Σχήμα 6.3: Προβολή του $v$ στον υποχώρο $U$

H απάντηση είναι ναι, όταν o υποχώρος $U$ του ${\mathbb{R}}^{m}$ έχει μία ορθογώνια βάση. Για να το δούμε αυτό, έστω ότι ${\rm dim}_{{\mathbb{R}}}U=n$ και ότι $\{u_{1},\ldots,u_{n}\}$ είναι μία ορθογώνια βάση για τον χώρο $U$ . Τότε το διάνυσμα

v^{\prime}=\operatorname{proj}_{u_{1}}(v)+\cdots+\operatorname{proj}_{u_{n}}(v)

ανήκει στο $U$ και $w=v-v^{\prime}$ είναι ορθογώνιο σε κάθε διάνυσμα του $U$ . Πράγματι, σύμφωνα με την άσκηση 5.4.10 αρκεί να αποδείξουμε ότι $\langle u_{i},w\rangle=0$ για $i=1,\ldots,n$ . Έχουμε

\langle w,u_{i}\rangle\;=\;\langle v,u_{i}\rangle-\sum_{j\in I}\frac{\langle v% ,u_{j}\rangle}{\langle u_{j},u_{j}\rangle}\;\langle u_{j},u_{i}\rangle\;=

=\;\langle v,u_{i}\rangle-\frac{\langle v,u_{i}\rangle}{\langle u_{i},u_{i}% \rangle}\;\langle u_{i},u_{i}\rangle\;=0.

Άρα δείξαμε ότι $v^{\prime}$ είναι ορθογώνια προβολή του $v$ στο $U$ , δηλ. ότι

{\rm proj}_{U}(v)=\frac{\langle v,u_{1}\rangle}{\langle u_{1},u_{1}\rangle}\;u% _{1}+\cdots+\frac{\langle v,u_{n}\rangle}{\langle u_{n},u_{n}\rangle}\;u_{n}.

(6.1.2.1)

Είναι φανερό ότι το $v$ ανήκει στο $U$ αν και μόνο αν $v=\operatorname{proj}_{u}(v)$ . Αποδεικνύεται εύκολα από το Πυθαγόρειο Θεώρημα ότι

\|v-{\rm proj}_{U}(v)\|\leq\|\ v-u\|,\ \forall\ u\in U\;.

Έτσι, για να βρούμε την απόσταση ενός σημείου $B(b_{1},\ldots,b_{m})$ από το $U$ , θέτουμε $v=(b_{1},\ldots,b_{m})$ και υπολογίζουμε το μήκος του διανύσματος $v-\operatorname{proj}_{U}(v)$ .

Παραδείγματα 6.1.3 .

1.

Έστω

$\;\;\;\;\;v_{1}=(\;\frac{1}{2}\;,\frac{1}{2}\;,\frac{1}{2}\;,\frac{1}{2}\;),\;% \;v_{2}=(\;\frac{1}{2}\;,\frac{1}{2}\;,-\frac{1}{2}\;,-\frac{1}{2}\;),$
$V=S\left(\{v_{1},v_{2}\}\right)$ και $w=(1,3,1,5)$ . Το σύνολο $(v_{1},v_{2})$ είναι ορθοκανονική βάση για το $V$ . Έχουμε ότι

$\operatorname{proj}_{v_{1}}(w)=5v_{1},\ \operatorname{proj}_{v_{2}}(w)=-v_{2}% \hbox{άρα}\operatorname{proj}_{V}(w)=5v_{1}+v_{2}\ .$
2.

Έστω $u_{1}=(1,1,0)$ , $u_{2}=(0,1,1)$ , $U=S\left(\{u_{1},u_{2}\}\right)$ και $w=(2,3,3)$ . Θα βρούμε τη προβολή $\operatorname{proj}_{U}(w)$ . Το σύνολο $(u_{1},u_{2})$ είναι βάση για το n $U$ αλλά δεν είναι ορθογώνια. Πρώτα απ' όλα λοιπόν πρέπει να βρούμε μία ορθογώνια βάση για το n $U$ . Παρατηρούμε ότι το διάνυσμα

$u_{2}-\operatorname{proj}_{u_{1}}(u_{2})=\frac{1}{2}(-1,1,2)$
είναι ορθογώνιο προς το $u_{1}$ , όπως άλλωστε και κάθε πολλαπλάσιό του. Άρα μία ορθογώνια βάση για το n $U$ αποτελείται από τα διανύσματα $u_{1}=(1,1,0)$ και $u_{2}^{\prime}=(-1,1,2))$ . Επομένως

$\operatorname{proj}_{u_{1}}(w)=\frac{5}{2}(1,1,0),\ \operatorname{proj}_{u_{2}% ^{\prime}}(w)=\frac{7}{6}(-1,1,2),$
άρα

$\operatorname{proj}_{U}(w)=\operatorname{proj}_{u_{1}}(w)+\operatorname{proj}_% {u_{2}^{\prime}}(w)=\frac{1}{3}(4,11,7)\;.\$
Συνεπώς

$w=\operatorname{proj}_{U}(w)+\left(w-\operatorname{proj}_{U}(w)\right)=\frac{1% }{3}(4,11,7)+\frac{1}{3}(2,-2,2)\ .$
Θα επεκτείνουμε τη βάση του $U$ σε μία ορθογώνια βάση για τον ${\mathbb{R}}^{3}$ . Όπως είδαμε παραπάνω, το διάνυσμα $\frac{1}{3}(2,-2,2)$ είναι ορθογώνιο προς κάθε διάνυσμα του $U$ . To ίδιο ισχύει και για κάθε πολλαπλάσιο του. Επομένως

$\big((1,1,0),(-1,1,2),(2,-2,2)\big)$
είναι μία ορθογώνια βάση για το n ${\mathbb{R}}^{3}$ . Παρατηρούμε ότι αφού $\operatorname{proj}_{U}(w)\neq w$ , το διάνυσμα $w\notin U$ . Θα υπολογίσουμε την απόσταση του σημείου $(2,3,3)$ (τελικό σημείο του $w$ ) από το επίπεδο του $U$ . H απόσταση του $(2,3,3)$ από το $U$ είναι το μήκος του $w-\operatorname{proj}_{U}(w)$ . Έχουμε ότι

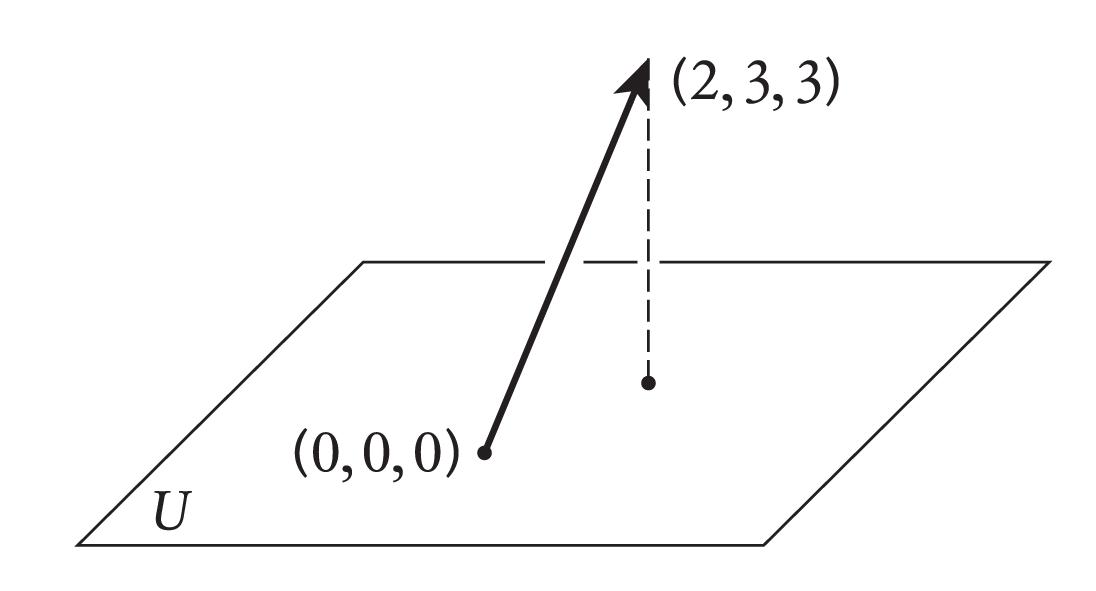
$\|w-\operatorname{proj}_{U}(w)\|=\|\frac{1}{3}(2,-2,2)\|=\frac{1}{3}\|2,-2,2)% \|=\frac{1}{3}\sqrt{12}=\frac{2}{3}\sqrt{3}\ .$

Σχήμα 6.4: H απόσταση του $(2,3,3)$ από τον $U$

To «πλησιέστερο» στο $(2,3,3)$ σημείο του $U$ είναι το τελικό σημείο του $\operatorname{proj}_{U}(w)$ , δηλ. το $1/3(4,11,7)$ .
3.

Έστω

$\;\;\;\;\;v_{1}=(\;\frac{1}{2}\;,\frac{1}{2}\;,\frac{1}{2}\;,\frac{1}{2}\;),\;% \;v_{2}=(\;\frac{1}{2}\;,\frac{1}{2}\;,-\frac{1}{2}\;,-\frac{1}{2}\;),$
$\;\;v_{3}=(\;\frac{1}{2}\;,-\frac{1}{2}\;,\frac{1}{2}\;,-\frac{1}{2}\;),\;\;v_% {4}=(\;\frac{1}{2}\;,-\frac{1}{2}\;,-\frac{1}{2}\;,\frac{1}{2}\;)$
και $v=(1,3,1,5)$ . Το σύνολο $D=(v_{1},v_{2},v_{3},v_{4})$ είναι ορθοκανονική βάση του ${\mathbb{R}}^{4}$ . Θα γράψουμε το $v$ ως γραμμικό συνδυασμό των στοιχείων της $D$ . Παρατηρούμε ότι $v=\operatorname{proj}_{{\mathbb{R}}^{4}}(v)$ και ότι

$\langle v_{1},v\rangle=5,\ \langle v_{2},v\rangle=1,\ \langle v_{3},v\rangle=-% 2,\ \langle v_{4},v\rangle=1\ .$
Χρησιμοποιώντας τον τύπο (6.1.2.1) βρίσκουμε ότι

$v=5v_{1}+v_{2}-2v_{3}+v_{1}\ .$

Στις εφαρμογές η εύρεση ορθοκανονικών βάσεων για υποχώρους του ${\mathbb{R}}^{m}$ είναι μεγάλης σημασίας και ιδιαίτερα για τις υπολογιστικές μεθόδους εύρεσης ιδιοτιμών και ιδιοδιανυσμάτων, όπως είναι η QR- ανάλυση πινάκων. Στο Παράδειγμα 6.1.3.2 υπολογίσαμε μία ορθογώνια βάση του υποχώρου $U$ του ${\mathbb{R}}^{2}$ δοθείσης μίας (μη ορθογώνιας) βάσης του $U$ . H μέθοδος που χρησιμοποιήσαμε γενικεύεται στον Αλγόριθμο Ορθοκανονικοποίησης των Gram - Schmidt.

Αλγόριθμος 6.1.1 Αλγόριθμος Ορθοκανονικοποίησης των Gram - Schmidt για τον υποχώρο

V

του

{\mathbb{R}}^{m}

Είσοδος: Μία βάση

\{v_{1},\ldots,v_{n}\}

για τον

V

Έξοδος: Μία ορθοκανονική βάση για τον

V

Βήμα 1 Θέτουμε

w_{1}=v_{1}

. Για

i=2,\ldots,n

, θέτουμε

V_{i-1}=S(\{w_{1},\ldots,w_{i-1}\})

και υπολογίζουμε

w_{i}=v_{i}-\operatorname{proj}_{V_{i-1}}(v_{i})=v_{i}-\operatorname{proj}_{w_% {1}}(v_{i})-\cdots-\operatorname{proj}_{w_{i-1}}(v_{i})\ .

Βήμα 2 Κανονικοποιούμε τα

w_{i}

για

i=1,\ldots,n

. Το σύνολο

\{\frac{w_{1}}{\|w_{1}\|}\;,\;\;\frac{w_{2}}{\|w_{2}\|}\;,\ldots,\;\frac{w_{ν}% }{\|w_{ν}\|}\}\

είναι ορθοκανονική βάση για τον $V$ .

Παρατηρούμε ότι

V_{i-1}=S(\{w_{1},\ldots,w_{i-1}\})=S(\{v_{1},\ldots,v_{i-1}\})

και ότι το $w_{i}$ είναι ορθογώνιο προς τα διανύσματα $w_{1},\ldots,w_{i-1},$ για $i=2,\ldots,n$ . Αναφέρουμε δύο παραλλαγές του αλγορίθμου 6.1.1.

i.)

Μπορούμε να αντικαταστήσουμε το $w_{i}$ με $\kappa w_{i}$ , όπου $0\neq\kappa\in{\mathbb{R}}$ , για $1\leq i<n$ . Αυτό γίνεται για ευκολία στους υπολογισμούς, εάν για παράδειγμα δεν επιθυμούμε κλάσματα. Δεν προχωράμε στο τελευταίο βήμα της κανονικοποίησης εάν μας ενδιαφέρει μία ορθογώνια βάση για τον $V$ που δεν είναι κατ' ανάγκη ορθοκανονική.
ii.)

Στην είσοδο του αλγορίθμου, αντί για βάση του $V$ μπορούμε να χρησιμοποιήσουμε ένα παράγον σύνολο του $V$ . Εάν το παράγον σύνολο περιέχει γραμμικά εξαρτημένα διανύσματα, τότε κατά την εφαρμογή του αλγορίθμου θα προκύψουν μηδενικά διανύσματα. Αγνοούμε τα μηδενικά διανύσματα και συνεχίζουμε με τα μη μηδενικά εναπομείναντα διανύσματα.

Παραδείγματα 6.1.4.

1.

Έστω

$v_{1}=(1,1,0,0),\;v_{2}=(1,1,-2,1)\;\;v_{3}=(0,-1,0,2),$
και $V=S(\{v_{1},v_{2},v_{3}\})$ . Τότε
2.

$w_{1}=v_{1}=(1,1,0,0)$ ,
3.

$w_{2}=v_{2}-\operatorname{proj}_{w_{1}}v_{2}=(1,1,-2,1)-\frac{2}{2}(1,1,0,0)=(% 0,0,-2,1)$ ,
4.

$w_{3}=v_{3}-\operatorname{proj}_{w_{1}}(v_{3})-\operatorname{proj}_{w_{2}}(v_{% 3})=$

$(0,-1,0,2)-\frac{-1}{2}(1,1,0,0)-\frac{2}{5}(0,0,-2,1)=(\frac{1}{2},-\frac{1}{% 2}\;,\frac{4}{5},\frac{8}{5})$
$=\frac{1}{10}(5,-5,8,16)\;.$

Μία ορθογώνια βάση του $V$ αποτελείται από τα διανύσματα

$(1,1,0,0),(0,0,-2,1),(5,-5,8,16),$
ενώ τα διανύσματα

$\frac{1}{\sqrt{2}}\;(1,1,0,0),\frac{1}{\sqrt{5}}\;(0,0,-2,1),\frac{1}{\sqrt{37% 0}}\;(5,-5,8,16)$
αποτελούν μία ορθοκανονική βάση του $V$ . Σημειώνουμε ότι για την ορθογώνια βάση του $V$ χρησιμοποιήσαμε το διάνυσμα $10w_{3}$ . Σημειώνουμε επίσης ότι δεν ελέγξαμε τη γραμμική ανεξαρτησία για το παράγον σύνολο του $V$ . Ο αλγόριθμος δεν παρήγαγε κάποιο μηδενικό διάνυσμα. Επομένως τα αρχικά διανύσματα ήταν γραμμικά ανεξάρτητα.
5.

Θα υπολογίσουμε μία ορθοκανονική βάση του υποχώρου

$V=\{\;(x,y,z)\in{\mathbb{R}}^{3}:\ \ x-5y-2z=0\}\ .$
Παρατηρούμε ότι

$V=\{\;(5y+2z,y,z):\ y,z\in{\mathbb{R}}\}=\{\;y(5,1,0)+z(2,0,1):\ y,z\in{% \mathbb{R}}\}=$
$=S(\{(5,1,0),(2,0,1)\}).$
Έστω $v_{1}=(5,1,0)$ , $v_{2}=(2,0,1)$ . Τότε

$\{v_{1},v_{2}-\operatorname{proj}_{v_{1}}(v_{2})\}=\{(5,1,0),(1,1,-2)\}$
είναι ορθογώνια βάση του $V$ , ενώ

$\{\frac{1}{\sqrt{5}}({2},0,1),\frac{1}{\sqrt{6}}(1,1-2)\}$
είναι ορθοκανονική βάση του $V$ .
6.

Έστω $v_{1}=(1,1,1)$ , $v_{2}=(2,1,0)$ , $v_{3}=(4,3,2)$ και $V=S(\{v_{1},v_{2},v_{3}\})$ . Σύμφωνα με την δεύτερη παραλλαγή του αλγορίθμου 6.1.1, έχουμε ότι
7.

$w_{1}=v_{1}$ ,
8.

$w_{2}=v_{2}-\operatorname{proj}_{w_{1}}(v_{2})=(1,0,-1)$ και
9.

$w_{3}=v_{3}-\operatorname{proj}_{w_{1}}(v_{3})-\operatorname{proj}_{w_{2}}(v_{% 2})=$

$(4,3,2)-\frac{9}{3}(1,1,1)-\frac{2}{2}(1,0,-1)=(0,0,0)\ .$
Αφού $w_{3}=0$ έπεται ότι $v_{3}=\operatorname{proj}_{S(\{w_{1},w_{2}\})}(v_{3})$ , άρα $v_{3}\in S(w_{1},w_{2}\})$ και κατά συνέπεια $V=S\left(\{w_{1},w_{2}\}\right)$ . Επομένως, μία ορθογώνια βάση του $V$ είναι το σύνολο $\{w_{1},w_{2}\}$ .

Έστω $V$ διανυσματικός υποχώρος του ${\mathbb{R}}^{m}$ και $w\in{\mathbb{R}}^{m}$ . Έχουμε στη διάθεσή μας μία μέθοδο για τον υπολογισμό μίας ορθοκανονικής βάσης για τον $V$ . O επόμενος αλγόριθμος δίνει μία μέθοδο για την εύρεση του $\operatorname{proj}_{V}(w)$ .

Αλγόριθμος 6.1.2 Αλγόριθμος εύρεσης του

\operatorname{proj}_{V}(w)

Είσοδος: Μία βάση για τον

V

και το διάνυσμα

w

Έξοδος: To διάνυσμα

\operatorname{proj}_{V}(w)

Βήμα 1 Χρησιμοποιούμε τον Αλγόριθμο 6.1.1, παραλλαγή i, για να βρούμε μία ορθογώνια βάση

\{w_{1},\ldots,w_{n}\}

για τον

V

Βήμα 2 Χρησιμοποιούμε τον τύπο 6.1.2.1 για να υπολογίσουμε το διάνυσμα

\operatorname{proj}_{V}(w)

Παράδειγμα 6.1.5 .

Θα βρούμε την προβολή του

e_{3}

στον υποχώρο

V=S(\{(1,1,1),(2,1,0)\})

. Είδαμε προηγουμένως ότι μία ορθογώνια βάση για τον

V

είναι το σύνολο

\{(1,1,1),(1,0,-1)\}

. Επομένως

\operatorname{proj}_{V}(e_{3})=\frac{1}{3}(1,1,1)-\frac{1}{2}(1,0,-1)=\frac{1}% {6}(-1,2,5)\;.

Αναφέρουμε τον επόμενο αλγόριθμο, που επιτρέπει τον υπολογισμό του διανύσματος

\operatorname{proj}_{V}(w)

, χωρίς τον υπολογισμό ορθογώνιας βάσης για τον

V

Αλγόριθμος 6.1.3 Αλγόριθμος εύρεσης του

\operatorname{proj}_{V}(w)

με χρήση γινομένου πινάκων.

Είσοδος: Ένα παράγον σύνολο για τον

V

και το διάνυσμα

w

Έξοδος: To διάνυσμα

\operatorname{proj}_{V}(w)

Βήμα 1 Έστω

V=S(\{v_{1},\ldots,v_{n}\})\subset{\mathbb{R}}^{m}

και

B=(e_{1},\ldots,e_{m})

. Θεωρούμε τον

m\times n

πίνακα

A=\begin{bmatrix}C_{B}(v_{1})&\cdots&C_{B}(v_{n})\end{bmatrix}

. Υπολογίζουμε τον

n\times n

πίνακα

A^{T}A

Βήμα 2 Βρίσκουμε μία λύση

(c_{1},\ldots,c_{n})

του συστήματος

(A^{T}A)X=A^{T}C_{B}(w)\;.

(6.1.5.1)

\operatorname{proj}_{V}(w)=c_{1}\cdot v_{1}+\cdots+c_{n}\cdot v_{n}\ .

Ο αλγόριθμος 6.1.3 χρήζει εξήγησης. Αφού

\operatorname{proj}_{V}(w)\in V=S(\{v_{1},\ldots,v_{n}\})

έπεται ότι υπάρχουν

c_{1},\ldots,c_{n}

έτσι ώστε

\operatorname{proj}_{V}(w)=c_{1}v_{1}+\cdots+c_{n}v_{n}

. Θα δείξουμε ότι

(c_{1},\ldots,c_{n})

είναι λύση του συστήματος 6.1.5.1. Πράγματι, το διάνυσμα

w-\operatorname{proj}_{V}(w)

είναι ορθογώνιο προς κάθε στοιχείο του

V

. Άρα

\langle v_{i},w-\operatorname{proj}_{V}(w)\rangle=0,\textrm{gia}i=1,\ldots,n\;.

Επομένως

\langle v_{i},w-c_{1}v_{1}-\cdots-c_{n}v_{n}\rangle=0,\textrm{gia}i=1,\ldots,n\

και

C_{B}(v_{i})^{T}\big(C_{B}(w)-c_{1}C_{B}(v_{1})-\cdots-c_{n}C_{B}(v_{n})\big)=% {0},\textrm{gia}i=1,\ldots,n\;.

(6.1.5.2) Έστω

C=\begin{bmatrix}c_{1}&\cdots&c_{n}\end{bmatrix}^{T}

. Τότε

c_{1}C_{B}(v_{1})+\cdots+c_{n}C_{B}(v_{n})=ΑC\;.

Άρα η σχέση 6.1.5.2 γίνεται

C_{B}(v_{i})^{T}\big(C_{B}(w)-AC\big)={0},\hbox{για}i=1,\ldots,n\

και

C_{B}(v_{i})^{T}C_{B}(w)=C_{B}(v_{i})^{T}(AC),\hbox{για}i=1,\ldots,n\ .

Όμως

C_{B}(v_{i})^{T}

είναι η

i

γραμμή του

A^{T}

. Επομένως, από την παραπάνω σχέση, προκύπτει ότι

Α^{Τ}C_{B}(w)=A^{T}(AC)\textrm{kai'ara}Α^{Τ}C_{B}(w)=(A^{T}A)C\;.

Δείξαμε λοιπόν ότι το σύστημα

(A^{T}A)X=Α^{Τ}C_{B}(w)

είναι συμβατό και ότι

C

είναι μία λύση του συστήματος 6.1.5.1. Παρατηρούμε ότι αν τα διανύσματα

v_{1},\ldots,v_{n}

δεν είναι βάση του

V

, τότε η λύση του συστήματος 6.1.5.1 δεν είναι μοναδική.

Παράδειγμα 6.1.6 .

Έστω

V=S\left(\{(1,1,1,1),(1,1,0,0)\}\right)

. Θα βρούμε το διάνυσμα

\operatorname{proj}_{V}(e_{1})

. Σύμφωνα με τον αλγόριθμο 6.1.2, μία ορθογώνια βάση του

V

αποτελείται από τα διανύσματα

v_{1}=(1,1,1,1)

και

v_{2}=(1,1,-1,-1)

. Έτσι

\operatorname{proj}_{V}(e_{1})=\operatorname{proj}_{v_{1}}(e_{1})+% \operatorname{proj}_{v_{2}}(e_{1})=\frac{1}{4}(1,1,1,1)+\frac{1}{4}(1,1,-1,-1)=

=\frac{1}{2}(1,1,0,0)\ .

Σύμφωνα με τον αλγόριθμο 6.1.3 ,

A=\begin{bmatrix}1&1\cr 1&1\cr 1&0\cr 1&0\end{bmatrix},\ C_{B}(e_{1})=\begin{% bmatrix}1\cr 0\cr 0\cr 0\end{bmatrix},\ A^{T}A=\begin{bmatrix}4&2\cr 2&2\end{% bmatrix},\ \textrm{kai}A^{T}C_{B}(e_{1})=\begin{bmatrix}1\cr 1\end{bmatrix}\;.

Λύνουμε το σύστημα

(A^{T}A)X=A^{T}C_{B}(w)\ .

Η ελαττωμένη κλιμακωτή μορφή του επαυξημένου πίνακα είναι

\left[\begin{array}[]{cc|c}1&0&0\cr 0&1&\frac{1}{2}\end{array}\right]

και η λύση του συστήματος είναι

(0,1/2)

. Άρα

\operatorname{proj}_{V}(e_{1})=0(1,1,1,1)+\frac{1}{2}(1,1,0,0)=\frac{1}{2}(1,1% ,0,0)\;.

Ασκήσεις Ενότητας 6.1

1.

Δίνεται η ορθογώνια βάση

$B=\{\;v_{1}=(3,1,-1),\;v_{2}=(1,-2,1),\;v_{3}=(1,4,7)\;\}$
του ${\mathbb{R}}^{3}$ . Να βρείτε την προβολή του $v=(a,b,c)\in{\mathbb{R}}^{3}$ σε κάθε ένα από τα διανύσματα $v_{1},v_{2},v_{3}$ καθώς και στον χώρο που παράγεται από τα $v_{1},v_{2}$ και τέλος να γράψετε το $v=\operatorname{proj}_{{\mathbb{R}}^{3}}(v)$ ως γραμμικό συνδυασμό των $v_{1},v_{2},v_{3}$ .

Λύση
2.

Έστω $v_{1}=(-3,0,4)$ , $v_{2}=(4,0,-3)$ , $v_{3}=(0,5,0)$ και $u=(1,2,3)$ . Να βρεθούν τα ${\rm proj}_{v_{1}}u$ , ${\rm proj}_{S(\{v_{2},v_{3}\})}u$ , και να γράψετε το $v=\operatorname{proj}_{{\mathbb{R}}^{3}}(v)$ ως γραμμικό συνδυασμό των $v_{1},v_{2},v_{3}$ .

Λύση
3.

Δίνεται η βάση $B=\{u_{1}=(1,0,1),\;u_{2}=(2,1,-3),\;u_{3}=(-1,1,0)\}$ του ${\mathbb{R}}^{3}$ . Να υπολογισθεί με τη μέθοδο των Gram-Schmidt μία ορθοκανονική βάση $B^{\prime}$ του ${\mathbb{R}}^{3}$ που προκύπτει από τη δοθείσα βάση.

Λύση
4.

Δίνονται τα στοιχεία $v=(0,1,2,-1)$ , $u=(1,0,0,2)$ , $w=(3,1,-2,1)$ . Αν $U=S(\{u,w\})$ , να βρεθεί το ${\rm proj}_{U}v$ .

Λύση
5.

Δίνεται το επίπεδο $U=S(\{v_{1},v_{2}\})$ του ${\mathbb{R}}^{3}$ όπου $v_{1}=(1,0,1)$ και $v_{2}=(1,1,2)$ . Να βρεθεί η ελάχιστη απόσταση του $(3,3,4)$ από το $U$ .

Λύση

6.2 Εφαρμογές

Σε αυτήν την ενότητα παρουσιάζουμε διάφορες εφαρμογές της διαγωνιοποίησης καθώς και της θεωρίας που αναπτύξαμε για τις ορθογώνιες προβολές διανυσμάτων.

Δυνάμεις Διαγωνιοποιήσιμων Πινάκων

Έστω $Α\in\mathcal{M}_{n}(\Bbbk)$ ένας διαγωνιοποιήσιμος πίνακας. Υπάρχουν λοιπόν πίνακες $S$ και $D$ έτσι ώστε

S^{-1}A\;S=D=\begin{bmatrix}d_{1}&&{\bf 0}\\ &\ddots&\\ {\bf 0}&&d_{n}\end{bmatrix}\textrm{kai'ara}A=S\;D\;S^{-1}.

Έστω ότι $m$ είναι θετικός ακέραιος. Τότε

D^{m}=\begin{bmatrix}d_{1}^{\;m}&&{\bf 0}\\ &\ddots&\\ {\bf 0}&&d_{n}^{\;m}\end{bmatrix},\;\;\;\forall\;m\in\mathbb{N}\ .

Συνεπώς

A^{m}=(S\;D\;S^{-1})^{m}=(S\;D\;S^{-1})(S\;D\;S^{-1})\cdots(S\;D\;S^{-1})=S\;D% ^{m}S^{-1}.

Αν ο $Α$ είναι αντιστρέψιμος πίνακας, τότε οι ιδιοτιμές του είναι μη μηδενικές, βλ. Πρόταση 5.1.7. Επομένως, o $D$ είναι αντιστρέψιμος και μπορούμε να θεωρήσουμε και αρνητικές δυνάμεις του $D$ . Παρατηρούμε ότι αν $m\in{\mathbb{N}}$ , τότε $D^{-m}=(D^{m})^{-1}$ και

D^{-m}=\begin{bmatrix}d_{1}^{-m}&&{\bf 0}\\ &\ddots&\\ {\bf 0}&&d_{n}^{-m}\end{bmatrix},\;\;\;\forall\;m\in\mathbb{N}\;.

Άρα

A^{-m}=(A^{m})^{-1}=(S\;D^{m}S^{-1})^{-1}=S\;D^{-m}S^{-1}.

Παράδειγμα 6.2.1 .

Έστω ότι $Α\in\mathcal{M}_{n}({\mathbb{C}})$ είναι διαγωνιοποιήσιμος με ιδιοτιμές $\pm 1$ και $\pm i$ . Θα δείξουμε ότι για κάθε $k\in\mathbb{Z}$

Α^{4κ}=I_{n}\ .

Πράγματι, παρατηρούμε ότι αφού o $Α$ είναι διαγωνιοποιήσιμος, ισχύει ότι

A=S\;D\;S^{-1},

όπου οι τιμές της κυρίας διαγωνίου του $D$ είναι οι ιδιοτιμές $\pm 1$ και $\pm i$ , (χωρίς να ξέρουμε πόσες φορές εμφανίζονται οι ιδιοτιμές ή με ποιά σειρά). Επομένως

A^{4κ}=S\;D^{4κ}S^{-1},\;\;\;\forall\;κ\in\mathbb{Z}.

Όμως

(\pm 1)^{4k}=1\textrm{kai}({\pm i})^{4k}=1\;.

Συνεπώς

D^{4k}=I_{n}\Rightarrow A^{4κ}=S\;D^{4κ}S^{-1}=S\;I_{n}S^{-1}=S\;S^{-1}=I_{n}\ .

Γεωμετρία και Γραφικά Υπολογιστών

Στον κλάδο γραφικά υπολογιστών της πληροφορικής, πολλές εφαρμογές χρειάζονται να τροποποιήσουν μία εικόνα αλλάζοντα στην θέση, τον προσανατολισμό ή και το μέγεθός της. Αυτό γίνεται εφαρμόζοντας έναν γεωμετρικό μετασχηματισμό στις συντεταγμένες που ορίζουν την εικόνα. Παρακάτω εξετάζουμε μία ειδική κατηγορία τέτοιων μετασχηματισμών που διατηρούν την κλίμακα της εικόνας. Μία ισομετρία (isometry) του ${\mathbb{R}}^{n}$ είναι μία συνάρτηση $T:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ που διατηρεί τις αποστάσεις, δηλ.

\|T(x)-T(y)\|=\|x-y\|\textrm{giak'aje}x,y\in{\mathbb{R}}^{n}\;.

H ισομετρία $T:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ δεν είναι κατ' ανάγκη γραμμική συνάρτηση. To βασικό παράδειγμα μίας ισομετρίας που δεν είναι γραμμική συνάρτηση είναι η μεταφορά (translation) κατά $\alpha$ , δηλ. η συνάρτηση

T:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n},T(x)=x+\alpha,\textrm{'opou}0% \neq\alpha\in{\mathbb{R}}^{n}

μεταφορά

Παράδειγμα 6.2.2 .

Στο επόμενο σχήμα 6.5 απεικονίζεται η μεταφορά στο ${\mathbb{R}}^{2}$ κατά το $\alpha=(1,1)$ .

Σχήμα 6.5: Μεταφορά κατά $(1,1)$ : $T(x_{1},x_{2})=(x_{1}+1,x_{2}+1)$ .

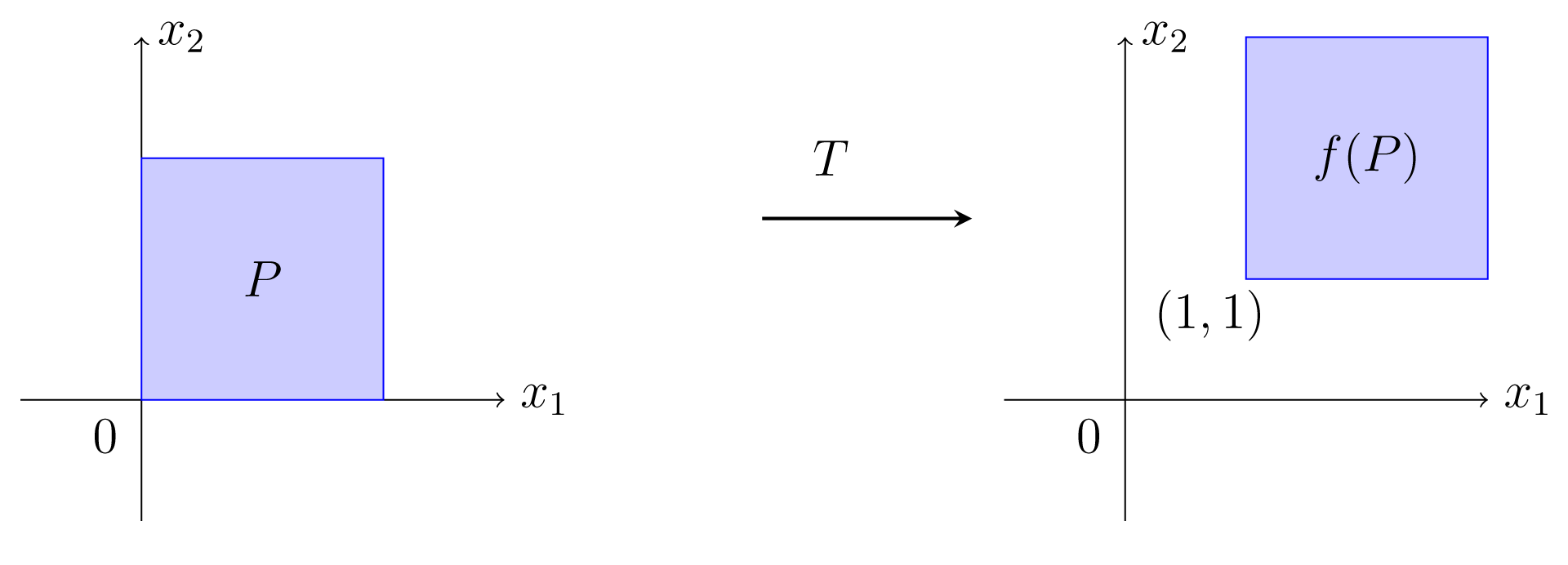
To επόμενο θεώρημα δείχνει τη σύνδεση ανάμεσα στις ισομετρίες και στις γραμμικές συναρτήσεις.

Θεώρημα 6.2.3.

Έστω $T:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ μία ισομετρία. Τότε η συνάρτηση $f:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ , $f(x)=T(x)-T({\bf 0})$ είναι ισομετρία και γραμμική συνάρτηση. Επομένως κάθε ισομετρία είναι σύνθεση μίας ορθογώνιας συνάρτησης και μίας μεταφοράς

Απόδειξη.

Είναι εύκολο να δει κανείς ότι η $f$ είναι ισομετρία. Πράγματι

\|f(v_{1})-f(v_{2})\|=\|T(v_{1})-T(v_{2})\|=\|v_{1}-v_{2}\|.

Παρατηρούμε ότι

f({\bf 0})=T({\bf 0})-T({\bf 0})={\bf 0}.

Συνεπώς η $f$ διατηρεί το μήκος των διανυσμάτων, αφού

\|f(v)\|=\|f(v)-f({\bf 0})\|=\|v-{\bf 0}\|=\|v\|,\textrm{giak'aje}v\in{\mathbb% {R}}^{2}.

Τέλος, παρατηρούμε ότι

\langle f(v),f(w)\rangle=\langle v,w\rangle.

Πράγματι:

\|f(v)-f(w)\|=\|v-w\|\Rightarrow\langle f(v)-f(w),f(v)-f(w)\rangle=\langle v-w% ,v-w\rangle

\Rightarrow\langle f(v),f(v)\rangle-2\langle f(v),f(w)\rangle+\langle f(w),f(w% )\rangle=\langle v,v\rangle-2\langle v,w\rangle+\langle w,w\rangle.

Αφού $\langle f(v),f(v)\rangle=\langle v,v\rangle$ και $\langle f(w),f(w)\rangle=\langle w,w\rangle$ , προκύπτει το ζητούμενο. Έστω, τώρα $B=(e_{1},\ldots,e_{n})$ , η κανονική βάση του ${\mathbb{R}}^{n}$ . Αν $w_{i}=f(e_{i})$ , για $i=1,\ldots,n$ , τότε από τα παραπάνω έπεται ότι το διατεταγμένο σύνολο $D=(w_{1},\ldots,w_{n})$ είναι ορθοκανονική βάση για τον ${\mathbb{R}}^{n}$ . Έστω $u\in{\mathbb{R}}^{n}$ και έστω ότι τα $c_{1},\ldots,c_{n}$ είναι οι συντεταγμένες του $f(u)$ ως προς τη βάση $D$ , δηλ. $f(u)=c_{1}w_{1}+\cdots+c_{n}w_{n}$ . Σύμφωνα με το Θεώρημα 5.4.5, $c_{i}=\langle f(u),w_{i}\rangle$ , για $i=1,\ldots,n$ . Όμως, από τα παραπάνω, γνωρίζουμε ότι

\langle f(u),w_{i}\rangle=\langle\langle f(u),f(e_{i})\rangle=\langle u,e_{i}% \rangle,\ i=1,\ldots,n.

Επομένως

f(u)=\langle u,e_{i}\rangle w_{i}\,.

Αν λοιπόν $u,v\in{\mathbb{R}}^{n}$ , τότε

f(u+v)=\sum\langle u+v,e_{i}\rangle w_{i}=\sum(\langle u,e_{i}\rangle+\langle v% ,e_{i}\rangle)w_{i}=

\sum\langle u,e_{i}\rangle w_{i}+\sum\langle v,e_{i}\rangle w_{i}=f(u)+f(v).

Ομοίως, o αναγνώστης καλείται να διαπιστώσει χρησιμοποιώντας τις ιδιότητες του εσωτερικού γινομένου ότι

f(cu)=cf(u),\textrm{gia}c\in{\mathbb{R}},u\in{\mathbb{R}}^{n}.

∎

Έστω $f:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ μία γραμμική συνάρτηση που είναι ισομετρία. Χρησιμοποιώντας το Πόρισμα 5.5.3, προκύπτει ότι

\langle f^{*}f(v),w\rangle=\langle f(v),f(w)\rangle=\langle v,w\rangle,\textrm% {giak'aje}v,w\in{\mathbb{R}}^{n}.

Άρα

\langle f^{*}f(v),w\rangle=\langle v,w\rangle\Rightarrow\langle f^{*}f(v)-v,w% \rangle=0,\textrm{giak'aje}w\in{\mathbb{R}}^{n}\;.

Συνεπώς $f^{*}f=\operatorname{id}_{V}$ , βλ. 5.4.1.1. Επομένως, o πίνακας της συνάρτησης $f$ ως προς την κανονική βάση $B$ του ${\mathbb{R}}^{n}$ είναι ορθογώνιος :

\overline{A_{B,B}^{f}}A_{B,B}^{f}=I_{n}.

Εξαιτίας αυτής της ιδιότητας καλούμε τις γραμμικές συναρτήσεις, που είναι ισομετρίες, ορθογώνιες (orthogonal linear transformations). Χωρίς απόδειξη, σημειώνουμε το παρακάτω ενδιαφέρον συμπέρασμα για τις ισομετρίες στο επίπεδο.

Θεώρημα 6.2.4 .

Αν $T:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ είναι ισομετρία, τότε η $T$ έχει μία από τις επόμενες μορφές :

1.

μεταφορά κατά ένα $a$ (translation),
2.

περιστροφή κατά γωνία $\theta$ (rotation),
3.

αντικατοπτρισμός ως προς μία ευθεία $L$ (reflection),
4.

σύνθεση ενός αντικατοπτρισμού ως προς μία ευθεία $L$ και μίας μεταφοράς που στέλνει τα σημεία της $L$ σε σημεία της $L$ (glide reflection).

Οι γεωμετρικοί μετασχηματισμοί που επιθυμούμε δεν είναι βέβαια όλοι ισομετρίες.

Παράδειγμα 6.2.5.

Θα βρούμε τον τύπο για τον γεωμετρικό μετασχηματισμό $T:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ , που διαστέλλει τα σχήματα του ${\mathbb{R}}^{2}$ με συντελεστή $2$ ως προς τον άξονα των $Y$ , τα περιστρέφει αριστερόστροφα κατ' αγωνία $\pi/4$ και τα μεταφέρει κατά to $(1,1/2)$ . Θα χρησιμοποιήσουμε τις γνώσεις μας από την Ενότητα 4.1. H γραμμική συνάρτηση της διαστολής αντιστοιχεί στον πίνακα

\left[\begin{array}[]{cc}1&0\cr 0&2\end{array}\right],

βλ. Παράδειγμα 4.1.6.5. H γραμμική συνάρτηση της περιστροφής αντιστοιχεί στον πίνακα

\left[\begin{array}[]{rr}\sqrt{2}/2&-\sqrt{2}/2\cr\sqrt{2}/2&\sqrt{2}/2\end{% array}\right]\begin{array}[]{c}\end{array},

βλ. Παράδειγμα 4.1.6.4. To γινόμενο των πινάκων, δηλ. o πίνακας

\left[\begin{array}[]{rr}\sqrt{2}/2&-\sqrt{2}\cr\sqrt{2}/2&\sqrt{2}\end{array}% \right]\begin{array}[]{c}\end{array},

αντιστοιχεί στην σύνθεση των γραμμικών συναρτήσεων. Συνδυάζοντας με την μεταφορά κατά to $(1,1/2)$ , βρίσκουμε ότι o γεωμετρικός μετασχηματισμός που επιθυμούμε έχει τύπο

T:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(\alpha,\beta)\mapsto% \left(\frac{\sqrt{2}}{2}\alpha-\sqrt{2}\beta+1,\frac{\sqrt{2}}{2}\alpha+\sqrt{% 2}\beta+\frac{1}{2}\right).

Σχήμα 6.6:O γεωμετρικός μετασχηματισμός $T$ .

Παραπέμπουμε στο σύγγραμμα [4] για περισσότερα επί του θέματος της Γεωμετρίας για γραφικά υπολογιστών.

Το πρόβλημα του Κυνηγού και της Λείας του

To μοντέλο κυνηγού και λείας (predator-prey model) περιγράφει ένα απλό δυναμικό σύστημα δύο πληθυσμών: των κυνηγών και της λείας. Οι κυνηγοί τρέφονται αποκλειστικά από τη λεία, ενώ η λεία δεν έχει άλλους εχθρούς και έχει απεριόριστες ποσότητες τροφής. Για παράδειγμα, αυτό το μοντέλο περιγράφει (απλοϊκά) ένα οικοσύστημα που αποτελείται από λύκους και αντιλόπες. Έστω ότι $x_{k}$ είναι ο πληθυσμός της λείας και $y_{k}$ είναι ο πληθυσμός του κυνηγού τον χρόνο $κ$ μετά τον χρόνο της αρχικής μέτρησης (χρόνος μηδέν) και έστω ότι το μοντέλο περιγράφεται από τις εξισώσεις:

\begin{array}[]{rrrr}y_{k+1}\;=&1/2\;y_{k}&+&1/100\;x_{k}\cr x_{k+1}\;=&-50/4% \;y_{k}&+&5/4\;x_{k}\ .\end{array}

Αν

A=\left[\begin{array}[]{cc}1/2&1/100\cr-50/4&5/4\end{array}\right]\;\;\;\mbox{% και}\;\;\;V_{k}=\left[\begin{array}[]{r}y_{k}\cr x_{k}\end{array}\right]\;,

τότε το παραπάνω πληθυσμιακό μοντέλο περιγράφεται από την εξίσωση

V_{k+1}=A\;V_{k}\;.

Έστω ότι ξεκινάμε με αρχικό πληθυσμό $y_{0}=50$ και $x_{0}=1600$ . Τα διανύσματα $V_{0}$ και $V_{1}$ περιγράφουν την αρχική κατάσταση και την κατάσταση ένα χρόνο αργότερα:

V_{0}=\left[\begin{array}[]{c}50\cr 1600\end{array}\right]\textrm{kai}V_{1}=% \left[\begin{array}[]{c}41\cr 1375\end{array}\right].

Παρατηρούμε ότι και οι δύο πληθυσμοί μειώθηκαν. Θα συνεχίσουν να μειώνονται οι πληθυσμοί έως ότου αφανιστούν και τα δύο είδη; Είναι φανερό ότι θέλουμε να μελετήσουμε το $V_{k}$ για μεγάλα $k$ . Δεν είναι δύσκολο να δούμε ότι $V_{k}=A^{k}V_{0}$ . Πράγματι,

V_{k}=A\;V_{k-1}=A\;(A\;V_{k-2})=A^{2}\;V_{k-2}=\cdots=A^{k}\;V_{0}\;.

Όμως, o $A$ διαγωνιοποιείται:

A=P\;D\;P^{-1},\textrm{'opou}D=\left[\begin{array}[]{cc}1&0\cr 0&3/4\end{array% }\right]\textrm{kai}P=\left[\begin{array}[]{cc}1&1\cr 50&25\end{array}\right].

Συνεπώς

A^{k}=P\;D^{k}\;P^{-1}\textrm{kai'ara}V_{k}=A^{k}\;V_{0}=P\;D^{k}\;P^{-1}\;V_{% 0}\;.

Αφού

D^{k}=\left[\begin{array}[]{cc}1^{k}&0\cr 0&(3/4)^{k}\end{array}\right]=\left[% \begin{array}[]{cc}1&0\cr 0&(3/4)^{k}\end{array}\right],

συμπεραίνουμε ότι για μεγάλα $k$ , o πίνακας $D^{k}$ πλησιάζει την τιμή $\left[\begin{array}[]{cc}1&0\cr 0&0\end{array}\right]$ . Άρα για μεγάλα $k$ , o $V_{k}$ πλησιάζει την τιμή

(P\left[\begin{array}[]{cc}1&0\cr 0&0\end{array}\right]P^{-1})\;V_{0}=\left[% \begin{array}[]{c}14\cr 700\end{array}\right].

To πληθυσμιακό σύστημα που μελετούμε θα ισορροπήσει. Παρατηρούμε ότι η ιδιότητα της ισορροπίας δεν εξαρτάται από τις αρχικές τιμές των $y_{k}$ και $x_{k}$ , αλλά από τον πίνακα $A$ των συντελεστών και τις ιδιοτιμές του.

Μαρκοβιανές Αλυσίδες

Έστω ότι ένα σύστημα αποτελείται από $k$ διακριτές καταστάσεις. Τις αριθμούμε $1,2\ldots,k$ . Μεταβαίνουμε από την κατάσταση $j$ στην κατάσταση $i$ με μία πιθανότητα $p_{ij}$ . To σύστημα αυτό είναι μία Μαρκοβιανή αλυσίδα (Markov chain). O πίνακας μετάβασης της Μαρκοβιανής αλυσίδας είναι o τετραγωνικός $k\times k$ πίνακας $P=(p_{ij})$ . Σημειώνουμε ότι το άθροισμα των στοιχείων κάθε στήλης του πίνακα $P$ είναι $1$ . Ένας τέτοιος πίνακας λέγεται στοχαστικός (stochastic). Στο επόμενο παράδειγμα περιγράφουμε μία απλή Μαρκοβιανή αλυσίδα με δύο καταστάσεις.

Παράδειγμα 6.2.6.

Θεωρούμε δύο καταστάσεις για τον καιρό μίας πόλης: στεγνός (κατάσταση1) ή βροχερός (κατάσταση2). Έστω ότι o πίνακας μετάβασης του συστήματος είναι

P=\left[\begin{array}[]{cc}0.94&0.02\\ 0.06&0.98\end{array}\right].

Έτσι, αν o καιρός είναι στεγνός τη μία μέρα, η πιθανότητα να είναι στεγνός την επομένη είναι $94\%$ ενώ ηπιθανότητα να είναι βροχερός είναι $6\%$ . Αν o καιρός είναι βροχερός τη μία μέρα, η πιθανότητα να είναι στεγνός την επομένη είναι $2\%$ ενώ η πιθανότητα να είναι βροχερός είναι $98\%$ . Έστω ότι o καιρός είναι βροχερός κάποια μέρα. Ποια είναι η πρόγνωση του καιρού μετά από 10 ημέρες; Αν η αρχική κατάσταση $x^{(0)}$ περιγράφεται από το διάνυσμα $x^{(0)}=\begin{bmatrix}0&1\end{bmatrix}^{T}$ , τότε το γινόμενο $x^{(1)}:=Px^{(0)}$ δείχνει την κατανομή των πιθανοτήτων την επόμενη μέρα. Έστω $x^{(n)}$ η κατανομή των πιθανοτήτων την $n$ -στη μέρα. Τότε

x^{(n)}=Px^{(n-1)}=P\;P\;x^{(n-2)}=P^{2}\;x^{(n-2)}=\cdots=P^{n}x^{(0)}\;.

Για να μπορέσουμε, λοιπόν, να απαντήσουμε στο ερώτημα που τέθηκε, δηλ. να βρούμε το $x^{(10)}$ , πρέπει να υπολογίσουμε τον πίνακα $P^{10}$ .

Γενικότερα, για να απαντήσουμε ερωτήματα όπως αυτό του παραδείγματος, θέλουμε να υπολογίσουμε δυνάμεις ενός στοχαστικού πίνακα $P$ . Υπολογιστικά αυτό γίνεται ιδιαίτερα πολύπλοκο. Ευτυχώς, έχουμε στη διάθεσή μας το επόμενο θεώρημα, που δίνουμε χωρίς απόδειξη,.

Θεώρημα 6.2.7 .

Έστω ότι $P$ είναι ένας πίνακας μετάβασης μίας Μαρκοβιανής αλυσίδας, τέτοιος ώστε τα στοιχεία του $P$ να είναι όλα θετικά. Τότε το $1$ είναι ίδιο τιμή του $P$ και o $P^{m}$ σταθεροποιείται για μεγάλες τιμές του $m$ . H οριακή κατάσταση του συστήματος είναι ανεξάρτητη από την αρχική κατανομή.

Θα δούμε πως μπορούμε να εφαρμόσουμε τα παραπάνω στο προηγούμενο παράδειγμα.

Παράδειγμα 6.2.8.

(Συνέχεια του Παραδείγματος 6.2.6.) Σύμφωνα με το Θεώρημα 6.2.7, o $P^{m}$ σταθεροποιείται, δηλ. $P^{m}=P^{m+1}$ , για μεγάλες τιμές του $m$ . Επομένως $x^{(m+1)}=x^{(m)}$ , αφού

x^{(m+1)}=P^{m}x^{(0)}=P^{m+1}x^{(0)}=x^{(m)}\;.

Όμως , $x^{(m+1)}=Px^{(m)}$ , άρα :

x^{(m)}=Px^{(m)},

δηλ. το $x^{(m)}$ είναι ιδιοδιάνυσμα του $P$ για την ιδιοτιμή $1$ . Θα χρησιμοποιήσουμε αυτό το ιδιοδιάνυσμα για να προσεγγίσουμε το $x^{(10)}$ . Παρατηρούμε ότι

V_{1}(P)=\{t(1,3):\ t\in{\mathbb{R}}\}.

Αφού το $x^{(m)}$ ανήκει στο $V_{1}(P)$ και είναι στοχαστικός πίνακας, τα άθροισμα των στοιχείων του είναι $1$ . Άρα

x^{(m)}=\begin{bmatrix}0.25\cr 0.75\end{bmatrix}

και η πιθανότητα μετά από 10 ημέρες o καιρός να είναι στεγνός είναι περίπου $25\%$ ενώ o καιρός θα είναι βροχερός με πιθανότητα περίπου $75\%$ .

Παραπέμπουμε τον ενιδαφερόμενο αναγνώστη στο σύγγραμμα[4] για περισσότερες λεπτομέρειες επί του θέματος.

Διαφορικές Εξισώσεις και Ιδιοτιμές

Έστω ένα απλό γραμμικό σύστημα $n$ διαφορικών εξισώσεων:

	$\displaystyle f_{1}^{\prime}(x)$	$\displaystyle=a_{11}f_{1}(x)+\cdots+a_{1n}f_{n}(x)$
	$\displaystyle\vdots$
	$\displaystyle f_{n}^{\prime}(x)$	$\displaystyle=a_{n1}f_{1}(x)+\cdots+a_{nn}f_{n}(x),$

όπου $f_{i}:{\mathbb{R}}\rightarrow{\mathbb{R}}$ είναι πραγματική διαφορίσιμη συνάρτηση και $f^{\prime}_{i}:{\mathbb{R}}\rightarrow{\mathbb{R}}$ είναι η παράγωγός της, για $1\leq i\leq n$ . Επιθυμούμε να βρούμε τους τύπους των $f_{i}$ , για $1\leq i\leq n$ . To σύστημα γράφεται ως

F^{\prime}=A\;F,

όπου

A=\begin{bmatrix}a_{11}&\cdots&a_{1n}\cr\vdots&\cdots&\vdots\cr a_{n1}&\cdots&% a_{nn}\end{bmatrix}\;,F=\begin{bmatrix}f_{1}(x)\cr\vdots\cr f_{n}(x)\end{% bmatrix}\textrm{kai}F^{\prime}=\begin{bmatrix}f_{1}^{\prime}(x)\cr\vdots\cr f_% {n}^{\prime}(x)\end{bmatrix}\;.

Όταν o πίνακας $A$ διαγωνιοποιείται, τότε η επίλυση του συστήματος $F^{\prime}=A\;F$ γίνεται εύκολα ως εφαρμογή της θεωρίας της διαγωνιοποίησης. H παρατήρηση - κλειδί για την επίλυση του συστήματος $F^{\prime}=A\;F$ είναι ότι αν

g(x)=c_{1}f_{1}(x)+\cdots c_{n}f_{n}(x),\textrm{t'ote}g^{\prime}(x)=c_{1}f_{1}% ^{\prime}(x)+\cdots c_{n}f_{n}^{\prime}(x).

Επομένως

G=PF\Rightarrow G^{\prime}=PF^{\prime}\ .

Τα επόμενα Παραδείγματα, θα διαφωτίσουν τη διαδικασίας επίλυσης του $F^{\prime}=A\;F$ .

Παραδείγματα 6.2.9 .

1.

Αν $f^{\prime}(x)=-5f(x)$ , τότε από τον διαφορικό λογισμό γνωρίζουμε ότι $f(x)=Ce^{-5x}$ . Αν δίνεται ότι $f(0)=2$ , τότε $2=Ce^{0}=C$ και $f(x)=2e^{-5x}$ .
2.

Έστω

$\;\;\;\;\;\;\;F^{\prime}=A\;F,\;\;\;{\textrm{όπου}}\;A=\begin{bmatrix}3&0\cr 0% &4\end{bmatrix},\;F=\begin{bmatrix}f_{1}(x)\cr f_{2}(x)\end{bmatrix}\textrm{% kai}F^{\prime}=\begin{bmatrix}f_{1}^{\prime}(x)\cr f_{2}^{\prime}(x)\end{% bmatrix}.$
To σύστημα $F^{\prime}=A\;F$ αποτελείται από τις εξισώσεις

$\displaystyle f_{1}^{\prime}(x)$ $\displaystyle=3f_{1}(x)$
$\displaystyle f_{2}^{\prime}(x)$ $\displaystyle=4f_{2}(x)$
και η λύση του είναι

$F=F=\begin{bmatrix}f_{1}(x)\cr f_{2}(x)\end{bmatrix}=\begin{bmatrix}C_{1}e^{3x% }\cr C_{2}e^{4x}\end{bmatrix}\ .$
Όταν προσδιορίζονται αρχικές συνθήκες, τότε μπορούμε να επιλύσουμε για $C_{1}$ και $C_{2}$ . Για παράδειγμα αν δίνεται ότι $f_{1}(0)=2$ και $f_{2}(0)=-1$ , τότε

$\displaystyle f_{1}(x)$ $\displaystyle=2e^{3x}$
$\displaystyle f_{2}(x)$ $\displaystyle=-e^{4x}\;.$
3.

Έστω το σύστημα

$\displaystyle f_{1}^{\prime}(x)$ $\displaystyle=2f_{1}(x)-f_{2}(x)$
$\displaystyle f_{2}^{\prime}(x)$ $\displaystyle=6f_{1}(x)-f_{2}(x).$
O πίνακας

$A=\left[\begin{array}[]{rr}2&-1\cr 6&-5\end{array}\right]$
είναι διαγωνιοποιήσιμος με ιδιοτιμές $1,-4$ και $A=PDP^{-1}$ , όπου

$D=\left[\begin{array}[]{rr}1&0\cr 0&-4\end{array}\right]\;\;\;\textrm{και}\;\;% \;P=\left[\begin{array}[]{rr}1&1\cr 1&6\end{array}\right].$
Θα λύσουμε πρώτα το σύστημα $G^{\prime}=D\;G$ , δηλ. θα βρούμε $g_{1}:{\mathbb{R}}\rightarrow{\mathbb{R}}$ , $g_{2}:{\mathbb{R}}\rightarrow{\mathbb{R}}$ που ικανοποιούν το σύστημα των διαφορικών εξισώσεων

$\displaystyle g_{1}^{\prime}(x)$ $\displaystyle=\ \ \ g_{1}(x)$
$\displaystyle g_{2}^{\prime}(x)$ $\displaystyle=-4g_{2}(x).$
Το σύστημα $G=D\;G$ έχει λύση

$\;G=F=\begin{bmatrix}g_{1}(x)\cr g_{2}(x)\end{bmatrix}=\left[\begin{array}[]{l% }C_{1}e^{x}\cr C_{2}e^{-4x}\end{array}\right].$
Εάν τώρα θέσουμε $F=P\;G$ , παρατηρούμε ότι $F^{\prime}=P\;G^{\prime}$ και ότι $F$ είναι λύση του αρχικού συστήματος. Πράγματι:

$F=P\;G\Rightarrow A\;F=(PDP^{-1})P\;G=(PD)(P^{-1})P\;G)=P(D\;G)=PG^{\prime}=F^% {\prime}\;.$
Επομένως η λύση του συστήματος $F^{\prime}=AF$ είναι $F=PG$ , δηλ.

$F=\left[\begin{array}[]{c}f_{1}(x)\\ f_{2}(x)\end{array}\right]=\left[\begin{array}[]{c}C_{1}e^{x}+C_{2}e^{-4x}\cr C% _{1}e^{x}+6C_{2}e^{-4x}\end{array}\right].$
Αν γνωρίζουμε κάποιες αρχικές τιμές για τις συναρτήσεις $f_{1},f_{2}$ , τότε μπορούμε να υπολογίσουμε τις σταθερές $C_{1},C_{2}$ . Πράγματι, έστω ότι $f_{1}(0)=2$ , $f_{2}(0)=-3$ . Τότε

$\displaystyle 2$ $\displaystyle=C_{1}+C_{2}$
$\displaystyle-3$ $\displaystyle=C_{1}+6C_{2}$
με λύση $C_{1}=3$ , $C_{2}=-1$ , οπότε

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;f_{1}(x)=3e^{x}-e^{-4x}\;\;\;\;% \hbox{και}\;\;\;\;f_{2}(x)=3e^{x}-6e^{-4x}.$

Απομονώνουμε την παρατήρηση του προηγούμενου παραδείγματος.

Αν $A=P\;DP^{-1}$ , τότε $G$ είναι λύση του $G^{\prime}=D\;G$ αν και μόνο αν $P G$ είναι λύση του $F^{\prime}=A\;F$ .

Τετραγωνικές Μορφές

Ένα πολυώνυμο με $n$ μεταβλητές και συντελεστές πραγματικούς αριθμούς λέγεται τετραγωνική μορφή (quadratic form) αν όλοι οι όροι του πολυωνύμου είναι βαθμού δύο ως προς τις μεταβλητές. Για παράδειγμα το πολυώνυμο

q(x_{1},x_{2},x_{3})=3x_{1}^{2}+4x_{2}^{2}+5x_{3}^{2}+5x_{1}x_{2}+x_{2}x_{3}

είναι μία τετραγωνική μορφή. O αναγνώστης καλείται να επιβεβαιώσει ότι

\left[\begin{array}[]{ccc}x_{1}&x_{2}&x_{3}\end{array}\right]\left[\begin{% array}[]{ccc}3&7/2&0\\ 7/2&4&1/2\\ 0&1/2&5\end{array}\right]\left[\begin{array}[]{c}x_{1}\\ x_{2}\\ x_{3}\end{array}\right]=\begin{bmatrix}3x_{1}^{2}+4x_{2}^{2}+5x_{3}^{2}+5x_{1}% x_{2}+2x_{2}x_{3}\end{bmatrix}.

Γράφουμε, λοιπόν,

q(x_{1},x_{2},x_{3})=X^{T}AX,

όπου

A=\left[\begin{array}[]{ccc}3&7/2&0\\ 7/2&4&1\\ 0&1&5\end{array}\right],\ X=\left[\begin{array}[]{c}x_{1}\\ x_{2}\\ x_{3}\end{array}\right].

Παρατηρούμε ότι o πίνακας $A$ είναι συμμετρικός. Στην κύρια διαγώνιο του $A$ εμφανίζονται οι συντελεστές των όρων $x_{i}^{2}$ του πολυωνύμου $q(x_{1},x_{2},x_{3})$ , για $1\leq i\leq 3$ . Αν $1\leq i\neq j\leq 3$ , τότε το στοιχείο $a_{ij}$ του $A$ είναι ίσο με το ήμισυ του συντελεστή του όρου $x_{i}x_{j}$ του $q(x_{1},x_{2},x_{3})$ . Γενικότερα, κάθε τετραγωνική μορφή

q(x_{1},x_{2},\ldots,x_{n})=\sum_{i=1}^{n}b_{i}x_{i}^{2}+\sum_{1\leq i<j\leq n% }^{n}2b_{ij}x_{i}x_{j}\;,

γράφεται ως

q(x_{1}\ldots,x_{n})=X^{T}A\;X\textrm{'opou}X^{T}=[\;x_{1}\;x_{2}\;\cdots\;x_{% n}\;]\textrm{kai}A=A^{T}.

Αν $c\in{\mathbb{R}}$ και $A=A^{T}\in\mathcal{M}_{n}({\mathbb{R}})$ , ποια είναι η γραφική αναπαράσταση στον ${\mathbb{R}}^{n}$ μίας εξίσωσης της μορφής

q(x_{1},x_{2},\ldots,x_{n})=c,\ \textrm{'opou}q(x_{1},x_{2},\ldots,x_{n})=X^{T% }A\;X\textrm{?}

Αφού o $A$ είναι συμμετρικός πίνακας, από το Φασματικό Θεώρημα, γνωρίζουμε ότι οι ιδιοτιμές του $A$ είναι πραγματικοί αριθμοί και o $A$ διαγωνιοποιείται ορθογώνια. Έστωότι $D=P^{T}AP$ είναι η ορθογώνια διαγωνιοποίηση του $A$ , όπου $D$ είναι o διαγώνιος πίνακας των ιδιοτιμών του $A$ και $P^{T}=P^{-1}$ . H αλλαγή συντεταγμένων $Y=P^{T}X$ μας επιτρέπει να αλλάξουμε την οπτική μας γωνία και να διαχωρίσουμε τις μεταβλητές. Πράγματι, αν $\lambda_{1},\ldots,\lambda_{n}$ είναι οι ιδιοτιμές του $A$ , τότε

X^{T}A\;X=X^{T}(PDP^{T})\;X=(X^{T}P)D(P^{T}X)=(P^{T}X)^{T}D(P^{T}X)=Y^{T}DY

και η τετραγωνική μορφή $q(x_{1},\ldots,x_{n})=X^{T}A\;X$ μετατρέπεται στην τετραγωνική μορφή

q(y_{1},\ldots,y_{n})=\lambda_{1}y_{1}^{2}+\cdots+\lambda_{n}y_{n}^{2}=Y^{T}D% \;Y\;.

To επόμενο παράδειγμα θα διαφωτίσει αυτήν τη διαδικασία, βλ. σύγγραμμα [2, Ενότητα 7.2.22].

Παράδειγμα 6.2.10.

Θα βρούμε το γράφημα της καμπύλης με εξίσωση

x_{1}^{2}+4x_{1}x_{2}+x_{2}^{2}-5=0\ .

Το πολυώνυμο $q(x_{1},x_{2})=x_{1}^{2}+4x_{1}x_{2}+x^{2}$ είναι τετραγωνική μορφή με πίνακα

A=\left[\begin{array}[]{cc}1&2\\ 2&1\end{array}\right]\begin{array}[]{c}\\ .\end{array}

Οι ιδιοτιμές του $A$ είναι $-1,3$ και

D=P^{T}A\;P=\left[\begin{array}[]{rc}-1&0\\ 0&3\end{array}\right]\textrm{'opou}P=\frac{1}{\sqrt{2}\;}\left[\begin{array}[]% {rc}-1&1\\ 1&1\end{array}\right].

Θέτουμε

Y=P^{T}X,\textrm{'opou}X=\begin{bmatrix}x_{1}\cr x_{2}\end{bmatrix}\textrm{kai% }Y=\begin{bmatrix}y_{1}\cr y_{2}\end{bmatrix}.

Me αυτήν την αλλαγή συντεταγμένων, η εξίσωση της καμπύλης είναι

-y_{1}^{2}+3y_{2}^{2}-5=0.

Στο παρακάτω σχήμα, παρουσιάζεται η γραφική παράσταση της καμπύλης ως προς τους άξονες $Y_{1}$ και $Y_{2}$ :

Σχήμα 6.7:Η καμπύλη $-y_{1}^{2}+3y_{2}^{2}-5=0.$ .

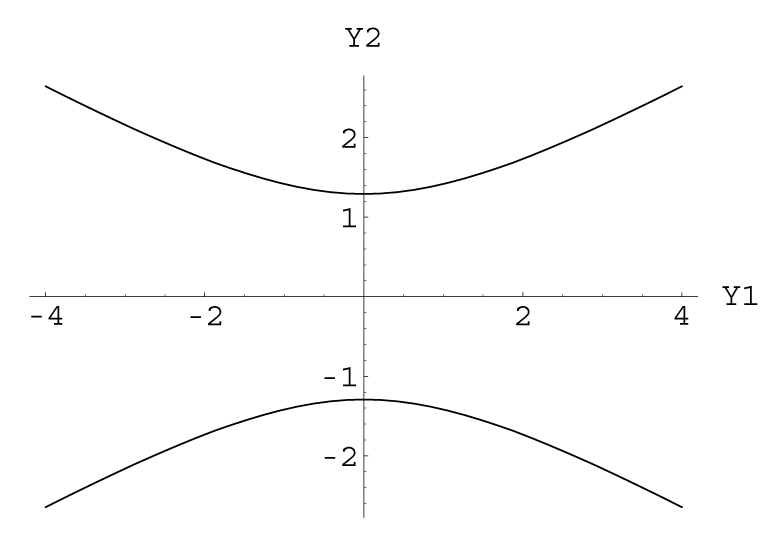
Ο άξονας $Y_{1}$ , δηλ. τα σημεία του ${\mathbb{R}}^{2}$ που ικανοποιούν την εξίσωση $Y_{2}=0$ , είναι τα σημεία της ευθείας $x_{1}=-x_{2}$ :

y_{2}=0\Leftrightarrow\frac{1}{\sqrt{2}}(x_{1}+x_{2})=0\Leftrightarrow x_{1}=-% x_{2}\ .

Αντίστοιχα ο άξονας $Y_{2}$ είναι η ευθεία $x_{1}=x_{2}$ :

\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y_{1}=0\Leftrightarrow\frac{% 1}{\sqrt{2}}(-x_{1}+x_{2})=0\Leftrightarrow x_{1}=x_{2}.\;\;\;\;\;\;\;\;\;\;\;% \;\;\;\;\;\;\;\;\;\;\;\;\;\;\Box

Επομένως για τη γραφική παράσταση της καμπύλης ως προς τους άξονες $X_{1}$ και $X_{2}$ πρέπει να περιστρέψουμε το σχήμα δεξιόστροφα κατά γωνία $\pi/4$ :

Σχήμα 6.8:Η καμπύλη $x_{1}^{2} + 4 x_{1} x_{2} + x_{2}^{2} - 5 = 0$ .

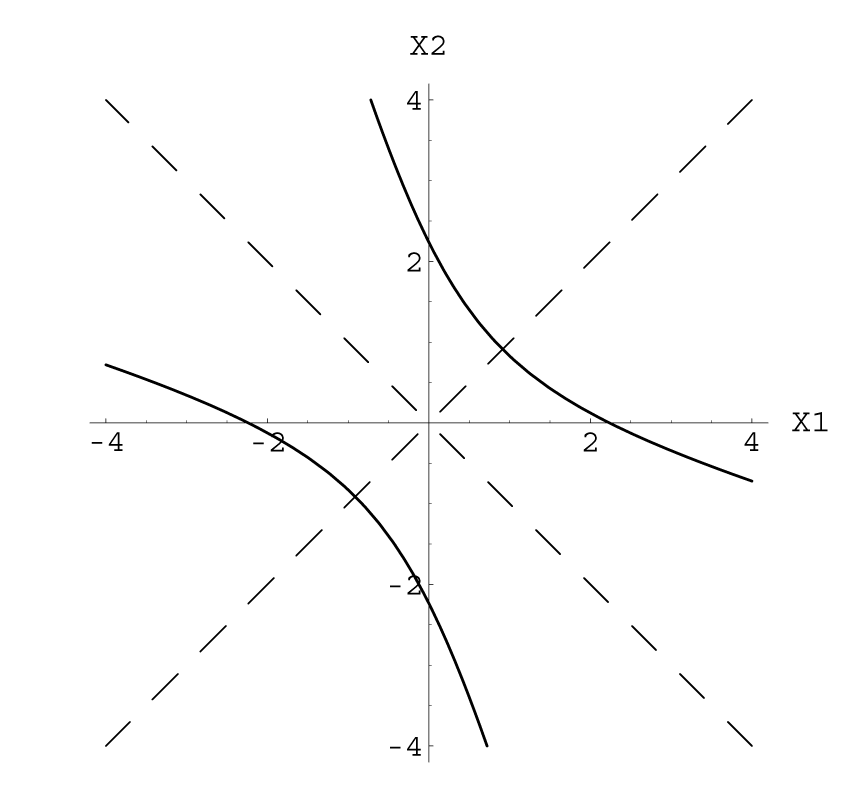
Παρατηρούμε ότι μία καμπύλη στο πραγματικό επίπεδο της μορφής

a_{1}y_{1}^{2}+a_{2}y^{2}=c,

όπου $c>0$ , εμπίπτει σε μία ακριβώς από τις παρακάτω κατηγορίες:

•

έλλειψη, όταν ta $a_{1},a_{2}$ έχουν το ίδιο πρόσημο,
•

υπερβολή, όταν ta $a_{1},a_{2}$ έχουν διαφορετικό πρόσημο.

Από την ανάλυση που κάναμε παραπάνω, μπορεί κανείς να δεί ότι μία καμπύλη στο επίπεδο με εξίσωση

q(x_{1},x_{2})-\gamma=0,

όπου $q(x_{1},x_{2})$ είναι τετραγωνική μορφή, θα ανήκει σε μία από τις δύο κατηγορίες, (ανάλογα με τα πρόσημα των ιδιοτιμών):

i.

έλλειψη, όταν οι ιδιοτιμές έχουν το ίδιο πρόσημο, ή
ii.

υπερβολή, όταν οι ιδιοτιμές έχουν διαφορετικά πρόσημα

Για περισσότερα επί κωνικών μορφών παραπέμπουμε τον αναγνώστη στην αντίστοιχη ιστοσελίδα της wikipedia.

Μέθοδος των Ελαχίστων Τετραγώνων

Θα χρησιμοποιήσουμε τη θεωρία της Ενότητας 6.1 για να βρούμε τη βέλτιστη προσέγγιση λύσης ενός μη συμβατού γραμμικού συστ'ήματος. Θυμίζουμε ότι αν $A\in M_{m\times n}({\mathbb{R}})$ , και $E\in M_{m\times 1}({\mathbb{R}})$ , τότε το σύστημα $AX=E$ είναι συμβατό αν και μόνο αν το $E$ ανήκει στον $\Sigma(A)$ , τον χώρο στηλών του $A$ , βλ. Πρόταση 3.2.9. Για την απλούστευση των συμβολισμών, θα χρησιμοποιήσουμε το ίδιο σύμβολο για την στήλη $E=\begin{bmatrix}c_{1}&\cdots&c_{m}\end{bmatrix}^{T}$ και για το διάνυσμα $E=(c_{1},\ldots,c_{m})$ . Έστω $v_{1},\ldots,v_{n}$ τα διανύσματα που αντιστοιχούν στις στήλες του $Α$ και έστω ότι το σύστημα $AX=E$ δεν είναι συμβατό. Αφού $E\notin\Sigma(A)$ , επιθυμούμε την «καλύτερη» μη λύση. Θέλουμε λοιπόν να βρούμε το στοιχείο του $\Sigma(A)$ που βρίσκεται πλησιέστερα του $E$ , δηλ. την προβολή $\operatorname{proj}_{\Sigma(A)}(E)$ . Ισοδύναμα, θέλουμε να υπολογίσουμε ta $z_{1},\ldots,z_{n}\in{\mathbb{R}}$ για τα οποία

\operatorname{proj}_{\Sigma(A)}(E)=z_{1}v_{1}+\cdots+z_{n}v_{n}.~{}

Σύμφωνα με τον Αλγόριθμο 6.1.3, το διάνυσμα $(z_{1},\ldots,z_{n})$ , για την προβολή του $E$ στον $\Sigma(A)$ , προκύπτει ως λύση του συστήματος

(A^{T}A)X=A^{T}Ε\ .

Ονομάζουμε τη λύση $(z_{1},\ldots,z_{n})$ βέλτιστη προσεγγιστική λύση (best approximation) του $AX=E$ . Η απόκλιση (το λάθος) είναι το μήκος της διαφοράς $E-\operatorname{proj}_{\Sigma(A)}(E)$ . Έτσι αν απόκλιση $\operatorname{proj}_{\Sigma(A)}(E)=(p_{1},\ldots,p_{m})$ τότε η απόκλιση είναι ίση με

\|E-\operatorname{proj}_{\Sigma(A)}(E)\|=\sqrt{(c_{1}-p_{1})^{2}+\cdots+(c_{m}% -p_{m})^{2}},

και για αυτό, η μέθοδος αυτή ονομάζεται μέθοδος των ελαχίστων τετραγώνων (method of least squares). Αποδείξαμε λοιπόν την παρακάτω πρόταση.

Πρόταση 6.2.11.

Έστω $AX=Ε$ ένα γραμμικό σύστημα, όπου $A\in M_{m\times n}({\mathbb{R}})$ και $Ε\in M_{m\times 1}({\mathbb{R}})$ . Τότε κάθε λύση του συστήματος

(A^{T}A)X=A^{T}Ε

είναι βέλτιστη προσεγγιστική λύση του $AX=B$ .

Παραδείγματα 6.2.12.

1.

Το σύστημα

$\begin{array}[]{rrc}x_{1}\;\;+&x_{2}\;=&1\\ 2x_{1}\;\;+&2x_{2}\;=&1\end{array}$

δεν έχει λύση. Έστω

$Α=\begin{bmatrix}1&1\cr 2&2\end{bmatrix},Ε=\begin{bmatrix}1\cr 1\end{bmatrix}\ .$
Τότε

$Α^{Τ}Α=\left[\begin{array}[]{cc}5&5\\ 5&5\end{array}\right],\hbox{και}A^{T}Ε=\left[\begin{array}[]{c}3\\ 3\end{array}\right]\ .$
Οι λύσεις του $(A^{T}A)X=A^{T}Ε$ είναι το σύνολο:

$\{(\frac{3}{5},0)+t(-1,1):\ t\in{\mathbb{R}}\}\ .$
Κάθε ένα από τα στοιχεία αυτού του συνόλου είναι βέλτιστη προσεγγιστική λύση του $AX=Ε$ . Μία συγκεκριμένη λύση είναι $(\frac{3}{5},0)$ . Για αυτήν τη λύση (όπως και για κάθε άλλη βέλτιστη προσεγγιστική λύση) έχουμε ότι

$A\begin{bmatrix}3/5\cr 0\end{bmatrix}=\begin{bmatrix}3/5\cr 6/5\end{bmatrix}% \neq\begin{bmatrix}1\cr 1\end{bmatrix}$
και η απόκλιση είναι $\sqrt{(2/5)^{2}+(-1/5)^{2}}=\sqrt{1/5}$ .
2.

Έστω τα σημεία $(1,1)$ , $(2,2)$ , $(3,4)$ . Είναι εύκολο να δει κανείς ότι δεν υπάρχει ευθεία $y=a_{0}+a_{1}x$ που να περνά και από τα τρία σημεία και το σύστημα

$\begin{array}[]{rrc}a_{0}\;\;+&a_{1}\;=&1\\ a_{0}\;\;+&2a_{1}\;=&2\\ a_{0}\;\;+&3a_{1}\;=&4\end{array}$
δεν έχει λύση. H βέλτιστη προσεγγιστική λύση του παραπάνω συστήματος καθορίζει την ευθεία ελαχίστων τετραγώνων (line of best fit) αυτών των σημείων. Έχουμε ότι

$Α=\left[\begin{array}[]{rr}1&1\\ 1&2\\ 1&3\end{array}\right],\;\;\;E=\left[\begin{array}[]{r}1\\ 2\\ 4\end{array}\right],\;\;A^{T}A=\left[\begin{array}[]{rc}3&6\\ 6&14\end{array}\right],\;\;A^{T}Ε=\left[\begin{array}[]{c}7\\ 17\end{array}\right].$
Επιλύουμε το σύστημα $(A^{T}A)X=A^{T}Ε$ . Η λύση αυτού του συστήματος είναι η $(-2/3,3/2)$ . Η ευθεία ελαχίστων τετραγώνων είναι η

$y=\displaystyle-\frac{2}{3}+\;\frac{3}{2}\;x\ .$
Παρατηρούμε ότι

$Α\begin{bmatrix}-\frac{2}{3}\cr\ \ \frac{3}{2}\end{bmatrix}=\frac{1}{6}\begin{% bmatrix}{5}\cr{14}\cr{23}\end{bmatrix}\neq\left[\begin{array}[]{r}1\\ 2\\ 4\end{array}\right]\;.$
Η απόκλιση είναι ίση με

$\sqrt{(1/6)^{2}+(-1/3)^{2}+(1/6)^{2}}=\sqrt{1/6}\ .$

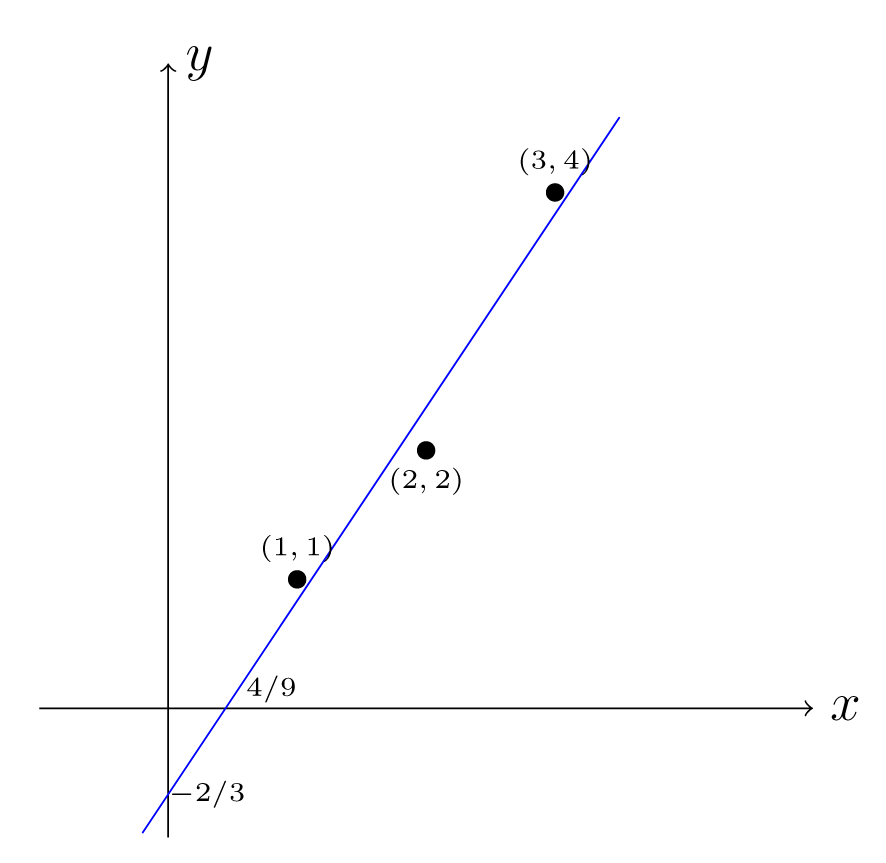
Σχήμα 6.9: H ευθεία ελαχίστων τετραγώνων $y=-\frac{2}{3}+\frac{3}{2}x$ .

Ασκήσεις Ενότητας 6.2

1.

Να υπολογίσετε τον πίνακα $A^{100}$ , όπου

$A=\begin{bmatrix}1&1&0\\ 0&i&2\cr 0&0&0\end{bmatrix}.$

Λύση
2.

Να αποδείξετε ότι αν $T:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι ισομετρία και $T({\bf 0})={\bf 0}$ , τότε

$T(cu)=cT(u),\textrm{gia}c\in{\mathbb{R}},u\in{\mathbb{R}}^{n}.$

Λύση
3.

Να βρείτε τον τύπο του γεωμετρικού μετασχηματισμού $T:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ , που προκύπτει ως η σύνθεση a) της αριστερόστροφης περιστροφής κατά $\pi/2$ , b) της συστολής του άξονα των $X$ κατά $1/2$ και g) της μεταφοράς κατά $(2,1)$ . Να σχεδιάσετε την απεικόνιση του μοναδιαίου τετραγώνου. Θα είχε διαφορά στην εικόνα μας αν κάναμε πρώτα τη μεταφορά;

Λύση
4.

Έστω ότι o πίνακας που αντιστοιχεί σε ένα πληθυσμιακό μοντέλο κυνηγού και λείας είναι

$\left[\begin{array}[]{cc}0.55&0.005\cr-18&1.2\end{array}\right].$
Να αποφασίσετε αν θα επιτευχθεί ισορροπία στο σύστημα και σε ποια τιμή.

Λύση
5.

Έστω ότι o πίνακας μετάβασης μίας Μαρκοβιανής αλυσίδας (δύο καταστάσεων) είναι o παρακάτω πίνακας:

$P=\left[\begin{array}[]{cc}0.70&0.23\cr 0.38&0.77\end{array}\right].$
Να βρείτε την οριακή τιμή του $P^{m}$ . Εάν σε κάποια φάση η κατανομή των πιθανοτήτων περιγράφεται από ton $\begin{bmatrix}0.4&0.6\end{bmatrix}$ , να προσεγγίσετε την κατανομή μετά από $100$ φάσεις.
6.

Να λυθεί το σύστημα των διαφορικών εξισώσεων

$\begin{array}[]{crcccc}f_{1}^{\prime}(x)\;\;=&3f_{1}(x)&+&2f_{2}(x)&+&2f_{3}(x% )\\ f_{2}^{\prime}(x)\;\;=&f_{1}(x)&+&4f_{2}(x)&+&2f_{3}(x)\\ f_{3}^{\prime}(x)\;\;=&-f_{1}(x)&-&2f_{2}(x)&&\end{array},$
αν $f_{1}(0)=1$ , $f_{2}(0)=-1$ και $f_{3}(0)=1$ .

Λύση
7.

Να βρείτε το είδος της καμπύλης που περιγράφεται από την εξίσωση $5x^{2}-4xy+8y^{2}=1$ .

Λύση
8.

Να βρείτε μία βέλτιστη προσεγγιστική λύση του συστήματος

$\begin{array}[]{lr}2x+\ \,5y+\ \,z=&1\cr 4x+10y+3z=&2\cr 6x+15y+4z=&2\end{% array}.$

Λύση
9.

Να βρείτε την ευθεία των ελαχίστων τετραγώνων για τα σημεία $(1,1),(2,2),(3,4),(4,5)$ .

Λύση

6.3 Σύντομα Ιστορικά Στοιχεία

Όπως είδαμε στα προηγούμενα κεφάλαια, οι εφαρμογές των ελαχίστων τετραγώνων και των τετραγωνικών μορφών υπήρξαν η κινητήριος δύναμη τον 19ο αιώνα για την ανάπτυξη της θεωρίας των ιδιοτιμών και των ιδιοχώρων συναρτήσεων από κορυφαίους μαθηματικούς της εποχής τους, όπως οι Gauss, Fourier, Cachy και άλλοι. To μοντέλο του κυνηγού και της λείας του, γνωστό και ως μοντέλο των Lotka - Volterra πρωτοεισήχθη από τον Lotka το 1925 στο βιβλίο του πάνω στα βιομαθηματικά, αρχικά μελετώντας οργανικά συστήματα με φυτά ως το θήραμα και φυτοφάγα ζώα ως τον κυνηγό. O Volterra ανεξάρτητα, παρουσίασε το ίδιο μοντέλο το 1926, μελετώντας τις αλλαγές στον πληθυσμό των ψαριών στην Αδριατική θάλασσα. To μοντέλο αυτό έχει χρησιμοποιηθεί για να μελετηθεί και προγραμματιστεί η αναπαραγωγή των αλκών και λύκων στο Βασιλικό Εθνικό Πάρκο στο νησί Isle, στο Michigan Ηνωμένων Πολιτειών. Οι Μαρκοβιανές αλυσίδες οφείλουν το όνομά τους στον Ρώσο μαθηματικό Andey Markov, o οποίος δούλεψε πάνω σε τέτοια προβλήματα στις αρχές του 20ου αιώνα.

Βιβλιογραφία

1.

H. Anton, C. Rorres, Elementary Linear Algebra, Applications Version, John Wiley and Sons, 1994.
2.

Θ. Θεοχάρη-Αποστολίδη, Χ. Χαραλάμπους, Β. Βαβατσούλας, Εισαγωγή στη Γραμμική Άλγεβρα, Θεσσαλονίκη 2006.
3.

V. Katz, Ιστορία των Μαθηματικών, Πανεπιστημιακές Εκδόσεις Κρήτης, 2013.
4.

F. Lin, K. Wyrwas, J. Irwin, C. Lilley, W.T. Hewitt, T.L.J. Howard, Geometry for Computer Graphics, Student Notes, The University of Manchester
5.

K. Nicholoson, Elementary Linear Algebra, McGraw-Hill, 2001.
6.

L.R. Rabiner, B.H. Juang, An Introduction to Hidden Markov Models,1986.
7.

Th. Shiffrin and M. R.Adams, Linear Alegbra, a Geometric Approach, W.H. Freeman and Company,2002.

	$\displaystyle f_{1}^{\prime}(x)$	$\displaystyle=3f_{1}(x)$
	$\displaystyle f_{2}^{\prime}(x)$	$\displaystyle=4f_{2}(x)$

	$\displaystyle f_{1}(x)$	$\displaystyle=2e^{3x}$
	$\displaystyle f_{2}(x)$	$\displaystyle=-e^{4x}\;.$

	$\displaystyle f_{1}^{\prime}(x)$	$\displaystyle=2f_{1}(x)-f_{2}(x)$
	$\displaystyle f_{2}^{\prime}(x)$	$\displaystyle=6f_{1}(x)-f_{2}(x).$

	$\displaystyle g_{1}^{\prime}(x)$	$\displaystyle=\ \ \ g_{1}(x)$
	$\displaystyle g_{2}^{\prime}(x)$	$\displaystyle=-4g_{2}(x).$

	$\displaystyle 2$	$\displaystyle=C_{1}+C_{2}$
	$\displaystyle-3$	$\displaystyle=C_{1}+6C_{2}$