Μια Εισαγωγή στη Γραμμική Άλγεβρα για τις Θετικές Επιστήμες

Κεφάλαιο 1Γραμμικά Συστήματα

Η επίλυση των γραμμικών συστημάτων αποτελεί ένα από τα κύρια θέματα μελέτης της Γραμμικής Άλγεβρας. Σε αυτό το κεφάλαιο θα μελετήσουμε τις βασικές τεχνικές επίλυσης των γραμμικών συστημάτων.

1.1 Γραμμικά Συστήματα

Σε αυτήν την ενότητα θα εισάγουμε τη βασική ορολογία που αφορά τα γραμμικά συστήματα εξισώσεων. Με $\Bbbk$ θα συμβολίζουμε είτε το σώμα των πραγματικών αριθμών $\mathbb{R}$ , είτε το σώμα των μιγαδικών αριθμών $\mathbb{C}$ . Ένα γραμμικό σύστημα (linear system) $m$ εξισώσεων με $n$ αγνώστους, με συντελεστές από το σώμα $\Bbbk$ , είναι ένα σύστημα γραμμικών εξισώσεων

\begin{matrix}\alpha_{11}\;x_{1}+\alpha_{12}\;x_{2}+\cdots+\alpha_{1n}\;x_{n}&% =\beta_{1}\\ \;\;\vdots&\vdots\cr\alpha_{m1}x_{1}+\alpha_{m2}x_{2}+\cdots+\alpha_{mn}x_{n}&% =\beta_{m},\end{matrix}

(1.1.0.1)

όπου όλοι οι συντελεστές $a_{ij}$ και όλες οι σταθερές $\beta_{i}$ ανήκουν στο $\Bbbk$ . Το $i$ παίρνει τιμές $1,\ldots,m$ , ενώ το $j$ παίρνει τιμές $1,\ldots,n$ . Τα $x_{1},\ldots,x_{n}$ είναι οι άγνωστοι του γραμμικού συστήματος. Λύση (solution) του συστήματος (1.1.0.1) στο $\Bbbk$ είναι μία διατεταγμένη $n$ -άδα $(\xi_{1},\xi_{2},\ldots,\xi_{n})$ στοιχείων του $\Bbbk$ , η οποία ικανοποιεί τις εξισώσεις (1.1.0.1), δηλ.

\alpha_{i1}\xi_{1}+\cdots+\alpha_{in}\xi_{n}=\beta_{i}\;,\;\;\;\;\text{ για κά% θε }1\leq i\leq m.

Ένα γραμμικό σύστημα είναι δυνατόν να έχει περισσότερες από μία λύσεις. Λέμε ότι το σύστημα (1.1.0.1) είναι συμβατό (consistent) αν έχει τουλάχιστον μία λύση. Αν δεν υπάρχει λύση, τότε λέμε ότι το σύστημα (1.1.0.1) είναι ασύμβατο (inconsistent).

Στη γλώσσα των πινάκων, το σύστημα (1.1.0.1) γράφεται συνοπτικά ως

AX=B,

(1.1.0.2)

όπου

A=\left[\begin{array}[]{ccc}\alpha_{11}&\cdots&\alpha_{1n}\\ \vdots&&\vdots\\ \alpha_{m1}&\cdots&\alpha_{mn}\end{array}\right],\;\;\;X=\left[\begin{array}[]% {c}x_{1}\\ \vdots\\ x_{n}\end{array}\right]\;\;\;\hbox{και}\;\;\;B=\left[\begin{array}[]{c}\beta_{% 1}\\ \vdots\\ \beta_{m}\end{array}\right].

O πίνακας $A$ έχει $m$ γραμμές, όσες και οι εξισώσεις του (1.1.0.1), και $n$ στήλες, όσοι είναι οι άγνωστοι του (1.1.0.1). Ο $Α$ γράφεται σε συντομογραφία $A=(a_{ij})$ και λέγεται πίνακας των συντελεστών (coefficient matrix) του συστήματος (1.1.0.2), ο πίνακας $B$ λέγεται πίνακας των σταθερών όρων (column of constants) του συστήματος (1.1.0.2), ενώ ο πίνακας

[A\ |\ B]=\left[\begin{array}[]{cccc}\alpha_{11}&\cdots&\alpha_{1n}&\beta_{1}% \\ \vdots&&\vdots&\vdots\\ \alpha_{m1}&\cdots&\alpha_{mn}&\beta_{m}\end{array}\right]

λέγεται επαυξημένος (extended) πίνακας του συστήματος (1.1.0.2). Θα γράφουμε τον επαυξημένο πίνακα $[A\ |\ B]$ και ως

[A\ |\ B]=\left[\begin{array}[]{ccc|c}\alpha_{11}&\cdots&\alpha_{1n}&\beta_{1}% \\ \vdots&&\vdots&\vdots\\ \alpha_{m1}&\cdots&\alpha_{mn}&\beta_{m}\end{array}\right],

για να τονίσουμε ότι η τελευταία στήλη είναι η στήλη των σταθερών όρων του συστήματος $AX=B$ . H $j$ στήλη του $Α$ συμβολίζεται με $\Sigma_{j}$ και αντιστοιχεί στη μεταβλητή $x_{j}$ . Τα στοιχεία της $\Sigma_{j}$ είναι οι συντελεστές του $x_{j}$ .

Παραδείγματα 1.1.1.

1.

Έστω το γραμμικό σύστημα

$\begin{array}[]{rcrcrcrcrcl}x_{1}&-&2x_{2}&&&&&+&4x_{5}&=&0\\ -x_{1}&+&2x_{2}&+&x_{3}&&&-&5x_{5}&=&0\\ -2x_{1}&+&4x_{2}&-&3x_{3}&+&x_{4}&-&2x_{5}&=&0\\ 3x_{1}&-&6x_{2}&+&4x_{3}&-&2x_{4}&+&2x_{5}&=&0\end{array},$ (1.1.1.1)
4 εξισώσεων με 5 αγνώστους, με συντελεστές από το ${\mathbb{R}}$ . Ο πίνακας των συντελεστών του συστήματος (1.1.1.1) είναι

$\left[\begin{array}[]{rrrrr}1&-2&0&0&4\\ -1&2&1&0&-5\\ -2&4&-3&1&-2\\ 3&-6&4&-2&2\end{array}\right],$
ενώ ο επαυξημένος πίνακας είναι

$\left[\begin{array}[]{rrrrrrr}1&-2&0&0&4&|&0\\ -1&2&1&0&-5&|&0\\ -2&4&-3&1&-2&|&0\\ 3&-6&4&-2&2&|&0\end{array}\right].\$
Το σύστημα (1.1.1.1) είναι συμβατό, αφού η 5-άδα $(0,0,0,0,0)$ ικανοποιεί κάθε μία από τις 4 εξισώσεις του (1.1.1.1). Μία άλλη λύση του συστήματος είναι το στοιχείο $(2,1,0,0,0)$ του ${\mathbb{R}}^{5}$ . Ο αναγνώστης μπορεί να επιβεβαιώσει ότι κάθε στοιχείο του ${\mathbb{R}}^{5}$ της μορφής $(2t,t,0,0,0)$ , για $t\in{\mathbb{R}}$ είναι λύση του συστήματος (1.1.1.1), αντικαθιστώντας τις τιμές $x_{1}=2t$ , $x_{2}=t$ , $x_{3}=0$ , $x_{4}=0$ , $x_{5}=0$ στις εξισώσεις του (1.1.1.1). Άρα το σύστημα (1.1.1.1) έχει άπειρες λύσεις. Η 5-άδα $(2,1,1,0,0)$ δεν είναι λύση του συστήματος (1.1.1.1), γιατί δεν ικανοποιεί τη δεύτερη εξίσωση:

$-2+2\cdot 1+1-5\cdot 0=1\neq 0.$
2.

Το γραμμικό σύστημα με επαυξημένο πίνακα τον

$\left[\begin{array}[]{rrrr}1&-1&|&1\\ 2&-2&|&0\end{array}\right]$
αντιστοιχεί στο γραμμικό σύστημα

$\begin{array}[]{rcrcrcrcrcl}x_{1}&-&x_{2}&=&1\\ 2x_{1}&-&2x_{2}&=&0\end{array}$ (1.1.1.2)
και είναι ασύμβατο όπως εύκολα μπορεί να επιβεβαιωθεί. Πράγματι, αν $(\xi_{1},\xi_{2})$ ήταν λύση του συστήματος (1.1.1.2), τότε σύμφωνα με την πρώτη εξίσωση $\xi_{1}=1+\xi_{2}$ , ενώ σύμφωνα με τη δεύτερη εξίσωση $2\xi_{1}=2\xi_{2}$ και $\xi_{1}=\xi_{2}$ . Συνδυάζοντας τις δύο εκφράσεις για το $\xi_{1}$ βλέπουμε ότι $\xi_{1}=1+\xi_{1}$ , άρα $0=1$ που είναι αδύνατον. Καταλήξαμε σε άτοπο γιατί υποθέσαμε ότι $(\xi_{1},\xi_{2})$ ήταν λύση του συστήματος (1.1.1.2). Άρα το σύστημα (1.1.1.2) δεν έχει λύση και είναι ασύμβατο.
3.

Έστω ότι ο επαυξημένος πίνακας ενός γραμμικού συστήματος είναι

$\left[\begin{array}[]{rrrrrrr}1&-2&0&0&4&|&0\\ -1&2&1&0&-5&|&0\\ -2&4&-3&1&-2&|&0\\ 0&0&0&0&0&|&1\end{array}\right].\$
Η τελευταία γραμμή του παραπάνω πίνακα αντιστοιχεί στην εξίσωση

$0\ x_{1}+0\ x_{2}+0\ x_{3}+0\ x_{4}=1,$
που δεν έχει λύση, αφού είναι αδύνατον να ισχύει $0=1$ . Άρα το γραμμικό σύστημα με τον παραπάνω επαυξημένο πίνακα είναι ασύμβατο. Γενικότερα, αν ο επαυξημένος πίνακας $[A\ |\ B]$ του γραμμικού συστήματος $AX=B$ έχει μία γραμμή της μορφής

$[\begin{array}[]{rrrrrr}0&0&\cdots&0&|&t\end{array}],\$
για κάποια σταθερά $t\neq 0$ , τότε το γραμμικό σύστημα είναι ασύμβατο.

Έστω ότι σε κάποιο γραμμικό σύστημα εξισώσεων αλλάζουμε τη θέση των εξισώσεων $i$ και $j$ . Στο νέο γραμμικό σύστημα η $i$ εξίσωση είναι η $j$ του αρχικού συστήματος και αντίστοιχα η $j$ εξίσωση του νέου συστήματος είναι η $i$ εξίσωση του αρχικού. Είναι ξεκάθαρο ότι το νέο γραμμικό σύστημα έχει ακριβώς τις ίδιες λύσεις όπως το αρχικό σύστημα. Ο επαυξημένος πίνακας του καινούριου συστήματος προκύπτει από τον επαυξημένο πίνακα του συστήματος (1.1.0.1) αντιμεταθέτοντας τις γραμμές $i$ και $j$ .

Στη συνέχεια εξετάζουμε πως επηρεάζονται οι λύσεις του συστήματος (1.1.0.1) αν πολλαπλασιάσουμε την $i$ εξίσωση με κάποιο μη μηδενικό στοιχείο $c$ του σώματος $\Bbbk$ . Το νέο σύστημα γραμμικών εξισώσεων διαφέρει από το παλιό μόνο στην $i$ εξίσωση. Δηλαδή η $i$ εξίσωση του συστήματος (1.1.0.1) είναι

\alpha_{i1}x_{1}+\cdots+\alpha_{in}x_{n}=\beta_{i}\ ,

(1.1.1.3)

ενώ η $i$ εξίσωση του καινούριου συστήματος είναι

(c\alpha_{i1})x_{1}+\cdots+(c\alpha_{in})x_{n}=c\beta_{i}\ .

(1.1.1.4)

Έτσι αν $(\xi_{1},\xi_{2},\ldots,\xi_{n})$ ικανοποιεί την εξίσωση (1.1.1.3) τότε

\alpha_{i1}\xi_{1}+\cdots+\alpha_{in}\xi_{n}=\beta_{i}\Rightarrow c(\alpha_{i1% }\xi_{1}+\cdots+c\alpha_{in}\xi_{n})=c\beta_{i}\Rightarrow\\ (c\alpha_{i1})\xi_{1}+\cdots+(c\alpha_{in})\xi_{n}=c\beta_{i},

(1.1.1.5)

δηλ. $(\xi_{1},\xi_{2},\ldots,\xi_{n})$ είναι λύση της εξίσωσης (1.1.1.4). To αντίστροφο αποδεικνύεται ακριβώς με τον ίδιο τρόπο, αφού η εξίσωση (1.1.1.3) προέρχεται από την εξίσωση (1.1.1.4) πολλαπλασιάζοντας την τελευταία με $c^{-1}$ . Εύκολα, λοιπόν, προκύπτει ότι οι λύσεις των δύο συστημάτων είναι ακριβώς οι ίδιες. Παρατηρούμε ότι ο επαυξημένος πίνακας του νέου συστήματος προκύπτει από τον αρχικό πίνακα αν πολλαπλασιάσουμε τα στοιχεία της $i$ γραμμής με $κ$ .

Τέλος, αν στην $i$ εξίσωση του συστήματος (1.1.0.1) προσθέσουμε $κ$ φορές την $l$ εξίσωση του συστήματος (1.1.0.1), προκύπτει ένα νέο σύστημα που διαφέρει από το παλιό μόνο στην $i$ εξίσωση. Έτσι τώρα η εξίσωση γίνεται

\ (\alpha_{i1}+κ\alpha_{l1})x_{1}+\cdots+(\alpha_{in}+k\alpha_{ln})x_{n}=\beta% _{i}+k\beta_{l}.

(1.1.1.6)

Και πάλι τα δύο συστήματα έχουν ακριβώς τις ίδιες λύσεις. Πράγματι, αν $\xi=(\xi_{1},\ldots,\xi_{n})$ είναι λύση του συστήματος (1.1.0.1), αρκεί να βεβαιώσουμε ότι η $\xi$ ικανοποιεί την $i$ εξίσωση του νέου συστήματος, αφού ήδη ικανοποιεί όλες τις άλλες. Αφού όμως η $\xi$ ικανοποιεί τις $i$ και $l$ εξισώσεις του συστήματος (1.1.0.1), ισχύει ότι

\alpha_{i1}\xi_{1}+\cdots+\alpha_{in}\xi_{n}=\beta_{i}\

(1.1.1.7)

και

\alpha_{l1}\xi_{1}+\cdots+\alpha_{ln}\xi_{n}=\beta_{l}.

(1.1.1.8)

Πολλαπλασιάζοντας τη σχέση (1.1.1.8) με $k$ προκύπτει ότι

κ\alpha_{l1}\xi_{1}+\cdots+κ\alpha_{ln}\xi_{n}=κ\beta_{l}.\

(1.1.1.9)

Προσθέτοντας τις σχέσεις (1.1.1.7) και (1.1.1.9), βρίσκουμε ότι

(\alpha_{i1}+κ\alpha_{l1})\xi_{1}+\cdots+(\alpha_{in}+κ\alpha_{ln})\xi_{n}=% \beta_{i}+κ\beta_{l},

δηλ. ικανοποιείται η (1.1.1.6). Για το αντίστροφο, δηλαδή για να δείξουμε ότι μία λύση του νέου συστήματος είναι και λύση του συστήματος (1.1.0.1), αρκεί να παρατηρήσουμε ότι από το νέο σύστημα μπορούμε να πάμε πίσω στο σύστημα (1.1.0.1), αφαιρώντας από την $i$ εξίσωση, $k$ φορές την $λ$ εξίσωση. Επομένως, το ζητούμενο προκύπτει από όσα είδαμε προηγουμένως. Συγκεντρώνουμε τις παρατηρήσεις μας στην επόμενη πρόταση.

Πρόταση 1.1.2.

Έστω $ΑX=B$ ένα γραμμικό σύστημα με συντελεστές από το $\Bbbk$ . Αν ο πίνακας $[Α^{\prime}|B^{\prime}]$ προκύπτει από τον πίνακα $[A|B]$ με οποιαδήποτε από τις επόμενες τρεις ενέργειες:

•

αντιμετάθεση δύο γραμμών του $[A|B]$ ,
•

πολλαπλασιασμό μίας γραμμής του $[A|B]$ με κάποιο μη μηδενικό στοιχείο του $\Bbbk$ ,
•

άθροισμα μίας γραμμής του $[A|B]$ με πολλαπλάσιο μίας άλλης γραμμής του $[A|B]$ ,

τότε το γραμμικό σύστημα $A^{\prime}X=B^{\prime}$ έχει ακριβώς τις ίδιες λύσεις με το σύστημα $AX=B$ .

Όταν όλες οι σταθερές στον πίνακα $Β$ είναι ίσες με 0, τότε γράφουμε $Β=\bf{0}$ και καλούμε το σύστημα $AX=\bf{0}$ ομογενές (homogeneous). Το σύστημα $AX=\bf{0}$ είναι συμβατό για οποιοδήποτε πίνακα $A$ , αφού το $(0,\ldots,0)$ είναι λύση. Σημειώνουμε μία ενδιαφέρουσα ιδιότητα των ομογενών συστημάτων:

Πρόταση 1.1.3.

Έστω το ομογενές σύστημα $AX=\bf{0}$ με συντελεστές από το σώμα $\Bbbk$ με λύσεις $v_{1}=(p_{1},\ldots,p_{n})$ , $v_{2}=(q_{1},\ldots,q_{n})$ . Τότε $\kappa v_{1}+\lambda v_{2}$ είναι λύση του $AX=\bf{0}$ , για $\kappa,\lambda\in\Bbbk$ .

Απόδειξη.

Έστω ότι η $i$ εξίσωση του συστήματος $AX={\bf 0}$ είναι $\alpha_{i1}\;x_{1}+\alpha_{i2}\;x_{2}+\cdots+\alpha_{in}\;x_{n}=0\ .$ Παρατηρούμε ότι $\kappa v_{1}+\lambda v_{2}=(kp_{1}+tq_{1},\ldots,kp_{n}+tq_{n})$ . Για να δείξουμε, λοιπόν, ότι $\kappa v_{1}+\lambda v_{2}$ είναι λύση του συστήματος $AX=\bf{0}$ , αρκεί να δείξουμε ότι $\alpha_{i1}\;(\kappa p_{1}+tq_{1})+\cdots+\alpha_{in}\;(\kappa p_{n}+\lambda q% _{n})=0\ .$ Όμως, $\alpha_{i1}\;p_{1}+\cdots+\alpha_{in}\;p_{n}=0\ \textrm{ και }\alpha_{i1}\;q_{% 1}+\cdots+\alpha_{in}\;q_{n}=0.$ Επομένως $\kappa\alpha_{i1}\;p_{1}+\cdots+\kappa\alpha_{in}\;p_{n}=0\ \textrm{ και }% \lambda\alpha_{i1}\;q_{1}+\cdots+\lambda\alpha_{in}\;q_{n}=0.$ Προσθέτοντας τις δύο εξισώσεις προκύπτει ότι:

(\kappa\alpha_{i1}\;p_{1}+\cdots+\kappa\alpha_{in}\;p_{n})+(\lambda\alpha_{i1}% \;q_{1}+\cdots+\lambda\alpha_{in}\;q_{n})=0\Rightarrow\\ (\kappa\alpha_{i1}\;p_{1}+\lambda\alpha_{i1}\;q_{1})+\cdots+(\kappa\alpha_{in}% \;p_{n}+\lambda\alpha_{in}\;q_{n})=0\Rightarrow\\ \alpha_{i1}\;(\kappa p_{1}+\lambda q_{1})+\cdots+\alpha_{in}\;(\kappa p_{n}+% \lambda q_{n})=0.

(1.1.3.1)

Επομένως $\kappa v_{1}+\lambda v_{2}$ είναι λύση του $AX=\bf{0}$ . ∎

Λέμε ότι ο συνδυασμός $\kappa v_{1}+\lambda v_{2}$ είναι γραμμικός συνδυασμός (linear combination) των $v_{1}$ και $v_{2}$ με συντελεστές $\kappa,\lambda\in\Bbbk$ .Παρατηρούμε ότι σύμφωνα με την Πρόταση 1.1.3 αν $v\neq(0,\ldots,0)$ είναι λύση του $A\,X=\bf 0$ , τότε $\kappa v$ είναι λύση του $A\,X=\bf 0$ για $\kappa\in\Bbbk$ . Επομένως ισχύει η επόμενη παρατήρηση.

Αν το σύστημα

A\,X=\bf 0

έχει μία μη μηδενική λύση, τότε

A\,X=\bf 0

έχει άπειρες λύσεις.

Ασκήσεις Ενότητας 1.1

1.

Να βρείτε τους επαυξημένους πίνακες των συστημάτων:

$\begin{array}[]{lrcrcrcl}{\rm i)}&x&+&y&+&z&=&0\\ &x&+&2y&-&z&=&0\\ &2x&+&3y&&&=&0\end{array}$ , $\;\;\;\;\begin{array}[]{lrcrcrcl}{\rm ii)}&x&+&y&+&z&=&1\\ &x&+&2y&-&z&=&2\\ &2x&+&3y&&&=&0\end{array}$ ,
$\begin{array}[]{lrcrcrcl}{\rm iii)}&x&-&y&+&&=&1\\ &x&+&y&-&z&=&2\end{array}$ .

Λύση
2.

Να γράyετε και να λύσετε στον ${\mathbb{R}}$ τα συστήματα με τους επόμενους επαυξημένους πίνακες.

${\rm i)}\left[\begin{array}[]{ccccc|c}0&0&1&0&0&0\\ 0&1&0&1&3&2\\ 0&3&0&0&0&1\end{array}\right]$ , $\;\;\;\;{\rm ii)}\left[\begin{array}[]{cc|r}1&2&1\\ 0&4&8\\ 1&5&-1\end{array}\right]$ .

Λύση
3.

Να βρείτε τις λύσεις του ομογενούς συστήματος $AX=0$ στον ${\mathbb{R}}$ , όταν $Α$ είναι ο μηδενικός $3\times 4$ πίνακας, δηλαδή ο πίνακας

$\left[\begin{array}[]{cccc}0&0&0&0\cr 0&0&0&0\cr 0&0&0&0\end{array}\right].$

Λύση

1.2 Στοιχειώδεις Πράξεις Γραμμών

$\;$ Σε αυτήν την ενότητα αυτή θα περιγράψουμε τον αλγόριθμο του Gauss. Ο αλγόριθμος αυτός χρησιμοποιείται προκειμένου να μεταβούμε από έναν $m\times n$ πίνακα $Α=(a_{ij})$ σε ένα νέο πίνακα με όσο το δυνατόν περισσότερα μηδενικά στοιχεία. Πρώτα θα ορίσουμε τους τρεις τύπους των στοιχειωδών πράξεων γραμμών που επιτρέπεται να χρησιμοποιούμε. Οι γραμμές του $Α$ συμβολίζονται με $\Gamma_{1},\ldots,\Gamma_{m}$ . Κάθε γραμμή του $Α$ είναι ένας $1\times n$ πίνακας. Έτσι

\Gamma_{i}=\begin{bmatrix}a_{i1}&\cdots&a_{in}\end{bmatrix},\textrm{ για }i=1,% \ldots,m.

Όταν γράφουμε $b\Gamma_{i}$ , εννοούμε ότι πολλαπλασιάζουμε όλα τα στοιχεία της γραμμής $\Gamma_{i}$ με το στοιχείο $b\in\Bbbk$ . Το αποτέλεσμα είναι ο $1\times n$ πίνακας

b\Gamma_{i}=\begin{bmatrix}ba_{i1}&\cdots&ba_{in}\end{bmatrix}.

Όταν γράφουμε $\Gamma_{i}+b\Gamma_{j}$ , εννοούμε ότι πολλαπλασιάζουμε τα στοιχεία της $\Gamma_{j}$ με το $b$ και στη συνέχεια τα προσθέτουμε στα αντίστοιχα στοιχεία της $\Gamma_{i}$ . Το αποτέλεσμα είναι ο $1\times n$ πίνακας

\Gamma_{i}+b\Gamma_{j}=\begin{bmatrix}a_{i1}+ba_{j1}&\cdots&a_{in}+ba_{jn}\end% {bmatrix}.

Ορισμός 1.2.1.

Έστω $Α=(a_{ij})$ ένας $m\times n$ πίνακας με στοιχεία από το $\Bbbk$ και $\Gamma_{1},\ldots,\Gamma_{m}$ οι γραμμές του $Α$ . Οι στοιχειώδεις πράξεις γραμμών (elementary row operations) ενός πίνακα $A$ είναι οι εξής:

τύπου 1: αντικατάσταση της γραμμής $\Gamma_{i}$ με τη γραμμή $\Gamma_{i}+a\Gamma_{j}$ , όπου $1\leq i,j\leq n$ και $a\in\Bbbk$ . Θα συμβολίζουμε τη πράξη αυτή με $\Gamma_{i}\rightarrow\Gamma_{i}+a\Gamma_{j}$ .
τύπου 2: αντιμετάθεση της γραμμής $\Gamma_{i}$ με τη γραμμή $\Gamma_{j}$ , όπου $1\leq i,j\leq n$ . Θα συμβολίζουμε τη πράξη αυτή με $\Gamma_{i}\leftrightarrow\Gamma_{j}$ .
τύπου 3: αντικατάσταση της γραμμής $\Gamma_{i}$ με τη γραμμή $b\Gamma_{i}$ , όπου $1\leq i\leq n$ και $0\neq b\in\Bbbk$ . Θα συμβολίζουμε τη πράξη αυτή με $\Gamma_{i}\rightarrow b\Gamma_{i}$ .

Στη στοιχειώδη πράξη γραμμών τύπου 1, η σειρά των δεικτών έχει μεγάλη σημασία: στη γραμμή $\Gamma_{i}$ προσθέτουμε το πολλαπλάσιο $a\Gamma_{j}$ της γραμμής $\Gamma_{j}$ . Αν το $a$ είναι μηδέν, τότε το αποτέλεσμα είναι η αρχική γραμμή $\Gamma_{i}$ . Στα επόμενα παραδείγματα, με $A\rightarrow B$ συμβολίζουμε τη μετάβαση στον πίνακα $Β$ από τον πίνακα $Α$ .

Παραδείγματα 1.2.2.

1.

$\;\;\;\;\left[\begin{array}[]{ccccc}1&0&1&3&2\\ 4&0&0&0&1\\ 0&1&1&0&0\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{2}\rightarrow\Gamma_{2}-4\Gamma_{1}}\end{array}\left[% \begin{array}[]{rrrrr}1&0&1&3&2\\ 0&0&-4&-12&-7\\ 0&1&1&0&0\end{array}\right]\begin{array}[]{c}\end{array}$ .
2.

$\;\;\;\;\left[\begin{array}[]{ccccc}1&0&1&3&2\\ 4&0&0&0&1\\ 0&1&1&0&0\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{2}\leftrightarrow\Gamma_{1}}\end{array}\left[\begin{% array}[]{rrrrr}4&0&0&0&1\\ 1&0&1&3&2\\ 0&1&1&0&0\end{array}\right]\begin{array}[]{c}\end{array}$ .
3.

$\;\;\;\;\left[\begin{array}[]{ccccc}1&0&1&3&2\\ 4&0&0&0&1\\ 0&1&1&0&0\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{3}\rightarrow 2\Gamma_{3}}\end{array}\left[\begin{% array}[]{rrrrr}1&0&1&3&2\\ 4&0&0&0&1\\ 0&2&2&0&0\end{array}\right]\begin{array}[]{c}\end{array}$ .

Λέμε ότι η γραμμή $\Gamma_{i}$ του $Α$ είναι μηδενική αν όλα τα στοιχεία της $\Gamma_{i}$ είναι μηδέν, δηλ.

\Gamma_{i}=\begin{bmatrix}0&\cdots&0\end{bmatrix}.

Στη συνέχεια προσδιορίζουμε πότε ένας πίνακας είναι σε κλιμακωτή μορφή γραμμών.

Ορισμός 1.2.3.

Ο πίνακας $A$ είναι σε κλιμακωτή μορφή γραμμών (row echelon form) αν έχει τις εξής ιδιότητες:

•

Σε κάθε γραμμή του $Α$ , το πρώτο μη μηδενικό στοιχείο, ξεκινώντας από τα αριστερά, είναι ίσο με $1$ . Ονομάζουμε το $1$ καθοδηγητική μονάδα καθοδηγητική μονάδα (leading one) της γραμμής.
•

Τα στοιχεία στην ίδια στήλη με μία καθοδηγητική μονάδα και κάτω από αυτήν, πρέπει να είναι ίσα με μηδέν.
•

Οι μηδενικές γραμμές, αν υπάρχουν, είναι οι τελευταίες γραμμές του πίνακα.

Ένας πίνακας $Α$ είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών αν

•

$A$ είναι σε κλιμακωτή μορφή γραμμών και
•

κάθε στήλη του $Α$ , με καθοδηγητική μονάδα, έχει όλα τα στοιχεία κάτω και επάνω από την καθοδηγητική μονάδα ίσα με μηδέν.

Αν o πίνακας $A$ είναι σε κλιμακωτή μορφή γραμμών, τότε η καθοδηγητική μονάδα της $\Gamma_{i}$ είναι δεξιότερα των καθοδηγητικών μονάδων των παραπάνω γραμμών, δηλ. των γραμμών $\Gamma_{j}$ , όπου $j\leq i$ . Τα επόμενα παραδείγματα αποσαφηνίζουν τις έννοιες που ορίσαμε προηγουμένως. Σε αυτά, κυκλώνουμε τις καθοδηγητικές μονάδες για να τις ξεχωρίζουμε.

Παραδείγματα 1.2.4.

1.

Ο μηδενικός $m\times n$ πίνακας $\bf 0$ , δηλ. ο $m\times n$ πίνακας που έχει όλα τα στοιχεία του ίσα με 0, είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών.
2.

Οι πίνακες

$A=\left[\begin{array}[]{cccc}0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0% pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0% }{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2&3\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture\end{array}\right]\;\;\;\hbox{και}\;\;\;C=% \left[\begin{array}[]{ccccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2&3&4&5\\ 0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2&3&0\\ 0&0&0&0&0\end{array}\right]$
είναι σε κλιμακωτή μορφή γραμμών αλλά όχι σε ελαττωμένη κλιμακωτή μορφή γραμμών.
3.

Οι πίνακες

$B=\left[\begin{array}[]{cccc}0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0% pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0% }{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2&0\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture\end{array}\right]\;\;\;\hbox{και}\;\;\;D=% \left[\begin{array}[]{ccccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&-2&6\\ 0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&3&-2\\ 0&0&0&0&0\end{array}\right]$
είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών.
4.

Οι πίνακες

$Ε=\left[\begin{array}[]{cccc}0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to% 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{% 0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}% \nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture\\ 0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2&3\end{array}\right]\;\;\;\hbox{και}\;\;% \;F=\left[\begin{array}[]{ccccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.% 0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{% 0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&3&4&5\\ 0&0&2&0&0\end{array}\right]$
δεν είναι σε κλιμακωτή μορφή γραμμών.

Ο στόχος μας είναι να φέρουμε τον πίνακα $A$ σε κλιμακωτή μορφή γραμμών. Ο στόχος αυτός πετυχαίνεται χρησιμοποιώντας τον αλγόριθμο του Gauss (Gaussian elimination algorithm).

Αλγόριθμος 1.2.1 Αλγόριθμος του Gauss

Είσοδος: Ένας

m\times n

πίνακας

Α

Έξοδος: Η ελαττωμένη κλιμακωτή μορφή του

Α

Βήμα 1 Αν ο

Α

είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών, τότε ο αλγόριθμος τερματίζει.

Βήμα 2 Βρίσκουμε την αριστερότερη μη μηδενική στήλη του

Α

Βήμα 3 Αντιμεταθέτουμε την πρώτη γραμμή με άλλη γραμμή αν χρειάζεται, έτσι ώστε στην πρώτη γραμμή της στήλης που εντοπίσαμε στο βήμα 2, να υπάρχει μη μηδενικό στοιχείο.

Βήμα 4 Αν το στοιχείο στην πρώτη γραμμή του βήματος 3 είναι το

a

, τότε πολλαπλασιάζουμε την πρώτη γραμμή με

1/a

και κατασκευάζουμε την καθοδηγητική μονάδα της πρώτης γραμμής.

Βήμα 5 Αφαιρούμε κατάλληλα πολλαπλάσια της πρώτης γραμμής από τις επόμενες γραμμές για να μηδενίσουμε τα στοιχεία της στήλης κάτω από την καθοδηγητική μονάδα της πρώτης γραμμής.

Βήμα 6 Επαναλαμβάνουμε τα προηγούμενα βήματα του αλγορίθμου, ξεκινώντας όμως από τη δεύτερη γραμμή του πίνακα που έχει προκύψει. Συνεχίζουμε με αυτόν τον τρόπο, έως ότου προκύψει πίνακας που είναι σε κλιμακωτή μορφή γραμμών.

Βήμα 7 Ξεκινώντας από την τελευταία μη μηδενική γραμμή του πίνακα του βήματος 6 και δουλεύοντας προς τα επάνω, αφαιρούμε κατάλληλα πολλαπλάσιο της γραμμής από τις προηγούμενες για να μηδενίσουμε τα στοιχεία επάνω από τη καθοδηγητική μονάδα.

Θα αποσαφηνίσουμε τον αλγόριθμο με τα επόμενα παραδείγματα.

Παραδείγματα 1.2.5.

1.

Θα εφαρμόσουμε τον αλγόριθμο του Gauss προκειμένου να φέρουμε τον πίνακα

$A=\left[\begin{array}[]{cccccc}0&0&1&0&0&0\\ 0&2&0&2&6&4\\ 0&3&0&0&0&1\end{array}\right]$
σε ελαττωμένη κλιμακωτή μορφή γραμμών. Η αριστερότερη μη μηδενική στήλη είναι η δεύτερη στήλη, ενώ το στοιχείο στη δεύτερη γραμμή αυτής της στήλης είναι μη μηδενικό. Έτσι στο βήμα 3 αντιμεταθέτουμε τις δύο πρώτες γραμμές, ενώ στο βήμα 4 διαιρούμε τη πρώτη γραμμή με το 2. Στη συνέχεια δείχνουμε τα βήματα του αλγορίθμου που φέρνουν τον $Α$ σε κλιμακωτή μορφή γραμμών, (βήματα 2-6).

$A\begin{array}[]{c}\\ \overrightarrow{\Gamma_{1}\leftrightarrow\Gamma_{2}}\end{array}\left[\begin{% array}[]{cccccc}0&2&0&2&6&4\\ 0&0&1&0&0&0\\ 0&3&0&0&0&1\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{1}\rightarrow\frac{1}{2}\Gamma_{1}}\end{array}\left[% \begin{array}[]{cccccc}0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&1&3&2\\ 0&0&1&0&0&0\\ 0&3&0&0&0&1\end{array}\right]$

$\begin{array}[]{c}\\ \overrightarrow{\Gamma_{3}\rightarrow\Gamma_{3}-3\Gamma_{1}}\end{array}\left[% \begin{array}[]{cccccc}0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&1&3&2\\ 0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0\\ 0&0&0&-3&-9&-5\end{array}\right]$

$\begin{array}[]{c}\\ \overrightarrow{\Gamma_{3}\rightarrow-\frac{1}{3}\Gamma_{3}}\end{array}A^{% \prime}=\left[\begin{array}[]{cccccc}0&\leavevmode\pgfpicture\makeatletter% \hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&1&3&2\\ 0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&3&\frac{5}{3}\end{array}\right]\ .$

Ο $Α^{\prime}$ είναι σε κλιμακωτή μορφή γραμμών. Για να φέρουμε τον $Α^{\prime}$ σε ελαττωμένη κλιμακωτή μορφή, αφαιρούμε από την πρώτη γραμμή την τρίτη:

$Α^{\prime}\begin{array}[]{c}\\ \overrightarrow{\Gamma_{1}\rightarrow\Gamma_{1}-\Gamma_{3}}\end{array}Α^{% \prime\prime}=\left[\begin{array}[]{cccccc}0&\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0&\frac{1}{3}\\ 0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&3&\frac{5}{3}\end{array}\right]\begin{% array}[]{c}\\ \\ .\end{array}$
Ο $Α^{\prime\prime}$ είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών.
2.

Ο πίνακας

$Α=\left[\begin{array}[]{cccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt% {\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{% 0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&-1&0&2\\ 0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&1\\ 0&0&0&0\end{array}\right]$
είναι ήδη σε ελαττωμένη κλιμακωτή μορφή γραμμών. Ο αλγόριθμος του Gauss επιστρέφει τον $Α$ .
3.

Εφαρμόζουμε τον αλγόριθμο του Gauss στον επόμενο πίνακα $Β$ :

$Β=\left[\begin{array}[]{ccccc}2&0&0&3&0\\ 4&0&0&4&2\\ 1&0&0&0&1\\ 0&0&0&1&0\end{array}\right]\begin{array}[]{c}\\ \\ \overrightarrow{\Gamma_{1}\rightarrow\frac{1}{2}\Gamma_{1}}\\ \end{array}\left[\begin{array}[]{ccccc}\leavevmode\pgfpicture\makeatletter% \hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&\frac{3}{2}&0\\ 4&0&0&4&2\\ 1&0&0&0&1\\ 0&0&0&1&0\end{array}\right]$

$\begin{array}[]{c}\\ \overrightarrow{\Gamma_{2}\rightarrow\Gamma_{2}-4\Gamma_{1}}\\ \Gamma_{3}\rightarrow\Gamma_{3}-\Gamma_{1}\end{array}\left[\begin{array}[]{% cccrc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&\frac{3}{2}&0\\ 0&0&0&-2&2\\ 0&0&0&-\frac{3}{2}&1\\ 0&0&0&1&0\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{2}\rightarrow-\frac{1}{2}\Gamma_{2}}\end{array}$

$\left[\begin{array}[]{cccrr}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&\frac{3}{2}&0\\ 0&0&0&1&-1\\ 0&0&0&-\frac{3}{2}&1\\ 0&0&0&1&0\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{3}\rightarrow\Gamma_{3}+\frac{3}{2}\Gamma_{2}}\\ \Gamma_{4}\rightarrow\Gamma_{4}-\Gamma_{2}\end{array}\left[\begin{array}[]{% ccccr}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&\frac{3}{2}&0\\ 0&0&0&\ \leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&-1\\ 0&0&0&0&-\frac{1}{2}\\ 0&0&0&0&1\end{array}\right]$

$\begin{array}[]{c}\\ \overrightarrow{\Gamma_{3}\rightarrow-2\Gamma_{3}}\end{array}\left[\begin{% array}[]{ccccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&\frac{3}{2}&\;0\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&-1\\ 0&0&0&0&\;\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture\\ 0&0&0&0&\;1\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{4}\rightarrow\Gamma_{4}-\Gamma_{3}}\\ \end{array}\left[\begin{array}[]{ccccc}\leavevmode\pgfpicture\makeatletter% \hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&\frac{3}{2}&0\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0\\ 0&0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture\\ 0&0&0&0&0\end{array}\right]$

$\begin{array}[]{c}\\ \overrightarrow{\Gamma_{1}\rightarrow\Gamma_{1}-\frac{2}{3}\Gamma_{2}}\end{% array}\left[\begin{array}[]{ccccc}\leavevmode\pgfpicture\makeatletter\hbox to % 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0% }{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}% \nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0&0\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0\\ 0&0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture\\ 0&0&0&0&0\end{array}\right].$
4.

Θεωρούμε τον $3\times 3$ -πίνακα

$Α=\left[\begin{array}[]{rrr}1&2&1\\ 0&4&8\\ 1&5&-1\end{array}\right]\begin{array}[]{c}\\ \\ .\end{array}$
Θα φέρουμε τον $Α$ σε ελαττωμένη κλιμακωτή μορφή γραμμών χρησιμοποιώντας μία παραλλαγή του αλγορίθμου του Gauss. Θα χρησιμοποιήσουμε την καθοδηγητική μονάδα της δεύτερης γραμμής (στη δεύτερη στήλη) για να κάνουμε μηδενικά ταυτόχρονα στην πρώτη και τρίτη γραμμή. Ο τρόπος αυτός συνήθως απαιτεί περισσότερες πράξεις από τον αλγόριθμο 1.2.1.

$Α\begin{array}[]{c}\\ \overrightarrow{\Gamma_{3}\rightarrow\Gamma_{3}-\Gamma_{1}}\end{array}\left[% \begin{array}[]{ccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2&1\\ 0&4&8\\ 0&3&-2\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{2}\rightarrow\frac{1}{4}\Gamma_{2}}\end{array}\left[% \begin{array}[]{ccr}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2&1\\ 0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2\\ 0&3&-2\end{array}\right]$

$\begin{array}[]{c}\\ \overrightarrow{\Gamma_{1}\rightarrow\Gamma_{1}-2\Gamma_{2}}\\ \Gamma_{3}\rightarrow\Gamma_{3}-3\Gamma_{2}\end{array}\left[\begin{array}[]{% ccr}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&-3\\ 0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&2\\ 0&0&-8\end{array}\right]\begin{array}[]{c}\\ \overrightarrow{\Gamma_{3}\rightarrow-\frac{1}{8}\Gamma_{3}}\end{array}\left[% \begin{array}[]{ccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&-3\\ 0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&\;2\\ 0&0&\;\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture\end{array}\right]$

$\begin{array}[]{c}\\ \overrightarrow{\Gamma_{1}\rightarrow\Gamma_{1}+3\Gamma_{3}}\\ \Gamma_{2}\rightarrow\Gamma_{2}-2\Gamma_{3}\end{array}\left[\begin{array}[]{% ccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0\\ 0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0\\ 0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture\end{array}\right].$

Σημειώνουμε ότι αν στον $A$ εφαρμόσουμε στοιχειώδεις πράξεις γραμμών και καταλήξουμε στον $Β$ , τότε αντιστρέφοντας τις πράξεις αυτές καταλήγουμε στον $Α$ από τον $Β$ , με στοιχειώδεις πράξεις γραμμών. Έτσι αν δύο πίνακες $Β$ , $C$ , προκύπτουν από τον $Α$ μετά από εφαρμογή στοιχειωδών πράξεων γραμμών, τότε μπορούμε να πάμε από τον $Β$ στον $C$ με εφαρμογή στοιχειωδών πράξεων γραμμών περνώντας ενδιάμεσα από τον $Α$ . Παρατηρούμε επίσης ότι αν οι $A^{\prime}$ και $A^{\prime\prime}$ είναι δύο πίνακες σε κλιμακωτή μορφή γραμμών έτσι ώστε o $A^{\prime}$ και o $A^{\prime\prime}$ να προκύπτουν από τον $Α$ μετά από εφαρμογές στοιχειωδών πράξεων γραμμών, τότε είναι δυνατόν $A^{\prime}\neq A^{\prime\prime}$ . Για παράδειγμα, στο 1.2.5.1, οι $A^{\prime}$ και $Α^{\prime\prime}$ είναι σε κλιμακωτή μορφή γραμμών και προέρχονται από τον $Α$ . Έχει, λοιπόν, σημασία η επόμενη πρόταση.

Πρόταση 1.2.6.

Έστω ότι οι πίνακες $Β$ , $C$ είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών και ότι οι $B$ και $C$ προέρχονται από τον $Α$ μετά από εφαρμογή στοιχειωδών πράξεων γραμμών. Τότε $B=C$ .

Απόδειξη.

Έστω ότι ο $Α$ είναι $m\times n$ . Θα χρησιμοποιήσουμε τη μέθοδο της μαθηματικής επαγωγής (mathematical induction) στο $n$ , τον αριθμό των στηλών του $Α$ . Δηλαδή, πρέπει να δείξουμε ότι η πρόταση ισχύει για την αρχική τιμή του $n$ (επαγωγικό βήμα) και υποθέτοντας ότι η πρόταση είναι αληθής για το $n=k$ (υπόθεση της επαγωγής), θα πρέπει στη συνέχεια να δείξουμε ότι η πρόταση ισχύει για $n=k+1$ . Η πρόταση είναι αληθής για $n=1$ , βλ. Άσκηση 1.2.1. Θα υποθέσουμε λοιπόν ότι η πρόταση ισχύει για τους $m\times k$ πίνακες. Στη συνέχεια θα αποδείξουμε ότι η πρόταση είναι αληθής όταν o $A$ είναι $m\times(k+1)$ και οι $Β$ , $C$ , πίνακες σε ελαττωμένη κλιμακωτή μορφή γραμμών, προέρχονται από τον $Α$ μετά από εφαρμογή στοιχειωδών πράξεων γραμμών. Είναι φανερό ότι οι πίνακες που αποτελούνται από τις πρώτες $k$ στήλες των $B$ και $C$ είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών και προέρχονται από τον πίνακα που αποτελείται από τις πρώτες $k$ στήλες του $Α$ μετά από εφαρμογή στοιχειωδών πράξεων γραμμών. Εφαρμόζουμε, λοιπόν, την υπόθεση της επαγωγής για να συμπεράνουμε ότι οι πρώτες $k$ στήλες των $Β$ και $C$ είναι ίσες. Άρα, οι διαφορές των $B$ και $C$ (αν υπάρχουν) βρίσκονται στην τελευταία $(k+1)$ -στήλη. Δουλεύοντας με την τελευταία μη μηδενική γραμμή του $Β$ , είναι εύκολο να δει κανείς ότι ταυτίζεται με την τελευταία μη μηδενική γραμμή του $C$ , εξαιτίας της θέσης της καθοδηγητικής μονάδας (είτε στη στήλη $(k+1)$ είτε σε προηγούμενη στήλη) και της παρατήρησης ότι οι γραμμές του $Β$ προέρχονται από τις γραμμές του $C$ μετά από εφαρμογή στοιχειωδών πράξεων γραμμών. Δηλαδή, οι τελευταίες γραμμές των $B$ και $C$ ταυτίζονται. Δουλεύοντας με αυτόν τον τρόπο από κάτω προς τα επάνω, προκύπτει ότι $B=C$ . ∎

Ο μοναδικός πίνακας σε ελαττωμένη κλιμακωτή μορφή γραμμών που προκύπτει από τον $Α$ με την εφαρμογή στοιχειωδών πράξεων γραμμών λέγεται η ελαττωμένη κλιμακωτή μορφή γραμμών του $Α$ .

Ορισμός 1.2.7.

Έστω $A\in M_{n\times m}(K)$ . Η βαθμίδα (rank) του πίνακα $Α$ λέγεται το πλήθος των καθοδηγητικών μονάδων στην ελαττωμένη κλιμακωτή μορφή του $A$ . Η βαθμίδα του $A$ συμβολίζεται με ${\rm\bf rank}(A)$ .

Είναι φανερό από την Πρόταση 1.2.6, ότι αν o $B$ προκύπτει από τον $Α$ με κάποια από τις τρεις στοιχειώδεις πράξεις γραμμών, τότε $\operatorname{rank}(A)=\operatorname{rank}(B)$ .

Παραδείγματα 1.2.8.

1.

Έστω $\bf 0$ ο μηδενικός $m\times n$ πίνακας. Τότε $\operatorname{rank}({\bf 0})=0$ .
2.

Έστω $B$ o πίνακας του Παραδείγματος 1.2.5.3. Τότε $\operatorname{rank}(B)=3$ .

Αν o $Β$ είναι η ελαττωμένη κλιμακωτή μορφή γραμμών του $m\times n$ πίνακα $Α$ , τότε κάθε μη μηδενική γραμμή του $Β$ έχει καθοδηγητική μονάδα και επομένως $\operatorname{rank}(B)\leq m$ . Επίσης αν μία στήλη του $B$ έχει καθοδηγητική μονάδα, τότε όλα τα άλλα στοιχεία της στήλης αυτής είναι μηδέν. Συνεπώς, κάθε στήλη του $Β$ έχει το πολύ μία καθοδηγητική μονάδα και επομένως $\operatorname{rank}(Β)\leq n$ . Αφού $\operatorname{rank}(A)=\operatorname{rank}(B)$ , συμπεραίνουμε ότι:

Αν $\bf Α$ είναι $\bf m\times n$ πίνακας, τότε $\bf\operatorname{{\bf rank}}(A)\leq\operatorname{{\bf min}}(m,n)$ .

Παρατήρηση 1.2.9.

Όπως με τις γραμμές του

Α

, μπορούμε να ορίσουμε ανάλογα τις στοιχειώδεις πράξεις στηλών (elementary column operations) του

Α

και στη συνέχεια να αναπτύξουμε τη θεωρία για την ελαττωμένη κλιμακωτή μορφή στηλών (column reduced echelon form) του

Α

, βλ. σύγγραμμα [2, Ορισμός 1.2.5]. Ο αλγόριθμος του Gauss προσαρμόζεται για να φέρει τον πίνακα

Α

σε ελαττωμένη κλιμακωτή μορφή στηλών.

Η ελαττωμένη κλιμακωτή μορφή γραμμών ενός πίνακα δεν ισούται κατ' ανάγκη με την ελαττωμένη κλιμακωτή μορφή στηλών του πίνακα.

Παράδειγμα 1.2.10.

Ο πίνακας

Α=\left[\begin{array}[]{cccc}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt% {\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{% 0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&4\\ 0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0\\ 0&0&0&0\end{array}\right]

είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών. Όμως, ο $Α$ δεν είναι σε ελαττωμένη κλιμακωτή μορφή στηλών. Οι επόμενες στοιχειώδεις πράξεις στηλών, φέρνουν τον $Α$ σε ελαττωμένη κλιμακωτή μορφή στηλών.

\;\;Α\begin{array}[]{c}\\ \overrightarrow{\Sigma_{4}\rightarrow\Sigma_{4}-4\Sigma_{1}}\\ \end{array}\begin{bmatrix}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0\cr 0&0&\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0\cr 0&0&0&0\end{bmatrix}\begin{array}[]{c% }\\ \overrightarrow{\Sigma_{2}\leftrightarrow\Sigma_{3}}\\ \end{array}\begin{bmatrix}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0\cr 0&\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0\cr 0&0&0&0\end{bmatrix}

Θα δούμε αργότερα ότι η ελαττωμένη κλιμακωτή μορφή γραμμών και η ελαττωμένη κλιμακωτή μορφή στηλών ενός πίνακα έχουν τον ίδιο αριθμό καθοδηγητικών μονάδων.

Ασκήσεις Ενότητας 1.2

1.

Να βρείτε όλους του $m\times 1$ πίνακες με στοιχεία από τον ${\mathbb{R}}$ σε ελαττωμένη κλιμακωτή μορφή γραμμών.

Λύση
2.

Να περιγράψετε όλους του $2\times 2$ πίνακες με στοιχεία από τον ${\mathbb{C}}$ σε ελαττωμένη κλιμακωτή μορφή γραμμών.

Λύση
3.

Να περιγράψετε όλους του $2\times 3$ πίνακες με στοιχεία από τον ${\mathbb{C}}$ σε ελαττωμένη κλιμακωτή μορφή στηλών.

Λύση
4.

Να φέρετε τους επόμενους πίνακες σε κλιμακωτή μορφή και σε ελαττωμένη κλιμακωτή μορφή γραμμών και να υπολογίσετε τη βαθμίδα τους.

$Α_{1}=\left[\begin{array}[]{ccc}2&1&1\\ 1&3&1\\ 1&1&4\end{array}\right],\;A_{2}=\left[\begin{array}[]{cccr}2&4&7&4\\ 1&2&3&1\\ 3&6&5&-5\end{array}\right],\;A_{3}=\left[\begin{array}[]{rrrrr}-3&8&\;\;6&-5&-% 3\\ 1&-2&\;\;0&3&1\\ 1&-1&\;\;3&2&-5\\ 2&-3&\;\;3&5&0\\ -1&5&\;\;9&0&-7\end{array}\right].$

$A_{4}=\left[\begin{array}[]{rrr}3&3&3\\ 1&2&-1\\ 0&1&-1\end{array}\right],\;\;A_{5}=\left[\begin{array}[]{rrrr}2&3&3&2\\ 1&1&1&0\\ 3&-2&4&1\\ 0&-5&1&-1\end{array}\right],\;\;A_{6}=\left[\begin{array}[]{rrrr}1&3&0&-3\\ 0&1&2&1\\ 0&9&5&0\\ 1&2&0&4\end{array}\right]\;.$

Λύση

1.3 Επίλυση Γραμμικών Συστημάτων

Στην ενότητα αυτή θα αναπτύξουμε μία μέθοδο επίλυσης γραμμικών συστημάτων χρησιμοποιώντας τον αλγόριθμο του Gauss. Από την Πρόταση 1.1.2 και τον τρόπο που ορίσαμε την ελαττωμένη κλιμακωτή μορφή γραμμών προκύπτει το εξής συμπέρασμα.

Πρόταση 1.3.1.

Έστω $ΑX=B$ ένα γραμμικό σύστημα με συντελεστές από το $\Bbbk$ και έστω $[R|B^{\prime}]$ η ελαττωμένη κλιμακωτή μορφή γραμμών του $[A|B]$ . Το γραμμικό σύστημα $RX=B^{\prime}$ έχει ακριβώς τις ίδιες λύσεις με το σύστημα $AX=B$ .

O αλγόριθμος (1.3.1) βασίζεται σε αυτή την πρόταση.

Αλγόριθμος 1.3.1 Αλγόριθμος για την επίλυση γραμμικών συστημάτων

Είσοδος: Ένα γραμμικό σύστημα

AX=B

Έξοδος: Το σύνολο των λύσεων του συστήματος

AX=B

Βήμα 1 Θεωρούμε τον επαυξημένο πίνακα

[A\ |\ B]

. Με στοιχειώδεις πράξεις γραμμών φέρνουμε τον

[A\ |\ B]

σε κλιμακωτή μορφή γραμμών

[A^{\prime}\ |\ B^{\prime}]

. Αν μία οποιαδήποτε γραμμή του

[A^{\prime}\ |\ B^{\prime}]

είναι της μορφής

[\begin{array}[]{cccccc}0&0&\cdots&0&|&a\end{array}]

όπου $a\neq 0$ , τότε το αρχικό σύστημα $ΑX=Β$ είναι ασύμβατο και ο αλγόριθμος τερματίζει. Διαφορετικά συνεχίζουμε στο επόμενο βήμα.

Βήμα 2 Φέρνουμε τον

[Α^{\prime}|Β^{\prime}]

σε ελαττωμένη κλιμακωτή μορφή γραμμών

[R|Β^{\prime\prime}]

. Οι άγνωστοι που αντιστοιχούν στις στήλες χωρίς καθοδηγητικές μονάδες γίνονται παράμετροι, δηλαδή τους επιτρέπουμε να λάβουν οποιαδήποτε τιμή από το

\Bbbk

και λέγονται ελεύθερες μεταβλητές (free variable).

Βήμα 3 Βρίσκουμε τις εξισώσεις που αντιστοιχούν στις μη μηδενικές γραμμές του

[R|Β^{\prime\prime}]

. Λύνουμε ως προς τις μεταβλητές που αντιστοιχούν στις καθοδηγητικές μονάδες. Οι λύσεις του αρχικού συστήματος είναι το σύνολο των

n

-άδων που προκύπτουν από το Βήμα 3.

Για να φέρουμε τον πίνακα $[A\ |\ B]$ στη μορφή $[A^{\prime}\ |\ B^{\prime}]$ του πρώτου βήματος, μπορούμε να χρησιμοποιήσουμε τον Αλγόριθμο του Gauss. Σύμφωνα με την Πρόταση 1.1.2, τα συστήματα $AX=B$ και $A^{\prime}X=B^{\prime}$ του πρώτου βήματος έχουν τις ίδιες λύσεις. Τα επόμενα παραδείγματα θα διαφωτίσουν τη διαδικασία εύρεσης λύσεων. Θα χρησιμοποιούμε " $\rightarrow\cdots\rightarrow$ " για να συμβολίσουμε τη συνολική διαδικασία που φέρνει έναν πίνακα σε ελαττωμένη κλιμακωτή μορφή γραμμών. Με $\bf 0$ θα συμβολίζουμε το μηδενικό πίνακα οποιασδήποτε διάστασης.

Παραδείγματα 1.3.2.

1. Θα βρούμε το σύνολο των λύσεων του επόμενου ομογενούς συστήματος επάνω από το σώμα

{\mathbb{R}}

\begin{array}[]{rcrcrcrcrcl}x_{1}&-&2x_{2}&&&&&+&4x_{5}&=&0\\ -x_{1}&+&2x_{2}&+&x_{3}&&&-&5x_{5}&=&0\\ -2x_{1}&+&4x_{2}&-&3x_{3}&+&x_{4}&-&2x_{5}&=&0\\ 3x_{1}&-&6x_{2}&+&4x_{3}&-&2x_{4}&+&2x_{5}&=&0.\end{array}

(1.3.2.1)

Παίρνοντας τον επαυξημένο πίνακα που αντιστοιχεί στο σύστημα (1.3.2.1) και κάνοντας στοιχειώδες πράξεις γραμμών βρίσκουμε:

[Α\;|\bf{0}]=\left[\begin{array}[]{rrrrr|r}1&-2&0&0&4&0\\ -1&2&1&0&-5&0\\ -2&4&-3&1&-2&0\\ 3&-6&4&-2&2&0\end{array}\right]\longrightarrow\cdots

\cdots\longrightarrow\left[\begin{array}[]{rrccr|r}\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&-2&0&0&4&0\\ 0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&-1&0\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&3&0\\ 0&0&0&0&0&0\end{array}\right]\begin{array}[]{r}\\ \\ \\ .\end{array}

Το αρχικό σύστημα (1.3.2.1) γίνεται ισοδύναμο με το σύστημα

\begin{array}[]{rrrrr}x_{1}&-2x_{2}&&&+4x_{5}\;=0\\ &&x_{3}&&-\;\;x_{5}\;=0\\ &&&x_{4}&+3x_{5}\;=0.\end{array}

Οι μεταβλητές

x_{2},x_{5}

είναι παράμετροι. Λύνοντας ως προς

x_{1}

x_{3}

x_{4}

, βρίσκουμε ότι

\begin{array}[]{ll}x_{1}&=2x_{2}-4x_{5}\\ x_{3}&=x_{5}\\ x_{4}&=-3x_{5}\end{array}.

(1.3.2.2)

Αν

(x_{1},\ldots,x_{5})

είναι λύση του συστήματος (1.3.2.1), τότε οι

x_{2},x_{5}

μπορούν να πάρουν τυχαίες τιμές από το

{\mathbb{R}}

, ενώ οι

x_{1},x_{3},x_{4}

περιορίζονται από τις σχέσεις (1.3.2.2). Η τυχαία λύση του συστήματος (1.3.2.1) είναι μία

5

-άδα της μορφής

(2x_{2}-4x_{5},x_{2},x_{5},-3x_{5},x_{5})\textrm{ όπου }\;x_{2},x_{5}\in{% \mathbb{R}}.

Το σύνολο των λύσεων του συστήματος (1.3.2.1) είναι το σύνολο

\displaystyle\{\;(2x_{2}-4x_{5},x_{2},x_{5},-3x_{5},x_{5})\;:\;x_{2},x_{5}\in{% \mathbb{R}}\}=\\ \displaystyle=\{(2x_{2},x_{2},0,0,0)+(-4x_{5},0,x_{5},-3x_{5},x_{5})\;:\;x_{2}% ,x_{5}\in{\mathbb{R}}\}=\\ \displaystyle=\{x_{2}(2,1,0,0,0)+x_{5}(-4,0,1,-3,1)\;:\;x_{2},x_{5}\in{\mathbb% {R}}\}\;.

Σημειώνουμε ότι οι λύσεις του ιδίου συστήματος επάνω από το

{\mathbb{C}}

είναι το σύνολο

\{x_{2}(2,1,0,0,0)+x_{5}(-4,0,1,-3,1)\;:\;x_{2},x_{5}\in{\mathbb{C}}\}.

2. Θα λύσουμε επάνω από το σώμα

{\mathbb{R}}

το γραμμικό σύστημα

\begin{array}[]{rcrcrcrcrcl}x_{1}&-&x_{2}&-&x_{3}&+&2x_{4}&-&2x_{5}&=&1\\ 2x_{1}&+&x_{2}&-&2x_{3}&+&x_{4}&+&x_{5}&=&2\\ x_{1}&-&4x_{2}&-&x_{3}&+&5x_{4}&-&7x_{5}&=&1\\ -\;x_{1}&+&x_{2}&+&x_{3}&-&x_{4}&+&3x_{5}&=&0\\ 2x_{1}&+&x_{2}&-&x_{3}&+&x_{4}&+&2x_{5}&=&3.\end{array}

(1.3.2.3)

Έστω

Α

ο πίνακας των συντελεστών και

Β

ο πίνακας των σταθερών του συστήματος (1.3.2.3). Τότε

[Α\;|Β]=\left[\begin{array}[]{rrrrr|r}1&-1&-1&2&-2&1\\ 2&1&-2&1&1&2\\ 1&-4&-1&5&-7&1\\ -1&1&1&-1&3&0\\ 2&1&-1&1&2&3\end{array}\right]\longrightarrow\cdots

\cdots\longrightarrow\left[\begin{array}[]{ccccr|r}\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0&-1/3&1\\ 0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&\;8/3&1\\ 0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&1&1\\ 0&0&0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{\pgfsys@beginscope% \colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0}{}% \pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox t% o 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&1&1\\ 0&0&0&0&0&0\end{array}\right]\begin{array}[]{r}\\ \\ \\ \\ .\end{array}

Παρατηρούμε ότι

\operatorname{rank}(A)=\operatorname{rank}([A\ |\ Β])=4

και το αρχικό σύστημα είναι ισοδύναμο με το σύστημα

\begin{array}[]{rrrrr}x_{1}&&&&-1/3\;x_{5}\;=\;1\\ &x_{2}&&&+8/3\;x_{5}\;=\;1\\ &&x_{3}&&+\;\;\;\;\;\;x_{5}\;=\;1\\ &&&x_{4}&+\;\;\;\;\;\;x_{5}\;=\;1.\\ \end{array}

Οι λύσεις του ομογενούς συστήματος

AX=\bf{0}

δίνονται από το σύνολο

\{\;(1/3x_{5},-8/3x_{5},-x_{5},-x_{5},x_{5}):\ \;x_{5}\in{\mathbb{R}}\}=

=\{x_{5}(1/3,-8/3,-1,-1,1):\ \;x_{5}\in{\mathbb{R}}\}.

Οι λύσεις του συστήματος

AX=B

δίνονται από το σύνολο

\{\;(1,1,1,1,0)+t\;(1/3,-8/3,-1,-1,1):\ \;t\in{\mathbb{R}}\}.

3. Θα λύσουμε επάνω από το

{\mathbb{R}}

το γραμμικό σύστημα

AX=B

, όπου

Α=\left[\begin{array}[]{rrrr}0&1&2&3\cr 0&0&1&1\end{array}\right],\quad B=% \begin{bmatrix}1&-1\end{bmatrix}\ .

H ελαττωμένη κλιμακωτή μορφή γραμμών του πίνακα

[Α\ |\ Β]

είναι ο πίνακας

\left[\begin{array}[]{rccr|r}0&\leavevmode\pgfpicture\makeatletter\hbox to 0.0% pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0% }{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&1&3\cr 0&0&\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&1&-1\end{array}\right].

Το αρχικό σύστημα γίνεται ισοδύναμο με το

\begin{matrix}x_{2}&&+x_{4}&\;=&3\cr&x_{3}&+x_{4}&\;=&-1\end{matrix}\ .

Οι μεταβλητές είναι

x_{1}

x_{4}

. Λύνουμε ως προς

x_{2}

x_{3}

και βρίσκουμε ότι

\begin{matrix}x_{2}&=&3-x_{4}\cr x_{3}&=&-1-x_{4}\end{matrix}\ .

Το σύνολο των λύσεων του συστήματος είναι το σύνολο

\{(x_{1},3-x_{4},-1-x_{4},x_{4}):\ x_{1},x_{4}\in{\mathbb{R}}\}=

\{x_{1}(1,0,0,0)+x_{4}(0,-1,-1,1)+(0,3,-1,0):\ x_{1},x_{4}\in{\mathbb{R}}\}.

4. Θα βρούμε τις λύσεις του γραμμικού συστήματος

AX=B

στον

{\mathbb{R}}

, όπου

Α=\begin{bmatrix}1&2\cr 0&1\end{bmatrix},\quad B=\begin{bmatrix}1\cr-1\end{% bmatrix}\ .

H ελαττωμένη κλιμακωτή μορφή γραμμών του πίνακα

[Α\ |\ Β]

είναι ο πίνακας

\left[\begin{array}[]{cc|r}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&3\cr 0&\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&-1\end{array}\right].

Το αρχικό σύστημα είναι ισοδύναμο με το

\begin{matrix}x_{1}&&\;=&3\cr&x_{2}&\;=&-1\ .\end{matrix}\

Η μοναδική λύση του συστήματος είναι το

(3,-1)

. Το σύνολο

\{(3,-1)\}

είναι το σύνολο των λύσεων του γραμμικού συστήματος

AX=B

. 5. Θα λύσουμε επάνω από το

{\mathbb{C}}

τα γραμμικά συστήματα

AX=\bf{0}

AX=B

και

ΑX=C

, όπου

Α=\begin{bmatrix}1&2&0\cr 1&3&0\cr 0&0&1\cr 0&0&0\end{bmatrix},\quad B=\begin{% bmatrix}1\cr 2\cr 1\cr 1\end{bmatrix},\quad C=\begin{bmatrix}1\cr 0\cr i\cr 0% \end{bmatrix}\ .

Θα λύσουμε τα συστήματα αυτά ταυτόχρονα αφού έχουν τον ίδιο πίνακα συντελεστών. Έτσι επαυξάνουμε τον

Α

κατά τρεις στήλες,

\begin{bmatrix}A\ |\ \bf{0}\ B\ C\end{bmatrix}

, και φέρνουμε αυτόν τον επαυξημένο πίνακα σε ελαττωμένη κλιμακωτή μορφή γραμμών:

\left[\begin{array}[]{rrr|rrr}1&2&0&0&1&1\cr 1&3&0&0&2&0\cr 0&0&1&0&1&i\cr 0&0% &0&0&1&0\end{array}\right]\ \longrightarrow\cdots\longrightarrow\left[\begin{% array}[]{ccc|rrr}\leavevmode\pgfpicture\makeatletter\hbox to 0.0pt{% \pgfsys@beginscope\colorlet{pgfstrokecolor}{.}\pgfsys@color@rgb@stroke{0}{0}{0% }{}\pgfsys@color@rgb@fill{0}{0}{0}{}\pgfsys@setlinewidth{0.4pt}{}\nullfont% \hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&0&-1&3\cr 0&\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&0&1&-1\cr 0&0&\leavevmode\pgfpicture% \makeatletter\hbox to 0.0pt{\pgfsys@beginscope\colorlet{pgfstrokecolor}{.}% \pgfsys@color@rgb@stroke{0}{0}{0}{}\pgfsys@color@rgb@fill{0}{0}{0}{}% \pgfsys@setlinewidth{0.4pt}{}\nullfont\hbox to 0.0pt{ \pgfsys@beginscope{ {{}}\hbox{\hbox{{\pgfsys@beginscope{{}{{{}}}{{}}{} {}{}{}{}{}{}{}{}{{}\pgfsys@moveto{8.666504pt}{0.0pt}\pgfsys@curveto{8.666504pt% }{4.786378pt}{4.786378pt}{8.666504pt}{0.0pt}{8.666504pt}\pgfsys@curveto{-4.786% 378pt}{8.666504pt}{-8.666504pt}{4.786378pt}{-8.666504pt}{0.0pt}\pgfsys@curveto% {-8.666504pt}{-4.786378pt}{-4.786378pt}{-8.666504pt}{0.0pt}{-8.666504pt}% \pgfsys@curveto{4.786378pt}{-8.666504pt}{8.666504pt}{-4.786378pt}{8.666504pt}{% 0.0pt}\pgfsys@closepath\pgfsys@moveto{0.0pt}{0.0pt}\pgfsys@stroke% \pgfsys@invoke{ }}{{{{}}{\pgfsys@beginscope\pgfsys@transformcm{1.0}{0.0}{0.0}{% 1.0}{-3.749943pt}{-2.499962pt}{}\pgfsys@hbox{23}{}\pgfsys@endscope}}}}% \pgfsys@endscope}}}}\pgfsys@endscope{{{}}}{}{}\hss}\pgfsys@discardpath{}{}{}% \pgfsys@endscope\hss}\endpgfpicture&0&1&i\cr 0&0&0&0&1&0\end{array}\right].

Έπεται ότι – το

(0,0,0)

είναι η μοναδική λύση του συστήματος

AX=\bf{0}

, – το σύστημα

ΑX=B

δεν είναι συμβατό. – το

(3,-1,i)

είναι η μοναδική λύση του συστήματος

AX=C

Η επόμενη πρόταση γενικεύει όσα είδαμε στα προηγούμενα παραδείγματα. Η απόδειξη της πρότασης προκύπτει άμεσα από τον ορισμό της βαθμίδας του πίνακα.

Έστω το γραμμικό σύστημα

ΑX=Β

, όπου

Α

ένας

m\times n

πίνακας. Τότε:

•

Το $ΑX=Β$ είναι συμβατό αν και μόνο αν $\operatorname{rank}(Α)=\operatorname{rank}([A\ |\ B])$ .
•

Αν $\operatorname{rank}(A)=m$ , τότε το $ΑX=Β$ είναι συμβατό.
•

Αν $\operatorname{rank}(Α)=\operatorname{rank}([A\ |\ B])=n$ , τότε το $ΑX=Β$ έχει ακριβώς μία λύση.
•

Αν ${\operatorname{rank}}(A)={\operatorname{rank}}([A\ |\ B])<n$ , τότε το $AX=Β$ έχει άπειρες λύσεις. Η γενική λύση του $AX=B$ εκφράζεται με $n-{\operatorname{rank}}(A)$ παραμέτρους.

Εφαρμόζουμε τα προηγούμενα στην περίπτωση του ομογενούς συστήματος $AX=\bf{0}$ , όπου όπου $Α$ ένας $m\times n$ πίνακας. Αφού $\operatorname{rank}(Α)=\operatorname{rank}([A\ |\ {\bf 0}])$ , το ομογενές σύστημα $AX=\bf{0}$ είναι συμβατό και βλέπουμε ότι το $(0,\ldots,0)$ είναι λύση του $AX=\bf{0}$ . Οποιαδήποτε στοιχειώδης πράξη γραμμών στον $[A\ |\ {\bf 0}]$ διατηρεί μηδενική την τελευταία στήλη. Έτσι για την επίλυση του $AX=\bf{0}$ μπορούμε να αγνοήσουμε την τελευταία στήλη έως το τρίτο βήμα του αλγορίθμου επίλυσης. Το $(0,\ldots,0)$ είναι η μοναδική λύση του $AX=\bf{0}$ αν δεν υπάρχουν παράμετροι, δηλ. αν $\operatorname{rank}(Α)=n$ . Συνεπώς ισχύει η εξής πρόταση.

Έστω

Α

ένας

m\times n

πίνακας και

R

η ελαττωμένη κλιμακωτή μορφή γραμμών του

A

. Τότε

•

Το σύστημα $AX=\bf{0}$ είναι (πάντα) συμβατό.
•

Το $(0,\ldots,0)$ είναι η μοναδική λύση του $AX=\bf{0}$ αν και μόνο αν $\operatorname{rank}(A)=n$ , δηλ. αν κάθε στήλη της ελαττωμένης κλιμακωτής μορφής γραμμών του $A$ έχει καθοδηγητική μονάδα.

Ασκήσεις Ενότητας 1.3

1.

Τα επόμενα συστήματα έχουν τον ίδιο πίνακα συντελεστών. Να λυθούν (ταυτόχρονα) τα τρία πρώτα επάνω από τον ${\mathbb{R}}$ . Για το τέταρτο σύστημα, να βρείτε συνθήκη(ες) στα $a,b,c\in{\mathbb{R}}$ έτσι ώστε να είναι συμβατό.

$\begin{array}[]{lrcrcrcl}{\rm i)}&x&+&y&+&z&=&0\\ &x&+&2y&-&z&=&0\\ &2x&+&3y&&&=&0\end{array}$ $\;\;\;\;\begin{array}[]{lrcrcrcl}{\rm ii)}&x&+&y&+&z&=&1\\ &x&+&2y&-&z&=&2\\ &2x&+&3y&&&=&0\end{array}$

$\begin{array}[]{lrcrcrcl}{\rm iii)}&x&+&y&+&z&=&1\\ &x&+&2y&-&z&=&2\\ &2x&+&3y&&&=&3\ .\end{array}$ $\;\;\;\;\begin{array}[]{lrcrcrcl}{\rm iv)}&x&+&y&+&z&=&a\\ &x&+&2y&-&z&=&b\\ &2x&+&3y&&&=&b\end{array}$

Λύση
2.

Να λυθεί το σύστημα

$\begin{array}[]{rcrcrcrcrcr}x_{1}&-&2\;x_{2}&+&x_{3}&+&3\;x_{4}&-&x_{5}&=&0\\ 2\;x_{1}&+&x_{2}&&&+&x_{4}&+&x_{5}&=&3\\ x_{1}&-&7\;x_{2}&+&3\;x_{3}&+&8\;x_{4}&-&4\;x_{5}&=&-3\\ -3\;x_{1}&-&4\;x_{2}&+&x_{3}&+&x_{4}&+&3\;x_{5}&=&0\end{array}.$

Λύση
3.

Δίνονται οι πίνακες

$A=\left[\begin{array}[]{rrrr}1&-2&0&1\\ 2&-5&-1&3\\ -3&4&0&1\\ 0&4&2&-6\end{array}\right],\;\;\;B=\left[\begin{array}[]{c}1\\ 0\\ 3\\ a\end{array}\right]\;\;\hbox{και}\;\;\;X=\left[\begin{array}[]{c}x\\ y\\ z\\ t\end{array}\right].$
Να βρείτε την τιμή του $a$ ώστε το σύστημα $AX=B$ να έχει λύση.

Λύση
4.

Έστω ότι ο επαυξημένος πίνακας του συστήματος $AX=B$ έχει κλιμακωτή μορφή γραμμών τον πίνακα

$\left[\begin{array}[]{ccccc|c}1&2&0&2&0&3\\ 0&0&1&2&0&1\end{array}\right]\begin{array}[]{c}\\ .\end{array}$
Να λυθεί το σύστημα.
5.

Έστω ότι το σύστημα $AX=B$ έχει σύνολο λύσεων to $S=\{(1,2,0,1)+t(1,1,1,2)+s(0,1,2,1):t,s\in{\mathbb{C}}\}$ . Να λυθεί το σύστημα $AX=\bf 0$ .

Λύση

1.4 Ευθείες και Επίπεδα στον ${\mathbb{R}}^{2}$ και ${\mathbb{R}}^{3}$

Στην ενότητα αυτή θα μελετήσουμε τα συστήματα των εξισώσεων που έχουν σύνολο λύσεων ευθείες ή επίπεδα στον ${\mathbb{R}}^{3}$ . Πρώτα, όμως, θα μελετήσουμε τις εξισώσεις ευθειών στον ${\mathbb{R}}^{2}$ .

Ευθείες στον ${\mathbb{R}}^{2}$

Μία ευθεία στον ${\mathbb{R}}^{2}$ είναι το σύνολο των λύσεων της γραμμικής εξίσωσης $ax+by=c$ , όπου κάποιο από τα $a, b$ δεν είναι μηδέν. Η εξίσωση αυτή είναι ένα πολύ απλό γραμμικό σύστημα. Ο πίνακας των συντελεστών του συστήματος $\begin{bmatrix}a&b\end{bmatrix}$ έχει βαθμίδα 1. Επομένως, η γενική λύση του συστήματος περιγράφεται με μία παράμετρο.

Παραδείγματα 1.4.1.

1.

Ο επαυξημένος πίνακας της εξίσωσης $x+y=2$ είναι ο πίνακας

$\begin{bmatrix}1&1&|&2\end{bmatrix}\ ,$
ο οποίος είναι ήδη σε ελαττωμένη κλιμακωτή μορφή γραμμών. Το σύνολο λύσεων του συστήματος είναι το σύνολο

$\{(2-y,y):\ y\in{\mathbb{R}}\}=\{y(-1,1)+(2,0):\ y\in{\mathbb{R}}\}.$
Η ευθεία $x+y=2$ απεικονίζεται στο επόμενο σχήμα:

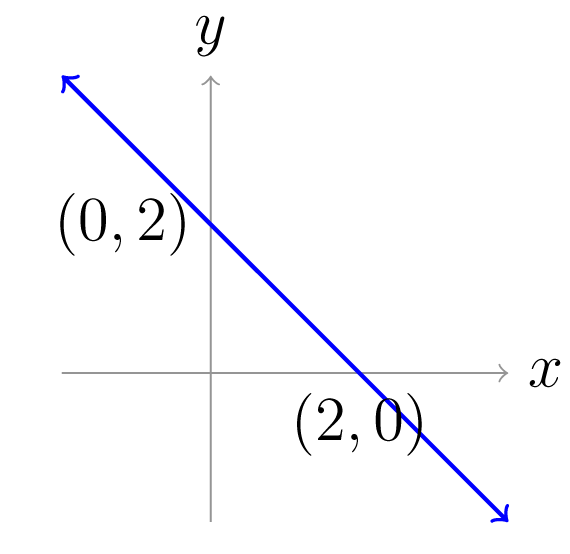
Σχήμα 1.1: H ευθεία $x+y=2$ .
2.

Ο επαυξημένος πίνακας της εξίσωσης $y=2$ είναι ο πίνακας $\begin{bmatrix}0&1&|&2\end{bmatrix}$ , ο οποίος είναι ήδη σε ελαττωμένη κλιμακωτή μορφή γραμμών. Το σύνολο είναι το σύνολο

$\{(t,2):\ \ \ t\in{\mathbb{R}}\}\$
και η ευθεία $y=2$ απεικονίζεται στο επόμενο σχήμα:

Σχήμα 1.2: H ευθεία $y=2$
3.

Η ευθεία

$L=\{(1,0)+t(1,1):\ t\in{\mathbb{R}}\}$
ικανοποιεί την εξίσωση $x-y=1$ . Πράγματι, αν $(x,y)\in L$ , τότε $x=1+t$ , $y=t$ , για κάποιο $t\in{\mathbb{R}}$ . Συνεπώς, $x=1+y\Rightarrow x-y=1$ . Η ευθεία $L$ είναι παράλληλη με την ευθεία

$\{t(1,1):\ t\in{\mathbb{R}}\}.$
Οι δύο ευθείες απεικονίζονται στο επόμενο σχήμα:

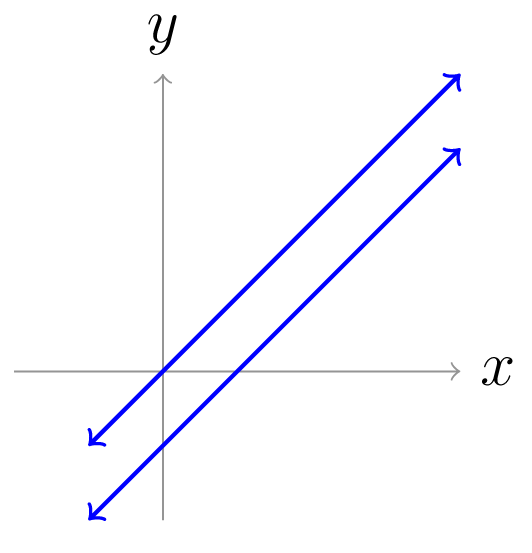
Σχήμα 1.3: Οι ευθείες $x-y=0$ και $x-y=1$

Ευθείες και Επίπεδα στον ${\mathbb{R}}^{3}$

Έστω τώρα ένα γραμμικό σύστημα με τρεις αγνώστους και $m$ εξισώσεις, με συντελεστές από τον ${\mathbb{R}}$ . Για ευκολία το γράφουμε ως $AX=B$ , όπου o $A$ είναι ένας $m\times n$ πίνακας. Γνωρίζουμε ότι $\operatorname{rank}A\leq 3$ , δηλ. $\operatorname{rank}A$ μπορεί να πάρει ακριβώς τέσσερις τιμές, με μέγιστη τιμή το $3$ και ελάχιστη τιμή το $0$ . Οι λύσεις του $AX=B$ (αν υπάρχουν) είναι σημεία του ${\mathbb{R}}^{3}$ . Όμως, o ${\mathbb{R}}^{3}$ έχει (a priori) τρεις βαθμούς ελευθερίας. Μία (μη μηδενική) γραμμική εξίσωση επιβάλλει μία συνθήκη που μειώνει τους βαθμούς ελευθερίας. Αν το σύστημα είναι ασύμβατο, τότε υπάρχουν συνθήκες που δεν μπορούν να ικανοποιηθούν ταυτόχρονα. Αν, όμως, το σύστημα είναι συμβατό, τότε υπάρχουν σημεία του ${\mathbb{R}}^{3}$ που ικανοποιούν ταυτόχρονα όλες τις συνθήκες. Έστω, λοιπόν, ότι το σύστημα $AX=B$ είναι συμβατό. Θα εξετάσουμε τι συμβαίνει, ανάλογα με τη βαθμίδα του $A$ .

i.)

Αν $\operatorname{rank}Α=3$ , τότε δεν υπάρχει κάποιος βαθμός ελευθερίας. To σύνολο των λύσεων αποτελείται από μία μοναδική τριάδα, δηλ. η λύση του $AX=B$ είναι ένα σημείο.
ii.)

Αν $\operatorname{rank}A=2$ , τότε υπάρχει μία παράμετρος και ένας βαθμός ελευθερίας και το σύνολο των λύσεων είναι της μορφής

$\{t(a_{1},a_{2},a_{3})+(a,b,c):t\in{\mathbb{R}}\}.$
H μία παράμετρος μας αναγκάζει να κινούμαστε στον τρισδιάστατο χώρο σε μία συγκεκριμένη κατεύθυνση. H γραφική αναπαράσταση του συνόλου των λύσεων του $AX=B$ είναι η ευθεία που διέρχεται από τα σημεία $(a,b,c)$ (για $t=0$ ) και $(a_{1}+a,a_{2}+b,a_{3}+c)$ (για $t=1$ ).
iii.)

Αν $\operatorname{rank}A=1$ , τότε υπάρχουν δύο παράμετροι και δύο βαθμοί ελευθερίας. To σύνολο των λύσεων του $AX=B$ είναι της μορφής

$\{t(a_{1},a_{2},a_{3})+s(b_{1},b_{2},b_{3})+(a,b,c):t\in{\mathbb{R}}\}.$

Οι δύο παράμετροι μας επιτρέπουν να κινηθούμε ελεύθερα προς δύο ανεξάρτητες κατευθύνσεις. H γραφική αναπαράσταση του συνόλου των λύσεων του $AX=B$ είναι το επίπεδο που περιέχει τα σημεία $(a,b,c)$ (για $t=0$ , $s=0$ ), $(a_{1}+a,a_{2}+b,a_{3}+c)$ (για $t=1$ , $c=0$ ) και $(b_{1}+a,b_{2}+b,b_{3}+c)$ (για $t=0$ , $c=1$ ) .
iv.)

Αν $\operatorname{rank}A=0$ , τότε όλες οι γραμμές του $A$ είναι μηδενικές, δηλ. o $A$ είναι o μηδενικός πίνακας. Αυτό σημαίνει ότι δεν υπάρχει κάποιος περιορισμός, οι βαθμοί ελευθερίας είναι τρεις και το σύνολο λύσεων του συστήματος είναι όλο το ${\mathbb{R}}^{3}$ .

Παραδείγματα 1.4.2.

1.

Το $x y$ επίπεδο στον ${\mathbb{R}}^{3}$ περιγράφεται από την εξίσωση $z=0$ . Η εξίσωση $z=0$ είναι ένα γραμμικό σύστημα με μία εξίσωση και τρεις αγνώστους με επαυξημένο πίνακα

$\left[\begin{array}[]{rrr|r}0&0&1&0\end{array}\right].$
O πίνακας των συντελεστών του συστήματος έχει βαθμίδα $1$ . Έτσι, το αντίστοιχο γραμμικό σύστημα έχει δύο βαθμούς ελευθερίας.
2.

Θα εξετάσουμε τις λύσεις της εξίσωσης $x+y=2$ στον ${\mathbb{R}}^{3}$ . (Σημειώνουμε ότι η εξίσωση $x+y=2$ στον ${\mathbb{R}}^{2}$ αντιστοιχεί σε μία ευθεία, όπως είδαμε στο Παράδειγμα 1.4.1.1). Ο επαυξημένος πίνακας του γραμμικού συστήματος $x+y=2$ στον ${\mathbb{R}}^{3}$ είναι

$\left[\begin{array}[]{rrr|r}1&1&0&2\end{array}\right].$
Το σύστημα είναι συμβατό, ο πίνακας των συντελεστών του συστήματος έχει βαθμίδα 1 και το σύνολο λύσεων είναι ένα επίπεδο $Ε$ :

$Ε=\{(2-y,y,z):\ y\in{\mathbb{R}}\}=\{(2,0,0)+y(-1,1,0)+z(0,0,1):\ y,z\in{% \mathbb{R}}\}\ ,$
που απεικονίζεται στο Σχήμα 1.4.

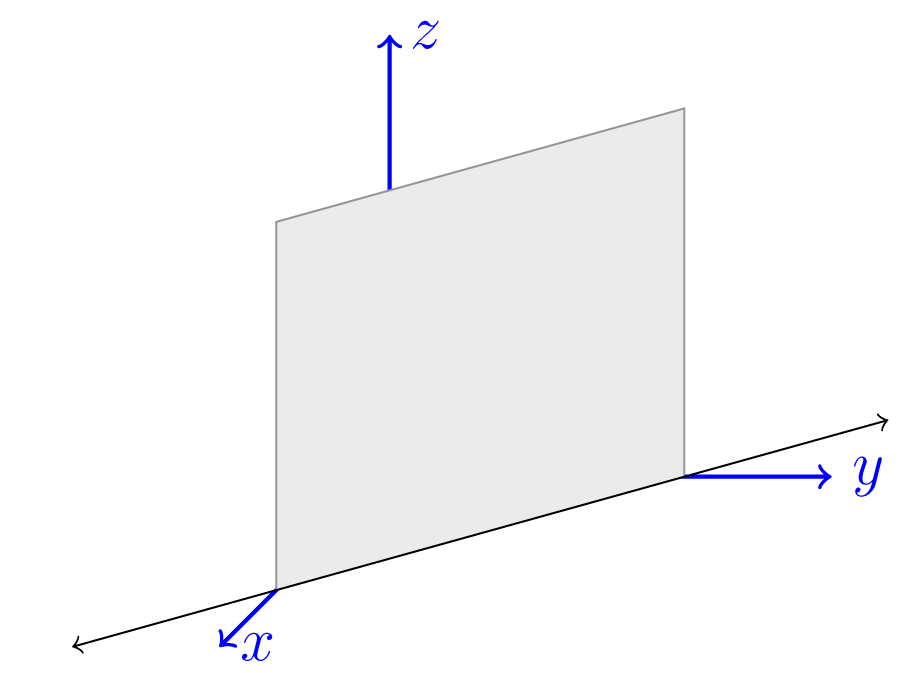
Σχήμα 1.4: Το επίπεδο $x+y=2$ στον ${\mathbb{R}}^{3}$

Στη συνέχεια, βρίσκουμε τα σημεία τομής του επιπέδου $E$ με το $x y$ επίπεδο ( $z=0$ ), δηλ. λύνουμε το γραμμικό σύστημα

$\begin{array}[]{rlc}x+y&&=2\\ &z&=0\end{array},$
που γράφουμε ως $AX=B$ . O επαυξημένος πίνακας του συστήματος είναι o

$\begin{bmatrix}A&|\ B\end{bmatrix}=\left[\begin{array}[]{rrr|c}1&1&0&2\\ 0&0&1&0\end{array}\right]$
και το σύνολο των λύσεων του συστήματος $AX=B$ είναι η ευθεία $L$ που δίνεται από την εξίσωση

$L=\{(2-y,y,0):\ y\in{\mathbb{R}}\}=\{(2,0,0)+y(-1,1,0):\ y\in{\mathbb{R}}\}.$
Η ευθεία $L$ περνά από τα σημεία $(2,0,0)$ , (για $t=0$ ), και $(1,1,1)$ , (για $t=1$ ). Σημειώνουμε ότι η $L$ είναι παράλληλη προς την ευθεία

$\{y(-1,1,0):\ y\in{\mathbb{R}}\},$
που είναι η λύση του ομογενούς συστήματος $AX=\bf 0$ .
3.

Οι εξισώσεις $x_{1}+2x_{2}+3x_{3}=1$ και $x_{1}+2x_{2}+x_{3}=2$ περιγράφουν δύο επίπεδα στον ${\mathbb{R}}^{3}$ . Για να βρούμε την τομή τους, θα βρούμε τα σημεία που ικανοποιούν ταυτόχρονα και τις δύο εξισώσεις. Θα λύσουμε λοιπόν το σύστημα

$\begin{array}[]{cccl}x_{1}&+2x_{2}&+3x_{3}&=1\cr x_{1}&+2x_{2}&+x_{3}&=2\end{% array}\begin{array}[]{r}\\ .\end{array}$
Φέρνουμε τον επαυξημένο πίνακα του προηγούμενου συστήματος σε ελαττωμένη κλιμακωτή μορφή γραμμών:

$\left[\begin{array}[]{rrrrr}1&2&3&|&1\cr 1&2&1&|&2\end{array}\right]% \rightarrow\left[\begin{array}[]{rrrrr}1&2&0&|&5/2\cr 0&0&1&|&-1/2\end{array}% \right].$
Επομένως

$\begin{array}[]{l}x_{1}\;=\;5/2-2x_{2}\\ x_{3}\;=\;-1/2\end{array}$
και οι λύσεις του συστήματος είναι το σύνολο

$L=\{\;(5/2,0,-1/2)+t(-2,1,0)\;:\;t\in{\mathbb{R}}\}.$
Συνεπώς, η τομή των επιπέδων $x_{1}+2x_{2}+3x_{3}=1$ και $x_{1}+2x_{2}+x_{3}=2$ είναι η ευθεία $L$ (βλ. Σχήμα 1.6). Παρατηρούμε ότι η $L$ διέρχεται από τα σημεία $(5/2,0,-1/2)$ ( $t=0$ ) και $(1/2,1,-1/2)$ ( $t=1$ ). Κάθε τιμή του $t\in{\mathbb{R}}$ δίνει ένα σημείο του ${\mathbb{R}}^{3}$ επί της $L$ .

Σχήμα 1.5: Τομή δύο επιπέδων
4.

Ο πίνακας συντελεστών για το ομογενές γραμμικό σύστημα $x=0$ , $y=0$ , $z=0$ , είναι ο πίνακας

$\begin{bmatrix}1&0&0\cr 0&1&0\cr 0&0&1\end{bmatrix}\ .$
H μοναδική λύση αυτού του συστήματος είναι το $(0,0,0)$ . Αφού $x=0$ περιγράφει το $y z$ επίπεδο, $y=0$ περιγράφει to $x z$ επίπεδο και αντίστοιχα $z=0$ περιγράφει to $x y$ επίπεδο, από την προηγούμενη ανάλυση προκύπτει ότι η τομή των τριών επιπέδων είναι η αρχή των αξόνων ${\bf 0}:(0,0,0)$ .

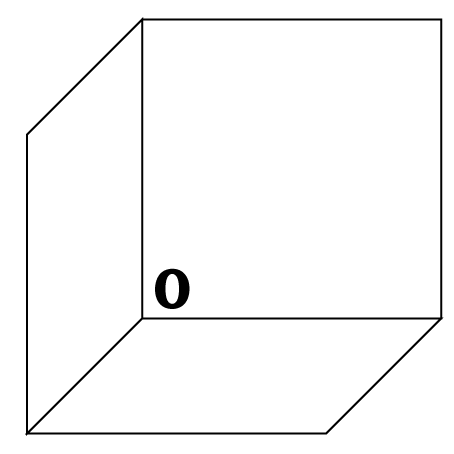
Σχήμα 1.6: Τομή των επιπέδων $x y$ , $x z$ , $y z$
5.

Θα υπολογίσουμε την τομή των τριών επιπέδων $x_{1}+x_{2}+x_{3}=0$ , $x_{1}+2x_{2}-x_{3}=1$ και $2x_{1}+3x_{2}=2$ του ${\mathbb{R}}^{3}$ . Φέρνουμε τον επαυξημένο πίνακα του γραμμικού συστήματος

$\begin{array}[]{cccl}x_{1}&+x_{2}&+x_{3}&=0\cr x_{1}&+2x_{2}&-x_{3}&=1\cr 2x_{% 1}&+3x_{2}&&=2\end{array}$
σε κλιμακωτή μορφή γραμμών:

$\left[\begin{array}[]{rrr|r}1&1&1&0\cr 1&2&-1&1\cr 2&3&0&2\end{array}\right]% \rightarrow\left[\begin{array}[]{rrr|r}1&1&1&0\cr 0&1&-2&1\cr 0&0&0&1\end{% array}\right].$
Το σύστημα αυτό δεν είναι συμβατό, άρα τα τρία επίπεδα δεν έχουν κάποιο κοινό σημείο και η τομή τους είναι το κενό σύνολο.
6.

Έστω τα σημεία $(1,0,0)$ , $(0,1,1)$ και $(0,0,1)$ στο ${\mathbb{R}}^{3}$ . Θα βρούμε την εξίσωση ενός επιπέδου που περνά από τα τρία αυτά σημεία. Η εξίσωση ενός επιπέδου στο ${\mathbb{R}}^{3}$ έχει την μορφή

$ax+by+cz=d\;\textrm{ 'h isod'unama }\;ax+by+cz-d=0.$
Επομένως, θέλουμε να βρούμε τα $a, b, c, d$ έτσι ώστε να ικανοποιούνται οι εξής εξισώσεις:

$\begin{array}[]{ccccl}a&&&-\,d&=0\cr&b&+c&-\,d&=0\cr&&\ c&-\,d&=0\;.\end{array}$ (1.4.2.1)
To γραμμικό σύστημα (1.4.2.1) είναι ομογενές, άρα είναι συμβατό. Φέρνουμε τον πίνακα των συντελεστών σε ελαττωμένη κλιμακωτή μορφή γραμμών:

$\begin{bmatrix}1&0&0&-1\cr 0&1&1&-1\cr 0&0&1&-1\end{bmatrix}\rightarrow\begin{% bmatrix}1&0&0&-1\cr 0&1&0&\ \;0\cr 0&0&1&-1\end{bmatrix}.$
Συνεπώς οι λύσεις του ομογενούς συστήματος (1.4.2.1) είναι το σύνολο

$\{(d,0,d,d):\ d\in{\mathbb{R}}\}=\{t(1,0,1,1):\ t\in{\mathbb{R}}\}.$
Έτσι, αν $t=1$ , βρίσκουμε τη λύση $(1,0,1,1)$ , δηλ. $a=c=d=1$ και $b=0$ . H εξίσωση του επιπέδου είναι

$x+z=1.$
Ο αναγνώστης καλείται να διαπιστώσει ότι όλες οι τιμές στο σύνολο των λύσεων δίνουν το ίδιο επίπεδο.

Ασκήσεις Ενότητας 1.4

1.

Να βρεθεί η εξίσωση της ευθείας $\{(1,4)+t(1,2):\ t\in{\mathbb{R}}\}$ .

Λύση
2.

Να βρεθεί η τομή των επιπέδων $x+2y-z=0$ , $x-y+z=1$ στο ${\mathbb{R}}^{3}$ .

Λύση
3.

Να βρεθεί η εξίσωση του επιπέδου που περνά από τα σημεία $(0,0,0)$ , $(1,0,0)$ και $(0,2,3)$ .

Λύση
4.

Να βρεθούν όλα τα επίπεδα που περνούν από τα σημεία $(0,0,0)$ , $(1,0,1)$ και $(2,0,2)$ . Να εξηγήσετε γιατί δεν υπάρχει μοναδικό επίπεδο που να περνά από αυτά τα σημεία.

Λύση

1.5 Πολυωνυμικές Καμπύλες

Το γράφημα ενός πολυωνύμου $f(x)=a_{0}+a_{1}x+\cdots+a_{n}x^{n}$ , όπου $a_{i}\in{\mathbb{R}}$ για $0\leq i\leq n$ και $a_{n}\neq 0$ , για $n\in{\mathbb{N}}$ , ονομάζεται πολυωνυμική καμπύλη βαθμού $n$ (polynomial curve of degree $n$ ). Τα σημεία μίας πολυωνυμικής καμπύλης είναι της μορφής $(a,b)\in{\mathbb{R}}^{2}$ όπου $b=f(a)$ . Στην ενότητα αυτή, θα δούμε πως να βρίσκουμε την πολυωνυμική καμπύλη βαθμού $n$ που διέρχεται από καθορισμένα σημεία. Αν τα σημεία αυτά προκύπτουν ως πειραματικά δεδομένα που έχουμε συγκεντρώσει, τότε η πολυωνυμική καμπύλη δίνει ένα μοντέλο (model) για το φαινόμενο του πειράματος και μπορεί να χρησιμοποιηθεί για να περιγράψει τη συμπεριφορά του φαινομένου.

Παράδειγμα 1.5.1.

Δίνονται τα σημεία $A(2,4)$ , $B(3,2)$ και $C(5,-8)$ . Θα βρούμε μία πολυωνυμική καμπύλη βαθμού 2 που διέρχεται από τα τρία αυτά σημεία. Στη συνέχεια θα αποδείξουμε ότι υπάρχουν άπειρες πολυωνυμικές καμπύλες βαθμού 3 που διέρχονται από αυτά τα σημεία. Πρώτα θα δείξουμε ότι δεν υπάρχει πολυωνυμική καμπύλη βαθμού $1$ , δηλ. μία ευθεία που να περιέχει τα $Α, Β, C$ .

•

Έστω $y=a_{0}+a_{1}x$ . Τα σημεία $Α, Β, C$ ανήκουν την καμπύλη του $y$ an ικανοποιούνται οι εξισώσεις

$\begin{array}[]{rrrr}a_{0}&+2a_{1}&=&4\\ a_{0}&+3a_{1}&=&2\\ a_{0}&+5a_{1}&=&-8\end{array}\begin{array}[]{l}\\ \\ .\end{array}$
Ο επαυξημένος πίνακας του συστήματος αυτού (με αγνώστους $α_{0}$ , $a_{1}$ ) είναι ο

$\left[\begin{array}[]{cc|c}1&2&4\\ 1&3&2\\ 1&5&-8\end{array}\right]\begin{array}[]{l}\\ \\ .\end{array}$
Παρατηρούμε ότι ο πίνακας των συντελεστών είναι $3\times 2$ και ότι έχει βαθμίδα 2, ενώ η βαθμίδα του επαυξημένου πίνακα είναι 3. Επομένως το σύστημα είναι ασύμβατο και δεν έχει λύση. Συνεπώς δεν υπάρχει πολυωνυμική καμπύλη βαθμού 1 που να διέρχεται από τα 3 αυτά σημεία.
•

Έστω $y=a_{0}+a_{1}x+a_{2}x^{2}$ . Τα σημεία $Α, Β, C$ ανήκουν την καμπύλη του $y$ , αν ικανοποιούνται οι εξισώσεις

$\begin{array}[]{rrclr}a_{0}&+2a_{1}&+4\;a_{2}&=&4\\ a_{0}&+3a_{1}&+\;9a_{2}&=&2\\ a_{0}&+5a_{1}&+25a_{2}&=&-8\end{array}.$
Φέρνουμε τον επαυξημένο πίνακα του συστήματος αυτού (με αγνώστους $α_{0}$ , $a_{1}$ , $a_{2}$ ) σε ελαττωμένη κλιμακωτή μορφή:

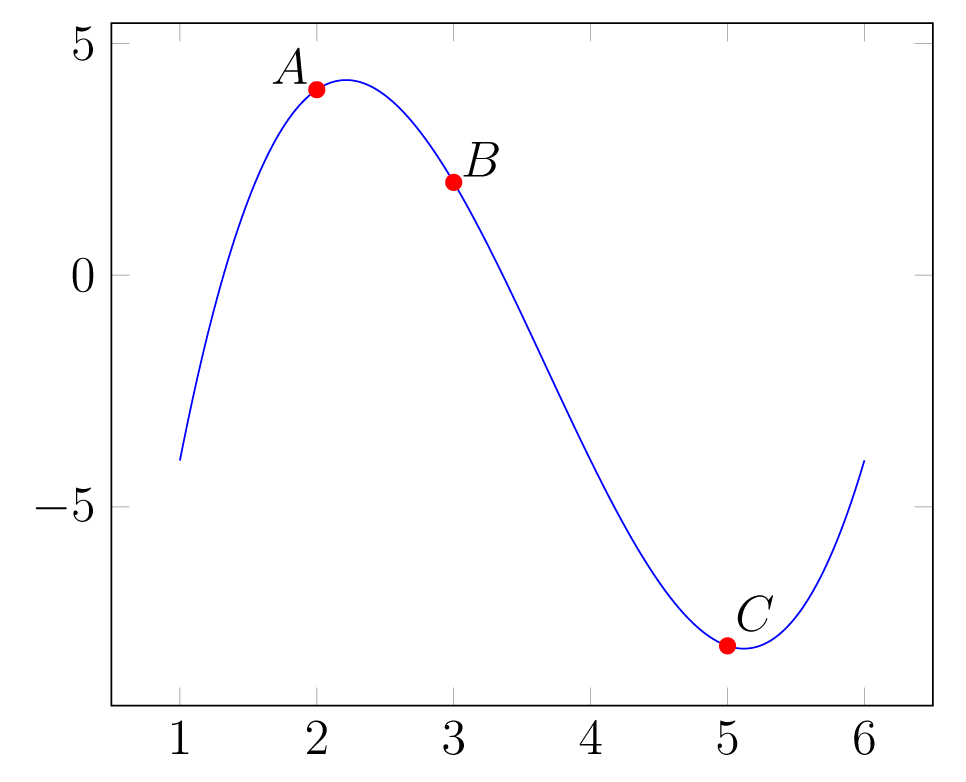
$\left[\begin{array}[]{ccc|r}1&2&4&4\\ 1&3&9&2\\ 1&5&25&-8\end{array}\right|\rightarrow\left|\begin{array}[]{ccc|r}1&0&0&2\\ 0&1&0&3\\ 0&0&1&-1\end{array}\right].$
Συνεπώς το σύστημα έχει τη μοναδική λύση $(2,3,-1)$ . Δηλ. $a_{0}=2$ , $a_{1}=3$ , $a_{2}=-1$ , και τα $A$ , $B$ , $C$ ανήκουν στην καμπύλη $\;y=2+3x-x^{2}$ (βλ. επόμενο σχήμα).

Σχήμα 1.7: H παραβολή $y=-x^{2}+3x+2$ .
•

Έστω ότι $y=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}$ . Τα σημεία $A$ , $B$ και $C$ ανήκουν στην καμπύλη του $y$ αν ικανοποιούνται οι εξισώσεις

$\begin{array}[]{lclcl}a_{0}+2\;a_{1}+&4\;a_{2}+&8\;a_{3}&=\;4\\ a_{0}+3\;a_{1}+&9\;a_{2}+&27a_{3}&=\;2\\ a_{0}+5\;a_{1}+&25a_{2}+&125a_{3}&=-8\;.\end{array}$ (1.5.1.1)
Η ελαττωμένη κλιμακωτή μορφή γραμμών του επαυξημένου πίνακα του συστήματος αυτού είναι

$\left[\begin{array}[]{cccc|c}1&0&0&30&2\\ 0&1&0&-31&3\\ 0&0&1&10&-1\end{array}\right].$
To σύνολο των λύσεων του γραμμικού συστήματος (1.5.1.1)είναι το σύνολο

$\{(2,3,-1,0)+α_{3}(-30,31,-10,1):\ a_{3}\in\mathbb{R}\}\ .$
Όταν $a_{3}=0$ τότε η $4$ -άδα $(2,3,-1,0)$ είναι η παραβολή που βρήκαμε προηγουμένως. Για κάθε άλλο $a_{3}\in\mathbb{R}$ βρίσκουμε μία πολυωνυμική καμπύλη βαθμού 3 που διέρχεται από τα τρία αυτά σημεία. Η πολυωνυμική καμπύλη βαθμού $\leq 3$ που περνά από τα $A, B, C$ είναι γράφημα του πολυωνύμου

$y=(2-30t)+(3+31t)x-(1+10t)x^{2}+tx^{3},$
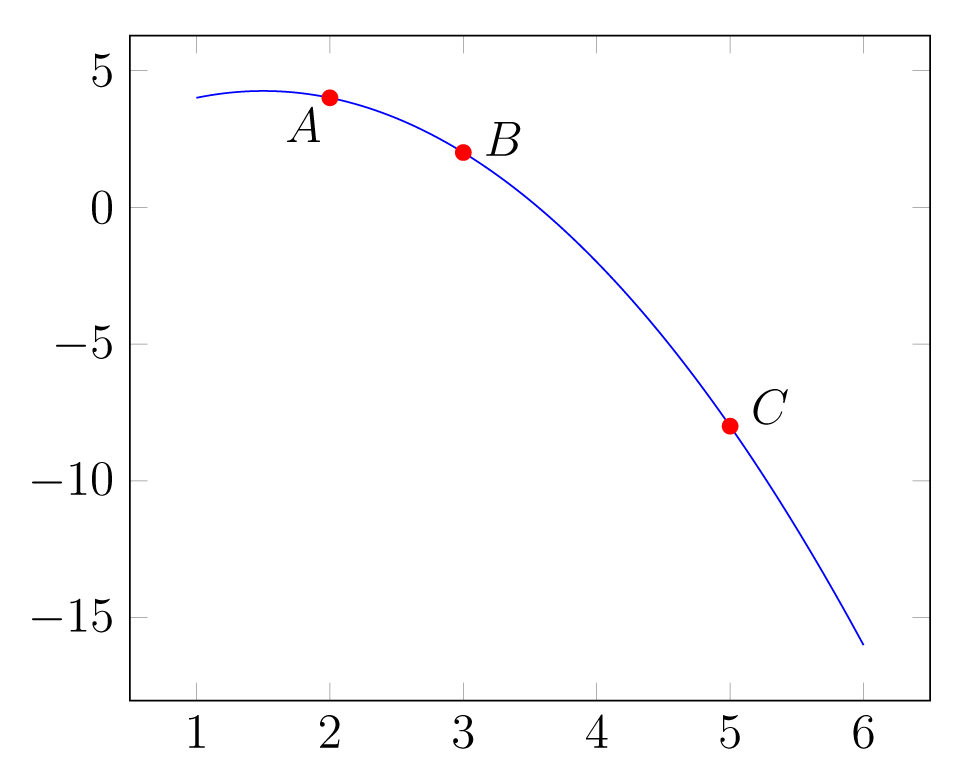
και υπάρχουν, λοιπόν, άπειρες καμπύλες βαθμού 3 που διέρχονται από τα $A, B, C$ . Όταν $t=1$ το πολυώνυμο είναι $\;y=-28+34x-11x^{2}+x^{3}$ και το γράφημά του είναι η καμπύλη του επόμενου σχήματος:

Σχήμα 1.8: H καμπύλη $y=-28+34x-11x^{2}+x^{3}$ .
•

Είναι φανερό ότι για $n\geq 3$ , υπάρχουν $a_{0},a_{1},\ldots,a_{n}$ , έτσι ώστε η καμπύλη του $f(x)=a_{0}+a_{1}x+\cdots+a_{n}x^{n}$ να διέρχεται από τα σημεία $A, B, C$ αφού η ελαττωμένη κλιμακωτή μορφή γραμμών του επαυξημένου πίνακα του αντίστοιχου συστήματος είναι

$\left[\begin{array}[]{cccrccc|c}1&0&0&30&*&\cdots&*&2\\ 0&1&0&-31&*&\cdots&*&3\\ 0&0&1&10&*&\cdots&*&-1\end{array}\right]$
και το σύστημα είναι συμβατό με άπειρες λύσεις.

Το Παράδειγμα 1.5.1 αφορά τρία συγκεκριμένα σημεία του ${\mathbb{R}}^{2}$ . Χρησιμοποιώντας τις ιδιότητες των οριζουσών που θα εισάγουμε στο επόμενο κεφάλαιο, θα δούμε ότι από $n$ διαφορετικά σημεία του ${\mathbb{R}}^{2}$ περνούν άπειρες πολυωνυμικές καμπύλες βαθμού $\geq n$ και ακριβώς μία πολυωνυμική καμπύλη βαθμού $n-1$ , βλ. Άσκηση2.3.6. Κλείνουμε αυτήν την ενότητα με ένα ερώτημα που αφορά τα σημεία $A, B, C$ του Παραδείγματος 1.5.1. Όπως είδαμε δεν υπάρχει ευθεία που να διέρχεται από τρία αυτά σημεία. Μήπως όμως μπορούμε να βρούμε την εξίσωση μίας ευθείας που να διέρχεται όσο γίνεται πιο κοντά από αυτά τα σημεία? Το ερώτημα αυτό έχει νόημα όταν είμαστε πεπεισμένοι ότι το μοντέλο μας είναι σωστό και ότι οι συντεταγμένες των σημείωνδεν έχουν δοθεί με απόλυτη ακρίβεια, από λάθος της μέτρησης ή εξαιτίας άλλων περιορισμών του υπολογιστικού συστήματος. Μπορούμε πράγματι να βρούμε μία ευθεία που να περιορίζει όσο το δυνατόν την απόκλιση. H ευθεία αυτή ονομάζεται ευθεία των ελαχίστων τετραγώνων και θα εξετάσουμε τον υπολογισμό της στην Ενότητα 6.2. Στο Σχήμα (1.9) απεικονίζεται η ευθεία των ελαχίστων τετραγώνων για τα σημεία $A, B, C$ του Παραδείγματος 1.5.1.

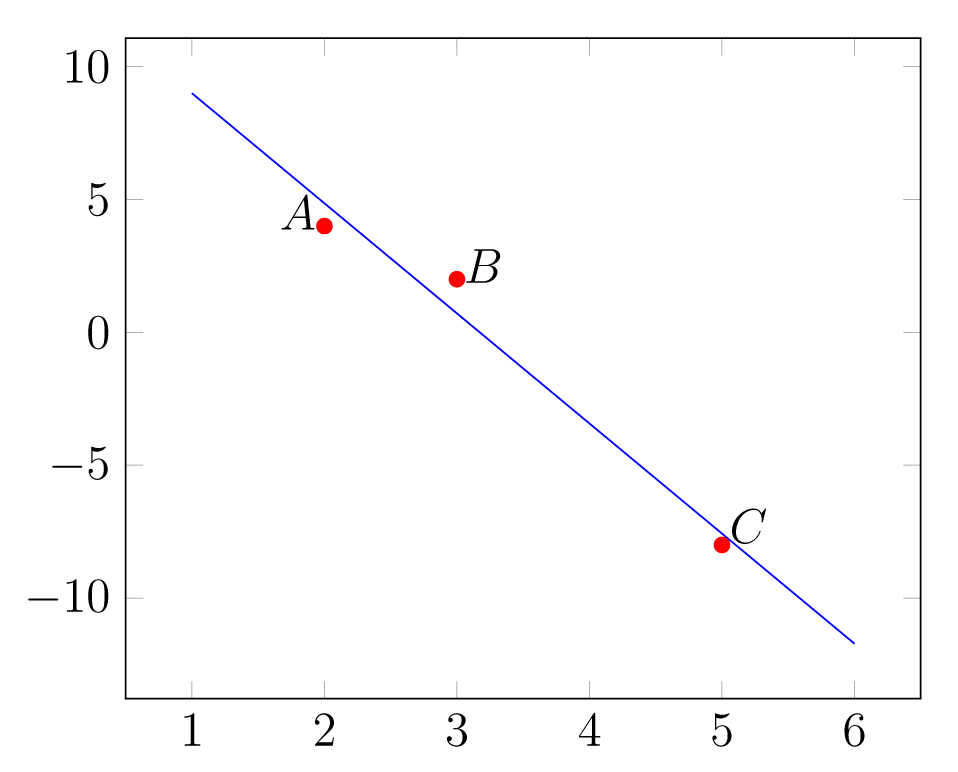Σχήμα 1.9: H ευθεία των ελαχίστων τετραγώνων για τα $A, B, C$ .

Ασκήσεις Ενότητας 1.5

1.

Να βρεθεί αν υπάρχει πολυωνυμική καμπύλη βαθμού το πολύ 2 που διέρχεται από τα σημεία $(-2,5)$ , $(1,-4)$ , $(3,0)$ .

Λύση
2.

Να βρεθεί πολυωνυμική καμπύλη βαθμού το πολύ 3 που διέρχεται από τα σημεία $(-1,0)$ , $(0,2)$ , $(1,2)$ , $(2,6)$ .

Λύση
3.

Να βρεθεί μία πολυωνυμική καμπύλη βαθμού 4 που διέρχεται από τα σημεία $(-1,0)$ , $(0,2)$ , $(1,2)$ , $(2,6)$ .

Λύση

1.6 Σύντομα Ιστορικά Στοιχεία

Το πρόβλημα της επίλυσης γραμμικών συστημάτων απασχόλησε τους μαθηματικούς από τα αρχαία χρόνια. Έχουν βρεθεί αρχαιολογικά ευρήματα που δείχνουν ότι ήδη από το 300 π.Χ. οι αρχαίοι Βαβυλώνιοι έλυναν προβλήματα δύο εξισώσεων με δύο αγνώστους. Είναι επίσης γνωστό ότι οι αρχαίοι Κινέζοι, μεταξύ του 200 π.Χ. και 100 π.Χ., εισήγαγαν την έννοια των πινάκων για την επίλυση τέτοιων συστημάτων. Στο βιβλίο «Εννέα Κεφάλαια της Μαθηματικής Τέχνης», που χρονολογείται στη Δυναστεία Han (206 π.Χ. έως 220 μ.Χ.), αναλύεται με παραδείγματα η μέθοδος που είχαν εφεύρει και που είναι πολύ κοντά στον αλγόριθμο του Gauss. Όμως τα επιτεύγματα των αρχαίων Κινέζων δεν έφτασαν στη Δύση και η πρόοδος στη Γραμμική Άλγεβρα ήταν αργή και αποσπασματική. Ενδεικτικά αναφέρουμε τη συνεισφορά του Ιταλού μαθηματικού Cardanο (1501-1576), που στο βιβλίο του «Ars Magna» (το Μεγάλο Έργο) το 1545 ασχολήθηκε με τη συστηματική επίλυση εξισώσεων με δύο αγνώστους. Σημαντική επίσης υπήρξε η συνεισφορά του Ελβετού μαθηματικού Cramer (1704-1755), ο οποίος το 1750 στην προσπάθειά να βρει την εξίσωση της καμπύλης που διέρχεται από κάποια σημεία, δημοσίευσε τον κανόνα που σήμερα είναι γνωστός με το όνομά του, βλ. Ενότητα 2.3. Τη μεγάλη ώθηση προς τα εμπρός, έδωσε η εργασία του μεγάλου Γερμανού μαθηματικού Gauss (1777-1855). Στις αρχές του 1801 ένας μυστήριος αστεροειδής παρατηρήθηκε από τον Ιταλό μοναχό Piazzi για 41 ημέρες και μετά εξαφανίστηκε. Έτσι ένα από τα μεγάλα προβλήματα που προσπαθούσαν να λύσουν οι αστρονόμοι της εποχής, ήταν να βρουν την τροχιά του αστεροειδή στον αχανή ουρανό Ο νεαρός Gauss χρησιμοποίησε τον αλγόριθμο του και τη μέθοδο των ελαχίστων τετραγώνων την άνοιξη του 1801, για να λύσει το μυστήριο της τροχιάς του αστεροειδούς, ο οποίος βρέθηκε και πάλι στο τέλος του έτους πολύ κοντά στις συντεταγμένες που προέβλεψε ο Gauss. Ο Gauss περιέγραψε κάποιες από τις ιδέες του το 1802. H εργασία του θεωρείται από τις πρώτες εργασίες που ασχολούνται με την επίλυση γραμμικών εξισώσεων χρησιμοποιώντας τεχνικές της μοντέρνας Γραμμικής Άλγεβρας. Για περισσότερα ιστορικά στοιχεία παραπέμπουμε στο σύγγραμμα [3].

Βιβλιογραφία

1.

H. Anton, C. Rorres, Elementary Linear Algebra, Applications Version, John Wiley and Sons, 1994.
2.

Θ. Θεοχάρη-Αποστολίδη, Χ. Χαραλάμπους, Β. Βαβατσούλας, Εισαγωγή στη Γραμμική Άλγεβρα, Θεσσαλονίκη 2006.
3.

V. Katz, Ιστορία των Μαθηματικών , Πανεπιστημιακές Εκδόσεις Κρήτης, 2013
4.

K. Nicholoson, Elementary Linear Algebra, McGraw-Hill, 2001.
5.

Th. Shiffrin and M. R.Adams, Linear Algebra, a Geometric Approach, W. H. Freeman and Company, 2002

Κεφάλαιο 1Γραμμικά Συστήματα

1.1 Γραμμικά Συστήματα

Παραδείγματα 1.1.1.

Πρόταση 1.1.2.

Πρόταση 1.1.3.

Απόδειξη.

Παρατήρηση 1.1.4

Ασκήσεις Ενότητας 1.1

1.2 Στοιχειώδεις Πράξεις Γραμμών

Ορισμός 1.2.1.

Παραδείγματα 1.2.2.

Ορισμός 1.2.3.

Παραδείγματα 1.2.4.

Παραδείγματα 1.2.5.

Πρόταση 1.2.6.

Απόδειξη.

Ορισμός 1.2.7.

Παραδείγματα 1.2.8.

Παρατήρηση 1.2.9.

Παράδειγμα 1.2.10.

Ασκήσεις Ενότητας 1.2

1.3 Επίλυση Γραμμικών Συστημάτων

Πρόταση 1.3.1.

Παραδείγματα 1.3.2.

Πρόταση 1.3.3.

Πρόταση 1.3.4.

Ασκήσεις Ενότητας 1.3

1.4 Ευθείες και Επίπεδα στον ${\mathbb{R}}^{2}$ και ${\mathbb{R}}^{3}$

Ευθείες στον ${\mathbb{R}}^{2}$

Παραδείγματα 1.4.1.

Ευθείες και Επίπεδα στον ${\mathbb{R}}^{3}$

Παραδείγματα 1.4.2.

Ασκήσεις Ενότητας 1.4

1.5 Πολυωνυμικές Καμπύλες

Παράδειγμα 1.5.1.

Ασκήσεις Ενότητας 1.5

1.6 Σύντομα Ιστορικά Στοιχεία

Βιβλιογραφία

Κεφάλαιο 1Γραμμικά Συστήματα

1.1 Γραμμικά Συστήματα

Παραδείγματα 1.1.1.

Πρόταση 1.1.2.

Πρόταση 1.1.3.

Απόδειξη.

Παρατήρηση 1.1.4

Ασκήσεις Ενότητας 1.1

1.2 Στοιχειώδεις Πράξεις Γραμμών

Ορισμός 1.2.1.

Παραδείγματα 1.2.2.

Ορισμός 1.2.3.

Παραδείγματα 1.2.4.

Παραδείγματα 1.2.5.

Πρόταση 1.2.6.

Απόδειξη.

Ορισμός 1.2.7.

Παραδείγματα 1.2.8.

Παρατήρηση 1.2.9.

Παράδειγμα 1.2.10.

Ασκήσεις Ενότητας 1.2

1.3 Επίλυση Γραμμικών Συστημάτων

Πρόταση 1.3.1.

Παραδείγματα 1.3.2.

Πρόταση 1.3.3.

Πρόταση 1.3.4.

Ασκήσεις Ενότητας 1.3

1.4 Ευθείες και Επίπεδα στον ℝ2 και ℝ3

Ευθείες στον ℝ2

Παραδείγματα 1.4.1.

Ευθείες και Επίπεδα στον ℝ3

Παραδείγματα 1.4.2.

Ασκήσεις Ενότητας 1.4

1.5 Πολυωνυμικές Καμπύλες

Παράδειγμα 1.5.1.

Ασκήσεις Ενότητας 1.5

1.6 Σύντομα Ιστορικά Στοιχεία

Βιβλιογραφία

1.4 Ευθείες και Επίπεδα στον ${\mathbb{R}}^{2}$ και ${\mathbb{R}}^{3}$

Ευθείες στον ${\mathbb{R}}^{2}$

Ευθείες και Επίπεδα στον ${\mathbb{R}}^{3}$