Μια Εισαγωγή στη Γραμμική Άλγεβρα για τις Θετικές Επιστήμες

Κεφάλαιο 4Γραμμικές Συναρτήσεις

Στο κεφάλαιο αυτό θα μελετήσουμε μία ειδική κατηγορία συναρτήσεων μεταξύ των $\Bbbk$ -διανυσματικών χώρων. Θα δούμε ότι οι συναρτήσεις αυτές καθορίζονται πλήρως από τις τιμές που λαμβάνουν τα στοιχεία των βάσεων. Για να τις μελετήσουμε θα αντιστοιχήσουμε πίνακες σε αυτές τις συναρτήσεις και θα χρησιμοποιήσουμε τα συμπεράσματά μας από τη θεωρία πινάκων (Κεφάλαιο 2) .

4.1 Γραμμικές Συναρτήσεις, I

Έστω $V$ , $W$ δύο $\Bbbk$ -διανυσματικοί χώροι. H δομή που έχουν αυτοί οι χώροι είναι σημαντική. Ποιές είναι, λοιπόν, οι ιδιότητες που επιθυμούμε να έχουν οι καλές συναρτήσεις $f:\ V\rightarrow W$ ; Δεν θέλει πολύ σκέψη για να αποφασίσουμε ότι θέλουμε οι ευθείες του $V$ να απεικονίζονται σε ευθείες του $W$ . Αφού, λοιπόν, οι ευθείες στο $V$ περιγράφονται ως πολλαπλάσια ενός διανύσματος, θέλουμε για κάθε $v\in V$ να ισχύει ότι

f(\kappa v)=\kappa f(v),\ \textrm{ gia }\kappa\in\Bbbk\;.

Σε αυτήν την ιδιότητα οφείλουν οι γραμμικές συναρτήσεις το όνομά τους. H άλλη ιδιότητα των καλών συναρτήσεων σχετίζεται με το άθροισμα των διανυσμάτων. Αθροίσματα στον $V$ οφείλουν να απεικονίζονται σε αθροίσματα στον $W$ . Επομένως απαιτούμε

f(v+u)=f(v)+f(u)

για οποιαδήποτε δύο διανύσματα $v,u\in V$ .

Ορισμός 4.1.1.

Έστω $V$ , $W$ δύο $\Bbbk$ -διανυσματικοί χώροι. Μία συνάρτηση $f:\ V\rightarrow W$ λέγεται γραμμική συνάρτηση (linear transformation) αν

i.

$f(v+u)=f(v)+f(u)$ ,
ii.

$f(\kappa v)=\kappa f(v)$ ,

για όλα τα $\kappa\in\Bbbk$ , $v,u\in V$ . Ισοδύναμα η συνάρτηση $f:\ V\rightarrow W$ είναι γραμμική συνάρτηση αν και μόνο αν

f(k\cdot v+t\cdot u)=k\cdot f(v)+t\cdot f(w),\;\;k,t\in\Bbbk,v,w\in V.

Στο επόμενο σχήμα θα επιχειρήσουμε να δώσουμε τη γεωμετρική εποπτεία για μία γραμμική συνάρτηση $f:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{3}$ . Αφού ευθείες του ${\mathbb{R}}^{2}$ απεικονίζονται σε ευθείες του ${\mathbb{R}}^{3}$ και αθροίσματα στον ${\mathbb{R}}^{2}$ απεικονίζονται σε αθροίσματα στον ${\mathbb{R}}^{3}$ , είναι φανερό ότι πρέπει να ισχύουν τα εξής:

•

η εικόνα του μηδενικού διανύσματος (σημείο) του ${\mathbb{R}}^{2}$ στον ${\mathbb{R}}^{3}$ είναι το μηδενικό διάνυσμα του ${\mathbb{R}}^{3}$ ,
•

όλα τα διανύσματα στο εσωτερικό του παραλληλογράμμου που ορίζεται από δύο διανύσματα $v, w$ απεικονίζονται σε διανύσματα που βρίσκονται στο εσωτερικό του παραλληλογράμμου που ορίζεται από τα $f(v)$ , $f(w)$ .

Σχήμα 4.1: H γραμμική συνάρτηση $f:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{3}$

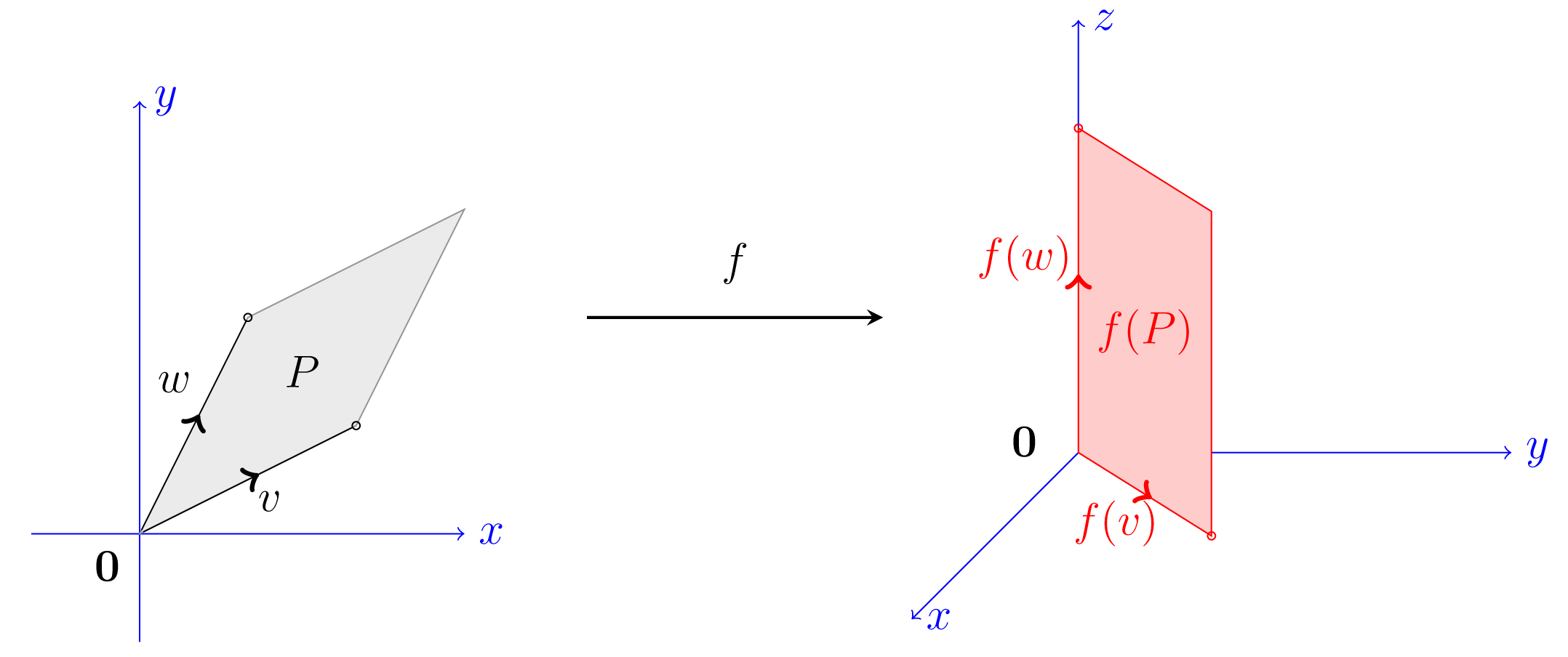
Έστω $f:V\rightarrow W$ μία γραμμική συνάρτηση. Γενικεύουμε την προηγούμενη παρατήρηση και θα δείξουμε ότι $f({\bf 0})={\bf 0}$ . Πράγματι αν $v\in V$ , τότε

\;\;f({\bf 0})=f(0v)=0f(v)={\bf 0}\ .\;\;

Αποδείξαμε λοιπόν ότι:

Αν $f:V\rightarrow W$ μία γραμμική συνάρτηση, τότε $f({\bf 0})={\bf 0}$ .

Παραδείγματα 4.1.2.

1.

Έστω $V, W$ δύο $\Bbbk$ -διανυσματικοί χώροι. Η συνάρτηση $V\rightarrow W$ , $v\mapsto\bf 0$ είναι γραμμική συνάρτηση και λέγεται μηδενική ή τετριμμένη συνάρτηση (trivial transformation) στον $V$ .
2.

Έστω $V$ $\Bbbk$ -διανυσματικός χώρος. Η συνάρτηση $\operatorname{id}_{V}:V\rightarrow V$ , $v\mapsto v$ είναι γραμμική συνάρτηση και λέγεται ταυτοτική συνάρτηση identity transformation) στον $V$ .
3.

H $f:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ , $(x,y)\mapsto(x+1,y)$ δεν είναι γραμμική συνάρτηση, αφού ${\bf 0}\mapsto(1,0)\neq{\bf 0}$ .
4.

Η συνάρτηση $f:\Bbbk^{3}\rightarrow\Bbbk^{2}$ , $(x,y,z)\mapsto(x-z,x+y)$ είναι γραμμική. Πράγματι:

$\displaystyle(x_{1},y_{1},z_{1})+(x_{2},y_{2}+z_{2})=(x_{1}+x_{2},y_{1}+y_{2},% z_{1}+z_{2})\mapsto\\ \displaystyle\left((x_{1}+x_{2})-(z_{1}+z_{2}),(x_{1}+x_{2})+(y_{1}+y_{2})% \right)\\ \displaystyle=(x_{1}-z_{1},x_{1}+y_{1})+(x_{2}-z_{2},x_{2}+y_{2})=f(x_{1},y_{1% },z_{1})+f(x_{2},y_{2},z_{2})$
και

$c(x,y,z)=(cx,cy,cz)\mapsto(cx-cz,cx+cy)=c(x-z,x+y)=cf(x,y,z)\;.$
5.

O αναγνώστης καλείται να επιβεβαιώσει ότι η συνάρτηση $\phi:\Bbbk^{n}\longrightarrow\mathcal{M}_{n\times 1}(\Bbbk)$ , $(b_{1},\ldots,b_{n})\ \mapsto\begin{bmatrix}b_{1}&\cdots&b_{n}\end{bmatrix}^{T}$ , της Παρατήρησης 3.2.8 είναι γραμμική συνάρτηση.

Έστω $f:\ V\rightarrow W$ μία γραμμική συνάρτηση, $B$ και $D$ διατεταγμένες βάσεις των $V$ και $W$ αντίστοιχα. Θα δείξουμε ότι όλες οι πληροφορίες της $f:V\rightarrow W$ αποθηκεύονται σε έναν $m\times n$ πίνακα, όπου $m={\rm dim}_{\Bbbk}W$ και $n={\rm dim}_{\Bbbk}W$ . O πίνακας αυτός συμβολίζεται με $A^{f}_{D,B}$ . Αν $Β=\big(v_{1},\ldots,v_{n}\big)$ , τότε η $ι$ στήλη του $A^{f}_{D,B}$ είναι ο $C_{D}\left(f(v_{i})\right)$ , δηλ.

[\;A^{f}_{D,B}=\left[\begin{array}[]{cccc}C_{D}\left(f(v_{1})\right)&\cdots&C_% {D}\left(f(v_{n})\right)\end{array}\right].\;]

Θα υπολογίσουμε τους πίνακες $A^{f}_{D,B}$ , για κάποιες από τις γραμμικές συναρτήσεις των Παραδειγμάτων 4.1.2.

Παραδείγματα 4.1.3.

1.

Έστω η μηδενική συνάρτηση $f:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{3}$ . Αν $B$ και $D$ είναι διατεταγμένες βάσεις των ${\mathbb{R}}^{2}$ και ${\mathbb{R}}^{3}$ o πίνακας της $f$ είναι ο μηδενικός $3\times 2$ πίνακας:

$A^{f}_{D,B}=\begin{bmatrix}0&0&0\cr 0&0&0\end{bmatrix}\ .$
2.

Αν o $V$ είναι διανυσματικός χώρος διάστασης $n$ , o $W$ είναι διανυσματικός χώρος διάστασης $m$ , $B$ και $D$ διατεταγμένες βάσεις των $V$ και $W$ και $f:\ V\rightarrow W$ η μηδενική συνάρτηση, τότε $A^{f}_{D,B}$ είναι o μηδενικός πίνακας στον $\mathcal{M}_{m\times n}(\Bbbk)$ .
3.

Έστω $V={\mathbb{R}}^{2}$ , $B=\big(v_{1},v_{2}\big)$ μία διατεταγμένη βάση του $V$ και $\operatorname{id}_{V}:\ V\rightarrow V$ ταυτοτική συνάρτηση στον $V$ . Αφού $\operatorname{id}_{V}(v_{1})=v_{1}$ και $\operatorname{id}_{V}(v_{2})=v_{2}$ , προκύπτει ότι

$A^{\operatorname{id}_{V}}_{B,B}=Ι_{2}\;.$
Έστω τώρα $B=\big(e_{1},e_{2}\big)$ και $D=\big(-e_{2},2e_{1}\big)$ . Αφού $id_{v}(e_{1})=e_{1}=0(-e_{2})+1/2(2e_{1})$ και $id_{v}(e_{2})=e_{2}=-(-e_{2})$ , έπεται ότι

$A^{\operatorname{id}_{V}}_{D,B}=\begin{bmatrix}0&-1\cr\frac{1}{2}&0\end{% bmatrix}.$
O αναγνώστης μπορεί να διαπιστώσει ότι

$A^{\operatorname{id}_{V}}_{Β,D}=\begin{bmatrix}0&2\cr-1&0\end{bmatrix}\textrm{% kai 'oti }\left(A^{\operatorname{id}_{V}}_{D,B}\right)^{-1}=A^{\operatorname{% id}_{V}}_{Β,D}\;.$
4.

Αν o $V$ είναι διανυσματικός χώρος διάστασης $n$ και $B$ είναι μία διατεταγμένη βάση του $V$ , τότε

$A^{\operatorname{id}_{V}}_{B,B}=Ι_{n}\;.$
5.

Θεωρούμε τη γραμμική συνάρτηση

$f:\Bbbk^{3}\rightarrow\Bbbk^{2}\;,\;\;\;\;(x,y,z)\mapsto(x-z,x+y).$
Έστω $Β=(e_{1},e_{2},e_{3})$ η κανονική βάση του $\Bbbk^{3}$ και $D=(\epsilon_{1},\epsilon_{2})$ η κανονική βάση του $\Bbbk^{2}$ . Τότε

$f(e_{1})=(1,1)=\epsilon_{1}+\epsilon_{2},\hbox{ άρα }C_{D}(f(e_{1}))=[1\ 1]^{T% }\ .$
Επίσης

$f(e_{2})=(0,1)=0\epsilon_{1}+1\epsilon_{2}.\hbox{ άρα }C_{D}(f(e_{2}))=[0\ 1]^{T}\ .$
Τέλος

$f(e_{3})=(-1,0)=-1\epsilon_{1}+0\epsilon_{2},\hbox{άρα }C_{D}(f(e_{3}))=[-1\ 0% ]^{T}\ .$
Άρα

$A^{f}_{D,B}=\left[\begin{array}[]{rrr}1&0&-1\\ 1&1&0\end{array}\right]\begin{array}[]{c}\end{array}.$
Παρατηρούμε ότι

$A^{f}_{D,B}\begin{bmatrix}x\cr y\cr z\end{bmatrix}=\left[\begin{array}[]{rrr}1% &0&-1\\ 1&1&0\end{array}\right]\begin{array}[]{c}\end{array}\begin{bmatrix}x\cr y\cr z% \end{bmatrix}=\left[\begin{array}[]{c}x-z\cr x+y\end{array}\right].$

Η επόμενη πρόταση είναι ιδιαίτερα χρήσιμη.

Πρόταση 4.1.4.

Έστω $f:\ V\rightarrow W$ μία γραμμική συνάρτηση, $B$ και $D$ διατεταγμένες βάσεις των $V$ και $W$ αντίστοιχα. Τότε για κάθε $v\in F$ ισχύει ότι

C_{D}(f(v))=A^{f}_{D,B}\ C_{B}(v).

Απόδειξη.

Έστω ότι $Β=\big(v_{1},\ldots,v_{n}\big)$ και ότι $v=k_{1}v_{1}+\cdots+k_{n}v_{n}$ , δηλ.

C_{B}(v)=\begin{bmatrix}k_{1}&\cdots&k_{n}\end{bmatrix}^{T}.

Αφού $f$ είναι γραμμική συνάρτηση, προκύπτει ότι

f(v)=f(k_{1}v_{1}+\cdots+k_{n}v_{n})=f(k_{1}v_{1})+\cdots+f(k_{n}v_{n})=k_{1}f% (v_{1})+\cdots+k_{n}f(v_{n}).

Αν $D=(w_{1},\ldots,w_{m})$ , τότε γράφοντας τα $f(v_{i})$ ως γραμμικούς συνδυασμούς των $w_{j}$ , για $1\leq j\leq m$ και $1\leq i\leq n$ , και συγκεντρώνοντας τους αντίστοιχους συντελεστές, προκύπτει ότι

C_{D}(f(v))=k_{1}C_{D}(f(v_{1}))+\cdots+k_{n}C_{D}(f(v_{n}))=A^{f}_{D,B}\ % \begin{bmatrix}k_{1}\cr\vdots\cr k_{n}\end{bmatrix}\ .

∎

Αντίστροφα αν καθορίσουμε διατεταγμένες βάσεις $Β=(v_{1},\ldots,v_{n})$ και $D=(w_{1},\ldots,w_{n})$ για τους χώρους $V$ και $W$ , τότε σε κάθε πίνακα $A=(\alpha_{ij})\in M_{m\times n}({\mathbb{R}})$ αντιστοιχεί μία γραμμική συνάρτηση $f:\ V\rightarrow W$ που ορίζεται από τη σχέση

C_{D}(f(v))=A\ C_{B}(v)\ .

(4.1.4.1)

H $i$ στήλη του $Α$ είναι ίση με $C_{D}\left(f(v_{i})\right)$ . Για παράδειγμα, η εικόνα του $f(v_{1})$ βρίσκεται από την πρώτη στήλη του $Α$ :

f(v_{1})=a_{11}w_{1}+a_{21}w_{2}+\cdots+a_{n1}w_{n}\ .

Με τον ίδιο τρόπο μπορούμε να υπολογίσουμε τις εικόνες $f(v_{i})$ για κάθε $v_{i}\in Β$ . Προκύπτει, λοιπόν, το εξής συμπέρασμα.

Πρόταση 4.1.5.

Έστω $A=(\alpha_{ij})\in M_{m\times n}(\Bbbk)$ , και $B$ , $D$ διατεταγμένες βάσεις για τους $V$ και $W$ αντίστοιχα. Τότε υπάρχει γραμμική συνάρτηση $f:\ V\rightarrow W$ έτσι ώστε $A^{f}_{D,B}=Α$ . Αντίστροφα, σε κάθε γραμμική συνάρτηση $f:\ V\rightarrow W$ αντιστοιχεί ένας $m\times n$ πίνακας $A\in M_{m\times n}(\Bbbk)$ .

Στα επόμενα παραδείγματα θα εντρυφήσουμε σε αυτές τις έννοιες.

Παραδείγματα 4.1.6.

1.

Έστω ότι $f:\ \Bbbk^{2}\rightarrow\Bbbk^{2}$ γραμμική συνάρτηση και ότι $f(e_{1})=(1,1)$ και $f(e_{2})=(1,2)$ . Έστω $Β$ η κανονική βάση του $\Bbbk^{2}$ . Τότε

$Α_{Β,Β}^{f}=\begin{bmatrix}1&1\cr 1&2\end{bmatrix}\ .$
Θα υπολογίσουμε την εικόνα του $v=(a,b)$ . Από τη Σχέση (4.1.4.1) έχουμε ότι

$C_{B}(f(v))=Α_{Β,Β}^{f}\begin{bmatrix}a\cr b\end{bmatrix}=\begin{bmatrix}a+b% \cr a+2b\end{bmatrix}$
και $f(a,b)=(a+b,a+2b)$ .
2.

Έστω ότι η γραμμική συνάρτηση $f:\Bbbk^{3}\rightarrow\Bbbk^{3}$ έχει πίνακα

$A^{φ}_{Β,Β}=\left[\begin{array}[]{rrr}1&2&5\\ 0&1&1\\ 3&0&2\end{array}\right],$
ως προς την κανονική βάση $B=(e_{1},e_{2},e_{3})$ του $R^{3}$ . Έπεται ότι

$f(e_{1})=(1,0,3),\;\;\;f(e_{2})=(2,1,0),\;\;\;f(e_{3})=(5,1,2).$
Άρα, αν $v=\kappa_{1}e_{1}+\kappa_{2}e_{2}+\kappa_{3}e_{3}$ , τότε

$C_{B}(v)=\begin{bmatrix}\kappa_{1}\cr\kappa_{2}\cr\kappa_{3}\end{bmatrix},% \quad C_{B}(f(v))=A\ C_{B}(v)=\begin{bmatrix}\kappa_{1}+2\kappa_{2}+5\kappa_{3% }\cr\kappa_{2}+\kappa_{3}\cr 3\kappa_{1}+2\kappa_{3}\end{bmatrix},$
και $f(v)=(\kappa_{1}+2\kappa_{2}+5\kappa_{3},\kappa_{2}+\kappa_{3},3\kappa_{1}+2% \kappa_{3})$ .
3.

Θεωρούμε τους ${\mathbb{R}}$ -διανυσματικούς χώρους $\Bbbk^{3}$ και $\Bbbk^{4}$ με αντίστοιχες διατεταγμένες κανονικές βάσεις $B=(e_{1},e_{2},e_{3})$ και $D=(\epsilon_{1},\epsilon_{2},\epsilon_{3},\epsilon_{4})$ . Έστω η γραμμική συνάρτηση $f:\Bbbk^{3}\rightarrow\Bbbk^{4}$ με πίνακα

$A^{f}_{D,B}=\begin{bmatrix}1&2&3\cr 4&5&6\cr 7&8&9\cr 10&11&12\end{bmatrix}% \begin{array}[]{c}\end{array}.$
Για τον αναλυτικό τύπο της $f$ έχουμε ότι

$A^{f}_{D,B}\begin{bmatrix}a\cr b\cr c\end{bmatrix}=\begin{bmatrix}a+2b+3c\cr 4% a+5b+6c\cr 7a+8b+9c\cr 10a+11b+12c\end{bmatrix}$
και άρα

$f(a,b,c)=(a+2b+3c,4a+5b+6c,7a+8b+9c,10a+11b+12c)\ .$
4.

Η αριστερόστροφη περιστροφή (counterclockwise rotation) κατά γωνία $\theta$ , είναι η συνάρτηση $r_{\theta}$ του ${\mathbb{R}}^{2}$ που περιστρέφει το διάνυσμα $Ο Α$ κατά γωνία $\theta$ με φορά αντίθετη των δεικτών του ρολογιού. Η γεωμετρική παράσταση της συνάρτησης δίνεται στο Σχήμα (4.2).

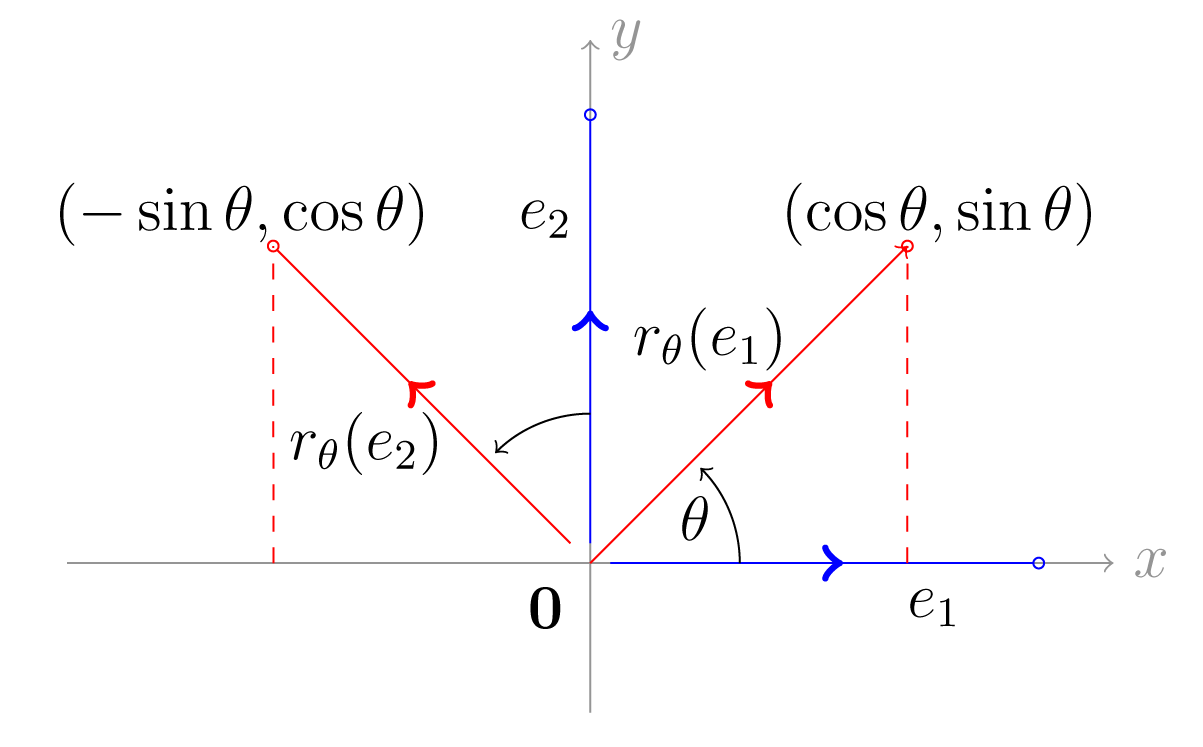
Σχήμα 4.2: Αριστερόστροφη περιστροφή κατά γωνία $\theta$

Επομένως

$r_{\theta}:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(\alpha,\beta% )\mapsto(\alpha^{\prime},\beta^{\prime}).$
Από τα όμοια τρίγωνα που σχηματίζονται δεν είναι δύσκολο να παρατηρήσει κάποιος ότι $(1,0)\mapsto(\cos\theta,\sin\theta)$ , ενώ $(0,1)\mapsto(-\sin\theta,\cos\theta)$ . Έτσι ο πίνακας που αντιστοιχεί στην $r_{\theta}$ ως προς τη κανονική βάση είναι

$\left[\begin{array}[]{rr}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta\end{array}\right]\begin{array}[]{c}\end{array}.$
και

$r_{\theta}(a,b)=(\cos\theta\ a-\sin\theta\ b,\sin\theta\ a+\cos\theta\ b)\;.$
5.

Η συνάρτηση

$f:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(\alpha,\beta)\mapsto(% k\alpha,\beta),$
για κάποιο θετικό πραγματικό αριθμό $k$ , λέγεται διαστολή (dilation) ως προς τον άξονα των Χ αν $k\geq 1$ , ενώ αν $0<k<1$ , τότε η $f$ λέγεται συστολή (contraction) ως προς τον άξονα των Χ. Ο πίνακας της $f$ ως προς τη κανονική βάση του ${\mathbb{R}}^{2}$ είναι ο

$\begin{bmatrix}κ&0\cr 0&1\end{bmatrix}\begin{array}[]{c}\end{array}$
και ο τύπος της $f$ είναι $f(a,b)=(κa,b)$ . Ανάλογα ορίζεται η συνάρτηση διαστολής ή συστολής ως προς τον άξονα των $Y$ .

Στη συνέχεια βλέπουμε το αποτέλεσμα της διαστολής ως προς τον άξονα των Χ με $k=2$ .

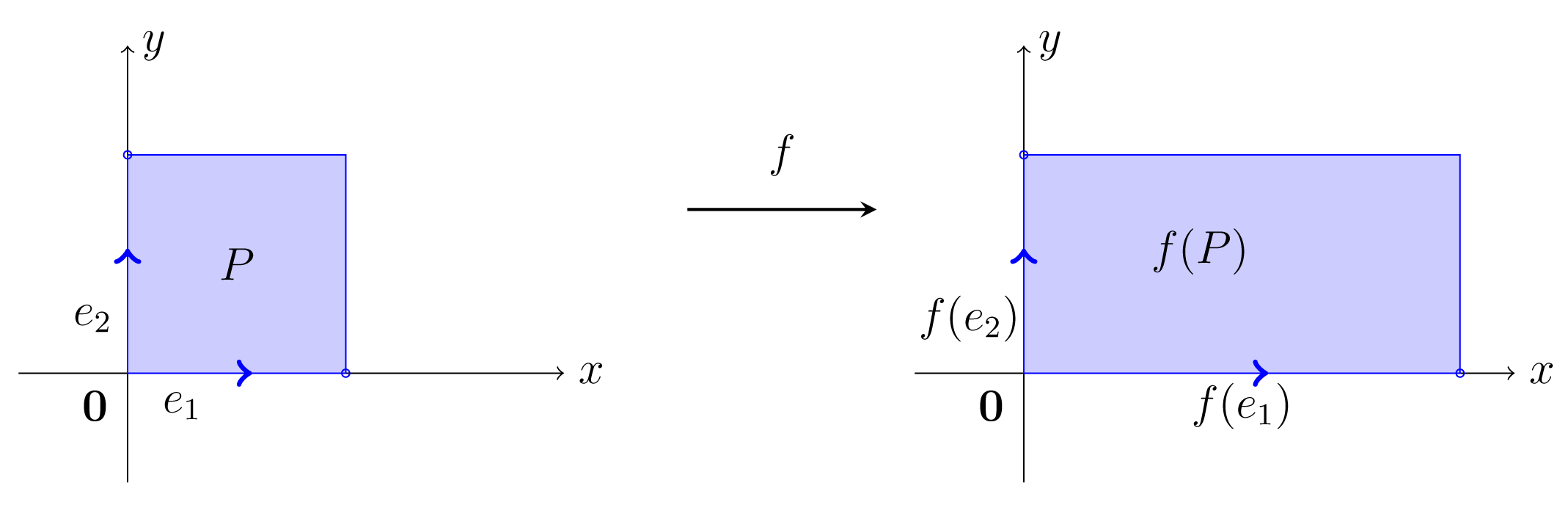
Σχήμα 4.3: Διαστολή ως προς τον άξονα των $X$ με συντελεστή $2$
6.

Έστω $m$ κάποιος πραγματικός αριθμός. Η συνάρτηση $φ:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ που απεικονίζει το διάνυσμα $\vec{ΟA}$ στο διάνυσμα $\vec{ΟΑ_{1}}$ επί της ευθείας με εξίσωση $y=mx$ έτσι ώστε $\vec{ΟΑ_{1}}$ να είναι ορθογώνιο στο $\vec{ΑΑ_{1}}$ , λέγεται προβολή (projection) στην προαναφερθείσα ευθεία. Γεωμετρικά η συνάρτηση αναπαριστάται όπως στο Σχήμα (4.4):

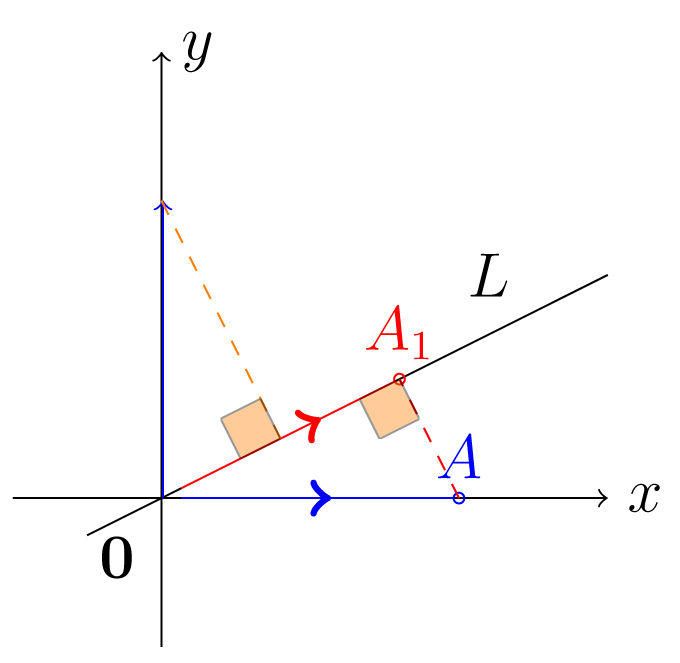
Σχήμα 4.4: Προβολή στην ευθεία $y=mx$

Στο επόμενο κεφάλαιο θα δούμε πως να υπολογίζουμε τις προβολές με τη βοήθεια των εσωτερικών γινομένων.
7.

Η συνάρτηση $f$ του $\Bbbk^{2}$ που αντιστοιχεί το $Ο A$ στο $ΟA^{\prime}$ που απέχει από την ευθεία με εξίσωση $y=mx$ όσο και το $Ο Α$ λέγεται αντικατοπτρισμός (reflection):

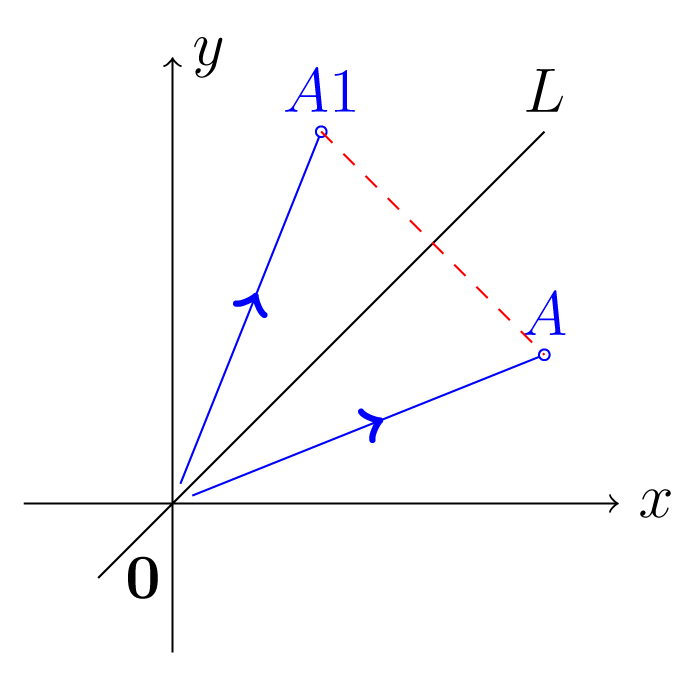
Σχήμα 4.5: Αντικατοπτρισμός ως προς την ευθεία $y=mx$

Θα βρούμε τον πίνακα του αντικατοπτρισμού $f$ ως προς τον άξονα των $X$ για τη κανονική βάση $B=\{e_{1},e_{2}\}$ του ${\mathbb{R}}^{2}$ , βλ. Σχήμα (4.6). Παρατηρούμε ότι $f(e_{1})=e_{1}$ ενώ $f(e_{2})=(0,-1)$ . Άρα

$Α_{Β,Β}=\begin{bmatrix}1&0\cr 0&-1\end{bmatrix},\textrm{ και epom'enwc }f(a,b)% =(a,-b)\;.$

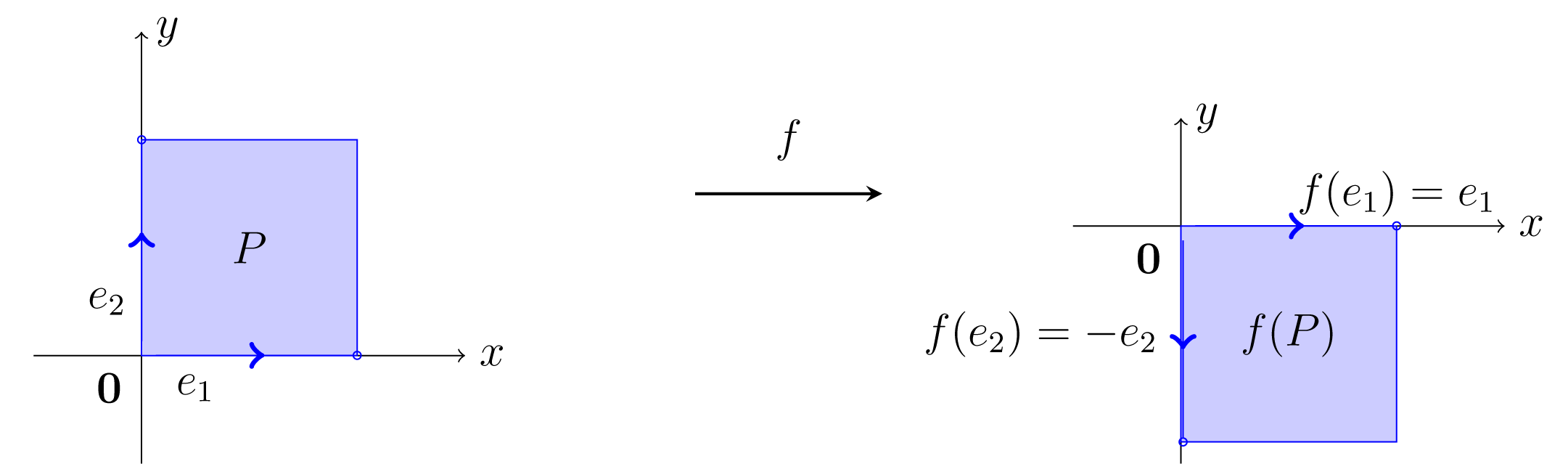
Σχήμα 4.6: Αντικατοπτρισμός ως προς τον άξονα των Q

Έστω ότι $V_{1}$ , $V_{2}$ , $V_{3}$ είναι $\Bbbk$ -διανυσματικοί χώροι και ότι $f:\ V_{1}\rightarrow V_{2}$ , $g:\ V_{2}\rightarrow V_{3}$ είναι γραμμικές συναρτήσεις. Δεν είναι δύσκολο να παρατηρήσει κάποιος ότι η σύνθεση $g\circ f:V_{1}\rightarrow V_{3}$ είναι γραμμική συνάρτηση. Αν $B, D, E$ είναι βάσεις για τους $V_{1},\ V_{2},\ V_{3}$ αντίστοιχα, τότε προκύπτει o επόμενος μνημονικός τύπος:

$\;\;Α^{(g\circ f)}_{Ε,Β}=Α^{g}_{E,D}A^{f}_{D,B}$ .

Παραδείγματα 4.1.7.

1.

Έστω $f:\ \Bbbk^{2}\rightarrow\Bbbk^{2}$ , $f(a,b)=(a,-b)$ , $g:\ \Bbbk^{2}\rightarrow\Bbbk^{3}$ , $g(a,b)=(a,b,a-b)$ και $B, D$ οι κανονικές βάσεις των χώρων $\Bbbk^{2}$ και $\Bbbk^{3}$ αντίστοιχα. Τότε

$Α^{f}_{Β,Β}=\begin{bmatrix}1&0\cr 0&-1\end{bmatrix},\ A^{g}_{D,B}=\begin{% bmatrix}1&0\cr 0&1\cr 1&-1\end{bmatrix},\ A^{g\circ f}_{D,B}=A^{g}_{D,B}\circ A% ^{f}_{B,B}=\begin{bmatrix}1&0\cr 0&-1\cr 1&1\end{bmatrix}\ .$
Άρα

$g\circ f:\ \Bbbk^{2}\rightarrow\Bbbk^{3},\quad(g\circ f)(a,b)=(a,-b,a+b)\ .$
2.
Θα υπολογίσουμε τον πίνακα που αντιστοιχεί στη γραμμική συνάρτηση $f:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ που προκύπτει από τις συνθέσεις των εξής γραμμικών συναρτήσεων:
- –
  
  $f_{1}$ : την αριστερόστροφη περιστροφή του ${\mathbb{R}}^{2}$ με γωνία $\theta=\pi/2$ ,
- –
  
  $f_{2}$ : τον αντικατοπτρισμό του ${\mathbb{R}}^{2}$ ως προς τον άξονα των $X$ ,
- –
  
  $f_{3}$ : τη διαστολή ως προς τον άξονα των $Y$ με συντελεστή 2.
Αντί να βρούμε τους πίνακες για κάθε μία από τις συναρτήσεις και στη συνέχεια να τους πολλαπλασιάσουμε, θα υπολογίσουμε την εικόνα για κάθε ένα από τα διανύσματα της κανονικής βάσης του ${\mathbb{R}}^{2}$ μετά από τη σύνθεση των τριών συναρτήσεων:

$\begin{matrix}e_{1}&\smash{\mathop{\longrightarrow}\limits^{f_{1}}}&e_{2}&% \smash{\mathop{\longrightarrow}\limits^{f_{2}}}&-e_{2}&\smash{\mathop{% \longrightarrow}\limits^{f_{3}}}&(0,-2)\cr e_{2}&\smash{\mathop{% \longrightarrow}\limits^{f_{1}}}&-e_{1}&\smash{\mathop{\longrightarrow}\limits% ^{f_{2}}}&-e_{1}&\smash{\mathop{\longrightarrow}\limits^{f_{3}}}&(-1,0)\end{% matrix}\ .$
Αν $Β$ είναι η κανονική βάση του $R^{2}$ , έπεται ότι $A^{f}_{Β,Β}=\left[\begin{array}[]{rr}0&-1\\ -2&0\end{array}\right]$ . Επομένως

$f:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(a,b)\mapsto(-b,-2a).$

Ασκήσεις Ενότητας 4.1

1.

Να αποδείξετε ότι η $f$ είναι γραμμική συνάρτηση, όπου $f:\Bbbk^{2}\rightarrow\Bbbk^{3}$ , $(x,y)\mapsto(x+y,y,3x)$ . Να αποδείξετε ότι αν $B$ είναι η κανονική βάση του $\Bbbk^{2}$ και $D$ η κανονική βάση του $\Bbbk^{3}$ , τότε

$A^{f}_{Β,D}=\begin{bmatrix}1&1\cr 0&1\cr 3&0\end{bmatrix}\ .$
2.

Έστω

$Α=\left[\begin{array}[]{cc}1&2\\ 3&4\end{array}\right]\begin{array}[]{c}\end{array}.$
Να βρεθεί η γραμμική συνάρτηση $f:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2}$ με πίνακα τον $Α$ .

Λύση
3.

Έστω

$Α=\left[\begin{array}[]{cccc}1&3&5&6\\ 3&1&0&-1\end{array}\right].$
Να οριστεί η γραμμική συνάρτηση $f:\mathbb{R}^{4}\rightarrow\mathbb{R}^{2}$ με πίνακα $Α$ . Να οριστεί η γραμμική συνάρτηση $g:\mathbb{R}^{2}\rightarrow\mathbb{R}^{4}$ με πίνακα $Α^{T}$ .

Λύση
4.

Έστω $f:\mathbb{R}^{3}\rightarrow\mathbb{R}^{4}$ όπου $f(a,b,c)=(a+b+c,b+c,a+2c,b+3c)$ . Να βρεθεί ο πίνακας της $f$ ως προς την κανονική βάση του ${\mathbb{R}}^{3}$ .

Λύση
5.

Έστω

$Α=\left[\begin{array}[]{cc}1&1\\ -2&1\end{array}\right]$
είναι o πίνακας μίας γραμμικής συνάρτηση $f:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2}$ . Να υπολογίσετε το $f(4,-3)$ .

Λύση
6.

Να βρεθεί η γραμμική συνάρτηση $f:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ που πρώτα περιστρέφει δεξιόστροφα ως προς γωνία $\pi/2$ , μετά διαστέλλει ως προς τον άξονα των Χ με συντελεστή 3, στη συνέχεια διαστέλλει ως προς τον άξονα των Υ με συντελεστή 2 και τέλος αντικατοπτρίζει ως προς τον άξονα των Υ. (Υπόδειξη: Να κάνετε το σχήμα και να βρείτε τις εικόνες των $e_{1}$ και $e_{2}$ ).

Λύση

4.2 Γραμμικές Συναρτήσεις, II

Σε αυτήν την ενότητα εισάγουμε την έννοια της εικόνας και του πυρήνα μίας γραμμικής συνάρτησης.

Ορισμός 4.2.1.

Έστω ότι $V$ , $W$ είναι $\Bbbk$ -διανυσματικοί χώροι και ότι $f:\ V\rightarrow W$ , $v\mapsto f(v)$ μία γραμμική συνάρτηση. Η εικόνα (image) της $f$ συμβολίζεται με ${\rm Im}f$ και είναι το σύνολο

{\rm Im}f=\{\;f(v)\;:\;v\in V\}\subseteq W.

Ο πυρήνας (kernel) της $f$ συμβολίζεται $\operatorname{Ker}f$ και είναι το σύνολο

\operatorname{Ker}f=\{\;v\in V\;:\;f(v)=0\}\subseteq V.

Θα υπολογίσουμε τον πυρήνα και την εικόνα σε κάποια χαρακτηριστικά Παραδείγματα.

Παραδείγματα 4.2.2.

1.

Έστω

$f:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{m}\;,\;\;\;\;v\mapsto{\bf 0},$
η τετριμμένη συνάρτηση στον ${\mathbb{R}}^{n}$ . Τότε $\operatorname{Ker}\ f={\mathbb{R}}^{n}$ , ενώ ${\rm Im}\ f=\{{\bf 0}\}$ .
2.

Έστω

$f:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{3}\;,\;\;\;\;(x,y)\mapsto(x,0,0)\;.$
Τότε

$\operatorname{Ker}f=S(\{(0,1)\})\hbox{ και }{\rm Im}f=\{S(\{(1,0,0)\})\ .$

Δεν είναι δύσκολο να παρατηρήσει κάποιος ότι τα σύνολα ${\rm Im}f$ και $\operatorname{Ker}f$ είναι υποχώροι των $W$ και $V$ αντίστοιχα. Πως ελέγχουμε όμως αν ένα διάνυσμα $w$ του $W$ είναι μέσα στην ${\rm Im}f$ ή αν ένα διάνυσμα $v$ του $V$ είναι μέσα στον $\operatorname{Ker}f$ ; Έστω ότι $Β$ και $D$ είναι διατεταγμένες βάσεις των $V$ και $W$ . Θα υποθέσουμε ότι ${\rm dim}_{\Bbbk}(V)=n$ , ${\rm dim}_{\Bbbk}(W)=m$ και ότι $B=(v_{1},\ldots,v_{n})$ . Στην Πρόταση 4.1.4 είδαμε ότι

A^{f}_{D,B}\ C_{B}(v)=C_{D}(f(v))\;.

Επομένως $w\in{\rm Im}f$ , δηλ. υπάρχει $v\in V$ τέτοιο ώστε $f(v)=w$ , αν και μόνο αν το γραμμικό σύστημα

A^{f}_{D,B}\ X=B,\textrm{ 'opou }B=C_{D}(w)

είναι συμβατό. Εάν αυτό συμβαίνει και $(x_{1},\ldots,x_{n})$ είναι λύση του συστήματος, τότε

C_{D}(w)=x_{1}C_{D}\left(f(v_{1})\right)+\cdots+x_{n}C_{D}\left(f(v_{n})\right).

Άρα το ζητούμενο διάνυσμα $v\in V$ προκύπτει ως o γραμμικός συνδυασμός

v=x_{1}v_{1}+\cdots x_{n}v_{n}\;.

Παρατηρούμε επίσης ότι $v\in\operatorname{Ker}f$ , δηλ. $f(v)=\bf 0$ , αν και μόνο αν

A^{f}_{D,B}\ C_{B}(v)={\bf 0}.

Επομένως για να βρούμε τα στοιχεία του $\operatorname{Ker}f$ υπολογίζουμε τον $\operatorname{null}(A^{f}_{D,B})$ . Αν το διάνυσμα $v=(x_{1},\ldots,x_{n})$ είναι λύση του $AX=\bf 0$ , τότε το $v\in\operatorname{null}(A^{f}_{D,B})$ και

v=x_{1}v_{1}+\cdots x_{n}v_{n}\in\operatorname{Ker}f.

Συγκεντρώνουμε αυτές τις παρατηρήσεις στην επόμενη πρόταση.

Πρόταση 4.2.3.

Έστω $f:\ V\rightarrow W$ , $v\mapsto f(v)$ μία γραμμική συνάρτηση, $Β$ και $D$ διατεταγμένες βάσεις των $V$ και $W$ αντίστοιχα. Τότε:

i)

το $w\in W$ ανήκει στον ${\rm Im}f$ αν και μόνο αν $C_{D}(w)$ παράγεται από τις στήλες του $A^{f}_{D,B}$
ii)

το $v\in V$ ανήκει στον $\operatorname{Ker}f$ του $V$ αν και μόνο αν $A^{f}_{D,B}C_{B}(v)=\bf 0$ .

Έχουμε δει ότι η βαθμίδα $\operatorname{rank}(A^{f}_{D,B})$ είναι ίση με τη διάσταση του χώρου στηλών του $A^{f}_{D,B}$ , βλ. Πρόταση 3.4.1. Επομένως o χώρος που παράγεται από τις στήλες του $A^{f}_{D,B}$ έχει διάσταση $\operatorname{rank}(A^{f}_{D,B})$ . Ως άμεση συνέπεια της Πρότασης 4.2.3, σημειώνουμε το εξής πόρισμα.

Πόρισμα 4.2.4.

i)

${\rm dim}_{\Bbbk}({\rm Im}f)=\operatorname{rank}(A^{f}_{D,B})$ .
ii)

${\rm dim}_{\Bbbk}(\operatorname{Ker}f)={\rm dim}_{\Bbbk}(\operatorname{null}(A))$

To επόμενο παράδειγμα θα ξεκαθαρίσει αυτές τις έννοιες.

Παράδειγμα 4.2.5.

Έστω η συνάρτηση

f:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(x,y,z)\mapsto(x-z,\;x% +y)\ ,

και έστω $B$ , $D$ οι κανονικές βάσεις του ${\mathbb{R}}^{3}$ και του ${\mathbb{R}}^{2}$ . Τότε

A^{f}_{D,B}=\begin{bmatrix}1&0&-1\cr 1&1&0\end{bmatrix}.

Είναι φανερό ότι $\operatorname{rank}(A^{f}_{D,B})=2$ . Επομένως, ο χώρος στηλών του $A^{f}_{D,B}$ είναι υποχώρος του ${\mathbb{R}}^{2}$ με διάσταση δύο, άρα $\Sigma\big(A^{f}_{D,B}\big)={\mathbb{R}}^{2}$ και κατά συνέπεια, ${\rm Im}f={\mathbb{R}}^{2}$ . Ας βρούμε αναλυτικά για ένα τυχαίο στοιχείο $w=(b_{1},b_{2})\in{\mathbb{R}}^{2}$ , ένα στοιχείο $v=(a_{1},a_{2},a_{3})\in{\mathbb{R}}^{3}$ έτσι ώστε $f(v)=w$ . Θεωρούμε τον επαυξημένο πίνακα $[A^{f}_{D,B}\ |\ C_{D}(w)]$ και τον φέρουμε σε ελαττωμένη κλιμακωτή μορφή γραμμών:

\left[\begin{array}[]{ccr|c}1&0&-1&b_{1}\cr 1&1&0&b_{2}\end{array}\right]% \rightarrow\left[\begin{array}[]{ccr|c}1&0&-1&b_{1}\cr 0&1&1&b_{2}-b_{1}\end{% array}\right].

Επομένως $v=(b_{1}+t,b_{2}-b_{1}-t,t)$ έχει την ιδιότητα $f(v)=w$ , όπου $t\in{\mathbb{R}}$ και υπάρχουν άπειρα διανύσματα του ${\mathbb{R}}^{3}$ που απεικονίζονται μέσω της $f$ στο $w$ .

Είδαμε ότι o $\operatorname{Ker}f$ είναι ο μηδενοχώρος του $A^{f}_{D,B}$ και αποτελείται από τις λύσεις του συστήματος $A^{f}_{D,B}X={\bf 0}$ . Επομένως

\operatorname{Ker}f=\{(x_{3},-x_{3},x_{3}):\ x_{3}\in{\mathbb{R}}\}=S(\{(1,-1,% 1)\})\ .

Παρατηρούμε ότι

{\rm dim}_{\Bbbk}(\operatorname{Ker}f)+{\rm dim}_{\Bbbk}({\rm Im}f)=3={\rm dim% }_{\Bbbk}({\mathbb{R}}^{3})\;.

H γραμμική συνάρτηση $f:\ V\rightarrow W$ είναι ένα προς ένα αν και μόνο αν διαφορετικά διανύσματα απεικονίζονται σε διαφορετικά στοιχεία. Έτσι αν $f$ είναι ένα προς ένα και $f(v_{1})=f(v_{2})$ , συμπεραίνουμε ότι $v_{1}=v_{2}$ .

Πρόταση 4.2.6.

Έστω $f:\ V\rightarrow W$ μία γραμμική συνάρτηση. Τότε η $f$ είναι ένα προς ένα αν και μόνο αν $\operatorname{Ker}f=\{{\bf 0}\}$ .

Απόδειξη.

Αν ${\bf 0}\neq v\in\operatorname{Ker}f$ τότε $f(v)=f({\bf 0})={\bf 0}$ και επομένως η $f$ δεν είναι ένα προς ένα. Αντίστροφα, ας υποθέσουμε ότι $\operatorname{Ker}f=\{{\bf 0}\}$ και έστω ότι $f(v_{1})=f(v_{2})$ . Τότε

f(v_{1})-f(v_{2})={\bf 0}\Leftrightarrow f(v_{1}-v_{2})={\bf 0}\Leftrightarrow v% _{1}-v_{2}\in\operatorname{Ker}f\{{\bf 0}\}.

Επομένως $v_{1}-v_{2}={\bf 0}$ και $v_{1}=v_{2}$ . ∎

Από τα προηγούμενα προκύπτει ότι ο πυρήνας μίας γραμμικής συνάρτησης $f$ μετράει πόσο απέχει η γραμμική συνάρτηση $f$ από το να είναι ένα προς ένα. Η $f:\ V\rightarrow W$ λέγεται επιμορφισμός (epimorphism) όταν ${\rm Im}f=W$ .

Πρόταση 4.2.7.

Έστω $f:\ V\rightarrow W$ μία γραμμική συνάρτηση, $Β$ και $D$ διατεταγμένες βάσεις των $V$ και $W$ αντίστοιχα. Τότε η $f$ είναι επιμορφισμός αν και μόνο αν ${\rm dim}_{\Bbbk}(W)=\operatorname{rank}(A^{f}_{D,B})$ .

Απόδειξη.

Όμως η $f$ είναι επιμορφισμός ακριβώς όταν ${\rm Im}f=W$ . Από το Πόρισμα 4.2.4 έπεται ότι η $f$ είναι επιμορφισμός αν και μόνο αν ${\rm dim}_{\Bbbk}(W)=\operatorname{rank}(A^{f}_{D,B})$ . ∎

Η $f:\ V\rightarrow W$ λέγεται ισομορφισμός (isomorphism) αν είναι ένα προς ένα και επιμορφισμός.

Παράδειγμα 4.2.8.

Έστω

f:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(x,y)\mapsto(x+2y,2x+3% y)\;.

Έστω $Β$ η κανονική βάση του ${\mathbb{R}}^{2}$ . Τότε

Α_{Β,Β}^{f}=\begin{bmatrix}1&2\cr 2&3\end{bmatrix}\ .

Αφού $\det(Α_{Β,Β}^{f})=-1$ , ο πίνακας $Α_{Β,Β}^{f}$ είναι αντιστρέψιμος πίνακας και $\operatorname{null}(Α_{Β,Β}^{f})=\{{\bf 0}\}$ . O χώρος στηλών του $Α_{Β,Β}^{f}$ είναι ο ${\mathbb{R}}^{2}$ . Άρα η $f$ είναι ένα προς ένα και επιμορφισμός, επομένως $f$ είναι ισομορφισμός.

Έστω $f:V\rightarrow W$ μία γραμμική συνάρτηση. Το επόμενο θεώρημα συνδέει τις διαστάσεις των υποχώρων ${\rm Im}f$ του $W$ και $\operatorname{Ker}f$ του $V$ .

Θεώρημα 4.2.9.

Έστω $f:V\rightarrow W$ μία γραμμική συνάρτηση. Τότε:

{\;\;n={\rm dim}_{\Bbbk}(V)={\rm dim}_{\Bbbk}(\operatorname{Ker}f)+{\rm dim}_{% \Bbbk}({\rm Im}f)\ .\;}

Απόδειξη.

Έστω $Α\in\mathcal{M}_{m\times n}(\Bbbk)$ ο πίνακας της συνάρτησης $f$ ως προς τις διατεταγμένες βάσεις $B$ και $D$ των $V$ και $W$ αντίστοιχα. Από το Θεώρημα 3.4.3, γνωρίζουμε ότι

\operatorname{rank}(A)+{\rm dim}(\operatorname{null}(A))=n\ .

(4.2.9.1)

Σύμφωνα με το Πόρισμα 4.2.4 $\operatorname{rank}(A)={\rm dim}_{\Bbbk}({\rm Im}f)$ και ${\rm dim}_{\Bbbk}(\operatorname{null}(A))={\rm dim}_{\Bbbk}(\operatorname{Ker}f)$ , επομένως προκύπτει το ζητούμενο. ∎

Τα επόμενα πορίσματα είναι άμεσες συνέπειες του Θεωρήματος 4.2.9.

Πόρισμα 4.2.10.

Αν $f:V\rightarrow W$ είναι ισομορφισμός, τότε

{\rm dim}_{\Bbbk}V={\rm dim}_{\Bbbk}W\;.

Απόδειξη.

Αφού $f$ είναι ισομορφισμός, έπεται ότι ${\rm dim}_{\Bbbk}(\operatorname{Ker}f)=0$ και ${\rm dim}_{\Bbbk}({\rm Im}f)={\rm dim}_{\Bbbk}(W)$ . Επομένως

{\rm dim}_{\Bbbk}(V)=0+{\rm dim}_{\Bbbk}(W)={\rm dim}_{\Bbbk}(W)\;.

∎

Μπορούμε, λοιπόν, να αποφασίσουμε αν $f:V\rightarrow W$ είναι ισομορφισμός, ελέγχοντας αν o πίνακας της συνάρτησης είναι αντιστρέψιμος.

Πόρισμα 4.2.11.

Έστω $V$ και $W$ διανυσματικοί χώροι με την ίδια διάσταση, $B$ διατεταγμένη βάση του $V$ και $D$ διατεταγμένη βάση του $W$ . Αν $f:V\rightarrow W$ είναι γραμμική συνάρτηση τότε η $f$ είναι ισομορφισμός αν και μόνο αν ο πίνακας $A_{D,B}^{f}$ είναι αντιστρέψιμος.

Απόδειξη.

Ο πίνακας $A_{D,B}^{f}$ είναι αντιστρέψιμος αν και μόνο αν $\operatorname{null}A_{D,B}^{f}=\{{\bf 0}\}$ , ισοδύναμα αν και μόνο αν $\operatorname{rank}(A_{D,B}^{f}\big)={\rm dim}_{\Bbbk}(W)$ , δηλ. αν $\operatorname{Ker}f=\{{\bf 0}\}$ και ${\rm Im}f=W$ . ∎

Στην προηγούμενη ενότητα, είδαμε ότι αν $B, D, E$ είναι διατεταγμένες βάσεις για τους $V_{1},\ V_{2},$ και $V_{3}$ αντίστοιχα, τότε

{\;\;Α^{g\circ f}_{Ε,Β}=Α^{g}_{E,D}A^{f}_{D,B}\ .\;\;}

Η παρατήρηση αυτή μας επιτρέπει να βρούμε την αντίστροφη συνάρτηση μίας γραμμικής συνάρτησης που είναι ισομορφισμός. Τονίζουμε ότι αν μία γραμμική συνάρτηση $f:V\rightarrow W$ είναι ισομορφισμός, τότε η συνάρτηση $f^{-1}:W\rightarrow V$ υπάρχει, αφού $f$ είναι αμφιμονότιμη και επιμορφισμός.

Πρόταση 4.2.12.

Έστω $f:\ V\rightarrow W$ ισομορφισμός, $B$ , $D$ διατεταγμένες βάσεις των $V$ και $W$ αντίστοιχα, $Α=A_{D,B}^{f}$ . Τότε $f^{-1}:\ W\rightarrow V$ είναι η γραμμική συνάρτηση με πίνακα $Α^{-1}$ ως προς τις διατεταγμένες βάσεις $D$ και $B$ των $W$ και $V$ αντίστοιχα, δηλ.

[Α^{f^{-1}}_{B,D}=(A_{D,B}^{f})^{-1}\ .]

Απόδειξη.

Έστω ότι $g:\ W\rightarrow V$ είναι η γραμμική συνάρτηση με πίνακα $A_{B,D}^{g}=A^{-1}$ . Τότε

A_{B,B}^{g\circ f}=A_{B,D}^{g}A_{D,B}^{f}=A^{-1}A=I_{n}

και επομένως

C_{B}\big(g\circ f\;(v)\big)=I_{n}\,C_{B}(v)=C_{B}(v)\ .

Συνεπώς, $g\circ f:\ V\rightarrow V$ , $v\mapsto v$ , δηλ. $g=f^{-1}$ . ∎

Παράδειγμα 4.2.13.

Θα υπολογίσουμε την αντίστροφη συνάρτηση της γραμμικής συνάρτησης $f:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2},\ (x,y)\mapsto(x+2y,2x+3y)$ . Έστω $Β$ η κανονική βάση του ${\mathbb{R}}^{2}$ . Τότε

Α=A_{Β,B}^{f}=\begin{bmatrix}1&2\cr 2&3\end{bmatrix}\ \ \longrightarrow\ \ A_{% B,B}^{f^{-1}}=(A)^{-1}=\begin{bmatrix}-3&2\cr 2&-1\end{bmatrix}\ .

Επομένως $f^{-1}(x,y)=(-3x+2y,2x-y)$ .

Έστω ότι οι $\Bbbk$ -διανυσματικοί χώροι $V$ , $W$ έχουν την ίδια διάσταση $n$ , και έστω $B$ , $D$ διατεταγμένες βάσεις των $V$ και $W$ αντίστοιχα. Θεωρούμε τη γραμμική συνάρτηση $f:\ V\rightarrow W$ έτσι ώστε $A_{D,B}^{f}=I_{n}$ . Αφού ο πίνακας $A_{D,B}^{f}$ είναι αντιστρέψιμος, έπεται ότι η γραμμική συνάρτηση $f$ είναι ισομορφισμός. Αποδείξαμε λοιπόν το επόμενο συμπέρασμα.

Θεώρημα 4.2.14.

Έστω ότι $V$ , $W$ είναι $\Bbbk$ -διανυσματικοί χώροι και ότι ${\rm dim}_{\Bbbk}(V)={\rm dim}_{\Bbbk}(W)$ . Τότε υπάρχει ισομορφισμός $f:V\rightarrow W$ . Ειδικότερα, αν ${\rm dim}_{\Bbbk}(V)$ , τότε o $V$ είναι ισόμορφος με τον $\Bbbk^{n}$ .

Αυτό σημαίνει ότι όταν δύο $\Bbbk$ -διανυσματικοί χώροι έχουν την ίδια διάσταση, τότε από αλγεβρική σκοπιά είναι πανομοιότυποι: μελετώντας τον έναν από τους δύο, μπορούμε να βγάλουμε συμπεράσματα που ισχύουν και για τους δύο. Παρατηρούμε επίσης ότι o ισομορφισμός του Θεωρήματος 4.2.14 δεν είναι μοναδικός. Αν κρατήσουμε τη βάση $B$ του $V$ σταθερή, τότε κάθε φορά που αλλάζουμε τη διάταξη σε οποιαδήποτε βάση του $W$ , παίρνουμε και έναν διαφορετικό ισομορφισμό. Υπάρχει λόγος να προτιμήσουμε κάποιον από τους ισομορφισμούς; H απάντηση σε αυτό το ερώτημα είναι θετική, λόγω των εφαρμογών, και η επιλογή της βάσης εξαρτάται κυρίως από τις γραμμικές συναρτήσεις που θέλουμε να μελετήσουμε. Θα δούμε, λοιπόν, την επίδραση που έχουν οι αλλαγές βάσεων (στις γραμμικές συναρτήσεις μεταξύ των δύο χώρων) στην επόμενη ενότητα.

Παραδείγματα 4.2.15.

1.

Έστω $v_{1}=(1,2,0)$ , $v_{2}=(0,0,1)$ , $V=S(\{v_{1},v_{2}\})$ . O χώρος $V$ είναι επίπεδο του ${\mathbb{R}}^{3}$ , $D=(v_{1},v_{2})$ είναι διατεταγμένη βάση του $V$ και ${\rm dim}V=2$ . Θα βρούμε έναν ισομορφισμό μεταξύ του ${\mathbb{R}}^{2}$ και του $V$ . Έστω $B=(e_{1},e_{2})$ η κανονική βάση του ${\mathbb{R}}^{2}$ . Παίρνουμε τη γραμμική συνάρτηση $f:\ {\mathbb{R}}^{2}\rightarrow V,$ όπου $f(e_{1})=(1,2,0)$ και $f(e_{2})=(0,0,1)$ . O αναλυτικός τύπος της $f$ προκύπτει από τη σχέση $f(a,b)=f(ae_{1}+be_{2})=af(e_{1})+bf(e_{2})=(a,2a,0)+(0,0,b)=(a,2a,b),$ ενώ

$A^{f}_{D,B}=\begin{bmatrix}1&0\cr 0&1\end{bmatrix}\ .$
Ο πίνακας $A^{f}_{D,B}$ είναι αντιστρέψιμος και η γραμμική συνάρτηση $f$ είναι ισομορφισμός.
2.

Έστω τώρα $V=S(\{(1,2,0),(0,0,1)\})$ και $W=S(\{(1,4,0),(0,0,1)\})$ . Παρατηρούμε ότι ${\rm dim}(V)={\rm dim}(W)=2$ . Θα βρούμε έναν ισομορφισμό $f:\ V\rightarrow W$ . Έστω η βάση $D=(v_{1},v_{2})$ του $V,$ όπου $v_{1}=(1,2,0)$ , $v_{2}=(0,0,1)$ και η βάση $E=(w_{1},w_{2})$ του $W,$ όπου $w_{1}=(1,4,0)$ , $w_{2}=(0,0,1)$ . Θεωρούμε τον αντιστρέψιμο πίνακα

$Α=\begin{bmatrix}0&1\cr 1&0\end{bmatrix}\$
και τη γραμμική συνάρτηση $f:V\rightarrow W$ έτσι ώστε $A_{E,D}^{f}=A$ . Έχουμε ότι $f(v_{1})=w_{2}$ και $f(v_{2})=w_{1}$ , ενώ $f(av_{1}+bv_{2})=af(v_{1})+bf(v_{2})$ άρα $f(a,2a,b)=(b,4b,a)$ . Η γραμμική συνάρτηση $f$ είναι ισομορφισμός.

Συγκεντρώνουμε τους ορισμούς και τα κυριότερα αποτελέσματα των γραμμικών συναρτήσεων στον επόμενο πίνακα.

i.

Η $f:V\rightarrow U$ λέγεται γραμμική συνάρτηση αν $f(v_{1}+v_{2})=f(v_{1})+f(v_{2})$ και $f(\kappa v)=\kappa f(v)$ για όλα τα $\kappa\in{\mathbb{R}}$ , $v_{1},v_{2},v\in V$ .
ii.

Αν $Β$ και $D$ είναι διατεταγμένες βάσεις των $V$ και $U$ αντίστοιχα, τότε η $f$ ορίζεται πλήρως από τις εικόνες των στοιχείων της $B$ . Ο πίνακας της $f$ ως προς τις βάσεις $D$ και $B$ συμβολίζεται $A^{f}_{D,B}$ και είναι ο $m\times n$ πίνακας

$A^{f}_{D,B}=\left[\begin{array}[]{ccc}C_{D}(f(v_{1}))&\cdots&C_{D}(f(v_{n}))% \end{array}\right],$
όπου $n={\rm dim}_{\Bbbk}(V)$ και $m={\rm dim}_{\Bbbk}(U)$ . Ισχύει ότι

$C_{D}(f(v))=A^{f}_{D,B}C_{B}(v)\;.$
iii.

Η $f$ είναι ένα προς ένα αν και μόνο αν $\operatorname{Ker}f=\{v\in V:\ f(v)=0\}$ ή ισοδύναμα αν και μόνο αν $\operatorname{null}(A_{f})=\{0\}$ . H $f$ είναι επιμορφισμός αν και μόνο αν ${\rm Im}f=U$ , δηλ. αν και μόνο αν $\operatorname{rank}(A^{f}_{D,B})={\rm dim}_{\Bbbk}(U)$ . Ισχύει ότι

${\rm dim}_{\Bbbk}({\rm Im}f)+{\rm dim}_{\Bbbk}(\operatorname{Ker}f)={\rm dim}_% {\Bbbk}(V)\;.$
iv.

Όταν ${\rm dim}_{\Bbbk}(V)={\rm dim}_{\Bbbk}(U)$ , συγκρίνοντας διαστάσεις προκύπτει ότι

$f\hbox{ ισομορφισμός }\Leftrightarrow f\hbox{ ένα προς ένα }\Leftrightarrow f% \hbox{ epiμορφισμός }\;.$
Επομένως η $f:V\rightarrow U$ είναι ισομορφισμός αν και μόνο αν ο πίνακας $A_{D,B}^{f}$ είναι αντιστρέψιμος και σε αυτήν την περίπτωση

$A_{Β,D}^{f^{-1}}=\big(A^{f}_{D,B}\big)^{-1}\;.$

Ασκήσεις Ενότητας 4.2

1.

Δίνεται η συνάρτηση

$f:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}\;,\;\;\;\;(x,y,z)\rightarrow(x+2% y,y-z,x+2z).$
Να υπολογίσετε μία βάση των $\operatorname{Ker}f$ και ${\rm Im}f$ .

Λύση
2.

Έστω η γραμμική συνάρτηση $f:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ , με

$f(x,y,z)=(x+3z,\;2x+y+5z,\;-y+2z),$
για $(x,y,z)\in{\mathbb{R}}^{3}$ . Να αποδείξετε ότι η $f$ είναι ισομορφισμός.
3.

Να βρεθεί ισομορφισμός $f:\ {\mathbb{R}}^{2}\rightarrow V,$ όπου $V=\{(x,y,z):\ x+y+z=0\}$ .

Λύση
4.

Να βρεθεί ισομορφισμός $f:\ V\rightarrow{\mathbb{R}}^{2},$ όπου $V=\{(x,y,z):\ x+y+z=0\}$ .

Λύση

4.3 Πίνακες Αλλαγής Βάσης

Έστω ότι οι $B$ , $B^{\prime}$ είναι δύο διατεταγμένες βάσεις του $\Bbbk$ -διανυσματικού χώρου $V$ και ότι αντίστοιχα οι $D$ , $D^{\prime}$ είναι διατεταγμένες βάσεις του $\Bbbk$ -διανυσματικού χώρου $U$ . Θεωρούμε τη γραμμική συνάρτηση $f:V\rightarrow U$ . Ποιά είναι η σχέση μεταξύ των πινάκων $A^{f}_{D,B}$ και $A^{f}_{D^{\prime}B^{\prime}}$ ; Με αυτό το ερώτημα θα ασχοληθούμε σε αυτή την ενότητα. Πρώτα, εξετάζουμε τον πίνακα που αντιστοιχεί στην ταυτοτική συνάρτηση $\operatorname{id}_{V}:V\rightarrow V$ ως προς δύο διατεταγμένες βάσεις $B$ και $B^{\prime}$ . Ονομάζουμε τον πίνακα $A^{\operatorname{id}_{V}}_{B,B}$ πίνακα μετάβασης (change of basis matrix) και τον συμβολίζουμε με $S_{B^{\prime}\leftarrow B}$ . $S_{B^{\prime}\leftarrow B}$ O πίνακας $S_{B^{\prime}\leftarrow B}$ είναι τετραγωνικός. O αριθμός γραμμών (και στηλών) του $S_{B^{\prime}\leftarrow B}$ είναι ίσος με $n$ όπου $n={\rm dim}_{\Bbbk}(V)$ . Αν $B=(v_{1},\ldots,v_{n})$ , τότε σύμφωνα με τον Πίνακα 4.2.1.ii, ισχύει ότι:

S_{B^{\prime}\leftarrow B}=\left[\begin{array}[]{cccc}C_{Β^{\prime}}(v_{1})&% \cdots&C_{Β^{\prime}}(v_{n})\end{array}\right].

Παρατηρούμε ότι

S_{B^{\prime}\leftarrow B}=I_{n}\Leftrightarrow B=B^{\prime}.

Έτσι, σύμφωνα πάλι με τον Πίνακα 4.2.1.iv, αφού

S_{B\leftarrow B^{\prime}}\;S_{B^{\prime}\leftarrow B}=S_{B\leftarrow B}=Ι_{n},

έπεται ότι:

$(S_{B^{\prime}\leftarrow B})^{-1}=S_{B\leftarrow B^{\prime}}$ .

Παραδείγματα 4.3.1.

1.

Έστω $Β=(e_{1},e_{2})$ η κανονική βάση του ${\mathbb{R}}^{2}$ και $B^{\prime}=(v_{1},v_{2})$ όπου $v_{1}=(1,2)$ , $v_{2}=(1,1)$ . Είναι πολύ εύκολο να βρούμε τον πίνακα $S_{B\leftarrow B^{\prime}}$ . Αφού $v_{1}=e_{1}+2e_{2}$ και $v_{2}=e_{1}+e_{2}$ , έπεται ότι

$S_{B\leftarrow B^{\prime}}=\begin{bmatrix}1&1\cr 2&1\end{bmatrix}\;.$
Επομένως

$S_{B^{\prime}\leftarrow B}=(S_{B\leftarrow B^{\prime}})^{-1}=\begin{bmatrix}-1% &1\cr 2&-1\end{bmatrix}\;.$
Σημειώνουμε την ερμηνεία των στηλών του $S_{B^{\prime}\leftarrow B}$ , ως τους πίνακες των συντεταγμένων των στοιχείων της βάσης $B$ ως προς τη βάση $B^{\prime}$ . Αφού

$S_{B^{\prime}\leftarrow B}=\left[\begin{array}[]{cc }C_{Β^{\prime}}(v_{1})&C_{% Β^{\prime}}(v_{2})\end{array}\right],$
έπεται ότι $e_{1}=-v_{1}+2v_{2}$ και ότι $e_{2}=v_{1}-v_{2}$ .
2.

Έστω $Β=(e_{1},e_{2},e_{3})$ η κανονική βάση του ${\mathbb{R}}^{2}$ και $B^{\prime}=(v_{1},v_{2},v_{3})$ όπου $v_{1}=(1,2,0)$ , $v_{2}=(1,1,0)$ , $v_{3}=e_{3}$ . Θα βρούμε τους πίνακες μετάβασης από τη μία βάση στην άλλη. Θα ξεκινήσουμε με τον απλούστερο από τους δύο πίνακες, τον $S_{B\leftarrow B^{\prime}}$ , που οι στήλες του είναι οι συντεταγμένες των στοιχείων της $B^{\prime}$ . Στη συνέχεια, βρίσκουμε τον $S_{B^{\prime}\leftarrow B}$ παίρνοντας τον αντίστροφο του $S_{B\leftarrow B^{\prime}}$ . O αναγνώστης καλείται να διαπιστώσει ότι

$S_{B\leftarrow B^{\prime}}=\begin{bmatrix}1&1&0\cr 2&1&0\cr 0&0&1\end{bmatrix}% \begin{array}[]{c}\end{array}\textrm{ και }S_{B^{\prime}\leftarrow B}=\left[% \begin{array}[]{rrr}-1&1&\;0\\ 2&-1&\;0\\ 0&0&\;1\end{array}\right]\begin{array}[]{c}\end{array}.$
Από τις στήλες του $S_{B^{\prime}\leftarrow B}$ συμπεραίνουμε ότι $e_{1}=-v_{1}+2v_{2}$ , $e_{2}=v_{1}-v_{2}$ και βέβαια $e_{3}=v_{3}$ .
3.

Στον $\mathcal{M}_{2\times 2}({\mathbb{C}})$ θεωρούμε τον επόμενο πίνακα $A$ και τον αντίστροφό του:

$Α=\left[\begin{array}[]{rr}3&2\\ 1&1\end{array}\right]\begin{array}[]{c}\end{array},\ Α^{-1}=\left[\begin{array% }[]{rr}1&-2\\ -1&3\end{array}\right]\begin{array}[]{c}\end{array}.$
Αφού ο $A$ είναι αντιστρέψιμος, οι στήλες του $Α$ είναι γραμμικά ανεξάρτητες, άρα $v_{1}=(3,1),\;v_{2}=(2,1)$ , είναι γραμμικά ανεξάρτητα στον ${\mathbb{C}}^{2}$ και $B^{\prime}=(v_{1},v_{2})$ είναι διατεταγμένη βάση, βλ. Πρόταση 3.5.10. Παρατηρούμε ότι:

$A=S_{B\leftarrow B^{\prime}}\textrm{ kai }A^{-1}=S_{B^{\prime}\leftarrow B}\;.$
Επομένως $e_{1}=v_{1}-v_{2}$ και $e_{2}=-2v_{1}+3v_{2}$ .

Μία χρήσιμη σχέση, συνέπεια της θεώρησης του πίνακα $S_{B^{\prime}\leftarrow B}$ ως πίνακα της ταυτοτικής συνάρτησης του $V$ και της Πρότασης 4.1.4 είναι η εξής:

[C_{B^{\prime}}(v)=S_{B^{\prime}\leftarrow B}\ C_{B}(v)\ .]

(4.3.1.1)

Παράδειγμα 4.3.2.

Έστω $Β=(e_{1},e_{2})$ η κανονική βάση του ${\mathbb{R}}^{2}$ , $w_{1}=(1,1),\ w_{2}=(1,-1)$ και $Β^{\prime}=(w_{1},w_{2})$ . Παρατηρούμε ότι $w_{1}=e_{1}+e_{2}$ , $w_{2}=e_{1}-e_{2}$ . Άρα

S_{B\leftarrow B^{\prime}}=\left[\begin{array}[]{rr}1&1\cr 1&-1\end{array}% \right]\textrm{ kai }S_{B^{\prime}\leftarrow B}=(S_{B\leftarrow B^{\prime}})^{% -1}=\left[\begin{array}[]{rr}1/2&1/2\\ 1/2&-1/2\end{array}\right].

Επομένως $e_{1}=1/2\,w_{1}+1/2\,w_{2}$ , $e_{2}=1/2\,w_{1}-1/2\,w_{2}$ . Έστω $v=(2,1)$ . Θα βρούμε τις συντεταγμένες του $v$ ως προς τη βάση $B^{\prime}$ . Αφού $v=2e_{1}+e_{2}$ , έπεται ότι

C_{B^{\prime}}(v)=S_{B^{\prime}\leftarrow B}\;C_{B}(v)=\left[\begin{array}[]{% rr}1/2&1/2\\ 1/2&-1/2\end{array}\right]\begin{bmatrix}2\cr 1\end{bmatrix}=\begin{bmatrix}3/% 2\cr 1/2\end{bmatrix},

δηλ. $v=3/2\,w_{1}+1/2\,w_{2}$ .

Έστω τώρα $w=3w_{1}+w_{2}$ . Τότε

C_{B}(u)=S_{B\leftarrow B^{\prime}}\;C_{B^{\prime}}(u)=\left[\begin{array}[]{% rr}1&1\cr 1&-1\end{array}\right]\begin{bmatrix}3\cr 1\end{bmatrix}=\begin{% bmatrix}4\cr 2\end{bmatrix},

άρα

w=4e_{1}+2e_{2}=(4,2).

Έστω, λοιπόν, $f:V\rightarrow U$ γραμμική συνάρτηση. Στη συνέχεια περιγράφουμε τη σχέση μεταξύ των πινάκων $A^{f}_{D,B}$ και $A^{f}_{D^{\prime}B^{\prime}}$ .

Πρόταση 4.3.3.

Έστω $f:\ V\rightarrow W$ μία γραμμική συνάρτηση, $Β$ , $Β^{\prime}$ δύο διατεταγμένες βάσεις του $V$ και $D$ , $D^{\prime}$ δύο διατεταγμένες βάσεις του $W$ . Τότε

{A^{f}_{D^{\prime},B^{\prime}}=S_{D^{\prime}\leftarrow D}\;A^{f}_{D,B}\;S_{B% \leftarrow B^{\prime}}\ .}

Απόδειξη.

Έστω ότι $B^{\prime}=(v_{1},\ldots,v_{n})$ , όπου $n={\rm dim}_{\Bbbk}(V)$ . Τότε

A^{f}_{D^{\prime},B^{\prime}}=\left[\begin{array}[]{ccc}C_{D^{\prime}}(f(v_{1}% ))&\cdots&C_{D^{\prime}}(f(v_{n}))\end{array}\right].

Για την $i$ στήλη του $A^{f}_{D^{\prime},B^{\prime}}$ , από τη σχέση (4.3.1.1), έχουμε ότι

C_{D^{\prime}}\left(f(v_{i})\right)=S_{D^{\prime}\leftarrow D}\;C_{D}\left(f(v% _{i})\right)\;.

(4.3.3.1)

Από την Πρόταση 4.1.4 έχουμε ότι

C_{D}\left(f(v_{i})\right)=A^{f}_{D,B}\;C_{B}(v_{i})\;.

Αντικαθιστώντας στην Έκφραση (4.3.3.1) προκύπτει ότι

C_{D^{\prime}}\left(f(v_{i})\right)=S_{D^{\prime}\leftarrow D}\;A^{f}_{D,B^{% \prime}}\;C_{B}(v_{i}).

Παρατηρούμε ότι $C_{B}(v_{i})$ είναι η $i$ στήλη του $S_{B\leftarrow B^{\prime}}$ , δηλ. η $i$ στήλη του $A^{f}_{D^{\prime},B^{\prime}}$ προκύπτει ως την $i$ στήλη του γινομένου πινάκων

S_{D^{\prime}\leftarrow D}\;A^{f}_{D,B}\;S_{B\leftarrow B^{\prime}}\;.

H πρότασή μας λοιπόν αποδείχθηκε. ∎

Ως ειδική περίπτωση της Πρότασης 4.3.3 εξετάζουμε ti συμβαίνει όταν $V=W$ και $Β=D$ ενώ $B^{\prime}=D^{\prime}$ . Θέτοντας $S=S_{B\leftarrow B^{\prime}}$ , προκύπτει το επόμενο συμπέρασμα:

Πόρισμα 4.3.4.

Έστω $f:\ V\rightarrow V$ μία γραμμική συνάρτηση και $Β$ , $Β^{\prime}$ δύο διατεταγμένες βάσεις του $V$ . Τότε υπάρχει αντιστρέψιμος πίνακας $S$ , έτσι ώστε

{A^{f}_{B^{\prime},B^{\prime}}=S^{-1}A^{f}_{B,B}\;S\ .}

(4.3.4.1)

Οι πίνακες $A^{f}_{B,B}$ , $A^{f}_{B^{\prime},B^{\prime}}$ είναι όμοιοι. Γενικότερα δύο πίνακες $A,A^{\prime}\in M_{n}(\Bbbk)$ λέγονται όμοιοι (similar) αν υπάρχει αντιστρέψιμος πίνακας $P\in M_{n}(\Bbbk)$ έτσι ώστε

A^{\prime}=P^{-1}A\;P\ .

Σημειώνουμε την επόμενη χρήσιμη πρόταση.

Πρόταση 4.3.5.

Έστω $A$ , $A^{\prime}$ δύο όμοιοι πίνακες. Τότε $\det A=\det A^{\prime}$ .

Απόδειξη.

Έστω ότι $A^{\prime}=P^{-1}A\;P$ για κάποιον αντιστρέψιμο πίνακα $P$ . Αφού $\det(P^{-1})\det P=1$ , έπεται ότι

$\det A^{\prime}=\det\left(P^{-1}A\;P\right)=\det(P^{-1})\,\det A\,\det P=\det A$ .

∎

Από τα προηγούμενα προκύπτει ότι αν $f:\ V\rightarrow V$ είναι μία γραμμική συνάρτηση και $Β$ , $Β^{\prime}$ δύο διατεταγμένες βάσεις του $V$ , τότε

\det(A^{f}_{B^{\prime},B^{\prime}})=\det(A^{f}_{B,B}).

Παραδείγματα 4.3.6.

1.
Δίνεται η γραμμική συνάρτηση

$f:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}\;,\;\;\;(x,y,z)\mapsto(x+3y-z,\;% 2x-y,\;y+2z).$
Έστω $B=(e_{1},e_{2},e_{3})$ η κανονική βάση του ${\mathbb{R}}^{3}$ . Αφού $f(e_{1})=(1,2,0)$ , $f(e_{2})=(3,-1,1)$ και $f(e_{3})=(-1,0,2)$ ,

$A^{f}_{B,B}=\left[\begin{array}[]{rrr}1&3&-1\\ 2&-1&0\\ 0&1&2\end{array}\right]\begin{array}[]{c}\end{array}.$
Έστω τώρα $v_{1}=(0,1,-1)$ , $v_{2}=(1,1,1)$ , $v_{3}=(2,0,-1)$ . Τα διανύσματα $v_{1},v_{2},v_{3}$ είναι γραμμικά ανεξάρτητα και $D=(v_{1},v_{2},v_{3})$ είναι διατεταγμένη βάση του ${\mathbb{R}}^{3}$ . Επίσης,

$S_{B\leftarrow D}=\left[\begin{array}[]{rrr}0&1&2\\ 1&1&0\\ -1&1&-1\end{array}\right]$
και

$S_{D\leftarrow B}=(S_{B\leftarrow D})^{-1}=\frac{1}{5}\left[\begin{array}[]{% rrr}-1&3&-2\\ 1&2&2\\ 2&-1&-1\end{array}\right].$
Άρα

$A^{f}_{D,B}=S_{D\leftarrow B}\;A^{f}_{B,B}\;S_{B\leftarrow B}=S_{D\leftarrow B% }\;A^{f}_{B,B}\;I_{3}=\frac{1}{5}\left[\begin{array}[]{rrr}5&-8&-3\\ 5&3&3\\ 0&6&-4\end{array}\right].$
Αφού

$A^{f}_{D,B}=\begin{bmatrix}C_{D}(f(e_{1}))&C_{D}(f(e_{2}))&C_{D}(f(e_{3}))\end% {bmatrix}^{T},$
έπεται ότι
- –
  
  $f(e_{1})=v_{1}+v_{2}$ ,
- –
  
  $f(e_{2})=\displaystyle{\frac{1}{5}}(-{8}v_{1}+{3}v_{2}+{6}v_{3})$ ,
- –
  
  $f(e_{3})=\displaystyle{\frac{1}{5}}(-{3}{5}v_{1}+{3}v_{2}-{4}$ .
Επίσης,

$A^{f}_{D,D}=S_{D\leftarrow B}\;A^{f}_{B,B}\;S_{B\leftarrow D}=\frac{1}{5}\left% [\begin{array}[]{rrr}-5&-6&13\cr 0&11&7\cr 10&2&4\end{array}\right].$
Επομένως
- –
  
  $f(v_{1})=-v_{1}+2v_{3}$ ,
- –
  
  $f(v_{2})=\frac{1}{5}(-6v_{1}+11v_{2}+2v_{3})$ , και
- –
  
  $f(v_{3})=\frac{1}{5}(13v_{1}+7v_{2}+4v_{3})$ .
2.

Έστω $v_{1}=(1,1),v_{2}=(-1,1)\in{\mathbb{C}}^{2}$ , $B$ η κανονική βάση του ${\mathbb{C}}^{2}$ και $D$ η βάση $(v_{1},v_{2})$ . Δίνεται η γραμμική συνάρτηση $f:{\mathbb{C}}^{2}\rightarrow{\mathbb{C}}^{2}$ , με την πληροφορία ότι $f(v_{1})=v_{1}$ και $f(v_{2})=2v_{2}$ . O πίνακας, λοιπόν, της $f$ ως προς τη βάση $D$ είναι ιδιαίτερα απλός:

$Α^{f}_{D,D}=\begin{bmatrix}1&0\cr 0&2\end{bmatrix}\;.$
Επιθυμούμε να βρούμε τον τύπο της $f$ . Αφού

$S_{B\leftarrow D}=\begin{bmatrix}1&-1\cr 1&1\end{bmatrix},\;S_{D\leftarrow B}=% (S_{B\leftarrow D})^{-1}=\frac{1}{2}\begin{bmatrix}\ \;1&1\cr-1&1\end{bmatrix}\;,$
έπεται ότι

$Α^{f}_{B,B}=S_{B\leftarrow D}\;A^{f}_{D,D}\;S_{D\leftarrow B}=\frac{1}{5}% \begin{bmatrix}3&1\cr 1&3\end{bmatrix}.$
Αφού $C_{B}f(a,b)=Α^{f}_{B,B}C_{B}(a,b)$ , έχουμε ότι:

$C_{B}f(a,b)=\frac{1}{2}\begin{bmatrix}3&1\cr 1&3\end{bmatrix}\;\begin{bmatrix}% a\cr b\end{bmatrix}=\frac{1}{2}\begin{bmatrix}3a+b\cr b+3a\end{bmatrix}$
και άρα

$f(a,b)=\frac{1}{2}(3a+b,b+3a)\;.$
Παρατηρούμε ότι o πίνακας της $f$ ως προς τη βάση $D$ είναι σαφώς απλούστερος από τον πίνακα της $f$ ως προς την κανονική βάση $Β$ .

Ένας $n\times n$ πίνακας $A$ με συντελεστές από το $\Bbbk$ είναι διαγωνιοποιήσιμος (diagonalizable), αν o $A$ είναι όμοιος με διαγώνιο πίνακα. Η γραμμική συνάρτηση $f:V\rightarrow V$ λέγεται διαγωνιοποιήσιμη (diagonalizable) αν υπάρχει μία διατεταγμένη βάση $D$ του $V$ , έτσι ώστε o $A^{f}_{D,D}$ να είναι διαγώνιος πίνακας. Ένα από τα σημαντικότερα προβλήματα που θα μας απασχολήσουν στο επόμενο κεφάλαιο, είναι η εύρεση κριτηρίων για το πότε ένας τετραγωνικός πίνακας και αντίστοιχα μία γραμμική συνάρτηση είναι διαγωνιοποιήσιμοι.

Ασκήσεις Ενότητας 4.3

1.

Έστω $B=(e_{1},e_{2},e_{3},e_{4})$ η συνήθης βάση του ${\mathbb{R}}$ -διανυσματικού χώρου ${\mathbb{R}}^{4}$ , $\epsilon_{1}=e_{1}+e_{4},\;\;\epsilon_{2}=e_{1}+3e_{2},\;\;\epsilon_{3}=3e_{1}% +e_{2},\;\;\epsilon_{4}=e_{1}+e_{2}+e_{3}+e_{4}$ , $D=(\epsilon_{1},\epsilon_{2},\epsilon_{3},\epsilon_{4})$ . Να βρεθούν οι πίνακες $S_{D\leftarrow B}$ και $S_{B\leftarrow D}$ .

Λύση
2.

Έστω $C=((1,1),(1,-1))$ και

$Α=\begin{bmatrix}1&2\cr 3&4\end{bmatrix}\ .$
Να βρεθεί η γραμμική συνάρτηση $f:\mathbb{R}^{2}\rightarrow\mathbb{R}^{2}$ , όταν $Α=Α_{f}=A_{C,C}$ .

Λύση
3.

Δίνεται ο ενδομορφισμός του ${\mathbb{R}}$ -διανυσματικού χώρου ${\mathbb{R}}^{3}$ ,

$f:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}\;,\;\;\;\;x\epsilon_{1}+y% \epsilon_{2}+z\epsilon_{3}\mapsto y\epsilon_{1}+z\epsilon_{2}+x\epsilon_{3}\;,$
όπου $\epsilon_{1}=(1,0,1),\;\;\epsilon_{2}=(1,1,0),\;\;\epsilon_{3}=(1,0,0)$ . Να ορίσετε την $f$ ως προς τη συνήθη βάση του ${\mathbb{R}}^{3}$ , δηλ. να περιγράψετε $f(e_{1})$ , $f(e_{2})$ , $f(e_{3})$ και να δώσετε τον τύπο $f(a,b,c)$ . Εάν η $f$ είναι ισομορφισμός να βρεθεί η $f^{-1}$ .

Λύση

4.4 Σύντομα Ιστορικά Στοιχεία

H μελέτη των γραμμικών συναρτήσεων, ως (γραμμική) αλλαγή του συστήματος των συντεταγμένων απασχόλησε τους γεωμέτρες τον 17ο και 18ο αιώνα για το πραγματικό επίπεδο και τον τρισδιάστατο χώρο. O Gauss (1777-1855) στο έργο του για τις τετραγωνικές μορφές, δηλ. τις συναρτήσεις της μορφής $f(x,y)=ax^{2}+bxy+cy^{2}$ , το 1801 μελέτησε πότε (γραμμικές) αλλαγές του συστήματος των συντεταγμένων δίνουν ισοδύναμες τετραγωνικές μορφές. Αποθήκευσε τις πληροφορίες της αλλαγής συντεταγμένων σε έναν πίνακα (άτυπα), αυτόν που σήμερα καλούμε πίνακα της γραμμικής συνάρτησης και απέδειξε ότι η ορίζουσα του πίνακα πρέπει να είναι ίση με το $1$ . Εφεξής, η εξέλιξη της ιστορίας των γραμμικών συναρτήσεων παρακολουθεί στενά και παράλληλα την ιστορία της θεωρίας των πινάκων και των διανυσματικών χώρων.

Για περισσότερα ιστορικά στοιχεία παραπέμπουμε στα συγγράμματα [3] και [4].

Βιβλιογραφία

1.

H. Anton, C. Rorres, Elementary Linear Algebra, Applications Version, John Wiley and Sons, 1994.
2.

Θ. Θεοχάρη-Αποστολίδη, Χ. Χαραλάμπους, Β. Βαβατσούλας, Εισαγωγή στη Γραμμική Άλγεβρα, Θεσσαλονίκη 2006.
3.

V. Katz, Ιστορία των Μαθηματικών, Πανεπιστημιακές Εκδόσεις Κρήτης, 2013.
4.

I. Kleiner, A History of Abstract Algebra, Birkhäuser Boston, 2007.
5.

K. Nicholoson, Elementary Linear Algebra, McGraw-Hill, 2001.
6.

Th. Shiffrin and M. R. Adams, Linear Algebra, a Geometric Approach, W. H. Freeman and Company, 2002.