Μια Εισαγωγή στη Γραμμική Άλγεβρα για τις Θετικές Επιστήμες

Κεφάλαιο 3Διανυσματικοί Χώροι

Έστω $\Bbbk$ όπως συνήθως το ${\mathbb{R}}$ ή το ${\mathbb{C}}$ .Στο κεφάλαιο αυτό θα μελετήσουμε την αλγεβρική δομή που αποκτά το σύνολο των στοιχείων του $\Bbbk^{n}$ και που οφείλεται στο άθροισμα και στο βαθμωτό γινόμενο με στοιχεία από το $\Bbbk$ . Τα στοιχεία του $\Bbbk^{n}$ είναι διανύσματα και το σύνολο $\Bbbk^{n}$ είναι διανυσματικός χώρος. Για τη συνέχεια, η γεωμετρική εποπτεία είναι ιδιαίτερα σημαντική καθώς μας καθοδηγεί ορθά προς τα ισχύοντα. Θα επιχειρήσουμε να την αξιοποιήσουμε στο έπακρο. Εφόσον έχουμε αποκτήσει εξοικείωση με τον $\Bbbk^{n}$ , θα μελετήσουμε αφηρημένους $\Bbbk$ -διανυσματικούς χώρους.

3.1 Διανύσματα στον ${\mathbb{R}}^{n}$

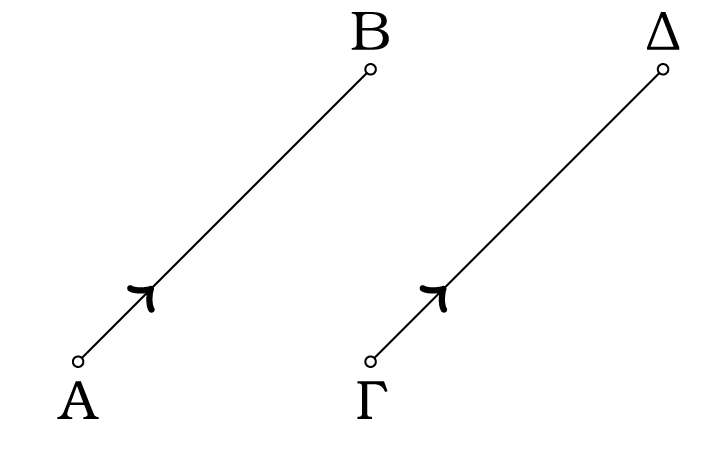
Τα διανύσματα (vectors) στον ${\mathbb{R}}^{n}$ , διάνυσμα όπου $n\in{\mathbb{N}}$ , είναι ευθύγραμμα τμήματα που χαρακτηρίζονται από το μήκος, την κλίση και τη φορά τους. Το ίδιο διάνυσμα μπορεί να αναπαρασταθεί με διαφορετικά αρχικά σημεία, όπως φαίνεται στο Σχήμα (3.1), όπου $\vec{AB}=\vec{\Gamma\Delta}$ .

Σχήμα 3.1:Το ίδιο διάνυσμα με διαφορετικά αρχικά σημεία

Αν $P(p_{1},\ldots,p_{n})$ και $Q(q_{1},\ldots,q_{n})$ είναι σημεία στον ${\mathbb{R}}^{n}$ , τότε το διάνυσμα με αρχικό σημείο $P$ και τελικό σημείο $Q$ γράφεται $\vec{PQ}$ και είναι η $n$ -άδα

\vec{PQ}:=(q_{1}-p_{1},\ldots,q_{n}-p_{n})\ .

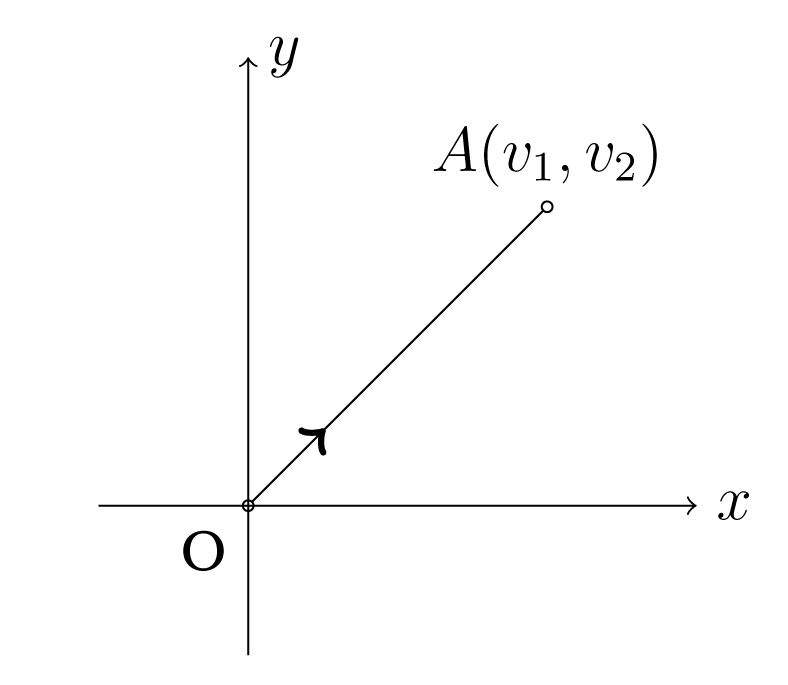
To βέλος στο $\vec{PQ}$ ορίζει το αρχικό και τελικό σημείο του διανύσματος, είναι όμως περιττό όταν δίνονται οι τιμές των συντεταγμένων του διανύσματος, δηλ. οι $q_{i}-p_{i}$ , για $i=1,\ldots,n$ . Αντίστροφα, έστω το διάνυσμα ${v}=(v_{1},\ldots,v_{n})$ στον $\mathbb{R}^{n}$ . Αν επιλέξουμε ως αρχικό σημείο του ${v}$ την αρχή των αξόνων $Ο(0,\ldots,0)$ , τότε το τελικό σημείο του ${v}$ είναι το σημείο $Α(v_{1},\ldots,v_{n})$ . Έτσι δημιουργούμε μία αμφιμονότιμη αντιστοιχία μεταξύ των σημείων του ${\mathbb{R}}^{n}$ και στα διανύσματα στον ${\mathbb{R}}^{n}$ , που έχουν αρχικό σημείο την αρχή των αξόνων. Στο επόμενο σχήμα απεικονίζεται το διάνυσμα $\vec{OA}=(v_{1},v_{2})$ , όπου $A$ είναι το σημείο $Α(v_{1},v_{2})$ του ${\mathbb{R}}^{2}$ .

Αν ${{\alpha}}=(a_{1},\ldots,a_{n})$ , ${\beta}=(b_{1},\ldots,b_{n})$ είναι δύο διανύσματα στον ${\mathbb{R}}^{n}$ ,τότε το άθροισμα (sum) των $\alpha$ και $\beta$ είναι το διάνυσμα $\alpha+\beta=(a_{1}+b_{1},\ldots,a_{n}+b_{n})$ .Γεωμετρικά, προσθέτουμε δύο διανύσματα στον ${\mathbb{R}}^{n}$ με τον κανόνα του παραλληλογράμμου, όπως φαίνεται στο Σχήμα (3.3). Έτσι, $\vec{ΟΑ}=\vec{B\Gamma}$ , ενώ $\vec{ΟΒ}=\vec{Α\Gamma}$ .

Σχήμα 3.3:To άθροισματων $\alpha$ και $\beta$ είναι το $\gamma$

Ο βαθμωτός πολλαπλασιασμός (scalar product) του ${{\alpha}}=(a_{1},\ldots,a_{n})$ με ένα στοιχείο $c$ του $\mathbb{R}$ , ορίζεται ως το διάνυσμα

c{{\alpha}}:=(ca_{1},\ldots,ca_{n})\ .

Το διάνυσμα $c{{\alpha}}$ είναι παράλληλο με το διάνυσμα ${{\alpha}}$ και το μήκος του αυξάνεται όταν $|c|>1$ , ενώ ελαττώνεται όταν $|c|<1$ . Όταν $c>0$ , η φορά του $c{{a}}$ είναι ίδια με τη φορά του ${{\alpha}}$ , ενώ είναι η αντίστροφη όταν $c<0$ .

Όταν $c=-1$ γράφουμε $-{{\alpha}}$ , δηλ. $-\alpha=(-a_{1},\ldots,-a_{n})$ . Έτσι, στο σύνολο των διανυσμάτων του ${\mathbb{R}}^{n}$ ορίζονται δύο πράξεις, η πρόσθεση και ο βαθμωτός πολλαπλασιασμός. Δεν είναι δύσκολο να επιβεβαιώσου με τα εξής:

1.

Ισχύει η προσεταιριστική ιδιότητα (associativity) για την πρόσθεση των διανυσμάτων, δηλ.

$\;{v}+({u}+{w})=({v}+{u})+{w}\ ,$
για όλα τα διανύσματα, ${v},{u},{w}$ , στον $\mathbb{R}^{n}$ .
2.

Το διάνυσμα ${0}=(0,\ldots,0)$ είναι το μηδενικό στοιχείο (zero element) της πρόσθεσης διανυσμάτων, δηλ.

$\;{0}+{v}={v}={v}+{0}\ ,$
για όλα τα διανύσματα ${v}$ στον $\mathbb{R}^{n}$ .
3.

Το διάνυσμα $-{v}$ είναι το αντίθετο (opposite) του ${v}$ ως προς την πρόσθεση, για κάθε διάνυσμα ${v}$ στον $\mathbb{R}^{n}$ , δηλ.

$\;-{v}+{v}={0}={v}+(-{v})\;.$
4.

Ισχύει η αντιμεταθετική ιδιότητα (commutativity) για την πρόσθεση διανυσμάτων:

$\;{v}+{u}={u}+{v}\;,$
για όλα τα ${v},{u}$ , διανύσματα στον $\mathbb{R}^{n}$ .
5.

Ισχύει η επιμεριστική ιδιότητα (distributivity) για την πρόσθεση διανυσμάτων και το βαθμωτό πολλαπλασιασμό:

$\;\kappa({v}+{u})=\kappa{v}+\kappa{u}\;,$
και

$\;(\kappa+\lambda)v=\kappa{v}+\lambda{v}\;,$
για κάθε $\kappa,\lambda\in\mathbb{R}$ και κάθε διάνυσμα ${v}$ , ${u}$ στον $\mathbb{R}^{n}$ .
6.

Ισχύει ότι

$\;\kappa(\lambda{v})=(\kappa\lambda){v}\;,$
για κάθε $\kappa,\lambda\in\mathbb{R}$ και ${v}$ στον $\mathbb{R}^{n}$ .
7.

Ισχύει ότι

$\;1{v}={v}\;,$
για κάθε διάνυσμα ${v}$ στον $\mathbb{R}^{n}$ .

Τις ιδιότητες αυτές ονομάζουμε ιδιότητες διανυσματικού χώρου (properties of a vector space). Το σύνολο των διανυσμάτων στον ${\mathbb{R}}^{n}$ είναι ο διανυσματικός χώρος ${\mathbb{R}}^{n}$ , (vector space ${\mathbb{R}}^{n}$ ). Όταν γράφουμε ${u}\in{\mathbb{R}}^{n}$ εννοούμε το διάνυσμα ${u}$ του διανυσματικού χώρου ${\mathbb{R}}^{n}$ . Αν το $U$ είναι ένα υποσύνολο διανυσμάτων στον ${\mathbb{R}}^{n}$ και

1.

${v}+{u}\in U$ , για κάθε $u,v\in U$ ,
2.

$cu\in U$ , για κάθε $u\in U$ και κάθε $c\in{\mathbb{R}}$ ,

τότε λέμε ότι o $U$ είναι διανυσματικός υποχώρος (subspace) του ${\mathbb{R}}^{n}$ . Για παράδειγμα, είναι εύκολο να δει κανείς ότι αν ${u}\in{\mathbb{R}}^{n}$ είναι διάνυσμα στον ${\mathbb{R}}^{n}$ , τότε το σύνολο

U=\{t{u}:\ t\in{\mathbb{R}}\}

είναι διανυσματικός υποχώρος του ${\mathbb{R}}^{n}$ . Λέμε ότι o $U$ είναι η ευθεία (line) που περνά από την αρχή των αξόνων και είναι παράλληλη προς το $u$ .

Σχήμα 3.5:H ευθεία $\{tu:\ t\in{\mathbb{R}}\}$

Παραδείγματα 3.1.1.

1.

Έστω ${v}=(2,3,1)$ . Η ευθεία που διέρχεται από την αρχή των αξόνων και το σημείο $v$ περιγράφεται από την εξίσωση

$U=\{(2t,3t,t):\ t\in\mathbb{R}\}=\{t{v}:\ t\in{\mathbb{R}}\}\,.$
Παρατηρούμε ότι η ευθεία $U$ είναι το σύνολο των λύσεων του ομογενούς γραμμικού συστήματος $AX=0$ , όπου

$A=\begin{bmatrix}1&0&-2\cr 0&1&-3\end{bmatrix}\ ,\textrm{βλ.~{}Ενότητα\ref{% lpinspace}.}$ , βλ. Ενότητα 1.4

Σχήμα 3.6: H ευθεία $\{t(2,3,1):\ t\in{\mathbb{R}}\}$
2.

Έστω $U$ το επίπεδο στον ${\mathbb{R}}^{3}$ που περιγράφεται ως το σύνολο

$U=\{(a,b,c)\in\mathbb{R}^{3}:\ 3a+b-2c=0\}.$
Στο Σχήμα (3.7) βλέπουμε τη γραφική αναπαράσταση του $U$ . Παρατηρούμε ότι το $(0,0,0)$ ανήκει στο $U$ . Ταυτίζουμε λοιπόν το $U$ με το σύνολο των διανυσμάτων του ${\mathbb{R}}^{3}$ , που έχουν αρχικό σημείο την αρχή των αξόνων και τελικό σημείο επί του $U$ .

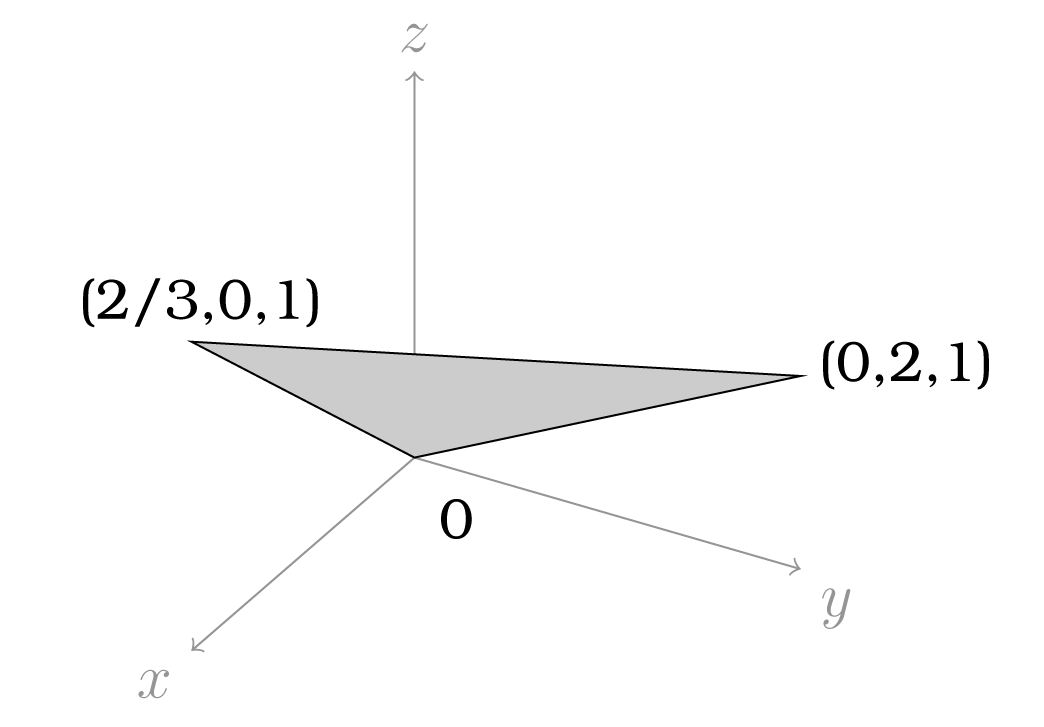
Σχήμα 3.7:To επίπεδο $\{(a,b,c):\ 3a+b-2c=0\}$

Αν $u=(u_{1},u_{2},u_{3})\in U$ , τότε $t(u_{1},u_{2},u_{3})\in U$ , για κάθε $t\in{\mathbb{R}}$ . Πράγματι,

$3u_{1}+u_{2}-2u_{3}=0\ \Rightarrow\ 3(tu_{1})+(tu_{2})-2(tu_{3})=0.$
Επίσης αν $u\in U$ και $w\in U$ τότε $u+w\in U$ . Πράγματι, έστω $u=(u_{1},u_{2},u_{3})$ και $w=(w_{1},w_{2},w_{3})$ . Τότε $3u_{1}+u_{2}-2u_{3}=0$ και $3w_{1}+w_{2}-2w_{3}=0$ . Επομένως

$3(u_{1}+w_{1})+(u_{2}-w_{2})-2(u_{3}+w_{3})=0\Rightarrow u+w\in U\;.$
Συνεπώς το $U$ είναι ${\mathbb{R}}$ -διανυσματικός υποχώρος του ${\mathbb{R}}^{n}$ .
3.

Έστω $L$ η ευθεία που δίνεται από την εξίσωση

$L=\{(1,3)+t(1,1):\ t\in\mathbb{R}\}.$
Η ευθεία $L$ είναι παράλληλη προς το διάνυσμα $(1,1)$ και διέρχεται από τα σημεία $A(1,3)$ , (για $t=0$ ), και $B(2,4)$ , (για $t=1$ ). H ευθεία $L$ δεν περνά από την αρχή των αξόνων. Έτσι το μηδενικό διάνυσμα δεν ανήκει στην $L$ και η $L$ δεν είναι διανυσματικός υποχώρος του ${\mathbb{R}}^{2}$ .

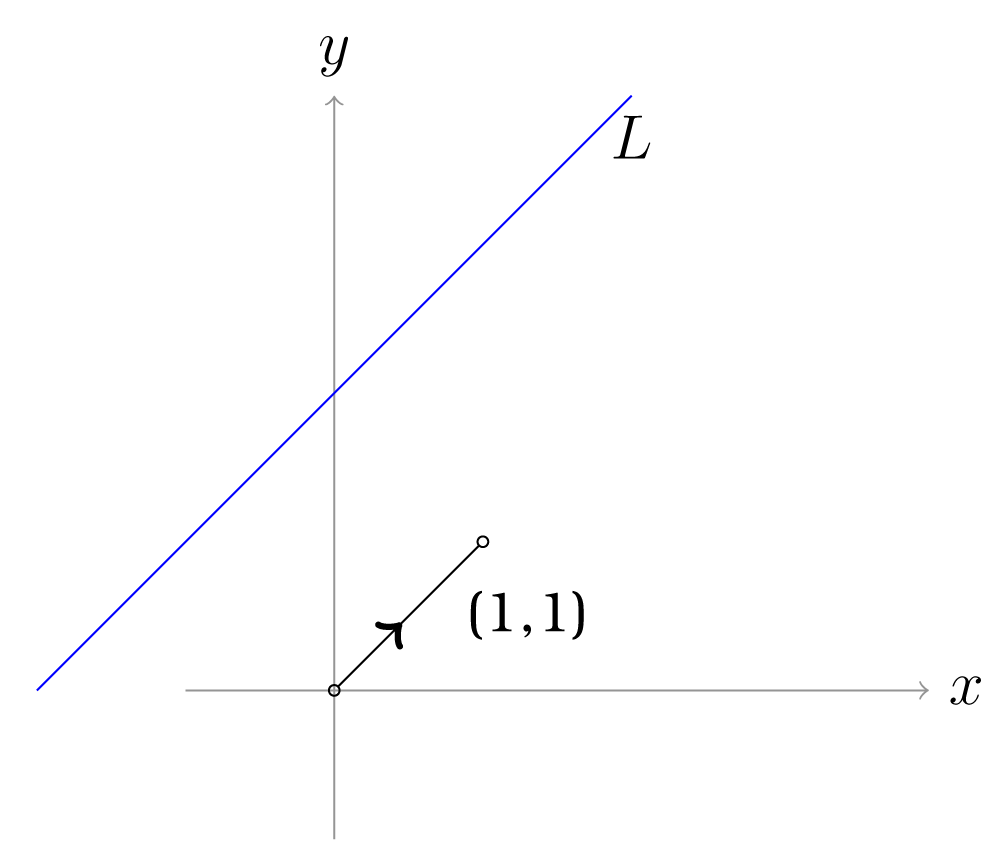
Σχήμα 3.8: H ευθεία $\{(1,3)+t(1,1):\ t\in{\mathbb{R}}\}$
4.

Το επίπεδο $Ε=\{\;(x,y,z)\in{\mathbb{R}}^{3}\;:\;x+y=2\;\}$ του Παραδείγματος I20.i2, δεν είναι υποχώρος του ${\mathbb{R}}^{3}$ , αφού ${\bf 0}\notin E$ (βλ. Σχήμα 1.4).

Με χρήση της θεωρίας των διανυσμάτων θα αποδείξουμε ότι το εμβαδόν ενός παραλληλογράμμου είναι ίσο με την απόλυτη τιμή της ορίζουσας του πίνακα. Πρώτα παρατηρούμε ότι ένα παραλληλόγραμμο καθορίζεται πλήρως από τρεις κορυφές και δύο ακμές. Αν $Α$ , $Β$ είναι δύο σημεία του ${\mathbb{R}}^{2}$ , τότε γράφουμε $Α Β$ για το ευθύγραμμο τμήμα που ενώνει τα δύο σημεία και $|ΑΒ|$ για το μήκος του $Α Β$ .

Πρόταση 3.1.2.

Έστω

M=\begin{bmatrix}a_{1}&b_{1}\cr a_{2}&b_{2}\end{bmatrix}\in{\cal{M}}_{2}({% \mathbb{R}})\

και $P_{M}$ το παραλληλόγραμμο με κορυφές τα σημεία $O(0,0)$ , $A(a_{1},a_{2})$ , $B(b_{1},b_{2})$ , και ακμές τα ευθύγραμμα τμήματα $Ο Α$ , $Ο Β$ . Τότε το εμβαδόν του $P_{M}$ ισούται με $|\det M|$ .

Απόδειξη.

Ως γνωστόν

\textrm{Εμβαδόν}P_{M}=\textrm{Bάσηtou$P_{M}$}\cdot\textrm{Ύψοςtou$P_{M}$}\ .

Έστω $\Gamma$ η τέταρτη κορυφή του $P_{M}$ . Θεωρούμε την ευθεία $L$ που περνάει από τα σημεία $Ο$ και $Β$ καθώς και την ευθεία $L^{\prime}$ που περνάει από τα σημεία $Α$ και $\Gamma$ . H ευθεία $L^{\prime}$ είναι παράλληλη προς το διάνυσμα $\vec{ΟΒ}$ και περιγράφεται ως το σύνολο

L^{\prime}=\{{(a_{1},a_{2})}+κ(b_{1},b_{2}):\ κ\in{\mathbb{R}}\}.

Έστω $C(c_{1},c_{2})$ τυχαίο σημείο επί της $L^{\prime}$ . Υπάρχει, λοιπόν, $k\in{\mathbb{R}}$ , τέτοιο ώστε

(c_{1},c_{2})=(a_{1}+kb_{1},a_{2}+kb_{2})\;.

Θεωρούμε το παραλληλόγραμμο $P_{1}$ με κορυφές τα σημεία $Ο$ , $Β$ , $C$ , και ακμές $Ο Β$ , $Ο C$ , βλ. Σχήμα (3.9).

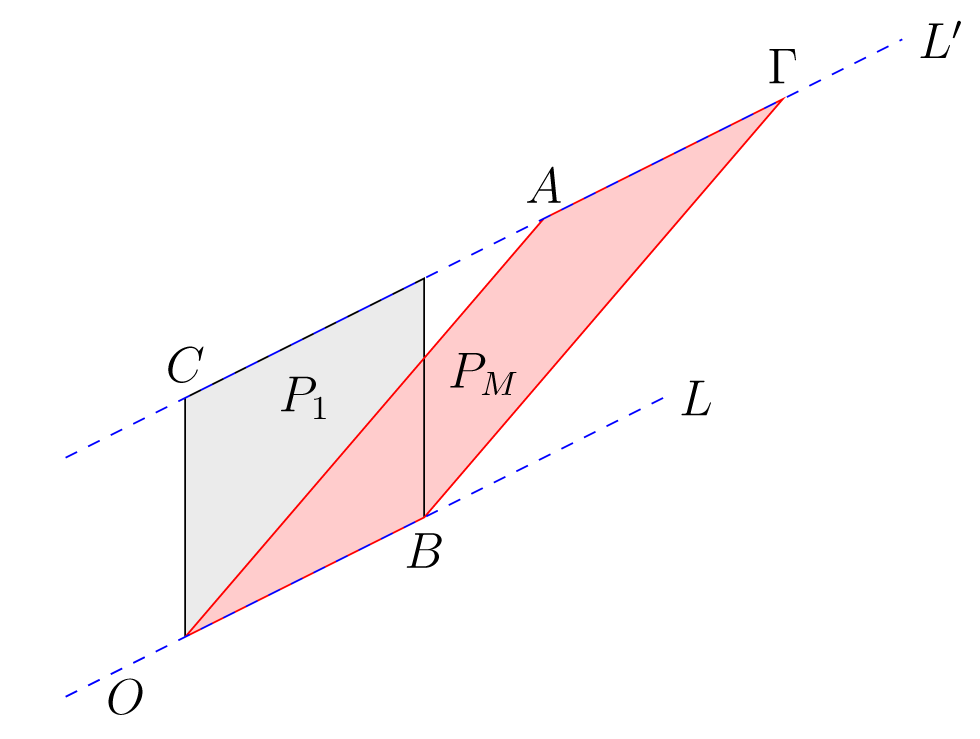
Σχήμα 3.9: Τα παραλληλόγραμμα $P$ και $P_{1}$

Παρατηρούμε ότι τα παραλληλόγραμμα $P_{M}$ και $P_{1}$ έχουν την ίδια βάση $|OB|$ . Αφού τα σημεία $Α$ και $C$ ανήκουν στην $L^{\prime}$ και η $L^{\prime}$ είναι παράλληλη προς την $L$ , έπεται ότι οι αποστάσεις των $Α$ και $C$ από την $L$ είναι ίσες. Άρα τα παραλληλόγραμμα $P_{M}$ και $P_{1}$ έχουν ίσα ύψη. Συνεπώς

\textrm{Εμβαδόν}P_{M}=\textrm{Eμβαδόν}P_{1}\;.

Σημειώνουμε ότι

M\begin{array}[]{c}\\ \overrightarrow{\Sigma_{1}\rightarrow\Sigma_{1}+k\Sigma_{2}}\end{array}M_{1}=% \begin{bmatrix}c_{1}&b_{1}\cr c_{2}&b_{2}\end{bmatrix}\textrm{kai}P_{1}=P_{M_{% 1}}\;\textrm{en'w}\det M=\det M_{1}\;.

Αντίστοιχα, θεωρώντας τον ανάστροφο του $M$ , παρατηρούμε ότι αν

M\begin{array}[]{c}\\ \overrightarrow{\Gamma_{2}\rightarrow\Gamma_{2}+k\Gamma_{1}}\end{array}M_{2},% \textrm{gia}k\in{\mathbb{R}}\;,

τότε

\det M=\det M_{2}\textrm{kai}\textrm{Εμβαδόν}P_{M}=\textrm{Eμβαδόν}P_{M_{2}}\;.

Σημειώνουμε ότι το $P_{M_{2}}$ έχει ακμή βάσης $Ο Α$ και δύο άλλες κορυφές επί της ευθείας που διέρχεται από τα σημεία $B$ και $\Gamma$ . Θα εφαρμόσουμε τις προηγούμενες παρατηρήσεις διαδοχικά. Την πρώτη φορά επιλέγουμε ως $C(0,c)$ το σημείο τομής της $L^{\prime}$ με τον άξονα των $y$ . Έτσι, το $P_{1}$ έχει ακμές $O B$ και $O C$ και αντιστοιχεί στον πίνακα:

M_{1}=\begin{bmatrix}0&b_{1}\cr c&b_{2}\end{bmatrix}\ .

Στη συνέχεια θεωρούμε το σημείο $\Delta$ , την τέταρτη κορυφή του $P_{1}$ . Βρίσκουμε το σημείο τομής της ευθείας

\{\vec{OB}+t\vec{B\Delta}:\ t\in{\mathbb{R}}\},

με τον άξονα των $x$ , έστω $D$ . Έτσι, $D=(d,0)$ και το αντίστοιχο παραλληλόγραμμο $P_{2}$ έχει ως κορυφές τα σημεία $O, C, D$ , βλ. Σχήμα (3.10).

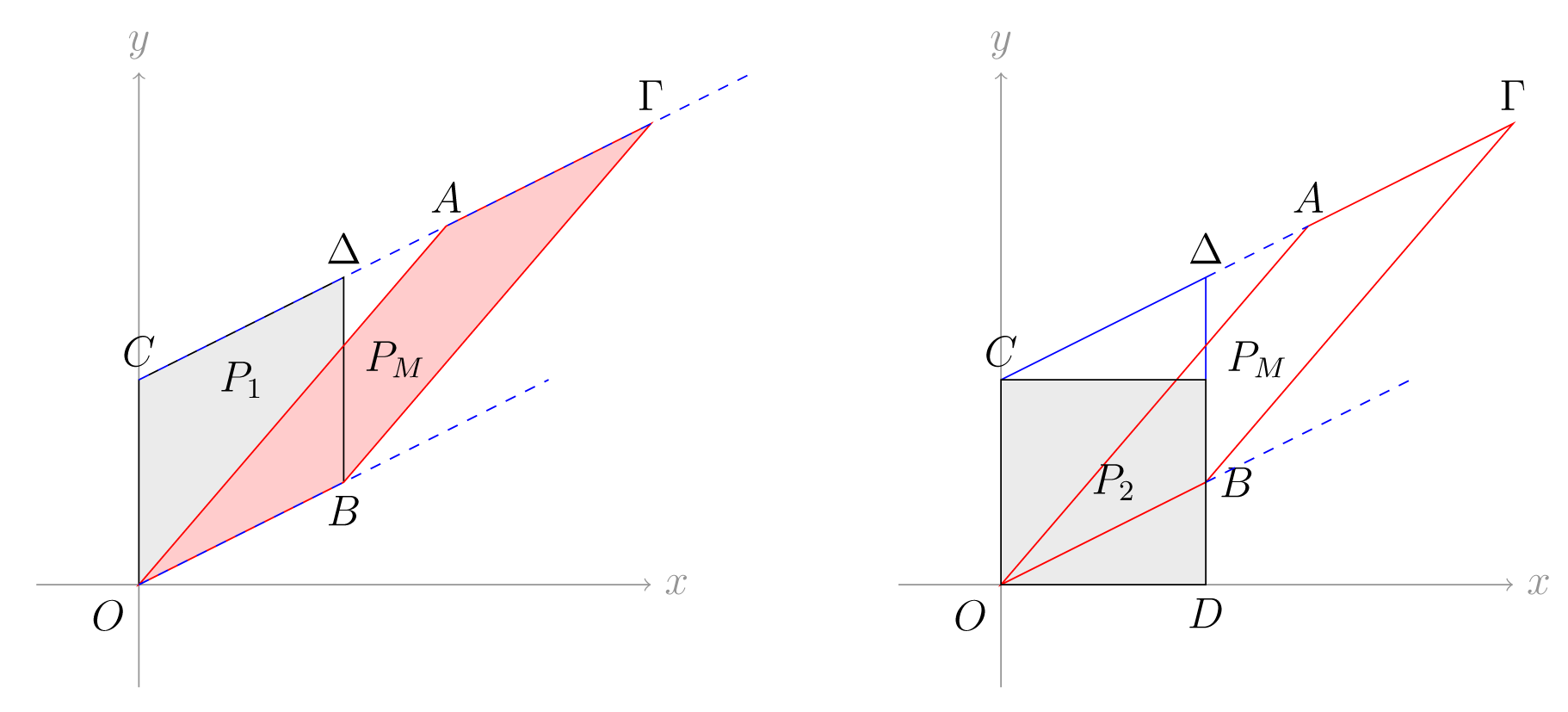
Σχήμα 3.10: Τα παραλληλόγραμμα $P_{M}$ , $P_{1}$ , $P_{2}$

Παρατηρούμε ότι

M_{2}=\begin{bmatrix}0&d\cr c&0\end{bmatrix}\ \textrm{και'oti}P_{M_{2}}=P_{2}.

Επομένως

\textrm{Εμβαδόν}P_{M}=\textrm{Eμβαδόν}P_{1}=\textrm{Eμβαδόν}P_{2}\

ενώ

\det M=\det M_{1}=\det M_{2}=-cd\ .

Αφού το $P_{2}$ είναι ορθογώνιο, έπεται ότι

\textrm{Eμβαδόν}P_{2}=|c||d|\Longrightarrow\textrm{Εμβαδόν}P_{M}=|\det M|\ .

Αποδείξαμε λοιπόν ότι η απόλυτη τιμή της ορίζουσας του $M$ είναι ίση με το εμβαδόν του παραλληλογράμμου $P_{M}$ .∎

Στον ${\mathbb{R}}^{3}$ , ένα παραλληλεπίπεδο καθορίζεται από τις συντεταγμένες τριών διανυσμάτων. Όπως προηγουμένως, μπορεί να αποδειχθεί ότι o όγκος του παραλληλεπιπέδου είναι ίσος με την απόλυτη τιμή της ορίζουσας του $3\times 3$ πίνακα των συντεταγμένων αυτών των τριών διανυσμάτων. Παρατηρούμε ότι τρία διανύσματα στον ${\mathbb{R}}^{3}$ ορίζουν ένα γνήσιο παραλληλεπίπεδο όταν δεν υπάρχει κάποιο επίπεδο που να περιέχει και τα τρία διανύσματα ταυτόχρονα. Σε αντίθετη περίπτωση, το στερεό παραλληλεπίπεδο καταρρέει και δεν έχει όγκο, ενώ η ορίζουσα του αντίστοιχου $3\times 3$ πίνακα είναι ίση με μηδέν.

Ασκήσεις Ενότητας 3.1

1.

Να δώσετε την εξίσωση της ευθείας $L=\{(1,2)+k(1,0):\ k\in{\mathbb{R}}\}$ στη μορφή $ax+by=c$ . Να εξετάσετε αν η $L$ είναι υποχώρος του ${\mathbb{R}}^{2}$ . Ομοίως για την ευθεία $L^{\prime}=\{(2,4)+k(1,2):\ k\in{\mathbb{R}}\}$ .

Λύση
2.

Να δώσετε την εξίσωση του επιπέδου $E_{1}=\{k(1,1,1)+t(1,0,1):\ k,t\in{\mathbb{R}}\}$ στη μορφή $ax+by+cz=d$ . Να εξετάσετε αν το $E_{1}$ είναι διανυσματικός υποχώρος του ${\mathbb{R}}^{3}$ . Ομοίως για τα επίπεδα $E_{1}=\{k(1,1,1)+t(1,0,1)+(3,1,3):\ k,t\in{\mathbb{R}}\}$ και $E_{2}=\{k(1,1,1)+t(1,0,1)+(3,2,3):\ k,t\in{\mathbb{R}}\}$ .

Λύση
3.

Να βρείτε το εμβαδόν του παραλληλογράμμου με κορυφές $(0,0)$ , $(1,3)$ , $(2,4)$ , $(3,7)$ .

Λύση
4.

Να βρείτε το εμβαδόν του παραλληλογράμμου με κορυφές $(1,1)$ , $(2,3)$ , $(1,5)$ , $(2,7)$ .

Λύση
5.

Να βρείτε τον όγκο του παραλληλεπιπέδου που ορίζεται από τα διανύσματα $(1,1,1)$ , $(0,2,1)$ , $(0,0,3)$ .

Λύση

3.2 Διανυσματικός Χώρος $\Bbbk^{n}$ και Υποχώροι

Στην ενότητα αυτή θα γενικεύσουμε στον ${\mathbb{C}}^{n}$ , όσα εξετάσαμε στην προηγούμενη ενότητα για τον ${\mathbb{R}}^{n}$ . Έτσι, θεωρούμε γενικότερα το σώμα $\Bbbk$ , όπου $\Bbbk={\mathbb{R}}$ ή ${\mathbb{C}}$ . Αν $v=(v_{1},\ldots,v_{n})$ , $w=(w_{1},\ldots,w_{n})\in\Bbbk^{n}$ , τότε ορίζουμε το άθροισμα (sum), $v+w$ , ως εξής:

v+w=(v_{1}+w_{1},\ldots,v_{n}+w_{n})\;.

Αντίστοιχα, αν $c\in\Bbbk$ , τότε ορίζουμε το βαθμωτό γινόμενο (scalar product), $c v$ , ως εξής:

cv=(cv_{1},\ldots,cv_{n})\;.

To σύνολο $\Bbbk^{n}$ γίνεται διανυσματικός χώρος διανυσματικός χώρος (vector space) όταν μελετάμε τη δομή που προκύπτει από αυτές τις δύο πράξεις. Τα στοιχεία του $\Bbbk^{n}$ θα λέγονται εφεξής διανύσματα (vectors). O επόμενος πίνακας συγκεντρώνει τις ιδιότητες που ικανοποιούνται στον διανυσματικό χώρο $\Bbbk^{n}$ . Me ${\bf 0}$ συμβολίζουμε το διάνυσμα $(0,\ldots,0)\in\Bbbk^{n}$ .

1.

${v}+({u}+{w})=({v}+{u})+{w}$ , για όλα τα ${v},{u},{w}\in\Bbbk^{n}$ .
2.

$\;{\bf 0}+{v}={v}={v}+{\bf 0}$ , για κάθε ${v}\in\Bbbk^{n}$ .
3.

$\;-{v}+{v}={\bf 0}={v}+(-{v})$ , για κάθε ${v}\in\Bbbk^{n}$ .
4.

$\;{v}+{u}={u}+{v}$ , για όλα τα ${v},{u}\in\Bbbk^{n}$ .
5.

$\;\kappa({v}+{u})=\kappa{v}+\kappa{u}$ , για κάθε $\kappa\in\Bbbk$ και όλα τα $v,u\in\Bbbk^{n}$ ,
$\;(\kappa+\lambda)v=\kappa{v}+\lambda{v}$ , για όλα τα $\kappa,\lambda\in\Bbbk$ και κάθε ${v}\in\Bbbk^{n}$ .
6.

$\;\kappa(\lambda{v})=(\kappa\lambda){v}$ , για όλα τα $\kappa,\lambda\in\Bbbk$ και κάθε ${v}\in\Bbbk^{n}$ .
7.

$\;1{v}={v}$ , για κάθε ${v}\in\Bbbk^{n}$ .

Για τη μελέτη μας εστιάζουμε σε κάποια υποσύνολα του $\Bbbk^{n}$ που ικανοποιούν δύο σημαντικές ιδιότητες.

Ορισμός 3.2.1.

Ένα μη κενό υποσύνολο $U$ του $\Bbbk^{n}$ λέγεται διανυσματικός υποχώρος (subspace) του $\Bbbk^{n}$ (ή απλώς υποχώρος) αν

i.

${u}+{w}\in U$ , για κάθε $u,w\in U$ ,
ii.

$\kappa u\in U$ , για κάθε $u\in U$ και κάθε $\kappa\in\Bbbk$ ,

Έστω o $U$ διανυσματικός υποχώρος του $\Bbbk^{n}$ . Από τις ιδιότητες του υποχώρου, προκύπτει ότι:

•

αν $u\in U$ , τότε $-u=(-1)u\in U$ .
•

${\bf 0}\in U$ , αφού $u-u={\bf 0}\in U$ .

Επομένως αν για κάποιο υποσύνολο $A$ του $\Bbbk^{n}$ μπορέσουμε και δείξουμε ότι ${\bf 0}\notin A$ , τότε το $A$ δεν είναι υποχώρος του $\Bbbk^{n}$ . Πως προκύπτουν, λοιπόν, οι υποχώροι; Σε αυτήν την ενότητα, θα μελετήσουμε τα διανύσματα που παράγουν τους διανυσματικούς υποχώρους του $\Bbbk^{n}$ .

Παράδειγμα 3.2.2.

Έστω $v\in\Bbbk^{n}$ ένα μη μηδενικό διάνυσμα. To σύνολο

L=\{\kappa v:\ \kappa\in\Bbbk\}\;

είναι υποχώρος του $\Bbbk^{n}$ . Πράγματι, δύο τυχαία στοιχεία του $L$ είναι της μορφής $\kappa_{1}v$ και $\kappa_{2}v$ για κάποια $\kappa_{1},\kappa_{2}\in\Bbbk$ . Επομένως

\kappa_{1}v+\kappa v=(\kappa_{1}+\kappa_{2})v\in L.

Αντίστοιχα για το βαθμωτό γινόμενο, έστω $\kappa v$ τυχαίο στοιχείο του $L$ για κάποια $\kappa\in\Bbbk$ , και έστω $c$ τυχαίο στοιχείο του $\Bbbk$ . Τότε

c(\kappa v)=(c\kappa)v\in L\;.

Γράφουμε $L=S\left(\{v\}\right)$ και λέμε ότι το σύνολο $\{v\}$ παράγει την $L$ . Δεν είναι δύσκολο να παρατηρήσει κάποιος ότι αν καθορίσουμε ένα μη μηδενικό $s\in\Bbbk$ , τότε

L=S\left(\{s\cdot v)\}\right)\;.

Σημειώνουμε ότι όταν $\Bbbk={\mathbb{R}}$ και $n=2$ ή $3$ , τότε $L$ είναι ευθεία στον ${\mathbb{R}}^{n}$ που διέρχεται από την αρχή των αξόνων, βλ. Παράδειγμα 3.1.1.1. Έτσι, o υποχώρος

S(\{(1,2)\})=\{\;(\kappa,2\kappa)\;:\;\kappa\in{\mathbb{R}}\;\}

είναι η ευθεία στον ${\mathbb{R}}^{2}$ που περνά από την αρχή των αξόνων και το σημείο $(1,2)$ . Αντίστοιχα, o υποχώρος

S(\{(\alpha_{1},\ldots,\alpha_{n})\})\subset{\mathbb{R}}^{n}

είναι η ευθεία στον ${\mathbb{R}}^{n}$ που περνά από την αρχή των αξόνων και το σημείο $(\alpha_{1},\ldots,\alpha_{n})$ .

Έστω τώρα $X$ είναι υποσύνολο διανυσμάτων του $\Bbbk^{n}$ . Ορίζουμε το υποσύνολο $S(X)\subset\Bbbk^{n}$ ως εξής:

{S(X)=\{\;\kappa_{1}x_{{1}}+\cdots+\kappa_{s}x_{{s}}\;:\;\kappa_{j}\in\Bbbk,\;% x_{{j}}\in X,1\leq j\leq s,\;s\in\mathbb{N}\}.}

Λέμε ότι το σύνολο $S(X)$ είναι o χώρος που παράγεται από το $X$ (space spanned by $X$ ) και λέμε ότι το $X$ παράγει $S(X)$ (spanning set) τον $S(X)$ . Τα στοιχεία του $S(X)$ λέγονται γραμμικοί συνδυασμοί (linear combinations) των στοιχείων του $X$ με συντελεστές από το $\Bbbk$ . Παρατηρούμε ότι:

S(\emptyset)=\{{\bf 0}\}\textrm{kai}X\subset S(X).

Δεν είναι δύσκολο να επιβεβαιώσουμε ότι το σύνολο $S(X)$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ . Πράγματι:

•

αν $u\in S(X)$ , τότε υπάρχουν $\kappa_{1},\ldots,\kappa_{s}\in\Bbbk$ και $x_{1},\ldots,x_{s}\in X$ τέτοια ώστε $v=\kappa_{1}x_{{1}}+\cdots+\kappa_{s}x_{{s}}$ . Αν $t\in\Bbbk$ , τότε

$tv=(t\kappa_{1})x_{{1}}+\cdots+(t\kappa_{s})x_{{s}}\in S(X)\;.$
•

αν $u,w\in S(X)$ , τότε υπάρχουν $\kappa_{1},\ldots,\kappa_{s}$ και $\lambda_{1},\ldots,\lambda_{t}\in\Bbbk$ καθώς και διανύσματα $x_{1},\ldots,x_{s}$ και $y_{1},\ldots,y_{t}\in X$ τέτοια ώστε $v=\kappa_{1}x_{{1}}+\cdots+\kappa_{s}x_{{s}}$ και $w=\lambda_{1}y_{{1}}+\cdots+\lambda_{t}y_{{t}}$ . Επομένως

$v+w=\kappa_{1}x_{{1}}+\cdots+\kappa_{s}x_{{s}}+\lambda_{1}y_{{1}}+\cdots+% \lambda_{t}y_{{t}}\in S(X)\;.$

Σημειώνουμε ότι αν $V$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ , τότε $S(V)\subset V$ . Συνεπώς

V\subset S(V)\subset V\ \Rightarrow V=S(V)\;.

Αποδείξαμε, λοιπόν, την επόμενη πρόταση.

Πρόταση 3.2.3.

Ένα υποσύνολο $V$ διανυσμάτων στο $\Bbbk^{n}$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ αν και μόνο αν $V=S(X)$ για κάποιο $X\subset\Bbbk^{n}$ .

Όταν o $V$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ , επιθυμούμε να βρούμε όσο το δυνατόν μικρότερα σε πλήθος υποσύνολα του $V$ που να παράγουν τον $V$ .

Παραδείγματα 3.2.4.

1.

Έστω $X=\{(1,0),(0,1)\}\subset{\mathbb{C}}^{2}$ . Θα δείξουμε ότι $S(X)={\mathbb{C}}^{2}$ . Πράγματι έστω $(a,b)\in{\mathbb{C}}^{2}$ . Τότε $a,b\in{\mathbb{C}}$ και

$(a,b)=a(1,0)+b(0,1)\in S(X)\;.$
Επομένως

${\mathbb{C}}^{2}\subset S(X)\subset{\mathbb{C}}^{2}\ \Rightarrow{\mathbb{C}}^{% 2}=S(X).$
Είναι φανερό ότι το διάνυσμα $(1,0)$ δεν παράγει τον ${\mathbb{C}}^{2}$ αφού το διάνυσμα $(0,1)\notin S\left(\{(1,0)\}\right)$ . Αντίστοιχα, $S\left(\{(0,1)\}\right)\neq{\mathbb{C}}^{2}$ αφού $(1,0)\notin S\left(\{(0,1)\right)$ . Επομένως δεν υπάρχει γνήσιο υποσύνολο του $X$ που να παράγει τον ${\mathbb{C}}^{2}$ . Αν δουλέψουμε στον ${\mathbb{R}}^{2}$ και θεωρήσουμε το $X=\{(1,0),(0,1)\}\subset{\mathbb{R}}^{2}$ , προκύπτει με τον ίδιο ακριβώς τρόπο ότι ${\mathbb{R}}^{2}=S(X)$ .
2.

Έστω $e_{i}$ το διάνυσμα στον $\Bbbk^{n}$ που έχει μονάδα για την $i$ συντεταγμένη και μηδέν σε όλες τις άλλες. Έτσι,

$e_{1}=(1,0,\cdots,0),\ e_{2}=(0,1,0,\cdots,0),\ \ldots,\ e_{n}=(0,\cdots,0,1)\;.$
Θεωρούμε το υποσύνολο $X=\{e_{1},e_{2},\ldots,e_{n}\}$ του $\Bbbk^{n}$ . Αν $(a_{1},\cdots,a_{n})\in\Bbbk^{n}$ , τότε

$(a_{1},\cdots,a_{n})=a_{1}e_{1}+\cdots+a_{n}e_{n}\in S(X)\;.$
Επομένως

$\Bbbk^{n}\subset S(X)\subset\Bbbk^{n}\ \Rightarrow\Bbbk^{n}=S(X).$
Αποδείξαμε λοιπόν ότι

$\Bbbk^{n}=S\left(\{(e_{1},\ldots,e_{n}\}\right).$
3.

Ο υποχώρος $\{{\bf 0}\}=S\left(\{{\bf 0}\}\right)$ λέγεται ο μηδενικός υποχώρος του $\Bbbk^{n}$ .
4.

Θα αποδείξουμε ότι

$S(\{(1,2),(2,4)\})=S(\{(1,2)\}).$
Πράγματι είναι φανερό ότι $S(\{(1,2)\})\subset S(X)$ . Επίσης,

$S(X)=\{\kappa(1,2)+\lambda(2,4):\ \kappa,\lambda\in\Bbbk\}=\{(\kappa+2\lambda,% 2\kappa+4\lambda):\ \kappa,\lambda\in\Bbbk\}=$
$\{(\kappa+2\lambda)\left(1,2\right):\ \kappa,\lambda\in\Bbbk\}=\{t(1,2):\ t\in% \Bbbk\}.$
Επομένως

$S(\{(1,2)\})\subset S(X)\subset S(\{(1,2)\})\ \Rightarrow S(\{(1,2)\})=S(X)\;.$
Παρατηρούμε ακόμη ότι

$S(X)=S(\{(2,4)\})=S(\{(3,6)\}),$
και άρα το διάνυσμα που παράγει τον $S(X)$ δεν είναι μοναδικό.
5.

Έστω $X=\{(1,2),(0,1)\}$ . Χρησιμοποιώντας τη θεωρία των γραμμικών συστημάτων, θα δείξουμε ότι $S(X)=\Bbbk^{2}$ . Πράγματι έστω $(\alpha,\beta)\in\Bbbk^{2}$ . Θα βρούμε $x_{1}$ , $x_{2}\in\Bbbk$ έτσι ώστε

$(\alpha,\beta)=x_{1}(1,2)+x_{2}(0,1)\ .$
Πρέπει, λοιπόν, να επιλύσουμε το γραμμικό σύστημα

$\begin{matrix}\ x_{1}&&=\alpha\cr 2x_{1}&+x_{2}&=\beta.\end{matrix}$
Αφού

$\left[\begin{array}[]{cc|c}1&0&\alpha\cr 2&1&\beta\end{array}\right]% \longrightarrow\left[\begin{array}[]{cc|c}1&0&\alpha\cr 0&1&\beta-2\alpha\end{% array}\right].$
προκύπτει ότι $x_{1}=\alpha$ , $x_{2}=\beta-2\alpha$ . Άρα

$(\alpha,\beta)=(\alpha,2\alpha+(\beta-2\alpha))=\alpha(1,2)+(\beta-2\alpha)(0,% 1)\ .$ (3.2.4.1)
Επομένως $S(X)=\Bbbk^{2}$ . O αναγνώστης καλείται να διαπιστώσει ότι

$e_{1}=1(1,2)-2(0,1)\ \textrm{kai}e_{2}=0(1,2)+1(0,1)\;,$
όπως προβλέπει η Σχέση (3.2.4.1).
6.

Έστω $X=\{u,w\}$ , όπου ${u},{w}$ είναι δύο μη μηδενικά διανύσματα του $\Bbbk^{2}$ και ${u}$ δεν είναι πολλαπλάσιο του $v$ . Θα αποδείξουμε ότι $S(X)=\Bbbk^{2}$ . Πράγματι, έστω ότι ${u}=(a_{1},a_{2})$ , ${w}=(b_{1},b_{2})$ όπου $a_{i},b_{i}\in\Bbbk$ , για $i=1,2$ και έστω ${h}=(c_{1},c_{2})\in\Bbbk^{2}$ . Παρατηρούμε ότι ${h}\in S(X)$ αν και μόνο αν υπάρχουν $k,t\in\Bbbk$ , έτσι ώστε

${h}=k{u}+t{w}\ .$
Αντικαθιστώντας τις συντεταγμένες των ${u},{w},{h}$ σε αυτήν την εξίσωση, βλέπουμε ότι η δυάδα $(k,t)$ πρέπει να είναι λύση του γραμμικού συστήματος

$\begin{matrix}xa_{1}+yb_{1}&=c_{1}\cr xa_{2}+yb_{2}&=c_{2}\;.\end{matrix}$ (3.2.4.2)
Αυτό θα συμβεί αν και μόνο αν σύστημα (3.2.4.2) είναι συμβατό. Ο πίνακας των συντελεστών είναι

$Α=\begin{bmatrix}a_{1}&b_{1}\cr a_{2}&b_{2}\end{bmatrix}\ .$
Παρατηρούμε ότι αν η ορίζουσα $\det A=a_{1}b_{2}-b_{1}a_{2}$ είναι μηδέν, τότε $(a_{2},b_{1})\neq k(b_{1},b_{2})$ για κάποιο $k\in\Bbbk$ . Όμως, από την υπόθεση αυτό δεν συμβαίνει, άρα $\operatorname{rank}(A)=2$ και ο πίνακας $A$ είναι αντιστρέψιμος. Συνεπώς, το Σύστημα (3.2.4.2) είναι συμβατό και έχει λύση. Άρα $h\in U$ και επομένως

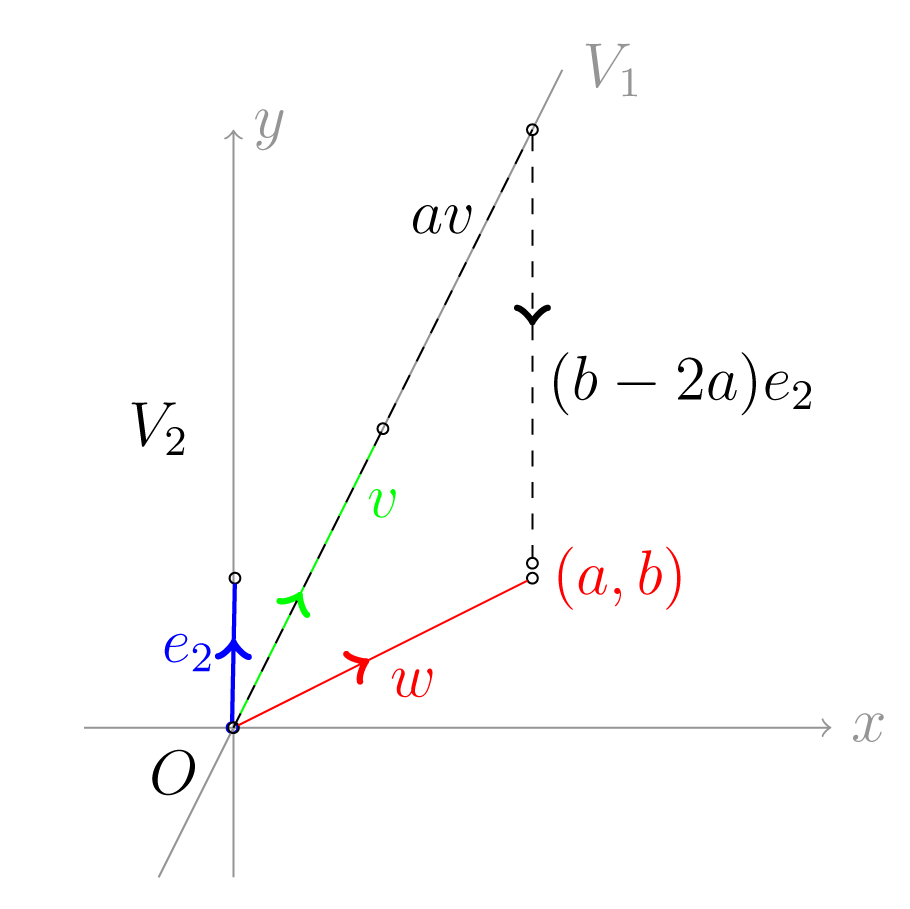
$\Bbbk^{2}\subset U\subset\Bbbk^{2}\ \Rightarrow U=\Bbbk^{2}\;.$
Σημειώνουμε ότι όταν $\Bbbk={\mathbb{R}}$ , μπορούμε να χρησιμοποιήσουμε γεωμετρικά επιχειρήματα για την απόδειξη. Πράγματι, έστω $h,u,w\in{\mathbb{R}}^{2}$ , όπως στο επόμενο σχήμα.

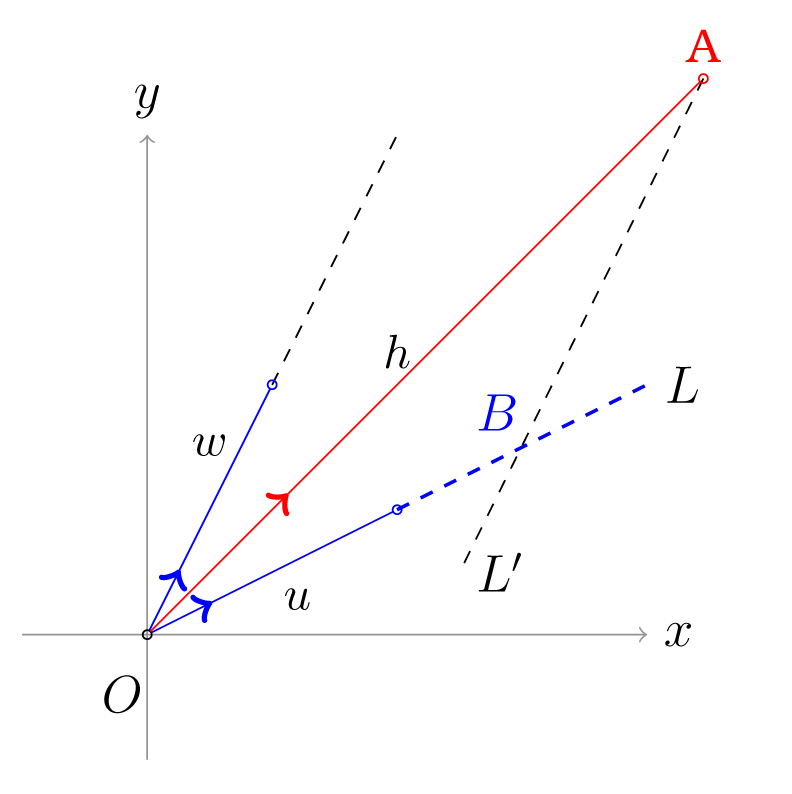
Σχήμα 3.11: $S(\{u,w\})={\mathbb{R}}^{2}$

Σημειώνουμε $Α$ , το τελικό σημείο του ${h}$ . Προεκτείνουμε το διάνυσμα ${u}$ στην ευθεία $L$ . Θεωρούμε $L^{\prime}$ , την ευθεία που είναι παράλληλη προς το ${w}$ και διέρχεται από το $A$ . Οι ευθείες $L$ και $L^{\prime}$ δεν είναι παράλληλες, αφού τα διανύσματα ${u}$ και ${w}$ δεν είναι παράλληλα. Επομένως οι $L$ και $L^{\prime}$ τέμνονται σε κάποιο σημείο, που σημειώνουμε με $Β$ . Αφού $\vec{OB}=ku$ , $\vec{OA}=tw$ για κάποια $k,t\in{\mathbb{R}}$ , έπεται ότι

${h}=\vec{OB}+\vec{BA}=k{u}+t{w}\in U\ .$
7.

Σε αυτό το παράδειγμα, θα βρούμε μία εξίσωση που ικανοποιείται από τα στοιχεία του $S\left(X\right)\subset{\mathbb{R}}^{3}$ όπου $X=\{(1,0,1),(0,2,0)\}$ . Αφού

$S(X)=\{\;\kappa(1,0,1)+\lambda(0,2,0)\;:\;\kappa,\lambda\in\Bbbk\;\},$
το διάνυσμα $(a,b,c)\in S(X)$ αν και μόνο αν υπάρχουν $\kappa$ , $\lambda$ έτσι ώστε το σύστημα

$\begin{bmatrix}1&0\cr 0&2\cr 1&0\end{bmatrix}\cdot\begin{bmatrix}\kappa\cr% \lambda\end{bmatrix}=\begin{bmatrix}a\cr b\cr c\end{bmatrix}$
είναι συμβατό. Αφού

$\left[\begin{array}[]{cc|c}1&0&α\cr 0&2&b\cr 1&0&c\end{array}\right]% \longrightarrow\left[\begin{array}[]{cc|c}1&0&α\cr 0&2&b\cr 0&0&c-a\end{array}% \right]\$
συμπεραίνουμε ότι το προηγούμενο σύστημα είναι συμβατό αν και μόνο αν $a-c=0$ , δηλ. αν $a=c$ . Επομένως

$S(X)=\{(α,b,α):\ α,b\in\Bbbk\}=\{(a,b,c)\in\Bbbk^{3}:\ a-c=0\}\ .$
O υποχώρος $S(X)$ είναι ένα επίπεδο που περνά από την αρχή των αξόνων και απεικονίζεται ως εξής:

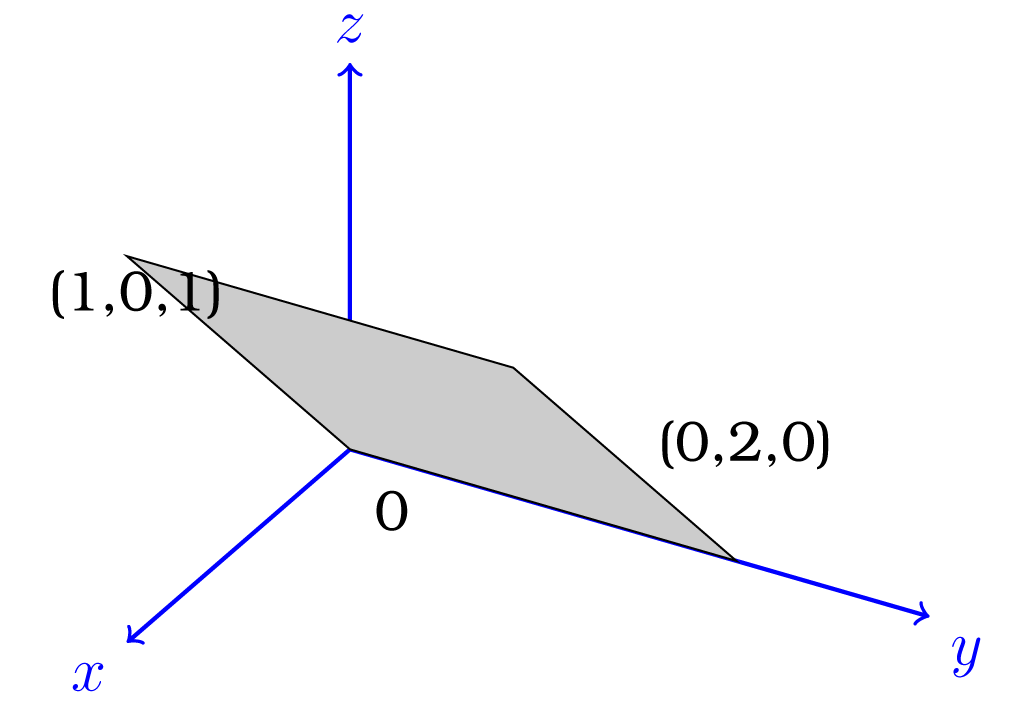
Σχήμα 3.12: $S\left(\{(1,0,1),(0,2,0)\}\right)=\{(a,b,a):\ a,b\in{\mathbb{R}}\}$
8.

Αντίστροφα, ξεκινώντας από μία εξίσωση που περιγράφει τα διανύσματα ενός διανυσματικού υποχώρου $U$ στον $\Bbbk^{3}$ , μπορούμε εύκολα να βρούμε δύο διανύσματα $u_{1},u_{2}$ έτσι ώστε $U=S\left(\{u_{1},u_{2}\}\right)$ . Θα δείξουμε τη διαδικασία για τον υποχώρο

$U=\{\;(x,y,z)\in\Bbbk^{3}\ :\;3x+y-2z=0\;\}\;.$
Αφού $3x+y-2z=0$ , έπεται ότι $-3x+2z=y$ . Έτσι αν $(x,y,z)\in U$ , τότε

$(x,y,z)=(x,-3x+2z,z)=x(1,-3,0)+z(0,2,1).$
Θέτουμε $u_{1}=(1,-3,0)$ , $u_{2}=(0,2,1)$ και παρατηρούμε ότι $u_{1},u_{2}\in U$ . Επομένως, αν $X=\{u_{1},u_{2}\}$ , τότε

$U=\{\;xu_{1}+zu_{2}\;:\;x,z\in\Bbbk\;\}=S(X)\ .$
To παράγον σύνολο $X$ δεν είναι μοναδικό. Εάν λύσουμε την εξίσωση $3x+y-2z=0$ ως προς το $z$ τότε βρίσκουμε ένα διαφορετικό σύνολο διανυσμάτων που παράγει το $U$ . Πράγματι

$z=1/2(3x+y)\Rightarrow(x,y,z)=(x,y,\frac{3x+y}{2})=x(1,0,\frac{3}{2})+y(0,1,% \frac{1}{2})$
και

$U=S(Y),\textrm{όπου}Y=\{(1,0,\frac{3}{2}),(0,1,\frac{1}{2})\})\ .$
Είναι επίσης εύκολο να δούμε ότι

$U=S(\{(2,0,3),(0,2,1)\})\ .$
Όταν $\Bbbk={\mathbb{R}}$ , το Σχήμα 3.13 απεικονίζει τον $U$ .

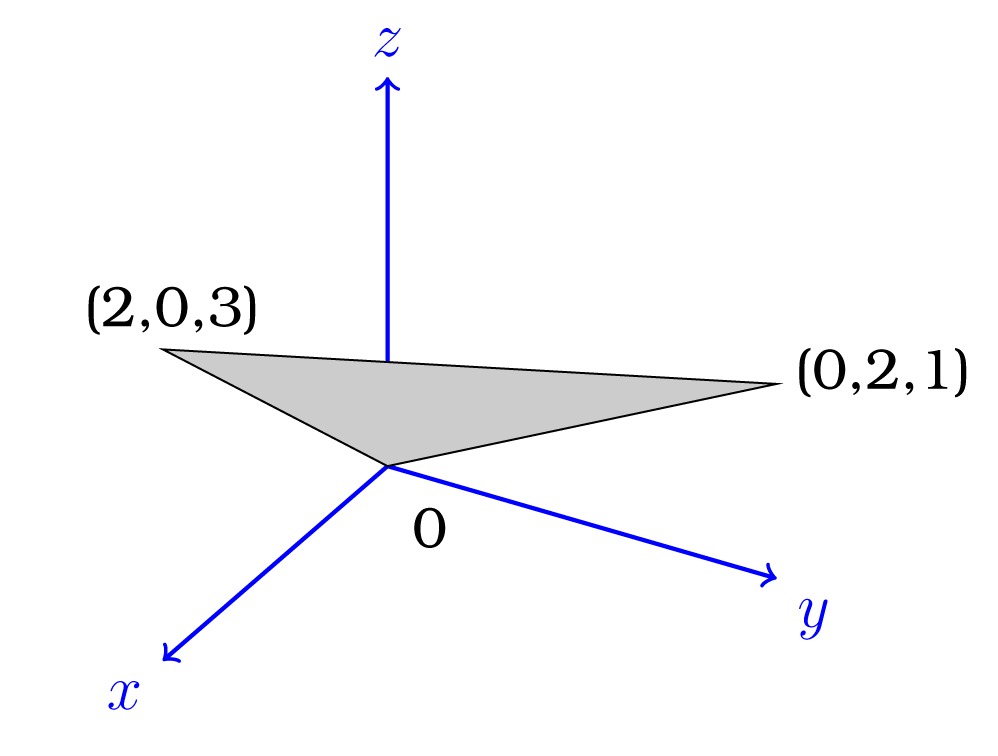
Σχήμα 3.13: $U=S\left(\{(2,0,3),(0,2,1)\}\right)$
9.

Έστω

$U=\{(a_{1},\ldots,a_{n})\in\Bbbk^{n}:\ a_{1}-a_{2}=0\}.$

Στις ασκήσεις o αναγνώστης καλείται να επιβεβαιώσει ότι το σύνολο $U$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ , βλ. Άσκηση 3.4.2. Παρατηρούμε ότι στον $\Bbbk^{2}$ , ένα διάνυσμα παράγει τον $U$ :
$U = {(a_{1}, a_{2}) \in k^{2} : a_{1} - a_{2} = 0} = {(a_{1}, a_{2}) \in k^{2} : a_{1} - a_{2} = 0} = {(a_{2}, a_{2}) : a_{2} \in k} = {a_{2} (1, 1) : a_{2} \in k} = S ({(1, 1)})$
Στον $k^{3}$ , όμως, χρειαζόμαστε δύο διανύσματα:
$U = {(a_{1}, a_{2}, a_{3}) \in k^{n} : a_{1} - a_{2} = 0} = {(a_{2}, a_{2}, a_{3}) : a_{2}, a_{3} \in k} = {a_{2} (1, 1, 0) + a_{3} (0, 1, 0) : a_{2}, a_{3} \in k} = S ({(1, 1, 0), (0, 0, 1)})$
Αντίστοιχα, στον $k^{n}$ χρειαζόμαστε $n - 1$ διανύσματα για να παράξουμε τον $U$ . Στο Σχήμα 3.14 βλέπουμε τη γραφική αναπαράσταση του $U$ στον $R^{2}$ και στον $R^{3}$ .

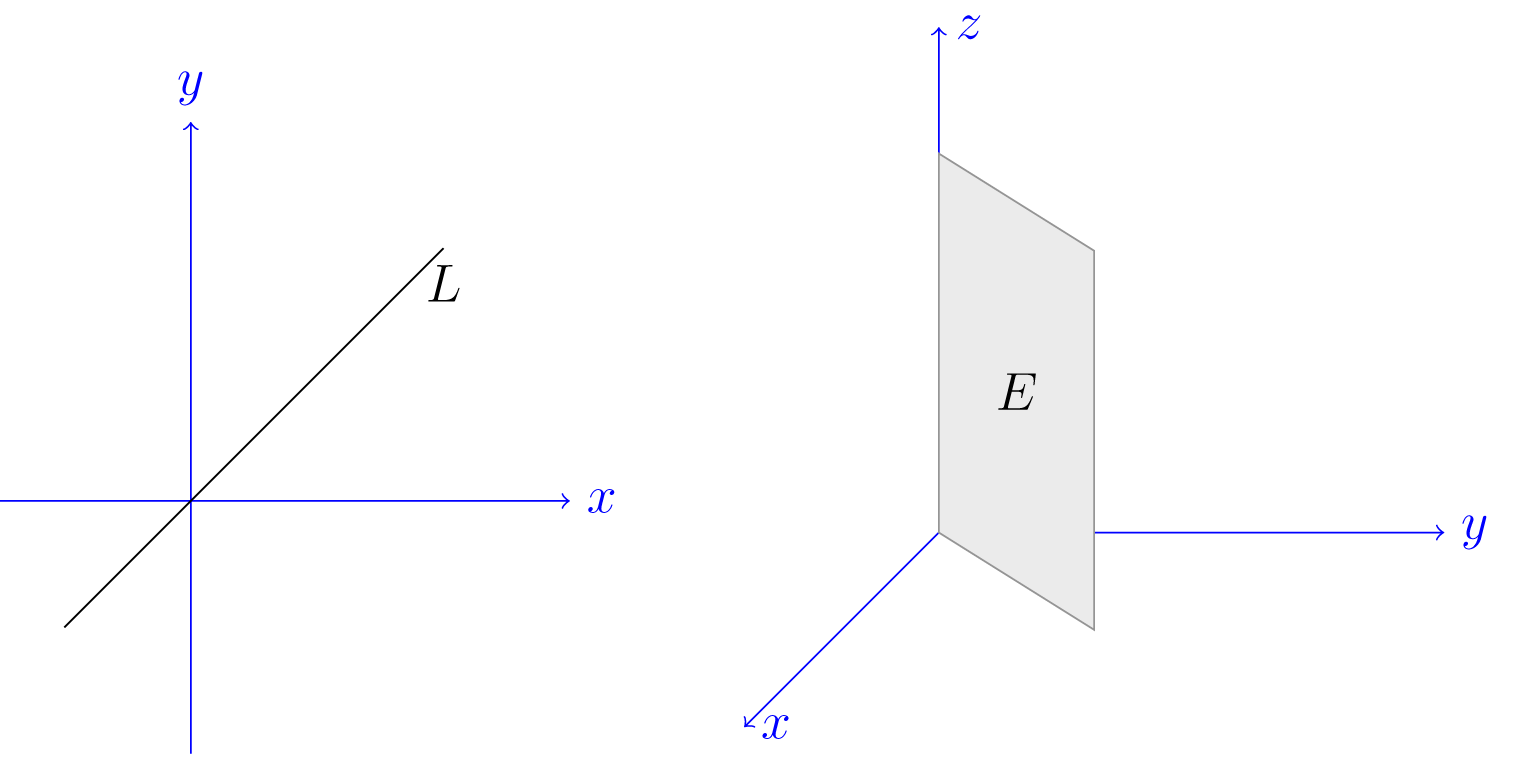
Σχήμα 3.14: Οι λύσεις της εξίσωσης $x-y=0$ στον ${\mathbb{R}}^{2}$ και στον ${\mathbb{R}}^{3}$

Στη συνέχεια ορίζουμε το άθροισμα (sum) και την τομή (intersection) δύο υποχώρων του $\Bbbk^{n}$ . Έστω $U$ και $W$ δύο υποχώροι του $\Bbbk^{n}$ . Το άθροισμα $U+W$ των $U$ και $W$ ορίζεται ως εξής:

U+W=\{\;u+w\;:\;u\in U\hbox{και}w\in W\;\}.

Παρατηρούμε ότι $U\subset U+W$ , αφού ${0}\in W$ και $u=u+{0}$ . Ομοίως $W\subset U+W$ . H επόμενη πρόταση, προκύπτει εύκολα από τους σχετικούς ορισμούς:

Αν

U=S(X_{1})

W=S(X_{2})

όπου

X_{1}

X_{2}

είναι υποσύνολα του

\Bbbk^{n}

, τότε

U+W=S(X_{1}\cup X_{2})

και άρα το άθροισμα $U+W$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ .

Η τομή $U\cap W$ ορίζεται ως εξής:

U\cap W=\{\;v\;:\;v\in U\hbox{και}v\in W\;\}\ .

Προκύπτει εύκολα ότι $U\cap W$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ . Στα Παραδείγματα θα δούμε ότι τα διανύσματα που ανήκουν στην τομή $U\cap W$ προκύπτουν ως λύσεις ενός ομογενούς συστήματος.

Παραδείγματα 3.2.5.

1.

Έστω $v=(1,2)$ , $e_{2}=(0,1)$ και

$V_{1}=\{\;(x,y)\in\Bbbk^{2}\;:\;2x-y=0\;\}=S(\{(1,2)\})=S(\{v\})$
και

$V_{2}=\{\;(x,y)\in\Bbbk^{2}\;:\;x=0\;\}=S(\{0,1)\}=S(\{e_{2}\}).$
Είναι εύκολο να δούμε ότι $V_{1}\cap V_{2}=\{{\bf 0}\}$ .Στο Παράδειγμα 3.2.4.5 είδαμε ότι $V_{1}+V_{2}=\Bbbk^{2}$ . Συγκεκριμένα είδαμε ότι αν $w=(\alpha,\beta)\in\Bbbk^{2}$ τότε

$w=\alpha\cdot v+(b-2a)\cdot e_{2}\;.$
Στο Σχήμα (3.15), απεικονίζουμε τους χώρους $V_{1}$ και $V_{2}$ στον ${\mathbb{R}}^{2}$ .

Σχήμα 3.15 : $V_{1}+V_{2}={\mathbb{R}}^{2}$ , $V_{1}\cap V_{2}={\bf 0}$
2.

Θεωρούμε τους υποχώρους
$V_{1}=\{\;(x,y,z)\in\Bbbk^{3}\;:\;x-z=0\;\}=S\left(\{v_{1},v_{2}\}\right)\;,$
$V_{2}=\{\;(x,y,z)\in\Bbbk^{3}\;:\;x+y+z=0\;\}=S\left(\{w_{1},w_{2}\}\right)\;,$
όπου $v_{1}=(1,0,1),v_{2}=(0,1,0)$ και $w_{1}=(1,0,-1),w_{2}=(0,1,-1)$ . Θα υπολογίσουμε την τομή $V_{1}\cap V_{2}$ . Είναι φανερό ότι $(x,y,z)\in V_{1}\cap V_{2}$ αν και μόνο αν

$\begin{array}[]{lcc}x&-z&=0\cr x+y&+z&=0\ .\end{array}$

Λύνοντας το σύστημα αυτό βρίσκουμε ότι

$V_{1}\cap V_{2}=\{\;(x,-2x,x)\;:\;x\in\Bbbk\;\}=\{x(1,-2,1):\;x\in\Bbbk\}.\$

Στη συνέχεια, θα αποδείξουμε ότι $V_{1}+V_{2}=\Bbbk^{3}$ . Καταρχήν παρατηρούμε ότι $(a,b,c)\in V_{1}+V_{2}$ αν και μόνο αν υπάρχουν $(x_{1},x_{2},x_{3},x_{4})$ έτσι ώστε

$(a,b,c)=x_{1}v_{1}+x_{2}v_{2}+x_{3}w_{1}+x_{4}w_{4}\ ,$
δηλ. αν και μόνο αν το σύστημα

$\begin{matrix}x_{1}&&+x_{3}&&=a\\ &x_{2}&&+x_{4}&=b\cr x_{1}&&-x_{3}&-x_{4}&=c\end{matrix}\$
είναι συμβατό. O πίνακας των συντελεστών του συστήματος είναι o πίνακας

$A=\left[\begin{array}[]{ccrr}1&0&1&0\cr 0&1&0&1\cr 1&0&-1&-1\end{array}\right]\;.$
Αφού ο $Α$ έχει βαθμίδα 3, έπεται ότι το σύστημα είναι συμβατό, για κάθε διάνυσμα $(a,b,c)\in\Bbbk^{3}$ . Επομένως $V_{1}+V_{2}=\Bbbk^{3}$ .

Έστω $Α=(a_{ij})\in\mathcal{M}_{m\times n}(\Bbbk)$ . O μηδενοχώρος (nullspace) του $Α$ συμβολίζεται με $\operatorname{null}(A)$ $\operatorname{null}(A)$ και είναι ο υποχώρος του $\Bbbk^{n}$ που παράγεται από τις λύσεις του ομογενούς συστήματος $AX={\bf 0}$ . Ο χώρος γραμμών (row space) του $A$ συμβολίζεται με $\Gamma(A)$ $\Gamma(A)$ και είναι ο υποχώρος του $\Bbbk^{n}$ που παράγεται από τα διανύσματα που αντιστοιχούν στις $m$ γραμμές του $A$ ,δηλ.

\Gamma(A):=S(\{(a_{11},a_{12},\cdots,a_{1n}),\ldots,(a_{m1},a_{m2},\cdots,a_{% mn})\})\subset\Bbbk^{n}.

O χώρος στηλών (column space) του $A$ συμβολίζεται με $\Sigma(A)$ $\Sigma(A)$ και είναι ο υποχώρος του $\Bbbk^{m}$ που παράγεται από τα διανύσματα που αντιστοιχούν στις $n$ στήλες του $A$ , δηλ.

\Sigma(A):=S(\{(a_{11},a_{21},\cdots,a_{m1}),\ldots,(a_{1n},a_{2n},\cdots,a_{% mn})\})\subset\Bbbk^{m}.

Σημειώνουμε την επόμενη χρήσιμη διαπίστωση.

O χώρος γραμμών του

Α

είναι ο χώρος στηλών του

A^{T}

, ενώ ο χώρος στηλών του

Α

είναι ο χώρος γραμμών του

A^{T}

, δηλ.

\Gamma(A)=\Sigma(A^{T})\textrm{kai}\Sigma(A)=\Gamma(A^{T}).

Από τον ορισμό γνωρίζουμε ότι κάθε λύση του $AX={\bf 0}$ ανήκει στον $\operatorname{null}(A)$ . To αντίστροφο είναι επίσης αληθές, όπως προκύπτει από την Πρόταση 1.1.3. Διατυπώνουμε αυτήν την διαπίστωση στην επόμενη πρόταση.

Πρόταση 3.2.6.

Έστω $Α=(a_{ij})\in\mathcal{M}_{m\times n}(\Bbbk)$ . Κάθε στοιχείο του $\operatorname{null}(A)$ είναι λύση του ομογενούς συστήματος $AX={\bf 0}$ .

Σημειώνουμε ότι αν $B\neq\bf 0$ , τότε το σύνολο των λύσεων του συστήματος $AX=B$ δεν είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ , αφού το ${\bf 0}$ δεν ανήκει στο σύνολο των λύσεων.

Παράδειγμα 3.2.7.

Θα υπολογίσουμε το μηδενοχώρο, το χώρο γραμμών και το χώρο στηλών του πίνακα $A$ όπου

Α=\begin{bmatrix}0&1&0&2\cr 0&0&1&0\cr 0&0&0&0\end{bmatrix}\in\mathcal{M}_{3% \times 4}({\mathbb{C}}).

Παρατηρούμε ότι ο πίνακας $Α$ είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών. Οι λύσεις του $AX=0$ είναι:

\{(x,y,z,w):\ y+2w=0,z=0,x,w\in\Bbbk\}=\{(x,-2w,0,w):\ x,w\in{\mathbb{C}}\}=

=\{x(1,0,0,0)+w(0,-2,0,1):\ x,w\in\Bbbk\}\ .

Επομένως

\operatorname{null}(A)=S\left(\{(1,0,0,0),(0,-2,0,1)\}\right)\ .

Έστω, τώρα,

v_{1}=(0,1,0,2),v_{2}=(0,0,1,0)

τα διανύσματα που αντιστοιχούν στις μη μηδενικές γραμμές του $Α$ και

w_{1}=(1,0,0),\ w_{2}=(0,1,0),\ w_{3}=(2,0,0)

τα διανύσματα που αντιστοιχούν στις μη μηδενικές στήλες του $Α$ . Τότε

\Gamma(A)=S\left(\{v_{1},v_{2},{\bf 0}\}\right)=S\left(\{v_{1},v_{2}\}\right)% \subset{\mathbb{C}}^{4}\

και

\Sigma(A)=S\left(\{{\bf 0},w_{1},w_{2},w_{3}\})=S(\{w_{1},w_{2},w_{3}\}\right)% =S\left(\{w_{1},w_{2}\}\right)\subset{\mathbb{C}}^{3}.

Για να εξηγήσουμε την τελευταία ισότητα σημειώνουμε ότι αν $u\in\Sigma(A)$ , τότε υπάρχουν $k,t,s\in\Bbbk$ , έτσι ώστε $u=k\cdot w_{1}+t\cdot w_{2}+s\cdot w_{3}$ . Επομένως, $u=(k+2s)\cdot w_{1}+t\cdot w_{2}$ , αφού $w_{3}=2w_{1}$ . O αναγνώστης καλείται να βρει την εξίσωση της οποίας το σύνολο των λύσεων είναι o $\Sigma(A)$ .

Παρατήρηση 3.2.8.

Πολλές φορές είναι χρήσιμο και βολικό να ταυτίζουμε τα στοιχεία του $\Bbbk^{n}$ με $n\times 1$ πίνακες με στοιχεία από το $\Bbbk$ . Θεωρούμε, λοιπόν, τη συνάρτηση $\phi:\Bbbk^{n}\longrightarrow\mathcal{M}_{n\times 1}(\Bbbk)$ , όπου

(b_{1},\ldots,b_{n})\ \mapsto\begin{bmatrix}b_{1}\cr\vdots\cr b_{n}\end{% bmatrix}.

Είναι φανερό ότι η συνάρτηση αυτή είναι ένα προς ένα (one to one) και επί (onto), δηλ. κάθε διάνυσμα του $\Bbbk^{n}$ αντιστοιχεί σε ακριβώς έναν πίνακα του $\mathcal{M}_{n\times 1}(\Bbbk)$ και αντίστροφα. Θα χρησιμοποιήσουμε αυτήν την αντιστοιχία πολλές φορές στη συνέχεια αυτού του συγγράμματος. Αν $v_{1},\ldots,v_{m}\in\Bbbk$ , γράφουμε

A=\begin{bmatrix}v_{1}&v_{2}&\cdots&v_{m}\end{bmatrix},

εννοώντας τον $n\times m$ πίνακα με στήλες τους πίνακες $\phi(v_{1}),\ldots,\phi(v_{m})$ . Για παράδειγμα, αν $v_{1}=(1,1)$ , $v_{2}=(1,2)$ , $v_{3}=(2,4)$ , τότε με $A=\begin{bmatrix}v_{1}&v_{2}&v_{3}\end{bmatrix}$ εννοούμε τον πίνακα

A=\begin{bmatrix}1&1&2\cr 1&2&4\end{bmatrix}\;.

$\begin{bmatrix}v_{1}&v_{2}&\cdots&v_{m}\end{bmatrix}$ Έστω $Α=(a_{ij})\in\mathcal{M}_{m\times n}(\Bbbk)$ και έστω $X=(x_{i})\in\mathcal{M}_{1\times n}(\Bbbk)$ . To γινόμενο $A X$ είναι το παρακάτω άθροισμα:

AX=\begin{bmatrix}a_{11}&\cdots&a_{1n}\cr\vdots&\ddots&\vdots\cr a_{n1}&\cdots% &a_{nn}\end{bmatrix}\begin{bmatrix}x_{1}\cr\vdots\cr x_{n}\end{bmatrix}=x_{1}% \begin{bmatrix}a_{11}\cr\vdots\cr a_{n1}\end{bmatrix}+\cdots+x_{n}\begin{% bmatrix}a_{1n}\cr\vdots\cr a_{nn}\end{bmatrix}.

Μπορούμε λοιπόν να συνοψίσουμε πότε ένα σύστημα $AX=B$ είναι συμβατό ως εξής:

Πρόταση 3.2.9.

Το σύστημα $AX=B$ είναι συμβατό αν και μόνο αν το διάνυσμα του $Β$ ανήκει στον $\Sigma(A)$ . To σύστημα $A^{T}X=C$ είναι συμβατό αν και μόνο αν το διάνυσμα του $C$ ανήκει στον $\Gamma(A)$ .

H χρησιμότητα της Πρότασης 3.2.9 έγκειται στο ότι μας επιτρέπει να υπολογίζουμε το χώρο γραμμών και στηλών ενός πίνακα.

Παράδειγμα 3.2.10.

Έστω

Α=\begin{bmatrix}0&1&0&2\cr 0&0&1&0\cr 0&0&0&0\end{bmatrix}

o πίνακας του Παραδείγματος 3.2.7. To σύστημα $ΑX=\begin{bmatrix}1&1&1\end{bmatrix}^{T}$ δεν είναι συμβατό, όπως είναι φανερό από τον επαυξημένο πίνακα

\left[\begin{array}[]{cccc|c}0&1&0&2&1\cr 0&0&1&0&1\cr 0&0&0&0&1\end{array}% \right].

Επομένως το διάνυσμα $(1,1,1)$ δεν ανήκει στον χώρο στηλών του πίνακα $Α$ . To διάνυσμα $(0,2,2,4)$ ανήκει στον χώρο γραμμών του πίνακα $Α$ , αφού το σύστημα

A^{T}X=\begin{bmatrix}0&2&2&4\end{bmatrix}^{T}

είναι συμβατό, όπως είναι φανερό από τον επαυξημένο πίνακα

\left[\begin{array}[]{ccc|c}0&0&0&0\cr 1&0&0&2\cr 0&1&0&2\cr 2&0&0&4\end{array% }\right].

Στα Παραδείγματα 3.2.4 είδαμε ότι το παράγον σύνολο $X$ του υποχώρου $U$ του $\Bbbk^{n}$ δεν είναι μοναδικά ορισμένο. Για τον ίδιο υποχώρο $U$ υπάρχουν (άπειρα τον αριθμό) σύνολα $X$ έτσι ώστε $S(X)=U$ . Τα σύνολα που παράγουν τον $U$ μπορεί να διαφέρουν και ως προς το πλήθος τους. Στην επόμενη ενότητα θα μας απασχολήσουν ερωτήματα που αφορούν την εύρεση συνόλων που παράγουν τον $U$ και έχουν το μικρότερο δυνατό πλήθος στοιχείων.

Ασκήσεις Ενότητας 3.2

1.

Να αποδείξετε ότι το σύνολο $L=\{\;(x,y,z)\in{\mathbb{R}}^{3}\;:\;x+y=1\;\}$ δεν είναι υποχώρος του ${\mathbb{R}}^{3}$ .

Λύση
2.

Να αποδείξετε ότι το σύνολο $U=\{(a_{1},\ldots,a_{n})\in\Bbbk^{n}:\ a_{1}-a_{2}=0\}$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ . Για $n=4$ να βρεθεί ένα παράγον σύνολο.

Λύση
3.

Να αποδείξετε ότι το σύνολο $L=\{\;(x,y,z)\in{\mathbb{R}}^{3}\;:\;x+y=0\;\}$ είναι υποχώρος του ${\mathbb{R}}^{3}$ και να βρείτε ένα παράγον σύνολο.

Λύση
4.

Δίνονται τα υποσύνολα

$U=\{\;(k,k,k)\;:\;k\in{\mathbb{R}}\;\}\;\;\;\hbox{και}\;\;\;V=\{\;(0,\lambda,% \mu)\;:\;\lambda,\mu\in{\mathbb{R}}\;\}$
του ${\mathbb{R}}^{3}$ . Να αποδείξετε ότι οι $U,\;V$ είναι υποχώροι του ${\mathbb{R}}^{3}$ . Να βρείτε σύνολα που παράγουν τους $U$ και $V$ . Να υπολογίσετε την τομή $U\cap V$ .

Λύση
5.

Να βρεθεί η εξίσωση του επιπέδου $S(\{(1,2,0),(1,0,1)\})$ .

Λύση
6.

Να αποδείξετε ότι για τα υποσύνολα

$X=\{(1,0),(1,1)\}\;\;\;\hbox{και}\;\;\;Y=\{(0,1),(1,2)\}$
του ${\mathbb{R}}^{2}$ ισχύει ότι $S(X)=S(Y)$ .

Λύση
7.

Να ελέγξετε αν το διάνυσμα $(1,2,3)$ είναι στο χώρο στηλών και γραμμών του πίνακα

$A=\begin{bmatrix}1&0&2\cr 1&1&3\cr 2&1&5\end{bmatrix}\ .$

Λύση

3.3 Βάσεις και Γραμμική Ανεξαρτησία, I

Στη προηγούμενη ενότητα είδαμε ότι οι μη μηδενικοί υποχώροι του $\Bbbk^{n}$ έχουν άπειρα το πλήθος παράγοντα σύνολα. Μας ενδιαφέρουν τα ελαχιστοτικά παράγοντα σύνολα. Τι εννοούμε με αυτό; Έστω ότι $V$ είναι διανυσματικός υποχώρος του $\Bbbk^{n}$ . Ένα παράγον σύνολο $X$ του $V$ είναι ελαχιστοτικό (minimal) αν δεν υπάρχει γνήσιο υποσύνολο (δηλ. διάφορο του $X$ ) του $X$ που να παράγει τον $V$ . Θα δούμε ότι όλα τα ελαχιστοτικά παράγοντα σύνολα του $V$ έχουν τον ίδιο αριθμό στοιχείων, μία ιδιαίτερα σημαντική ιδιότητα για θεωρητικούς αλλά και υπολογιστικούς λόγους.

Ορισμός 3.3.1.

Έστω ότι o $V$ είναι μη μηδενικός διανυσματικός υποχώρος του $\Bbbk^{n}$ και ότι $Β$ είναι ένα υποσύνολο διανυσμάτων του $V$ έτσι ώστε $V=S(B)$ . Αν δεν υπάρχει γνήσιο υποσύνολο $B^{\prime}$ του $B$ έτσι ώστε $V=S(B^{\prime})$ να παράγει τον $V$ , τότε λέμε ότι το σύνολο $Β$ είναι βάση (basis) του $V$ . Ορίζουμε τη βάση του μηδενικού υποχώρου του $\Bbbk^{n}$ να είναι το κενό σύνολο $\emptyset$ .

Τονίζουμε ότι το κενό σύνολο είναι βάση μόνο για το μηδενικό υποχώρο του $\Bbbk^{n}$ . Όταν η σειρά των στοιχείων σε μία βάση είναι καθορισμένη, τότε λέμε ότι η βάση είναι διατεταγμένη (ordered basis). Χρησιμοποιούμε παρενθέσεις αντί για αγκύλες για να δηλώνουμε τα διατεταγμένα σύνολα.

Παραδείγματα 3.3.2.

1.

Έστω $V$ η ευθεία $S(\{v\})$ , όπου $v\neq\bf 0$ . To $\{v\}$ παράγει το n $V$ και $V\neq 0$ . Αφού το μόνο γνήσιο υποσύνολο του $\{v\}$ είναι το κενό σύνολο $\emptyset$ , έπεται ότι το σύνολο $\{v\}$ είναι βάση για το $V$ .
2.

Έστω $V=S(\{(1,2),(2,4)\})$ , όπως στο Παράδειγμα 3.2.4.4. Αφού $V=S(\{(1,2)\})$ , το σύνολο $\{(1,2),(2,4)\}$ δεν είναι βάση του $V$ . To σύνολο $Β=\{(1,2)\}$ είναι βάση του $V$ .
3.

Στο Παράδειγμα 3.2.4.2, είδαμε ότι $\Bbbk^{n}=S(X)$ όπου $X=\{e_{1},\ldots e_{n}\}$ και

$e_{1}=(1,0,0,\ldots,0),\;e_{2}=(0,1,0,\ldots,0),\ldots,\;e_{n}=(0,0,\ldots,0,1)\$
Έστω $X^{\prime}\varsubsetneqq X$ και έστω ότι $e_{i}\notin X^{\prime}$ , για κάποιο $i$ . Τότε είναι φανερό ότι $e_{i}$ δεν είναι γραμμικός συνδυασμός των στοιχείων του $X^{\prime}$ και $e_{i}\notin S(X^{\prime})$ . Επομένως $S(X^{\prime})\neq\Bbbk^{n}$ . Αποδείξαμε λοιπόν ότι $\{e_{1},\ldots,e_{n}\}$ είναι βάση για τον $\Bbbk^{n}$ .

Η κανονική βάση (canonical basis) για τον $\Bbbk^{n}$ είναι η διατεταγμένη βάση
$Β=\big(e_{1},\ldots,e_{n}\big)$ .
4.

Έστω $X=\{v_{1}=(1,2,0),\;v_{2}=(0,1,2),\;v_{3}=(2,5,2)\}$ και $V=S(X)$ . O αναγνώστης καλείται να επιβεβαιώσει ότι

$v_{3}=2v_{1}+v_{2}\textrm{kai'ara}S(\{v_{1},v_{2}\})=V.$
Αφού, το γνήσιο υποσύνολο $\{v_{1},v_{2}\}\subsetneq X$ παράγει τον $V$ , συμπεραίνουμε ότι το $X$ δεν είναι βάση για τον $V$ . O αναγνώστης καλείται να διαπιστώσει ότι: (a) $V\neq S(\{v_{2}\})$ , και (b) $V\neq S(\{v_{2}\})$ , συνεπώς $\{v_{1},v_{2}\}$ είναι βάση για τον $V$ .

Πως όμως μπορούμε στη γενική περίπτωση, ξεκινώντας από ένα παράγον σύνολο $X$ για το διανυσματικό υποχώρο $V$ του $\Bbbk^{n}$ , να βρούμε μία βάση για τον $V$ ; Αναλύουμε τι συνέβη στο τελευταίο παράδειγμα. Έστω ότι το σύνολο $X$ δεν είναι βάση για το χώρο $V=S(X)$ . Υπάρχει, λοιπόν, $Β\subsetneq X$ , έτσι ώστε $S(B)=S(X)$ . Αφού $Β\neq X$ υπάρχει $v\in X\setminus B$ . Τότε όμως $v\in S(B)$ , (αφού $S(B)=S(X)$ και $v\in S(X)$ ). Συμπεραίνουμε ότι το $v$ είναι γραμμικός συνδυασμός των διανυσμάτων του $B$ , δηλ.

v=\kappa_{1}v_{1}+\cdots+\kappa_{m}v_{m},\hbox{giak'apoia}\ v_{i}\in B\textrm{% kai}\kappa_{i}\in\Bbbk\textrm{'opou}1\leq i\leq m\ .

Επομένως

v-\kappa_{1}v_{1}-\kappa_{2}v_{2}-\cdots-\kappa_{m}v_{m}={\bf 0}\ .

Υπάρχει λοιπόν ένας γραμμικός συνδυασμός διανυσμάτων του $X$ που δίνει το μηδενικό διάνυσμα, όπου o συντελεστής του $v$ είναι μη μηδενικός. Αντίστροφα, αν $V=S(X)$ και υπάρχει μία σχέση της μορφής

\kappa_{1}v_{1}+\kappa_{2}v_{2}+\cdots+\kappa_{m}v_{m}={\bf 0}\;,

(3.3.2.1)

μεταξύ των $v_{1},\ldots,v_{n}$ του $X$ , όπου $\kappa_{1}\neq 0$ , τότε λύνοντας ως προς το $v_{1}$ και διαιρώντας με το $\kappa_{1}$ , προκύπτει ότι

v_{1}=-\frac{\kappa_{2}}{\kappa_{1}}v_{2}-\cdots-\frac{\kappa_{m}}{\kappa_{1}}% v_{m}\ .

Επομένως, όταν και όπου εμφανίζεται το $v_{1}$ , μπορούμε να το αντικαταστήσουμε με την προηγούμενη έκφραση. Άρα

V=S(X\setminus\{v_{1}\})\ .

Για να δηλώσουμε αυτήν την ιδιαιτερότητα, δίνουμε τους εξής ορισμούς.

Ορισμός 3.3.3.

Έστω $v_{1},v_{2},\ldots,v_{m}$ στοιχεία του υποχώρου $V$ του $\Bbbk^{n}$ . Αν

\kappa_{1}v_{1}+\kappa_{2}v_{2}+\cdots+\kappa_{m}v_{m}={\bf 0}\;,

(3.3.3.1)

όπου τουλάχιστον ένα από τα $\kappa_{1},\kappa_{2},\ldots,\kappa_{m}\in\Bbbk$ δεν είναι μηδέν, τότε η (3.3.3.1) λέγεται (μη μηδενική) σχέση γραμμικής εξάρτησης (linear dependence equation) ανάμεσα στα $v_{1},v_{2},\ldots,v_{n}$ και τα διανύσματα $v_{1},v_{2},\ldots,v_{n}$ καλούνται γραμμικά εξαρτημένα (linearly dependent).

Όταν τα $v_{1},v_{2},\ldots,v_{n}$ είναι γραμμικά εξαρτημένα, τότε κάθε σύνολο που τα περιέχει λέγεται γραμμικά εξαρτημένο σύνολο (linearly dependent set). Παρατηρούμε ότι το $\bf 0$ είναι γραμμικά εξαρτημένο, αφού

1\,{\bf 0}={\bf 0}

είναι μη μηδενική σχέση γραμμικής εξάρτησης. Δεν είναι δύσκολο να συμπεράνει κανείς ότι το $\bf 0$ είναι το μοναδικό διάνυσμα που είναι (μόνο του) γραμμικά εξαρτημένο.

Παρατήρηση 3.3.4.

Έστω ότι $v_{1},v_{2},\ldots,v_{m}$ είναι διανύσματα του $\Bbbk^{n}$ και έστω ότι

A=\begin{bmatrix}v_{1}&v_{2}&\cdots&v_{m}\end{bmatrix}\;.

Τα $\kappa_{1},\kappa_{2},\ldots,\kappa_{m}$ ικανοποιούν την Έκφραση (3.3.3.1) ακριβώς όταν $(\kappa_{1},\kappa_{2},\ldots,\kappa_{m})$ είναι λύση του $AX=\bf 0$ . Σύμφωνα με την Πρόταση 1.3.4, το σύστημα $AX={\bf 0}$ έχει μη μηδενική λύση ακριβώς όταν $\operatorname{rank}(A)\neq m$ . Αποδείξαμε λοιπόν το εξής συμπέρασμα.

Τα

v_{1},\ldots,v_{m}

είναι γραμμικά εξαρτημένα

\Longleftrightarrow

\operatorname{rank}\left(\begin{bmatrix}v_{1}&\cdots&v_{m}\end{bmatrix}\right)<m

Θυμίζουμε ότι η βαθμίδα ενός πίνακα είναι το πολύ ίση με τον αριθμό των γραμμών του πίνακα, βλ. Ενότητα 1.2. Επομένως, αν μας δίνονται

m

διανύσματα στον

\Bbbk^{n}

και

m>n

, τότε τα διανύσματα είναι με βεβαιότητα γραμμικά εξαρτημένα.

Αν τα $v_{1},v_{2},\ldots,v_{n}$ δεν είναι γραμμικά εξαρτημένα, τότε λέμε ότι είναι γραμμικά ανεξάρτητα (linearly independent) και ότι το σύνολο $\{v_{1},v_{2},\ldots,v_{m}\}$ είναι γραμμικά ανεξάρτητο σύνολο (linearly independent set). Έστω ότι $v_{1},\ldots,v_{n}\in\Bbbk^{n}$ είναι γραμμικά ανεξάρτητα και ότι $A=\begin{bmatrix}v_{1}&\cdots&v_{n}\end{bmatrix}$ . Τότε $\operatorname{rank}(A)=n$ και άρα o $A$ είναι αντιστρέψιμος πίνακας. Από την Πρόταση 3.2.9, συμπεραίνουμε ότι κάθε διάνυσμα του $\Bbbk^{n}$ μπορεί να γραφεί ως γραμμικός συνδυασμός των $v_{1},\ldots,v_{n}$ . Συνοψίζοντας, ισχύει το εξής συμπέρασμα:

Πρόταση 3.3.5.

Έστω τα διανύσματα $v_{1},\ldots,v_{m}$ του $\Bbbk^{n}$ και $A=\begin{bmatrix}v_{1}&\cdots&v_{m}\end{bmatrix}$ . Ισχύουν τα εξής:

i)

Τα $v_{1},\ldots,v_{m}$ είναι γραμμικά ανεξάρτητα αν και μόνο αν $\operatorname{rank}(A)=m$ .
ii)

Αν $n<m$ , τότε τα $v_{1},\ldots,v_{m}$ είναι γραμμικά εξαρτημένα.
iii)

Αν $n=m$ , τότε τα $v_{1},\ldots,v_{m}$ είναι γραμμικά ανεξάρτητα αν και μόνο αν $\det A\neq 0$ .
iv)

Αν $n=m$ και $\det A\neq 0$ , τότε $S(\{v_{1},\ldots,v_{m}\})=\Bbbk^{n}$ .

Θα εφαρμόσουμε αυτά τα κριτήρια στα επόμενα Παραδείγματα.

Παραδείγματα 3.3.6.

1.

Τα στοιχεία $v_{1}=(1,2)$ και $v_{2}=(2,4)$ του $\Bbbk^{2}$ είναι γραμμικά εξαρτημένα, αφού $v_{2}=2v_{1}$ και $2v_{1}-v_{2}=0$ . Η δυάδα $(2,-1)$ είναι λύση του ομογενούς συστήματος $ΑX={\bf 0}$ όπου $A=\begin{bmatrix}v_{1}|&v_{2}\end{bmatrix}$ . Στη συνέχεια γράφουμε τον πίνακα $Α$ και τη μετάβαση του σε ελαττωμένη κλιμακωτή μορφή γραμμών.

$A=\begin{bmatrix}1&2\cr 2&4\end{bmatrix}\ \longrightarrow\begin{bmatrix}1&2\cr 0% &0\end{bmatrix}.$
Είναι φανερό ότι $\operatorname{rank}A=1$ .
2.

Τα διανύσματα $e_{1},\ldots,e_{n}$ είναι γραμμικά ανεξάρτητα, αφού

$\begin{bmatrix}e_{1}|&e_{2}|&\cdots&|e_{n}\end{bmatrix}=I_{n}\$
και $\operatorname{rank}(I_{n})=n$ .
3.

Έστω $v_{1}=(1,2,0),\;v_{2}=(0,1,2),\;v_{3}=(2,5,2)$ . Τα διανύσματα $v_{1},v_{2},v_{3}$ είναι γραμμικά εξαρτημένα, αφού $v_{3}=2v_{1}+v_{2}$ και άρα

$2v_{1}+v_{2}-v_{3}=0\ .$ (3.3.6.1)
Στη συνέχεια γράφουμε τον πίνακα $Α=\begin{bmatrix}v_{1}|&v_{2}&|v_{3}\end{bmatrix}$ και τη μετάβαση του σε ελαττωμένη κλιμακωτή μορφή γραμμών.

$A=\begin{bmatrix}1&0&2\cr 2&1&5\cr 0&2&2\end{bmatrix}\rightarrow\begin{bmatrix% }1&0&2\cr 0&1&1\cr 0&0&0\end{bmatrix}\ .$
Παρατηρούμε ότι οι λύσεις του συστήματος $AX={\bf 0}$ δίνουν το σύνολο

$\{(-2t,-t,t):\ t\in{\mathbb{R}}\}$
και ότι $t=-1$ δίνει τη σχέση γραμμικής εξάρτησης (3.3.6.1).
4.

Τα διανύσματα $v_{1}=(1,2,2)$ , $v_{2}=(1,3,5)$ , $v_{3}=(0,4,9)$ είναι γραμμικά ανεξάρτητα αφού ο πίνακας

$A=\begin{bmatrix}1&1&0\cr 2&3&4\cr 2&5&9\end{bmatrix}$
έχει βαθμίδα τρία.

Έστω, λοιπόν, ότι $V=S(B)$ . Πότε είναι το $B$ βάση του $V$ ; Έχουμε ήδη εξετάσει τι πρέπει να συμβαίνει και η επόμενη πρόταση δίνει την πλήρη απάντηση.

Πρόταση 3.3.7.

Έστω ότι $V=S(Β)$ . To $Β$ είναι βάση του $V$ αν και μόνο αν τα στοιχεία του $V$ είναι γραμμικά ανεξάρτητα.

Έστω ότι $V=S(X)$ . Για να βρούμε μία βάση για τον $V$ , θα εστιάσουμε σε γραμμικά ανεξάρτητα υποσύνολα $Β$ του $X$ έτσι ώστε $Β\cup\{v\}$ να είναι γραμμικά εξαρτημένο, για κάθε $v\in X\setminus B$ .

Παράδειγμα 3.3.8.

Στο Παράδειγμα 3.3.8.4, είδαμε ότι τα διανύσματα $v_{1}=(1,2,2)$ , $v_{2}=(1,3,5)$ , $v_{3}=(0,4,9)$ είναι γραμμικά ανεξάρτητα. Επομένως αν $D=\{v_{1},v_{2},v_{3}\}$ , τότε το $D$ είναι βάση για τον διανυσματικό χώρο $V=S(D)$ . O πίνακας $Α=\begin{bmatrix}v_{1}|&v_{2}&|v_{3}\end{bmatrix}$ είναι αντιστρέψιμος. Επομένως το σύστημα $AX=Β$ είναι συμβατό για κάθε $B$ . Σύμφωνα με την Πρόταση 3.2.9, κάθε διάνυσμα του $\Bbbk^{3}$ ανήκει στο χώρο στηλών του $Α$ . Αυτό σημαίνει ότι κάθε διάνυσμα του $\Bbbk^{3}$ ανήκει στον $V$ . Αποδείξαμε λοιπόν ότι

V=\Bbbk^{3}\hbox{καιότιto$D$είναιβάσηγιατοn}\Bbbk^{3}\ .

Είναι δυνατόν ο διανυσματικός υποχώρος $V$ του $\Bbbk^{n}$ να έχει δύο βάσεις με διαφορετικό αριθμό στοιχείων; Ας εξερευνήσουμε λίγο αυτήν την περίπτωση. Έστω ότι $B_{1}=\{v\}$ και ότι $B_{2}=\{w_{1},w_{2}\}$ είναι δύο βάσεις του $V$ . Αφού $w_{1}\in V$ και $Β_{1}$ είναι βάση του $V$ , έπεται ότι $w_{1}=t_{1}v$ . Ομοίως $w_{2}=t_{2}v$ . Επίσης αφού $w_{2}\neq{\bf 0}$ (γιατί;) έχουμε ότι $t_{2}\neq 0$ . Τότε όμως

w_{1}-\frac{t_{1}}{t_{2}}w_{2}=t_{1}v-\frac{t_{1}}{t_{2}}t_{2}v={\bf 0}\

είναι μία μη μηδενική σχέση γραμμικής εξάρτησης μεταξύ των στοιχείων της βάσης $B_{2}$ και αυτό είναι άτοπο. Αυτή είναι και η βασική ιδέα της απόδειξης του επόμενου πολύ σημαντικού θεωρήματος. Για την πλήρη απόδειξη, ο αναγνώστης παραπέμπεται στη βιβλιογραφία, βλ. για παράδειγμα το σύγγραμμα [2, Ενότητα 2.4].

Θεώρημα 3.3.9.

Κάθε διανυσματικός υποχώρος του $\Bbbk^{n}$ έχει μία βάση. Όλες οι βάσεις ενός διανυσματικού υποχώρου έχουν το ίδιο πλήθος στοιχείων.

O αριθμός των στοιχείων της βάσης είναι εξαιρετικά σημαντική έννοια.

Ορισμός 3.3.10.

Έστω $V$ ένας διανυσματικός υποχώρος του $\Bbbk^{n}$ . Το πλήθος των στοιχείων μίας βάσης του $V$ λέγεται διάσταση (dimension) του $V$ και συμβολίζεται ${\rm dim}_{\Bbbk}(V)$ ${\rm dim}_{\Bbbk}(V)$ .

Η διάσταση του μηδενικού υποχώρου του $\Bbbk^{n}$ είναι το μηδέν, γιατί δεχθήκαμε ότι το κενό σύνολο είναι βάση αυτού του υποχώρου. Κάθε άλλος υποχώρος έχει διάσταση ένα θετικό ακέραιο, δηλ. αν $V\neq 0$ τότε ${\rm dim}_{\Bbbk}(V)>0$ .

Παραδείγματα 3.3.11.

1.

${\rm dim}_{\Bbbk}(\Bbbk^{n})=n$
2.

Έστω $V$ υποχώρος του $\Bbbk^{2}$ . Αν ${\rm dim}_{\Bbbk}(V)=2$ , τότε $V=\Bbbk^{2}$ . Αν ${\rm dim}_{\Bbbk}(V)=1$ , τότε o $V=S(\{v\})$ , όπου $v\neq\bf 0$ . Αν ${\rm dim}_{\Bbbk}(V)=0$ , τότε $V=\{{\bf 0}\}$ . Αυτοί είναι και οι μοναδικοί τύποι υποχώρων που έχει ο $\Bbbk^{2}$ .
3.

Οι γνήσιοι υποχώροι του $\Bbbk^{3}$ έχουν διάσταση μικρότερη του 3. Έστω $V$ υποχώρος του $\Bbbk^{3}$ . Αν ${\rm dim}_{\Bbbk}(V)=0$ , τότε o $V$ είναι ο μηδενικός υποχώρος. Αν ${\rm dim}_{\Bbbk}(V)=1$ , τότε $V=S(\{v\})$ όπου $v\neq\bf 0$ . Αν ${\rm dim}_{\Bbbk}(V)=2$ , τότε $V=S(\{v_{1},v_{2}\})$ όπου $v_{1}$ , $v_{2}$ δεν είναι παράλληλα διανύσματα. Αν ${\rm dim}_{\Bbbk}(V)=3$ , τότε $V=\Bbbk^{3}$ .

Υπάρχουν δύο βασικοί τρόποι για την εύρεση βάσης ενός διανυσματικού υποχώρου $V=S(X)$ του $\Bbbk^{n}$ . Τους συνοψίζουμε στους αλγορίθμους (3.3.1) και (3.3.2).

Αλγόριθμος 3.3.1 Αλγόριθμος εύρεσης βάσης για τον υποχώρο

{\bf S(X)}\subset\Bbbk^{n}

ως υποσύνολο του

X

Είσοδος:

X=\{v_{1},\ldots,v_{m}\}\subset\Bbbk^{n}

Έξοδος: Μία βάση

B

για τον

S(X)

με

B\subset X

Βήμα 1 Θεωρούμε τον

n\times m

πίνακα

Α=\begin{bmatrix}v_{1}\ |&v_{2}\ |&\cdots\ |&v_{m}\end{bmatrix}

Βήμα 2 Φέρνουμε τον

A

σε κλιμακωτή μορφή γραμμών.

Βήμα 3 Έστω ότι οι καθοδηγητικές μονάδες βρίσκονται στις στήλες

j_{1},\ldots,j_{t}

. Τα διανύσματα

v_{j_{1}},\ldots,v_{j_{t}}

αποτελούν βάση του

S(X)

Είναι φανερό ότι ο αλγόριθμος (3.3.1) δίνει προτεραιότητα επιλογής στα πρώτα κατά σειρά διανύσματα. Έτσι αν θέλουμε να επιλέξουμε μία βάση που να περιέχει κάποια συγκεκριμένα γραμμικά ανεξάρτητα διανύσματα, τα γράφουμε ως τις πρώτες στήλες του $A$ .

Παράδειγμα 3.3.12.

Έστω τα διανύσματα $v_{1}=(1,2,0,1)$ , $v_{2}=(0,1,3,-1)$ , $v_{3}=(1,1,-3,2)$ και $X=\{v_{1},v_{2},v_{3}\}$ , $V=S(X)$ . Θα βρούμε μία βάση για τον $V$ . Θεωρούμε τον πίνακα

Α = [\begin{array}{crr} 1 & 0 & 1 \\ 2 & 1 & 1 \\ 0 & 3 & - 3 \\ 1 & - 1 & 2 \end{array}] .

H κλιμακωτή μορφή γραμμών του πίνακα $A$ είναι ο πίνακας

R = [\begin{array}{ccr} 1 ◯ & 0 & 1 \\ 0 & 1 ◯ & - 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}] .

Παρατηρούμε ότι οι καθοδηγητικές μονάδες στον πίνακα $R$ βρίσκονται στην πρώτη και δεύτερη στήλη του $R$ . Έτσι ${v_{1}, v_{2}}$ είναι μία βάση για τον $V$ και $\dim_{R} (V) = 2$ .

Αφού ${v_{1}, v_{2}}$ είναι βάση για τον $V$ , το $v_{3}$ γράφεται ως γραμμικός συνδυασμός των $v_{1}$ και $v_{2}$ . Επιθυμούμε, λοιπόν, να βρούμε $k_{1}, k_{2} \in R$ έτσι ώστε $v_{3} = k_{1} v_{1} + k_{2} v_{2}$ . Για να βρούμε τους συντελεστές $k_{1}$ , $k_{2}$ αρκεί να λύσουμε το σύστημα

[\begin{matrix} 1 & 0 \\ 2 & 1 \\ 0 & 3 \\ 1 & - 1 \end{matrix}] X = [\begin{matrix} 1 \\ 1 \\ - 3 \\ 2 \end{matrix}] .

(3.3.12.1)

Παρατηρούμε ότι o $A$ είναι o επαυξημένος πίνακας του συστήματος (3.3.12.1). Οι λύσεις προκύπτουν από τον $R$ . To $(1,-1)$ είναι λύση και άρα

v_{3}=v_{1}-v_{2}\ .

Άρα

v_{1}-v_{2}-v_{3}=0\

είναι μη μηδενική σχέση γραμμικής εξάρτησης των $v_{1},v_{2},v_{3}$ . Παροτρύνουμε τον αναγνώστη να παρατηρήσει ότι η τρίτη στήλη του $R$ είναι η διαφορά της δεύτερης στήλης του $R$ από την πρώτη και ότι οι αντίστοιχες σχέσεις ισχύουν για τις στήλες του $Α$ .

Είναι φανερό ότι η βάση που θα πάρουμε, όταν το $X$ είναι γραμμικά εξαρτημένο σύνολο, εξαρτάται από τη διάταξη των στοιχείων του $X$ και των αντίστοιχων στηλών του $Α$ . Η μέθοδος του αλγορίθμου αυτού στηρίζεται στην παρατήρηση ότι η βάση του $V=S(X)$ είναι ένα μέγιστο γραμμικά ανεξάρτητο υποσύνολο του $X$ . Ένα σημαντικό πλεονέκτημα αυτής της μεθόδου είναι ότι η βάση που προκύπτει είναι υποσύνολο του $X$ . Είναι επίσης πολύ εύκολο να βρούμε τις σχέσεις γραμμικής εξάρτησης μεταξύ των διανυσμάτων του $X$ από την ελαττωμένη κλιμακωτή μορφή γραμμών του $Α$ .

Παρατήρηση 3.3.13.

Έστω ότι $S(X)=V$ και έστω ότι αλλάζουμε κάποιο από τα διανύσματα του $X$ με έναν από τους εξής τρόπους:

•

αλλάζοντας τη σειρά των διανυσμάτων του $X$ ,
•

προσθέτοντας σε ένα διάνυσμα του $X$ πολλαπλάσιο ενός άλλου διανύσματος του $X$ ,
•

πολλαπλασιάζοντας ένα διάνυσμα του $X$ με κάποιο $0\neq\kappa\in\Bbbk$ .

Αν $X_{1}$ είναι το νέο σύνολο που προκύπτει από αυτήν την αλλαγή, τότε είναι εύκολο να παρατηρήσει κάποιος ότι $S(X_{1})=S(X)=V$ .

Σε αυτήν την παρατήρηση στηρίζεται η επόμενη μέθοδος εύρεσης βάσης του $V=S(X)$ .

Αλγόριθμος 3.3.2 Αλγόριθμος εύρεσης βάσης για τον υποχώρο

{\bf S(X)}\subset\Bbbk^{n}

σε κλιμακωτή μορφή.

Είσοδος:

X=\{v_{1},\ldots,v_{m}\}\subset\Bbbk^{n}

Έξοδος: Βάση για το διανυσματικό υποχώρο

S(X)

του

\Bbbk^{n}

Βήμα 1 Θεωρούμε τον πίνακα

Α=\begin{bmatrix}v_{1}\ |&v_{2}\ |&\cdots\ |&v_{m}\end{bmatrix}

Βήμα 2 Φέρνουμε τον

Α^{Τ}

σε ελαττωμένη κλιμακωτή μορφή γραμμών

R

Βήμα 3 Έστω ότι

t=\operatorname{rank}(A^{T})

και ότι

\Gamma_{1},\Gamma_{2},\ldots,\Gamma_{t}

είναι οι μη μηδενικές γραμμές του

R

. Τα αντίστοιχα διανύσματα αποτελούν βάση για τον

S(X)

Εξαιτίας της θέσης των καθοδηγητικών μονάδων, μπορούμε εύκολα να δούμε ότι τα διανύσματα με τις καθοδηγητικές μονάδες δεν μπορούν να προκύψουν από γραμμικούς συνδυασμούς των υπολοίπων. H βάση που προκύπτει από τον προηγούμενο αλγόριθμο δεν είναι πάντα υποσύνολο του $X$ . Το πλεονέκτημα, όμως, αυτής της μεθόδου είναι ότι τα στοιχεία της βάσης είναι σχετικά απλά, αφού οι συντεταγμένες τους έχουν πολλά μηδενικά.

Παράδειγμα 3.3.14.

Έστω $V=S(X)$ ο διανυσματικός χώρος του Παραδείγματος 3.3.12. Τότε

Α^{Τ}=\left[\begin{array}[]{rrrr}1&2&0&1\\ 0&1&3&-1\\ 1&1&-3&2\end{array}\right]\begin{array}[]{c}\\ \\ .\end{array}

Η ελαττωμένη κλιμακωτή μορφή γραμμών του $Α^{Τ}$ είναι o πίνακας

\left[\begin{array}[]{rrrr}1&0&-6&3\\ 0&1&3&-1\\ 0&0&0&0\end{array}\right].

Επομένως το σύνολο $\{(1,0,-6,3),(0,1,3,-1)\}$ είναι βάση του $V$ .

Ασκήσεις Ενότητας 3.3

1.

Να εξετάσετε αν τα στοιχεία

$u_{1}=(1,0,2,1),\;\;u_{2}=(0,0,2,4),\;\;u_{3}=(0,1,0,2),\;\;u_{4}=(2,0,4,2)$
του ${\mathbb{R}}^{4}$ είναι γραμμικά ανεξάρτητα. Να δώσετε τις σχέσεις εξάρτησης που υπάρχουν μεταξύ των διανυσμάτων.

Λύση
2.

Δίνονται τα στοιχεία

$v_{1}=(1,2,0,1),\;\;\;v_{2}=(0,1,3,-1),\;\;\;v_{3}=(1,1,-3,2)$
του ${\mathbb{R}}^{4}$ . Να βρείτε μία σχέση γραμμικής εξάρτησης για τα στοιχεία αυτά και μία βάση για το διανυσματικό υποχώρο $S(\{v_{1},v_{2},v_{3}\})$ του ${\mathbb{R}}^{3}$ .

Λύση
3.
Να βρείτε μία βάση, για κάθε έναν από τους εξής διανυσματικούς χώρους.
1. (a)
  
  $\;\;U_{1}=\{\;(x,y)\in{\mathbb{R}}^{2}\;/\;2x+y=0\;\}$ .
2. (b)
  
  $\;\;U_{2}=\{\;(x,y,z)\in{\mathbb{R}}^{3}\;/\;x+y+3z=0\;\}$ .
3. (c)
  
  $\;\;U_{3}=S\{(1,0,2,1),(3,1,0,0),(2,0,1,4)\}$ .
Λύση

3.4 Βάσεις και Γραμμική Ανεξαρτησία, II

Στην ενότητα αυτή θα χρησιμοποιήσουμε τα συμπεράσματα της θεωρίας μας, για να αποδείξουμε μία πολύ σημαντική σχέση που συνδέει τη βαθμίδα ενός πίνακα $A$ με τη βαθμίδα του αναστρόφου $A^{T}$ και με τη διάσταση του $\operatorname{null}(A)$ . Θα δούμε, επίσης, πως συνδέεται η διάσταση του αθροίσματος με τη διάσταση της τομής δύο διανυσματικών υποχώρων του ${\mathbb{R}}^{n}$ . Τέλος, θα ορίσουμε τον πίνακα των συντεταγμένων ενός διανύσματος ως προς μία διατεταγμένη βάση. Έστω $Α$ είναι τυχαίος $m\times n$ πίνακας και $\Gamma(A)\subset{\mathbb{R}}^{n}$ , ο χώρος γραμμών του $A$ . Σύμφωνα με τον αλγόριθμο (3.3.1), για να βρούμε τη βάση του $\Gamma(A)$ , γράφουμε τα διανύσματα που παράγουν τον $\Gamma(A)$ ως στήλες, δηλ. θεωρούμε τον $A^{T}$ . Σύμφωνα με αυτόν τον αλγόριθμο, επιλέγουμε $\operatorname{rank}(A^{T})$ το πλήθος γραμμές από τις αρχικές γραμμές του $A$ , για τη βάση του $\Gamma(A)$ , δηλ.

{\rm dim}_{{\mathbb{R}}}\left(\Gamma(A)\right)=\operatorname{rank}(A^{T})\;.

Σύμφωνα, όμως, με τον αλγόριθμο (3.3.2), για τη βάση του $\Gamma(A)$ , κρατάμε τον $A$ ως έχει και τον φέρνουμε σε ελαττωμένη κλιμακωτή μορφή γραμμών $R$ . Στη συνέχεια επιλέγουμε τις μη μηδενικές γραμμές του $R$ για τη βάση του $\Gamma(A)$ . Επομένως η βάση του $\Gamma(A)$ που επιλέγουμε με αυτόν τον τρόπο έχει $\operatorname{rank}(R)=\operatorname{rank}(A)$ στοιχεία. Σύμφωνα με το Θεώρημα 3.5.7, όλες οι βάσεις του $\Gamma(A)$ έχουν το ίδιο πλήθος στοιχείων. Άρα

{\rm dim}_{{\mathbb{R}}}\left(\Gamma(A)\right)=\operatorname{rank}(A^{T})=% \operatorname{rank}(A)\;.

H ίδια ανάλυση μπορεί να γίνει και για το χώρο στηλών του $A$ , $\Sigma(A)$ . Συνεπώς

{\rm dim}_{{\mathbb{R}}}\left(\Sigma(A)\right)=\operatorname{rank}(A^{T})=% \operatorname{rank}(A)\;.

Αποδείξαμε λοιπόν την εξής πρόταση.

Πρόταση 3.4.1.

Έστω $A\in\mathcal{M}_{m\times n}({\mathbb{R}})$ . Τότε

\operatorname{rank}(A)=\operatorname{rank}(A^{T})

και οι διαστάσεις του χώρου γραμμών του $A$ και του χώρου στηλών του $A$ είναι ίσες με $\operatorname{rank}(A)$ .

Όπως θα δούμε στο επόμενο παράδειγμα, η διαφορά $n-\operatorname{rank}(A)$ είναι η διάσταση του $\operatorname{null}(A)$ .

Παραδείγματα 3.4.2.

Έστω ο πίνακας

Α = [\begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 0 & 1 & 3 & - 1 \\ 1 & 1 & - 3 & 2 \end{array}] \begin{matrix}  \end{matrix} .

Η ελαττωμένη κλιμακωτή μορφή γραμμών του $Α$ είναι ο πίνακας $R$ , όπου $R = [\begin{array}{ccrr} 1 ◯ & 0 & - 6 & 3 \\ 0 & 1 ◯ & 3 & - 1 \\ 0 & 0 & 0 & 0 \end{array}]$ .

Αφού οι καθοδηγητικές μονάδες είναι στην πρώτη και δεύτερη στήλη, το σύνολο ${(1, 0, 1), (2, 1, 1)}$ είναι βάση για το χώρο στηλών του $Α$ και κατά συνέπεια είναι βάση για το χώρο γραμμών του $Α^{T}$ . Αντίστοιχα, το σύνολο ${(1, 0, - 6, 3), (0, 1, 3, - 1)}$ είναι βάση για το χώρο γραμμών του $Α$ και για τον χώρο στηλών του $Α^{T}$ . Έστω τώρα

v_{1} = (1, 0, 1), v_{2} = (2, 1, 1), v_{3} = (0, 3, - 3), v_{4} = (1, - 1, 2)

τα διανύσματα που αντιστοιχούν στις στήλες του $A$ . Η τρίτη και τέταρτη στήλη του $R$ , δηλ. οι στήλες του $R$ χωρίς καθοδηγητική μονάδα, μπορούν να γραφούν ως συνδυασμός των άλλων δύο. Πράγματι, έστω $\Sigma_{i}$ οι στήλες του $R$ , για $i=1,\ldots,4$ . Βλέπουμε ότι

\Sigma_{3}=-6\,\Sigma_{1}+3\,\Sigma_{2}\hbox{και}\Sigma_{4}=3\,\Sigma_{1}-% \Sigma_{2}\;.

Επομένως

6\,\Sigma_{1}-3\,\Sigma_{2}-\Sigma_{3}=0\hbox{και}\Sigma_{1}-\Sigma_{2}-\Sigma% _{4}=0\ .

Παρατηρούμε ότι έχουμε αντίστοιχες σχέσεις γραμμικής εξάρτησης για τις στήλες του $Α$ και ότι

6\,v_{1}-3\,v_{2}-v_{3}=0\hbox{και}v_{1}-v_{2}-v_{4}=0\;.

Αυτό βέβαια είναι αναμενόμενο, γιατί όπως είδαμε, στην Παρατήρηση 3.3.4, οι σχέσεις γραμμικής εξάρτησης μεταξύ των $v_{1},\ldots,v_{4}$ αντιστοιχούν σε λύσεις του ομογενούς συστήματος $AX=\bf 0$ που είναι ίδιες με τις λύσεις του $RX=\bf 0$ (Πρόταση 1.3.4). Οι ελεύθερες μεταβλητές βρίσκονται στις στήλες τρία και τέσσερα. Άρα

\displaystyle\operatorname{null}(A)=\{(6z-3w,-3z+w,z,w):\ z,w\in{\mathbb{R}}\}% =\{z(6,-3,1,0)+\\ \displaystyle w(-3,1,0,1):\ z,w\in{\mathbb{R}}\}=S\left(\{(6,-3,1,0),(-3,1,0,1% )\}\right)\ .

Έστω $u_{1}=(6,-3,1,0)$ , $u_{2}=(-3,1,0,1)$ . Θα δείξουμε ότι το σύνολο $\{u_{1},u_{2}\}$ είναι βάση για τον $\operatorname{null}(A)$ . Πράγματι, είναι φανερό ότι τα διανύσματα αυτά δεν είναι το ένα πολλαπλάσιο του άλλου και άρα $u_{1}$ , $u_{2}$ είναι γραμμικά ανεξάρτητα. Παρατηρούμε ότι για το συμπέρασμα αυτό ήταν αρκετό να σημειώσουμε τις τιμές των $u_{1}$ , $u_{2}$ στην τρίτη και τέταρτη συντεταγμένη. Οι τιμές αυτές, $0$ στο ένα διάνυσμα και $1$ στο άλλο και το ανάπαλιν, είναι η κύρια αιτία που το ένα διάνυσμα δεν είναι πολλαπλάσιο του άλλου. Τα προηγούμενα γενικεύονται εύκολα στο εξής συμπέρασμα.

Θεώρημα 3.4.3.

Έστω $A\in\mathcal{M}_{m\times n}({\mathbb{R}})$ . Τότε

{\operatorname{rank}}(A)+{\rm dim}_{{\mathbb{R}}}\ (\operatorname{null}(A))=n.

Στο επόμενο παράδειγμα θα υπολογίσουμε την τομή δύο διανυσματικών υποχώρων του ${\mathbb{R}}^{n}$ .

Παράδειγμα 3.4.4.

Σε αυτό το παράδειγμα θα εξετάσουμε τον υπολογισμό της τομής δύο διανυσματικών χώρων. Έστω $V=S(\{v_{1},v_{2}\})$ και $W=S(\{w_{1},w_{2}\})$ όπου $v_{1}=(1,1,0,-1)$ , $v_{2}=(1,2,3,0)$ , $w_{1}=(1,2,2,-2)$ , $w_{2}=(0,-1,-2,1)$ . Θεωρούμε τον πίνακα $Α=\begin{bmatrix}v_{1}&v_{2}&w_{1}&w_{2}\end{bmatrix}$ , δηλ.

Α=\begin{bmatrix}1&1&1&0\cr 1&2&2&-1\cr 0&3&2&-2\cr-1&0&-2&1\end{bmatrix}\;.

Παρατηρούμε ότι $\Sigma(A)=V+W$ . H ελαττωμένη κλιμακωτή μορφή γραμμών του $Α$ είναι ο πίνακας $R$ :

R=\begin{bmatrix}1&0&0&1\cr 0&1&0&0\cr 0&0&1&-1\cr 0&0&0&0\end{bmatrix}\ .

Αφού $\operatorname{rank}(A)=3$ , έπεται ότι ${\rm dim}_{{\mathbb{R}}}(V+W)=3$ . Από τη θέση των καθοδηγητικών μονάδων στον $R$ βλέπουμε ότι μία βάση για τον $V+W$ είναι το σύνολο $\{v_{1},v_{2},w_{1}\}$ . Από τον πίνακα $R$ μπορούμε επίσης να συμπεράνουμε ότι

w_{2}=v_{1}-w_{1}\Rightarrow v_{1}-w_{1}-w_{2}={\bf 0}\Rightarrow v_{1}=w_{1}+% w_{2}\ .

Επομένως $v_{1}\in W$ και άρα $v_{1}\in V\cap W$ . Αντίστροφα, κάθε διάνυσμα στην τομή $V\cap W$ δίνει μία σχέση γραμμικής εξάρτησης μεταξύ των στηλών του $A$ . Σύμφωνα με την Παρατήρηση 3.3.4, οι σχέσεις γραμμικής εξάρτησης προκύπτουν από τον $\operatorname{null}(A)$ . Από τη μορφή του $R$ όμως, είναι φανερό ότι όλες οι σχέσεις γραμμικής εξάρτησης είναι πολλαπλάσια της σχέσης που ήδη γράψαμε. Επομένως

V\cap W=S(\{v_{1}\}).

Γενικεύοντας όσα είδαμε στο προηγούμενο παράδειγμα, διατυπώνουμε την εξής πρόταση:

Θεώρημα 3.4.5.

Έστω ότι $U$ και $W$ είναι υποχώροι του $\Bbbk^{n}$ . Τότε

{{\rm dim}_{\Bbbk}(U+W)={\rm dim}_{\Bbbk}(U)+{\rm dim}_{\Bbbk}(W)-{\rm dim}_{% \Bbbk}(U\cap W)\ .}

Απόδειξη.

Θα σκιαγραφήσουμε την απόδειξη. Θεωρούμε τον πίνακα $A$ , όπου οι πρώτες ${\rm dim}_{\Bbbk}(U)$ στήλες του αντιστοιχούν στα διανύσματα μίας βάσης του $U$ και οι επόμενες ${\rm dim}_{\Bbbk}(W)$ στήλες του αντιστοιχούν στα διανύσματα μίας βάσης του $W$ . Έτσι, συνολικά o $A$ έχει $n$ γραμμές και $({\rm dim}_{\Bbbk}(U)+{\rm dim}_{\Bbbk}W)$ στήλες. Φέρνουμε τον $Α$ σε ελαττωμένη κλιμακωτή μορφή γραμμών $R$ . Ο αριθμός των καθοδηγητικών μονάδων του $A$ είναι ίσος με ${\rm dim}_{\Bbbk}(U+W)$ . Για κάθε στήλη του $R$ χωρίς καθοδηγητική μονάδα υπάρχει μία εξίσωση που περιγράφει αυτήν τη στήλη ως γραμμικό συνδυασμό των προηγούμενων στηλών. H εξίσωση αυτή δίνει μία σχέση γραμμικής εξάρτησης μεταξύ των διανυσμάτων της βάσης του $U$ και της βάσης του $W$ . Διαχωρίζοντας τα διανύσματα της βάσης του $U$ από τη βάση του $W$ , προκύπτει ένας συνδυασμός διανυσμάτων της βάσης του $U$ που είναι επίσης συνδυασμός διανυσμάτων της βάσης του $W$ , δηλ. ένα διάνυσμα στην τομή $U\cap W$ . Αντίστροφα, κάθε διάνυσμα στην τομή $U\cap W$ δίνει μία σχέση γραμμικής εξάρτησης μεταξύ των στηλών του $A$ . Σύμφωνα με την Παρατήρηση 3.3.4, οι σχέσεις γραμμικής εξάρτησης προκύπτουν από τον $\operatorname{null}(A)$ . Έτσι, προκύπτει ότι

{\rm dim}_{\Bbbk}(U\cap W)={\rm dim}_{\Bbbk}\left(\operatorname{null}(A)\right% )\;.

Εφαρμόζοντας το Θεώρημα 3.4.3, προκύπτει η ζητούμενη σχέση.∎

H απόδειξη του Θεωρήματος 3.4.5 μας επιτρέπει να διατυπώσουμε τον επόμενο αλγόριθμο εύρεσης βάσης για τους υποχώρους $U+W$ και $U\cap W$ . Σημειώνουμε ότι ${\rm dim}_{\Bbbk}(U+W)\geq{\rm dim}_{\Bbbk}(U)$ και ότι ${\rm dim}_{\Bbbk}(U+W)={\rm dim}_{\Bbbk}(U)$ αν και μόνο αν $W\subset U$ .

Αλγόριθμος 3.4.1 Αλγόριθμος εύρεσης βάσεων για τους υποχώρους

U+W

και

U\cap W

του

\Bbbk^{n}

Είσοδος: Βάσεις

\{v_{1},\ldots,v_{m}\}

\{w_{1},\ldots,w_{r}\}

για τους

U

και

W

αντίστοιχα.

Έξοδος: Βάσεις για τους

U+W

U\cap W

Βήμα 1 Θεωρούμε τον

n\times(m+r)

πίνακα

Α=\begin{bmatrix}v_{1}&\cdots&v_{m}&w_{1}&\cdots&w_{r}\end{bmatrix}

Βήμα 2 Φέρνουμε τον

Α

σε ελαττωμένη κλιμακωτή μορφή γραμμών

R

Βήμα 3 Έστω ότι οι καθοδηγητικές μονάδες βρίσκονται στις στήλες

i_{1},\ldots,i_{t}

, όπου

t=\operatorname{rank}(A)

. Για τη βάση του

U+W

, επιλέγουμε τα αντίστοιχα διανύσματα από το σύνολο

\{v_{1},\ldots,v_{m},w_{1},\ldots,w_{r}\}

Βήμα 4 Αν μία στήλη του

R

δεν έχει καθοδηγητική μονάδα, τότε γράφουμε τη στήλη ως γραμμικό συνδυασμό των στηλών με καθοδηγητική μονάδα. Αποκόπτουμε το συνδυασμό που αφορά τις πρώτες

m

στήλες και γράφουμε τον αντίστοιχο συνδυασμό των

\{v_{1},\ldots,v_{m}\}

. Επαναλαμβάνουμε για όλες τις στήλες χωρίς καθοδηγητική μονάδα. Τα διανύσματα που προκύπτουν από αυτήν τη διαδικασία είναι βάση για τον

U\cap W

Παράδειγμα 3.4.6.

Έστω $U$ o χώρος που παράγεται από τα διανύσματα $v_{1}=(1,0,0)$ , $v_{2}=(0,1,0)$ και $W$ o χώρος που παράγεται από τα διανύσματα $w_{1}=(1,1,0)$ , $w_{2}=(0,0,1)$ . Τότε ο πίνακας

Α=\begin{bmatrix}1&0&1&0\cr 0&1&1&0\cr 0&0&0&1\end{bmatrix}

είναι ήδη σε ελαττωμένη κλιμακωτή μορφή γραμμών. Αφού $\operatorname{rank}Α=3$ , έπεται ότι ${\rm dim}_{{\mathbb{R}}}(U+W)=3$ και επομένως $U+W={\mathbb{R}}^{3}$ . Παρατηρούμε ότι οι καθοδηγητικές μονάδες του $A$ είναι στην πρώτη, δεύτερη και τέταρτη στήλη και ότι τα αντίστοιχα διανύσματα $v_{1},v_{2},w_{2}$ είναι η συνήθης κανονική βάση του ${\mathbb{R}}^{3}$ . Αφού ${\rm dim}_{{\mathbb{R}}}(U+W)=3$ , έπεται ότι

{\rm dim}_{{\mathbb{R}}}(U\cap W)=4-3=1\;.

H τρίτη στήλη του $A$ δεν έχει καθοδηγητική μονάδα. Επομένως

\Sigma_{3}=\Sigma_{1}+\Sigma_{2}

και $w_{3}=v_{1}+v_{2}$ . Άρα $U\cap W=S(\{v_{1}+v_{2}\})$ .

Σε κάποιες περιπτώσεις μας ενδιαφέρει να επεκτείνουμε τη βάση ενός υποχώρου σε βάση ολόκληρου του $\Bbbk^{n}$ . Σημειώνουμε τον εξής αλγόριθμο για αυτές τις περιπτώσεις.

Αλγόριθμος 3.4.2 Αλγόριθμος επέκτασης βάσης του

U

σε βάση του

\Bbbk^{n}

Είσοδος: Βάση

\{v_{1},\ldots,v_{m}\}

για τον

U

Έξοδος: Μία βάση

D

για τον

\Bbbk^{n}

τέτοια ώστε

\{v_{1},\ldots,v_{m}\}\subset D

Βήμα 1 Θεωρούμε τον

n\times(m+n)

πίνακα

Α=\begin{bmatrix}v_{1}\ |&\cdots\ |&v_{m}\ |&e_{1}\ |&\cdots\ |&e_{n}\end{bmatrix}

, όπου

e_{1},\ldots,e_{n}

τα στοιχεία της κανονικής βάσης του

\Bbbk^{n}

Βήμα 2 Φέρνουμε τον

Α

σε ελαττωμένη κλιμακωτή μορφή γραμμών

R

Βήμα 3 Έστω ότι οι καθοδηγητικές μονάδες βρίσκονται στις στήλες

i_{1},\ldots,i_{n}

. Επιλέγουμε τα αντίστοιχα διανύσματα από το σύνολο

\{v_{1},\ldots,v_{m},e_{1},\ldots,e_{r}\}

Παράδειγμα 3.4.7.

Έστω $v=(1,1,0)$ και $W=S(\{v\})$ . To $\{v\}$ είναι βάση για το $W$ . Θα επεκτείνουμε τη βάση του $W$ σε μία βάση του ${\mathbb{R}}^{3}$ . Αφού $\{e_{1},e_{2},e_{3}\}$ παράγει τον ${\mathbb{R}}^{3}$ , κάθε υπερσύνολο του $\{e_{1},e_{2},e_{3}\}$ παράγει τον ${\mathbb{R}}^{3}$ . Επομένως το σύνολο $X=\{v,e_{1},e_{2},e_{3}\}$ παράγει τον ${\mathbb{R}}^{3}$ . Θα χρησιμοποιήσουμε τον Αλγόριθμο (3.4.2). Αφού

A=\begin{bmatrix}1&1&0&0\cr 1&0&1&0\cr 0&0&0&1\end{bmatrix}\rightarrow\cdots% \rightarrow\begin{bmatrix}1&0&1&0\cr 0&1&-1&0\cr 0&0&0&1\end{bmatrix}\;,

έπεται ότι το σύνολο $\{v,e_{1},e_{3}\}$ είναι βάση για τον ${\mathbb{R}}^{3}$ .

Έστω $V$ ένας διανυσματικός υποχώρος του $\Bbbk^{n}$ , διάστασης $m$ , και έστω $B$ μία διατεταγμένη βάση του $V$ : $Β=\left(v_{1},\ldots,v_{m}\right)$ . Θα αποδείξουμε ότι κάθε διάνυσμα του $V$ γράφεται με μοναδικό τρόπο ως συνδυασμός των στοιχείων της $B$ . Έστω, λοιπόν , $v\in V$ . Αφού $B$ είναι βάση του $V$ , υπάρχουν $\kappa_{1},\ldots,\kappa_{n}\in\Bbbk$ έτσι ώστε

v=\kappa_{1}v_{1}+\cdots+\kappa_{m}v_{m}\;.

(3.4.6.1)

Έστω επίσης ότι:

v=\kappa_{1}^{\prime}v_{1}+\cdots+\kappa_{m}^{\prime}v_{m}.\

(3.4.6.2)

Αφαιρώντας τη σχέση (3.4.6.2) από τη σχέση (3.4.6.1) προκύπτει ότι

{\bf 0}=(\kappa_{1}-\kappa_{1}^{\prime})v_{1}+\cdots+(\kappa_{m}-\kappa_{m}^{% \prime})v_{m}\ .

Αφού το $B$ είναι γραμμικά ανεξάρτητο σύνολο, η σχέση αυτή πρέπει να είναι η μηδενική. Επομένως $\kappa_{i}=\kappa_{i}^{\prime}$ , για $i=1,\ldots,m$ . Αυτό σημαίνει ότι οι συντελεστές $\kappa_{1},\ldots,\kappa_{m}\in\Bbbk$ της σχέσης (3.4.6.1) είναι μοναδικοί. Αποδείξαμε λοιπόν το εξής συμπέρασμα:

Αν

B=\left(v_{1},\ldots,v_{m}\right)

είναι μία διατεταγμένη βάση του

V

, τότε κάθε

v\in V

μπορεί να γραφεί με μοναδικό τρόπο ως

v=\kappa_{1}v_{1}+\cdots+\kappa_{m}v_{m}

m\times 1

πίνακας

\begin{bmatrix}\kappa_{1}&\cdots&\kappa_{m}\end{bmatrix}^{T}

λέγεται πίνακας των συντεταγμένων (coordinate matrix) του

v

ως προς τη βάση

B=(v_{1},\ldots,v_{m})

και συμβολίζεται με

C_{B}(v)

. Τονίζουμε ότι o πίνακας

C_{B}(v)

έχει

m

γραμμές, όπου

m

είναι η διάσταση του

V

, παρότι

v\in\Bbbk^{n}

. Αντίστροφα, αν

C_{B}(v)=\left[\begin{array}[]{ccc}\kappa_{1}&\cdots&\kappa_{m}\end{array}% \right]^{T}\textrm{t'ote}v=\kappa_{1}v_{1}+\cdots+\kappa_{m}v_{m}\;.

Από τα προηγούμενα και την Πρόταση 3.2.9 προκύπτει το εξής αποτέλεσμα:

Αν

v\in V

και

B=(v_{1},\ldots,v_{m})

είναι διατεταγμένη βάση του

V

, τότε o

C_{B}(v)

προκύπτει ως η μοναδική λύση του συστήματος

AX=[v]

, όπου

Α=\begin{bmatrix}v_{1}&\cdots&v_{m}\end{bmatrix}

Στα Παραδείγματα που ακολουθούν υπολογίζουμε πίνακες συντεταγμένων σε διάφορες περιπτώσεις.

Παραδείγματα 3.4.8.

1.

Έστω $v=(1,1)$ , $B=\{v\}$ και $V=S(B)$ . To διάνυσμα $w=(3,3)$ ανήκει στον $V$ και $C_{B}(w)=[3]$ , αφού $w=3v$ . Έστω τώρα τα σύνολα $B_{1}=\{(1/2,1/2)\}$ , $B_{2}=\{(-1,-1)\}$ και $B_{3}=\{w\}$ . Τότε το $B_{i}$ είναι βάση του $V$ , για $i=1,\ldots,3$ . Είναι εύκολο να διαπιστώσει κανείς ότι

$C_{B_{1}}(w)=[6],\ C_{B_{2}}(w)=[-3],\ C_{B_{3}}(w)=[1]\;,$
ενώ

$C_{B}(v)=[1],\ C_{B_{1}}(v)=[2],\ C_{B_{3}}(v)=[1/3].$
2.

Έστω $B=\big(e_{1},e_{2}\big)$ η κανονική βάση του ${\mathbb{R}}^{2}$ και $v=(1,2)\in{\mathbb{R}}^{2}$ . Τότε

$C_{B}(e_{1})=\begin{bmatrix}1\cr 0\end{bmatrix},\quad C_{B}(e_{2})=\begin{% bmatrix}0\cr 1\end{bmatrix},\quad C_{B}(v)=\begin{bmatrix}1\cr 2\end{bmatrix}\;.$
αφού

$e_{1}=1\,e_{1}+0\,e_{2},\ e_{2}=0\,e_{1}+1\,e_{2},\ v=1\,e_{1}+2\,e_{2}\;.$
3.

Έστω τώρα η διατεταγμένη βάση $D=\big(e_{1},w\big)$ του ${\mathbb{R}}^{2}$ , όπου $w=(0,-1)$ και $v=(1,2)$ , όπως προηγουμένως. Τότε

$C_{D}(e_{1})=\begin{bmatrix}1\cr 0\end{bmatrix},\quad C_{D}(e_{2})=\begin{% bmatrix}\ \;0\cr-1\end{bmatrix},\quad C_{D}(v)=\begin{bmatrix}\ \;1\cr-2\end{% bmatrix},$
αφού

$e_{1}=1\,e_{1}+0\,w,\ e_{2}=0\,e_{1}-1\,w,\ v=1\,e_{1}-2\,w\;.$
4.

Έστω $v=(1,1)$ και $w=(2,3)$ . To σύνολο $Β=\big(v,w\big)$ είναι βάση για τον ${\mathbb{C}}^{2}$ . Θα βρούμε τις συντεταγμένες του $(4,5i)$ ως προς αυτήν τη βάση. Θέλουμε να γράψουμε το $(4,5i)$ ως συνδυασμό των $v$ , $w$ . Παίρνουμε τον πίνακα με στήλες τα τρία διανύσματα και τον φέρνουμε σε ελαττωμένη κλιμακωτή μορφή γραμμών.

$\left[\begin{array}[]{cc|c}1&2&4\cr 1&3&5i\end{array}\right]\rightarrow\cdots% \rightarrow\left[\begin{array}[]{cc|c}1&0&-4-10i\cr 0&1&-4+5i\end{array}\right].$
Άρα $(4,5i)=(-4-10i)v+(-4+5i)w$ και

$C_{B}(4,5i)=\begin{bmatrix}-4-10i\cr-4+5i\end{bmatrix}.$
5.

Έστω η βάση $B=(v,w)$ του επιπέδου $E$ στον ${\mathbb{R}}^{3}$ που δίνεται από την εξίσωση $x+y-z=0$ στον ${\mathbb{R}}^{3}$ , όπου $v=(1,0,1)$ και $w=(0,1,1)$ . To διάνυσμα $u=(2,2,4)\in E$ και αφού

$\left[\begin{array}[]{cc|c}1&0&2\cr 0&1&2\cr 1&1&4\end{array}\right]% \rightarrow\cdots\rightarrow\left[\begin{array}[]{cc|c}1&0&2\cr 0&1&2\cr 0&0&0% \end{array}\right],$
έπεται ότι $C_{B}(u)=\begin{bmatrix}2&2\end{bmatrix}^{T}$ .

Έστω τώρα ότι $V$ είναι διανυσματικός υποχώρος του ${\mathbb{R}}^{n}$ . Κάθε γραμμικός συνδυασμός διανυσμάτων του $V$ ανήκει στο $V$ . Έστω, λοιπόν, ότι $D$ είναι μία διατεταγμένη βάση του $V$ και ότι $u_{1},\ldots,u_{t}$ είναι τυχαία διανύσματα του $V$ , ενώ $\kappa_{1},\ldots,\kappa_{t}$ τυχαία στοιχεία του ${\mathbb{R}}$ . Είναι εύκολο να επιβεβαιώσει κανείς ότι

C_{D}(\kappa_{1}u_{1}+\cdots+\kappa_{t}u_{t})=\kappa_{1}C_{D}(u_{1})+\cdots+% \kappa_{t}C_{D}(u_{t})\;.

Δηλώνουμε την παρατήρηση αυτή ως εξής:

\kappa_{1}C_{D}(u_{1})+\cdots+\kappa_{t}C_{D}(u_{t})=\begin{bmatrix}C_{D}(u_{1% })&\cdots&C_{D}(u_{t})\end{bmatrix}\begin{bmatrix}\kappa_{1}\cr\vdots\cr\kappa% _{t}\end{bmatrix}=C_{D}(\kappa_{1}u_{1}+\cdots+\kappa_{t}u_{t})\,.

H παρατήρηση αυτή θα φανεί ιδιαίτερα χρήσιμη στη συνέχεια.

Ασκήσεις Ενότητας 3.4

1.

Δίνονται οι υποχώροι $V$ και $W$ του ${\mathbb{R}}$ -διανυσματικού χώρου ${\mathbb{R}}^{5}$ με ${\rm dim}_{{\mathbb{R}}}V=3$ και ${\rm dim}_{{\mathbb{R}}}W=3$ . Να αποδείξετε ότι υπάρχει στοιχείο $v\neq 0$ του ${\mathbb{R}}^{5}$ τέτοιο ώστε $v\in V\cap U$ .

Λύση
2.

Να βρείτε μία βάση για τους υποχώρους $U+V$ και $U\cap W$ του ${\mathbb{R}}^{4}$ , όπου

$U=S(\{(1,0,2,1),(1,1,0,0),(0,0,1,0)\}$
και

$W=S(\{(0,0,2,1),(2,2,0,0),(0,0,0,1)\}.$

Λύση
3.
Να βρείτε $C_{B}(e_{1})$ και $C_{B}(e_{2})$ όταν
1. (a)
  
  $Β=(e_{1},e_{2})$ ,
2. (b)
  
  $Β=(e_{2},e_{1})$ ,
3. (c)
  
  $Β=((1,-1),(0,2))$ .
  
  Λύση
4.

Έστω $D=(v_{1},v_{2})$ διατεταγμένη βάση του ${\mathbb{R}}^{2}$ . Να βρείτε $C_{D}(5w_{1}-w_{2})$ όταν

$C_{D}(w_{1})=\begin{bmatrix}2\cr 3\end{bmatrix},\quad C_{D}(w_{2})=\begin{% bmatrix}4\cr 5\end{bmatrix}.$

Λύση
5.
Να βρείτε το διάνυσμα $v\in{\mathbb{R}}^{3}$ με $C_{B}(v)=\begin{bmatrix}1&1&2\end{bmatrix}^{T}$ , όταν
1. (a)
  
  $Β=(e_{1},e_{2},e_{3})$ .
2. (b)
  
  $B=(e_{1}+e_{2},e_{3},e_{2})$ .
Λύση
6.

Έστω η διατεταγμένη βάση $D=\left((1,0,1),(0,1,0)\right)$ για το επίπεδο $U=\{(x,y,z):\;x-z=0\}$ .Να βρεθεί ο πίνακας των συντεταγμένων των $w_{1}=(2,2,2)$ και $w_{2}(2,5,2)$ ως προς τη $D$ .

Λύση
7.

Να βρείτε μία βάση για τους $\Gamma(A)$ , $\Sigma(A)$ και $\operatorname{null}(A)$ όπου

$A=\begin{bmatrix}1&1&1&2&3\cr 2&2&2&5&6\end{bmatrix}\in\mathcal{M}_{2\times 5}% (\Bbbk)\;.$
Να ερμηνεύσετε τα στοιχεία της βάσης του $\operatorname{null}(A)$ ως σχέσεις εξάρτησης των στηλών του $A$ .

Λύση
8.

Για κάθε $m\times n$ πίνακα $A$ και $n\times k$ πίνακα $B$ με συντελεστές από το $\Bbbk$ , να αποδείξετε ότι ${\rm dim}_{\Bbbk}\operatorname{null}(AB)\geq{\rm dim}_{\Bbbk}\operatorname{% null}(B)$ .

Λύση
9.

Για κάθε $m\times n$ πίνακα $A$ και $n\times k$ πίνακα $B$ , να αποδείξετε ότι $\operatorname{rank}(AB)\leq\min(\operatorname{rank}(A),\operatorname{rank}(B))$ . (Υπόδειξη: Να χρησιμοποιήσετε την προηγούμενη άσκηση, το Θεώρημα 3.4.3 και την Πρόταση 3.4.1.)

Λύση

3.5 $\Bbbk$ -Διανυσματικοί Χώροι

Στις προηγούμενες ενότητες αυτού του κεφαλαίου μελετήσαμε τον $\Bbbk^{n}$ και τους υποχώρους του. O παρατηρητικός αναγνώστης ίσως έχει εντοπίσει τις ομοιότητες μεταξύ των ιδιοτήτων που περιγράφονται στον Πίνακα 3.2.1 και στις ιδιότητες του συνόλου των $\mathcal{M}_{n\times m}(\Bbbk)$ πινάκων όπως περιγράφονται στις Προτάσεις 2.1.4 και 2.1.9. H ανάλυση για τους υποχώρους και τις βάσεις στηρίχθηκε σε αυτές τις ιδιότητες. Έτσι εύλογα γενικεύουμε το προηγούμενο έργο μας.

Ορισμός 3.5.1.

Έστω $V$ ένα σύνολο με μία πράξη πρόσθεσης ( $V\times V\rightarrow V$ ) και μία πράξη βαθμωτού πολλαπλασιασμού ( $\Bbbk\times V\rightarrow V$ ). To $V$ λέγεται διανυσματικός χώρος επάνω από το $\Bbbk$ ή για συντομία $\Bbbk$ -διανυσματικός χώρος ( $\Bbbk$ -vector space) αν ικανοποιούνται οι εξής ιδιότητες:

i.

${v}+({u}+{w})=({v}+{u})+{w}$ ,για όλα τα ${v},{u},{w}\in V$ .
ii.

Υπάρχει μοναδικό ${\bf 0}\in V$ , έτσι ώστε $\;{\bf 0}+{v}={v}={v}+{\bf 0}$ , για κάθε ${v}\in V$ .
iii.

Για κάθε $v\in V$ , υπάρχει μοναδικό $-v\in V$ , έτσι ώστε $\;-{v}+{v}={\bf 0}={v}+(-{v})$ .
iv.

$\;{v}+{u}={u}+{v}$ για όλα τα ${v},{u}\in V$ .
v.

$\;\kappa({v}+{u})=\kappa{v}+\kappa{u}$ για κάθε $\kappa\in\Bbbk$ και όλα τα ${v},{u}\in V$
$\;(\kappa+\lambda)v=\kappa{v}+\lambda{v}$ , για όλα τα $\kappa,\lambda\in\Bbbk$ και κάθε ${v}\in V$ .
vi.

$\;\kappa(\lambda{v})=(\kappa\lambda){v}$ , για όλα τα $\kappa,\lambda\in\Bbbk$ και ${v}\in V$ .
vii.

$\;1{v}={v}$ , για κάθε ${v}\in V$ .

Παραδείγματα 3.5.2.

1.

Όπως είδαμε o $\Bbbk^{n}$ είναι $\Bbbk$ -διανυσματικός χώρος για κάθε $n\in{\mathbb{N}}$ .
2.

To σύνολο $\mathcal{M}_{n\times m}(\Bbbk)$ είναι $\Bbbk$ -διανυσματικός χώρος με τη συνήθη πρόσθεση και σκαλιανό πολλαπλασιασμό.
3.

Έστω $\Bbbk[x]$ το σύνολο των πολυωνύμων με συντελεστές από το $\Bbbk$ . Αν $f(x),g(x)\in\Bbbk[x]$ , τότε ορίζουμε το άθροισμα $(f+g)(x)$ ως το πολυώνυμο $f(x)+g(x)$ . Αν $f(x)=\sum_{i}a_{i}x^{i}\in\Bbbk[x]$ και $c\in\Bbbk$ , τότε ορίζουμε το βαθμωτό γινόμενο $r\cdot f(x)$ ως το πολυώνυμο $\sum_{i}(ca_{i})x^{i}$ . O $\Bbbk[x]$ είναι $\Bbbk$ -διανυσματικός χώρος.
4.

Έστω ${\mathbb{R}}^{\mathbb{R}}$ το σύνολο των πραγματικών συναρτήσεων, δηλ. των συναρτήσεων από το ${\mathbb{R}}$ στο $R$ . Αν $f,g\in V$ , τότε ορίζουμε το άθροισμα $f+g$ ως τη συνάρτηση $f+g:\ {\mathbb{R}}\rightarrow R$ , όπου $(f+g)(a)=f(a)+g(a)$ , για $a\in{\mathbb{R}}$ . Αν $f\in V$ και $r\in{\mathbb{R}}$ , τότε ορίζουμε το βαθμωτό γινόμενο $r\cdot f$ ως τη συνάρτηση $r\cdot f:\ {\mathbb{R}}\rightarrow R$ , όπου $(r\cdot f)(a)=f(ra)$ , για $a\in{\mathbb{R}}$ .O $V$ είναι ${\mathbb{R}}$ -διανυσματικός χώρος.
5.

To σώμα των μιγαδικών αριθμών είναι ${\mathbb{R}}$ -διανυσματικός χώρος, με τη συνήθη πρόσθεση και (βαθμωτό) πολλαπλασιασμό.

Στη συνέχεια γενικεύουμε την έννοια του διανυσματικού υποχώρου.

Ορισμός 3.5.3.

Ένα μη κενό υποσύνολο $U$ του $V$ λέγεται $\Bbbk$ -διανυσματικός υποχώρος ( $\Bbbk$ -subspace) του $V$ αν

i.

${u}+{w}\in U$ ,για όλα τα $u,w\in U$ ,
ii.

$cu\in U$ ,για κάθε $u\in U$ και κάθε $c\in\Bbbk$ ,

Πρόταση 3.5.4.

To μη κενό υποσύνολο $U$ του $V$ είναι $\Bbbk$ -διανυσματικός υποχώρος αν και μόνο αν $U$ είναι $\Bbbk$ -διανυσματικός χώρος.

Για κάθε έναν από τους διανυσματικούς υποχώρους του προηγούμενου παραδείγματος, θα δώσουμε Παραδείγματα υποχώρων.

Παραδείγματα 3.5.5.

1.

Οι υποχώροι του $\Bbbk^{n}$ είναι οι $\Bbbk$ -διανυσματικοί υποχώροι.
2.

To σύνολο των πολυωνύμων στον $\Bbbk[x]$ που έχουν βαθμό $\leq m$ είναι $\Bbbk$ -διανυσματικός υποχώρος του $\Bbbk[x]$ .
3.

To σύνολο των διαγώνιων $n\times n$ πινάκων με συντελεστές από το $\Bbbk$ είναι $\Bbbk$ -διανυσματικός υποχώρος του $\mathcal{M}_{n}(\Bbbk)$ . To ίδιο και τα σύνολα των άνω και κάτω τριγωνικών πινάκων.
4.

To σύνολο των συνεχών πραγματικών συναρτήσεων είναι $\Bbbk$ -διανυσματικός υποχώρος του ${\mathbb{R}}^{\mathbb{R}}$ .
5.

O ${\mathbb{R}}$ είναι ${\mathbb{R}}$ -διανυσματικός υποχώρος του ${\mathbb{C}}$ .

Έστω $X$ ένα υποσύνολο του $\Bbbk$ -διανυσματικού χώρου $V$ . Τότε

{S(X)=\{\;\kappa_{1}x_{{1}}+\cdots+\kappa_{s}x_{{s}}\;:\;\kappa_{j}\in\Bbbk,\;% x_{{j}}\in X,1\leq j\leq s,\;s\in\mathbb{N}\}.}

Καλούμε τον αναγνώστη να παρατηρήσει ότι το $s$ στην περιγραφή του $S(X)$ δεν είναι κάποιος σταθερός φυσικός αριθμός, αλλά είναι μεταβλητή και επιτρέπεται να πάρει οποιαδήποτε τιμή από το ${\mathbb{N}}$ . Τα στοιχεία του $S(X)$ είναι γραμμικοί συνδυασμοί των στοιχείων του $X$ με συντελεστές από το $\Bbbk$ . Στην περίπτωση που $X=\emptyset$ , τότε $S(X)=\{{\bf 0}\}$ . Εύκολα αποδεικνύεται η εξής πρόταση.

Πρόταση 3.5.6.

To υποσύνολο $U$ του $V$ είναι $\Bbbk$ -διανυσματικός υποχώρος του $V$ αν και μόνο αν υπάρχει $X\subset V$ έτσι ώστε $U=S(X)$

Τονίζουμε ότι αν o $V$ είναι $\Bbbk$ -διανυσματικός χώρος, τότε

0v={\bf 0}\;.

Αν και στον $\Bbbk^{n}$ η σχέση αυτή ήταν προφανής, για γενικούς διανυσματικούς χώρους χρήζει απόδειξης. Πράγματι, σύμφωνα με τον Ορισμό 3.5.1 (Ιδιότητα v) προκύπτει ότι

0v+0v=(0+0)v=0v,

ενώ από την μοναδικότητα του ${\bf 0}$ (Ιδιότητα ii), προκύπτει ότι

0v={\bf 0}.

Τα $v_{1},v_{2},\ldots,v_{m}$ του $V$ λέγονται γραμμικά ανεξάρτητα (linearly independent) αν δεν υπάρχει μη μηδενική σχέση γραμμικής εξάρτησης μεταξύ των $v_{1},v_{2},\ldots,v_{n}$ , δηλ. αν

\kappa_{1}v_{1}+\kappa_{2}v_{2}+\cdots+\kappa_{m}v_{m}={\bf 0}\;,

τότε $\kappa_{1}=\kappa_{2}=\ldots=\kappa_{m}=0$ . Μία βάση (basis) του $\Bbbk$ -διανυσματικού χώρου $V$ είναι ένα υποσύνολο $B$ του $V$ έτσι ώστε $V=S(B)$ και τα στοιχεία του $V$ να είναι γραμμικά ανεξάρτητα. Αποδεικνύεται (σχεδόν) όπως και για τους υποχώρους του $\Bbbk^{n}$ το εξής θεώρημα.

Θεώρημα 3.5.7.

Έστω $V$ ένας $\Bbbk$ -διανυσματικός χώρος. O $V$ έχει μία βάση. Αν μία βάση του $V$ είναι πεπερασμένο σύνολο, τότε όλες οι βάσεις του $V$ έχουν το ίδιο πλήθος στοιχείων.

Ανο $V$ έχει μία πεπερασμένη βάση, τότε το πλήθος των στοιχείων της λέγεται $\Bbbk$ -διάσταση ( $\Bbbk$ -dimension) του $V$ και συμβολίζεται ${\rm dim}_{\Bbbk}(V)$ ${\rm dim}_{\Bbbk}(V)$ . Αν o $V$ έχει μία άπειρη βάση, τότε λέμε ότι $V$ έχει άπειρη διάσταση και γράφουμε ${\rm dim}_{\Bbbk}(V)=\infty$ .

Παραδείγματα 3.5.8.

1.

${\rm dim}_{\Bbbk}(\Bbbk^{n})=n$ .
2.

To σύνολο $B=\{1,i\}$ είναι μία βάση για τον ${\mathbb{R}}$ -διανυσματικό χώρο ${\mathbb{C}}$ . Πράγματι ${\mathbb{C}}=\{a+bi:\alpha,b\in{\mathbb{R}}\}$ . Αφού $a+bi=a\cdot 1+b\cdot i$ βλέπουμε ότι ${\mathbb{C}}=S(B)$ . Επίσης $a+bi=0\Leftrightarrow a=b=0$ . Άρα τα $1,i$ είναι γραμμικά ανεξάρτητα. Επομένως $B$ είναι βάση για το ${\mathbb{C}}$ και ${\rm dim}_{{\mathbb{R}}}({\mathbb{C}})=2$ . Παρατηρούμε ότι ${\rm dim}_{\mathbb{C}}{\mathbb{C}}=1$ .
3.

Μία βάση του ${\mathbb{R}}[x]$ είναι το άπειρο σύνολο

$\{1,x,x^{2},\ldots,\}$
και ${\rm dim}_{{\mathbb{R}}}{\mathbb{R}}[x]=\infty$ .
4.

Θα γράψουμε μία βάση για τον $\Bbbk$ -διανυσματικό χώρο $\mathcal{M}_{2\times 3}(\Bbbk)$ και θα δείξουμε ότι ${\rm dim}_{\Bbbk}(\mathcal{M}_{2\times 3}(\Bbbk))=6$ . Θεωρούμε τους εξής έξι πίνακες:

$E_{1}=\left[\begin{array}[]{ccc}1&0&0\cr 0&0&0\end{array}\right],\quad E_{2}=% \left[\begin{array}[]{ccc}0&1&0\cr 0&0&0\end{array}\right],\quad E_{3}=\left[% \begin{array}[]{ccc}0&1&0\cr 0&0&0\end{array}\right],\quad$
$E_{4}=\left[\begin{array}[]{ccc}0&0&0\cr 1&0&0\end{array}\right],\quad E_{5}=% \left[\begin{array}[]{ccc}0&0&0\cr 0&1&0\end{array}\right],\quad E_{6}=\left[% \begin{array}[]{ccc}0&0&0\cr 0&0&1\end{array}\right].$
Είναι εύκολο να δει κανείς ότι ένας τυχαίος πίνακας του $\mathcal{M}_{2\times 3}(\Bbbk)$ είναι γραμμικός συνδυασμός των πινάκων αυτών αφού

$\left[\begin{array}[]{ccc}a&b&c\cr d&e&f\end{array}\right]=aE_{1}+bE_{2}+cE_{3% }+dE_{4}+eE_{5}+fE_{6}\ .$
Είναι επίσης εύκολο να δείξει κανείς ότι οι πίνακες $E_{1},\ldots,E_{6}$ είναι γραμμικά ανεξάρτητα στοιχεία του $\mathcal{M}_{2\times 3}(\Bbbk)$ , αφού

$\kappa_{1}E_{1}+\cdots+\kappa_{6}E_{m}={\bf 0}\Rightarrow\left[\begin{array}[]% {ccc}\kappa_{1}&\kappa_{2}&\kappa_{3}\cr\kappa_{4}&\kappa_{5}&\kappa_{6}\end{% array}\right]=\left[\begin{array}[]{ccc}0&0&0\cr 0&0&0\end{array}\right]$
και άρα $\kappa_{1}=\kappa_{2}=\cdots=\kappa_{6}=0$ . Επομένως $\{E_{1},\ldots,E_{6}\}$ είναι βάση για τον $\mathcal{M}_{2\times 3}(\Bbbk)$ .

Στο επόμενο κεφάλαιο θα δείξουμε ότι από αλγεβρική σκοπιά δεν μπορούμε να ξεχωρίσουμε δύο διανυσματικούς χώρους που έχουν την ίδια διάσταση επάνω από το $\Bbbk$ . Έτσι, αρκεί να μελετήσουμε έναν από αυτούς για να βγάλουμε συμπεράσματα για όλους. Έστω $B=(v_{1},\ldots,v_{m})$ μία διατεταγμένη βάση (ordered basis) του $\Bbbk$ -διανυσματικού χώρου $V$ , δηλ. μία βάση που είναι διατεταγμένο σύνολο. Αν

v=\kappa_{1}v_{1}+\cdots+\kappa_{m}v_{m}\;,

τότε οι συντελεστές $\kappa_{1},\ldots,\kappa_{m}\in{\mathbb{R}}$ είναι μοναδικοί και o $m\times 1$ πίνακας

\;C_{B}(v)=\left[\begin{array}[]{ccc}\kappa_{1}\\ \vdots\\ \kappa_{m}\end{array}\right],

λέγεται πίνακας των συντεταγμένων (coordinate matrix) του $v$ ως προς τη βάση $B$ .

Παραδείγματα 3.5.9.

1.

Έστω $B=(E_{1},\ldots,E_{6})$ και $B^{\prime}=(E_{2},E_{1},E_{3},\ldots,E_{6})$ δύο διατεταγμένες βάσεις του $\mathcal{M}_{2\times 3}(\Bbbk)$ όπου τα $E_{1},\ldots,E_{6}$ είναι όπως στο Παράδειγμα 3.5.8.4. Αν $A=\begin{bmatrix}1&2&5\cr 0&2&8\end{bmatrix}$ τότε

$C_{B}(A)=\left[\begin{array}[]{c}1\cr 2\cr 5\cr 0\cr 2\cr 8\end{array}\right]% \textrm{kai}C_{B^{\prime}}(A)=\left[\begin{array}[]{c}2\cr 1\cr 5\cr 0\cr 2\cr 8% \end{array}\right].$
2.

Έστω $E=\{(x,y,x+y):\ x,y\in{\mathbb{R}}^{2}\}$ το επίπεδο στον ${\mathbb{R}}^{2}$ με διατεταγμένη βάση $B=\left((1,0,1),(0,1,1)\right)$ . Τότε για το $v=(2,1,3)\in E$ ισχύει ότι $C_{B}(v)=\begin{bmatrix}2\cr 1\end{bmatrix}$ .

Σημειώνουμε την επόμενη σημαντική παρατήρηση, για τα $w,w_{1},\ldots,w_{t}\in V$ .

Αν $w=\kappa_{1}w_{1}+\cdots+\kappa_{t}w_{t}$ , τότε $C_{B}(w)=\kappa_{1}C_{B}(w_{1})+\cdots+\kappa_{1}C_{B}(w_{t})$ .

Ειδικότερα, αν

κ_{1} w_{1} + \dots + κ_{t} w_{t} = 0,

τότε

κ_{1} C_{B} (w_{1}) + \dots + κ_{1} C_{B} (w_{t}) = [\begin{matrix} 0 \\ ⋮ \\ 0 \end{matrix}] .

To αντίστροφο επίσης ισχύει. Σημειώνουμε, λοιπόν, το επόμενο συμπέρασμα.

Πρόταση 3.5.10.

Έστω Β μια διατεταγμένη βάση του k-διανυσματικού χώρου W, όπου

\dim_{k} (W) = m

. Τότε:

1.

Τα διανύσματα $w_{1}, \dots, w_{t} \in W$ είναι γραμμικά εξαρτημένα αν και μόνο αν οι στήλες $C_{B} (w_{1}), \dots, C_{B} (w_{t}) \in M_{m \times 1} (k)$ είναι γραμμικά εξαρτημένες.
2.

Τα διανύσματα $w_{1}, \dots, w_{t} \in W$ είναι γραμμικά ανεξάρτητα αν και μόνο αν οι στήλες $C_{B} (w_{1}), \dots, C_{B} (w_{t}) \in M_{m \times 1} (k)$ είναι γραμμικά ανεξάρτητες.

Ασκήσεις Ενότητας 3.5

1.

Να αποδείξετε ότι το σύνολο των πολυωνύμων με συντελεστές από το ${\mathbb{R}}$ που έχουν βαθμό $6$ δεν είναι υποχώρος του ${\mathbb{R}}[x]$ . Να αποδείξετε ότι το σύνολο $\{1,x,\ldots,x^{6}\}$ είναι βάση για τον υποχώρο των πολυωνύμων με συντελεστές από το ${\mathbb{R}}$ που έχουν βαθμό $\leq 6$ . Να γενικεύσετε για τον υποχώρο των πολυωνύμων με συντελεστές από το ${\mathbb{R}}$ που έχουν βαθμό $\leq m$ .

Λύση
2.

Να βρείτε μία βάση για τον $\mathcal{M}_{n\times m}(\Bbbk)$ και να αποδείξετε ότι

${\rm dim}_{\Bbbk}\left(\mathcal{M}_{n\times m}(\Bbbk)\right)=nm.$

Λύση
3.

Να βρείτε μία βάση για το χώρο των διαγωνίων $n\times n$ πινάκων και να αποδείξετε ότι έχει διάσταση $n$ .

Λύση
4.

Να βρείτε μία βάση για το χώρο των άνω τριγωνικών $2\times 2$ πινάκων και να αποδείξετε ότι έχει διάσταση $3$ . Να γενικεύσετε για το χώρο των άνω τριγωνικών $n\times n$ πινάκων.

3.6 Σύντομα Ιστορικά Στοιχεία

H Καρτεσιανή Γεωμετρία ανακαλύφθηκε το 1636 από τους Γάλλους μαθηματικούς Fermat (1601-1665) και Descartes (1596-1650) και επηρέασε βαθιά την εξέλιξη των μαθηματικών. Ενάμιση αιώνα αργότερα, στις αρχές του 19ου αιώνα, με το έργο του Βοημού μαθηματικού Bolzano (1782-1848) το 1804 εμφανίστηκαν οι απαρχές της θεωρίας των διανυσμάτων. Στο βιβλίο του o Bolzano το 1804 εισάγει την ιδέα των πράξεων σε ευθείες και επίπεδα χωρίς αναφορά σε συγκεκριμένο σύστημα συντεταγμένων, όπως επέβαλε η αναλυτική Καρτεσιανή Γεωμετρία. H ιδέα για τους διανυσματικούς χώρους εμφανίστηκε αχνά στη δουλειά του Γερμανού μαθηματικού Möbius (1790-1868) με κατευθυνόμενα ευθύγραμμα τμήματα το 1827 και το 1828. O Ελβετός λογιστής στο επάγγελμα και ερασιτέχνης μαθηματικός Argand (1768-1822) το 1814 παρουσίασε τους μιγαδικούς αριθμούς ως ζεύγη πραγματικών αριθμών, δηλ. αντιμετώπισε τον ${\mathbb{C}}$ ως ${\mathbb{R}}$ -διανυσματικό χώρο διάστασης 2, αν και ο όρος διανυσματικός χώρος δεν είχε ακόμα εφευρεθεί. O Ιρλανδός μαθηματικός Hamilton (1805-1865) ανακάλυψε τον τετραδιάστατο διανυσματικό χώρο των τετραδικών αριθμών το 1843 και από την χαρά του, χάραξε την ανακάλυψή του σε έναν βράχο κατά τη διάρκεια του περιπάτου που έκανε μαζί με τη γυναίκα του στη γέφυρα του Broome. Στο έργο του Πολωνού μαθηματικού Grassman (1809-1877) το 1844 οφείλουμε τους κανόνες που ορίζουν τους διανυσματικούς χώρους. To έργο αυτό φαίνεται να χρησιμοποίησε o Γάλλος μαθηματικός Cauchy (1789-1857) το 1853 χωρίς αναφορά στον Grassman. O πρώτος που έδωσε τον αξιωματικό ορισμό των διανυσματικών χώρων είναι o Ιταλός μαθηματικός Peano (1858-1932) το1888. Εκτός του ορισμού, o Peano αποδεικνύει ότι κάθε διανυσματικός πεπερασμένης διάστασης έχει μία βάση και δίνει Παραδείγματα διανυσματικών χώρων άπειρης διάστασης. Για περισσότερα ιστορικά στοιχεία παραπέμπουμε στα συγγράμματα [3] και [4].

Βιβλιογραφία

1.

H. Anton, C. Rorres, Elementary Linear Algebra, Applications Version, John Wiley and Sons,1994.
2.

Θ. Θεοχάρη-Αποστολίδη, Χ. Χαραλάμπους, Β. Βαβατσούλας, Εισαγωγή στη Γραμμική Άλγεβρα, Θεσσαλονίκη 2006.
3.

V. Katz, Ιστορία των Μαθηματικών, Πανεπιστημιακές Εκδόσεις Κρήτης, 2013.
4.

I. Kleiner, A History of Abstract Algebra, Birkhäuser, 2007.
5.

K. Nicholoson, Elementary Linear Algebra, McGraw-Hill, 2001.
6.

Th. Shiffrin and M. R. Adams, Linear Algebra, a Geometric Approach, W.H.Freeman and Company, 2002.

Κεφάλαιο 3Διανυσματικοί Χώροι

3.1 Διανύσματα στον ℝn

Παραδείγματα 3.1.1.

Πρόταση 3.1.2.

Απόδειξη.

Ασκήσεις Ενότητας 3.1

3.2 Διανυσματικός Χώρος kn και Υποχώροι

Ορισμός 3.2.1.

Παράδειγμα 3.2.2.

Πρόταση 3.2.3.

Παραδείγματα 3.2.4.

Παραδείγματα 3.2.5.

Πρόταση 3.2.6.

Παράδειγμα 3.2.7.

Παρατήρηση 3.2.8.

Πρόταση 3.2.9.

Παράδειγμα 3.2.10.

Ασκήσεις Ενότητας 3.2

3.3 Βάσεις και Γραμμική Ανεξαρτησία, I

Ορισμός 3.3.1.

Παραδείγματα 3.3.2.

Ορισμός 3.3.3.

Παρατήρηση 3.3.4.

Πρόταση 3.3.5.

Παραδείγματα 3.3.6.

Πρόταση 3.3.7.

Παράδειγμα 3.3.8.

Θεώρημα 3.3.9.

Ορισμός 3.3.10.

Παραδείγματα 3.3.11.

Παράδειγμα 3.3.12.

Παρατήρηση 3.3.13.

Παράδειγμα 3.3.14.

Ασκήσεις Ενότητας 3.3

3.4 Βάσεις και Γραμμική Ανεξαρτησία, II

Πρόταση 3.4.1.

Θεώρημα 3.4.3.

Παράδειγμα 3.4.4.

Θεώρημα 3.4.5.

Απόδειξη.

Παράδειγμα 3.4.6.

Παράδειγμα 3.4.7.

Παραδείγματα 3.4.8.

Ασκήσεις Ενότητας 3.4

3.5 k -Διανυσματικοί Χώροι

Ορισμός 3.5.1.

Παραδείγματα 3.5.2.

Ορισμός 3.5.3.

Πρόταση 3.5.4.

Παραδείγματα 3.5.5.

Πρόταση 3.5.6.

Θεώρημα 3.5.7.

Παραδείγματα 3.5.8.

Παραδείγματα 3.5.9.

Πρόταση 3.5.10.

Ασκήσεις Ενότητας 3.5

3.6 Σύντομα Ιστορικά Στοιχεία

Βιβλιογραφία

3.1 Διανύσματα στον ${\mathbb{R}}^{n}$

3.2 Διανυσματικός Χώρος $\Bbbk^{n}$ και Υποχώροι

3.5 $\Bbbk$ -Διανυσματικοί Χώροι