Μια Εισαγωγή στη Γραμμική Άλγεβρα για τις Θετικές Επιστήμες

Κεφάλαιο 5Ιδιοτιμές, Ιδιοδιανύσματα

Σε αυτό το κεφάλαιο μελετούμε τις ιδιοτιμές και τα ιδιοδιανύσματα ενός τετραγωνικού πίνακα. Ως συνήθως, $\Bbbk$ είναι το σώμα ${\mathbb{R}}$ ή το σώμα ${\mathbb{C}}$ .

5.1 Ιδιοτιμές και Ιδιοδιανύσματα

Έστω $V$ ένας $\Bbbk$ -διανυσματικός χώρος και $\phi:V\rightarrow V$ μία γραμμική συνάρτηση. Σε αυτήν την ενότητα θα δούμε πως εντοπίζουμε μη μηδενικά διανύσματα $v$ που οι εικόνες τους, $\phi(v)$ , είναι διανύσματα παράλληλα προς τα ίδια τα $v$ . Τα διανύσματα αυτά τα ονομάζουμε ιδιοδιανύσματα της $\phi$ . Στο Σχήμα 5.1 με μπλε χρώμα απεικονίζεται ένα ιδιοδιάνυσμα $v$ της $\phi$ , ενώ με κόκκινο χρώμα απεικονίζεται η εικόνα του.

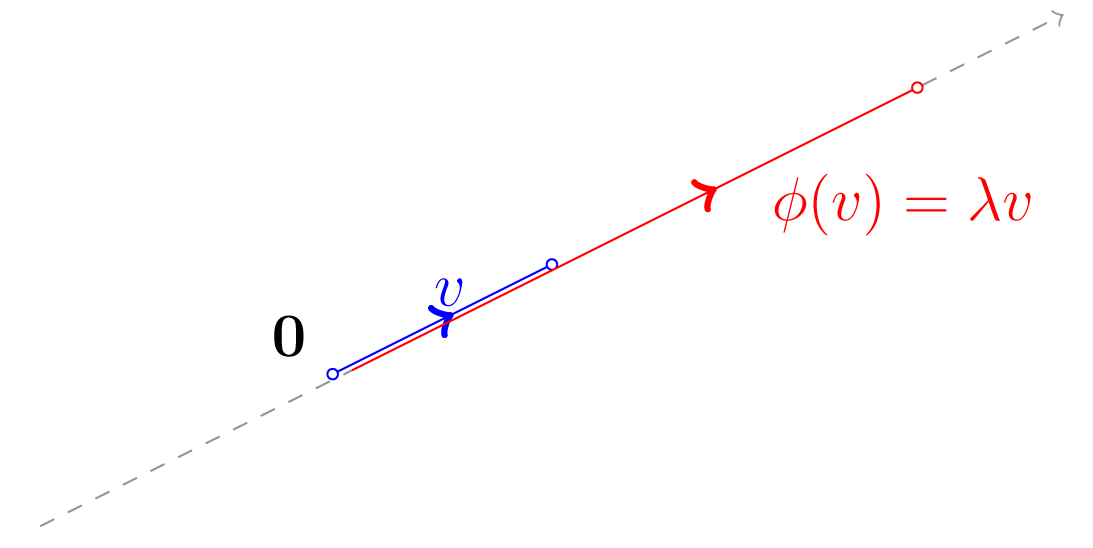
Σχήμα 5.1: Ιδιοδιάνυσμα για την ιδιοτιμή $\lambda$

Ορισμός 5.1.1.

Έστω $V$ ένας $\Bbbk$ -διανυσματικός χώρος και $\phi:V\rightarrow V$ μία γραμμική συνάρτηση. To $\lambda\in\Bbbk$ λέγεται ιδιοτιμή (eigenvalue) της $\phi$ , αν υπάρχει $v\in V$ , $v\neq 0$ , έτσι ώστε

\phi(v)=\lambda v.

(5.1.1.1)

Το $v$ της Σχέσης (5.1.1.1) λέγεται ιδιοδιάνυσμα (eigenvector) της $\phi$ για την ιδιοτιμή $\lambda$ .

Παραδείγματα 5.1.2.

1.

Η ταυτοτική συνάρτηση $\operatorname{id}_{V}:\ V\rightarrow V$ , $\operatorname{id}_{V}(v)=v$ έχει το $1$ για ιδιοτιμή, ενώ κάθε $v\neq{\bf 0}\in V$ είναι ιδιοδιάνυσμα για την ιδιοτιμή 1. Είναι φανερό ότι η γραμμική συνάρτηση $\operatorname{id}_{V}:V\rightarrow V$ δεν έχει άλλη ιδιοτιμή.
2.

Κάθε μη μηδενικό στοιχείο $v$ του $V$ είναι ιδιοδιάνυσμα για τη μηδενική (τετριμμένη) συνάρτηση $f:\ V\rightarrow V$ για την ιδιοτιμή $0$ αφού $f(v)={\bf 0}$ . Είναι φανερό ότι η μόνη ιδιοτιμή της μηδενικής συνάρτησης είναι το $0$ .

Έχοντας μελετήσει στο προηγούμενο κεφάλαιο τη στενή σχέση μεταξύ των γραμμικών συναρτήσεων και των πινάκων, δίνουμε στη συνέχεια τους αντίστοιχους ορισμούς για τους τετραγωνικούς πίνακες.

Ορισμός 5.1.3.

Αν $Α\in\mathcal{M}_{n}(\Bbbk)$ , τότε $b=\begin{bmatrix}b_{1}&\cdots&b_{n}\end{bmatrix}^{T}\in\mathcal{M}_{n\times 1}% (\Bbbk)$ λέγεται ιδιοδιάνυσμα (eigenvector) του $A$ για την ιδιοτιμή (eigenvalue) $\lambda$ , αν $b\neq\bf{0}$ και $A\;b=\lambda b$ , δηλ.

A\begin{bmatrix}b_{1}\cr\vdots\cr b_{n}\end{bmatrix}=\lambda\begin{bmatrix}b_{% 1}\cr\vdots\cr b_{n}\end{bmatrix}\ .

(5.1.3.1)

Σύμφωνα με το Θεώρημα 4.2.14, κάθε $\Bbbk$ -διανυσματικός χώρος $V$ διάστασης $n$ είναι ισόμορφος με τον $\Bbbk^{n}$ . Για να απλοποιήσουμε, λοιπόν, τους συμβολισμούς μας, θα περιοριστούμε στην περίπτωση που $V=\Bbbk^{n}$ . Σημειώνουμε την επόμενη πρόταση.

Πρόταση 5.1.4.

Έστω $\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}$ μία γραμμική συνάρτηση , $D$ μία διατεταγμένη βάση του $\Bbbk^{n}$ . To $v\in\Bbbk^{n}$ είναι ιδιοδιάνυσμα της $\phi$ για την ιδιοτιμή $\lambda$ αν και μόνο αν $C_{D}(v)$ είναι ιδιοδιάνυσμα του πίνακα $A^{\phi}_{D,D}$ για την ιδιοτιμή $\lambda$ . Ειδικότερα, αν $B$ είναι η κανονική βάση του $\Bbbk^{n}$ , τότε $(b_{1},\ldots,b_{n})$ είναι ιδιοδιάνυσμα της $\phi$ αν και μόνο αν $b=\begin{bmatrix}b_{1}&\cdots&b_{n}\end{bmatrix}^{T}$ είναι ιδιοδιάνυσμα του $A^{\phi}_{B,B}$ .

Απόδειξη.

Έστω ότι το $v$ είναι ιδιοδιάνυσμα της $\phi$ για την ιδιοτιμή $\lambda$ , δηλ. $\phi(v)=\lambda v$ . Τότε $v\neq{\bf 0}$ , άρα $C_{D}(v)\neq{\bf 0}$ . Είναι φανερό ότι $C_{D}(\lambda v)=\lambda\;C_{D}(v)$ . Από την Πρόταση 4.1.4, έχουμε ότι:

Α^{\phi}_{D,D}\;C_{D}(v)=C_{D}(\phi(v))=C_{D}(\lambda v)=\lambda\;C_{D}(v)\;.

Άρα το $C_{D}(v)$ είναι ιδιοδιάνυσμα του $Α^{\phi}_{D,D}$ . To αντίστροφο προκύπτει με τον ίδιο ακριβώς τρόπο.

Για το τελευταίο συμπέρασμα της πρότασης σημειώνουμε ότι αν $B$ είναι η κανονική βάση του $\Bbbk^{n}$ και $v=(b_{1},\ldots,b_{n})$ , τότε $C_{B}(v)=\begin{bmatrix}b_{1}&\cdots&b_{n}\end{bmatrix}^{T}$ . ∎

Στα επόμενο παραδείγματα θα δούμε πως βρίσκουμε τα ιδιοδιανύσματα και τις ιδιοτιμές, χρησιμοποιώντας την παρατήρηση αυτή και τη γεωμετρική εποπτεία για το πραγματικό επίπεδο και τον πραγματικό τρισδιάστατο χώρο.

Παραδείγματα 5.1.5.

1.

O μοναδιαίος πίνακας $I_{n}$ έχει την ιδιοτιμή 1 με ιδιοδιάνυσμα κάθε $v\neq 0\in\Bbbk^{n}$ . Σημειώνουμε ότι o $I_{n}$ είναι o πίνακας της ταυτοτικής συνάρτησης $\operatorname{id}_{\Bbbk^{n}}:\Bbbk^{n}\rightarrow\Bbbk^{n}$ , $\operatorname{id}(v)=v$ ως προς την κανονική βάση.
2.

O μηδενικός $n\times n$ πίνακας

${\bf 0}=\begin{bmatrix}0&\cdots&0\cr\vdots&\ddots&\vdots\cr 0&\cdots&0\end{bmatrix}$
έχει την ιδιοτιμή 0 με ιδιοδιάνυσμα κάθε $v\neq 0\in\Bbbk^{n}$ . Σημειώνουμε ότι o $\bf 0$ είναι o πίνακας της μηδενικής συνάρτησης $\Bbbk^{n}\rightarrow\Bbbk^{n}$ , $v\mapsto\bf 0$ ως προς οποιαδήποτε βάση.
3.

Η γραμμική συνάρτηση $f:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ που περιστρέφει αριστερόστροφα κατά γωνία $\displaystyle{{\pi}/{4}}$ τα στοιχεία του ${\mathbb{R}}^{2}$ (βλ. Σχήμα 5.2) δεν έχει ιδιοτιμές και ιδιοδιανύσματα. Για το συμπέρασμα αυτό αρκεί να παρατηρήσουμε τη γραφική απεικόνιση της συνάρτησης: όταν $v\neq 0$ τότε $f(v)$ και $v$ ορίζουν δύο ευθείες που σχηματίζουν μεταξύ τους γωνία $\pi/4$ . Άρα δεν υπάρχει $\lambda$ έτσι ώστε $f(v)=\lambda\ v$ .

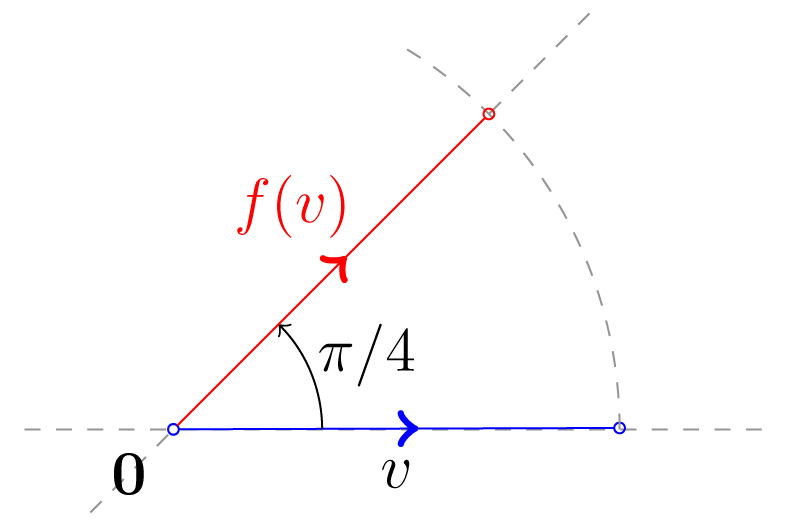
Σχήμα 5.2: Αριστερόστροφη περιστροφή κατά γωνία $\pi/4$

Έστω

$A=A^{f}_{BB}=\frac{\sqrt{2}}{2}\left[\begin{array}[]{cc}1&-1\cr 1&1\end{array}% \right].$
Αφού η $f$ δεν έχει ιδιοτιμές και ιδιοδιανύσματα, ούτε o $A$ έχει ιδιοτιμές και ιδιοδιανύσματα στον ${\mathbb{R}}$ .
4.

Έστω $f:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ η προβολή στην ευθεία $y=mx$ , όπως απεικονίζεται στο Σχήμα 4.4.

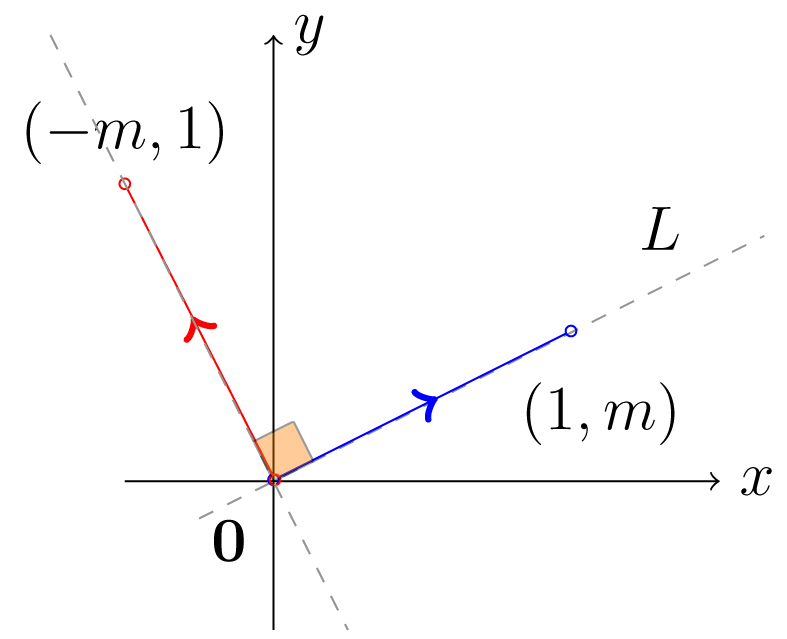
Σχήμα 5.3: Προβολή στον ${\mathbb{R}}^{2}$ στην ευθεία $y=mx$

Η ευθεία $y=mx$ περνά από την αρχή των αξόνων $O(0,0)$ και το σημείο $(1,m)$ . Είναι λοιπόν παράλληλη προς το διάνυσμα $(1,m)$ και κάθετη προς το διάνυσμα $(-m,1)$ . Από τη γραφική απεικόνιση της συνάρτησης, συμπεραίνουμε ότι η $f$ έχει δύο ιδιοτιμές: το 1 και το 0. Πράγματι αν $v_{1}=(1,m)$ τότε $f(v_{1})=v_{1}$ και άρα το $v_{1}$ είναι ιδιοδιάνυσμα για το 1. Αντίστοιχα αν $v_{2}=(-m,1)$ τότε $f(v_{2})=0$ και το $v_{2}$ είναι ιδιοδιάνυσμα για την ιδιοτιμή 0. Γενικότερα, τα πολλαπλάσια του $v_{1}$ είναι όλα ιδιοδιανύσματα για την τιμή 1, ενώ τα πολλαπλάσια του $v_{2}$ είναι ιδιοδιανύσματα της $f$ για την ιδιοτιμή 0.

Στη συνέχεια θα βρούμε τον τύπο της $f$ . Έστω $D=(v_{1},v_{2})$ . Ο πίνακας $Α^{f}_{D,D}$ είναι διαγώνιος, με τις ιδιοτιμές να εμφανίζονται ως στοιχεία της κυρίας διαγωνίου. Πράγματι $f(v_{1})=v_{1}$ και $f(v_{2})=0$ , επομένως

$C_{D}(f(v_{1}))=\begin{bmatrix}1\cr 0\end{bmatrix}\hbox{ και }C_{D}(f(v_{2}))=% \begin{bmatrix}0\cr 0\end{bmatrix}\ .$
Άρα

$Α^{f}_{D,D}=\begin{bmatrix}1&0\cr 0&0\end{bmatrix}\ .$
Έστω τώρα $B=(e_{1},e_{2})$ ,

$S=S_{B\leftarrow D}=\begin{bmatrix}1&-m\cr m&1\end{bmatrix}\ .$
Τότε

$Α^{f}_{Β,Β}=S\;A^{f}_{B,B}\;S^{-1}=\frac{1}{1+m^{2}}\begin{bmatrix}1&m\cr m&m^% {2}\end{bmatrix}\ .$
Αφού

$Α^{f}_{Β,Β}\;\begin{bmatrix}a\cr b\end{bmatrix}=\frac{1}{1+m^{2}}\begin{% bmatrix}a+mb\cr ma+m^{2}b\end{bmatrix}\;,$
έπεται ότι

$f(a,b)=\frac{1}{1+m^{2}}(a+mb,ma+m^{2}b)\;.$
5.

Έστω $f:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ o αντικατοπτρισμός ως προς την ευθεία $y=mx$ , όπως απεικονίζεται στο Σχήμα 5.4.

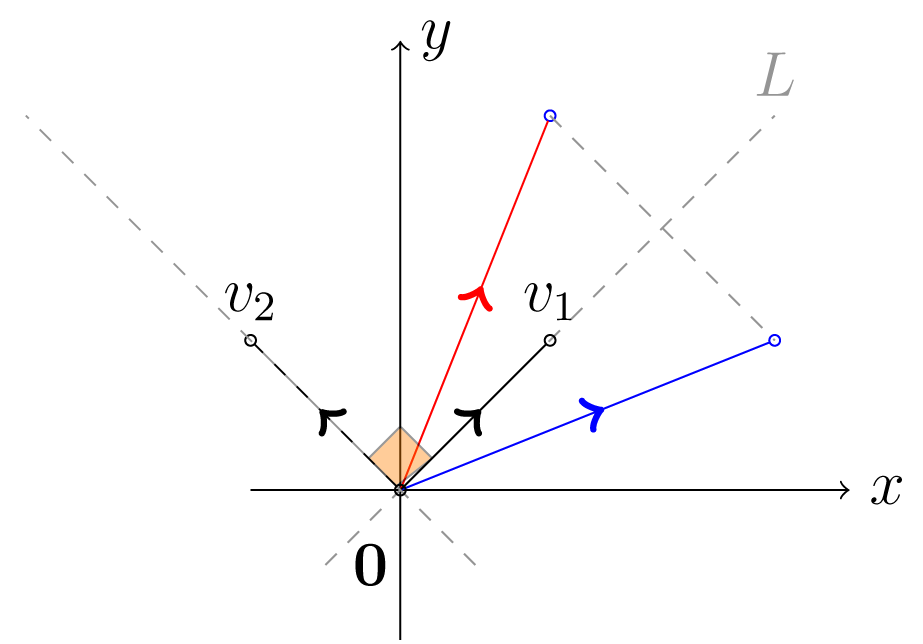
Σχήμα 5.4: Αντικατοπτρισμός ως προς την ευθεία $y=mx$

H $f$ έχει την ιδιοτιμή 1 με ιδιοδιανύσματα τα πολλαπλάσια του $v_{1}=(1,m)$ , και την ιδιοτιμή -1 με ιδιοδιανύσματα τα πολλαπλάσια του $v_{2}=(-m,1)$ . Έτσι ως προς τη βάση $D=(v_{1},v_{2})$ έχουμε ότι

$Α^{f}_{D,D}=\begin{bmatrix}1&0\cr 0&-1\end{bmatrix}\ .$
Έστω $Β$ η κανονική βάση του ${\mathbb{R}}^{2}$ και $S=S_{B\leftarrow D}$ . Τότε

$S=\begin{bmatrix}1&-m\cr m&1\end{bmatrix}$
και

$A^{f}_{B,B}=S\;A^{f}_{D,D}\;S^{-1}=\frac{1}{1+m^{2}}\begin{bmatrix}1-m^{2}&2m% \cr 2m&m^{2}-1\end{bmatrix}\;.$
Αφού

$A^{f}_{B,b}\begin{bmatrix}a\cr b\end{bmatrix}=\frac{1}{1+m^{2}}\begin{bmatrix}% a(1-m^{2})+2bm\cr 2am+b(m^{2}-1)\end{bmatrix}\;,$
o αναλυτικός τύπος της $f$ είναι

$f(a,b)=\frac{1}{1+m^{2}}(a(1-m^{2})+2bm,2am+b(m^{2}-1))\;.$

Αν το $\lambda$ είναι ιδιοτιμή της γραμμικής συνάρτησης $\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}$ , τότε o ιδιοχώρος (eigenspace) $V_{\lambda}(\phi)$ της $\phi$ , $V_{\lambda}(\phi)$ , είναι το σύνολο

V_{\lambda}(\phi):=\{v\in\Bbbk^{n}:\ \phi(v)=\lambda v\}\;.

Ο $V_{\lambda}(\phi)$ είναι, λοιπόν, το σύνολο όλων των ιδιοδιανυσμάτων της $\phi$ για την ιδιοτιμή $\lambda$ , μαζί με το ${\bf 0}$ . Αντίστοιχα, αν $A$ είναι ένας $n\times n$ πίνακας,

V_{\lambda}(A):=\{b\in\mathcal{M}_{n\times 1}(\Bbbk):\ Ab=\lambda b\}\;.

$V_{\lambda}(A)$ Αφού σε κάθε $n\times n$ πίνακα αντιστοιχεί μία γραμμική συνάρτηση $\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}$ και αντίστροφα, είναι φανερό ότι ιδιότητες του $V_{\lambda}(\phi)$ μεταφράζονται σε ιδιότητες του $V_{\lambda}(A)$ και τανάπαλιν. Παρατηρούμε ότι o $V_{\lambda}(\phi)$ είναι διανυσματικός χώρος. Πράγματι:

•

αν $v_{1},v_{2}\in V_{\lambda}(\phi)$ , τότε $\phi(v_{1}+v_{2})=\phi(v_{1})+\phi(v_{2})=\lambda v_{1}+\lambda v_{2}=\lambda(% v_{1}+v_{2})$ και επομένως $v_{1}+v_{2}\in V_{\lambda}(\phi)$ .
•

Επίσης, αν $v\in V_{\lambda}(\phi)$ και $\kappa\in\Bbbk$ , τότε $\phi(\kappa v)=\kappa\phi(v)=\kappa(\lambda v)=(\kappa\lambda)v=\lambda(\kappa v% )=\lambda\phi(v)$ και επομένως $\kappa v\in V_{\lambda}(\phi)$ .

Τέλος, μία ενδιαφέρουσα ιδιότητα των χώρων $V_{\lambda}(\phi)$ , είναι ότι παραμένουν αναλλοίωτοι (invariant) από τη δράση της $\phi$ , δηλ.

\phi\left(V_{\lambda}(\phi)\right)\subset V_{\lambda}(\phi).

Παραδείγματα 5.1.6.

1.

Δίνεται η γραμμική συνάρτηση

$\phi:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(x,y)\mapsto(2x+y,4% x+2y).$
Έστω $Β=(e_{1},e_{2})$ η κανονική βάση του ${\mathbb{R}}^{2}$ . Τότε

$A_{B,B}^{\phi}=\begin{bmatrix}2&1\cr 4&2\end{bmatrix}$
Παρατηρούμε ότι

$\phi(1,-2)=(0,0)=0(1,-2)\ ,$
δηλ. το $0$ είναι ιδιοτιμή και $v_{1}=(1,-2)$ είναι ιδιοδιάνυσμα της $\phi$ για την ιδιοτιμή $0$ όπως βέβαια και κάθε άλλο (μη μηδενικό) στοιχείο του $\operatorname{Ker}\phi$ . Επίσης,

$\phi(1,2)=(4,8)=4(1,2)\ ,$
δηλ. το $4$ είναι ιδιοτιμή του $\phi$ και $v_{2}=(1,2)$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $4$ . Τα $v_{1},v_{2}$ είναι γραμμικά ανεξάρτητα και παράγουν τον ${\mathbb{R}}^{2}$ . Άρα $D=(v_{1},v_{2})$ είναι βάση του ${\mathbb{R}}^{2}$ . Επομένως

$Α_{D,D}^{\phi}=\begin{bmatrix}0&0\cr 0&4\end{bmatrix}\ ,$
και

$Α_{D,D}^{\phi}=S^{-1}\;A_{B,B}^{\phi}\;S\textrm{ 'opou }S=S_{B\leftarrow D}=% \begin{bmatrix}\ \;1&1\cr-2&2\end{bmatrix}\ .$
O αναγνώστης καλείται να αποδείξει ότι $V_{0}(\phi)=S(\{(v_{1}\})$ και ότι $V_{4}(\phi)=S(\{v_{2}\})$ .
2.

Δίνεται η γραμμική συνάρτηση

$\phi:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(x,y)\mapsto(2x,3y).$
Έστω $Β=(e_{1},e_{2})$ η κανονική βάση του ${\mathbb{R}}^{2}$ . Παρατηρούμε ότι

$A=A_{B,B}^{\phi}=\begin{bmatrix}2&0\cr 0&3\end{bmatrix}\;$
είναι διαγώνιος πίνακας.: $\phi(e_{1})=2e_{1}$ και $\phi(e_{2})=3e_{2}$ . Επομένως, $e_{1}$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $2$ , ενώ το $e_{2}$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $3$ . O αναγνώστης καλείται να αποδείξει ότι

$V_{2}(\phi)=S(\{e_{1}\})\textrm{ kai }V_{3}(\phi)=S(\{e_{2}\})\ .$
3.

Έστω $\phi:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ , $\phi(x,y,z)=(3x,3y,z)$ και $Β=(e_{1},e_{2},e_{3})$ η κανονική βάση του ${\mathbb{R}}^{3}$ . Παρατηρούμε ότι

$A_{B,B}^{\phi}=\begin{bmatrix}3&0&0\cr 0&3&0\cr 0&0&1\end{bmatrix}\ .$
O $A_{B,B}^{\phi}$ είναι διαγώνιος και τα $e_{1}$ , $e_{2}$ είναι ιδιοδιανύσματα για την ιδιοτιμή $3$ , ενώ το $e_{3}$ είναι ιδιοδιάνυσμα για την ιδιοτιμή 1. O αναγνώστης καλείται να αποδείξει ότι

$V_{3}(\phi)=S(\{e_{1},e_{2}\}),\ V_{1}(\phi)=S(\{e_{3}\})\ .$
4.

Θα γενικεύσουμε τις παρατηρήσεις μας για τους διαγώνιους πίνακες και τις ιδιοτιμές τους. Έστω ότι $f:\ \Bbbk^{n}\rightarrow\Bbbk^{n}$ είναι γραμμική συνάρτηση με την ιδιότητα ότι υπάρχει $D=(v_{1},\ldots,v_{n})$ διατεταγμένη βάση του $\Bbbk^{n}$ έτσι ώστε το $v_{i}$ να είναι ιδιοδιάνυσμα της $f$ , για $i=1,\ldots,n$ . Έστω ότι $\lambda_{i}$ είναι η ιδιοτιμή της $f$ που αντιστοιχεί στο $v_{i}$ , για $i=1,\ldots,n$ . Αφού $f(v_{i})=\lambda_{i}v_{i}$ , o πίνακας των συντεταγμένων του $f(v_{i})$ ως προς τη βάση $D$ έχει την εξής μορφή:

$\begin{array}[]{lc}C_{D}(f(v_{i}))=&\begin{bmatrix}0&\cdots&{\ \ \lambda_{i}}&% \cdots&0\end{bmatrix}^{T}\cr&\begin{array}[]{c}\uparrow\\ {\text{$i$-j'esh}}\end{array}\end{array}$
και επομένως o $Α^{f}_{D,D}$ είναι διαγώνιος πίνακας,

$A^{f}_{D,D}=\begin{bmatrix}\lambda_{1}&&{0}\\ &\ddots&\\ {0}&&\lambda_{n}\end{bmatrix}\ .$

Αντίστροφα, αν $D=(v_{1},\ldots,v_{n})$ είναι βάση του $\Bbbk^{n}$ , $f:\ \Bbbk^{n}\rightarrow\Bbbk^{n}$ και

$A^{f}_{D,D}=\begin{bmatrix}\lambda_{1}&&{O}\\ &\ddots&\\ {O}&&\lambda_{n}\end{bmatrix}\;,$
τότε $f(v_{i})=\lambda_{i}v_{i}$ , για $i=1,\ldots,n$ . Επομένως το $v_{i}$ είναι ιδιοδιάνυσμα της $f$ για την ιδιοτιμή $\lambda_{i}$ , για $i=1,\ldots,n$ .
5.

Έστω $\phi:V\rightarrow V$ μία γραμμική συνάρτηση του $V$ και έστω ότι το $0$ είναι ιδιοτιμή του $\phi$ . Υπάρχει λοιπόν ${\bf 0}\neq v\in V$ έτσι ώστε $\phi(v)=0\;v={\bf 0}$ . Επομένως $v\in\operatorname{Ker}\phi$ και $\operatorname{Ker}\phi\neq\{{\bf 0}\}$ . Αντίστροφα, αν $v\in\operatorname{Ker}\phi$ και $v\neq{\bf 0}$ , τότε $\phi(v)={\bf 0}$ και το $v$ είναι ιδιοδιάνυσμα που αντιστοιχεί στην ιδιοτιμή $0$ . Καταλήγουμε έτσι στο εξής συμπέρασμα:

Το $0$ είναι ιδιοτιμή της γραμμικής συνάρτησης $\phi:V\rightarrow V$ αν και μόνο αν η $\phi$ δεν είναι ένα προς ένα. Ισοδύναμα, το $0$ είναι ιδιοτιμή του τετραγωνικού πίνακα $Α$ αν και μόνο αν $\det A=0$ .
6.

Έστω ότι $\phi:V\rightarrow V$ είναι ισομορφισμός. Αν το $\lambda$ είναι ιδιοτιμή της $\phi$ και $v$ είναι ιδιοδιάνυσμα της $\phi$ για το $\lambda$ , τότε (όπως θα δούμε) το $\lambda^{-1}$ είναι ιδιοτιμή της $\phi^{-1}$ και το $v$ είναι ιδιοδιάνυσμα της $\phi^{-1}$ για το $\lambda^{-1}$ . Πράγματι, έστω ότι το $v$ είναι ιδιοδιάνυσμα της $\phi$ που αντιστοιχεί στην ιδιοτιμή $\lambda$ . Αφού η γραμμική συνάρτηση $\phi:V\rightarrow V$ είναι ισομορφισμός, έπεται ότι $\lambda\neq 0$ . Επομένως

$\phi^{-1}(v)=\phi^{-1}((\lambda^{-1}\lambda)v)=\lambda^{-1}\phi^{-1}(\phi(v))=% \lambda^{-1}\operatorname{id}_{V}(v)=\lambda^{-1}v.$
Δείξαμε λοιπόν ότι:

Αν $\phi:V\rightarrow V$ είναι ισομορφισμός και το $\lambda$ είναι ιδιοτιμή της $\phi$ με ιδιοδιάνυσμα $v$ , τότε το $\lambda^{-1}$ είναι ιδιοτιμή του $\phi^{-1}:V\rightarrow V$ με ιδιοδιάνυσμα το $v$ .
7.

Δίνεται η γραμμική συνάρτηση $\phi:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ , με $\phi(x,y)=(y,-2x+3y)$ . O πίνακας $A$ της $\phi$ ως προς την κανονική βάση $B$ του ${\mathbb{R}}^{2}$ είναι

$A=\begin{bmatrix}0&-2\cr 1&3\end{bmatrix}\;.$
O αναγνώστης καλείται να επιβεβαιώσει ότι το $2$ είναι ιδιοτιμή του $A$ και της $\phi$ και ότι κάθε μη μηδενικό διάνυσμα επί της ευθείας $\{t(1,-1):t\in{\mathbb{R}}\}$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $2$ . H $\phi^{-1}:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ , δίνεται από τον τύπο $\;\phi^{-1}(x,y)=\displaystyle\frac{1}{2}(3x-y,2x)$ . O αναγνώστης καλείται να επιβεβαιώσει ότι το $\displaystyle\frac{1}{2}$ είναι ιδιοτιμή της $\phi^{-1}$ .
8.

Έστω o $2\times 2$ μιγαδικός πίνακας

$A=\begin{bmatrix}i&1\cr 0&1+i\end{bmatrix}\ .$
To $e_{1}$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $i$ και το $(1,1)$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $1+ι$ .
9.

Έστω o $2\times 2$ μιγαδικός πίνακας

$A=\begin{bmatrix}0&i\cr-i&1\end{bmatrix}\ .$
O αναγνώστης καλείται να επιβεβαιώσει ότι $\pm 1$ είναι ιδιοτιμές του $A$ .
10.

Έστω $A\in\mathcal{M}_{n}({\mathbb{C}})$ και $\lambda$ ιδιοτιμή του $A$ . Τότε το $\overline{\lambda}$ είναι ιδιοτιμή του $\overline{A}$ . Πράγματι, έστω ότι $b$ είναι ιδιοδιάνυσμα του $A$ για την ιδιοτιμή $\lambda$ . Τότε $Α\;b=\lambda b$ και συνεπώς

$\overline{Α\;b}={\overline{\lambda b}}\Rightarrow\overline{Α}\;\overline{b}=% \overline{\lambda}\;\overline{b},$
δηλ. το $\overline{b}$ είναι ιδιοδιάνυσμα του $\overline{A}$ για την ιδιοτιμή $\overline{\lambda}$ .
11.

Έστω $A\in\mathcal{M}_{n}({\mathbb{C}})$ ένας πίνακας, τέτοιος ώστε $A=\overline{A}^{T}$ . O $A$ λέγεται αυτοπροσαρτημένος (self-adjoint). Θα αποδείξουμε ότι οι ιδιοτιμές του $A$ είναι πραγματικοί αριθμοί.

Απόδειξη.

Έστω ότι το $b$ είναι ιδιοδιάνυσμα του $Α$ για την ιδιοτιμή $\lambda\in{\mathbb{C}}$ . Για να δείξουμε ότι το $\lambda$ είναι πραγματικός αριθμός, θα αποδείξουμε ότι $\lambda=\overline{\lambda}$ . Υπολογίζουμε το γινόμενο ${(Ab)^{T}\;\overline{b}}$ :

${(Ab)^{T}\overline{b}}=(\lambda b)^{Τ}\overline{b}=\lambda(b^{T}\overline{b})\;.$ (5.1.6.1)
Από το προηγούμενο παράδειγμα γνωρίζουμε ότι $\overline{\lambda}$ είναι ιδιοτιμή του $\overline{A}$ και ότι $\overline{b}$ είναι ιδιοδιάνυσμα για το $\overline{\lambda}$ . Από την υπόθεση, $\overline{A}^{T}=A$ . Συνεπώς $\overline{A}=A^{T}$ . Θα υπολογίσουμε τώρα το γινόμενο ${(Ab)^{T}\;\overline{b}}$ , χρησιμοποιώντας αυτές τις παρατηρήσεις.

$(Ab)^{T}\overline{b}=(b^{T}A^{T})\overline{b}=b^{T}(\overline{A}\;\overline{b}% )=b^{T}(\overline{\lambda}\ \overline{b})=\overline{\lambda}(b^{T}\overline{b}% )\ .$ (5.1.6.2)
Από τις Εκφράσεις (5.1.6.1) και (5.1.6.2) προκύπτει ότι

$\lambda(b^{T}\overline{b})=\overline{\lambda}(b^{T}\overline{b})\Rightarrow(% \lambda-\overline{\lambda})(b^{T}\overline{b})={\bf 0}.$
Όμως, $b^{T}\overline{b}\neq 0$ (βλ. Παράδειγμα 2.1.10.2) και άρα $\lambda=\overline{\lambda}$ . Αυτό σημαίνει ότι $\lambda\in{\mathbb{R}}$ και το ζητούμενο αποδείχθηκε.

∎

Αποδείξαμε λοιπόν ότι:

Αν $A\in\mathcal{M}_{n}({\mathbb{C}})$ είναι αυτοπροσαρτημένος πίνακας τότε οι ιδιοτιμές του $A$ είναι πραγματικοί αριθμοί. Αν $A\in\mathcal{M}_{n}({\mathbb{R}})$ είναι συμμετρικός πίνακας, τότε οι ιδιοτιμές του $A$ είναι πραγματικοί αριθμοί.
12.

O συμμετρικός πίνακας

$A=\begin{bmatrix}i&0\cr 0&2i\end{bmatrix}$
δεν είναι αυτοπροσαρτημένος, (προσοχή: $A=A^{T}$ , όμως $A\notin\mathcal{M}_{n}({\mathbb{R}})$ ). Οι ιδιοτιμές του $A$ είναι οι μιγαδικοί αριθμοί $i,2i$ .

στη συνέχεια γενικεύουμε το συμπέρασμα του Παραδείγματος 5.1.5. 5.

Πρόταση 5.1.7.

Έστω $A\in\mathcal{M}_{n}(\Bbbk)$ . Το $\lambda$ είναι ιδιοτιμή του $Α$ αν και μόνο αν $\det(A-\lambda I_{n})=0$ . Αντίστοιχα, αν $\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}$ είναι μία γραμμική συνάρτηση και $A$ είναι o πίνακας της $\phi$ ως προς οποιαδήποτε διατεταγμένη βάση του $\Bbbk^{n}$ , τότε το $\lambda$ είναι ιδιοτιμή της $\phi$ αν και μόνο αν $\det(A-\lambda I_{n})=0$ . Αν το $\lambda$ είναι ιδιοτιμή του $Α$ , τότε τα ιδιοδιανύσματα του $Α$ για την ιδιοτιμή $\lambda$ , είναι οι μη μηδενικές λύσεις του $A-\lambda I_{n}=0$ .

Απόδειξη.

Έστω ότι $b$ είναι ιδιοδιάνυσμα για τον $Α$ που αντιστοιχεί στην ιδιοτιμή $\lambda$ . Τονίζουμε ότι $b\neq{\bf 0}$ . Ισχύει ότι

Αb=\lambda b\Leftrightarrow Αb-\lambda b={\bf 0}\Leftrightarrow Αb-\lambda I_{% n}={\bf 0}\Leftrightarrow(A-\lambda I_{n})b={\bf 0}.

Συνεπώς το ομογενές σύστημα $(A-\lambda I_{n})X={\bf 0}$ έχει τη μη μηδενική λύση, $b$ . Αυτό μπορεί να γίνει μόνο όταν $A-\lambda I_{n}$ δεν είναι αντιστρέψιμος και $\det(A-\lambda I_{n})={0}$ . Για την αντίστροφη κατεύθυνση, παρατηρούμε ότι όλες οι συνεπαγωγές στον συλλογισμό μας αντιστρέφονται. ∎

Παραδείγματα 5.1.8.

1.

O πίνακας

$A=\begin{bmatrix}1&-1\cr 1&\ \;1\end{bmatrix}\in\mathcal{M}_{2}({\mathbb{R}})$
δεν έχει ιδιοτιμές και ιδιοδιανύσματα στον ${\mathbb{R}}$ . Πράγματι,

$\det(A-\lambda I_{2})=\det\left(\begin{bmatrix}1-\lambda&-1\cr 1&\ 1-\lambda% \end{bmatrix}\right)=(1-\lambda)^{2}+1=\lambda^{2}-2\lambda+2$
δεν έχει ρίζες στον ${\mathbb{R}}$ , αφού η διακρίνουσα του $\lambda^{2}-2\lambda+2$ είναι αρνητικός αριθμός. To πολυώνυμο $\lambda^{2}-2\lambda+2$ έχει όμως δύο μιγαδικές ρίζες, τις $1\pm i$ . Επομένως, $A\in\mathcal{M}_{2\times 2}({\mathbb{C}})$ έχει δύο ιδιοτιμές στον ${\mathbb{C}}$ . O αναγνώστης καλείται να διαπιστώσει ότι $(i,1)\in{\mathbb{C}}^{2}$ είναι ιδιοδιάνυσμα του $A$ για την ιδιοτιμή $1+i$ , ενώ $(-i,1)\in{\mathbb{C}}^{2}$ είναι ιδιοδιάνυσμα του $A$ για την ιδιοτιμή $1-i$ .
2.

Έστω ότι $A, B$ είναι δύο όμοιοι $n\times n$ πίνακες και ότι $B=P^{-1}AP$ για κάποιον αντιστρέψιμο πίνακα $P$ . Αν $b$ είναι ιδιοδιάνυσμα του $A$ για την ιδιοτιμή $\lambda$ , τότε $P^{-1}b$ είναι ιδιοδιάνυσμα του $B$ για την ιδιοτιμή $\lambda$ .

Απόδειξη.

Αφού $b$ είναι ιδιοδιάνυσμα του $A$ για την ιδιοτιμή $\lambda$ , $Ab=\lambda b$ . Επομένως:

$\displaystyle B(P^{-1}b)=(P^{-1}AP)(P^{-1}b)=(P^{-1}A)(P\;P^{-1}b)=(P^{-1}A)(I% _{n}\;b)\\ \displaystyle=P^{-1}(A\;b)=P^{-1}(\lambda b)=\lambda(P^{-1}b)\;.$
∎

Σημειώνουμε το συμπέρασμα που προκύπτει από τα προηγούμενα.

Όμοιοι πίνακες έχουν τις ίδιες ιδιοτιμές.

Παρατηρούμε ότι σύμφωνα με την Πρόταση 5.1.7,

V_{\lambda}(\phi)={\rm null}(Α-\lambda I_{n})\

και μάλιστα, αφού o $V_{\lambda}(\phi)$ περιέχει ένα τουλάχιστον μη μηδενικό ιδιοδιάνυσμα, ισχύει ότι

{\rm dim}_{\Bbbk}V_{\lambda}(\phi)\geq 1\;.

Ασκήσεις Ενότητας 5.1

1.

Έστω η γραμμική συνάρτηση $\phi:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ που περιστρέφει τα διανύσματα αριστερόστροφα κατά γωνία $\pi$ . Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της $\phi$ .

Λύση
2.

Έστω η γραμμική συνάρτηση $\phi:\ {\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ που αντικατοπτρίζει τα διανύσματα ως προς το επίπεδο $y=0$ . Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της $\phi$ .

Λύση
3.

Να υπολογισθούν οι ιδιοτιμές και τα ιδιοδιανύσματα των εξής γραμμικών συναρτήσεων
1. (a)
  
  $\phi:{\mathbb{C}}^{2}\rightarrow{\mathbb{C}}^{2}$ , $\;\;(x,y)\mapsto(x+4y,2x+3y)$ .
2. (b)
  
  $\psi:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ , $\;\;(a,b,c)\mapsto(b,c,a)$ .
3. (c)
  
  $f:R^{3}\rightarrow R^{3}$ , $\;\;(x,y,z)\mapsto(2x+y,y-z,2y+4z)$ .
Λύση
4.
Να υπολογισθούν οι ιδιοτιμές και τα ιδιοδιανύσματα των εξής πινάκων:
1. (a)
  
  $\begin{bmatrix}1&2\\ 3&2\end{bmatrix}$ ,
2. (b)
  
  $\begin{bmatrix}-2&2\\ -2&3\end{bmatrix}$ ,
3. (c)
  
  $\begin{bmatrix}1&i\\ -i&1\end{bmatrix}$ .
Λύση
5.

Έστω $Α$ ένας $n\times n$ πίνακας, $\lambda$ μία ιδιοτιμή του $Α$ και $X$ είναι ένα ιδιοδιάνυσμα του $Α$ που αντιστοιχεί στην ιδιοτιμή $\lambda$ . Να αποδείξετε ότι το $\lambda+k$ είναι μία ιδιοτιμή του $Α+kI_{n}$ και ότι $X$ είναι ιδιοδιάνυσμα του $Α+kI_{n}$ . Επίσης να αποδείξετε ότι το $\lambda^{m}$ είναι μία ιδιοτιμή του $A^{m}$ και ότι $X$ είναι ιδιοδιάνυσμα του $A^{m}$ που αντιστοιχεί στο $\lambda^{m}$ .

Λύση
6.

Έστω $A$ ένας $n\times n$ πίνακας και $\lambda$ είναι μία ιδιοτιμή του 3 $Α$ . Να αποδείξετε ότι το $\lambda^{2}-\lambda+2$ είναι μία ιδιοτιμή του πίνακα $3Α^{2}-Α+2Ι_{n}$ .

Λύση

5.2 Ιδιοχώροι και το Χαρακτηριστικό Πολυώνυμο

Έστω $\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}$ μία γραμμική συνάρτηση. Για να βρούμε τις ιδιοτιμές της $\phi$ , βασιζόμαστε στις Προτάσεις 5.1.4 και 5.1.7 και προχωράμε ως εξής:

•

βρίσκουμε τον πίνακα $A$ της $\phi$ , ως προς την κανονική (ή οποιαδήποτε άλλη διατεταγμένη βάση) του $\Bbbk^{n}$ ,
•

υπολογίζουμε την ορίζουσα του πίνακα $A-xI_{n}$ ,
•

βρίσκουμε τις τιμές των $\lambda$ που μηδενίζουν την ορίζουσα $\det(A-xI_{n})$ .

Για να βρούμε τα ιδιοδιανύσματα της $\phi$ όταν γνωρίζουμε τις ιδιοτιμές, μπορούμε να λύσουμε τα συστήματα $AX=\lambda X$ για κάθε ιδιοτιμή του $A$ . Υπάρχει μήπως κάποιος αποτελεσματικότερος τρόπος; Για να απαντήσουμε σε αυτό το ερώτημα, θα ορίσουμε το χαρακτηριστικό πολυώνυμο του $A$ . Σημειώνουμε ότι o πίνακας $A-xI_{n}$ είναι o $n\times n$ πίνακας

A-xI_{n}=\begin{bmatrix}\alpha_{11}-x&\alpha_{12}&\cdots&\alpha_{1n}\cr\alpha_% {21}&\alpha_{22}-x&\cdots&\alpha_{2n}\cr\vdots&\vdots&&\vdots\cr\alpha_{n1}&% \alpha_{n2}&\cdots&\alpha_{nn}-x\end{bmatrix}\;.

Επομένως $\det(A-xI_{n})$ είναι ένα πολυώνυμο στον $\Bbbk[x]$ , βαθμού $n$ . Το πολυώνυμο αυτό συμβολίζεται με $P_{A}(x)$ , δηλ.

P_{A}(x):=\det(A-xI_{n}),

(5.2.0.1)

και λέγεται χαρακτηριστικό πολυώνυμο (characteristic polynomial) του $A$ . Γράφουμε $P_{\phi}(x)$ για το $P_{A}(x)$ όταν θέλουμε να δώσουμε την έμφαση στην $\phi$ . Οι ιδιοτιμές του $Α$ μηδενίζουν το $P_{A}(x)$ και είναι οι ρίζες του $P_{A}(x)$ . $P_{A}(x)$ Παρατηρούμε ότι το $P_{A}(x)$ έχει την εξής μορφή:

P_{A}(x)=(-1)^{n}x^{n}+\alpha_{n-1}x^{n-1}+\cdots+\alpha_{1}x+\alpha_{0}\;.

O σταθερός όρος του $P_{A}(x)$ , $a_{0}$ , είναι ίσος με την ορίζουσα του $A$ . Πράγματι,

P_{A}(0)=\alpha_{0}=\det(A-0I_{n})=\det A\;.

Ενδιαφέρον επίσης έχει o συντελεστής $a_{n-1}$ του $P_{A}(x)$ . Από τον υπολογισμό της ορίζουσας του $A-xI_{n}$ προκύπτει ότι o $a_{n-1}$ είναι με προσέγγιση προσήμου το ίχνος του $A$ :ίχνος

\alpha_{n-1}=(-1)^{n-1}(\alpha_{11}+\cdots+\alpha_{nn})=(-1)^{n-1}\;% \operatorname{Tr}(A)\ .

Παραδείγματα 5.2.1.

1.

Έστω

$A=\begin{bmatrix}1&2\cr 0&i\end{bmatrix}\ .$
Τότε

$Α-xI_{2}=\begin{bmatrix}1-x&2\cr 0&i-x\end{bmatrix}\Rightarrow P_{A}(x)=(1-x)(% i-x)=x^{2}-(1+i)x+i\;.$
Οι ιδιοτιμές του $A$ είναι οι $1$ και $i$ . Έστω $\phi:{\mathbb{C}}^{2}\rightarrow{\mathbb{C}}^{2}$ , $\phi(a,b)=(a,2a+ib)$ . Αν $B$ είναι η κανονική βάση του ${\mathbb{C}}^{2}$ , τότε $A=A^{\phi}_{B,B}$ . Επομένως

$P_{\phi}(x)=x^{2}-(1+i)x+i\;.$
2.

Έστω

$A=\begin{bmatrix}1&0&2\cr 0&2&3\cr 0&2&3\end{bmatrix}\ .$
Τότε

$Α-xI_{3}=\begin{bmatrix}1-x&0&2\cr 0&2-x&3\cr 0&2&3-x\end{bmatrix}$
και $\det(A-xI_{3})=$

$(1-x)\big((2-x)(3-x)-6\big)=-x(x-1)(x-5)=-x^{3}+6x^{2}-6x\ .$
3.

Έστω $Α\in\mathcal{M}_{n}(\Bbbk)$ . Τότε

$\det(A-xI_{n})=\det(A-xI_{n})^{T}=\det(A^{T}-xI_{n})\;.$
Δείξαμε λοιπόν ότι

Οι πίνακες $A$ και $A^{T}$ έχουν το ίδιο χαρακτηριστικό πολυώνυμο.
4.

Είδαμε ότι ο σταθερός όρος του πολυωνύμου $P_{A}(x)$ είναι ίσος με την ορίζουσα του $Α$ . Σύμφωνα με την Πρόταση 5.1.7, το $0$ είναι ιδιοτιμή του $Α$ αν και μόνο αν $\det A=0$ . Επομένως

O πίνακας $A$ είναι αντιστρέψιμος αν και μόνο αν ο σταθερός όρος του $P_{A}(x)$ είναι διάφορος του μηδενός.

Πόσες ιδιοτιμές έχει μία γραμμική συνάρτηση $\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}$ ; Αντίστοιχα πόσες ιδιοτιμές έχει ένας $n\times n$ πίνακας $A$ ; Σύμφωνα με τα όσα έχουμε εξετάσει προηγουμένως o αριθμός των ιδιοτιμών του $\phi$ και αντίστοιχα του $A$ είναι ακριβώς o o αριθμός των ριζών του $P_{\phi}(x)$ και αντίστοιχα του $P_{A}(x)$ ). Πόσες λοιπόν ρίζες έχει ένα πολυώνυμο βαθμού $n$ ; H απάντηση εξαρτάται από το σώμα επάνω από το οποίο δουλεύουμε και δίνεται από την επόμενη πρόταση.

Πρόταση 5.2.2.

Αν $\phi:{\mathbb{C}}^{n}\rightarrow{\mathbb{C}}^{n}$ είναι μία γραμμική συνάρτηση, τότε η $\phi$ έχει ακριβώς $n$ μιγαδικές ιδιοτιμές. Αν $\phi:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι μία γραμμική συνάρτηση, τότε η $\phi$ έχει το πολύ $n$ πραγματικές ιδιοτιμές. Αντίστοιχα αν $Α\in\mathcal{M}_{n}({\mathbb{C}})$ τότε ο $Α$ έχει ακριβώς $n$ μιγαδικές ιδιοτιμές. Αν $Α\in\mathcal{M}_{n}({\mathbb{R}})$ τότε ο $Α$ έχει το πολύ $n$ πραγματικές ιδιοτιμές.

Απόδειξη.

Για την απόδειξη, πρέπει να αναφερθούμε στο Θεμελιώδες Θεώρημα της Άλγεβρας. Σύμφωνα με το θεώρημα αυτό, Θεμελιώδες Θεώρημα της Άλγεβρας ένα πολυώνυμο $p(x)\in{\mathbb{C}}[x]$ βαθμού $n$ με συντελεστές από το ${\mathbb{C}}$ έχει ακριβώς $n$ ρίζες στο ${\mathbb{C}}$ , μετρημένες σύμφωνα με την πολλαπλότητά τους. Βεβαίως, αν $p(x)\in{\mathbb{R}}[x]$ , τότε $p(x)\in{\mathbb{C}}[x]$ . Επομένως το $p(x)$ έχει ακριβώς $\deg p(x)$ μιγαδικές ρίζες και κάποιες από αυτές μπορεί να είναι πραγματικοί αριθμοί, ίσως όμως όχι όλες. Συνεπώς αν $p(x)\in{\mathbb{R}}[x]$ , τότε $p(x)$ έχει το πολύ $\deg p(x)$ πραγματικές ρίζες. Αφού $P_{A}(x)$ έχει βαθμό $n$ , το συμπέρασμα της πρότασης και για τις δύο περιπτώσεις προκύπτει από τις προηγούμενες παρατηρήσεις. ∎

Στα επόμενα παραδείγματα θα κάνουμε χρήση αυτής της πληροφορίας.

Παραδείγματα 5.2.3.

1.

Έστω ότι $Α\in\mathcal{M}_{n}({\mathbb{C}})$ και ότι οι ιδιοτιμές του $A$ είναι οι $\lambda_{1},\ldots,\lambda_{n}\in{\mathbb{C}}$ . Αφού λοιπόν o αρχικός συντελεστής του $P_{A}(x)$ είναι το $(-1)^{n}$ , έπεται ότι

$P_{A}(x)=(-1)^{n}(x-\lambda_{1})\cdots(x-\lambda_{n}).$
Αναπτύσσοντας αυτό το γινόμενο, προκύπτει ότι o συντελεστής του όρου $x^{n-1}$ είναι ίσος με το

$(-1)^{n-1}(\lambda_{1}+\cdots+\lambda_{n}),$
ενώ o σταθερός όρος του $P_{A}(x)$ , o $P_{A}(0)$ , είναι ίσος με το γινόμενο

$(-1)^{n}(0-\lambda_{1})\cdots(0-\lambda_{n})=(-1)^{n}(-1)^{n}(\lambda_{1}% \cdots\lambda_{n})=\lambda_{1}\cdots\lambda_{n}.$
Προηγουμένως είδαμε ότι o συντελεστής του όρου $x^{n-1}$ είναι $(-1)^{n-1}\operatorname{Tr}(A)$ και ότι o σταθερός όρος του $P_{A}(x)$ είναι ίσος με την ορίζουσα του $A$ . Επομένως αποδείξαμε την επόμενη σχέση μεταξύ της ορίζουσας του $A$ και της ιδιοτιμής του $A$ .

Αν $Α\in\mathcal{M}_{n}({\mathbb{C}})$ και οι ιδιοτιμές του $A$ είναι οι $\lambda_{1},\ldots,\lambda_{n}$ , τότε

$\operatorname{Tr}(A)=\lambda_{1}+\cdots+\lambda_{n}$ και $\det A=\lambda_{1}\cdots\lambda_{n}$ .
2.

Δίνεται ο πίνακας

$A=\begin{bmatrix}3-a&3b&c\\ c&a&i\\ i&c+i&-1\end{bmatrix}\$
μαζί με την πληροφορία ότι $\det A=2$ και ότι μία ιδιοτιμή του $A$ είναι ίση με $2$ . Από την Πρόταση 5.2.2 γνωρίζουμε ότι o $A$ έχει τρεις συνολικά μιγαδικές ιδιοτιμές. Θα υπολογίσουμε τις άλλες δύο.

Έστω ότι $\lambda_{1},\lambda_{2}$ είναι οι άλλες δύο ιδιοτιμές του $Α$ . Τότε

$2=\det A=2\lambda_{1}\lambda_{2},\;\;2=\operatorname{Tr}A=2+\lambda_{1}+% \lambda_{2}\ .$
Επομένως

$\lambda_{1}=-\lambda_{2},\hbox{ kai }\lambda_{1}^{2}=-1$
και οι άλλες δύο ιδιοτιμές του $Α$ είναι $\pm i$ .

Όπως έχουμε δει, όμοιοι πίνακες έχουν τις ίδιες ιδιοτιμές, βλ. Παράδειγμα 5.1.8.2. Ισχύει όμως κάτι πιο ισχυρό, όπως δείχνει η επόμενη πρόταση.

Πρόταση 5.2.4.

Όμοιοι πίνακες έχουν το ίδιο χαρακτηριστικό πολυώνυμο.

Απόδειξη.

Έστω ότι $A,B\in\mathcal{M}_{n}(\Bbbk)$ είναι δύο όμοιοι πίνακες. Θα αποδείξουμε ότι $\det(A-xI_{n})=\det(B-xI_{n})$ . Αφού $A, B$ είναι όμοιοι, υπάρχει αντιστρέψιμος πίνακας $S$ τέτοιος ώστε

B=S^{-1}A\;S\ .

Θα δείξουμε ότι $\det(Β-xI_{n})=\det(A-xI_{n})$ . Πράγματι

\det(Β-xI_{n})=\det(S^{-1}A\;S-xS^{-1}S)=\det(S^{-1}A\;S-S^{-1}xI_{n}S)=

=\det(S^{-1}(A-xI_{n})S)=\det(S^{-1}|\det(A-xI_{n})\det(S)=\det(A-xI_{n})\;.

Αποδείξαμε λοιπόν ότι οι όμοιοι πίνακες $A$ και $B$ έχουν το ίδιο χαρακτηριστικό πολυώνυμο. ∎

Έστω $\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}$ μία γραμμική συνάρτηση. Οι πίνακες της $\phi$ ως προς διαφορετικές βάσεις του $\Bbbk^{n}$ είναι όμοιοι, (Πόρισμα 4.3.4). Σύμφωνα με την προηγούμενη πρόταση, μπορούμε να επιλέξουμε οποιαδήποτε βάση του $\Bbbk^{n}$ και θα βρούμε ακριβώς το ίδιο πολυώνυμο $P_{\phi}(x)$ . O επόμενος αλγόριθμος συγκεντρώνει τα βήματα για τον υπολογισμό των ιδιοτιμών και των ιδιοδιανυσμάτων της $\phi$ .

Αλγόριθμος 5.2.1 Αλγόριθμος υπολογισμού ιδιοχώρων της γραμμικής συνάρτησης

\bf\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}

Είσοδος: Μια γραμμική συνάρτηση

\bf\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}

Έξοδος: Μια βάση για τους ιδιοχώρους της

\bf\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}

Βήμα 1 Έστω

A = [\begin{matrix} ϕ (e_{1}) & \dots & ϕ (e_{n}) \end{matrix}]

Βήμα 2 Βρίσκουμε το πολυώνυμο

P_{A} (x) = P_{ϕ} (x)

υπολογίζοντας την ορίζουσα

d e t (A - x I_{n})

Βήμα 3 Βρίσκουμε τις ιδιοτιμές του

Α

στον k, λύνοντας την εξίσωση

P_{A} (x) = 0

Βήμα 4 Για κάθε

λ

που είναι ιδιοτιμή του

A

, βρίσκουμε μια βάση για το μηδενοχώρο του

A - λ I_{n}

V_{λ} (ϕ) = n u l l (A - λ I_{n})

Στα παραδείγματα που ακολουθούν θα δούμε τον αλγόριθμο στη πράξη.

Παραδείγματα 5.2.5.

1.

Έστω $\phi:\ {\mathbb{C}}^{2}\rightarrow{\mathbb{C}}^{2}$ , $\phi(a,b)=(a+2b,ib)$ . Υπολογίζουμε τις εικόνες $\phi(e_{1})$ και $\phi(e_{2})$ . Αφού $\phi(e_{1})=(1,i)$ και $\phi(e_{2})=(2,i)$ , αν $B$ είναι η κανονική βάση του ${\mathbb{C}}^{2}$ και $Α=Α^{\phi}_{B,B}$ , τότε

$A=\begin{bmatrix}1&2\cr 0&i\end{bmatrix}\ .$
Όπως είδαμε στο Παράδειγμα 5.2.1.1,

$P_{A}(x)=(1-x)(i-x)$
και $A$ έχει τις ιδιοτιμές $1$ και $i$ . Έτσι

$V_{1}(A)=\operatorname{null}(A-I_{2})=\operatorname{null}\begin{bmatrix}0&2\cr 0% &i-1\end{bmatrix}=\operatorname{null}\begin{bmatrix}0&1\cr 0&0\end{bmatrix}=\{% t(1,0):\ t\in{\mathbb{C}}\}\$
ενώ

$\displaystyle V_{i}(A)=\operatorname{null}(A-iI_{2})=\operatorname{null}\begin% {bmatrix}1-i&2\cr 0&0\end{bmatrix}=\operatorname{null}\begin{bmatrix}1&1+i\cr 0% &0\end{bmatrix}\\ \displaystyle=\{t(-1-i,1):\ t\in{\mathbb{C}}\}\;.$

Παρατηρούμε ότι αν $v_{1}=(1,0)$ , $v_{2}=(-1-i,1)$ , τότε $D=(v_{1},v_{2})$ είναι διατεταγμένη βάση του ${\mathbb{C}}^{2}$ από ιδιοδιανύσματα της $\phi$ και άρα

$Α^{\phi}_{D,D}=\begin{bmatrix}1&0\cr 0&i\end{bmatrix}\ .$
Αφού ο πίνακας $Α^{\phi}_{D,D}$ είναι διαγώνιος, η γραμμική συνάρτηση $\phi$ είναι διαγωνιοποιήσιμη.
2.

Θα προσδιορίσουμε τους ιδιοχώρους της γραμμικής συνάρτησης

$\phi:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(x,y)\mapsto(2x+y,x% +2y).$
Ο πίνακας του $\phi$ ως προς τη συνήθη βάση του ${\mathbb{R}}^{2}$ είναι ο

$A=\begin{bmatrix}2&1\\ 1&2\end{bmatrix}.$
Αφού $A=A^{T}$ , o $A$ έχει ακριβώς δύο πραγματικές ιδιοτιμές, βλ. Παράδειγμα 5.1.5.11. Πράγματι, υπολογίζουμε και παραγοντοποιούμε το χαρακτηριστικό πολυώνυμο της $\phi$ :

$P_{\phi}(x)=\det\begin{bmatrix}2-x&1\\ 1&2-x\end{bmatrix}=(2-x)^{2}-1=x^{2}-4x+3=(x-1)(x-3).$
Επομένως οι ιδιοτιμές του $A$ είναι το $1$ και το $3$ . Φέρνουμε τον πίνακα $A-1I_{2}$ σε ελαττωμένη κλιμακωτή μορφή γραμμών:

$\left[\begin{array}[]{cc}1&1\\ 1&1\end{array}\right]\longrightarrow\left[\begin{array}[]{cc}1&1\\ 0&0\end{array}\right].$
O ιδιοχώρος του $\phi$ που αντιστοιχεί στην ιδιοτιμή 1, είναι o

$V_{1}(\phi)=\{\;(-x_{2},x_{2}):x_{2}\in\Bbbk\}=S(\{(-1,1)\})=S(\{v\}),$
όπου $v=(-1,1)$ .

Για τον χώρο $V_{3}(\phi)$ , φέρνουμε τον πίνακα $A-3I_{2}$ σε ελαττωμένη κλιμακωτή μορφή γραμμών

$\left[\begin{array}[]{rr}-1&1\\ 1&-1\end{array}\right]\longrightarrow\left[\begin{array}[]{rr}1&-1\\ 0&0\end{array}\right],$
άρα

$V_{3}(\phi)=\{\;(x_{2},x_{2}):\ x_{2}\in\Bbbk\}=S(\{(1,1)\})=S(\{u\}),$
όπου $u=(1,1)$ .

Τα ιδιοδιανύσματα $\{v,u\}$ είναι βάση για τον ${\mathbb{R}}^{2}$ και o $Α$ είναι διαγωνιοποιήσιμος και όμοιος με τον

$\begin{bmatrix}1&0\cr 0&3\end{bmatrix}\ .$
3.

Θα προσδιορίσουμε τις ιδιοτιμές και τους ιδιοχώρους του πίνακα

$A=\left[\begin{array}[]{cc}1&1\\ 1&0\end{array}\right]\in\mathcal{M}_{2}({\mathbb{R}}).$
Το χαρακτηριστικό πολυώνυμο του $A$ είναι το

$\left|\begin{array}[]{cr}1-x&1\\ 1&-x\end{array}\right|=-x+x^{2}-1=\left(x-\frac{1+\sqrt{5}}{2}\right)\left(x-% \frac{1-\sqrt{5}}{2}\right).$
Οι ιδιοτιμές του $Α$ είναι $\;\displaystyle\lambda_{1}=\frac{1+\sqrt{5}}{2}\;$ και $\;\displaystyle\lambda_{2}=\frac{1-\sqrt{5}}{2}\;$ .

Για να βρούμε τον ιδιοχώρο $V_{\lambda_{1}}$ λύνουμε το σύστημα $(Α-\lambda_{1}Ι_{2})X={\bf O}$ . H ελαττωμένη κλιμακωτή μορφή γραμμών του $Α-\lambda_{1}Ι_{2}$ είναι:

$\begin{bmatrix}1&\frac{-1-\sqrt{5}}{2}\\ 0&0\end{bmatrix}$
και άρα

$V_{\lambda_{1}}(A)=\{(\frac{1+\sqrt{5}}{2}x_{2},x_{2})\;:\;x_{2}\in{\mathbb{R}% }\}=S(\{(\frac{1+\sqrt{5}}{2},1)\})$
$=S(\{(1+\sqrt{5},2)\}).$
Αντίστοιχα

$V_{\lambda_{2}}(A)=S(\{(\frac{1-\sqrt{5}}{2},1)\})=S(\{(1-\sqrt{5},2)\}).$
Ο πίνακας $Α$ είναι διαγωνιοποιήσιμος και όμοιος με τον πίνακα

$\begin{bmatrix}\lambda_{1}&0\cr 0&\lambda_{2}\end{bmatrix}\ .$
4.

Ο πίνακας

$A=\left[\begin{array}[]{rr}0&-1\\ 1&0\end{array}\right]\in\mathcal{M}_{2}({\mathbb{R}})$
έχει χαρακτηριστικό πολυώνυμο το

$P_{A}(x)=\left|\begin{array}[]{rr}-x&-1\\ 1&-x\end{array}\right|=x^{2}+1\ .$
Το πολυώνυμο $P_{A}(x)$ δεν έχει ρίζες στον ${\mathbb{R}}$ και ο $Α$ δεν είναι διαγωνιοποιήσιμος στον ${\mathbb{R}}$ . Τα $\pm i\in{\mathbb{C}}$ είναι ρίζες του $P_{A}(x)$ στον ${\mathbb{C}}$ και άρα ο $Α$ έχει ιδιοτιμές τους μιγαδικούς αριθμούς $\pm i$ και είναι διαγωνιοποιήσιμος στον ${\mathbb{C}}$ . Οι αντίστοιχοι ιδιοχώροι είναι

$V_{i}(Α)=\{\;(ix_{2},x_{2}):\ x_{2}\in{\mathbb{C}}\}=S(\{(i,1)\}),$
και

$V_{-i}(Α)=\{\;(ix_{2},x_{2}):\ x_{2}\in{\mathbb{C}}\}=S(\{(-i,1)\}).$
5.

Έστω $\phi:\ {\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ , $\phi(a,b,c)=(a+2c,2b+3c,2b+3c)$ , $B$ η κανονική βάση του ${\mathbb{R}}^{3}$ και $Α=Α^{\phi}_{B,B}$ . Τότε

$A=\begin{bmatrix}1&0&2\cr 0&2&3\cr 0&2&3\end{bmatrix}$
και όπως είδαμε στο Παράδειγμα 5.2.1.2, $P_{A}(x)=-x(x-1)(x-5)$ . Επομένως οι ιδιοτιμές του $Α$ είναι $0$ , $1$ , $5$ .

$V_{0}(A)=\operatorname{null}(A-0\;I_{3})=\operatorname{null}A=\operatorname{% null}\begin{bmatrix}1&0&2\cr 0&2&3\cr 0&2&3\end{bmatrix}=\operatorname{null}% \begin{bmatrix}1&0&2\cr 0&1&\frac{3}{2}\cr 0&0&0\end{bmatrix}\ .$
Επομένως

$V_{0}(A)=\{t(-2,-\frac{3}{2},1):\ t\in{\mathbb{R}}\}\ .$
Επίσης

$V_{1}(A)=\operatorname{null}(A-1\;I_{3})=\operatorname{null}\begin{bmatrix}0&0% &2\cr 0&1&3\cr 0&2&2\end{bmatrix}=\operatorname{null}\begin{bmatrix}0&1&0\cr 0% &0&1\cr 0&0&0\end{bmatrix}\ .$
Επομένως

$V_{1}(A)=\{t(1,0,0):\ t\in{\mathbb{R}}\}\ .$
Τέλος

$V_{5}(A)=\operatorname{null}(A-5\;I_{3})=\operatorname{null}\begin{bmatrix}-4&% 0&2\cr 0&-3&3\cr 0&2&-2\end{bmatrix}=\operatorname{null}\begin{bmatrix}1&0&-% \frac{1}{2}\cr 0&1&-1\cr 0&0&0\end{bmatrix}$
και

$V_{5}(A)=\{t(\frac{1}{2},1,1):\ t\in{\mathbb{R}}\}\ .$
Παρατηρούμε ότι an

$v_{1}=(-2,-\frac{3}{2},1),v_{2}=(1,0,0),v_{3}=(\frac{1}{2},1,1)$
τότε $D=(v_{1},v_{2},v_{3})$ είναι διατεταγμένη βάση του ${\mathbb{R}}^{3}$ από ιδιοδιανύσματα της $\phi$ και

$Α^{\phi}_{D,D}=\begin{bmatrix}0&0&0\cr 0&1&0\cr 0&0&5\end{bmatrix}\ .$
Αφού ο πίνακας $Α^{\phi}_{D,D}$ είναι διαγώνιος, η $\phi$ είναι διαγωνιοποιήσιμη.
6.

Έστω

$Α=\left[\begin{array}[]{rrr}4&0&1\\ -2&1&0\\ -2&0&1\end{array}\right]\in M_{3}({\mathbb{R}}).$
Το χαρακτηριστικό πολυώνυμο $P_{A}(x)$ του $Α$ είναι το

$P_{A}(x)=\left|\begin{array}[]{ccc}4-x&0&1\\ -2&1-x&0\\ -2&0&1-x\end{array}\right|=(1-x)[(4-x)(1-x)+2]\Rightarrow$
$\Rightarrow P_{A}(x)=(1-x)(x-2)(x-3).$
Επομένως οι ιδιοτιμές του $A$ είναι είναι οι

$\lambda_{1}=1,\;\;\;\lambda_{2}=2,\;\;\;\lambda_{3}=3.$
Αφού ο πίνακας $A$ έχει τρεις διακεκριμένες ιδιοτιμές είναι διαγωνιοποιήσιμος. Πράγματι, οι ιδιοχώροι του $A$ είναι οι

$\begin{array}[]{ll}V_{1}=\{\;(0,\kappa,0):\;\kappa\in{\mathbb{R}}\}&=\;S(\{(0,% 1,0)\}),\\ V_{2}=\{\;(-\frac{1}{2}\kappa,\kappa,\kappa):\;\kappa\in{\mathbb{R}}\}&=\;S(\{% (-\frac{1}{2},1,1)\}),\\ V_{3}=\{\;(-\kappa,\kappa,\kappa):\;\kappa\in{\mathbb{R}}\}&=\;S(\{(-1,1,1)\})% \;.\end{array}$
Τα ιδιοδιανύσματα

$\varepsilon_{1}=(0,1,0),\;\;\varepsilon_{2}=(-\frac{1}{2},1,1),\;\;\varepsilon% _{3}=(-1,1,1)$
αποτελούν βάση του ${\mathbb{R}}^{3}$ . Έστω $D=(\varepsilon_{1},\varepsilon_{2},\varepsilon_{3})$ . Ο $A$ είναι όμοιος με τον πίνακα

$Ε=\left[\begin{array}[]{rrr}1&0&0\\ 0&2&0\\ 0&0&3\end{array}\right]\;,$
και

$Ε=S^{-1}A\;S$
όπου

$S=S_{B\leftarrow D}=\left[\begin{array}[]{rrr}0&-1/2&-1\\ 1&1&1\\ 0&1&1\end{array}\right]\;.$

Έστω $\lambda$ ιδιοτιμή του $A\in\mathcal{M}_{n}(\Bbbk)$ . Τότε $P_{A}(\lambda)=0$ και $P_{A}(x)=(x-\lambda)q_{1}(x)$ για κάποιο $q_{1}(x)\in\Bbbk[x]$ . Αν $q_{1}(\lambda)=0$ , τότε $q_{1}(x)=(x-\lambda)q_{2}(x)$ για κάποιο $q_{2}(x)\in\Bbbk[x]$ και $P_{A}(x)=(x-\lambda)^{2}q_{2}(x)$ . Συνεχίζοντας καταυτόν τον τρόπο, καταλήγουμε ότι υπάρχει ένας φυσικός αριθμός $m_{\lambda}\in{\mathbb{N}}$ τέτοιος ώστε

P_{A}(x)=(x-\lambda)^{m_{\lambda}}q(x)\;,\textrm{ 'opou }q(x)\in\Bbbk[x]\;,% \textrm{ kai }q(\lambda)\neq 0\;.

Σημειώνουμε ότι $1\leq m_{\lambda}\leq n$ . O φυσικός αυτός αριθμός $m_{\lambda}$ λέγεται αλγεβρική πολλαπλότητα (algebraic multiplicity) της ιδιοτιμής $\lambda$ . Αν λοιπόν $\lambda_{1},\ldots,\lambda_{k}$ είναι οι διακεκριμένες ιδιοτιμές του $A$ στο $\Bbbk$ , τότε υπάρχει $h(x)\in\Bbbk[x]$ τέτοιο ώστε

\deg P_{A}(x)=(x-\lambda_{1})^{m_{\lambda_{1}}}\cdots(x-\lambda_{k})^{m_{% \lambda_{k}}}\;h(x)

και άρα

m_{\lambda_{1}}+\cdots+m_{\lambda_{k}}\leq n.

Παρατηρούμε επίσης ότι αφού $V_{\lambda}(A)\neq\{{\bf 0}\}$ , $m_{\lambda}$ $n_{\lambda}$ έπεται ότι

n_{\lambda}:={\rm dim}_{\Bbbk}V_{\lambda}(A)\geq 1\;.

O φυσικός αριθμός $n_{\lambda}$ λέγεται η γεωμετρική πολλαπλότητα (geometric multiplicity) της $\lambda$ . Με χρήση της μεθόδου της μαθηματικής επαγωγής αποδεικνύεται ότι

Θεώρημα 5.2.6.

Αν το $\lambda$ είναι ιδιοτιμή του $A$ , τότε $m_{\lambda}\geq n_{\lambda}\geq 1$ , δηλ.

\textrm{ h algebrik'h pollapl'othta tou $\lambda$ }\geq\textrm{ th gewmetrik'h% pollapl'othta tou $\lambda$.}

Για την απόδειξη της παραπάνω ανισότητας παραπέμπουμε στο σύγγραμμα [2, Πρόταση 5.2.5].

Παράδειγμα 5.2.7.

Έστω

A=\begin{bmatrix}4&0&0&0&0\cr 0&4&1&0&0\cr 0&0&4&5&0\cr 0&0&0&0&5\end{bmatrix}.

Τότε $P_{A}(x)=(x-2)^{3}(x-3)^{2}$ και επομένως η αλγεβρική πολλαπλότητα του $4$ είναι το $3$ ενώ η αλγεβρική πολλαπλότητα του $5$ είναι το 2. O αναγνώστης καλείται να διαπιστώσει ότι η γεωμετρική πολλαπλότητα του $4$ είναι ίση με το $2$ ενώ η γεωμετρική πολλαπλότητα του $5$ είναι το $2$ .

Ασκήσεις Ενότητας 5.2

1.

Δίνεται ο πίνακας

$A=\begin{bmatrix}a&b&0\\ c&1-a&2i\\ i&c+1&1\end{bmatrix}\ .$
Αν $\det A=8$ και μία ιδιοτιμή του $A$ είναι το 2 να βρεθούν οι υπόλοιπες ιδιοτιμές.

Λύση
2.

Να βρείτε τους ιδιοχώρους του πίνακα

$Α=\begin{bmatrix}2&1&0\cr 0&1&-1\cr 0&2&4\end{bmatrix}\in\mathcal{M}_{3}({% \mathbb{R}}).$

Λύση
3.

Να αποδείξετε ότι όμοιοι πίνακες έχουν το ίδιο ίχνος και την ίδια ορίζουσα χρησιμοποιώντας την Πρόταση 5.2.4.

Λύση
4.

Να βρείτε τις αλγεβρικές και γεωμετρικές πολλαπλότητες των ιδιοτιμών του πίνακα

$A=\begin{bmatrix}1&1&2&0&0\cr 0&1&1&0&0\cr 0&0&1&0&0\cr 0&0&0&1&3\cr 0&0&0&3&1% \end{bmatrix}.$

Λύση

5.3 Διαγωνιοποιήσιμοι Πίνακες

Θυμίζουμε ότι o $n\times n$ πίνακας $A$ είναι διαγωνιοποιήσιμος αν o $A$ είναι όμοιος με διαγώνιο πίνακα. Σε αυτήν την ενότητα θα εξερευνήσουμε πότε μία γραμμική συνάρτηση $\phi:\ \Bbbk^{n}\rightarrow\Bbbk^{n}$ είναι διαγωνιοποιήσιμη. Σύμφωνα με το Παράδειγμα 5.1.6.3, η $\phi$ είναι διαγωνιοποιήσιμη αν και μόνο αν o $\Bbbk^{n}$ έχει μία διατεταγμένη βάση $D$ από ιδιοδιανύσματα της $\phi$ . Τονίζουμε ότι αν το ιδιοδιάνυσμα $v_{i}$ κατέχει την $i$ θέση στο διατεταγμένο σύνολο $D$ , τότε το $\lambda_{i}$ εμφανίζεται στην $i$ γραμμή και στήλη του διαγώνιου πίνακα $Α^{\phi}_{D,D}$ .

Παραδείγματα 5.3.1.

1.

Έστω ότι $\phi:{\mathbb{C}}^{2}\rightarrow{\mathbb{C}}^{2}$ , $\phi(a,b)=(a+2b,ib)$ . Όπως είδαμε στο Παράδειγμα 5.2.5.1, η $\phi$ είναι διαγωνιοποιήσιμη με ιδιοτιμές $1$ και $i$ και αντίστοιχα ιδιοδιανύσματα $v_{1}$ και $v_{2}$ . Έστω τώρα $D_{1}=(v_{1},v_{2})$ και $D_{2}=(v_{2},v_{1})$ . Τότε

$Α^{\phi}_{D_{1},D_{1}}=\begin{bmatrix}1&0\cr 0&i\end{bmatrix},\textrm{ en'w }Α% ^{\phi}_{D_{2},D_{2}}=\begin{bmatrix}i&0\cr 0&1\end{bmatrix}\;.$
2.

Έστω $\phi:\ {\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ , μία διαγωνιοποιήσιμη γραμμική συνάρτηση με ιδιοτιμές $\lambda_{1}$ , $\lambda_{2}$ , $\lambda_{3}$ και αντίστοιχα ιδιοδιανύσματα $v_{1}$ , $v_{2}$ , $v_{3}$ . Αν $D_{1}=(v_{1},v_{2},v_{3})$ και $D_{2}=(v_{3},v_{1},v_{2})$ , τότε

$Α^{\phi}_{D_{1},D_{1}}=\begin{bmatrix}\lambda_{1}&0&0\cr 0&\lambda_{2}&0\cr 0&% 0&\lambda_{3}\end{bmatrix},\textrm{ en'w }Α^{\phi}_{D_{2},D_{2}}=\begin{% bmatrix}\lambda_{3}&0&0\cr 0&\lambda_{1}&0\cr 0&0&\lambda_{2}\end{bmatrix}\;.$

H επόμενη πρόταση αποδεικνύει ότι δεν υπάρχει σχέση γραμμικής εξάρτησης μεταξύ μη μηδενικών διανυσμάτων από διαφορετικούς ιδιοχώρους.

Πρόταση 5.3.2.

Έστω $\phi:\Bbbk^{n}\rightarrow\Bbbk^{n}$ μία γραμμική συνάρτηση. Αν τα $w_{1}$ , $w_{2},\ldots,$ $w_{\kappa}$ είναι ιδιοδιανύσματα του $V$ που αντιστοιχούν σε διακεκριμένες ιδιοτιμές $\lambda_{1}$ , $\lambda_{2},\ldots,$ $\lambda_{\kappa}$ , τότε τα $w_{1},w_{2}$ , $\ldots,w_{\kappa}$ είναι γραμμικά ανεξάρτητα.

Απόδειξη.

Θα δώσουμε τη βασική ιδέα της απόδειξης, αποδεικνύοντας αναλυτικά την περίπτωση δύο ιδιοδιανυσμάτων δύο διαφορετικών ιδιοτιμών και σημειώνοντας ότι η γενική περίπτωση γίνεται ανάλογα. Έστω ότι

\mu_{1}w_{1}+\mu_{2}w_{2}={\bf 0},

(5.3.2.1)

όπου $\mu_{1},\mu_{2}\in\Bbbk$ . Θα αποδείξουμε ότι $\mu_{1}=\mu_{2}=0$ . Πράγματι,

\phi(\mu_{1}w_{1}+\mu_{2}w_{2})=\phi({\bf 0})=\phi({\bf 0})\Rightarrow\mu_{1}% \phi(w_{1})+\mu_{2}\phi(w_{2})={\bf 0}\Rightarrow

\mu_{1}\lambda_{1}w_{1}+\mu_{2}\lambda_{2}w_{2}={\bf 0}.

(5.3.2.2)

Πολλαπλασιάζουμε τη Σχέση (5.3.2.1) με $\lambda_{2}$ και την αφαιρούμε από τη Σχέση (5.3.2.2). Έτσι

\mu_{1}(\lambda_{1}-\lambda_{2})w_{1}={\bf 0}\ .

Όμως $w_{1}$ είναι ιδιοδιάνυσμα και άρα $w_{1}\neq{\bf 0}$ . Έπεται ότι $\mu_{1}(\lambda_{1}-\lambda_{2})={\ 0}$ . Άρα $\mu_{1}=0$ αφού $\lambda_{1}\neq\lambda_{2}$ . Αντικαθιστούμε στη Σχέση (5.3.2.1) και με τον ίδιο τρόπο καταλήγουμε ότι $\mu_{2}=0$ . ∎

Άμεση συνέπεια της προηγούμενης πρότασης είναι το εξής θεώρημα.

Θεώρημα 5.3.3.

Έστω $A\in\mathcal{M}_{n}(\Bbbk)$ και $\lambda_{1},\ldots,\lambda_{k}\in\Bbbk$ οι διακεκεριμένες ιδιοτιμές του $A$ στο $\Bbbk$ . O $Α$ είναι διαγωνιοποιήσιμος αν και μόνο αν

{\\ {\rm dim}_{\Bbbk}V_{\lambda_{1}}(A)+\cdots+{\rm dim}_{\Bbbk}V_{\lambda_{k}}(A)% =n\;.}

Σημειώνουμε δύο ειδικές περιπτώσεις του Θεωρήματος 5.3.3.

Πόρισμα 5.3.4.

Έστω ότι $A\in\mathcal{M}_{n}(\Bbbk)$ .

i)

Αν o $A$ έχει $n$ διαφορετικές ιδιοτιμές, τότε ο $Α$ είναι διαγωνιοποιήσιμος.
ii)

Αν o $A$ είναι διαγωνιοποιήσιμος, τότε η γεωμετρική πολλαπλότητα κάθε ιδιοτιμής του $A$ είναι ίση με την αλγεβρική πολλαπλότητα της ιδιοτιμης.

Απόδειξη.

Από το Θεώρημα 5.2.6 προκύπτει ότι

k\leq n_{\lambda_{1}}+\cdots+m_{\lambda_{k}}=m_{\lambda_{1}}+\cdots+m_{\lambda% _{k}}\leq n.

Επομένως αν o $A$ είναι διαγωνιοποιήσιμος τότε

m_{\lambda_{1}}=n_{\lambda_{1}},\ldots,m_{\lambda_{k}}=n_{\lambda_{k}}\;,

ενώ αν $n=k$ , τότε $n_{\lambda_{i}}=m_{\lambda_{i}}=1$ , για $i=1,\ldots,n$ και o $A$ είναι διαγωνιοποιήσιμος. ∎

Στα παραδείγματα που ακολουθούν θα εφαρμόσουμε τα παραπάνω.

Παραδείγματα 5.3.5.

1.

Θεωρούμε τη γραμμική συνάρτηση

$\phi:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}\;,\;\;\;\;(x,y,z)\mapsto 4(x,% y,z)$
του ${\mathbb{R}}$ -διανυσματικού χώρου ${\mathbb{R}}^{3}$ . Ο πίνακας της $\phi$ ως προς τη συνήθη βάση του ${\mathbb{R}}^{3}$ είναι ο

$A=\left[\begin{array}[]{ccc}4&0&0\\ 0&4&0\\ 0&0&4\end{array}\right]\begin{array}[]{c}\\ \\ ,\end{array}$
και το χαρακτηριστικό πολυώνυμο είναι το $P_{Α}(x)=(4-x)^{3}$ . Έτσι η μόνη ιδιοτιμή της $\phi$ είναι το $4$ και αφού $A-4I_{3}={\bf 0}$ έπεται ότι $V_{4}(\phi)=\operatorname{null}(A-4I_{3})={\mathbb{R}}^{3}$ .
2.

Έστω

$Α=\begin{bmatrix}4&0&1\cr 0&4&0\cr 0&0&4\end{bmatrix}\ .$
Τότε $P_{A}(x)=(4-x)^{3}$ και η μόνη ιδιοτιμή του $Α$ είναι το $4$ . Επίσης

$Α-4Ι_{3}=\begin{bmatrix}0&0&1\cr 0&0&0\cr 0&0&0\end{bmatrix}$
και $V_{4}(A)=\{(s,t,0):\ s,t\in{\mathbb{R}}\}=S(\{e_{1},e_{2}\})$ . O πίνακας $Α$ δεν είναι διαγωνιοποιήσιμος γιατί δεν υπάρχει βάση του ${\mathbb{R}}^{3}$ που να αποτελείται από ιδιοδιανύσματα του $Α$ .
3.

Θα υπολογίσουμε τις ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής συνάρτησης $f:\ {\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ , $f(a,b,c)=(3a+2b+2c,a+4b+2c,-a-2b)$ . Έστω $Β$ η κανονική βάση του ${\mathbb{R}}^{3}$ και έστω

$A=Α_{Β,Β}^{f}=\left[\begin{array}[]{rrr}3&2&2\\ 1&4&2\\ -1&-2&0\end{array}\right]\begin{array}[]{c}\\ \\ .\end{array}$
Το χαρακτηριστικό πολυώνυμο $P_{A}(x)$ είναι το

$\left|\begin{array}[]{ccr}3-x&\;\;2&2\\ \;\;1&4-x&2\\ -1&-2&-x\end{array}\right|=12-16x+7x^{2}-x^{3}=(2-x)^{2}(3-x),$
και οι ιδιοτιμές του $A$ είναι το $2$ και το $3$ . Φέρνουμε τον πίνακα $A-2I_{3}$ σε ελαττωμένη κλιμακωτή μορφή γραμμών:

$A-2I_{3}=\left[\begin{array}[]{rrr}1&2&2\\ 1&2&2\\ -1&-4&0\end{array}\right]\longrightarrow\left[\begin{array}[]{ccc}1&2&2\\ 0&0&0\\ 0&0&0\end{array}\right]\begin{array}[]{c}\\ \\ ,\end{array}$
επομένως το σύνολο των λύσεων του συστήματος $(A-2I_{3})X={\bf 0}$ είναι το

$V_{2}(Α)=\{\;(-2x_{2}-2x_{3},x_{2},x_{3}):\ x_{2},x_{3}\in{\mathbb{R}}\}=$
$\{\;t(-2,1,0)+s(-2,0,1):\ t,s\in{\mathbb{R}}\}.$
Όμοια φέρνουμε τον πίνακα $A-3I_{3}$ σε ελαττωμένη κλιμακωτή μορφή γραμμών:

$A-3I_{3}=\left[\begin{array}[]{rrr}0&2&2\\ 1&1&2\\ -1&-2&-3\end{array}\right]\longrightarrow\left[\begin{array}[]{ccc}1&0&1\\ 0&1&1\\ 0&0&0\end{array}\right]\begin{array}[]{c}\\ \\ ,\end{array}$
και ο ιδιοχώρος που αντιστοιχεί στην ιδιοτιμή $3$ είναι ο

$V_{3}(Α)=S(\{(-1,-1,1)\}).$
Αφού

${\rm dim}(V_{2}(A))+{\rm dim}(V_{3}(A))=3$
έπεται ότι

$V_{2}(A)+V_{3}(A)={\mathbb{R}}^{3}$
και ότι η $f$ είναι διαγωνιοποιήσιμη. Θεωρούμε τα ιδιοδιανύσματα $v_{1}=(-2,1,0)$ , $v_{2}=(-2,0,1)$ (για την ιδιοτιμή $2$ ) και $v_{3}=(-1,-1,1)$ (για την ιδιοτιμή $3$ ) και τις διατεταγμένες βάσεις $D=(v_{1},v_{2},v_{3})$ , $E=(v_{2},v_{3},v_{1})$ του ${\mathbb{R}}^{3}$ . Τότε

$A^{f}_{D,D}=\begin{bmatrix}2&0&0\cr 0&2&0\cr 0&0&3\end{bmatrix}\textrm{ en'w }% A^{f}_{E,E}=\begin{bmatrix}2&0&0\cr 0&3&0\cr 0&0&2\end{bmatrix}\;.$
Οι τρεις πίνακες $Α^{f}_{B,B}$ , $A^{f}_{D,D}$ , $A^{f}_{E,E}$ είναι όμοιοι ανά ζεύγη. O αναγνώστης καλείται να βρει τους πίνακες μετάβασης.
4.

Έστω o πίνακας

$A=\left[\begin{array}[]{rrcc}2&0&0&0\\ 0&-2&1&0\\ 0&-5&2&0\\ 0&0&0&2\end{array}\right]\ .$
Τότε $P_{A}(x)==(2-x)^{2}(x^{2}+1)$ . Παρατηρούμε ότι η μοναδική ιδιοτιμή του $Α$ στον ${\mathbb{R}}$ είναι το 2, ενώ στον ${\mathbb{C}}$ οι ιδιοτιμές του $Α$ είναι το $2$ και το $\pm i$ . Επομένως o $A$ δεν είναι διαγωνιοποιήσιμος στον ${\mathbb{R}}$ . Εθετάζουμε στη συνέχεια αν o $A$ είναι διαγωνιοποιήσιμος στον ${\mathbb{C}}$ .

Για να βρούμε μία βάση για τον ιδιοχώρο $V_{2}(A)$ , φέρνουμε τον πίνακα $A-2I_{4}$ σε ελαττωμένη κλιμακωτή μορφή γραμμών:

$\left[\begin{array}[]{rrcc}0&0&0&0\\ 0&-4&1&0\\ 0&-5&0&0\\ 0&0&0&0\end{array}\right]\longrightarrow\left[\begin{array}[]{rrcc}0&1&0&0\\ 0&0&1&0\\ 0&0&0&0\\ 0&0&0&0\end{array}\right]\begin{array}[]{c}\\ \\ \\ .\end{array}$
Επομένως

$V_{2}(Α)=\operatorname{null}(A-2I_{4})=\{\;(x_{1},0,0,x_{4}):\;x_{1},x_{4}\in{% \mathbb{C}}\}=S(\{(1,0,0,0),(0,0,0,1)\}).$
Για να βρούμε τον ιδιοχώρο $V_{i}(A)$ παρατηρούμε ότι μετά από στοιχειώδεις πράξεις γραμμών, η ελαττωμένη κλιμακωτή μορφή γραμμών του $A-iI_{4}$ είναι

$\begin{bmatrix}1&0&0&0\cr 0&1&\frac{2-i}{5}&0\cr 0&0&0&1\cr 0&0&0&0\end{bmatrix}$
και άρα

$V_{i}(Α)=\{\;x_{3}(0,\frac{-2+i}{5},1,0)\;:\;t\in{\mathbb{C}}\}=\{k(0,-2+i,5,0% ):\ k\in{\mathbb{C}}\}.$
Αντίστοιχα, βρίσκουμε ότι o ιδιοχώρος για την ιδιοτιμή $-i$ είναι

$V_{-i}(Α)=\{\;t(0,-2-i,5,0)\;:\;t\in{\mathbb{C}}\}.$
Ο $Α$ είναι διαγωνιοποιήσιμος στον $C$ , αφού τα ιδιοδιανύσματα

$(1,0,0,0),\ (0,0,0,1),\ (0,-2+i,5,0),\ (0,-2-i,5,0)$
είναι γραμμικά ανεξάρτητα και αποτελούν βάση για τον ${\mathbb{C}}^{4}$ . Ο πίνακας $Α$ στον ${\mathbb{C}}$ είναι όμοιος με τον πίνακα

$\begin{bmatrix}2&0&0&0\cr 0&2&0&0\cr 0&0&i&0\cr 0&0&0&-i\end{bmatrix}\ .$

Παραθέτουμε το επόμενο θεώρημα χωρίς απόδειξη, τονίζουμε όμως ότι πρόκειται για ένα από τα σημαντικότερα θεωρήματα της Γραμμικής Άλγεβρας. To θεώρημα αυτό δείχνει ότι μπορούμε να συνδυάσουμε γραμμικά τις δυνάμεις του $A$ για να προκύψει o μηδενικός πίνακας. Για την απόδειξη, παραπέμπουμε τον αναγνώστη στο σύγγραμμα [2, Ενότητα 5.3].

Θεώρημα 5.3.6.

(Cayley-Hamilton) Έστω ότι $A\in M_{n\times n}(\Bbbk)$ και ότι

P_{A}(x)=(-1)^{n}x^{n}+\alpha_{n-1}x^{n-1}+\cdots+\alpha_{1}x+\alpha_{0},

είναι το χαρακτηριστικό πολυώνυμο του $A$ . Τότε

(-1)^{n}Α^{n}+\alpha_{n-1}Α^{n-1}+\cdots+\alpha_{1}Α+\alpha_{0}Ι_{n}

είναι o μηδενικός πίνακας, δηλ. $P_{A}(A)=\bf 0$ .

Στα επόμενα παραδείγματα θα εξετάσουμε διαφορετικές εφαρμογές του Θεωρήματος των Cayley-Hamilton.

Παραδείγματα 5.3.7.

1.

Έστω

$A=\begin{bmatrix}1&1\cr 0&2\end{bmatrix}\;.$
Τότε $P_{A}(x)=x^{2}-3x+2$ . Παρατηρούμε ότι

$A^{2}-3A+2I_{2}=\begin{bmatrix}1&3\cr 0&4\end{bmatrix}-3\begin{bmatrix}1&1\cr 0% &2\end{bmatrix}+\begin{bmatrix}2&0\cr 0&2\end{bmatrix}=\begin{bmatrix}0&0\cr 0% &0\end{bmatrix}={\bf 0},$
διαπιστώνουμε λοιπόν την ισχύ του Θεωρήματος των Cayley-Hamilton σε αυτό το συγκεκριμένο απλό παράδειγμα. Παρατηρούμε επίσης ότι

$\displaystyle A^{2}-3A+2I_{2}={\bf 0}\Rightarrow A^{2}-3A=-2I_{2}\Rightarrow(A% -3I_{2})A=2I_{2}\Rightarrow\\ \displaystyle\frac{1}{2}\;(A-3I_{2})A=I_{2}\Rightarrow A^{-1}=\frac{1}{2}\;(A-% 3I_{2})\;.$
2.

Έστω

$Α=\begin{bmatrix}1&\;0&2\\ 0&-1&1\\ 0&\;1&0\end{bmatrix}\;.$
Τότε $P_{Α}(x)=-x^{3}+2x-1$ και σύμφωνα με το Θεώρημα των Cayley-Hamilton

$-Α^{3}+2Α-Ι_{3}={\bf 0}.$
Αφού o σταθερός όρος του $P_{A}(x)$ είναι διάφορος του μηδενός, o $A$ είναι αντιστρέψιμος. Θα υπολογίσουμε τον $A^{-1}$ χρησιμοποιώντας την προηγούμενη σχέση μεταξύ των δυνάμεων του $A$ .

$\displaystyle-Α^{3}+2Α-Ι_{3}={\bf 0}\Rightarrow-Α^{3}+2Α=Ι_{3}\Rightarrow Α(-Α% ^{2}+2Ι_{3})=Ι_{3}.$
Επομένως

$A^{-1}=-Α^{2}+2Ι_{3}.$
3.

Έστω ότι

$P_{A}(x)=(-1)^{n}x^{n}+\alpha_{n-1}x^{n-1}+\cdots+\alpha_{1}x+\alpha_{0}\;.$
Από το Θεώρημα των Cayley-Hamilton έπεται ότι

$\displaystyle P_{A}(A)={\bf 0}\Rightarrow(-1)^{n}A^{n}+\alpha_{n-1}A^{n-1}+% \cdots+\alpha_{1}A+\alpha_{0}I_{n}={\bf 0}\Rightarrow\\ \\ \displaystyle A^{n}=(-1)^{n+1}\alpha_{n-1}A^{n-1}+\cdots+(-1)^{n+1}\alpha_{1}A% +(-1)^{n+1}\alpha_{0}I_{n}\;.$
Επομένως ο $A^{n}$ εκφράζεται ως γραμμικός συνδυασμός των $I_{n},A,\ldots,A^{n-1}$ . Πολλαπλασιάζοντας τις δύο πλευρές της προηγούμενης ισότητας με $Α$ και αντικαθιστώντας το $A^{n}$ βλέπουμε ότι

$A^{n+1}=(\alpha^{2}_{n-1}+\alpha_{n-1}\alpha_{n-2})A^{n-1}+\cdots+\alpha_{n-1}% \alpha_{0}Ι_{n}\;.$
Άρα και o $A^{n+1}$ εκφράζεται ως γραμμικός συνδυασμός των $I_{n},A,\ldots,A^{n-1}$ . Γενικότερα, όλες οι δυνάμεις $Α^{m}$ όπου $m\geq n$ μπορούν να γραφούν ως γραμμικοί συνδυασμοί των δυνάμεων $I_{n},A,\ldots,A^{n-1}$ .

To ίδιο ισχύει και για το $A^{-1}$ όταν o $A$ είναι αντιστρέψιμος. Πράγματι, ο $A$ είναι αντιστρέψιμος αν και μόνο αν $\alpha_{0}\neq 0$ . Σε αυτήν την περίπτωση,

$(-1)^{n}A^{n}+\alpha_{n-1}A^{n-1}+\cdots+\alpha_{1}A=-\alpha_{0}I_{n}\ .$
Βγάζοντας κοινό παράγοντα το $Α$ (από το αριστερό μέρος της ισότητας) βρίσκουμε ότι

$A\left((-1)^{n}A^{n-1}+\alpha_{n-1}A^{n-2}+\cdots+\alpha_{1}I_{n}\right)=-% \alpha_{0}I_{n},$
δηλ.

$A^{-1}=-\frac{1}{\alpha_{0}}\;((-1)^{n}A^{n-1}+\alpha_{n-1}A^{n-2}+\cdots+% \alpha_{1}I_{n}).$
4.

Έστω

$Α=\begin{bmatrix}0&0&i\\ i&0&0\\ 0&-1&0\end{bmatrix}\ .$

Το χαρακτηριστικό πολυώνυμο του πίνακα $Α$ είναι

$\det\begin{bmatrix}-x&0&i\\ i&-x&0\\ 0&-1&-x\end{bmatrix}=(-x)(-x)^{2}-i\cdot i=-x^{3}+1.$
Σύμφωνα με το θεώρημα των Cayley-Hamilton

$-Α^{3}+Ι_{3}={\bf 0}$
και άρα $Α^{3}=I_{3}$ . Αν $m\in{\mathbb{N}}$ , τότε o $m$ μπορεί να γραφεί μοναδικά ως $m=3\kappa+r$ , όπου $r=0,1,2$ και $\kappa\in{\mathbb{N}}$ . Επομένως για $m\in\mathbb{N}$ έχουμε τις εξής περιπτώσεις:

$A^{m}=\begin{cases}Α^{3\kappa}=(Α^{3})^{\kappa}=I_{3}^{\;\kappa}=I_{3}\cr Α^{3% \kappa+1}=(Α^{3})^{\kappa}A=A\cr Α^{3\kappa+2}=(Α^{3})^{\kappa}A^{2}=A^{2}\;.% \end{cases}$
Έτσι οι διακεκριμένες δυνάμεις του πίνακα $Α$ είναι οι $Ι_{3},Α,A^{2}$ . Αφού $A^{3}=Ι_{3}$ , προκύπτει ότι $A\;A^{2}=Ι_{3}$ , άρα $A^{-1}=A^{2}$ .

O πίνακας $J\in\mathcal{M}_{k}({\mathbb{C}})$ λέγεται μπλοκ του Jordan (Jordan block) για το $\lambda$ αν o $J$ έχει την εξής μορφή:

J=\begin{bmatrix}\lambda&1&0&\cdots&0&0\cr 0&\lambda&1&\cdots&0&0\cr 0&0&% \lambda&\cdots&0&0\cr\vdots&&&\ddots&&\vdots\cr 0&0&0&\cdots&\lambda&1\cr 0&0&% 0&\cdots&0&\lambda\end{bmatrix}.

Ένα σημαντικό αποτέλεσμα αφορά την ταξινόμηση των πινάκων σε ανάλυση μπλοκ πινάκων του Jordan. To αναφέρουμε στη συνέχεια χωρίς απόδειξη.

Θεώρημα 5.3.8.

Έστω $A\in\mathcal{M}_{n}({\mathbb{C}})$ και έστω $P_{A}(x)=(x-\lambda_{1})^{m_{1}}\cdots(x-\lambda_{s})^{m_{s}}$ , όπου $\lambda_{1},\ldots,\lambda_{s}\in{\mathbb{C}}$ είναι οι διακεκριμμένες ιδιοτιμές του $A$ . Έστω επίσης ότι $n_{i}={\rm dim}_{{\mathbb{C}}}V_{\lambda_{i}}(A)$ , για $i=1,\ldots,s$ . Υπάρχει αντιστρέψιμος πίνακας $P$ τέτοιος ώστε

P^{-1}AP=\begin{bmatrix}J_{1}&0&\cdots&0\cr 0&J_{2}&\cdots&0\cr\vdots&&\ddots&% 0\cr 0&0&\cdots&J_{r}\end{bmatrix},

όπου, για $j=1,\ldots,r$ , o υποπίνακας $J_{j}$ του $J$ είναι μπλοκ του Jordan για κάποια από τις ιδιοτιμές του $A$ . Ισχύουν τα εξής για την ιδιοτιμή $\lambda_{i}$ ( $i=1,\ldots,s$ ):

i)

O αριθμός των μπλοκ του Jordan για την $\lambda_{i}$ είναι ίσος με $n_{i}$ ,
ii)

η $\lambda_{i}$ εμφανίζεται ακριβώς $m_{i}$ φορές στη διαγώνιο των μπλοκ του Jordan για τη $\lambda_{i}$ .

O πίνακας $P^{-1}AP$ είναι μοναδικός και λέγεται η κανονική μορφή του Jordan (Jordan canonical form) για τον $A$ .

Στο επόμενο παράδειγμα εφαρμόζουμε το Θεώρημα 5.3.8 για έναν $3\times 3$ πίνακα.

Παράδειγμα 5.3.9.

Έστω ότι $P_{A}(x)=(x-2)^{3}$ . Τότε o $A$ είναι όμοιος με ακριβώς έναν από τους εξής πίνακες:

J_{1}=\begin{bmatrix}2&0&0\cr 0&2&0\cr 0&0&2\end{bmatrix},\ \ J_{2}=\begin{% bmatrix}2&0&0\cr 0&2&1\cr 0&0&2\end{bmatrix},\ \ J_{3}=\begin{bmatrix}2&1&0\cr 0% &2&1\cr 0&0&2\end{bmatrix}.

Και στις τρεις περιπτώσεις, η αλγεβρική πολλαπλότητα του $2$ είναι ίση με το $3$ . O πίνακας $A$ είναι διαγωνιοποιήσιμος μόνο όταν η κανονική μορφή του Jordan του $A$ είναι o $J_{1}$ , όταν δηλ. η γεωμετρική πολλαπλότητα του $2$ είναι $3$ . O $J_{1}$ αποτελείται από τρία μπλοκ του Jordan, όλα $1\times 1$ πίνακες. Όταν η γεωμετρική πολλαπλότητα του $2$ είναι δύο, τότε η κανονική μορφή του Jordan του $A$ είναι o $J_{2}$ . O $J_{2}$ αποτελείται από δύο μπλοκ του Jordan: το πρώτο είναι ένας $1\times 1$ πίνακας, το δεύτερο είναι ένας $2\times 2$ πίνακας. Τέλος, όταν η γεωμετρική πολλαπλότητα του $2$ είναι ένα, τότε η κανονική μορφή του Jordan του $A$ είναι o $J_{3}$ . O $J_{3}$ αποτελείται από ένα $3\times 3$ μπλοκ του Jordan.

Παραπέμπουμε τον αναγνώστη στο σύγγραμμα [6] για περισσότερα επί του θέματος αυτού.

Ασκήσεις Ενότητας 5.3

1.

Έστω η γραμμική συνάρτηση $\phi:\ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ που περιστρέφει τα διανύσματα αριστερόστροφα κατά γωνία $\pi$ . Είναι η $\phi$ διαγωνιοποιήσιμη;

Λύση
2.

Έστω η γραμμική συνάρτηση $\phi:\ {\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ που αντικατοπτρίζει τα διανύσματα ως προς το επίπεδο $y=0$ . Είναι η $\phi$ διαγωνιοποιήσιμη;

Λύση
3.

Να υπολογίσετε για ποιές τιμές των $a, b$ διαγωνιοποιείται ο πίνακας

$\begin{bmatrix}a&1\\ 0&b\end{bmatrix}\in\mathcal{M}_{2}({\mathbb{R}}).$

Λύση
4.

Να εξετάσετε αν ο πίνακας

$Α=\left[\begin{array}[]{rrr}2&1&0\cr 0&1&-1\cr 0&2&4\end{array}\right]$
είναι διαγωνιοποιήσιμος.

Λύση
5.

Να εξετάσετε αν ο πίνακας

$Α=\left[\begin{array}[]{rr}1&i\cr-i&2\end{array}\right]$
είναι διαγωνιοποιήσιμος.

Λύση
6.

Έστω ότι το χαρακτηριστικό πολυώνυμο του πίνακα $A$ είναι το

$x^{4}-2x^{3}+x+4.$
Να υπολογίσετε τον αριθμό των γραμμών του $A$ , τη βαθμίδα $\operatorname{rank}(A)$ και να εκφράσετε τον $A^{-1}$ ως γραμμικό συνδυασμό δυνάμεων του $A$ .

Λύση
7.

Με εφαρμογή του Θεωρήματος των Cayley-Hamilton να υπολογίσετε τον αντίστροφο του πίνακα

$Α=\left[\begin{array}[]{rrr}1&-2&2\\ -1&0&1\\ 3&-4&-3\end{array}\right]$
και να γράψετε τον $A^{4}$ ως γραμμικό συνδυασμό των πινάκων $I_{3},A,A^{2}$ .

Λύση
8.

Να βρείτε τις κανονικές μορφές του Jordan που μπορεί να έχει o πίνακας $A\in\mathcal{M}_{5}({\mathbb{C}})$ όταν $P_{A}(x)=(x-3)^{2}(x+1)^{3}$ .

Λύση

5.4 Ορθογώνιοι Πίνακες και Εσωτερικό Γινόμενο στον ${\mathbb{R}}^{n}$

Ο τετραγωνικός πίνακας $A\in\mathcal{M}_{n}({\mathbb{R}})$ λέγεται ορθογώνιος (orthogonal) αν

A^{T}A=I_{n}\;\;\;\;\hbox{ή ισοδύναμα αν }\;\;\;\;A^{-1}=A^{T}.

Είναι φανερό ότι $A$ είναι ορθογώνιος πίνακας αν και μόνο an $A^{T}$ είναι ορθογώνιος πίνακας, βλ. Άσκηση 5.4.2.

Παραδείγματα 5.4.1.

1.

O $I_{n}$ είναι ορθογώνιος πίνακας.
2.

Έστω

$A=\left[\begin{array}[]{rrr}1/\sqrt{3}&-2/\sqrt{6}&0\\ 1/\sqrt{3}&1/\sqrt{6}&-1/\sqrt{2}\\ 1/\sqrt{3}&1/\sqrt{6}&1/\sqrt{2}\end{array}\right].$
O αναγνώστης καλείται να επιβεβαιώσει ότι $A\;A^{T}=I_{3}$ και άρα o $Α$ είναι ορθογώνιος πίνακας και

$Α^{-1}=Α^{Τ}=\left[\begin{array}[]{rrr}1/\sqrt{3}&1/\sqrt{3}&1/\sqrt{3}\\ -2/\sqrt{6}&1/\sqrt{6}&1/\sqrt{6}\\ 0&-1/\sqrt{2}&1/\sqrt{2}\end{array}\right]\;.$
3.

Έστω o $Α\in\mathcal{M}_{n}({\mathbb{R}})$ ορθογώνιος πίνακας. Αφού $A^{T}\ A=I_{n}$ έπεται ότι

$\displaystyle\det A^{T}\ A=\det I_{n}=1\Rightarrow\det A^{T}\det A=1% \Rightarrow\det A\det A=1\\ \displaystyle\Rightarrow\det A=\pm 1\;.$

Μία σημαντική ιδιότητα των ορθογώνιων πινάκων είναι ότι οι ιδιοτιμές τους μπορούν να πάρουν δύο μόνο τιμές, τις $\pm 1$ , βλ. Άσκηση 5.3.3. Για να μπορέσουμε, όμως, να αποδείξουμε το προηγούμενο, θα χρειαστεί να αναπτύξουμε τη θεωρία του εσωτερικού γινομένου στον ${\mathbb{R}}^{n}$ και να περιγράψουμε το γινόμενο $A^{T}A$ με τη χρήση του εσωτερικού γινομένου.

Το σύνηθες εσωτερικό γινόμενο (standard inner product) στον ${\mathbb{R}}^{n}$ είναι η συνάρτηση

\langle\ ,\ \rangle:{\mathbb{R}}^{n}\times{\mathbb{R}}^{n}\rightarrow{\mathbb{% R}},\hbox{ όπου }

\langle(\alpha_{1},\ldots,\alpha_{n}),\;(\beta_{1},\ldots,\beta_{n})\rangle\;=% \alpha_{1}\beta_{1}+\cdots+\alpha_{n}\beta_{n}\;.

Για παράδειγμα, στον ${\mathbb{R}}^{2}$

\langle(1,2),(3,-1)\rangle=1\cdot 3+2\cdot(-1)=1\;,\langle(1,2),(1,2)\rangle=5\ .

Ομοίως στον ${\mathbb{R}}^{n}$ για κάθε $n\in{\mathbb{N}}$ , έχουμε ότι:

\langle\;(\alpha_{1},\ldots,\alpha_{n}),(\alpha_{1},\ldots,\alpha_{n})\;% \rangle=\alpha_{1}^{2}+\cdots+\alpha_{n}^{2}\ .

Έστω ότι $v,u,w\in{\mathbb{R}}^{n}$ , $\kappa,\lambda\in{\mathbb{R}}$ . Είναι εύκολο να δούμε ότι ικανοποιούνται οι ιδιότητες του επόμενου πίνακα.

i)

$\langle v,v\rangle\;\geq 0$ , $\forall v\in{\mathbb{R}}^{n}$ και $\langle v,v\rangle=0$ αν και μόνο αν $v={\bf 0}$ .
ii)

$\langle v,u\rangle=\langle u,v\rangle$ , $\forall v,w\in{\mathbb{R}}^{n}$
iii)

$\langle\kappa v+\lambda w,u\rangle=\kappa\langle v,u\rangle+\lambda\langle w,u\rangle$ , $\forall v,w\in{\mathbb{R}}^{n}$ , $\forall\kappa,\lambda\in{\mathbb{R}}$ ,
iv)

$\langle v,\kappa u+\lambda w\rangle\;=\kappa\langle v,u\rangle+\lambda\langle v% ,w\rangle$ , $\forall v,w\in{\mathbb{R}}^{n}$ , $\forall\kappa,\lambda\in{\mathbb{R}}$ ,
v)

$\langle v,{\bf 0}\rangle=0$ , $\forall v\in{\mathbb{R}}^{n}$ .

Ως άμεση συνέπεια της πρώτης ιδιότητας του εσωτερικού γινομένου, προκύπτει ότι

\textrm{ an }\langle v,w\rangle=0,\textrm{ gia k'aje }w\in{\mathbb{R}}^{n},% \textrm{ t'ote }v=0.

(5.4.1.1)

Το μήκος (norm) του $v$ norm συμβολίζεται $\|v\|$ $\|v\|$ και είναι ίσο με $\sqrt{\langle v,v\rangle}$ . To διάνυσμα $v$ λέγεται κανονικό (normal) αν $\|v\|=1$ . Αν $w\in{\mathbb{R}}^{n}$ είναι μη μηδενικό διάνυσμα, τότε o αναγνώστης μπορεί εύκολα να διαπιστώσει ότι το διάνυσμα

\frac{1}{\|w\|}w

είναι κανονικό και παράλληλο προς το $w$ . Η απόσταση (distance) απόσταση δύο διανυσμάτων $v,u\in{\mathbb{R}}^{n}$ είναι το μήκος του διανύσματος $v-u$ και συμβολίζεται $d(v,u)$ δηλ. $d(v,u)=\|u-v\|$ . Μπορεί να αποδειχθεί η επόμενη ανισότητα, που είναι γνωστή ως ανισότητα των Cauchy-Schwarz (Cauchy-Schwarz inequality):

-\|u\|\|v\|\leq\langle u,v\rangle\leq\|u\|\|v\|\ .

Έτσι ισχύει ότι

-1\leq\frac{\langle u,v\rangle}{\|u\|\|v\|}\leq 1\ .

Αναφέρουμε επίσης την τριγωνική ανισότητα (triangle inequality) που προκύπτει εύκολα από την ανισότητα των Cauchy-Schwarz:

\|v+u\|\leq\|v\|+\|u\|\ .

Αν $v$ , $u\neq 0$ τότε γωνία (angle) των $v$ και $u$ ορίζεται η γωνία $\theta$ για την οποία $0\leq\theta\leq\pi$ και

\cos\theta=\frac{\langle u,v\rangle}{\|u\|\|v\|}\;.

Παράδειγμα 5.4.2.

Έστω $v=(1,0,1)$ , $u=(-1,1,0)$ . Τότε $\|u\|=\|u\|=\sqrt{2}$ και $d(u,v)=\sqrt{6}$ .

\cos\theta=\frac{\langle v,u\rangle}{\|v\|\|u\|}=\frac{-1}{\sqrt{2}\sqrt{2}}=-% \frac{1}{2}\;

και άρα $\theta\displaystyle=\pi-\frac{\pi}{3}=\frac{2\pi}{3}$ .

Σχήμα 5.5: Τα διανύσματα $u$ και $v$ στον ${\mathbb{R}}^{3}$

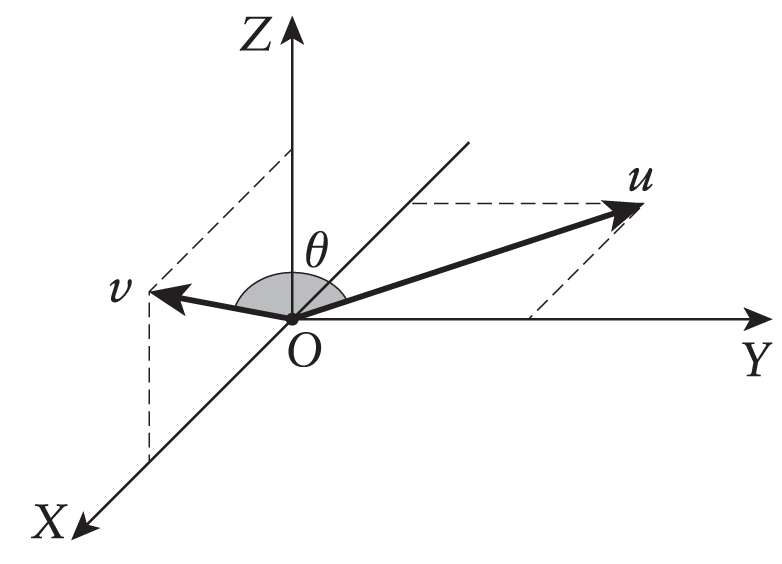
Τα διανύσματα $u$ , $v$ δεν είναι κανονικά. Τα διανύσματα όμως

u^{\prime}=\frac{1}{\sqrt{2}}(1,0,1),\ \ \ v^{\prime}=\frac{1}{\sqrt{2}}(-1,1,0)

είναι κανονικά και σχηματίζουν την ίδια γωνία όπως τα $u$ και $v$ .

Δύο διανύσματα $v$ , $u$ λέγονται ορθογώνια (orthogonal) όταν

\langle v,u\rangle=0\;.

Είναι εύκολο να αποδείξει κανείς ότι όταν τα διανύσματα $v$ , $u$ είναι ορθογώνια, τότε ισχύει το παρακάτω συμπέρασμα, γνωστό ως το Πυθαγόρειο Θεώρημα, βλ. Άσκηση 5.4.2.

Αν $u,v\in{\mathbb{R}}^{n}$ είναι ορθογώνια διανύσματα τότε $\|u+v\|^{2}=\|u\|^{2}+\|v\|^{2}$ .

Αν $D$ είναι διατεταγμένη βάση του ${\mathbb{R}}^{n}$ , τότε η $D$ λέγεται ορθογώνια βάση (orthogonal basis) του ${\mathbb{R}}^{n}$ , αν τα διανύσματα της $D$ είναι ανά δύο ορθογώνια. Αν η $D$ είναι ορθογώνια βάση του ${\mathbb{R}}^{n}$ και κάθε διάνυσμα της $D$ είναι κανονικό, τότε η $D$ λέγεται ορθοκανονική βάση (orthonormal basis) του ${\mathbb{R}}^{n}$ .

Παράδειγμα 5.4.3.

Είναι φανερό ότι η κανονική βάση $B=(e_{1},\ldots,e_{n})$ του ${\mathbb{R}}^{n}$ είναι ορθοκανονική. Πράγματι, $e_{1},\ldots,e_{n}$ είναι κανονικά αφού $\|e_{i}\|=1$ , για $i=1,\ldots,n$ και

\langle e_{i},e_{j}\rangle\;=\begin{cases}0,\;\hbox{για }i\neq j\\ 1,\;\hbox{για }i=j\end{cases}

δηλ. $e_{i},e_{j}$ είναι ανά δύο ορθογώνια για $1\leq i<j\leq n$ .

Όταν o $V$ είναι διανυσματικός υποχώρος του ${\mathbb{R}}^{n}$ γενικεύουμε τους προηγούμενους ορισμούς. Έτσι, αν $D$ είναι μία διατεταγμένη βάση του $V$ τότε η $D$ λέγεται ορθογώνια βάση (orthogonal basis) του $V$ αν τα διανύσματα της $D$ είναι ανά δύο ορθογώνια και η $D$ λέγεται ορθοκανονική βάση (orthonormal basis) του $V$ αν $D$ είναι ορθογώνια βάση και κάθε διάνυσμα της $D$ είναι κανονικό. Σημειώνουμε την επόμενη παρατήρηση.

Κάθε ορθογώνια βάση του $V$ γίνεται ορθοκανονική αν κανονικοποιήσουμε (normalize) τα στοιχεία της, δηλ. αν διαιρέσουμε τα στοιχεία της βάσης με το μήκος τους.

Παραδείγματα 5.4.4.

1.

Έστω $v_{1}=(1,1)$ , $v_{2}=(1,-1)$ . Αφού $\langle v_{1},v_{2}\rangle=0$ και $v_{1},v_{2}$ είναι γραμμικά ανεξάρτητα έπεται ότι $D=\{v_{1},v_{2}\}$ είναι ορθογώνια βάση του ${\mathbb{R}}^{2}$ . Το μήκος και των δύο διανυσμάτων της βάσης είναι $\|v_{1}\|=\|v_{2}\|=\sqrt{2}$ . Η βάση $D$ δεν είναι ορθοκανονική. Κανονικοποιούμε, θεωρώντας τα διανύσματα $w_{1}=1/\sqrt{2}(1,1)$ , $w_{2}=1/\sqrt{2}(1,-1)$ . Το σύνολο $\{w_{1},w_{2}\}$ είναι τώρα ορθοκανονική βάση του ${\mathbb{R}}^{2}$ .
2.

Έστω $v_{1}=1/{\sqrt{3}}(1,1,1)$ , $v_{2}=1/{\sqrt{6}}(-2,1,1)$ , $v_{3}=1/{\sqrt{2}}(0,-1,1)$ . Είναι εύκολο να δούμε ότι τα προηγούμενα διανύσματα είναι ανά δύο ορθογώνια. Θα δείξουμε ότι $v_{1}$ , $v_{2}$ , $v_{3}$ είναι γραμμικά ανεξάρτητα. Πράγματι, ο πίνακας

$A=\begin{bmatrix}1/{\sqrt{3}}&-2/{\sqrt{6}}&0\cr 1/{\sqrt{3}}&1/{\sqrt{6}}&-1/% {\sqrt{2}}\cr 1/{\sqrt{3}}&1/{\sqrt{6}}&1/{\sqrt{2}}\end{bmatrix}$
είναι ορθογώνιος (Παράδειγμα 5.4.1), και επομένως αντιστρέψιμος. Άρα τα $v_{1},v_{2},v_{3}$ είναι γραμμικά ανεξάρτητα, βλ. Πρόταση 3.3.5. Επίσης $\|v_{1}\|=\|v_{2}\|=\|v_{3}\|=1$ . Έπεται ότι το σύνολο $\{v_{1},v_{2},v_{3}\}$ είναι ορθοκανονική βάση του ${\mathbb{R}}^{3}$ .
3.

Έστω o υποχώρος $V$ του ${\mathbb{R}}^{3}$ που ορίζεται ως το σύνολο

$V=\{(x,y,z)\in{\mathbb{R}}^{3}:\ x+y-z=0\}\ .$
Αν $v_{1}=(1,0,1)$ , $v_{2}=(0,1,1)$ , τότε $\big(v_{1},v_{2}\big)$ είναι διατεταγμένη βάση για τον $V$ αλλά όχι ορθογώνια βάση για τον $V$ . Παρατηρούμε, όμως, ότι

$w=(-1,2,1)=-v_{1}+2v_{2}\in V$
και ότι $\langle v_{1},w\rangle=0$ , άρα $\{v_{1},w\}$ είναι ορθογώνια βάση για τον $V$ . Επομένως

$\{\frac{1}{\sqrt{2}}v_{1},\frac{1}{\sqrt{6}}w\}$
είναι ορθοκανονική βάση για τον $V$ .

To επόμενο θεώρημα δείχνει τη χρησιμότητα της εύρεσης ορθογώνιας βάσης.

Θεώρημα 5.4.5.

Έστω ότι $V$ υποχώρος του ${\mathbb{R}}^{n}$ και ότι τα διανύσματα $v_{1},\ldots,v_{t}\in V$ είναι ανά δύο ορθογώνια. Τότε τα διανύσματα $v_{1},\ldots,v_{t}$ είναι γραμμικά ανεξάρτητα και

v=\kappa_{1}v_{1}+\cdots+\kappa_{t}v_{t}\Longrightarrow\kappa_{i}=\frac{% \langle v,v_{i}\rangle}{\|v_{i}\|^{2}}\textrm{ gia }i=1,\ldots,t\;.

Απόδειξη.

Έστω ότι

\kappa_{1}v_{1}+\cdots+\kappa_{t}v_{t}={\bf 0}

(5.4.5.1)

Θα δείξουμε ότι οι συντελεστές $\kappa_{1},\ldots,\kappa_{t}$ είναι $0$ . Θα πάρουμε το εσωτερικό γινόμενο με το διάνυσμα $v_{1}$ και των δύο πλευρών της έκφρασης (5.4.5.1). Αφού

\langle v_{1},\kappa_{1}v_{1}+\cdots+\kappa_{t}v_{t}\rangle=\langle v_{1},{\bf 0% }\rangle=0

έπεται ότι

\langle v_{1},\kappa_{1}v_{1}\rangle+\cdots+\langle v_{1},\kappa_{t}v_{t}% \rangle=0

και

\kappa_{1}\langle v_{1},v_{1}\rangle+\cdots+\kappa_{t}\langle v_{1},v_{t}% \rangle=0\ ,

άρα

\kappa_{1}1+\kappa_{2}0+\cdots+\kappa_{t}0=0\Rightarrow\kappa_{1}=0\ .

Είναι φανερό ότι μπορούμε να επαναλάβουμε τα προηγούμενα παίρνοντας το εσωτερικό γινόμενο με κάθε ένα από τα διανύσματα $v_{1},\ldots,v_{t}$ και να δείξουμε ότι $\kappa_{1}=\cdots=\kappa_{t}=0$ . Επομένως τα διανύσματα $v_{1},\ldots,v_{t}$ είναι γραμμικά ανεξάρτητα.

Έστω τώρα $v=\kappa_{1}v_{1}+\cdots+\kappa_{t}v_{t}$ . Παίρνοντας το εσωτερικό γινόμενο με το $v_{i}$ προκύπτει ότι:

\langle v,v_{i}\rangle=\langle\kappa_{1}v_{1}+\cdots+\kappa_{t}v_{t},v_{i}% \rangle=\kappa_{i}\langle v_{i},v_{i}\rangle\Longrightarrow\kappa_{i}=\frac{% \langle v,v_{i}\rangle}{\langle v_{i},v_{i}\rangle}

από όπου προκύπτει και το ζητούμενο. ∎

Έστω $Β=(e_{1},\ldots,e_{n})$ η κανονική βάση του ${\mathbb{R}}^{n}$ . Το γινόμενο των πινάκων $C_{B}(u)^{Τ}C_{B}(v)$ είναι ένας $1\times 1$ πίνακας με μοναδικό στοιχείο το αποτέλεσμα του εσωτερικού γινομένου των $u$ , $v$ , δηλ.

C_{B}(u)^{Τ}C_{B}(v)=C_{B}(v)^{T}C_{B}(u)=[\langle v,u\rangle]\ .

Εξαιτίας αυτής της παρατήρησης και για συντομογραφία γράφουμε:

\langle v,u\rangle=v^{T}u\;.

Γενικότερα, αν $A\in\mathcal{M}_{n}({\mathbb{R}})$ και $Α=\begin{bmatrix}C_{B}(v_{1})&\ldots&C_{B}(v_{n})\end{bmatrix}$ , τότε

Α^{Τ}\ Α=\begin{bmatrix}v_{1}^{T}\,v_{1}&\ldots&v_{1}^{T}\,v_{n}\cr\vdots&&% \vdots\cr v_{n}^{T}\,v_{1}&\ldots&v_{n}^{T}\,v_{n}\end{bmatrix}.

Προκύπτει λοιπόν το εξής κριτήριο:

Πρόταση 5.4.6.

To σύνολο $D=\{v_{1},\ldots,v_{n}\}\subset{\mathbb{R}}^{n}$ είναι ορθογώνια βάση του ${\mathbb{R}}^{n}$ αν και μόνο αν o $A^{T}A$ είναι διαγώνιος πίνακας, όπου

Α=\begin{bmatrix}C_{B}(v_{1})&\cdots&C_{B}(v_{n})\end{bmatrix}\;.

To σύνολο $D$ είναι ορθοκανονική βάση του ${\mathbb{R}}^{n}$ αν και μόνο αν $A^{T}A=I_{n}$ , δηλ. αν και μόνο αν ο $Α$ είναι ορθογώνιος πίνακας.

H προηγούμενη πρόταση γενικεύεται ως εξής για το διανυσματικό υποχώρο $V$ του ${\mathbb{R}}^{n}$ .

Πρόταση 5.4.7.

Έστω $B$ η κανονική βάση του ${\mathbb{R}}^{n}$ , $V$ ένας διανυσματικός υποχώρος του ${\mathbb{R}}^{n}$ , με ${\rm dim}_{{\mathbb{R}}}V=m$ . Ένα υποσύνολο $D=\{v_{1},\ldots,v_{m}\}\subset V$ είναι ορθογώνια βάση του $V$ αν και μόνο αν o $A^{T}A$ είναι διαγώνιος $m\times m$ πίνακας, όπου

Α=\begin{bmatrix}C_{B}(v_{1})&\ldots&C_{B}(v_{m})\end{bmatrix}\;.

To σύνολο $D$ είναι ορθοκανονική βάση του ${\mathbb{R}}^{n}$ αν και μόνο αν $A^{T}A=I_{m}$ , δηλ. αν και μόνο αν ο $Α$ είναι ορθογώνιος πίνακας.

Είναι πλέον φανερό ότι αν οι στήλες του $A$ είναι ορθοκανονική βάση του ${\mathbb{R}}^{n}$ , τότε και οι γραμμές του $A$ είναι ορθοκανονική βάση του ${\mathbb{R}}^{n}$ .

Παραδείγματα 5.4.8.

1.

Στο Παράδειγμα 5.4.1 είδαμε ότι o

$A=\left[\begin{array}[]{rrr}1/\sqrt{3}&-2/\sqrt{6}&0\cr 1/\sqrt{3}&1/\sqrt{6}&% -1/\sqrt{2}\\ 1/\sqrt{3}&1/\sqrt{6}&1/\sqrt{2}\end{array}\right]$
είναι ορθογώνιος πίνακας. Συνεπώς

$\left(\frac{1}{\sqrt{3}}(1,1,1),\frac{1}{\sqrt{6}}(-2,1,1),\frac{1}{\sqrt{2}}(% 0,-1,1)\right)$
και

$\left((\frac{1}{\sqrt{3}},\ \frac{2}{\sqrt{6}},0),\ (\frac{1}{\sqrt{3}},\frac{% 1}{\sqrt{6}},-\frac{1}{\sqrt{2}}),\ (\frac{1}{\sqrt{3}},\frac{1}{\sqrt{6}},% \frac{1}{\sqrt{2}})\right),$
είναι δύο ορθοκανονικές βάσεις του ${\mathbb{R}}^{3}$ .
2.

Στο Παράδειγμα 5.4.4.3 είδαμε ότι

$\left(\frac{1}{\sqrt{2}}(1,0,1),\ \frac{1}{\sqrt{6}}(-1,2,1)\right)$
είναι ορθοκανονική βάση για το επίπεδο

$V=\{(x,y,z)\in{\mathbb{R}}^{3}:\ x+y-z=0\}\;.$
Έστω $B$ η κανονική βάση του ${\mathbb{R}}^{3}$ . O πίνακας $A$ της Πρότασης 5.4.7 είναι o $3\times 2$ πίνακας

$A=\displaystyle\left[\begin{array}[]{rr}{1}/{\sqrt{2}}&{-1}/{\sqrt{6}}\cr 0&{2% }/{\sqrt{6}}\cr{1}/{\sqrt{2}}&{1}/{\sqrt{6}}\end{array}\right].$
O αναγνώστης καλείται να διαπιστώσει ότι $A^{T}A=I_{2}$ .

Πως γενικεύονται τα προηγούμενα όταν o $V$ είναι ένας ${\mathbb{R}}$ -διανυσματικός χώρος; Αν $V$ είναι ένας ${\mathbb{R}}$ -διανυσματικό χώρος, τότε λέμε ότι o $V$ είναι Ευκλείδειος διανυσματικός χώρος (Euclidean vector space) αν μπορεί να ορισθεί ένα εσωτερικό γινόμενο (inner product) στον $V$ , εσωτερικό γινόμενο δηλ. μία συνάρτηση $\langle\ ,\rangle:V\times V\rightarrow{\mathbb{R}}$ για την οποία ισχύουν ιδιότητες, αντίστοιχες με αυτές του εσωτερικού γινομένου που μελετήσαμε στον ${\mathbb{R}}^{n}$ και τους υποχώρους του, βλ. Πίνακα 5.4.1. Στον επόμενο πίνακα έχουμε συγκεντρώσει αυτές τις ιδιότητες.

i.)

$\langle v,v\rangle\;\geq 0$ , $\forall v\in V$ και $\langle v,v\rangle=0$ αν και μόνο αν $v={\bf 0}$ .
ii.)

$\langle v,u\rangle=\langle u,v\rangle$ , $\forall v,w\in V$
iii.)

$\langle\kappa v+\lambda w,u\rangle=\kappa\langle v,u\rangle+\lambda\langle w,u\rangle$ , $\forall v,w\in V$ , $\forall\kappa,\lambda\in{\mathbb{R}}$ ,
iv.)

$\langle v,\kappa u+\lambda w\rangle\;=\kappa\langle v,u\rangle+\lambda\langle v% ,w\rangle$ , $\forall v,w\in V$ , $\forall\kappa,\lambda\in{\mathbb{R}}$ ,
v.)

$\langle v,{\bf 0}\rangle=0$ , $\forall v\in V$ .

Παραδείγματα 5.4.9.

1.

O ${\mathbb{R}}^{n}$ με το σύνηθες εσωτερικό γινόμενο.
2.

To σύνολο $V$ των συνεχών πραγματικών συναρτήσεων με πεδίο ορισμού το κλειστό διάστημα $[a,b]$ είναι Ευκλείδειος διανυσματικός χώρος με εσωτερικό γινόμενο

$\langle\;,\;\rangle:V\times V\rightarrow{\mathbb{R}},\ \langle f,g\rangle=\int% _{a}^{b}f(t)g(t)dt\;.$

Όλα τα συμπεράσματα αυτής της ενότητας επεκτείνονται με το φυσικότερο τρόπο σε Ευκλείδειους διανυσματικούς χώρους. Παραπέμπουμε τον αναγνώστη στα συγγράμματα της βιβλιογραφίας για περισσότερες λεπτομέρειες.

Μπορούμε, όμως, γενικότερα να ορίσουμε το σύνηθες εσωτερικό γινόμενο στον ${\mathbb{C}}^{n}$ και την έννοια του εσωτερικού γινομένου για τους ${\mathbb{C}}$ -διανυσματικούς χώρους. Το σύνηθες εσωτερικό γινόμενο (standard inner product) στον ${\mathbb{C}}^{n}$ ορίζεται ως εξής:

\langle(\alpha_{1},\ldots,\alpha_{n}),\;(\beta_{1},\ldots,\beta_{n})\rangle\;=% \alpha_{1}\overline{\beta_{1}}+\cdots+\alpha_{n}\overline{\beta_{n}}\;.

Λέμε ότι o ${\mathbb{C}}$ -διανυσματικός χώρος $V$ είναι Ερμητιανός διανυσματικός χώρος (Hermitian vector space) αν σε αυτόν ορίζεται ένα εσωτερικό ή ερμητιανό γινόμενο (inner product), δηλ. μία συνάρτηση $\langle\ ,\ \rangle:V\times V\rightarrow{\mathbb{C}}$ για την οποία ισχύουν οι ιδιότητες του επόμενου πίνακα.

i.)

$\langle v,v\rangle\in{\mathbb{R}}^{+}$ , $\forall v\in V$ και $\langle v,v\rangle=0$ αν και μόνο αν $v={\bf 0}$ .
ii.)

$\langle v,u\rangle=\overline{\langle u,v\rangle}$ , $\forall v,w\in V$ .
iii.)

$\langle\kappa v+\lambda w,u\rangle=\kappa\langle v,u\rangle+\lambda\langle w,u\rangle$ , $\forall v,w\in V$ , $\forall\kappa,\lambda\in{\mathbb{R}}$ .
iv.)

$\langle v,\kappa u+\lambda w\rangle\;=\overline{\kappa}\langle v,u\rangle+% \overline{\lambda}\langle v,w\rangle$ , $\forall v,w\in V$ , $\forall\kappa,\lambda\in{\mathbb{R}}$ .
v.)

$\langle v,{\bf 0}\rangle=0$ , $\forall v\in V$ .

Ένας πίνακας $A\in\mathcal{M}_{n}({\mathbb{C}})$ λέγεται ορθογώνιος (orthogonal) αν

A\overline{(A^{T})}=Ι_{n}.

Όπως σε έναν Ευκλείδειο διανυσματικό χώρο, έτσι και σε έναν Ερμητιανό διανυσματικό χώρο έχουμε τις έννοιες μίας ορθογώνιας και ορθοκανονικής βάσης. Τονίζουμε ότι αν o $A\in\mathcal{M}_{n}({\mathbb{R}})$ είναι ορθογώνιος στον ${\mathbb{R}}$ , τότε είναι ορθογώνιος και στον ${\mathbb{C}}$ . Έτσι, σύνολα που είναι ορθογώνιες (ορθοκανονικές) βάσεις στον ${\mathbb{R}}^{n}$ είναι ορθογώνιες (ορθοκανονικές) βάσεις στον ${\mathbb{C}}^{n}$ . Είναι όμως απαραίτητο για την ισχύ της θεωρίας μας, να χρησιμοποιούμε τους συζυγείς αναστρόφους πίνακες, όταν δουλεύουμε με μιγαδικούς αριθμούς.

Παράδειγμα 5.4.10.

O αναγνώστης καλείται να επιβεβαιώσει ότι o πίνακας

A=\frac{1}{\sqrt{2}}\begin{bmatrix}1&i\cr i&1\end{bmatrix}

είναι ορθογώνιος και ότι οι στήλες του $A$ δίνουν μία ορθοκανονική βάση του ${\mathbb{C}}^{2}$ .

Ασκήσεις Ενότητας 5.4

1.

Έστω $v=(1,2,3,4)$ . Να βρείτε $\|v\|$ , $\|3v\|$ , $\|\frac{1}{5}v\|$ , $d(u,v)$ .

Λύση
2.

Αν $u,v\in{\mathbb{R}}^{n}$ είναι ορθογώνια, τότε από τις ιδιότητες του εσωτερικού γινομένου, να αποδείξετε το Πυθαγόρειο Θεώρημα, δηλ. ότι

$\|u+v\|^{2}=\|u\|^{2}+\|v\|^{2}\;.$

Λύση
3.

Να αποδείξετε ότι τα $v_{1}=(-3,0,4)$ , $v_{2}=(4,0,-3)$ , $v_{3}=(0,5,0)$ δίνουν μία ορθογώνια βάση του ${\mathbb{R}}^{3}$ .

Λύση
4.

Αν $Α$ είναι ορθογώνιος πίνακας τότε να αποδείξετε ότι $A^{T}$ είναι ορθογώνιος πίνακας.

Λύση
5.

Για τον πίνακα

$A=\left[\begin{array}[]{cc}1&5\\ 5&1\end{array}\right]$
να βρείτε ένα διαγώνιο πίνακα $D$ και ένα πίνακα $P$ έτσι ώστε $D=P^{T}AP$ .

Λύση
6.

Να διαγωνιοποιήσετε ορθογώνια τον πίνακα

$\left[\begin{array}[]{ccc}1&0&0\\ 0&3&2\\ 0&2&6\end{array}\right].$

Λύση
7.

Έστω $V$ o χώρος των συνεχών πραγματικών συναρτήσεων στο διάστημα $[-\pi,\pi]$ με εσωτερικό γινόμενο

$\langle\;,\;\rangle:V\times V\rightarrow{\mathbb{R}},\ \langle f,g\rangle=\int% _{-\pi}^{\pi}f(t)g(t)dt\;.$

Να αποδείξετε ότι τα στοιχεία του (άπειρου) συνόλου

$\{1,\cos x,\sin x,\cos(2x),\sin(2x),\ldots,\cos(nx),\sin(nx),\ldots\;,\}$
είναι ανά δύο ορθογώνια. Να συμπεράνετε ότι ${\rm dim}_{{\mathbb{R}}}(V)=\infty$ .
8.

Να βρείτε ορθογώνιους πίνακες $A_{1}\in\mathcal{M}_{2}({\mathbb{R}})$ (αν υπάρχουν) τέτοιοι ώστε

$A_{1}=\begin{bmatrix}1/2&1/2\cr b&d\end{bmatrix},A_{2}=\begin{bmatrix}1/4&a\cr b% &d\end{bmatrix}.$

Λύση
9.

Να βρείτε μία ορθογώνια βάση στον ${\mathbb{C}}^{3}$ που να περιέχει το διάνυσμα $(1,0,i)$ .

Λύση
10.

Έστω ότι $\{u_{1},\ldots,u_{n}\}$ βάση για τον υποχώρο $U$ του ${\mathbb{R}}^{m}$ και έστω ότι $w\in{\mathbb{R}}^{m}$ . Να αποδείξετε ότι $\langle w,u\rangle=0$ , για κάθε $u\in U$ , αν και μόνο αν $\langle w,u_{i}\rangle=0$ , για $i=1,\ldots,n$ .
11.

Έστω ότι $h:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι γραμμική συνάρτηση. An

$\langle h(v),w\rangle=0,\textrm{ gia }v,w\in{\mathbb{R}}^{n},$
τότε $h=0_{{\mathbb{R}}^{n}}$ και $h(v)={\bf 0}$ , για $v\in{\mathbb{R}}^{n}$ . Να συμπεράνετε ότι αν $g:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι γραμμική συνάρτηση και

$\langle g(v),w\rangle=\langle v,w\rangle,\textrm{ gia }v,w\in{\mathbb{R}}^{n},$
τότε $g=\operatorname{id}_{{\mathbb{R}}^{n}}$ και $g(v)=v$ , για $v\in{\mathbb{R}}^{n}$ .

Λύση

5.5 Φασματικό Θεώρημα

Έστω ότι $\phi:\ {\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι μία γραμμική συνάρτηση, $Β$ είναι η κανονική βάση του ${\mathbb{R}}^{n}$ , και $Α=A_{B,B}^{\phi}$ . Ορίζουμε την προσαρτημένη γραμμική συνάρτηση (adjoint linear map) του $\phi$ , να είναι η γραμμική συνάρτηση $\phi^{*}$ $\phi^{*}:\ {\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ , με πίνακα

A_{B,B}^{\phi^{*}}=Α^{Τ}\;.

Παράδειγμα 5.5.1.

Έστω η γραμμική συνάρτηση $\phi:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}$ , $\phi(x,y)=(x+2y,3x-y)$ . Αν $Β$ είναι η κανονική βάση του ${\mathbb{R}}^{2}$ , τότε

A_{B,B}^{\phi}=\begin{bmatrix}1&2\cr 3&-1\end{bmatrix}\ .

Επομένως

A_{B,B}^{\phi^{*}}=\begin{bmatrix}1&3\cr 2&-1\end{bmatrix}\hbox{και}\phi^{*}:% \ {\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2},\ \ \phi^{*}(x,y)=(x+3y,2x-y)\;.

Μία σημαντική ιδιότητα του εσωτερικού γινομένου αφορά τις γραμμικές συναρτήσεις και τις προσαρτημένες συναρτήσεις.

Θεώρημα 5.5.2.

Έστω ότι $\phi:\ {\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι γραμμική συνάρτηση. Τότε

\langle\phi(v),w\rangle=\langle v,\phi^{*}(w)\rangle\;\textrm{gia}v,w\in{% \mathbb{R}}^{n}.

Απόδειξη.

Θα δείξουμε ότι

\phi(v)^{T}\;w=v^{T}\;\phi^{*}(w)\;

και ισοδύναμα ότι

C_{B}(\phi(v))^{T}\;C_{B}(w)=C_{B}(v)^{T}\;C_{B}(\phi^{*}(w))\;.

Από την Πρόταση 4.1.4, έπεται ότι

C_{B}(\phi(v))=Α\;C_{B}(v)\textrm{και}C_{B}(\phi^{*}(w))=A^{T}\;C_{B}(w)\;,

όπου $A=A_{B,B}^{\phi}$ . Άρα

\left(Α\ C_{B}(v)\right)^{Τ}C_{B}(w)=\left(C_{B}(v)^{T}A^{T}\right)C_{B}(w)=C_% {B}(v)^{T}\left(A^{T}C_{B}(w)\right)

και το ζητούμενο αποδείχθηκε.∎

Στη γλώσσα των πινάκων, μπορούμε να διατυπώσουμε το Θεώρημα 5.5.2 ως εξής:

Έστω ότι $A\in\mathcal{M}_{n}({\mathbb{R}})$ και $v\in{\mathbb{R}}^{n}$ . Τότε $\langle A\,v,v\rangle=\langle v,A^{T}v\rangle$ .

Είναι φανερό ότι $({\phi^{*}})^{*}=\phi$ . Άμεση λοιπόν συνέπεια του Θεωρήματος 5.5.2 είναι το επόμενο πόρισμα.

Πόρισμα 5.5.3.

Έστω ότι $\phi:\ {\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι γραμμική συνάρτηση. Τότε

\langle\phi^{*}(v),w\rangle=\langle v,\phi(w)\rangle\;\textrm{gia}v,w\in{% \mathbb{R}}^{n}.

Ειδικότερα

\langle\phi^{*}\phi(v),w\rangle=\langle\phi(v),\phi(w)\rangle\;\textrm{gia}v,w% \in{\mathbb{R}}^{n}.

Στη συνέχεια εξετάζουμε υπό ποιες συνθήκες μία γραμμική συνάρτηση $\phi:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ έχει $n$ ορθογώνια ιδιοδιανύσματα. Όταν αυτό συμβαίνει λέμε ότι η $\phi$ (και ο αντίστοιχος πίνακας ως προς οποιαδήποτε βάση του ${\mathbb{R}}^{n}$ ) είναι ορθογώνια διαγωνιοποιήσιμη (orthogonal diagonalizable). Τα $n$ ορθογώνια ιδιοδιανύσματα του ${\mathbb{R}}^{n}$ καθορίζουν ένα νέο σύστημα συντεταγμένων που διευκολύνει τη μελέτη της συνάρτησης. Από όσα έχουμε εξετάσει νωρίτερα και το Παράδειγμα 5.1.6.11 προκύπτει το εξής συμπέρασμα.

Πρόταση 5.5.4.

Ένας πίνακας $Α\in\mathcal{M}_{n}({\mathbb{R}})$ είναι ορθογώνια διαγωνιοποιήσιμος αν υπάρχει ορθογώνιος πίνακας $P\in\mathcal{M}_{n}({\mathbb{R}})$ έτσι ώστε

P^{T}A\;P=\begin{bmatrix}\lambda_{1}&&{0}\\ &\ddots&\\ {0}&&\lambda_{n}\end{bmatrix}\;.

Τα $\lambda_{1},\ldots,\lambda_{n}$ στην προηγούμενη έκφραση είναι οι ιδιοτιμές του $Α$ και είναι πραγματικοί αριθμοί. Οι στήλες του $P$ αντιστοιχούν σε ιδιοδιανύσματα του $Α$ .

Ο $Α$ είναι λοιπόν ορθογώνια διαγωνιοποιήσιμος όταν υπάρχει μία ορθοκανονική βάση του ${\mathbb{R}}^{n}$ που να αποτελείται από ιδιοδιανύσματα του $Α$ . To επόμενο θεώρημα δίνει μία ικανή και αναγκαία συνθήκη για να είναι ένας πίνακας ορθογώνια διαγωνιοποιήσιμος. To θεώρημα είναι γνωστόv ως το Φασματικό θεώρημα (spectral theorem). Για την αναλυτική απόδειξη του θεωρήματος παραπέμπουμε στο σύγγραμμα [2 , Θεώρημα 7.2.18]

Θεώρημα 5.5.5 (Φασματικό Θεώρημα).

Ο πίνακας $Α\in\mathcal{M}_{n}({\mathbb{R}})$ είναι ορθογώνια διαγωνιοποιήσιμος αν και μόνο αν $Α=Α^{Τ}$ .

Στη συνέχεια, στο Θεώρημα 5.5.6, θα αποδείξουμε μία ειδική περίπτωση του Φασματικού Θεωρήματος.

Θεώρημα 5.5.6.

Έστω ότι $Α\in\mathcal{M}_{2}({\mathbb{R}})$ και $A=A^{T}$ . Τότε o $A$ έχει δύο ορθογώνια ιδιοδιανύσματα.

Απόδειξη.

Έστω ότι $Α\in\mathcal{M}_{2}({\mathbb{R}})$ και $A=A^{T}$ . Στο Παράδειγμα 5.1.6.11 είδαμε ότι οι ιδιοτιμές του $Α$ είναι πραγματικοί αριθμοί. Έστω ότι $\lambda_{1}$ είναι μία από τις ιδιοτιμές του $Α$ και ότι $X_{1}=\begin{bmatrix}a_{1}&b_{1}\end{bmatrix}^{T}$ είναι ιδιοδιάνυσμα του $Α$ για την ιδιοτιμή $\lambda_{1}$ . Θεωρούμε τον ορθογώνιο πίνακα

P=\begin{bmatrix}a_{1}&-b_{1}\cr b_{1}&\ \;a_{1}\end{bmatrix}\ .

Θα δείξουμε ότι $X_{2}=\begin{bmatrix}-b_{1}&1_{1}\end{bmatrix}^{T}$ είναι ιδιοδιάνυσμα του $A$ . Έστω $v_{1}=(a_{1},b_{1})$ , $v_{2}=(-b_{1},a_{1})$ και $B$ η κανονική βάση του ${\mathbb{R}}^{2}$ . Έτσι, $X_{1}=C_{B}(v_{1})$ , $X_{2}=C_{B}(v_{2})$ . Για να δείξουμε ότι $X_{2}$ είναι ιδιοδιάνυσμα του $A$ αρκεί να δείξουμε ότι $AX_{2}=tX_{2}$ για κάποιον πραγματικό αριθμό $t$ . Θέτουμε $Y=AX_{2}$ Αφού $(v_{1},v_{2})$ είναι βάση του ${\mathbb{R}}^{2}$ , υπάρχουν $\kappa$ , $t\in{\mathbb{R}}$ έτσι ώστε $Y=\kappa X_{1}+tX_{2}$ . Ο στόχος μας, λοιπόν, είναι να δείξουμε ότι $\kappa=0$ . Για να τον πετύχουμε, θα υπολογίσουμε το γινόμενο $Y^{T}X_{1}=\left(AX_{2}\right)^{T}X_{1}$ . Κάνοντας τις πράξεις βρίσκουμε ότι

(AX_{2})^{T}X_{1}=X_{2}^{T}(A^{T}X_{1})=X_{2}^{T}(AX_{1})=X_{2}^{T}(\lambda_{1% }X_{1})=\lambda_{1}(X_{2}^{T}X_{1})={\bf 0}\ .

Αντικαθιστώντας $\kappa X_{1}+tX_{2}$ στη θέση του $AX_{2}$ βρίσκουμε ότι

(AX_{2})^{T}X_{1}=(\kappa X_{1}+tX_{2})^{Τ}X_{1}=(\kappa X_{1}^{T}+tX_{2}^{T})% X_{1}

=\kappa(X_{1}^{T}X_{1})+t(X_{2}^{T}X_{1})=\kappa(X_{1}^{T}X_{1})+t{\bf 0}=% \kappa(X_{1}^{T}X_{1})\ .

Αφού $X_{1}^{T}X_{1}\neq{\bf 0}$ και $\kappa(X_{1}^{T}X_{1})={\bf 0}$ έπεται ότι $\kappa=0$ . Άρα $AX_{2}=τX_{2}$ και το $X_{2}$ είναι ιδιοδιάνυσμα του $Α$ για την ιδιοτιμή $t$ . Επομένως ο $2\times 2$ πίνακας $Α$ έχει δύο ορθογώνια ιδιοδιανύσματα και είναι ορθογώνια διαγωνιοποιήσιμος.∎

Έστω ότι $B$ είναι η κανονική βάση του ${\mathbb{R}}^{n}$ και έστω ότι $\phi:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι μία γραμμική συνάρτηση. Παρατηρούμε ότι

A_{B,B}^{\phi}=({A_{B,B}^{\phi}})^{T}\textrm{ankaim'onoan}\phi=\phi^{*}.

H γραμμική συνάρτηση $\phi:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ λέγεται αυτοπροσαρτημένη (self-adjoint) an $\phi=\phi^{*}$ ενώ o πίνακας $A\in\mathcal{M}_{n}({\mathbb{R}})$ λέγεται αυτοπροσαρτημένος αν $A=A^{T}$ . Σύμφωνα με το Θεώρημα 5.5.5 η συνάρτηση $\phi:{\mathbb{R}}^{n}\rightarrow{\mathbb{R}}^{n}$ είναι ορθογώνια διαγωνιοποιήσιμη αν και μόνο αν η $\phi$ είναι αυτοπροσαρτημένη.

Παραδείγματα 5.5.7.

1.

Στο Παράδειγμα 5.2.5.2 δείξαμε ότι η συνάρτηση

$\phi:{\mathbb{R}}^{2}\rightarrow{\mathbb{R}}^{2}\;,\;\;\;\;(x,y)\mapsto(2x+y,x% +2y)$
είναι διαγωνιοποιήσιμη και ότι

$P^{T}\;A_{b,B}^{\phi}\;P=\begin{bmatrix}1&0\cr 0&3\end{bmatrix}\;,$
όπου

$P=\frac{1}{\sqrt{2}}\begin{bmatrix}-1&1\cr\ \;1&1\end{bmatrix}\;.$
Τα ιδιοδιανύσματα για τις ιδιοτιμές $1$ και $3$ της $\phi$ είναι ορθογώνια και $\phi=\phi^{*}$ .
2.
Θεωρούμε τον πίνακα

$Α=\left[\begin{array}[]{rrr}1&-1&0\\ -1&2&-1\\ 0&-1&1\end{array}\right].$
Παρατηρούμε ότι $Α=Α^{Τ}$ . Υπολογίζουμε το χαρακτηριστικό πολυώνυμο του $Α$ .

$P_{A}(x)=\left|\begin{array}[]{ccc}1-x&-1&\;\;0\\ -1&2-x&-1\\ \;\;0&-1&1-x\end{array}\right|=(1-x)[(2-x)(1-x)-1]+[-(1-x)]$
$\Rightarrow P_{A}(x)=(1-x)x(x-3).$
Οι ρίζες $\lambda_{1}=1$ , $\lambda_{2}=0$ , $\lambda_{3}=3$ του $P_{A}(x)$ είναι οι ιδιοτιμές του $A$ . Υπολογίζουμε τους ιδιοχώρους $V_{1}(A),V_{0}(A),V_{3}(A)$ του $Α$ . Έχουμε ότι
- –
  
  $V_{1}(A)=\{\;(-\kappa,0,\kappa)\;:\;\kappa\in\mathbb{R}\}=S(\{(-1,0,1)\})$ ,
- –
  
  $V_{0}(A)=\{\;(\kappa,\kappa,\kappa)\;:\;\kappa\in\mathbb{R}\}=S(\{(1,1,1)\})$ , και
- –
  
  $V_{3}(A)=\{\;(\kappa,-2\kappa,\kappa)\;:\;\kappa\in\mathbb{R}\}=S(\{(1,-2,1)\}$ .
Επιλέγουμε ένα διάνυσμα από κάθε ιδιοχώρο και βρίσκουμε μία βάση του ${\mathbb{R}}^{3}$ . An $\varepsilon_{1}=(-1,0,1)$ , $\varepsilon_{2}=(1,1,1)$ , $\varepsilon_{3}=(1,-2,1)$ , τότε $(\varepsilon_{1},\varepsilon_{2},\varepsilon_{3})$ είναι ορθογώνια βάση του ${\mathbb{R}}^{3}$ . Για $i=1,\ldots,3$ , διαιρούμε τα $\varepsilon_{i}$ με το μήκος τους και βρίσκουμε μία ορθοκανονική βάση του ${\mathbb{R}}^{3}$ από ιδιοδιανύσματα του $Α$ :

$\left(\;\frac{1}{\sqrt{2}}(-1,0,1),\;\;\frac{1}{\sqrt{3}}(1,1,1),\;\;\frac{1}{% \sqrt{6}}(1,-2,1)\;\right)\ .$
Ο πίνακας

$S=\left[\begin{array}[]{rrr}-{1}/{\sqrt{2}}&1/{\sqrt{3}}&1/{\sqrt{6}}\\ 0&1/{\sqrt{3}}&-{2}/{\sqrt{6}}\\ 1/{\sqrt{2}}&1/{\sqrt{3}}&1/{\sqrt{6}}\end{array}\right],$
είναι ορθογώνιος και

$S^{T}A\;S=\left[\begin{array}[]{rrr}1&0&0\\ 0&0&0\\ 0&0&3\end{array}\right].$
3.

Έστω $\phi:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ , $\phi(x,y,z)=(x,2y+4z,4y+3z)$ . O πίνακας της $\phi$ ως προς την κανονική βάση $B$ του ${\mathbb{R}}^{3}$ είναι o

$Α=\begin{bmatrix}1&0&0\cr 0&2&4\cr 0&4&3\end{bmatrix}\ .$
Αφού $Α=Α^{Τ}$ , o $Α$ είναι ορθογώνια διαγωνιοποιήσιμος και η $\phi=\phi^{*}$ είναι αυτοπροσαρτημένη γραμμική συνάρτηση. Παρατηρούμε ότι

$P_{A}(x)=(1-x)(x^{2}-5x-10)$
και ότι οι ιδιοτιμές του $Α$ είναι οι

$\lambda_{1}=1,\lambda_{2}=\frac{5+\sqrt{65}}{2},\ \lambda_{3}=\frac{5-\sqrt{65% }}{2}\;.$
H ελαττωμένη κλιμακωτή μορφή γραμμών του $A-I_{3}$ είναι o πίνακας

$\begin{bmatrix}0&1&0\cr 0&0&1\cr 0&0&0\end{bmatrix}\;.$
Έπεται ότι $V_{1}(A)=\{t(1,0,0):\ t\in{\mathbb{R}}\}$ και ότι $v_{1}=(1,0,0)$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $1$ . Στοιχειώδεις πράξεις γραμμών φέρνουν τον πίνακα $Α-\lambda_{2}I_{3}$ στη μορφή

$\begin{bmatrix}1&0&0\cr 0&{-1+\sqrt{65}}/{2}&4\cr 0&0&0\end{bmatrix}\;.$
Ο πίνακας αυτός δεν είναι σε ελαττωμένη κλιμακωτή μορφή γραμμών. Παρόλα αυτά μας δίνει όλες τις πληροφορίες που χρειαζόμαστε για να υπολογίσουμε τον ιδιοχώρο $V_{\lambda_{2}}(A)$ . Πράγματι αν $(x,y,z)\in V_{\lambda_{2}}(A)$ τότε από τη πρώτη γραμμή του πίνακα αυτού προκύπτει ότι $x=0$ , ενώ από τη δεύτερη γραμμή προκύπτει ότι

$\frac{-1+\sqrt{65}}{2}y+4z=0\Rightarrow z=\frac{1-\sqrt{65}}{8}y\ .$
Άρα

$V_{\lambda_{2}}(A)=\{t(0,1,\frac{1-\sqrt{65}}{8}):\ t\in{\mathbb{R}}\}=\{s(0,8% ,{1-\sqrt{65}}):\ s\in{\mathbb{R}}\}\$
και $v_{2}=(0,8,{1-\sqrt{65}})$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $\lambda_{2}$ . Ομοίως

$V_{\lambda_{3}}(A)=\{t(0,8,{1+\sqrt{65}}):\ t\in{\mathbb{R}}\}\$
και $v_{3}=(0,8,{1+\sqrt{65}})$ είναι ιδιοδιάνυσμα για την ιδιοτιμή $\lambda_{3}$ . Το σύνολο

$(v_{1},v_{2},v_{3})$
είναι ορθογώνια βάση του ${\mathbb{R}}^{3}$ που αποτελείται από ιδιοδιανύσματα του $A$ . Κανονικοποιούμε και βρίσκουμε μία ορθοκανονική βάση του ${\mathbb{R}}^{3}$ :

$((1,0,0),\frac{1}{\sqrt{130-2\sqrt{65}}}(0,8,{1-\sqrt{65}}),\frac{1}{\sqrt{130% +2\sqrt{65}}}(0,8,{1+\sqrt{65}})).$
Ο πίνακας

$P=\begin{bmatrix}1&0&0\cr 0&\frac{8}{\sqrt{130-2\sqrt{65}}}&\frac{8}{\sqrt{130% +2\sqrt{65}}}\cr 0&\frac{1-\sqrt{65}}{\sqrt{130-2\sqrt{65}}}{})&\frac{1+\sqrt{% 65}}{\sqrt{130+2\sqrt{65}}}\end{bmatrix}$
είναι ορθογώνιος και

$\begin{bmatrix}1&0&0\cr 0&\lambda_{2}&0\cr 0&0&\lambda_{3}\end{bmatrix}=P^{T}% AP\ .$

To Θεώρημα 5.5.5 προσδιορίζει πότε ακριβώς ένας πίνακας με στοιχεία πραγματικούς αριθμούς είναι ορθογώνια διαγωνιοποιήσιμος. Θέτουμε το αντίστοιχο ερώτημα για πίνακες με στοιχεία μιγαδικούς αριθμούς. An $A\in\mathcal{M}_{n}({\mathbb{C}})$ , πότε έχειο ${\mathbb{C}}^{n}$ μία βάση ορθογώνιων ιδιοδιανυσμάτων του $A$ ; O $A\in\mathcal{M}_{n}({\mathbb{C}})$ λέγεται ορθογώνια διαγωνιοποιήσιμος (orthogonal diagonalizable), αν υπάρχει ένας πίνακας $P$ έτσι ώστε $P^{-1}=\overline{(P^{T})}$ και

\overline{(P^{T})}AP=\begin{bmatrix}\lambda_{1}&\cdots&0\cr 0&\vdots\cr&&% \lambda_{n}\end{bmatrix}.

Οι στήλες του $P$ είναι ιδιοδιανύσματα του $A$ και $\lambda_{1},\ldots,\lambda_{n}$ είναι τα ιδιοδιανύσματα του $A$ . O $A$ λέγεται αυτοπροσαρτημένος ή Ερμητιανός (Hermitian) an $A=\overline{(A^{T})}$ . Στο Παράδειγμα 5.1.6.11 δείξαμε ότι an $A$ είναι αυτοπροσαρτημένος, τότε ο $Α$ έχει πραγματικές ιδιοτιμές. Μπορεί να αποδειχθεί ότι ισχύει το αντίστοιχο του Θεωρήματος 5.5.2 για τους μιγαδικούς $n\times n$ πίνακες και το σύνηθες εσωτερικό γινόμενο στον ${\mathbb{C}}^{n}$ .

Θεώρημα 5.5.8.

Αν $A\in\mathcal{M}_{n}({\mathbb{C}})$ και $v\in{\mathbb{C}}^{n}$ , τότε $\langle A\,v,v\rangle=\langle v,\overline{A^{T}}v\rangle$ .

Όπως στην απόδειξη του Φασματικού Θεωρήματος προκύπτει ότι αν o $A$ είναι αυτοπροσαρτημένος τότε o $A$ είναι ορθογώνια διαγωνιοποιήσιμος. Το αντίστροφο όμως δεν ισχύει. Υπάρχουν πίνακες στο $\mathcal{M}_{n}({\mathbb{C}})$ που είναι ορθογώνια διαγωνιοποιήσιμοι και που δεν είναι αυτοπροσαρτημένοι. Ποια είναι η κοινή ιδιότητα αυτών των πινάκων; Ένας πίνακας $A\in\mathcal{M}_{n}({\mathbb{C}})$ λέγεται κανονικός (normal) αν ισχύει η ακόλουθη συνθήκη:

A\;\overline{A}^{T}=\overline{A}^{T}\;A\;.

Είναι φανερό ότι an $A=\overline{(A^{T})}$ τότε o $A$ είναι κανονικός. Μπορεί, λοιπόν, κανείς να αποδείξει την εξής σημαντική πρόταση.

Θεώρημα 5.5.9.

Ένας πίνακας $Α\in\mathcal{M}_{n}({\mathbb{C}})$ είναι ορθογώνια διαγωνιοποιήσιμος αν και μόνο αν o $A$ είναι κανονικός. Ειδκότερα, an $A=\overline{(A^{T})}$ , τότε o $A$ είναι ορθογώνια διαγωνιοποιήσιμος.

Για την απόδειξη της προηγούμενης πρότασης, παραπέμπουμε στο σύγγραμμα [2, Θεώρημα 7.3.11].

Παραδείγματα 5.5.10.

O πίνακας

A=\begin{bmatrix}1&1&0\cr 0&1&1\cr 1&0&1\end{bmatrix}

είναι κανονικός και δεν είναι αυτοπροσαρτημένος. Στην Άσκηση 5.5.7, o αναγνώστης καλείται να διαγωνιοποιήσει ορθογώνια ton $A$ .

Σημειώνουμε ότι οι ιδιοτιμές ενός κανονικού πίνακα δεν είναι κατ' ανάγκη πραγματικοί αριθμοί. Παρατηρούμε, όμως, ότι οι ορθογώνιοι πίνακες είναι κανονικοί. Επίσης, οι ιδιοτιμές ενός ορθογώνιου πίνακα έχουν μέτρο $1$ , βλ. Άσκηση 5.5.5. Ισχύει, λοιπόν, το επόμενο συμπέρασμα.

Πόρισμα 5.5.11.

Έστω $A$ ένας ορθογώνιος $n\times n$ πίνακας. Τότε o $A$ είναι ορθογώνια διαγωνιοποιήσιμος. Οι ιδιοτιμές του $A$ έχουν μέτρο $1$ .

Ασκήσεις Eνότητας 5.5

1.

Έστω $\phi:{\mathbb{R}}^{3}\rightarrow{\mathbb{R}}^{3}$ , $\phi(x,y,z)=(x+2y,x+y+z,y-x)$ . Να βρεθεί o τύπος της $\phi^{*}$ .

Λύση
2.

Έστω $A\in\mathcal{M}_{m\times n}({\mathbb{R}})$ . Να αποδείξετε ότι $\operatorname{null}(A)=\operatorname{null}(A^{T}A)$ . Να συμπεράνετε ότι $\operatorname{rank}(A^{T}A)=\operatorname{rank}(A)$ .
3.

Έστω $A\in\mathcal{M}_{n}({\mathbb{R}})$ ορθογώνιος πίνακας, $\lambda$ ιδιοτιμή του $Α$ και $v$ ιδιοδιάνυσμα του $Α$ για την ιδιοτιμή $\lambda$ . Εξετάζοντας το εσωτερικό γινόμενο $\langle Av,Av\rangle$ να αποδείξετε ότι $\lambda=\pm 1$ .

Λύση
4.

Να βρείτε έναν ορθογώνια διαγωνιοποιήσιμο πίνακα $A$ στον $\mathcal{M}_{3}({\mathbb{R}})$ με πρώτη γραμμή $\begin{bmatrix}1&2&3\end{bmatrix}$ . Να βρείτε τις ιδιοτιμές του $A$ και βάσεις για τους ιδιοχώρους του.

Λύση
5.

Έστω $A\in\mathcal{M}_{n}({\mathbb{C}})$ ορθογώνιος πίνακας και $\lambda$ μία ιδιοτιμή του $Α$ . Να αποδείξετε ότι $\|\lambda\|=1$ . (Υπόδειξη: Άσκηση 3)

Λύση
6.

Να βρείτε έναν ορθογώνια διαγωνιοποιήσιμο πίνακα $A$ στον $\mathcal{M}_{2}({\mathbb{C}})$ με πρώτη γραμμή $\begin{bmatrix}1&1+3i\end{bmatrix}$ . Να βρείτε τις ιδιοτιμές του $A$ και βάσεις για τους ιδιοχώρους του.

Λύση
7.

Να διαγωνιοποιήσετε ορθογώνια τον

$A=\begin{bmatrix}1&1&0\cr 0&1&1\cr 1&0&1\end{bmatrix}.$

5.6 Σύντομα Ιστορικά Στοιχεία

Οι ιδιοτιμές εμφανίστηκαν για πρώτη φορά στη μελέτη των τετραγωνικών μορφών και των διαφορικών εξισώσεων. H σημασία της ύπαρξης των ιδιοδιανυσμάτων έγινε αντιληπτή τον 18ο αιώνα από τους Euler και Lagrange. Στις αρχές του 19ου αιώνα o Cauchy αντιλήφθηκε ότι τα αποτελέσματά τους μπορούν να χρησιμοποιηθούν για την ταξινόμηση των κωνικών επιφανειών, ενώ o Fourier εφάρμοσε τις ιδέες τους στο βιβλίο του Αναλυτική Θεωρία της Θερμότητας. O όρος χαρακτηριστικό πολυώνυμο οφείλεται στον Cauchy, o οποίος και απέδειξε το Φασματικό Θεώρημα. O Hermite εισήγαγε τους Ερμητιανούς πίνακες το 1855 και στις αρχές του 20ου αιώνα o Hilbert επέκτεινε τη θεωρία σε άπειρους πίνακες. O όρος eigenvectors οφείλεται σε αυτόν. H κανονική μορφή του Jordαν εμφανίστηκε στη δουλειά του Jordan το 1870.

Βιβλιογραφία

1.

H. Anton, C. Rorres, Elementary Linear Algebra, Applications Version, John Wiley and Sons, 1994.
2.

Θ. Θεοχάρη-Αποστολίδη, Χ. Χαραλάμπους, Β. Βαβατσούλας, Εισαγωγή στη Γραμμική Άλγεβρα, Θεσσαλονίκη 2006.
3.

V. Katz, Ιστορία των Μαθηματικών, Πανεπιστημιακές Εκδόσεις Κρήτης, 2013.
4.

K. Nicholoson, Elementary Linear Algebra, McGraw-Hill, 2001.
5.

Th. Shiffrin and M. R.Adams, Linear Algebra, a Geometric Approach, W. H. Freeman and Company, 2002.
6.

S. H. Weintraub, Jordan Canonical Form, Theory and Practice, Morgan & Claypool Publishers, 2009.

Κεφάλαιο 5Ιδιοτιμές, Ιδιοδιανύσματα

5.1 Ιδιοτιμές και Ιδιοδιανύσματα

Ορισμός 5.1.1.

Παραδείγματα 5.1.2.

Ορισμός 5.1.3.

Πρόταση 5.1.4.

Απόδειξη.

Παραδείγματα 5.1.5.

Παραδείγματα 5.1.6.

Απόδειξη.

Πρόταση 5.1.7.

Απόδειξη.

Παραδείγματα 5.1.8.

Απόδειξη.

Ασκήσεις Ενότητας 5.1

5.2 Ιδιοχώροι και το Χαρακτηριστικό Πολυώνυμο

Παραδείγματα 5.2.1.

Πρόταση 5.2.2.

Απόδειξη.

Παραδείγματα 5.2.3.

Πρόταση 5.2.4.

Απόδειξη.

Παραδείγματα 5.2.5.

Θεώρημα 5.2.6.

Παράδειγμα 5.2.7.

Ασκήσεις Ενότητας 5.2

5.3 Διαγωνιοποιήσιμοι Πίνακες

Παραδείγματα 5.3.1.

Πρόταση 5.3.2.

Απόδειξη.

Θεώρημα 5.3.3.

Πόρισμα 5.3.4.

Απόδειξη.

Παραδείγματα 5.3.5.

Θεώρημα 5.3.6.

Παραδείγματα 5.3.7.

Θεώρημα 5.3.8.

Παράδειγμα 5.3.9.

Ασκήσεις Ενότητας 5.3

5.4 Ορθογώνιοι Πίνακες και Εσωτερικό Γινόμενο στον ℝn

Παραδείγματα 5.4.1.

Παράδειγμα 5.4.2.

Παράδειγμα 5.4.3.

Παραδείγματα 5.4.4.

Θεώρημα 5.4.5.

Απόδειξη.

Πρόταση 5.4.6.

Πρόταση 5.4.7.

Παραδείγματα 5.4.8.

Παραδείγματα 5.4.9.

Παράδειγμα 5.4.10.

Ασκήσεις Ενότητας 5.4

5.5 Φασματικό Θεώρημα

Παράδειγμα 5.5.1.

Θεώρημα 5.5.2.

Απόδειξη.

Πόρισμα 5.5.3.

Πρόταση 5.5.4.

Θεώρημα 5.5.5 (Φασματικό Θεώρημα).

Θεώρημα 5.5.6.

Απόδειξη.

Παραδείγματα 5.5.7.

Θεώρημα 5.5.8.

Θεώρημα 5.5.9.

Παραδείγματα 5.5.10.

Πόρισμα 5.5.11.

Ασκήσεις Eνότητας 5.5

5.6 Σύντομα Ιστορικά Στοιχεία

Βιβλιογραφία

5.4 Ορθογώνιοι Πίνακες και Εσωτερικό Γινόμενο στον ${\mathbb{R}}^{n}$