Next: 6.8 Η ανισότητα Bernstein. Up: 6. Σύγκλιση των μερικών Previous: 6.6 Άλλες συνθήκες που Contents Index
Το πρώτο και βασικότερο αποτέλεσμα που αφορά τους συντελεστές Fourier
μιας ![]() συνάρτησης είναι το ακόλουθο:
συνάρτησης είναι το ακόλουθο:
Μια απόδειξη αυτού έχουμε περιγράψει στο Πρόβλημα 1.38. Με αυτά που έχουμε μάθει μέχρι τώρα μια άλλη απόδειξη προκύπτει για τους παρακάτω λόγους: (α) σίγουρα ισχύει για τριγωνομετρικά πολυώνυμα (η ακολουθία των συντελεστών Fourier τους όχι μόνο συγκλίνει στο 0 αλλά είναι και τελικά ίση με μηδέν) (β) τα τριγωνομετρικά πολυώνυμα είναι πυκνά στο χώρο
Γενικά όσο πιο «ομαλή» είναι μια συνάρτηση (όσο πιο «συνεχής», όσο πιο παραγωγίσιμη, κλπ) τόσο πιο γρήγορα φθίνουν οι συντελεστές Fourier της. Τα αποτελέσματα που θα δούμε παρακάτω κάνουν την παραπάνω γενική αρχή πιο συγκεκριμένη.
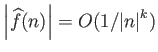 .
Η βελτίωση οφείλεται σε χρήση του Λήμματος Riemann-Lebesgue (Θεώρημα 6.6).
Αφού έχουμε από το Θεώρημα 3.1 για
.
Η βελτίωση οφείλεται σε χρήση του Λήμματος Riemann-Lebesgue (Θεώρημα 6.6).
Αφού έχουμε από το Θεώρημα 3.1 για
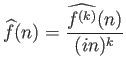
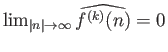 που συνεπάγεται το ζητούμενο.
που συνεπάγεται το ζητούμενο.
Το Πρόβλημα 5.9 αποτελεί επίσης μια έκφραση της αρχής «ομαλότητα συνεπάγεται
μείωση των συντελεστών Fourier»: αν
![]() τότε ισχύει
τότε ισχύει
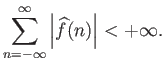
Το να είναι μια συνάρτηση
![]() Lipschitz,
το να υπάρχει δηλ. πεπερασμένος αριθμός
Lipschitz,
το να υπάρχει δηλ. πεπερασμένος αριθμός ![]() ώστε να ισχύει
ώστε να ισχύει
Απόδειξη.
Παρατηρούμε πρώτα ότι
![]() .
Έχουμε λοιπόν
.
Έχουμε λοιπόν
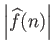 |
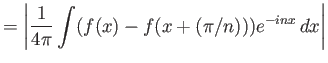 |
|
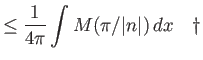 |
||
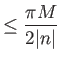 |
Αν
![]() λέμε ότι μια συνάρτηση
λέμε ότι μια συνάρτηση
![]() είναι Lipschitz-
είναι Lipschitz-![]() αν
υπάρχει πεπερασμένη σταθερά
αν
υπάρχει πεπερασμένη σταθερά ![]() τ.ώ. να ισχύει
τ.ώ. να ισχύει
(β) Αν μια συνάρτηση
![]() ικανοποιεί την (6.10) για κάποιο
ικανοποιεί την (6.10) για κάποιο ![]() δείξτε
ότι η συνάρτηση είναι αναγκαστικά σταθερή (και άρα δεν έχει ιδιαίτερη χρησιμότητα να μιλάμε για
συναρτήσεις που είναι Lipschitz-
δείξτε
ότι η συνάρτηση είναι αναγκαστικά σταθερή (και άρα δεν έχει ιδιαίτερη χρησιμότητα να μιλάμε για
συναρτήσεις που είναι Lipschitz-![]() με
με ![]() ).
).
Υπόδειξη: Για το (β) δείξτε ότι η παράγωγος της ![]() είναι παντού ίση με 0.
είναι παντού ίση με 0.
Στο επόμενο θεώρημα η μείωση των συντελεστών Fourier είναι αποτέλεσμα της μονοτονίας της συνάρτησης (η οποία πρέπει συνεπώς να θεωρείται κάποιο είδος ομαλότητας).
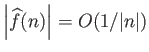 .
Πιο συγκεκριμένα, αν
.
Πιο συγκεκριμένα, αν
Απόδειξη.
Το δείχνουμε πρώτα όταν η συνάρτηση ![]() είναι κλιμακωτή και αύξουσα (ή φθίνουσα; αυτό δεν έχει καμιά σημασία
οπότε περιοριζόμαστε από δω και πέρα σε αύξουσες).
Αν η συνάρτηση είναι της μορφής
είναι κλιμακωτή και αύξουσα (ή φθίνουσα; αυτό δεν έχει καμιά σημασία
οπότε περιοριζόμαστε από δω και πέρα σε αύξουσες).
Αν η συνάρτηση είναι της μορφής
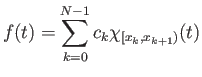
![$\displaystyle \widehat{\chi_{[a,b]}}(n) = \frac{i}{2\pi n}(e^{-ibn}-e^{-ian})
$](img1781.png)
Για να δείξουμε το ζητούμενο για οποιαδήποτε
![]() που είναι αύξουσα στο
που είναι αύξουσα στο
![]() χρειαζόμαστε το ακόλουθο αποτέλεσμα προσέγγισης.
χρειαζόμαστε το ακόλουθο αποτέλεσμα προσέγγισης.
Υπόδειξη: Για κάθε φυσικό ![]() ορίζουμε τη διαμέριση
ορίζουμε τη διαμέριση
![]() με
με
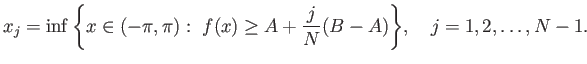
Με δεδομένο το αποτέλεσμα του Προβλήματος 6.12 η απόδειξη του Θεωρήματος 6.10
συμπληρώνεται ως εξής. Αν η ![]() είναι όπως στην εκφώνηση του Θεωρήματος και η
είναι όπως στην εκφώνηση του Θεωρήματος και η ![]() όπως στο Πρόβλημα
6.12 τότε
όπως στο Πρόβλημα
6.12 τότε
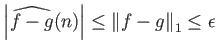 ενώ για την
ενώ για την
Έχουμε δει, σε διάφορες μορφές της, την αρχή ότι η ομαλότητα της συνάρτησης συνεπάγεται
ένα ρυθμό μείωσης των συντελεστών Fourier. Φυσιολογικά γεννιέται το ερώτημα αν υπάρχει
όριο στο πόσο αργά μπορεί μια ακολουθία συντελεστών Fourier να συγκλίνει στο 0, όπως
προβλέπει το Λήμμα Riemann-Lebesgue (Θεώρημα 6.6).
Συνέπεια του επόμενου Θεωρήματος 6.11 και του Προβλήματος 6.13
είναι ότι δεν υπάρχει τέτοιο όριο και ότι υπάρχουν ![]() συναρτήσεις των οποίων οι συντελεστές
Fourier συγκλίνουν στο 0 όσο αργά θέλουμε.
συναρτήσεις των οποίων οι συντελεστές
Fourier συγκλίνουν στο 0 όσο αργά θέλουμε.
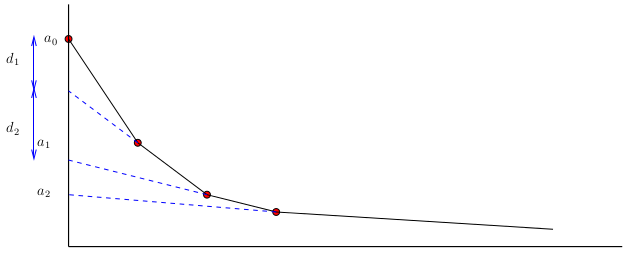
Σχήμα 6.3: Πώς γράφουμε μια κυρτή ακολουθία σαν άθροισμα «τριγώνων»
Παρατηρούμε κατ' αρχήν ότι οι συντελεστές Fourier ενός πυρήνα του Fejér ![]() είναι μια
άρτια κυρτή ακολουθία, όπως και η
είναι μια
άρτια κυρτή ακολουθία, όπως και η ![]() . Έπειτα δείχνουμε ότι η ακολουθία
. Έπειτα δείχνουμε ότι η ακολουθία ![]() μπορεί να γραφεί σαν
άθροισμα
μπορεί να γραφεί σαν
άθροισμα
Ο ευκολότερος τρόπος είναι να δει κανείς ότι ισχύει κάτι τέτοιο είναι να παρατηρήσει (δείτε Σχήμα 6.3)
ότι μια κυρτή πολυγωνική γραμμή (όπως αυτή που ορίζουν τα σημεία ![]() .
.![]() ) μπορεί να γραφεί
σαν άθροισμα από τρίγωνα όπως φαίνεται στο Σχήμα. Οι αριστερές πλευρές των τριγώνων είναι πάνω στον
άξονα των
) μπορεί να γραφεί
σαν άθροισμα από τρίγωνα όπως φαίνεται στο Σχήμα. Οι αριστερές πλευρές των τριγώνων είναι πάνω στον
άξονα των ![]() και έχουν μήκος
και έχουν μήκος ![]() και οι πλευρές τους προκύπτουν αν προεκτείνουμε τις πλευρές
και οι πλευρές τους προκύπτουν αν προεκτείνουμε τις πλευρές
![]() -
-![]() της πολυγωνικής γραμμής προς τα αριστερά μέχρι να τμήσουν τον άξονα των
της πολυγωνικής γραμμής προς τα αριστερά μέχρι να τμήσουν τον άξονα των ![]() .
.
Αν τώρα θέσουμε
Υπόδειξη: Το να είναι η ακολουθία ![]() .
.![]() , κυρτή ισοδυναμεί με το να είναι η μη αρνητική ακολουθία
, κυρτή ισοδυναμεί με το να είναι η μη αρνητική ακολουθία
Αντίθετα με την περίπτωση του Θεωρήματος 6.11 όπου η ακολουθία
![]() είναι άρτια, αν μια συνάρτηση έχει περιττή ακολουθία συντελεστών Fourier
τότε αυτοί υπόκεινται σε κάποια ελάχιστη ταχύτητα σύγκλισης στο 0.
είναι άρτια, αν μια συνάρτηση έχει περιττή ακολουθία συντελεστών Fourier
τότε αυτοί υπόκεινται σε κάποια ελάχιστη ταχύτητα σύγκλισης στο 0.
Απόδειξη.
Αφού
![]() έπεται ότι η συνάρτηση
έπεται ότι η συνάρτηση
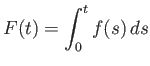
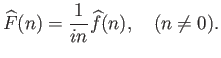
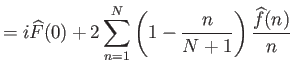 |
||
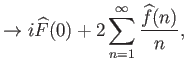 |
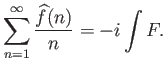
Το επόμενο εύκολο πόρισμα του Θεωρήματος 6.12 είναι το πρώτο αποτέλεσμα που συναντάμε
από το οποίο φαίνεται ότι υπάρχουν ακολουθίες που συγκλίνουν στο 0 και οι οποίες δεν
είναι ακολουθίες συντελεστών Fourier κάποιας ![]() συνάρτησης. Πάρτε για παράδειγμα
συνάρτησης. Πάρτε για παράδειγμα
![]() στο Πόρισμα 6.3.
στο Πόρισμα 6.3.
Mihalis Kolountzakis 2015-11-28