Next: Βιβλιογραφία Up: 6. Σύγκλιση των μερικών Previous: 6.7 Ρυθμός μείωσης των Contents Index
Απόδειξη.
Θα αποδείξουμε πρώτα την ασθενέστερη ανισότητα
Ας είναι
![]() τ.ώ. να ισχύει
τ.ώ. να ισχύει

Σχήμα 6.4: Οι συντελεστές Fourier της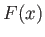
Μια καλή επιλογή είναι η συνάρτηση ![]() της οποίας οι συντελεστές Fourier φαίνονται στο Σχήμα
6.4.
της οποίας οι συντελεστές Fourier φαίνονται στο Σχήμα
6.4.
Η συνάρτηση αυτή μπορεί να γραφεί ως
Για να αποδειξουμε την (6.17) θα χρειαστεί να βρούμε μια άλλη συνάρτηση ![]() η οποία
να ικανοποιεί την (6.19) και να έχει
η οποία
να ικανοποιεί την (6.19) και να έχει ![]() νόρμα οσοδήποτε κοντά στο
νόρμα οσοδήποτε κοντά στο ![]() (αντί για
(αντί για ![]() που έχουμε
ήδη καταφέρει).
που έχουμε
ήδη καταφέρει).
Έστω λοιπόν
![]() .
Ορίζουμε μια νέα συνάρτηση
.
Ορίζουμε μια νέα συνάρτηση ![]() τ.ώ. να ισχύει
τ.ώ. να ισχύει ![]() όπως πριν (αυτό ισοδυναμεί με το ότι
όπως πριν (αυτό ισοδυναμεί με το ότι
![]() για
για
![]() ) και τέτοια ώστε
) και τέτοια ώστε

Σχήμα 6.5: Οι συντελεστές Fourier τηςείναι αυτοί της
«ανοιγμένοι» κατά
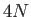
Υπόδειξη: Σχεδιάστε πρώτα τους συντελεστές Fourier της συνάρτησης
![]() ,
χρησιμοποιώντας το Σχήμα 6.5 και τα Προβλήματα 2.20
και 2.21.
,
χρησιμοποιώντας το Σχήμα 6.5 και τα Προβλήματα 2.20
και 2.21.
Υπόδειξη: Συμπληρώστε τις λεπτομέρειες στα παρακάτω.
(α) Η μάζα του πυρήνα ![]() «συγκεντρώνεται» κοντά στο 0
(δείτε Ορισμό 4.1 του τι σημαίνει «καλός πυρήνας», ιδιότητα 3)
άρα η μάζα του
«συγκεντρώνεται» κοντά στο 0
(δείτε Ορισμό 4.1 του τι σημαίνει «καλός πυρήνας», ιδιότητα 3)
άρα η μάζα του ![]() συγκεντρώνεται στα
σημεία
συγκεντρώνεται στα
σημεία
![]() ,
,
![]() .
Πρακτικά αυτό σημαίνει ότι για ένα ολοκλήρωμα της μορφής
.
Πρακτικά αυτό σημαίνει ότι για ένα ολοκλήρωμα της μορφής
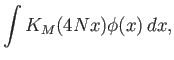
(β) Για
![]() «κοντά» σε ένα σημείο της μορφής
«κοντά» σε ένα σημείο της μορφής
![]() το
το
![]() είναι κοντά
στο 0 ή στο
είναι κοντά
στο 0 ή στο ![]() .
(Αν
.
(Αν ![]() ή
ή ![]() τότε είναι κοντά στο 0 και είναι κοντά στο
τότε είναι κοντά στο 0 και είναι κοντά στο ![]() αν
αν ![]() ή
ή ![]() .)
Άρα, λόγω της παρατήρησης στο (α), το ολοκλήρωμα
.)
Άρα, λόγω της παρατήρησης στο (α), το ολοκλήρωμα
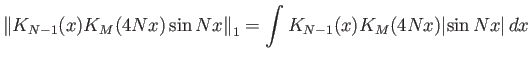
(γ) Χρησιμοποιούμε την ταυτότητα
![]() και γράφουμε το προηγούμενο ολοκλήρωμα ως
και γράφουμε το προηγούμενο ολοκλήρωμα ως
Mihalis Kolountzakis 2015-11-28