4.7 Cesáro μέσοι όροι της σειράς Fourier και το θεώρημα του Fejér

Το Θεώρημα 4.6, εφαρμοσμένο στην ακολουθία των μερικών αθροισμάτων της σειράς Fourier μιας συνάρτησης,

$$S_N(f)(x) = \sum_{k=-N}^N \widehat{f}(k) e^{ikx},$$

μας λέει ότι αν το όριο

$$\alpha = \lim_{N\to\infty}S_N(f)(x)$$

υπάρχει για κάποιο $x \in {\mathbb{R}}$ τότε υπάρχει και το όριο των μέσων όρων των $S_N{f}(x)$

$$\sigma_N(f)(x) = \frac{1}{N+1} \sum_{n=0}^N S_n(f)(x)$$ (4.19)

και είναι πάλι το $\alpha$.

Άσκηση 4.9   Δείξτε ότι

$$\sigma_N(f)(x) = \sum_{k=-N}^N \left(1-\frac{{\left\vert{k}\right\vert}}{N+1}\right) \widehat{f}(k) e^{ikx}.$$ (4.20)

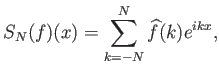
Ενδέχεται όμως να υπάρχει το όριο των μέσων (4.19) (λέγονται συνήθως Cesáro μέσοι της $f$ στο $x$) χωρίς να υπάρχει το όριο των $S_N(f)(x)$ και αυτό ακριβώς είναι που καθιστά τους Cesáro μέσους ένα χρήσιμο υποκατάστατο των μερικών αθροισμάτων. Στην περίπτωση που ισχύει

$$\alpha = \lim_{N\to\infty}\sigma_N(f)(x)$$

λέμε ότι η σειρά Fourier της $f$ στο σημείο $x$ είναι Cesáro αθροίσιμη στο $\alpha$. Εν γένει περιμένουμε η φυσιολογική συμπεριφορά να είναι $\alpha = f(x)$. Η πρώτη περίπτωση που αυτό συμβαίνει είναι ακριβώς όταν $f \in C({\mathbb{T}})$ και αυτό είναι το περιεχόμενο κλασικού θεωρήματος του Fejér.

Θεώρημα 4.7 (Fejér)   Αν $f \in C({\mathbb{T}})$ τότε $\sigma_n(f)(x) \to f(x)$ ομοιόμορφα για $x \in {\mathbb{R}}$. Με άλλα λόγια

$${\left\Vert{\sigma_n(f) - f}\right\Vert}_{L^\infty({\mathbb{T}})} \to 0 (n\to\infty).$$ (4.21)

Το Θεώρημα του Fejér μας δίνει μια νέα απόδειξη του θεωρήματος της Μοναδικότητας 4.1 για συνεχείς συναρτήσεις.

Πόρισμα 4.5 (Μοναδικότητα)   Αν $f,g \in C({\mathbb{T}})$ και για κάθε $n\in{\mathbb{Z}}$ έχουμε $\widehat{f}(n) = \widehat{g}(n)$ τότε $f(x) = g(x)$ για κάθε $x \in {\mathbb{R}}$.

Απόδειξη του Πορίσματος 4.5.
Αφού οι δύο συναρτήσεις έχουν τους ίδιους συντελεστές Fourier οι ποσότητες $\sigma_n(f)(x)$ και $\sigma_n(g)(x)$ θα ταυτίζονται για κάθε $x \in {\mathbb{R}}$ αφού αυτές ορίζονται μέσω των συντελεστών Fourier της κάθε συνάρτησης. Αφού $f(x) = \lim_{n\to\infty}\sigma_n(f)(x)$ και $g(x) = \lim_{n\to\infty}\sigma_n(g)(x)$ για κάθε $x \in {\mathbb{R}}$ έπεται ότι $f(x) = g(x)$.

Πόρισμα 4.6 (Μοναδικότητα στο $L^1({\mathbb{T}})$)   Αν $f \in L^1({\mathbb{T}})$ και $\widehat{f}(n) = 0$ για κάθε $n\in{\mathbb{Z}}$ τότε $f=0$ σχεδόν παντού.

Απόδειξη.
Από τον ορισμό (4.19) προκύπτει ότι $\sigma_n(f)=0$ για κάθε $n\in{\mathbb{N}}$ και άρα, από το Πόρισμα 4.8 παρακάτω για $p=1$, προκύπτει ότι $f=0$ σ.π.

Ένα άλλο πολύ χρήσιμο πόρισμα του Θεωρήματος του Fejér 4.7 είναι το ακόλουθο ανάλογο του θεωρήματος του Weierstrass (ότι τα αλγεβρικά πολυώνυμα προσεγγίζουν ομοιόμορφα κάθε συνεχή συνάρτηση σε κλειστό και φραγμένο διάστημα).

Πόρισμα 4.7   Τα τριγωνομετρικά πολυώνυμα είναι πυκνά στο χώρο $C({\mathbb{T}})$ με την ομοιόμορφη ($L^\infty$) μετρική.

Απόδειξη του Πορίσματος 4.7.
Αν $f \in C({\mathbb{T}})$ τότε οι συναρτήσεις $\sigma_n(f)(x)$ είναι τριγωνομετρικά πολυώνυμα και προσεγγίζουν ομοιόμορφα την $f$.

Άσκηση 4.10   Αν $f \in L^p({\mathbb{T}})$, $1 \le p < +\infty$, δείξτε ότι υπάρχει ακολουθία τριγωνομετρικών πολυωνύμων $p_n$ τ.ώ. ${\left\Vert{p_n-f}\right\Vert}_{L^p({\mathbb{T}})} \to 0$.

Υπόδειξη: Χρησιμοποιήστε το Πόρισμα 4.7 και το γεγονός ότι οι συνεχείς συναρτήσεις είναι πυκνές στους χώρους $L^p({\mathbb{T}})$ με τις αντίστοιχες μετρικές.