Next: 2. Τριγωνομετρικά πολυώνυμα Up: 1. Μέτρο και ολοκλήρωμα Previous: 1.2 Ολοκλήρωμα Lebesgue Contents Index
Μέχρι στιγμής έχουμε δει τον χώρο ![]() , όπου
, όπου
![]() έχει
έχει ![]() ,
που απαρτίζεται από όλες
τις συναρτήσεις
,
που απαρτίζεται από όλες
τις συναρτήσεις
![]() που είναι ολοκληρώσιμες, ισχύει δηλ. για αυτές
που είναι ολοκληρώσιμες, ισχύει δηλ. για αυτές
![]() .
Αν τώρα
.
Αν τώρα
![]() ορίζουμε το χώρο
ορίζουμε το χώρο ![]() να απαρτίζεται από όλες τις συναρτήσεις
να απαρτίζεται από όλες τις συναρτήσεις
![]() για τις οποίες
για τις οποίες
![]() .
Η
.
Η ![]() νόρμα της
νόρμα της
![]() είναι η ποσότητα
είναι η ποσότητα
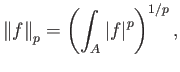
Απαραίτητο λοιπόν είναι να ισχύει η «τριγωνική ανισότητα»
Τέλος, για να μπορεί να παίξει η ποσότητα
![]() το ρόλο της απόστασης ανάμεσα
στις
το ρόλο της απόστασης ανάμεσα
στις
![]() πρέπει οπωσδήποτε να ισχύει και η συνεπαγωγή
πρέπει οπωσδήποτε να ισχύει και η συνεπαγωγή
Η μόνη μας διέξοδος εδώ είναι να αγνοήσουμε τις επουσιώδεις διαφορές ανάμεσα σε δύο
συναρτήσεις, θεωρούμε δηλ. δύο συναρτήσεις ![]() και
και ![]() ίδιες αν διαφέρουν οι τιμές τους
μόνο σε ένα σύνολο από
ίδιες αν διαφέρουν οι τιμές τους
μόνο σε ένα σύνολο από ![]() που έχουν μέτρο 0.
Λέμε τότε ότι οι δύο συναρτήσεις είναι ίσες «σχεδόν παντού» (συντομογραφία: σ.π. ή a.e. στα
Αγγλικά για το almost everywhere).
που έχουν μέτρο 0.
Λέμε τότε ότι οι δύο συναρτήσεις είναι ίσες «σχεδόν παντού» (συντομογραφία: σ.π. ή a.e. στα
Αγγλικά για το almost everywhere).
Αν θα θέλαμε να είμαστε λίγο πιο αυστηροί θα ορίζαμε μια σχέση ισοδυναμίας ανάμεσα σε συναρτήσεις,
όπου δύο συναρτήσεις θεωρούνται ισοδύναμες αν υπάρχει σύνολο ![]() , με
, με ![]() , τ.ώ. για
, τ.ώ. για
![]() έχουμε
έχουμε
![]() . Τα στοιχεία του χώρου
. Τα στοιχεία του χώρου ![]() είναι κλάσεις ισοδυναμίας αυτής της σχέσης
ισοδυναμίας που μόλις ορίσαμε.
είναι κλάσεις ισοδυναμίας αυτής της σχέσης
ισοδυναμίας που μόλις ορίσαμε.
Υπόδειξη: Εξετάστε τα σύνολα
![]() και δείξτε ότι κάποιο από αυτά
πρέπει να έχει θετικό μέτρο.
και δείξτε ότι κάποιο από αυτά
πρέπει να έχει θετικό μέτρο.
Πρέπει εδώ να αναφέρουμε ότι το Θεώρημα 1.5 είναι συνέπεια της πολύ σημαντικής ανισότητας του Hölder.
Ειδική περίπτωση (![]() ) της ανισότητας Hölder είναι η πάρα πολύ σημαντική
ανισότητα Cauchy-Schwarz.
) της ανισότητας Hölder είναι η πάρα πολύ σημαντική
ανισότητα Cauchy-Schwarz.
Υπόδειξη:
Αποδείξτε κάτι γενικότερο. Αν
![]() είναι μια γνησίως αύξουσα συνάρτηση
(και άρα υπάρχει η αντίστροφη
είναι μια γνησίως αύξουσα συνάρτηση
(και άρα υπάρχει η αντίστροφη ![]() η οποία είναι επίσης γνησίως αύξουσα και ορισμένη
στο
η οποία είναι επίσης γνησίως αύξουσα και ορισμένη
στο ![]() ) τότε για κάθε
) τότε για κάθε
![]() ισχύει
ισχύει
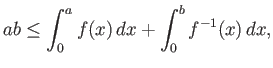
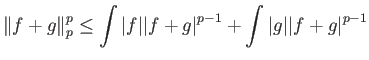
Για να ορίσουμε και τον χώρο
![]() χρειαζόμαστε την έννοια του ουσιώδους supremum
μιας συνάρτησης, το οποίο είναι, κατά κάποιο τρόπο, το supremum της συνάρτησης που όμως
δεν επηρεάζεται από επουσιώδεις αλλαγές στη συνάρτηση. Για να ορίσουμε λοιπόν το
χρειαζόμαστε την έννοια του ουσιώδους supremum
μιας συνάρτησης, το οποίο είναι, κατά κάποιο τρόπο, το supremum της συνάρτησης που όμως
δεν επηρεάζεται από επουσιώδεις αλλαγές στη συνάρτηση. Για να ορίσουμε λοιπόν το
![]() , όπου
, όπου
![]() μια συνάρτηση ορισμένη στο
μια συνάρτηση ορισμένη στο ![]() , ορίζουμε κατ' αρχήν το σύνολο
, ορίζουμε κατ' αρχήν το σύνολο
Ο χώρος
![]() (με
(με ![]() )
είναι ο χώρος όλων των συναρτήσεων
)
είναι ο χώρος όλων των συναρτήσεων
![]() για τις οποίες
για τις οποίες
![]() .
Ορίζουμε τέλος την sup-νόρμα ή άπειρο-νόρμα της
.
Ορίζουμε τέλος την sup-νόρμα ή άπειρο-νόρμα της ![]()
Δείξτε επίσης ότι η τριγωνική ανισότητα (Θεώρημα 1.5)
ισχύει και για ![]() .
.
Υπόδειξη:
![]() . Εφαρμόστε την ανισότητα
Hölder με εκθέτες
. Εφαρμόστε την ανισότητα
Hölder με εκθέτες ![]() και το συζυγή του.
και το συζυγή του.
Γιατί έχουμε επιλέξει αυτή την ονομασία για το χώρο ![]() , ένα όνομα του ίδιου τύπου με
τους χώρους
, ένα όνομα του ίδιου τύπου με
τους χώρους ![]() , με
, με ![]() , που όμως είναι χώροι που ορίζονται εντελώς διαφορετικά, με
ένα ολοκλήρωμα δηλαδή; Οι χώροι
, που όμως είναι χώροι που ορίζονται εντελώς διαφορετικά, με
ένα ολοκλήρωμα δηλαδή; Οι χώροι ![]() είναι όντως σε πολλά πράγματα αρκετά διαφορετικοί από
τον
είναι όντως σε πολλά πράγματα αρκετά διαφορετικοί από
τον ![]() και ακόμη κι όταν συμπεριφέρονται παρόμοια η απόδειξη γι' αυτό είναι διαφορετική
στην περίπτωση του πεπερασμένου
και ακόμη κι όταν συμπεριφέρονται παρόμοια η απόδειξη γι' αυτό είναι διαφορετική
στην περίπτωση του πεπερασμένου ![]() απ' ό,τι στην περίπτωση του
απ' ό,τι στην περίπτωση του ![]() . Αυτό
είναι φυσιολογικό μια και ορίζονται πολύ διαφορετικά.
Η απάντηση στο ερώτημα της ονομασίας έγκειται στο Πρόβλημα 1.33
και στο Πρόβλημα 1.35 που ακολουθεί.
. Αυτό
είναι φυσιολογικό μια και ορίζονται πολύ διαφορετικά.
Η απάντηση στο ερώτημα της ονομασίας έγκειται στο Πρόβλημα 1.33
και στο Πρόβλημα 1.35 που ακολουθεί.
Από την ανισότητα Minkowski προκύπτει ότι οι χώροι ![]() είναι διανυσματικοί χώροι
και οι αντίστοιχες νόρμες τούς καθιστούν παράλληλα και μετρικούς χώρους.
Είναι πολύ σημαντικό ότι αυτοί είναι πλήρεις χώροι (χώροι Banach).
Ό,τι και να είναι το σύνολο
είναι διανυσματικοί χώροι
και οι αντίστοιχες νόρμες τούς καθιστούν παράλληλα και μετρικούς χώρους.
Είναι πολύ σημαντικό ότι αυτοί είναι πλήρεις χώροι (χώροι Banach).
Ό,τι και να είναι το σύνολο
![]() (με θετικό μέτρο)
αν
(με θετικό μέτρο)
αν ![]() είναι μια συνεχής συνάρτηση στο
είναι μια συνεχής συνάρτηση στο ![]() που έχει συμπαγή φορέα
(υπάρχει δηλ. πεπερασμένος αριθμός
που έχει συμπαγή φορέα
(υπάρχει δηλ. πεπερασμένος αριθμός ![]() τέτοιος ώστε η
τέτοιος ώστε η ![]() μηδενίζεται εκτός του διαστήματος
μηδενίζεται εκτός του διαστήματος
![]() ) τότε
) τότε
![]() για κάθε
για κάθε
![]() .
Το ακόλουθο θεώρημα πυκνότητας είναι πάρα πολύ σημαντικό για τις εφαρμογές.
.
Το ακόλουθο θεώρημα πυκνότητας είναι πάρα πολύ σημαντικό για τις εφαρμογές.
Για
![]() ο γραμμικός υπόχωρος των συνεχών συναρτήσεων με φραγμένο φορέα είναι πυκνός
στο χώρο
ο γραμμικός υπόχωρος των συνεχών συναρτήσεων με φραγμένο φορέα είναι πυκνός
στο χώρο ![]() . Δηλαδή, για κάθε
. Δηλαδή, για κάθε
![]() και για κάθε
και για κάθε
![]() υπάρχει συνεχής
υπάρχει συνεχής
![]() με φραγμένο φορέα τ.ώ.
με φραγμένο φορέα τ.ώ.
Υπόδειξη: Χρησιμοποιήστε την πυκνότητα των συνεχών συναρτήσεων με φραγμένο φορέα (Θεώρημα 1.8) καθώς και το ότι κάθε συνεχής συνάρτηση σε φραγμένο κλειστό διάστημα είναι και ομοιόμορφα συνεχής.
Υπόδειξη: Δείξτε το πρώτα αν ![]() είναι συνεχής συνάρτηση με φραγμένο φορέα και έπειτα χρησιμοποιήστε
το Θεώρημα 1.8.
είναι συνεχής συνάρτηση με φραγμένο φορέα και έπειτα χρησιμοποιήστε
το Θεώρημα 1.8.
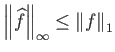 .
Δείξτε ότι
.
Δείξτε ότι
Υπόδειξη: Δείξτε το πρώτα με απ' ευθείας υπολογισμό στην περίπτωση που
![]() , για
, για
![]() . Χρησιμοποιήστε το γεγονός ότι ο μετασχηματισμός Fourier
είναι γραμμική πράξη για να το αποδείξετε για κατά τμήματα σταθερές συναρτήσεις με φραγμένο φορέα.
Έπειτα χρησιμοποιήστε το Πρόβλημα 1.36.
. Χρησιμοποιήστε το γεγονός ότι ο μετασχηματισμός Fourier
είναι γραμμική πράξη για να το αποδείξετε για κατά τμήματα σταθερές συναρτήσεις με φραγμένο φορέα.
Έπειτα χρησιμοποιήστε το Πρόβλημα 1.36.
Με ελάχιστες διαφορές αποδεικνύεται το ίδιο θεώρημα και στο
![]() . Σε αυτή την περίπτωση
το
. Σε αυτή την περίπτωση
το ![]() στον εκθέτη του εκθετικού ερμηνεύεται ως το εσωτερικό γινόμενο των
στον εκθέτη του εκθετικού ερμηνεύεται ως το εσωτερικό γινόμενο των
![]() .
.
Υπόδειξη:
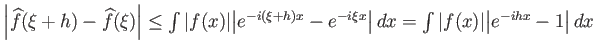 . Για
. Για ![]() ο 2ος παράγοντας στο ολοκλήρωμα
συγκλίνει στο 0 για κάθε
ο 2ος παράγοντας στο ολοκλήρωμα
συγκλίνει στο 0 για κάθε
![]() . Χρησιμοποιήστε το Θεώρημα Κυριαρχημένης Σύγκλισης
1.3 για να δείξετε ότι το ολοκλήρωμα πάει στο 0.
Η ομοιομορφία ως προς
. Χρησιμοποιήστε το Θεώρημα Κυριαρχημένης Σύγκλισης
1.3 για να δείξετε ότι το ολοκλήρωμα πάει στο 0.
Η ομοιομορφία ως προς
![]() προκύπτει απ' το ότι το φράγμα (που πάει στο 0) δεν
εξαρτάται από το
προκύπτει απ' το ότι το φράγμα (που πάει στο 0) δεν
εξαρτάται από το ![]() .
.
Ισχύουν κι εδώ οι παρατηρήσεις του Προβλήματος 1.38 όσον αφορά
τη, σχεδόν αυτόματη, γενίκευση στο
![]() .
.
Mihalis Kolountzakis 2015-11-28