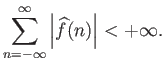Μπορούμε τώρα να δείξουμε ένα ακόμη Θεώρημα το οποίο συνδέει την ομαλότητα μιας συνάρτησης με το μέγεθος
των συντελεστών Fourier της. Το πρώτο τέτοιο θεώρημα που είδαμε είναι το Θέωρημα 3.1.
Απόδειξη.
Η μέθοδος είναι και πάλι η ολοκλήρωση κατά μέρη. Για 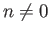 έχουμε
έχουμε
αφού ο πρώτος προσθετέος μηδενίζεται λόγω της περιοδικότητας της συνάρτησης.
Επίσης
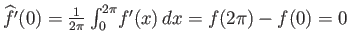 και πάλι λόγω της περιοδικότητας.
και πάλι λόγω της περιοδικότητας.
Άσκηση 3.19
Η απαίτηση στο Θεώρημα 3.3 να είναι συνεχής η παράγωγος της  είναι ισχυρότερη
απ' ό,τι πραγματικά χρειάζεται. Υποθέστε ότι
είναι ισχυρότερη
απ' ό,τι πραγματικά χρειάζεται. Υποθέστε ότι
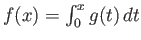 , για
, για
![$ x \in [0,2\pi]$](img760.png) ,
για μια συνάρτηση
,
για μια συνάρτηση
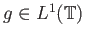 με
με
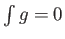 (ώστε να είναι η
(ώστε να είναι η  περιοδική) και δείξτε
ότι
περιοδική) και δείξτε
ότι
Υπόδειξη: Αντί για ολοκλήρωση κατά μέρη χρησιμοποιήστε το θεώρημα του Fubini (δείτε
1.4).
Μπορούμε να εκφράσουμε το Θεώρημα 3.3 και με τη βοήθεια των κατάλληλων γραμμικών τελεστών:
και
όπου ο διαφορικός τελεστής 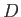 είναι από το χώρο
είναι από το χώρο
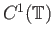 στο χώρο
στο χώρο
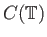 και ο
πολλαπλασιαστής
και ο
πολλαπλασιαστής 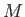 είναι από το χώρο των διπλών (δηλ.
είναι από το χώρο των διπλών (δηλ.
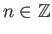 ) ακολουθιών στόν εαυτό του.
Το Θεώρημα 3.3 παίρνει πολύ απλά τη μορφή
) ακολουθιών στόν εαυτό του.
Το Θεώρημα 3.3 παίρνει πολύ απλά τη μορφή
Απόδειξη.
Αν
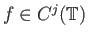 τότε έχουμε από επαναλαμβανόμενη χρήση του Θεωρήματος 3.3
τότε έχουμε από επαναλαμβανόμενη χρήση του Θεωρήματος 3.3
άρα έχουμε για 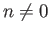 ότι
ότι
και χρησιμοποιώντας το προφανές φράγμα
παίρνουμε
Το ότι το ολοκλήρωμα που εμφανίζεται στον αριθμητή είναι πεπερασμένο είναι συνέπεια της συνέχειας
της 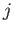 -τάξης παραγώγου
-τάξης παραγώγου 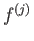 .
.
Άρα, αν
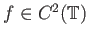 έχουμε
έχουμε
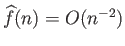 το οποίο συνεπάγεται
το οποίο συνεπάγεται
Έχουμε λοιπόν, ως συνέπεια του Πορίσματος 3.1
και του Θεωρήματος 3.2 το ακόλουθο.
Πόρισμα 3.2
Αν
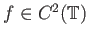 τότε η σειρά Fourier της
τότε η σειρά Fourier της  συγκλίνει απόλυτα και ομοιόμορφα
σε μια συνεχή συνάρτηση που έχει τους ίδιους συντελεστές Fourier με την
συγκλίνει απόλυτα και ομοιόμορφα
σε μια συνεχή συνάρτηση που έχει τους ίδιους συντελεστές Fourier με την  .
.
Mihalis Kolountzakis
2015-11-28
![]() έχουμε
έχουμε
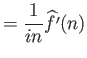
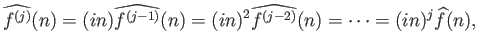
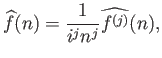
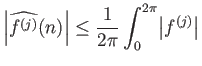
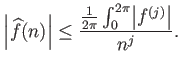
![]() έχουμε
έχουμε
![]() το οποίο συνεπάγεται
το οποίο συνεπάγεται