Next: 6.7 Ρυθμός μείωσης των Up: 6. Σύγκλιση των μερικών Previous: 6.5 Αρχή τοπικότητας Contents Index
Η σύγκλιση των Cesáro μέσων της ![]() στην ίδια την
στην ίδια την ![]() είναι εξασφαλισμένη
απλά και μόνο από τη συνέχεια της
είναι εξασφαλισμένη
απλά και μόνο από τη συνέχεια της ![]() από το Θεώρημα του Fejér
(Θεώρημα 4.7).
Το επόμενο θεώρημα μας συνδέει, υπό συνθήκες, τη σύγκλιση των μερικών αθροισμάτων
της σειράς Fourier με τη σύγκλιση των Cesáro μέσων.
από το Θεώρημα του Fejér
(Θεώρημα 4.7).
Το επόμενο θεώρημα μας συνδέει, υπό συνθήκες, τη σύγκλιση των μερικών αθροισμάτων
της σειράς Fourier με τη σύγκλιση των Cesáro μέσων.
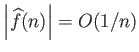 τότε οι ακολουθίες
τότε οι ακολουθίες
Απόδειξη.
Από το Θεώρημα 4.6 έχουμε ότι οποτεδήποτε
![]() τότε και
τότε και
![]() αφού η ακολουθία
αφού η ακολουθία
![]() αποτελείται από τους
αριθμητικούς μέσους της ακολουθιας
αποτελείται από τους
αριθμητικούς μέσους της ακολουθιας ![]() . Άρα αρκεί να υποθέσουμε ότι
. Άρα αρκεί να υποθέσουμε ότι
![]() και να αποδείξουμε από αυτό ότι
και να αποδείξουμε από αυτό ότι
![]() .
.
Η συνθήκη
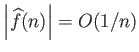 συνεπάγεται ότι για κάθε
συνεπάγεται ότι για κάθε
![]() υπάρχει
υπάρχει ![]() τ.ώ. να ισχύει
τ.ώ. να ισχύει
Υπόδειξη: Αρκεί να το δείξετε με
![]() στη θέση της ακολουθίας
στη θέση της ακολουθίας
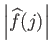 .
Εκτιμήστε τώρα το άθροισμα με ολοκλήρωμα.
.
Εκτιμήστε τώρα το άθροισμα με ολοκλήρωμα.
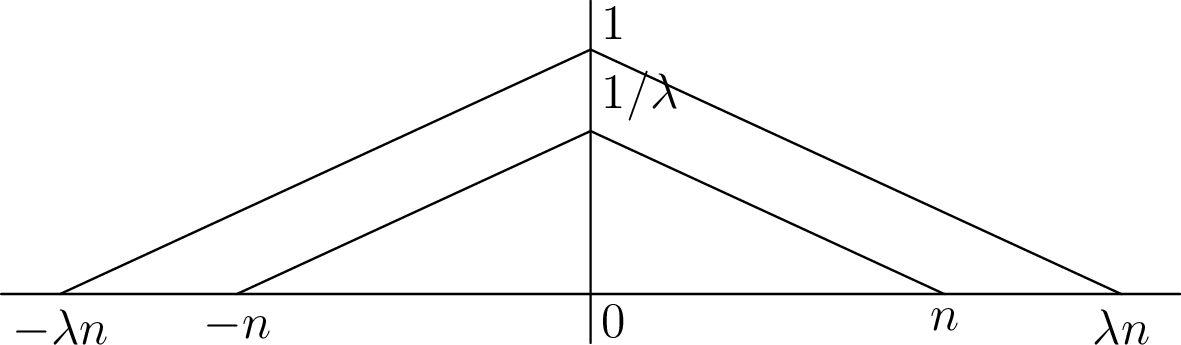
Σχήμα 6.1: Οι συντελεστές Fourier των πυρήνων του Fejérκαι
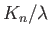
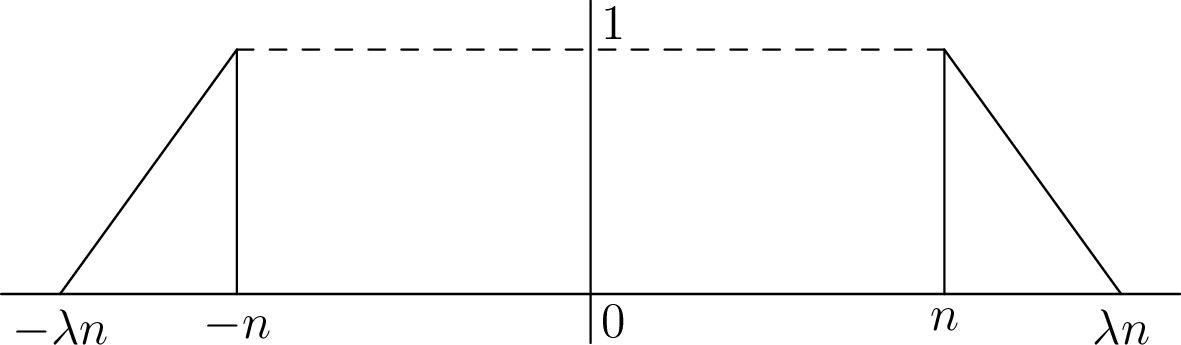
Σχήμα 6.2: Οι συντελεστές Fourier της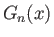
Ισχύει τώρα η ταυτότητα (υποθέστε για απλότητα ότι ![]() είναι ακέραιος; δεν αλλάζει τίποτε ουσιαστικό
αν δεν είναι και περιπλέκεται πολύ το γράψιμο)
είναι ακέραιος; δεν αλλάζει τίποτε ουσιαστικό
αν δεν είναι και περιπλέκεται πολύ το γράψιμο)
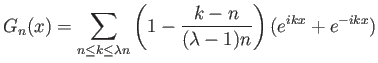
Παίρνοντας συνέλιξη με την ![]() η ταυτότητα (6.7) μας δίνει την
η ταυτότητα (6.7) μας δίνει την
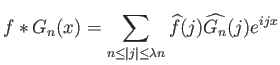
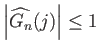 ,
,
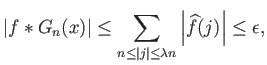
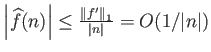 λόγω της παραγωγισιμότητας της
λόγω της παραγωγισιμότητας της 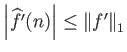 )
άρα από το Θεώρημα
6.5 η
)
άρα από το Θεώρημα
6.5 η
Το Πόρισμα 6.2 είναι επίσης συνέπεια του αποτελέσματος
του Προβλήματος 5.9: κάθε ![]() συνάρτηση έχει σειρά
Fourier που είναι απολύτως συγκλίνουσα, άρα και ομοιόμορφα συγκλίνουσα.
συνάρτηση έχει σειρά
Fourier που είναι απολύτως συγκλίνουσα, άρα και ομοιόμορφα συγκλίνουσα.
Mihalis Kolountzakis 2015-11-28