Next: 5.2 Εφαρμογή: Η ισοπεριμετρική Up: 5. Η θεωρία Previous: 5. Η θεωρία Contents Index
Αν
![]() το εσωτερικό τους γινόμενο είναι η ποσότητα
το εσωτερικό τους γινόμενο είναι η ποσότητα
Μια ακολουθία
![]() ονομάζεται ορθογώνιο σύστημα αν τα στοιχεία της είναι
ανά δύο κάθετα. Λέγεται ορθοκανονικό σύστημα αν τα στοιχεία της έχουν επιπλέον νόρμα 1.
ονομάζεται ορθογώνιο σύστημα αν τα στοιχεία της είναι
ανά δύο κάθετα. Λέγεται ορθοκανονικό σύστημα αν τα στοιχεία της έχουν επιπλέον νόρμα 1.
Το εσωτερικό γινόμενο είναι μια διγραμμική μορφή, είναι δηλ. γραμμικό ως προς το πρώτο και το δεύτερο μέλος χωριστά:
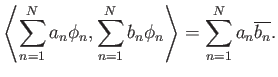
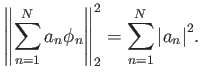
Υπόδειξη: Τετραγωνίστε και χρησιμοποιήστε την ανισότητα Cauchy-Schwarz.
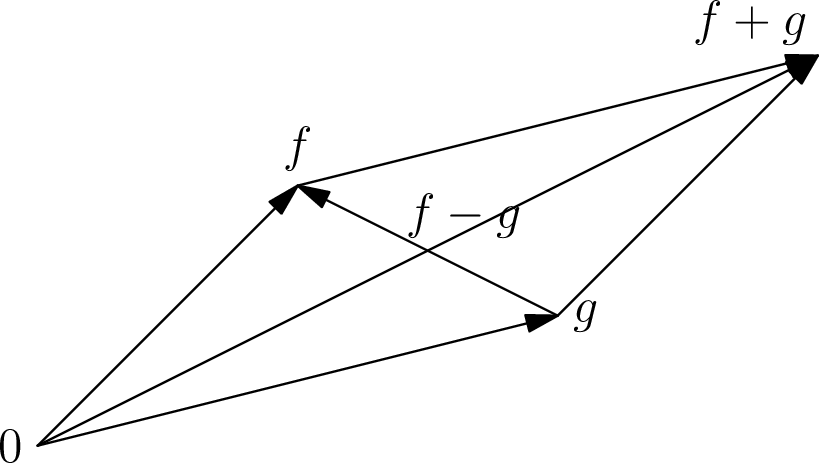
Σχήμα 5.1: Το άθροισμα δύο διανυσμάτωνκαι
και η διαφορά τους ως οι διαγώνιοι ενός παραλληλογράμμου
Το εσωτερικό γινόμενο είναι συνεχές ως πρός τα δύο ορίσματά του στην τοπολογία της νόρμας ![]() .
Αυτό σημαίνει ότι αν
.
Αυτό σημαίνει ότι αν
![]() και
και
![]() τότε και
τότε και
Ο γραμμικός χώρος
![]() με τη μετρική που ορίζεται από την
με τη μετρική που ορίζεται από την ![]() νόρμα είναι πλήρης χώρος
(αυτό δεν το αποδεικνύουμε εδώ).
Συνέπεια της πληρότητας είναι το παρακάτω.
νόρμα είναι πλήρης χώρος
(αυτό δεν το αποδεικνύουμε εδώ).
Συνέπεια της πληρότητας είναι το παρακάτω.
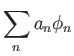
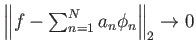 για
για
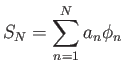
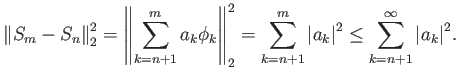
Είναι εύκολο να δούμε με απλές πράξεις ότι οι εκθετικές συναρτήσεις
Παρατηρήστε επίσης ότι για ![]() έχουμε
έχουμε
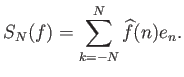
Απόδειξη.
| 0 | |||
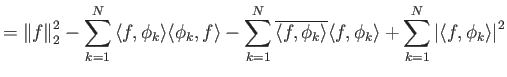 |
|||
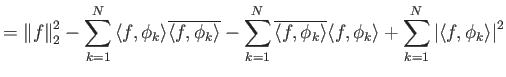 |
|||
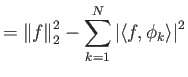 |
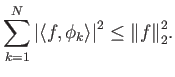
Οι εκθετικές συναρτήσεις
![]() ,
,
![]() , αποτελούν πλήρες ορθοκανονικό σύστημα.
Πράγματι, αν
, αποτελούν πλήρες ορθοκανονικό σύστημα.
Πράγματι, αν ![]() είναι κάθετη σε κάθε
είναι κάθετη σε κάθε ![]() αυτό σημαίνει ότι
αυτό σημαίνει ότι
![]() είναι 0
για κάθε
είναι 0
για κάθε
![]() , και από το Θεώρημα Μοναδικότητας στο
, και από το Θεώρημα Μοναδικότητας στο
![]() (Πόρισμα 4.6)
προκύπτει
(Πόρισμα 4.6)
προκύπτει ![]() .
.
Υπόδειξη:
Για την κατεύθυνση «αν» (πυκνότητα γραμμικών συνδυασμών συνεπάγεται
τη μη ύπαρξη μη μηδενικού διανύσματος ορθογώνιου ως προς όλα τα ![]() )
χρειάζεστε απλά τη συνέχεια του εσωτερικού γινομένου.
Για την άλλη κατεύθυνση, υποθέστε ότι δεν ισχύει η πυκνότητα και
χρησιμοποιήστε την ανισότητα του Bessel
για να κατασκευάσετε μια μη μηδενική συνάρτηση ορθογώνια ως προς όλα τα
)
χρειάζεστε απλά τη συνέχεια του εσωτερικού γινομένου.
Για την άλλη κατεύθυνση, υποθέστε ότι δεν ισχύει η πυκνότητα και
χρησιμοποιήστε την ανισότητα του Bessel
για να κατασκευάσετε μια μη μηδενική συνάρτηση ορθογώνια ως προς όλα τα ![]() .
.
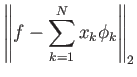
Απόδειξη.
Από την ανισότητα του Bessel προκύπτει ότι οι συναρτήσεις
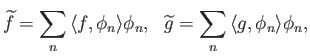
Μπορεί κανείς να δει το Θεώρημα 5.2 ως μια ισομετρία
Ο χώρος
![]() είναι ο γραμμικός χώρος όλων των ακολουθιών
είναι ο γραμμικός χώρος όλων των ακολουθιών ![]() ,
,
![]() , για τις οποίες
ισχύει
, για τις οποίες
ισχύει
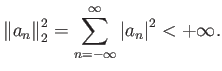
Δεν υπάρχει αντίστοιχο τέτοιο θεώρημα για χώρους ![]() με
με ![]() . Υπό μία έννοια
ο χώρος
. Υπό μία έννοια
ο χώρος ![]() είναι ο μόνος στον οποίο η νόρμα της συνάρτησης είναι τόσο προφανής αν κανείς
γνωρίζει τους συντελεστές Fourier της συνάρτησης.
Η ύπαρξη της ισότητας του Parseval είναι που κάνει την περίπτωση του
είναι ο μόνος στον οποίο η νόρμα της συνάρτησης είναι τόσο προφανής αν κανείς
γνωρίζει τους συντελεστές Fourier της συνάρτησης.
Η ύπαρξη της ισότητας του Parseval είναι που κάνει την περίπτωση του
![]() τόσο
πιο «εύκολη» από τους άλλους χώρους (μιλάμε για την ανάλυση Fourier πάντα αν και αυτό είναι
μάλλον γενικότερη διαπίστωση).
τόσο
πιο «εύκολη» από τους άλλους χώρους (μιλάμε για την ανάλυση Fourier πάντα αν και αυτό είναι
μάλλον γενικότερη διαπίστωση).
Υπόδειξη: Χρησιμοποιήστε την ισότητα του Parseval.
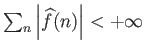 .
.
Υπόδειξη:
Χρησιμοποιήστε την ταυτότητα Parseval για να βρείτε, μέσω της ανισότητας Cauchy-Schwarz,
ένα κατάλληλο άνω φράγμα για την ποσότητα
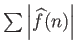 .
.
Mihalis Kolountzakis 2015-11-28