Next: 6.6 Άλλες συνθήκες που Up: 6. Σύγκλιση των μερικών Previous: 6.4 Σύγκλιση κατά Contents Index
Απόδειξη.
Ορίζουμε
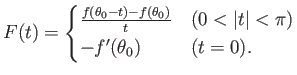
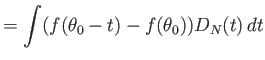 |
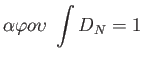 |
||
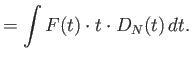 |
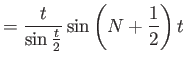 |
||
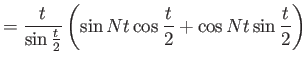 |
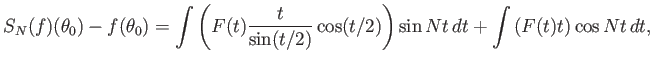
Αν μια ![]() συνάρτηση
συνάρτηση ![]() ικανοποιεί την (6.4) τότε, και μόνο τότε, η συνάρτηση
ικανοποιεί την (6.4) τότε, και μόνο τότε, η συνάρτηση
![]() είναι φραγμένη σε μια περιοχή του μηδενός. Το επόμενο αποτέλεσμα μας λέει ότι
ουσιαστικά αρκεί η ολοκληρωσιμότητα αυτής της συνάρτησης, που είναι βέβαια μια γενικότερη ιδιότητα.
είναι φραγμένη σε μια περιοχή του μηδενός. Το επόμενο αποτέλεσμα μας λέει ότι
ουσιαστικά αρκεί η ολοκληρωσιμότητα αυτής της συνάρτησης, που είναι βέβαια μια γενικότερη ιδιότητα.
Απόδειξη.
Μπορούμε χωρίς βλάβη της γενικότητας να προσθέσουμε μια σταθερά στην ![]() , την
, την
![]() , και να μεταφέρουμε
το
, και να μεταφέρουμε
το ![]() στο 0, ώστε η συνθήκη μας να γίνει
στο 0, ώστε η συνθήκη μας να γίνει
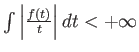 .
.![]() , και θέλουμε
να αποδείξουμε ότι
, και θέλουμε
να αποδείξουμε ότι
![]() .
.
Έχουμε
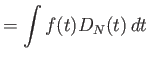 |
||
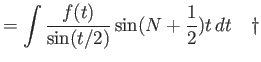 |
||
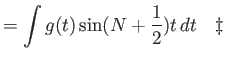 |
||
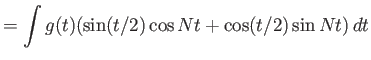 |
||
![$\displaystyle = \int f(t)\cos Nt dt + \int [g(t)\cos(t/2)] \sin Nt dt$](img1719.png) |
Mihalis Kolountzakis 2015-11-28