Next: 4.7 Cesáro μέσοι όροι Up: 4. Αθροισιμότητα σειρών Fourier Previous: 4.5 Μέσοι όροι των Contents Index
Για να παρακάμψουμε τα πολλά εμπόδια που υπάρχουν στη σύγκλιση των μερικών αθροισμάτων της σειράς Fourier μελετάμε τους μέσους όρους τους.
Απόδειξη.
Εύκολα βλέπει κανείς ότι μπορεί να υποθέσει ![]() .
Έστω
.
Έστω
![]() και
και ![]() τ.ώ. αν
τ.ώ. αν ![]() να ισχύει
να ισχύει
![]() .
Γράφουμε
.
Γράφουμε
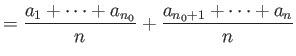 |
||
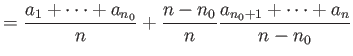 |
||
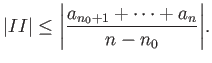
Για να δούμε ότι η σύγκλιση της ακολουθίας ![]() δε συνεπάγεται τη σύγκλιση της
δε συνεπάγεται τη σύγκλιση της ![]() αρκεί
να κοιτάξουμε το παράδειγμα της ακολουθίας
αρκεί
να κοιτάξουμε το παράδειγμα της ακολουθίας
![]() για την οποία οι μέσοι όροι συγκλίνουν
στο
για την οποία οι μέσοι όροι συγκλίνουν
στο ![]() ενώ η ίδια η ακολουθία δε συγκλίνει.
ενώ η ίδια η ακολουθία δε συγκλίνει.