Next: 4.11 Το Θεώρημα του Up: 4. Αθροισιμότητα σειρών Fourier Previous: 4.9 Εφαρμογή: Το θεώρημα Contents Index
Είναι πολύ εύκολο να φτιάξει κανείς μια συνάρτηση που δεν είναι πουθενά παραγωγίσιμη: η χαρακτηριστική συνάρτηση
των ρητών
![]() είναι μια τέτοια συνάρτηση. Όμως η συνάρτηση αυτή δεν είναι πουθενά παραγωγίσιμη για ένα κάπως
τετριμμένο (όχι ενδιαφέροντα δηλ.) λόγο: δεν είναι πουθενά συνεχής, αφού το άνω όριο σε κάθε σημείο είναι 1 και το
κάτω είναι 0.
Είναι πολύ πιο ενδιαφέρον να έχουμε παντού συνέχεια της συνάρτησης και πουθενά παραγωγισιμότητα, και σε αυτή την παράγραφο
θα δούμε ένα παράδειγμα, που λίγο-πολύ οφείλεται στον Weierstrass,
τέτοιας συνάρτησης χρησιμοποιώντας τεχνικές της αρμονικής ανάλυσης.
είναι μια τέτοια συνάρτηση. Όμως η συνάρτηση αυτή δεν είναι πουθενά παραγωγίσιμη για ένα κάπως
τετριμμένο (όχι ενδιαφέροντα δηλ.) λόγο: δεν είναι πουθενά συνεχής, αφού το άνω όριο σε κάθε σημείο είναι 1 και το
κάτω είναι 0.
Είναι πολύ πιο ενδιαφέρον να έχουμε παντού συνέχεια της συνάρτησης και πουθενά παραγωγισιμότητα, και σε αυτή την παράγραφο
θα δούμε ένα παράδειγμα, που λίγο-πολύ οφείλεται στον Weierstrass,
τέτοιας συνάρτησης χρησιμοποιώντας τεχνικές της αρμονικής ανάλυσης.
Η ομοιόμορφη σύγκλιση της σειράς είναι φανερή αφού
![]() αφού
αφού ![]() .
Πριν αποδείξουμε τη μη παραγωγισιμότητα ας δοκιμάσουμε να παραγωγίσουμε τη σειρά όρο προς όρο. Προκύπτει
η σειρά
.
Πριν αποδείξουμε τη μη παραγωγισιμότητα ας δοκιμάσουμε να παραγωγίσουμε τη σειρά όρο προς όρο. Προκύπτει
η σειρά
Ορίζουμε πρώτα το λεγόμενο πυρήνα του de la Vallée Poussin ο οποίος ορίζεται μέσω του πυρήνα του Fejér ως εξής:
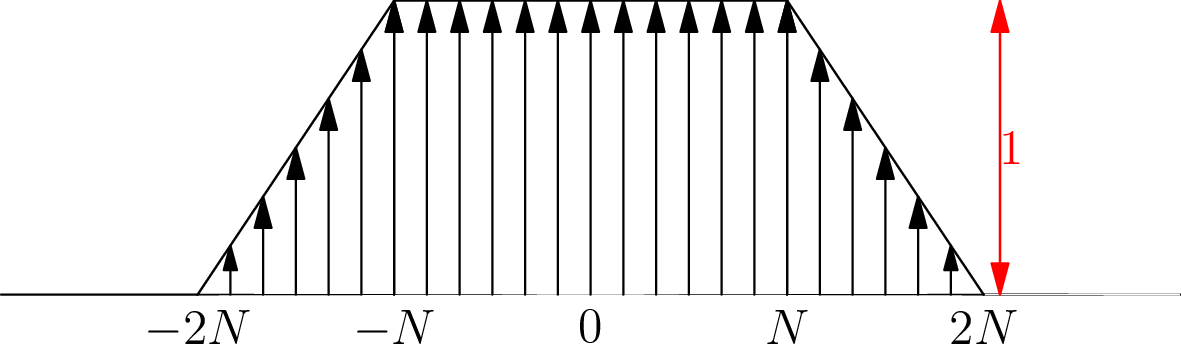
Σχήμα 4.8: Οι συντελεστές Fourier του πυρήνα του de la Vallée Poussinγια
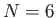
Το ότι οι συντελεστές Fourier της ![]() είναι ίσοι με 1 μέχρι το
είναι ίσοι με 1 μέχρι το ![]() και φθίνουν γραμμικά μέχρι το
και φθίνουν γραμμικά μέχρι το ![]() κάνει τους de la Vallée Poussin μέσους
κάνει τους de la Vallée Poussin μέσους
![]() να μοιάζουν αφενός με τα μερικά αθροίσματα
να μοιάζουν αφενός με τα μερικά αθροίσματα ![]() αλλά να έχουν και κάποιες από τις καλές ιδιότητες των Cesáro μέσων
αλλά να έχουν και κάποιες από τις καλές ιδιότητες των Cesáro μέσων
![]() .
.
Υπόδειξη: Εκφράστε το ![]() ως ένα μέσο de la Vallée Poussin της
ως ένα μέσο de la Vallée Poussin της ![]() και
χρησιμοποιήστε το Πρόβλημα 4.20.
και
χρησιμοποιήστε το Πρόβλημα 4.20.
Εφαρμόζοντας το Πρόβλημα 4.2 βλέπουμε ότι
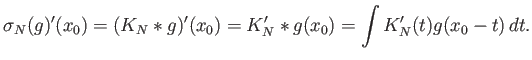
![$\displaystyle \sigma_N(g)'(x_0) = \int K_N'(t) \left[ g(x_0-t) - g(x_0) \right] dt.
$](img1083.png)
Από την (4.32) και την (4.34) παίρνουμε
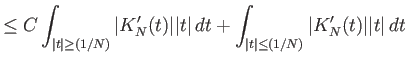 |
||
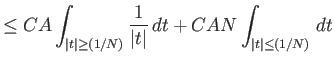 |
||
Ας υποθέσουμε τώρα ότι το ![]() υπάρχει, για τη συνάρτηση (4.27).
Χρησιμοποιώντας το Πρόβλημα 4.23 παίρνουμε αντίφαση ανάμεσα στην (4.35)
και στο συμπέρασμα του Λήμματος 4.1, για
υπάρχει, για τη συνάρτηση (4.27).
Χρησιμοποιώντας το Πρόβλημα 4.23 παίρνουμε αντίφαση ανάμεσα στην (4.35)
και στο συμπέρασμα του Λήμματος 4.1, για ![]() και
και
![]() ,
αφού με βάση το Λήμμα 4.1
η ποσότητα (4.35) είναι
,
αφού με βάση το Λήμμα 4.1
η ποσότητα (4.35) είναι ![]() ενώ από το Πρόβλημα 4.23 είναι ίση με
ενώ από το Πρόβλημα 4.23 είναι ίση με
![]() ,
που δεν είναι
,
που δεν είναι ![]() .
Η απόδειξη του Θεωρήματος 4.11 είναι πλήρης.
.
Η απόδειξη του Θεωρήματος 4.11 είναι πλήρης.
Mihalis Kolountzakis 2015-11-28