4.3 Συνέλιξη στον κύκλο
Αν 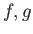 είναι
είναι  -περιοδικές συναρτήσεις η συνέλιξή τους ορίζεται διαφορετικά από τον τύπο
(4.5) ο οποίος δε θα έκανε νόημα σε αυτή την περίπτωση μια και οι
-περιοδικές συναρτήσεις η συνέλιξή τους ορίζεται διαφορετικά από τον τύπο
(4.5) ο οποίος δε θα έκανε νόημα σε αυτή την περίπτωση μια και οι  -περιοδικές συναρτήσεις
δεν είναι ολοκληρώσιμες πάνω σε ολόκληρο το
-περιοδικές συναρτήσεις
δεν είναι ολοκληρώσιμες πάνω σε ολόκληρο το
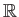 (εκτός από τη μηδενική συνάρτηση).
Ορίζουμε λοιπόν
(εκτός από τη μηδενική συνάρτηση).
Ορίζουμε λοιπόν
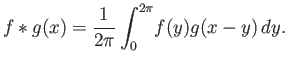 |
(4.6) |
Τι συνθήκες πρέπει να βάλουμε για τις  και
και 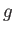 ώστε να κάνει νόημα το ολοκλήρωμα;
Η εύκολη λύση κι εδώ είναι να απαιτήσουμε να είναι κι οι δύο συνεχείς, αλλά αυτό είναι
περιοριστικό. Μια λύση κι εδώ είναι να ζητάμε η μια από αυτές να είναι ολοκληρώσιμη και η άλλη
φραγμένη (άρα και ολοκληρώσιμη αφού μιλάμε για φραγμένο διάστημα ολοκλήρωσης).
ώστε να κάνει νόημα το ολοκλήρωμα;
Η εύκολη λύση κι εδώ είναι να απαιτήσουμε να είναι κι οι δύο συνεχείς, αλλά αυτό είναι
περιοριστικό. Μια λύση κι εδώ είναι να ζητάμε η μια από αυτές να είναι ολοκληρώσιμη και η άλλη
φραγμένη (άρα και ολοκληρώσιμη αφού μιλάμε για φραγμένο διάστημα ολοκλήρωσης).
Όπως και στην περίπτωση συνέλιξης συναρτήσεων ορισμένων πάνω σε όλο το
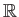 κι εδώ ορίζουμε
τη συνέλιξη δύο οποιωνδήποτε συναρτήσεων στο
κι εδώ ορίζουμε
τη συνέλιξη δύο οποιωνδήποτε συναρτήσεων στο
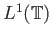 φτάνει να είμαστε διατεθειμένοι
να αποδεχτούμε ότι η συνάρτησή μας ορίζεται απλά σχεδόν παντού, όχι παντού.
φτάνει να είμαστε διατεθειμένοι
να αποδεχτούμε ότι η συνάρτησή μας ορίζεται απλά σχεδόν παντού, όχι παντού.
Θεώρημα 4.3
Για τη συνέλιξη 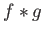 δύο συναρτήσεων
δύο συναρτήσεων
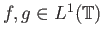 ισχύουν τα ακόλουθα.
ισχύουν τα ακόλουθα.
- Η συνέλιξη
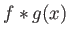 ορίζεται σχεδόν για κάθε
ορίζεται σχεδόν για κάθε
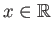 και έχουμε
και έχουμε
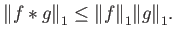 |
(4.7) |
- Αν επιπλέον
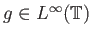 τότε
η συνέλιξη
τότε
η συνέλιξη 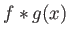 ορίζεται για κάθε
ορίζεται για κάθε
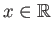 , είναι ουσιωδώς φραγμένη ολοκληρώσιμη συνάρτηση και ισχύει
, είναι ουσιωδώς φραγμένη ολοκληρώσιμη συνάρτηση και ισχύει
 |
(4.8) |
Επίσης η συνάρτηση 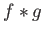 είναι ομοιόμορφα συνεχής στο
είναι ομοιόμορφα συνεχής στο
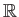 .
.
- (Αντιμεταθετικότητα)Ισχύει
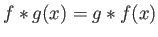 σχεδόν για κάθε
σχεδόν για κάθε
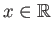 και η συνάρτηση
και η συνάρτηση 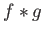 είναι επίσης
είναι επίσης  -περιοδική
αν την ορίσουμε κατάλληλα σε ένα σύνολο μέτρου 0.
-περιοδική
αν την ορίσουμε κατάλληλα σε ένα σύνολο μέτρου 0.
- (Γραμμικότητα)Η συνέλιξη είναι γραμμική και ως προς τα δύο ορίσματά της. Ισχύει δηλαδή, αν
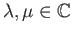
και ομοίως για γραμμικό συνδυασμό ως προς το πρώτο όρισμα,
οποτεδήποτε ορίζεται καλώς το δεξί μέλος.
- (Προσεταιριστικότητα)Αν
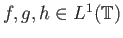 τότε
τότε
Απόδειξη.
Απόδειξη του 4.3.1.
Όπως στο Θεώρημα 4.2.
Απόδειξη του 4.3.2.
Για να δείξουμε τη συνέχεια της  παρατηρούμε ότι
παρατηρούμε ότι
Τέλος θυμόμαστε ότι ο τελεστής 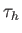 της μεταφοράς κατά
της μεταφοράς κατά 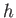 είναι συνεχής σε όλους τους χώρους
είναι συνεχής σε όλους τους χώρους 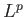 ,
και άρα η ποσότητα
,
και άρα η ποσότητα
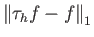 μπορεί να γίνει όσο μικρή θέλουμε
αρκεί το
μπορεί να γίνει όσο μικρή θέλουμε
αρκεί το 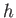 να είναι αρκετά μικρό.
Εφ' όσον δεν υπάρχει εξάρτηση από το
να είναι αρκετά μικρό.
Εφ' όσον δεν υπάρχει εξάρτηση από το 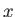 η συνέχεια είναι ομοιόμορφη στο
η συνέχεια είναι ομοιόμορφη στο
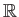 .
.
Απόδειξη του 4.3.3.
Για την αντιμεταθετικότητα κάνουμε την αλλαγή μεταβλητής 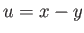 στο ολοκλήρωμα (4.6)
και χρησιμοποιούμε το γεγονός ότι αν μια συνάρτηση είναι
στο ολοκλήρωμα (4.6)
και χρησιμοποιούμε το γεγονός ότι αν μια συνάρτηση είναι  -περιοδική τότε το ολοκλήρωμά της
πάνω σε κάθε διάστημα μήκους
-περιοδική τότε το ολοκλήρωμά της
πάνω σε κάθε διάστημα μήκους  είναι το ίδιο.
Η
είναι το ίδιο.
Η  -περιοδικότητα της
-περιοδικότητα της 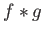 είναι άμεση συνέπεια της περιοδικότητας της
είναι άμεση συνέπεια της περιοδικότητας της 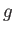 (και ισχύει και στην
περίπτωση της συνέλιξης στην ευθεία όταν η
(και ισχύει και στην
περίπτωση της συνέλιξης στην ευθεία όταν η  είναι ολοκληρώσιμη στο
είναι ολοκληρώσιμη στο
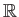 και η
και η 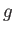 είναι
είναι  -περιοδική).
-περιοδική).
Απόδειξη του 4.3.4.
Αφήνεται ως άσκηση για τον αναγνώστη.
Απόδειξη του 4.3.5.
(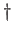 : εναλλαγή σειράς ολοκλήρωσης,
: εναλλαγή σειράς ολοκλήρωσης, 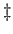 : αλλαγή μεταβλητής
: αλλαγή μεταβλητής 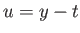 ).
Για να αιτιολογήσουμε την εναλλαγή σειράς ολοκλήρωσης παραπάνω
αρκεί να δείξουμε (θ. Fubini) ότι το πολλαπλό ολοκλήρωμα
).
Για να αιτιολογήσουμε την εναλλαγή σειράς ολοκλήρωσης παραπάνω
αρκεί να δείξουμε (θ. Fubini) ότι το πολλαπλό ολοκλήρωμα
είναι πεπερασμένο. Αυτό είναι συνέπεια διπλής εφαρμογής της
ανισότητας (4.7).
Δίνουμε ακόμη χωρίς απόδειξη την παρακάτω πολύ χρήσιμη ανισότητα.
Θεώρημα 4.4 (Ανισότητα Young)
Αν
![$ p, q, r \in [1, +\infty]$](img888.png) ικανοποιούν τη σχέση
ικανοποιούν τη σχέση
τότε ισχύει
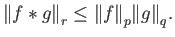 |
(4.9) |
Παρατήρηση 4.1
Σε ένα θεώρημα όπως το Θεώρημα 4.4 που για κάποια συνάρτηση δίνεται ότι κάποια νόρμα της είναι πεπερασμένη (η 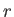 -νόρμα της
-νόρμα της 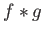 στην περίπτωση της ανισότητας Young) συνέπεια του Θεωρήματος (που συχνά δε δηλώνεται ρητά) είναι ότι η συνάρτηση αυτή ανήκει στον αντίστοιχο χώρο (στην περίπτωση της ανισότητα Young έπεται λοιπόν ότι η
στην περίπτωση της ανισότητας Young) συνέπεια του Θεωρήματος (που συχνά δε δηλώνεται ρητά) είναι ότι η συνάρτηση αυτή ανήκει στον αντίστοιχο χώρο (στην περίπτωση της ανισότητα Young έπεται λοιπόν ότι η 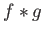 ανήκει στο χώρο
ανήκει στο χώρο
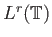 όταν
όταν
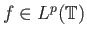 και
και
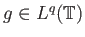 .
.
Παρατηρήστε ότι οι περιπτώσεις 1 και 2
του Θεωρήματος 4.3
είναι ειδικές περιπτώσεις της ανισότητας του Young για
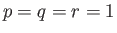 και
και
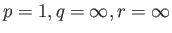 .
.
Αξίζει επίσης να σημειώσουμε το εξής πόρισμα της ανισότητας του Young για 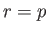 .
. .
.
Η ισχυρή σχέση που έχει η έννοια της συνέλιξης με την Ανάλυση Fourier οφείλεται στην
επόμενη πολύ σημαντική πρόταση
η οποία μας λέει ότι η πράξη της συνέλιξης στο πεδίο του «χρόνου» μεταφράζεται σε κατά σημείο
πολλαπλασιασμό στο πεδίο «Fourier» ή στο πεδίο συχνοτήτων.
Απόδειξη.
Έχουμε
(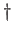 : αλλαγή σειράς ολοκλήρωσης,
: αλλαγή σειράς ολοκλήρωσης, 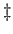 : αλλαγή μεταβλητής
: αλλαγή μεταβλητής 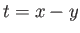 ).
Η αλλαγή σειράς ολοκλήρωσης αιτιολογείται από το θ. Fubini αφού το αντίστοιχο ολοκλήρωμα
όπου οι συναρτήσεις έχουν αντικατασταθεί από το μέτρο τους συγκλίνει.
).
Η αλλαγή σειράς ολοκλήρωσης αιτιολογείται από το θ. Fubini αφού το αντίστοιχο ολοκλήρωμα
όπου οι συναρτήσεις έχουν αντικατασταθεί από το μέτρο τους συγκλίνει.
Άσκηση 4.2
Αν
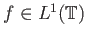 ,
,
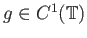 δείξτε ότι
δείξτε ότι
 και ότι
και ότι
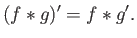 |
(4.12) |
Υπόδειξη: Εκφράστε τη διαφορά
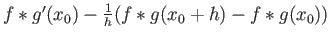 σαν ένα ολοκλήρωμα
και χρησιμοποιήστε το Θεώρημα Κυριαρχημένης Σύγκλισης για να δείξετε ότι πάει στο 0
για
σαν ένα ολοκλήρωμα
και χρησιμοποιήστε το Θεώρημα Κυριαρχημένης Σύγκλισης για να δείξετε ότι πάει στο 0
για 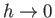 .
.
Άσκηση 4.3
Δείξτε ότι αν  είναι τριγωνομετρικό πολυώνυμο και
είναι τριγωνομετρικό πολυώνυμο και
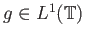 τότε η συνέλιξη
τότε η συνέλιξη
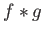 είναι τριγωνομετρικό πολυώνυμο βαθμού
είναι τριγωνομετρικό πολυώνυμο βαθμού
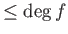 .
.
Mihalis Kolountzakis
2015-11-28
![]() είναι
είναι ![]() -περιοδικές συναρτήσεις η συνέλιξή τους ορίζεται διαφορετικά από τον τύπο
(4.5) ο οποίος δε θα έκανε νόημα σε αυτή την περίπτωση μια και οι
-περιοδικές συναρτήσεις η συνέλιξή τους ορίζεται διαφορετικά από τον τύπο
(4.5) ο οποίος δε θα έκανε νόημα σε αυτή την περίπτωση μια και οι ![]() -περιοδικές συναρτήσεις
δεν είναι ολοκληρώσιμες πάνω σε ολόκληρο το
-περιοδικές συναρτήσεις
δεν είναι ολοκληρώσιμες πάνω σε ολόκληρο το
![]() (εκτός από τη μηδενική συνάρτηση).
Ορίζουμε λοιπόν
(εκτός από τη μηδενική συνάρτηση).
Ορίζουμε λοιπόν
![]() κι εδώ ορίζουμε
τη συνέλιξη δύο οποιωνδήποτε συναρτήσεων στο
κι εδώ ορίζουμε
τη συνέλιξη δύο οποιωνδήποτε συναρτήσεων στο
![]() φτάνει να είμαστε διατεθειμένοι
να αποδεχτούμε ότι η συνάρτησή μας ορίζεται απλά σχεδόν παντού, όχι παντού.
φτάνει να είμαστε διατεθειμένοι
να αποδεχτούμε ότι η συνάρτησή μας ορίζεται απλά σχεδόν παντού, όχι παντού.
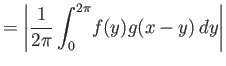
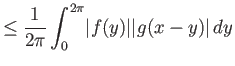
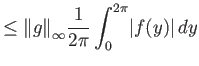
![]() στο ολοκλήρωμα (4.6)
και χρησιμοποιούμε το γεγονός ότι αν μια συνάρτηση είναι
στο ολοκλήρωμα (4.6)
και χρησιμοποιούμε το γεγονός ότι αν μια συνάρτηση είναι ![]() -περιοδική τότε το ολοκλήρωμά της
πάνω σε κάθε διάστημα μήκους
-περιοδική τότε το ολοκλήρωμά της
πάνω σε κάθε διάστημα μήκους ![]() είναι το ίδιο.
Η
είναι το ίδιο.
Η ![]() -περιοδικότητα της
-περιοδικότητα της ![]() είναι άμεση συνέπεια της περιοδικότητας της
είναι άμεση συνέπεια της περιοδικότητας της ![]() (και ισχύει και στην
περίπτωση της συνέλιξης στην ευθεία όταν η
(και ισχύει και στην
περίπτωση της συνέλιξης στην ευθεία όταν η ![]() είναι ολοκληρώσιμη στο
είναι ολοκληρώσιμη στο
![]() και η
και η ![]() είναι
είναι ![]() -περιοδική).
-περιοδική).
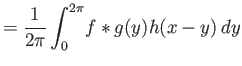
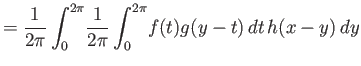
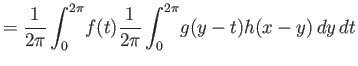
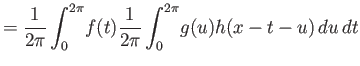
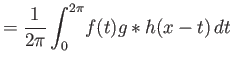
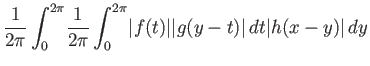
![]() και
και
![]() .
.
![]() .
.![]() .
.
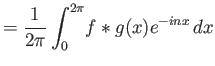
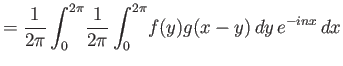
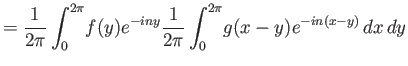
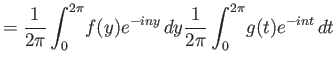
![]() σαν ένα ολοκλήρωμα
και χρησιμοποιήστε το Θεώρημα Κυριαρχημένης Σύγκλισης για να δείξετε ότι πάει στο 0
για
σαν ένα ολοκλήρωμα
και χρησιμοποιήστε το Θεώρημα Κυριαρχημένης Σύγκλισης για να δείξετε ότι πάει στο 0
για ![]() .
.