4.9 Εφαρμογή: Το θεώρημα ισοκατανομής του Weyl

Ορισμός 4.2   Έστω $x \in {\mathbb{R}}$. Το ακέραιο μέρος του $x$ ορίζεται ως εξής:

$${\left\lfloor{x}\right\rfloor} = \max{\left\{{n\in{\mathbb{Z}}: n\le x}\right\}}.$$

Το κλασματικό μέρος του $x$ είναι η ποσότητα

$${\left\{{x}\right\}} = x - {\left\lfloor{x}\right\rfloor}.$$

Γράφουμε επίσης $x \bmod 1 = {\left\{{x}\right\}}$.

Προφανώς ισχύει ${\left\{{x}\right\}} \in [0,1)$.

Ορισμός 4.3   Μια ακολουθία πραγματικών αριθμών $0 \le x_n \le 1$, $n=1,2,\ldots$, λέγεται ισοκατανεμημένη αν για κάθε αριθμούς $a, b$ με $0\le a \le b \le 1$ ισχύει

$$\lim_{N\to\infty}\frac{{\left\vert{{\left\{{n: 1\le n \le N \& x_n \in [a,b]}\right\}}}\right\vert}}{N} = b-a.$$

Αν $x_n \in {\mathbb{R}}$ λέμε ότι η $x_n$ είναι ισοκατανεμημένη mod 1 αν η ακολουθία των κλασματικών μερών ${\left\{{x_n}\right\}}$ είναι ισοκατανεμημένη.

Το νόημα του προηγούμενου ορισμού είναι ότι μια ακολουθία είναι ισοκατανεμημένη στο διάστημα $[0,1]$ αν το πλήθος των όρων της που πέφτουν μέσα σε ένα διάστημα $[a,b]$, αν κοιτάξουμε ένα μεγάλο αρχικό κομμάτι της ακολουθίας, είναι περίπου ανάλογο του μήκους του διαστήματος $b-a$.

Άσκηση 4.13   Δείξτε ότι η ακολουθία

$$0, \frac{1}{2}, 0, \frac{1}{3}, \frac{2}{3}, 0, \frac{1}{4}, \frac{2}{4}, \frac{3}{4}, \ldots$$

είναι ισοκατανεμημένη.

Άσκηση 4.14   Περιγράψτε μια ακολουθία $x_n \in [0,1]$ που να είναι πυκνή στο $[0,1]$ αλλά να μην είναι ισοκατανεμημένη.

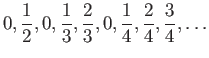
Σκοπός μας εδώ είναι αποδείξουμε το ακόλουθο πολύ σημαντικό θεώρημα.

Θεώρημα 4.9 (Weyl)   Αν $\alpha$ άρρητος τότε η ακολουθία

$$n\alpha, n=1,2,\ldots,$$

είναι ισοκατανεμημένη mod 1.

Στο παρακάτω σχήμα μπορείτε να δείτε τα κλασματικά μέρη ${\left\{{i\sqrt2}\right\}}$, $i=1,2,\ldots,20$.

Το θεώρημα 4.9 θα το αποδείξουμε χρησιμοποιώντας εργαλεία αρμονικής ανάλυσης. Υπάρχει και στοιχειώδης τρόπος να αποδειχτεί αλλά (α) αυτός δεν είναι σε καμία περίπτωση πιο εύκολος και (β) δεν έχει τις δυνατότητες επέκτασης που έχει η μέθοδος που θα δούμε. Το θεώρημα 4.9 είναι άμεση συνέπεια του Θεωρήματος 4.10.

Θεώρημα 4.10 (Κριτήριο ισοκατανομής του Weyl)   Έστω $x_n \in {\mathbb{R}}$, $n=1,2,\ldots$. Τα ακόλουθα είναι ισοδύναμα:

(α)

Η $x_n$ είναι ισοκατανεμημένη mod 1.

(β)

Για κάθε συνεχή και 1-περιοδική συνάρτηση $f$ ισχύει

$$\frac{1}{N}\sum_{n=1}^N f(x_n) \to \int_0^1 f(x) dx.$$ (4.25)

(γ)

Για κάθε $k\in{\mathbb{Z}}\setminus{\left\{{0}\right\}}$ ισχύει

$$\frac{1}{N}\sum_{n=1}^N e^{i2\pi k x_n} \to 0.$$ (4.26)

Άσκηση 4.15   Δείξτε ότι το Θεώρημα 4.9 έπεται από το Θεώρημα 4.10.

Υπόδειξη: Επαληθεύστε την ιδιότητα (γ) του Θεωρήματος 4.10 για την ακολουθία $n\alpha$, $\alpha\notin{\mathbb{Q}}$.

Άσκηση 4.16   Δείξτε ότι η ακολουθία $n\alpha$, $n=1,2,\ldots$, δεν είναι ισοκατανεμημένη mod 1 αν $\alpha \in {\mathbb{Q}}$.

Απόδειξη του Θεωρήματος 4.10.

(α) $\Rightarrow$ (β)

Παρτηρούμε ότι η ιδιότητα της ισοκατανομής mod 1 μπορεί να γραφεί ως εξής:

$$\lim_{N\to\infty}\frac{1}{N}\sum_{n=1}^N \chi_{[a,b]}({\left\{{x_... ...}) = \int_0^1 \chi_{[a,b]}(x) dx, (\gamma\iota\alpha 0\le a\le b \le 1).$$

Αυτό συνεπάγεται ότι η (4.25) ισχύει για κάθε συνάρτηση $f$ που γράφεται ως πεπερασμένος γραμμικός συνδυασμός χαρακτηριστικών κλειστών διαστημάτων, δηλ. για κάθε τμηματικά σταθερή συνάρτηση ορισμένη στο $[0,1]$. Όμως οι τμηματικά σταθερές συναρτήσεις είναι ομοιόμορφα πυκνές στις συνεχείς συναρτήσεις στο $[0,1]$ και εύκολα προκύπτει ότι η ιδιότητα (4.25) μεταβιβάζεται και στα ομοιόμορφα όρια συναρτήσεων για τις οποίες ισχύει.

Άσκηση 4.17   Αποδείξτε με λεπτομέρεια τον ισχυρισμό της προηγούμενης παραγράφου, ότι δηλ. η (4.25) ισχύει για όλες τις συνεχείς συναρτήσεις επειδή ισχύει για ένα υποσύνολο αυτών που είναι ομοιόμορφα πυκνό.

(β) $\Rightarrow$ (α)

Έστω $[a,b] \subseteq (0,1)$ και $\epsilon>0$ αρκετά μικρό. Προσεγγίζουμε από πάνω και από κάτω τη συνάρτηση $\chi_{[a,b]}$ (που δεν είναι συνεχής)

$$f \le \chi_{[a,b]} \le g$$

από τις συνεχείς (τραπεζοειδείς) συναρτήσεις $f$ και $g$ όπως φαίνονται στο παρακάτω Σχήμα.

Σχήμα 4.7: Οι συναρτήσεις $f$ και $g$ της απόδειξης.

Η συνάρτηση $f$ είναι ίση με 0 εκτός του $[a,b]$, είναι ίση με $1$ στο διάστημα $[a+\epsilon,b-\epsilon]$ και είναι γραμμική και συνεχής στα δύο διαστήματα $[a, a+\epsilon]$ και $[b-\epsilon, b]$. Ομοίως η $g$ είναι ίση με $1$ εντός του $[a,b]$, είναι ίση με 0 εκτός του διαστήματος $[a-\epsilon, b+\epsilon]$ και είναι γραμμική και συνεχής στα δύο διαστήματα $[a-\epsilon, a]$ και $[b, b+\epsilon]$.

Εφαρμόζουμε την (4.25) για τις συνεχείς συναρτήσεις $f$ και $g$ και παίρνουμε ως συνέπεια ότι το liminf και το limsup της ποσότητας

$$\frac{1}{N} \sum_{n=1}^N \chi_{[a,b]}({\left\{{x_n}\right\}})$$

είναι ανάμεσα στις τιμές $\int f$ και $\int g$ οι οποίες, για $\epsilon\to 0$, συγκλίνουν στο $\int\chi_{[a,b]}$.

(β) $\Rightarrow$ (γ)

Προφανές.

(γ) $\Rightarrow$ (β)

Εδώ χρησιμοποιούμε το γεγονός (συνέπεια του Θεωρήματος του Fejér 4.7) ότι τα τριγωνομετρικά πολυώνυμα προσεγγίζουν ομοιόμορφα όλες τις συνεχείς και περιοδικές συναρτήσεις. Για να είμαστε λίγο πιο ακριβείς, το Θεώρημα 4.7 αναφέρεται σε $2\pi$-περιοδικές συναρτήσεις και στα τριγωνομετρικά πολυώνυμα που είναι πεπερασμένοι γραμμικοί συνδυασμοί των συναρτήσεων $e^{inx}$, $n\in{\mathbb{Z}}$, ενώ εδώ αναφερόμαστε σε $1$-περιοδικές συναρτήσεις και σε τριγωνομετρικά πολυώνυμα που είναι πεπερασμένοι γραμμικοί συνδυασμοί των συναρτήσεων $e^{2\pi i nx}$, $n\in{\mathbb{Z}}$, αλλά είναι σχεδόν προφανές ότι το θεώρημα ισχύει και στην 1-περιοδική περίπτωση.

Αφού λοιπόν η (4.25) ισχύει για όλες τις μη σταθερές εκθετικές συναρτήσεις (αφού $\int e^{2\pi i k x} dx = 0$ για $k\neq 0$) και αφού προφανώς ισχύει και για τις σταθερές, έπεται ότι η (4.25) ισχύει για όλα τα τριγωνομετρικά πολυώνυμα και, κατ' επέκταση σε όλες τις 1-περιοδικές συνεχείς συναρτήσεις, λόγω της πυκνότητας, στην ομοιόμορφη μετρική, των τριγωνομετρικών πολυωνύμων σε αυτές.

Άσκηση 4.18   Έστω $a\neq 0$ ένας πραγματικός αριθμός και $0<\rho<1$. Δείξτε ότι η ακολουθία ${\left\{{an^{\rho}}\right\}}$ είναι ισοκατανεμημένη.

Υπόδειξη: Χρησιμοποιήστε το κριτήριο ισοκατανομήςτου Weyl (Θεώρημα 4.10). Εκτιμήστε το άθροισμα που εμφανίζεται από το αντίστοιχο ολοκλήρωμα, το οποίο υπολογίζεται ακριβώς, και δείξτε ότι το σφάλμα είναι $O(N^{\rho})$.