Next: 4.9 Εφαρμογή: Το θεώρημα Up: 4. Αθροισιμότητα σειρών Fourier Previous: 4.7 Cesáro μέσοι όροι Contents Index
Σε αναλογία με τη σχέση
![]() για τα μερικά αθροίσματα μπορούμε να
γράψουμε
για τα μερικά αθροίσματα μπορούμε να
γράψουμε
![]() , όπου
, όπου ![]() είναι ο πυρήνας του Fejér
είναι ο πυρήνας του Fejér
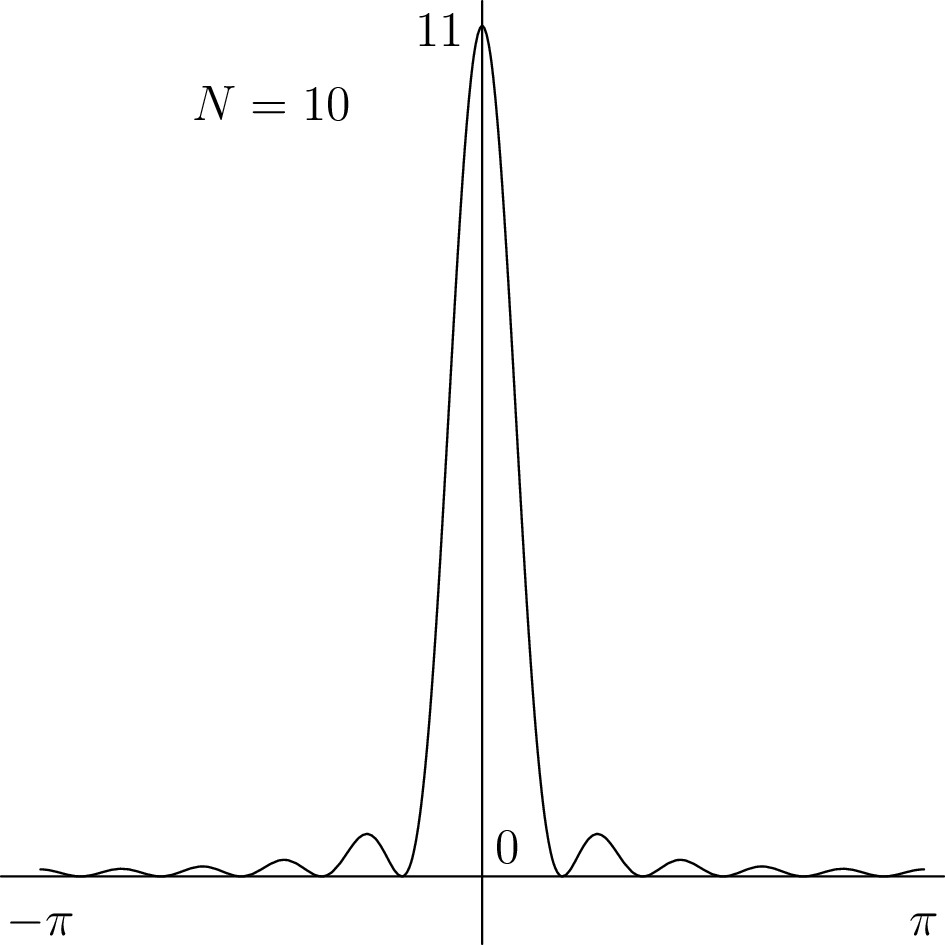
Σχήμα 4.5: Ο πυρήνας του Fejér για
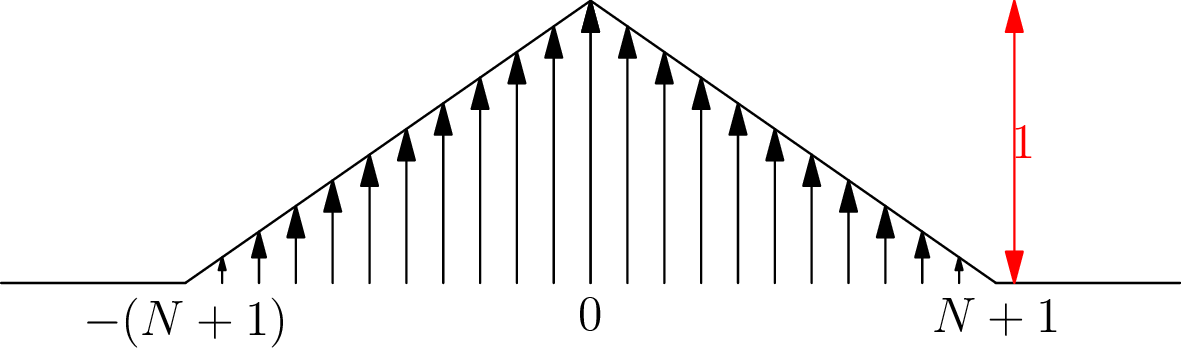
Σχήμα 4.6: Οι συντελεστές Fourier του πυρήνα του Fejérγια
Είναι πολύ σημαντικό ότι, όπως φαίνεται από την (4.23), ο πυρήνας του Fejér είναι μη αρνητική συνάρτηση, της οποίας το ολοκλήρωμα είναι
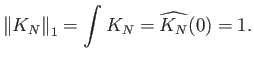
Έχουμε ήδη δει ότι ο πυρήνας του Fejér ικανοποιεί τις δύο πρώτες ιδιότητες. Για να δείξουμε και την ιδιότητα 4.1.3 παρατηρούμε ότι ο τύπος (4.23) συνεπάγεται την ανισότητα
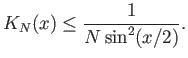
Το Θεώρημα του Fejér έπεται τώρα από το ακόλουθο γενικότερο αποτέλεσμα.
Απόδειξη.
Πρέπει να δείξουμε ότι
![]() ομοιόμορφα ως προς
ομοιόμορφα ως προς ![]() .
.
Έστω
![]() . Από την ομοιόμορφη συνέχεια της
. Από την ομοιόμορφη συνέχεια της ![]() έπεται ότι υπάρχει
έπεται ότι υπάρχει ![]() τ.ώ. αν
τ.ώ. αν
![]() τότε να ισχύει
τότε να ισχύει
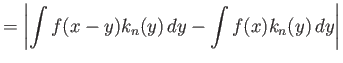 |
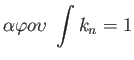 |
||
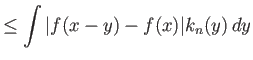 |
|||
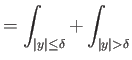 |
|||
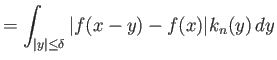 |
||
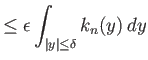 |
||
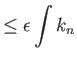 |
||
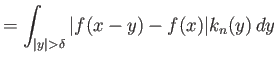 |
||
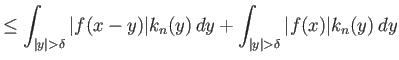 |
||
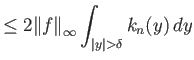 |
||
Έστω ![]() ,
,
![]() και
και
![]() τ.ώ.
τ.ώ.
![]() .
Αυτό είναι εφικτό λόγω της πυκνότητας των συνεχών συναρτήσεων στους χώρους
.
Αυτό είναι εφικτό λόγω της πυκνότητας των συνεχών συναρτήσεων στους χώρους
![]() ,
,
![]() .
.
Έχουμε
Από το Θεώρημα 4.7 έπεται ότι για ![]() αρκετά μεγάλο ισχύει
αρκετά μεγάλο ισχύει
Mihalis Kolountzakis 2015-11-28