Next: 5. Η θεωρία Up: 4. Αθροισιμότητα σειρών Fourier Previous: 4.10 Εφαρμογή: Μια συνεχής Contents Index
Το πολύ σημαντικό θεώρημα του Weierstrass στο οποίο αναφερθήκαμε όταν αποδείξαμε το αντίστοιχο για τριγωνομετρικά πολυώνυμα είναι το παρακάτω.
![$\displaystyle {\left\Vert{g}\right\Vert _\infty} = \sup_{x\in[a,b]} {\left\vert{g(x)}\right\vert}.
$](img1105.png)
Η πρώτη απόδειξη του θεωρήματος του Weierstrass που θα δούμε οφείλεται στον Landau.
Έστω
![]() συνεχής.
συνεχής.
Κάνουμε κατ' αρχήν την παρατήρηση ότι μπορούμε να υποθέσουμε ότι το ![]() είναι όποιο συγκεκριμένο διάστημα μας βολεύει, για παράδειγμα το
είναι όποιο συγκεκριμένο διάστημα μας βολεύει, για παράδειγμα το ![]() . Ο λόγος γι' αυτό είναι ότι μπορούμε
να αντιστοιχίσουμε τα σημεία
. Ο λόγος γι' αυτό είναι ότι μπορούμε
να αντιστοιχίσουμε τα σημεία
![]() με τα στοιχεία
με τα στοιχεία
![]() με μια αφφινική απεικόνιση (μια
απεικόνιση δηλ. που είναι της μορφής
με μια αφφινική απεικόνιση (μια
απεικόνιση δηλ. που είναι της μορφής
![]() ), την
), την
Αν τώρα
![]() είναι συνεχής τότε και η συνάρτηση
είναι συνεχής τότε και η συνάρτηση
Μπορούμε επίσης χωρίς βλάβη της γενικότητας να υποθέσουμε ότι
![]() .
Αυτό συμβαίνει γιατί μπορούμε να αφαιρέσουμε από την
.
Αυτό συμβαίνει γιατί μπορούμε να αφαιρέσουμε από την ![]() ένα κατάλληλο πρωτοβάθμιο πολυώνυμο
ώστε να πετύχουμε αυτή τη συνθήκη. Ακριβέστερα, αν η
ένα κατάλληλο πρωτοβάθμιο πολυώνυμο
ώστε να πετύχουμε αυτή τη συνθήκη. Ακριβέστερα, αν η
![]() είναι οποιαδήποτε
συνεχής συνάρτηση τότε θέτουμε
είναι οποιαδήποτε
συνεχής συνάρτηση τότε θέτουμε
Ορίζουμε τώρα (θυμόμαστε ότι η ![]() μηδενίζεται έξω από το διάστημα
μηδενίζεται έξω από το διάστημα ![]() )
)
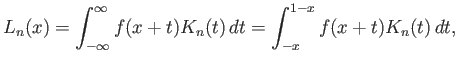
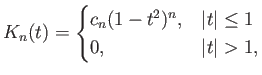
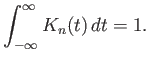
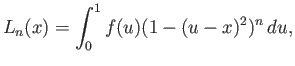
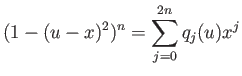
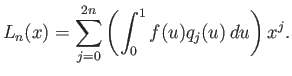
Η συνάρτηση ![]() (για την ακρίβεια, η ακολουθία συναρτήσεων
(για την ακρίβεια, η ακολουθία συναρτήσεων ![]() ) είναι αυτό που ονομάζεται προσέγγιση
της μονάδας, έχει δηλ. τις παρακάτω ιδιότητες:
) είναι αυτό που ονομάζεται προσέγγιση
της μονάδας, έχει δηλ. τις παρακάτω ιδιότητες:
Απόδειξη.
Γράφουμε
![]() (αφού
(αφού
![]() ) και έτσι,
αν
) και έτσι,
αν ![]() είναι οποιοδήποτε,
είναι οποιοδήποτε,
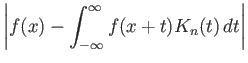 |
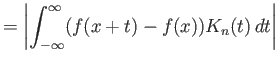 |
|
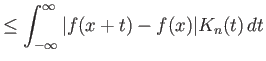 |
||
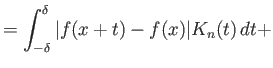 |
||
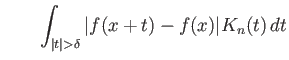 |
||
Για τον πρώτο όρο έχουμε λόγω της συνέχειας της ![]() στο
στο ![]() ότι υπάρχει
ότι υπάρχει ![]() ώστε
ώστε
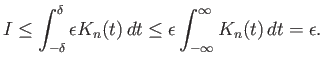
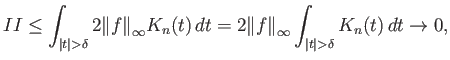
Στην εκτίμηση του ![]() ο δείκτης
ο δείκτης ![]() πέρα από τον οποίο ισχύει
πέρα από τον οποίο ισχύει
![]() δεν εξαρτάται
από το
δεν εξαρτάται
από το ![]() αλλά μόνο από το
αλλά μόνο από το ![]() και το
και το ![]() είτε η
είτε η ![]() είναι ομοιόμορφα συνεχής είτε όχι (αφού το μόνο
που χρησιμοποιούμε από την
είναι ομοιόμορφα συνεχής είτε όχι (αφού το μόνο
που χρησιμοποιούμε από την ![]() είναι ότι είναι φραγμένη).
είναι ότι είναι φραγμένη).
Όμως η επιλογή του ![]() έγινε όταν φράξαμε το
έγινε όταν φράξαμε το ![]() και εκεί το
και εκεί το ![]() εξαρτάται από το
εξαρτάται από το ![]() ,
εκτός αν η συνάρτηση
,
εκτός αν η συνάρτηση ![]() υποτεθεί ομοιόμορφα συνεχής οπότε το
υποτεθεί ομοιόμορφα συνεχής οπότε το ![]() εξαρτάται μόνο από το
εξαρτάται μόνο από το ![]() .
Σε αυτή την περίπτωση έχουμε ταυτόχρονα
.
Σε αυτή την περίπτωση έχουμε ταυτόχρονα
![]() για κάθε
για κάθε
![]() και άρα η σύγκλιση
και άρα η σύγκλιση
Η απόδειξη του Θεωρήματος του Weierstrass (Θεώρημα 4.12) είναι πλήρης.
Εφαρμόζοντας το Θεώρημα 4.13 παίρνουμε την ομοιόμορφη σύγκλιση των
πολυωνύμων ![]() στην
στην ![]() στο διάστημα
στο διάστημα ![]() .
.
Υπόδειξη: Ένα πολυώνυομο ![]() που είαι φραγμένο στο
που είαι φραγμένο στο
![]() είναι αναγκαστικά σταθερά.
είναι αναγκαστικά σταθερά.
Η δεύτερη απόδειξη του θεωρήματος του Weierstrass (Θεώρημα 4.12)
που θα δούμε οφείλεται στον Bernstein και είναι πολύ ενδιαφέρουσα γιατί συνδέει τη θεωρία Πιθανοτήτων με την πολυωνυμική προσέγγιση που θέλουμε να πετύχουμε. Επίσης τα πολυώνυμα που δίνει ως προσέγγιση της ![]() είναι πολύ απλό να περιγραφούν.
είναι πολύ απλό να περιγραφούν.
Υποθέτουμε και πάλι ότι η
![]() είναι συνεχής (δε χρειάζεται αυτή τη φορά να κανονικοποιήσουμε
την
είναι συνεχής (δε χρειάζεται αυτή τη φορά να κανονικοποιήσουμε
την ![]() ώστε να μηδενίζεται στα άκρα του διαστήματος). Ορίζουμε τα πολυώνυμα Bernstein της
ώστε να μηδενίζεται στα άκρα του διαστήματος). Ορίζουμε τα πολυώνυμα Bernstein της ![]() να είναι η ακολουθία πολυωνύμων
να είναι η ακολουθία πολυωνύμων ![]() που δίδεται από
που δίδεται από
Για την απόδειξη θα χρειαστεί να ερμηνεύσουμε τα πολυώνυμα του Bernstein σε πιθανοθεωρητική γλώσσα.
Ας υποθέσουμε ότι έχουμε ένα νόμισμα το οποίο φέρνει κορώνα με πιθανότητα
![]() και το ρίχνουμε
και το ρίχνουμε
![]() φορές. Η τυχαία μεταβλητή
φορές. Η τυχαία μεταβλητή ![]() μετράει το πόσες κορώνες φέραμε σε αυτό το πείραμα. Προφανώς ισχύει
πάντα
μετράει το πόσες κορώνες φέραμε σε αυτό το πείραμα. Προφανώς ισχύει
πάντα
![]() και εύκολα βλέπει κανείς ότι η
και εύκολα βλέπει κανείς ότι η ![]() ακολουθεί τη λεγόμενη διωνυμική
κατανομή, έχουμε δηλαδή για
ακολουθεί τη λεγόμενη διωνυμική
κατανομή, έχουμε δηλαδή για
![]()
![$\displaystyle {{\bf {Pr}}\left[{B_{x,n} = k}\right]} = \begin{cases}{n \choose ...
...u 0 \le k \le n 0 & \alpha\lambda\lambda\iota\omega\varsigma \end{cases}.
$](img1177.png)
Κάνουμε επίσης την παρατήρηση ότι, αν γράψουμε ![]() για την δείκτρια τυχαία μεταβλητή που είναι 1 αν φέρουμε
κορώνα στην
για την δείκτρια τυχαία μεταβλητή που είναι 1 αν φέρουμε
κορώνα στην ![]() ρίψη και 0 αν φέρουμε γράμματα στην
ρίψη και 0 αν φέρουμε γράμματα στην ![]() ρίψη, ισχύει
ρίψη, ισχύει
![$ {{\bf E}\left[{{\left\vert{X}\right\vert}}\right]} \le {{\bf E}\left[{{\left\vert{X}\right\vert}^2}\right]}^{1/2}$](img1191.png) για μια διακριτή τυχαία μεταβλητή
για μια διακριτή τυχαία μεταβλητή
Υπόδειξη: Οι δύο ποσότητες που μας ενδιαφέρουν είναι οι
![$\displaystyle {{\bf E}\left[{{\left\vert{X}\right\vert}}\right]} = \sum_{k\in{\mathbb{Z}}} {\left\vert{k}\right\vert} {{\bf {Pr}}\left[{X=k}\right]}
$](img1192.png)
![$\displaystyle {{\bf E}\left[{{\left\vert{X}\right\vert}^2}\right]} = \sum_{k\in{\mathbb{Z}}} {\left\vert{k}\right\vert}^2 {{\bf {Pr}}\left[{X=k}\right]}.
$](img1193.png)
Παρατηρούμε τώρα ότι υπάρχει η εξής σχέση ανάμεσα στα πολυώνυμα Bernstein, την τυχαία μεταβλητή ![]() και τη συνάρτηση
και τη συνάρτηση ![]() :
:
![$\displaystyle {{\bf E}\left[{\phi(X)}\right]} = \sum_{k \in {\mathbb{Z}}} \phi(k) {{\bf {Pr}}\left[{X=k}\right]},
$](img1196.png)
Από την (4.40) γίνεται τώρα φανερό το γιατί πρέπει να περιμένουμε τη σύγκλιση
Γράφουμε ![]() για το ενδεχόμενο
για το ενδεχόμενο
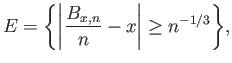
Υπόδειξη: Χρησιμοποιήστε το φράγμα
![]() και την τιμή
και την τιμή
![]() και εφαρμόστε την
ανισότητα (4.39) για το ενδεχόμενο
και εφαρμόστε την
ανισότητα (4.39) για το ενδεχόμενο ![]() γραμμένο στη μορφή
γραμμένο στη μορφή
Φράσσουμε τώρα τη διαφορά της συνάρτησής μας και της προσέγγισής της από ένα πολυώνυμο Bernstein:
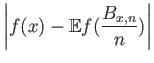 |
![$\displaystyle = {\left\vert{f(x) - \sum_{k=0}^n f(k/n){{\bf {Pr}}\left[{B_{x,n}=k}\right]}}\right\vert}$](img1207.png) |
|
![$\displaystyle = {\left\vert{\sum_{k=0}^n f(x){{\bf {Pr}}\left[{B_{x,n}=k}\right...
...t} (\alpha\varphi o \upsilon \sum_k {{\bf {Pr}}\left[{B_{x,n}=k}\right]}=1)$](img1208.png) |
||
![$\displaystyle = {\left\vert{\sum_{k=0}^n (f(x)-f(k/n)) {{\bf {Pr}}\left[{B_{x,n}=k}\right]}}\right\vert}$](img1209.png) |
||
![$\displaystyle \le \sum_{k=0}^n {\left\vert{f(x)-f(k/n)}\right\vert} \cdot {{\bf {Pr}}\left[{B_{x,n}=k}\right]} \dagger$](img1210.png) |
||
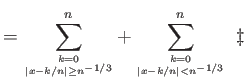 |
||
Έστω
![]() . Θα δείξουμε ότι αν το
. Θα δείξουμε ότι αν το ![]() είναι αρκετά μεγάλο τότε τα αθροίσματα
είναι αρκετά μεγάλο τότε τα αθροίσματα ![]() και
και ![]() φράσσονται από
φράσσονται από ![]() .
.
Για να φράξουμε το ![]() χρησιμοποιούμε την ομοιόμορφη συνέχεια της
χρησιμοποιούμε την ομοιόμορφη συνέχεια της ![]() (η οποία είναι συνέπεια της συνέχειας της
(η οποία είναι συνέπεια της συνέχειας της
![]() σε κλειστό διάστημα, δείτε το Πρόβλημα 4.28): για κάθε
σε κλειστό διάστημα, δείτε το Πρόβλημα 4.28): για κάθε
![]() υπάρχει
υπάρχει ![]() τ.ώ. αν
τ.ώ. αν
![]() να έπεται ότι
να έπεται ότι
![]() .
Αν λοιπόν το
.
Αν λοιπόν το ![]() είναι αρκετά μεγάλο ώστε να ισχύει
είναι αρκετά μεγάλο ώστε να ισχύει
![]() τότε στο άθροισμα
τότε στο άθροισμα ![]() η ποσότητα
η ποσότητα
![]() φράσσεται από
φράσσεται από ![]() οπότε ισχύει
οπότε ισχύει
![$\displaystyle I \le \epsilon \sum_{k=0 \atop {\left\vert{x-k/n}\right\vert}\ge ...
...]} \le \epsilon \sum_{k=0}^n {{\bf {Pr}}\left[{B_{x,n}=k}\right]}
= \epsilon.
$](img1216.png)
Για τον όρο ![]() φράσσουμε την ποσότητα
φράσσουμε την ποσότητα
![]() από
από
![]() (η συνάρτηση
(η συνάρτηση ![]() είναι φραγμένη αφού
είναι συνεχής σε κλειστό διάστημα, οπότε
είναι φραγμένη αφού
είναι συνεχής σε κλειστό διάστημα, οπότε
![]() ) και έχουμε
) και έχουμε
![$\displaystyle II \le 2{\left\Vert{f}\right\Vert _\infty} \sum_{k=0 \atop {\left...
...{{\bf {Pr}}\left[{E}\right]} \le 2{\left\Vert{f}\right\Vert _\infty} n^{-1/3}.
$](img1219.png)
Υπόδειξη: Για να αποδείξετε την ομοιόμορφη συνέχεια της ![]() πρέπει να χρησιμοποιήσετε τη συμπάγεια
φραγμένου κλειστού διαστήματος
πρέπει να χρησιμοποιήσετε τη συμπάγεια
φραγμένου κλειστού διαστήματος ![]() : κάθε ακολουθία
: κάθε ακολουθία
![]() έχει υπακολουθία η οποία συγκλίνει
(αναγκαστικά σε κάποιο σημείο του
έχει υπακολουθία η οποία συγκλίνει
(αναγκαστικά σε κάποιο σημείο του ![]() ).
).
Υποθέστε ότι η ![]() δεν είναι ομοιόμορφα συνεχής. Αυτό σημαίνει ότι για κάποιο
δεν είναι ομοιόμορφα συνεχής. Αυτό σημαίνει ότι για κάποιο
![]() υπάρχουν
υπάρχουν
![]() τ.ώ.
τ.ώ.
![]() αλλά με
αλλά με
Όσον αφορά τις συναρτήσεις ![]() και
και ![]() που πρέπει να βρείτε μπορείτε να δοκιμάσετε τις
που πρέπει να βρείτε μπορείτε να δοκιμάσετε τις
![]() και
και ![]() .
.
Το να πούμε ότι μια συνάρτηση είναι συνεχής σε κάποιο σύνολο είναι μια ποιοτική και όχι ποσοτική δήλωση. Είναι μια ιδιότητα που η συνάρτηση την έχει ή όχι. Κατά κάποιον τρόπο όμως υπάρχουν συναρτήσεις που είναι «πιο συνεχείς» από άλλες, όπως για παράδειγμα η πράσινη συνάρτηση στο Σχήμα 4.9 είναι πιο συνεχής από την κόκκινη συνάρτηση στο ίδιο Σχήμα, μεταβάλλεται δηλ. πιο αργά.
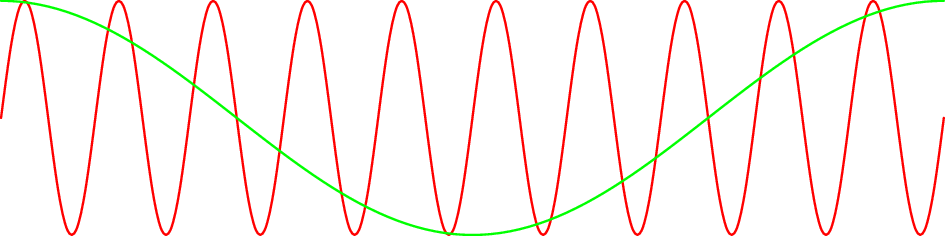
Σχήμα 4.9: Μια συνάρτηση (πράσινη) που είναι «πιο συνεχής» από μια άλλη
Η έννοια του μέτρου συνέχειας μιας συνάρτησης παίζει ακριβώς αυτό το ρόλο της ποσοτικοποίησης του πόσο γρήγορα αλλάζει μια συνάρτηση όταν αλλάζει η μεταβλητή.
Η ποσότητα
Η συνάρτηση
![]() μπορεί να μην είναι πεπερασμένη ακόμη κι όταν η συνάρτηση
μπορεί να μην είναι πεπερασμένη ακόμη κι όταν η συνάρτηση ![]() είναι συνεχής στο
είναι συνεχής στο ![]() .
Για παράδειγμα, εύκολα μπορεί κανείς να δει ότι αν
.
Για παράδειγμα, εύκολα μπορεί κανείς να δει ότι αν ![]() , ορισμένη για
, ορισμένη για
![]() , τότε για κάθε
, τότε για κάθε ![]() ισχύει
ισχύει
![]() . Δείτε όμως το Πρόβλημα 4.30.
. Δείτε όμως το Πρόβλημα 4.30.
Υπόδειξη: Χρησιμοποιήστε το θεώρημα μέσης τιμής για να φράξετε τη διαφορά
![]() .
.
Το μέτρο συνέχειας της ![]() είναι υποπροσθετική συνάρτηση.
είναι υποπροσθετική συνάρτηση.
Το Θεώρημα του Weierstrass (Θεώρημα 4.12) δε μας δίνει κάποια εκτίμηση για το πόσο μεγάλο μπορεί να είναι το «σφάλμα»
![]() όταν η
όταν η ![]() είναι μια συνεχής συνάρτηση στο διάστημα
είναι μια συνεχής συνάρτηση στο διάστημα ![]() και το
και το ![]() είναι πολυώνυμο βαθμού
είναι πολυώνυμο βαθμού ![]() .
Σημαντικό ερώτημα είναι το πόσο μικρή μπορεί να γίνει αυτή η ποσότητα αν
μας επιτρέπεται να διαλέξουμε κατάλληλα το πολυώυμο
.
Σημαντικό ερώτημα είναι το πόσο μικρή μπορεί να γίνει αυτή η ποσότητα αν
μας επιτρέπεται να διαλέξουμε κατάλληλα το πολυώυμο ![]() . Με άλλα λόγια μας ενδιαφέρει
η ποσότητα
. Με άλλα λόγια μας ενδιαφέρει
η ποσότητα
Όπως κάναμε και στην απόδειξη του θεωρήματος του Weierstrass μέσω των πολυωνύμων του
Bernstein, μπορούμε κι εδώ, χωρίς βλάβη της γενικότητας, να πάρουμε
![]() ,
πράγμα το οποίο απλουστεύει τους υπολογισμούς.
,
πράγμα το οποίο απλουστεύει τους υπολογισμούς.
Ξεκινάμε χρησιμοποιώντας της σχέση (4.40).
![$\displaystyle = \sum_{k=0}^n {\left\vert{f(x)-f(k/n)}\right\vert} {{\bf {Pr}}\left[{B_{x,n}=k}\right]} (A2)$](img1269.png) |
||
![$\displaystyle \le \sum_{k=0}^n \omega_f({\left\vert{x-\frac{k}{n}}\right\vert}) {{\bf {Pr}}\left[{B_{x,n}=k}\right]}$](img1270.png) |
||
![$\displaystyle = \sum_{k=0}^n \omega_f(\lambda\frac{1}{\sqrt{n}}) {{\bf {Pr}}\left[{B_{x,n}=k}\right]} (A3)$](img1271.png) |
||
![$\displaystyle \le \omega_f(1/\sqrt{n}) \sum_{k=0}^n (1+\sqrt{n}{\left\vert{x-\frac{k}{n}}\right\vert}){{\bf {Pr}}\left[{B_{x,n}=k}\right]} (A4)$](img1272.png) |
||
![$\displaystyle = \omega_f(1/\sqrt{n}) (1+\sqrt{n}{{\bf E}\left[{x-\frac{B_{x,n}}{n}}\right]})$](img1273.png) |
||
![$\displaystyle = \omega_f(1/\sqrt{n}) (1+\frac{1}{\sqrt{n}}{{\bf E}\left[{B_{x,n}-nx}\right]})$](img1274.png) |
||
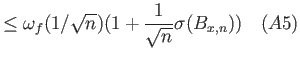 |
||
Mihalis Kolountzakis 2015-11-28