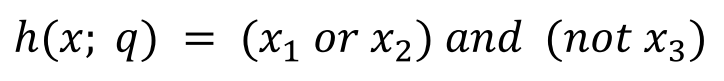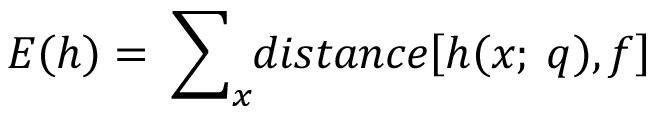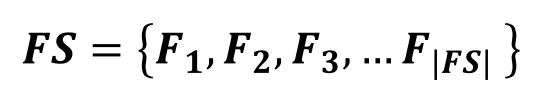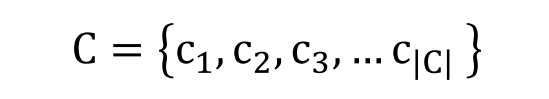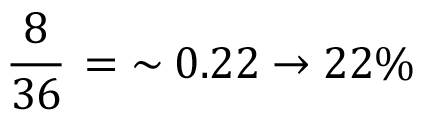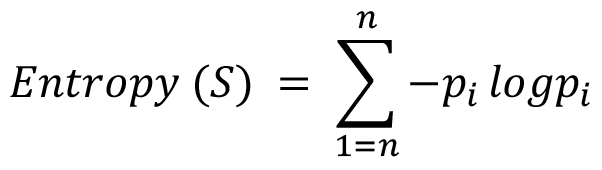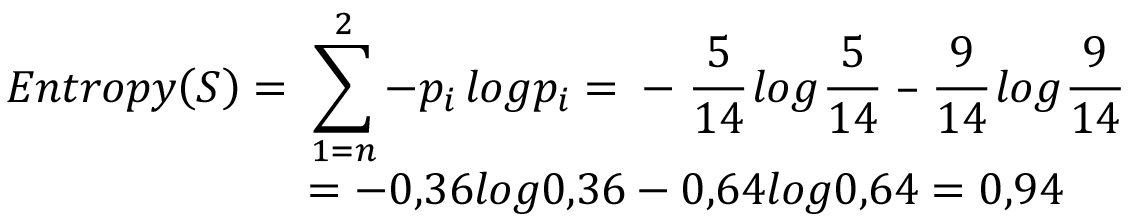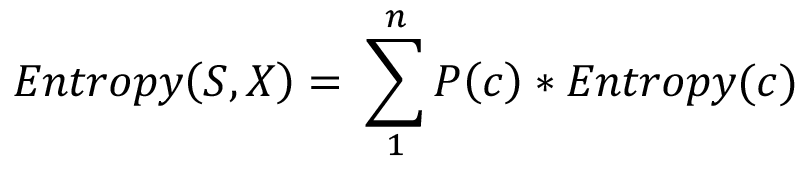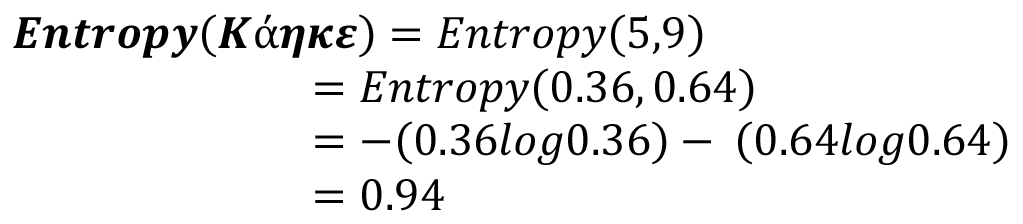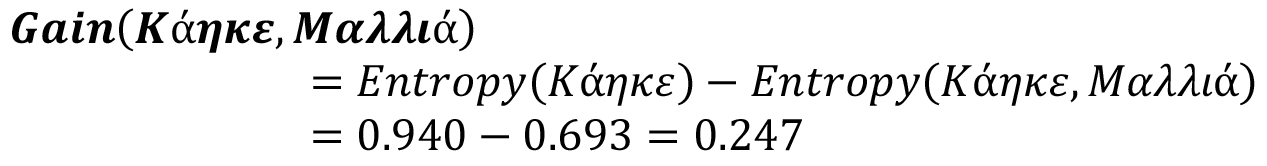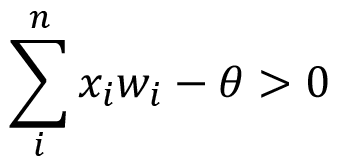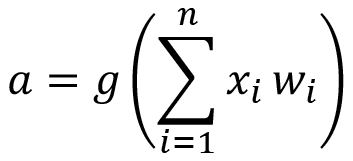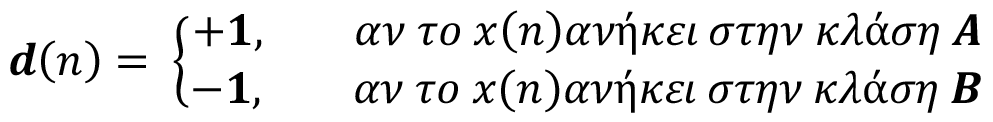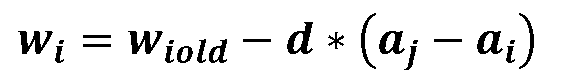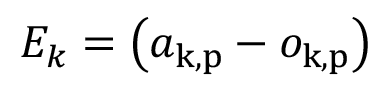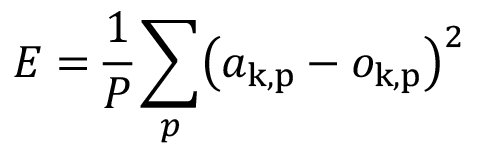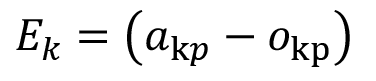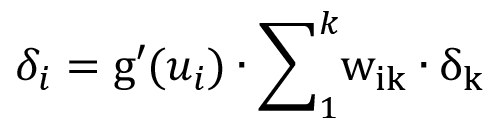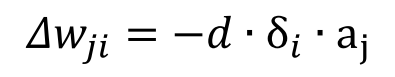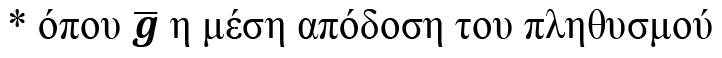ΚΕΦΑΛΑΙΟ 4 - Μηχανική Μάθηση

Σύνοψη

Η επίλυση προβλημάτων με ευφυείς προσεγγίσεις βασίζεται στη δυνατότητα των συστημάτων να μαθαίνουν. Στο κεφάλαιο αυτό σκιαγραφείται η επιστημονική περιοχή της Μηχανικής Μάθησης (Machine Learning) και ιδιαίτερα αυτή της Επαγωγικής Μάθησης (Inductive Learning). Στο πλαίσιο αυτό, παρουσιάζονται αλγόριθμοι που υποστηρίζουν την Επιβλεπόμενη Επαγωγική Μάθηση με παραδείγματα, όπως τα Δένδρα Απόφασης (Decision Trees), πρακτικές Επαγωγικής Μάθησης Μέσω Συνάφειας με Περιπτώσεις, όπως η Συλλογιστική Βασισμένη σε Περιπτώσεις (Case-Based Reasoning), συστήματα Μη Συμβολικής ΤΝ, όπως τα Νευρωνικά Δίκτυα (Neural Networks),αλγόριθμοι Εξελικτικής Μάθησης, όπως οι Γενετικοί Αλγόριθμοι (Genetic Algorithms).

Προαπαιτούμενη γνώση

Αναπαράσταση γνώσης, επίλυση προβλημάτων.

4.1 Εισαγωγή

Η Μάθηση (Learning) είναι μία από τις θεμελιώδεις ιδιότητες της νοήμονος συμπεριφοράς του ανθρώπου. Παρά τις μελέτες και τις έρευνες επί χρόνια από τους επιστήμονες του πεδίου της Γνωστικής Ψυχολογίας και τους φιλοσόφους, η έννοια της μάθησης δεν έχει γίνει πλήρως κατανοητή. Πώς, λοιπόν, θα μπορούσαν οι επιστήμονες του χώρου της ΤΝ να δημιουργήσουν υπολογιστικά συστήματα ικανά να μάθουν, να επιτύχουν, δηλαδή, τη λεγόμενη Μηχανική Μάθηση (Machine Learning).

Αυτή μπορεί να οριστεί ως:

 

το φαινόμενο κατά το οποίο ένα σύστημα βελτιώνει την απόδοσή του κατά την εκτέλεση μιας συγκεκριμένης εργασίας, χωρίς να υπάρχει ανάγκη να προγραμματιστεί εκ νέου.

 

Βάσει του ορισμού αυτού, η Μηχανική Μάθηση έχει ως σκοπό τη δημιουργία μηχανών ικανών να μαθαίνουν, να βελτιώνουν, δηλαδή, την απόδοσή τους σε κάποιους τομείς μέσω της αξιοποίησης προηγούμενης γνώσης και εμπειρίας. Ένας σχετικός γενικός ορισμός Μηχανικής Μάθησης δίνεται από τον Mitchell (1997):

 

«Ένα πρόγραμμα υπολογιστή λέμε ότι μαθαίνει από την εμπειρία Ε ως προς κάποια κλάση εργασιών Τ και μέτρο απόδοσης Ρ, αν η απόδοσή του σε εργασίες από το Τ, όπως μετριέται από το Ρ, βελτιώνεται μέσω της εμπειρίας Ε.»

 

Στην Επαγωγική Μάθηση (Inductive Learning), με τη διαδικασία της επαγωγής (induction) ο άνθρωπος μαθαίνει κατανοώντας το περιβάλλον του μέσω παρατηρήσεων και δημιουργεί μια απλοποιημένη (αφαιρετική) εκδοχή του που ονομάζεται νοητικό μοντέλο (mental model). Επιπλέον, o άνθρωπος έχει τη δυνατότητα να οργανώνει και να συσχετίζει τις εμπειρίες και τις παρατηρήσεις του δημιουργώντας νέες δομές που ονομάζονται νοητικά πρότυπα (mental patterns), με αξιοποίηση και του επαγωγικού και του απαγωγικού συλλογισμoύ. Στη δημιουργία νέων προτύπων από παλαιά βασίζονται οι τρόποι μάθησης που εξαρτώνται σε μεγαλύτερο ή μικρότερο βαθμό από την προϋπάρχουσα γνώση για ένα πρόβλημα, όπως είναι η μάθηση από επεξηγήσεις και η μάθηση από περιπτώσεις.

Σε σχέση με την ανθρώπινη ικανότητα προς μάθηση, οι φιλόσοφοι θέτουν το ερώτημα: «Πώς μπορεί ένας επαγωγικός συλλογισμός που οδηγεί στη μάθηση να αξιολογηθεί ως προς την ορθότητά του;». Αντίστοιχα, οι ψυχολόγοι ρωτούν: «Πώς αποθηκεύει ο εγκέφαλος τα αποτελέσματα της διαδικασίας της μάθησης, δηλαδή τα νοητικά μοντέλα και τα πρότυπα;». Στο χώρο της ΤΝ απλώς ρωτούν: «Πώς μπορεί μία μηχανή να δημιουργήσει νέα μοντέλα και πρότυπα μάθησης από συγκεκριμένα παραδείγματα και πόσο αξιόπιστα είναι αυτά τα μοντέλα και πρότυπα στην πράξη;».

Με βάση τα παραπάνω, μπορεί να δοθεί ο ακόλουθος εναλλακτικός ορισμός για τη Μηχανική Μάθηση:

 

Μηχανική Μάθηση ονομάζεται η ικανότητα ενός υπολογιστικού συστήματος να δημιουργεί μοντέλα ή πρότυπα από ένα σύνολο δεδομένων.

 

Ως κλάδος της ΤΝ, η Μηχανική Μάθηση ασχολείται με τη μελέτη αλγορίθμων που βελτιώνουν τη συμπεριφορά τους σε κάποια εργασία που τους έχει ανατεθεί χρησιμοποιώντας την εμπειρία τους.

Όσον αφορά τη σχεδίαση των συστημάτων Μηχανικής Μάθησης, για τα συστήματα που ανήκουν στη συμβολική ΤΝ, η δυνατότητα μάθησης προσδιορίζεται ως η ικανότητα πρόσκτησης επιπλέον γνώσης, που επιφέρει μεταβολές στην υπάρχουσα καταχωρημένη γνώση είτε αλλάζοντας χαρακτηριστικά της είτε με αυξομείωσή της. Στην περίπτωση των συστημάτων ΤΝ που ανήκουν στη Μη Συμβολική ΤΝ (όπως η περίπτωση των Τεχνητών Νευρωνικών Δικτύων), ως μάθηση προσδιορίζεται η δυνατότητα που διαθέτουν τα συστήματα στο να μετασχηματίζουν την εσωτερική τους δομή, παρά στο να μεταβάλλουν κατάλληλα τη γνώση που έχει καταχωρηθεί μέσα σε αυτά κατά το σχεδιασμό τους.

Αν και απέχουμε πάρα πολύ από τη δημιουργία μηχανών που μαθαίνουν τόσο καλά όσο ο άνθρωπος, για συγκεκριμένες περιοχές μάθησης έχουν αναπτυχθεί αλγόριθμοι οι οποίοι έχουν επιτρέψει την εμφάνιση σύγχρονων εμπορικών εφαρμογών με σημαντική επιτυχία. Επιπλέον, τα αποτελέσματα από τις εφαρμογές της ΤΝ αρχίζουν ήδη να είναι ορατά και να δίνουν απαντήσεις σε αναπάντητα, έως τώρα, ερωτήματα των άλλων κλάδων που διερευνούν την ικανότητα του ανθρώπου να μαθαίνει.

Ο τομέας της Μηχανικής Μάθησης αναπτύσσει, επίσης, επιτυχώς την Εξελικτική Μάθηση (Evolutionary Learning), η οποία μιμείται διαδικασίες φυσικής αναπαραγωγικής σε έμβια όντα. Χρησιμοποιείται κυρίως σε προβλήματα βελτιστοποίησης. Στην Εξελικτική Μάθηση κυριαρχούν οι γενετικοί αλγόριθμοι που θα παρουσιαστούν στο τέλος του κεφαλαίου.

Εκτός της ίδιας της ΤΝ, μεταξύ των επιστημονικών κλάδων που επωφελούνται από τα επιτεύγματα στον τομέα της Μηχανικής Μάθησης συγκαταλέγονται οι: Εξόρυξη Δεδομένων, Πιθανότητες και Στατιστική, Θεωρία της Πληροφορίας, Αριθμητική Βελτιστοποίηση, Θεωρία της Πολυπλοκότητας, Θεωρία Ελέγχου (προσαρμοστική), Ψυχολογία (εξελικτική, γνωστική), Νευροβιολογία και Γλωσσολογία.

4.2 Είδη Μηχανικής Μάθησης

Εν γένει, ο τομέας της Μηχανικής Μάθησης αναπτύσσει τρεις τρόπους μάθησης, ανάλογους με τους τρόπους με τους οποίους μαθαίνει ο άνθρωπος: επιβλεπόμενη μάθηση, μη επιβλεπόμενη μάθηση και ενισχυτική μάθηση. Πιο αναλυτικά:

• Επιβλεπόμενη Μάθηση (Supervised Learning) είναι η διαδικασία όπου ο αλγόριθμος κατασκευάζει μια συνάρτηση που απεικονίζει δεδομένες εισόδους (σύνολο εκπαίδευσης) σε γνωστές επιθυμητές εξόδους, με απώτερο στόχο τη γενίκευση της συνάρτησης αυτής και για εισόδους με άγνωστη έξοδο. Χρησιμοποιείται σε προβλήματα:
  • Ταξινόμησης (Classification)
  • Πρόγνωσης (Prediction)
  • Διερμηνείας (Interpretation)
    

• Μη Επιβλεπόμενη Μάθηση (Unsupervised Learning), όπου ο αλγόριθμος κατασκευάζει ένα μοντέλο για κάποιο σύνολο εισόδων υπό μορφή παρατηρήσεων χωρίς να γνωρίζει τις επιθυμητές εξόδους. Χρησιμοποιείται σε προβλήματα:
  • Ανάλυσης Συσχετισμών (Association Analysis)
  • Ομαδοποίησης (Clustering)

• Ενισχυτική Μάθηση (Reinforcement Learning), όπου ο αλγόριθμος μαθαίνει μια στρατηγική ενεργειών μέσα από άμεση αλληλεπίδραση με το περιβάλλον. Χρησιμοποιείται κυρίως σε προβλήματα Σχεδιασμού (Planning), όπως για παράδειγμα ο έλεγχος κίνησης ρομπότ και η βελτιστοποίηση εργασιών σε εργοστασιακούς χώρους.

Για κάθε πρόβλημα προς επίλυση στο χώρο της Μηχανικής Μάθησης υπάρχει ένας κατάλληλος τρόπος μάθησης και για κάθε τρόπο μάθησης υπάρχει τουλάχιστον ένας κατάλληλος αλγόριθμος που μπορεί να χρησιμοποιηθεί.

Όλοι οι αλγόριθμοι Μηχανικής Μάθησης διαχειρίζονται τη γνώση αναπαριστώντας την με κάποιον από τους τρόπους που έχουμε ήδη παρουσιάσει στο κεφάλαιο 2 για την αναπαράσταση της γνώσης ή με άλλους πιο μαθηματικοποιημένους τρόπους που θεωρούνται από τον συγκεκριμένο αλγόριθμο καταλληλότεροι να την εκφράσουν. Ορισμένοι αλγόριθμοι δέχονται ως είσοδο μόνο παρατηρήσεις και άλλοι λαμβάνουν υπόψη τους λίγο ή περισσότερο την προϋπάρχουσα γνώση. Μια προσπάθεια κατάταξης των αλγορίθμων με κριτήριο τον τρόπο μάθησης βασισμένο περισσότερο ή λιγότερο στην υπάρχουσα γνώση δίνεται παρακάτω:

Στο σχήμα 4.1, αποτυπώνεται ο γενικός τρόπος λειτουργίας των αλγορίθμων Μηχανικής Μάθησης. Η βασικότερη φάση κάθε αλγόριθμου είναι η εκπαίδευση, όπου ο αλγόριθμος χρησιμοποιεί ως είσοδο ένα σύνολο δεδομένων εκπαίδευσης (training set) προς επίτευξη του σκοπού του, τη δημιουργία νέας γνώσης. Επιπλέον, μπορεί είτε να χρησιμοποιήσει λιγότερο ή περισσότερο την υπάρχουσα γνώση είτε να μην τη χρησιμοποιήσει καθόλου.

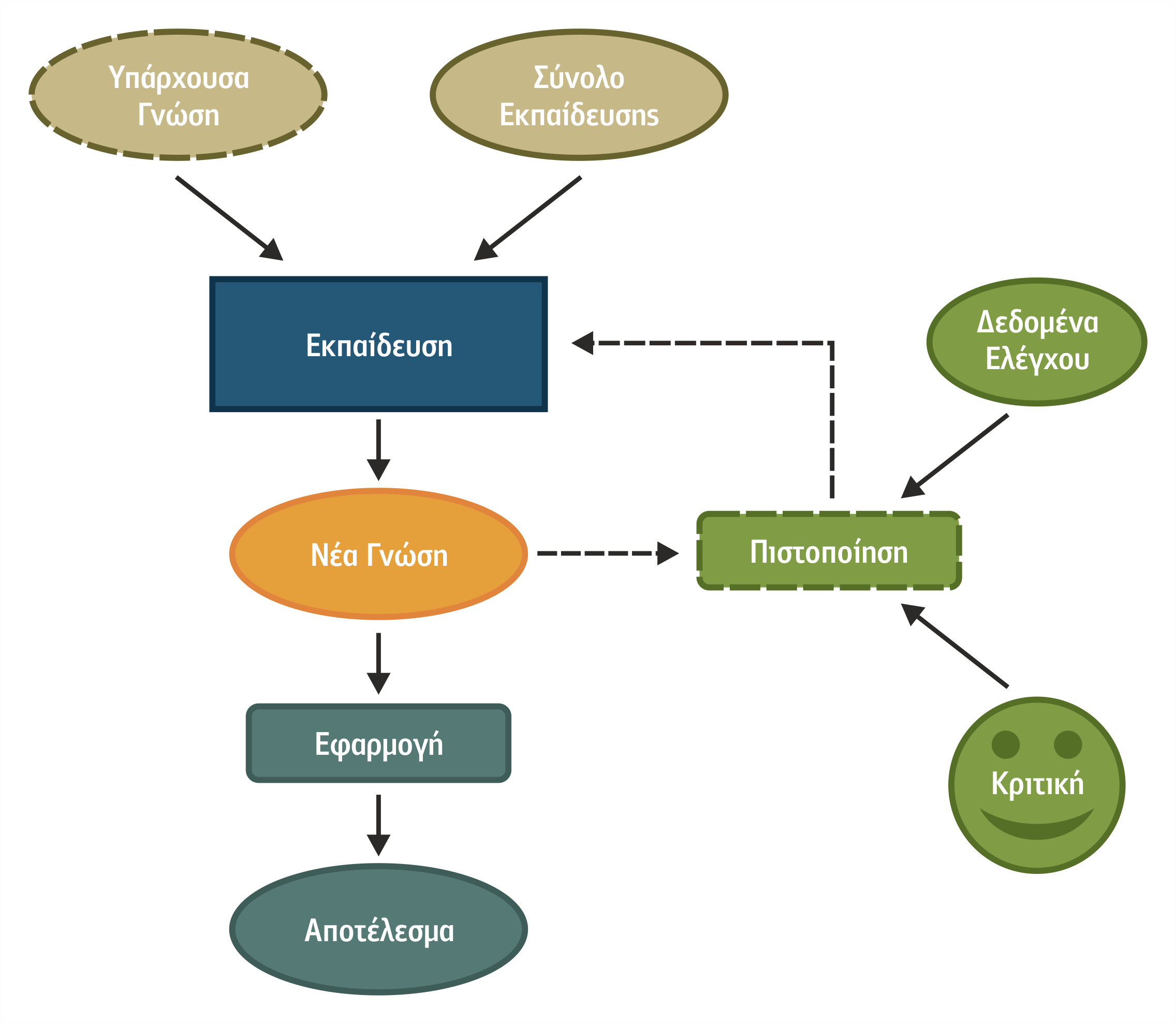
Σχήμα 4.1 Φάσεις Μηχανικής Μάθησης

Την εκπαίδευση ακολουθεί η φάση της πιστοποίησης της παραγόμενης νέας γνώσης. Συνήθως, η πιστοποίηση πραγματοποιείται καταρχάς από τον ίδιο τον αλγόριθμο μέσω διαδικασιών ανάκλησης (recall) με τη βοήθεια δεδομένων ελέγχου (test data) και, στη συνέχεια, μέσω κριτικής που κάνει ο χρήστης βάσει των γνώσεων που διαθέτει για το πρόβλημα που επιχειρεί να λύσει ο αλγόριθμος. Τέλος, η νέα γνώση δίνεται προς χρήση σε εφαρμογές στις οποίες είναι απαραίτητη, για να λυθούν πραγματικά προβλήματα.

4.3 Αλγόριθμοι Επιβλεπόμενης Επαγωγικής Μάθησης

Ένας από τους συνηθέστερους τρόπους Μηχανικής Μάθησης είναι μέσω επαγωγών οι οποίες παρέχουν δια του προτασιακού λογισμού ένα μηχανισμό εξαγωγής (όχι απαραίτητα σωστών) λογικών συμπερασμάτων από παραδείγματα.

Οι αλγόριθμοι Επαγωγικής Μάθησης (Inductive Learning algorithms) είναι ένα είδος αλγορίθμων που αναπτύχθηκε στο πλαίσιο της ΤΝ και ιδιαίτερα στο χώρο της Μηχανικής Μάθησης. Σκοπός των αλγορίθμων αυτών είναι η κατάληξη σε αποφάσεις σχετικές με τις σχέσεις που κυριαρχούν μέσα σε ένα σύνολο παραδειγμάτων που έχουν συγκεντρωθεί από παρατηρήσεις. Οι αλγόριθμοι επιβλεπόμενης Επαγωγικής Μάθησης εφαρμόζονται κυρίως σε προβλήματα ταξινόμησης (classification problems) και σε προβλήματα παρεμβολής (regression problems). Δημιουργούνται μοντέλα πρόβλεψης διακριτών τάξεων κατά την κατηγοριοποίηση και αριθμητικών τιμών κατά την παρεμβολή. Για προβλήματα πρόβλεψης, χρησιμοποιείται κυρίως μια παραλλαγή τους, οι αλγόριθμοι ημι-επιβλεπόμενης Μηχανικής Μάθησης, οι οποίοι λειτουργούν με σύνολο εκπαίδευσης μέσα στο οποίο υπάρχουν παραδείγματα μη γνωστές εξόδους.

Στην επιβλεπόμενη Επαγωγική Μάθηση (supervised Inductive Learning) το σύστημα πρέπει να «μάθει», δηλαδή να κατασκευάσει ένα νέο μοντέλο υπό μορφή μιας συνάρτησης πρόγνωσης (predictor function), η οποία θα απεικονίζει δεδομένες εισόδους σε γνωστές, επιθυμητές εξόδους, με απώτερο στόχο τη γενίκευση της συνάρτησης αυτής και για εισόδους με άγνωστη έξοδο. Για τη συνάρτηση πρόγνωσης ισχύουν τα ακόλουθα:

• Κάθε είσοδος, δεδομένη ή μη, που μπορεί να δεχθεί η συνάρτηση χαρακτηρίζεται ως στιγμιότυπο (instance), δημιουργώντας έτσι ένα σύνολο στιγμιότυπων.
• Οι είσοδοι περιγράφονται με βάση τα γνωρίσματα (attributes) που διαθέτουν και έχουν χαρακτηριστεί ως σημαντικά από την αρχή της μελέτης του προβλήματος που καλείται να επιλύσει το σύστημα.
• Οι δεδομένες είσοδοι συγκεντρώνονται από παρατηρήσεις και αποτελούν το λεγόμενο σύνολο εκπαίδευσης (training set) που αποτελεί υποσύνολο του συνόλου στιγμιότυπων.
• Το υπόλοιπο μέρος του συνόλου στιγμιότυπων αποτελεί το σύνολο ελέγχου (test set) που θα χρησιμοποιηθεί κατά τη φάση πιστοποίησης.
• Η συνάρτηση που απεικονίζει μια είσοδο από το σύνολο εκπαίδευσης στη γνωστή της έξοδο καλείται συνάρτηση στόχου (goal function).
• Η τιμή που επιστρέφει η συνάρτηση στόχου για ένα στιγμιότυπο από το σύνολο στιγμιότυπων, δίνεται σε μια μεταβλητή που καλείται μεταβλητή στόχου (goal variable).
• Στην επιβλεπόμενη μάθηση, η συμπεριφορά της συνάρτησης στόχου βελτιώνεται μέσω διαδικασιών εκπαίδευσης με τη βοήθεια της συνάρτησης λάθους (error function) που εντοπίζει τη διαφορά της μεταβλητής στόχου από την επιθυμητή έξοδο.

Εναλλακτική ορολογία που χρησιμοποιείται στο κεφάλαιο αυτό:

• Στιγμιότυπα (instances)

  Επίσης αναφέρονται ως παραδείγματα ή δείγματα (examples)

• Γνωρίσματα (attributes)

  Επίσης γνωστά ως χαρακτηριστικά (features), προσόντα (qualifications), μεταβλητές (variables), ανεξάρτητες μεταβλητές (independent variables), μεταβλητές εισόδου (input variables), συμεταβλητές (covariates)

• Μεταβλητή στόχου (goal variable)

  Επίσης γνωστή ως κατηγόρημα στόχου (goal predicate), εξαρτημένη μεταβλητή (dependent variable), τάξη κατηγοριοποίησης (classification class)

• Συνάρτηση λάθους (error function)

  Επίσης γνωστή ως αντικειμενική συνάρτηση (objective function), συνάρτηση απώλειας (loss function).

Αν υποθέσουμε ότι:

• h η συνάρτηση πρόγνωσης που θέλουμε να «μάθουμε»,
• f η συνάρτηση στόχου,
• D το σύνολο εκπαίδευσης,
• x ένα στιγμιότυπο σε μορφή ενός διανύσματος q των χαρακτηριστικών του.

Τότε, καταρχάς, η έμμεση απεικόνιση του x προς το f(x) μάς είναι άγνωστη. Διαθέσιμα είναι μόνο ζεύγη εκπαίδευσης του τύπου

Αυτό που θέλουμε να μάθουμε είναι η συνάρτηση h(x; q) που υλοποιεί μια γενικευμένη απεικόνιση από το x στο f.

Αν h(x; q) είναι «κοντά» στο f(x) για όλα τα στιγμιότυπα x του συνόλου ελέγχου, συμπεραίνουμε ότι τα χαρακτηριστικά q είναι οι παράμετροι που πρέπει να λάβει υπόψη της η συνάρτηση πρόβλεψης h(..). Ένα παράδειγμα συνάρτησης πρόγνωσης δίνεται παρακάτω, όπου q(x1 x2 x3) το διάνυσμα των χαρακτηριστικών του x:

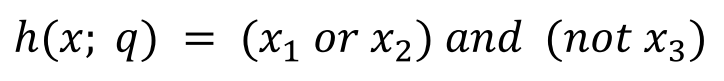
Μια εμπειρική συνάρτηση λάθους E θα μπορούσε να υπολογίζεται ως ακολούθως:

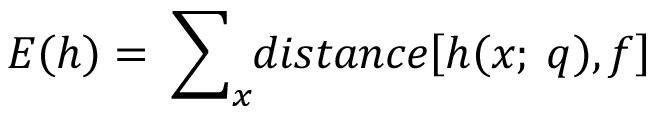
όπου distance είναι η συνάρτηση που υπολογίζει τη διαφορά της πρόγνωσης από την πραγματική τιμή που επιστρέφει η συνάρτηση στόχου f για ένα x από το σύνολο εκπαίδευσης. Η Ε επιστρέφει το άθροισμα όλων των διαφορών που αφορούν τα ζεύγη εκπαίδευσης μέσα στο D.

Γνωστότεροι αλγόριθμοι Επιβλεπόμενης Επαγωγικής Μάθησης είναι:

• Δένδρα Απόφασης (DecisionTrees),
• Μάθηση βασισμένη σε Επεξηγήσεις (Explanation-Based Learning),
• Μάθηση βασισμένη σε Περιπτώσεις (Case-Based Learning),
• Μάθηση Νευρωνικών δικτύων (π.χ. για Backpropagation Neural Networks),
• Μάθηση Μέσω Στατιστικών Μεθόδων (π.χ. μάθηση κατά Bayes),
• Συλλογική Μάθηση από Ενδυνάμωση (Boosting) κ.ά.

Στη συνέχεια θα αναφερθούμε στα Δένδρα Απόφασης.

4.3.1 Δένδρα Απόφασης

Τα Δένδρα Απόφασης-ΔΑ (Decision Trees) είναι ο γνωστότερος αλγόριθμος επιβλεπόμενης Επαγωγικής Μάθησης και έχει εφαρμοστεί με επιτυχία σε πολλούς τομείς όπου απαιτείται ταξινόμηση: ενδεικτικά, στην αναγνώριση προσώπων σε εικόνες, στην ιατρική για διάγνωση περιστατικών, για προβλέψεις απαραίτητες στη διαφήμιση, για προώθηση προϊόντων και, γενικότερα, για εξόρυξη γνώσης. Ο αλγόριθμος ΔΑ οδηγεί στη δημιουργία μιας δενδροειδούς μορφής που τα φύλλα της αποτελούν κατηγορίες ταξινόμησης (classes). Η δενδροειδής αυτή μορφή μπορεί να αναγνωστεί και ως ένα σύνολο κανόνων που καλούνται κανόνες ταξινόμησης (classification rules) και να δώσει μια πειστική απάντηση στο ερώτημα:

 

Πώς μπορεί μία μηχανή να δημιουργήσει γενικούς κανόνες από συγκεκριμένες παρατηρήσεις και πόσο αξιόπιστοι είναι αυτοί οι κανόνες στην πράξη;

 

Βασικές προϋποθέσεις για τη λειτουργία ενός αλγόριθμου επαγωγικής μάθησης είναι:

• καθορισμός ενός συνόλου χαρακτηριστικών (features set - FS) ως των προϋποθέσεων του επιδιωκόμενου προς εξαγωγή κανόνα ταξινόμησης:

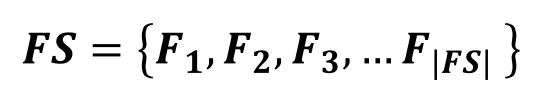
• ύπαρξη προκαθορισμένων διακριτών κατηγοριών ταξινόμησης (classes – C) ως στόχου του διαχωρισμού τον οποίο θα επιδιώξει ο αλγόριθμος και, στη συνέχεια, ως συμπερασμάτων (conclusions) των κανόνων στους οποίους θα οδηγήσει η αναγνώριση της δενδροειδούς μορφής που θα αναπτύξει ο αλγόριθμος:

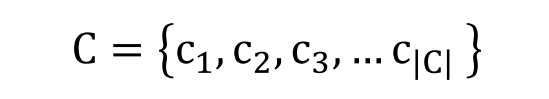
• ύπαρξη επαρκούς αριθμού δειγμάτων που θα προκύψουν από παρατηρήσεις και θα χρησιμοποιηθούν για τη δημιουργία του εκπαιδευτικού συνόλου (training set - ΤS).

Παράδειγμα προβλήματος που μπορεί να λύσει ένας αλγόριθμος ΔΑ

Έστω ότι μια διαφημιστική εταιρία έχει σκοπό να ετοιμάσει μια αφίσα, για να διαφημίσει ένα αντηλιακό, και θέλει να επιλέξει για την αφίσα ένα μοντέλο, άντρα ή γυναίκα, που θα φωτογραφηθεί σε μια παραλία εκτεθειμένο κάτω από τον ήλιο και παρόλα αυτά να μην έχει καεί .

Το μεγαλύτερο πρόβλημα που συνήθως προκύπτει και απαιτεί επίλυση είναι η δυσχέρεια στην εύρεση των εμφανισιακών χαρακτηριστικών που πρέπει να έχει το μοντέλο, για να είναι πειστικό στο ρόλο του. Αν δεν υπάρχει διαθέσιμη σχετική γνώση ή η υπάρχουσα δεν είναι ολοκληρωμένη, ώστε να δώσει απάντηση στο παραπάνω πρόβλημα, τότε απαιτείται η παραγωγή νέας γνώσης με επαγωγικό τρόπο συνήθως μέσα από παρατηρήσεις.

Στην περίπτωση κατά την οποία επιλεγεί ο αλγόριθμος των ΔΑ, τότε πρέπει να καθοριστούν:

• ως πρώτο βήμα πρέπει να αποφασιστούν οι κατηγορίες ταξινόμησης στις οποίες θα καταλήξει ο διαχωρισμός: στο πρόβλημά μας, οι κατηγορίες ταξινόμηση είναι δύο, αν το δείγμα που αφορά η παρατήρηση έχει καεί από τον ήλιο ή όχι.
• στη συνέχεια, τα υπόλοιπα εμφανισιακά χαρακτηριστικά που πρέπει να παρατηρηθούν κατά τη συγκέντρωση δειγμάτων και τα οποία θα χρησιμοποιήσει ο αλγόριθμος σε κάθε βήμα διαχωρισμού, ώστε να καταλήξει σε ένα σύνολο δειγμάτων με κοινά χαρακτηριστικά: στο παράδειγμά μας, θα είναι το χρώμα των μαλλιών, των ματιών και του δέρματος, και, επιπλέον, αν το δείγμα έχει χρησιμοποιήσει αντηλιακό ή όχι.

Βάσει των επιλεγμένων χαρακτηριστικών και των κατηγοριών ταξινόμησης, θα ακολουθήσει η συγκέντρωση των δειγμάτων που συνήθως γίνεται δια της παρατήρησης ή από συμπλήρωση ερωτηματολογίων. Στο παράδειγμά μας, η συγκέντρωση θα γίνει σε συνδυασμό, δηλαδή ο υπεύθυνος συγκέντρωσης θα παρατηρεί λουόμενους, θα σημειώνει τα χαρακτηριστικά τους, θα τους ρωτά για τη χρήση αντηλιακού και θα τους κατατάσσει σε κατηγορίες καμένων και μη καμένων. Στον πίνακα 4.1 έχει αποτυπωθεί ένα τέτοιο μικρό σύνολο δειγμάτων εκπαίδευσης για τις ανάγκες παρουσίασης της μεθόδου.

Πίνακας 4.1 Συγκεντρωτικός πίνακας δειγμάτων για εκπαίδευση αλγόριθμου ΔΑ

Σε ένα σύνολο παραμέτρων, όπου τα χαρακτηριστικά είναι πολλά και παίρνουν πολλές τιμές, οι δυνατοί συνδυασμοί που μπορεί να προκύψουν είναι πολλοί. Στο παράδειγμά μας, το χαρακτηριστικό «Μαλλιά» παίρνει 3 τιμές (ξανθά, καστανά, κόκκινα), το χαρακτηριστικό «Μάτια» 3 τιμές (πράσινα, μπλε, μαύρα), το χαρακτηριστικό «Δέρμα» 2 τιμές (σκούρο, ανοιχτό) και το χαρακτηριστικό «Αντηλιακό» 2 τιμές (ναι, όχι). Οι συνδυασμοί είναι τριάντα έξι (3x3x2x2=36). Επομένως, αν έχει δοθεί το σύνολο των 8 δειγμάτων του ανωτέρω πίνακα προς εκπαίδευση σε ένα σύστημα που κάνει αναγνώριση χρησιμοποιώντας πιθανότητες, μία νέα περίπτωση έχει πιθανότητα να αναγνωριστεί περίπου 22%:

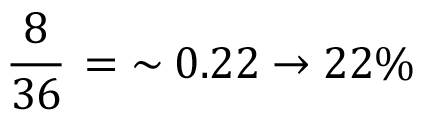
Τα ΔΑ έρχονται να δώσουν λύση στην αναγνώριση της νέας περίπτωσης, παράγοντας γενικευμένους κανόνες αναγνώρισης που στην περίπτωσή μας θα καθορίσουν το πότε κάποιος καίγεται από τον ήλιο και πότε όχι και θα αποτελούσαν μία λύση στην προσπάθεια της μηχανής να κατατάσσει κάθε νέα περίπτωση χρησιμοποιώντας αυτόν τον κανόνα. Ένα τέτοιο επιτυχημένο δένδρο αναγνώρισης για το πρόβλημά μας είναι αυτό του σχήματος 4.2.

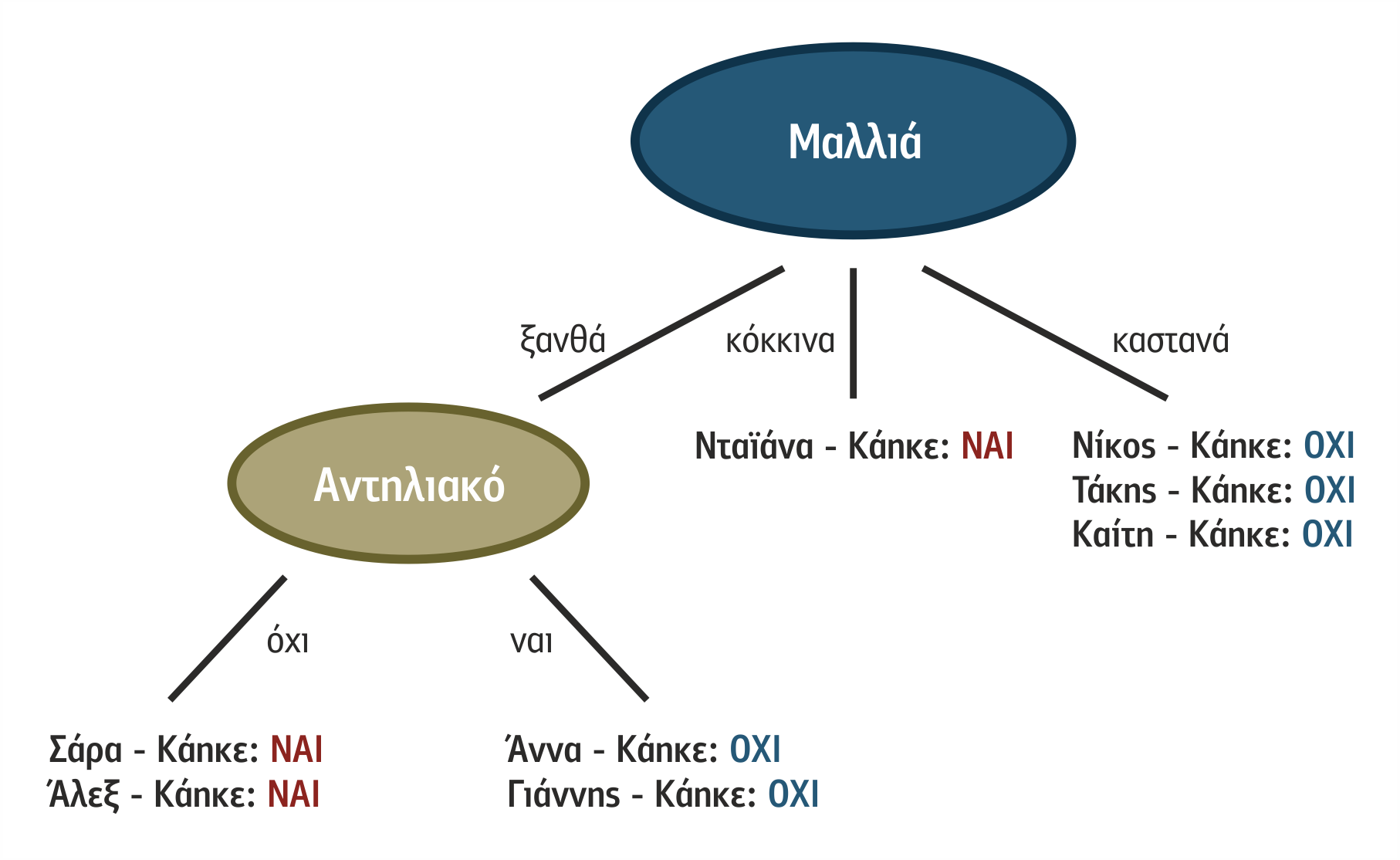
Σχήμα 4.2 Δένδρο απόφασης για το πρόβλημα της διαφήμισης αντηλιακού

Στην ουσία, ο αλγόριθμος των ΔΑ δημιουργεί μια δενδροειδή μορφή όπως προαναφέραμε, σε κάθε κόμβο της οποίας επιχειρείται ο περαιτέρω διαχωρισμός των μη κατηγοριοποιημένων δειγμάτων του συνόλου εκπαίδευσης που έχουν συγκεντρωθεί εκεί. Η δενδροειδής αυτή μορφή καλείται δένδρο απόφασης (decision tree) και όταν ο αλγόριθμων πετυχαίνει έναν πλήρη διαχωρισμό δειγμάτων τότε στα φύλλα της συγκεντρώνονται μόνο ομοιογενή δείγματα, δηλαδή δήγματα της ίδιας κατηγορίας. Κάθε φύλλο του ΔΑ με ομοιογενή δείγματα επιτρέπει την εξαγωγή ενός συμπεράσματος που μπορεί να εκφραστεί ως κανόνας που εκφράζει τον τρόπο προσδιορισμού μιας συγκεκριμένης κατηγορίας βάσει των χαρακτηριστικών της. Για παράδειγμα, το αριστερότερο φύλλο του δένδρου στου σχήματος 2.2 περιέχει ομοιογενή δείγματα άρα το συμπέρασμα που εξάγεται υπό μορφή κανόνα είναι το ακόλουθο:

 

ΑΝ Μαλλιά ξανθά

και Αντηλιακό όχι

ΤΟΤΕ περίπτωση καίγεται

 

Εάν για το πρόβλημα του παραδείγματός μας υπάρχουν 10 δείγματα συγκεντρωμένα μέσα στο σύνολο εκπαίδευσης, όπως αυτά που είναι καταχωρημένα μέσα στον πίνακα 4.2, τότε ο αλγόριθμος θα δημιουργήσει ένα δένδρο απόφασης σαν αυτό που παρουσιάζεται στο σχήμα 4.2, όπου δίπλα σε κάθε εσωτερικό κόμβο αναφέρονται τα δείγματα που αναμένουν για διαχωρισμό και δίπλα σε κάθε φύλλο αναφέρονται τα πλήρως διαχωρισμένα δείγματα, δηλαδή δείγματα μιας ζητούμενης κατηγορίας (ΝΑΙ, ΟΧΙ).

Για την περιγραφή ενός δένδρου αναγνώρισης μπορούμε να πούμε ότι:

• Η ρίζα του δένδρου είναι ένα από τα χαρακτηριστικά που ο αλγόριθμος κρίνει προσφορότερο να επιλέξει πρώτα.
• Κάθε εσωτερικός κόμβος του δένδρου ονοματίζεται με το όνομα ενός νέου χαρακτηριστικού που δεν έχει ήδη χρησιμοποιηθεί στο συγκεκριμένο κλαδί του δένδρου.
• Κάθε ακμή ονοματίζεται με μια διαφορετική τιμή που μπορεί να πάρει το χαρακτηριστικό του κόμβου από τον οποίο ξεκινάει.
• Κάθε φύλλο αντιστοιχεί σε μια κατηγορία ταξινόμησης.

Για τη δημιουργία ενός δένδρου απόφασης, ο αλγόριθμος χρησιμοποιεί την τεχνική «διαίρει και βασίλευε», όπως φαίνεται και στον αλγόριθμο που ακολουθεί:

Αλγόριθμος δένδρου απόφασης

όπου

• C κατηγορία ταξινόμησης
• TS το σύνολο δειγμάτων εκπαίδευσης
• FS το σύνολο των χαρακτηριστικών του TS, και
• Fi ένα επιλεγμένο χαρακτηριστικό του οποίου οι τιμές v1, v2, v3, …vn διαμερίζουν το σύνολο TS σε υποσύνολα TS1, TS2, TS3,… TSn

Η σωστή επιλογή χαρακτηριστικών, ο επαρκής αριθμός αυτών και των συγκεντρωμένων δειγμάτων αποτελούν κλειδί για μια αποτελεσματική λειτουργία του αλγόριθμου.

Ένας από τους πιο γνωστούς αλγόριθμους δημιουργίας Δένδρων Απόφασης είναι ο ID3 (Quinlan, 1986).

Ο αλγόριθμος ID3

Ο αλγόριθμος ID3 (Iterative Dichotomizer 3) αναπτύχθηκε αρχικά στο Πανεπιστήμιο του Σίδνεϋ από τον J. Ross Quinlan και βασίζεται στον αλγόριθμο Concept Learning System (CLS) που αποτελεί τυπικό αλγόριθμο δημιουργίας ΔΑ.

Αυτό που διαθέτει επιπλέον ο ID3 είναι η ευρετική αναζήτηση χαρακτηριστικού για διαχωρισμό. Δηλαδή, σε κάθε κόμβο του δένδρου αναζητά μεταξύ των χαρακτηριστικών του συνόλου δειγμάτων εκπαίδευσης αυτό το χαρακτηριστικό το οποίο διαχωρίζει καλύτερα τα δεδομένα δείγματα. Εάν το χαρακτηριστικό διαχωρίζει πλήρως το σύνολο εκπαίδευσης, τότε ο ID3 σταματά. Αλλιώς, λειτουργεί αναδρομικά στα n (όπου n = αριθμός των πιθανών τιμών ενός χαρακτηριστικού) διαχωρισμένα υποσύνολα, για να εντοπίσει το «καλύτερό» τους χαρακτηριστικό. Ο αλγόριθμος εφαρμόζει αναδρομικά μια άπληστη αναζήτηση, δηλαδή επιλέγει το καλύτερο χαρακτηριστικό και δεν ανατρέχει σε προηγούμενα χαρακτηριστικά που έχει χρησιμοποιήσει στη δεδομένη πορεία του για να τα επανεξετάσει.

Τα χαρακτηριστικά του αλγόριθμου ID3 είναι τα ακόλουθα:

• Μεγαλώνει επαναληπτικά ένα μικρό σύνολο εκπαίδευσης από δεδομένα που υπάρχουν σε μία περιορισμένη βάση δειγμάτων.
• Αφαιρεί χαρακτηριστικά που περιέχονται στην κατηγορία προς ταξινόμηση με σκοπό τη συμπίεση της βάσης.
• Χρησιμοποιεί στατιστικές μεθόδους (Shannon’s Information Statistic, μεγέθη εντροπία και κέρδος πληροφορίας), για να επιλέξει χαρακτηριστικά για διαχωρισμό.

Ο ID3, όπως και κάθε άλλος επαγωγικός αλγόριθμος, μπορεί να κατηγοριοποιήσει λανθασμένα ένα νέο στιγμιότυπο για πολλούς διαφορετικούς λόγους. Ο πιο απλός είναι να μην έχει γίνει καλός σχεδιασμός και η συγκέντρωση των δειγμάτων να μην έχει βασιστεί σε σωστά χαρακτηριστικά. Το πρόβλημα δεν αφορά τον αλγόριθμο, αλλά οδηγεί σε κακής ποιότητας συμπεράσματα στα φύλλα του δένδρου που παράγει. Άλλος λόγος είναι ότι μη επαρκές πλήθος των δειγμάτων θα οδηγήσει σε πρόωρες συγκλίσεις και υπεραπλουστευμένα συμπεράσματα. Τέλος, βασικότερο πρόβλημα για το οποίο ευθύνεται ο αλγόριθμος είναι η κακή επιλογή μεθόδου για τον ευρετικό ή συνήθως στατιστικό εντοπισμό του «καλού» χαρακτηριστικού.

Επιλογή χαρακτηριστικού

Προκειμένου να αποφασιστεί η καλύτερη επιλογή χαρακτηριστικού, ο αλγόριθμος ID3 βασίζεται στις έννοιες εντροπία και κέρδος πληροφορίας.

Εντροπία

Η εντροπία πληροφορίας (information entropy) χαρακτηρίζει το βαθμό αβεβαιότητας ενός συνόλου δεδομένων S: ενός συνόλου δεδομένων S:

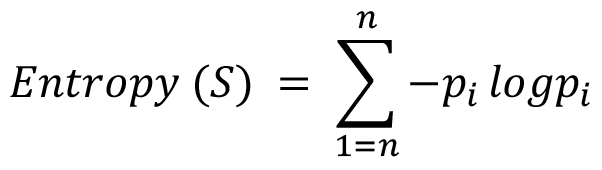
όπου p1, p2,…pi οι πιθανότητες του κάθε ενδεχομένου που περιλαμβάνεται στο σύνολο.

 

Ο αλγόριθμος ID3 χρησιμοποιεί την εντροπία ως μέτρο ομοιογένειας των τιμών του αρχικού συνόλου δεδομένων προς κάποιο χαρακτηριστικό, καθώς και τα υποσύνολα που προκύπτουν σε κάθε βήμα μετά την ταξινόμηση.

Εάν όλα τα δείγματα του συνόλου εκπαίδευσης είναι ομοιογενή ως προς μια κατηγορία, τότε η εντροπία του ισούται με μηδέν. Εάν οι κατηγορίες είναι διαφορετικές και τα δείγματα που ανήκουν σε καθεμία έχουν το ίδιο πλήθος, τότε η εντροπία είναι 1.

Στη δυαδική περίπτωση, όπου οι κατηγορίες είναι δύο, η εντροπία δίνεται από τη συνάρτηση:

 

 

Παράδειγμα, έστω δοχείο με N μπάλες με πιθανότητα ενδεχομένου η μπάλα να είναι λευκή N(p) και να είναι μαύρη N(1-p). Τότε ισχύει:

• Αν οι μπάλες είναι όλες μαύρες ή όλες άσπρες, δηλαδή p=1 ή (1-p)=1,τότε Εντροπία=0
• Αν οι μπάλες είναι μισές μαύρες και μισές άσπρες, δηλαδή p=(1-p)= ½ (πιθανότητα επιλογής 50%) τότε Εντροπία=1 (μέγιστη)

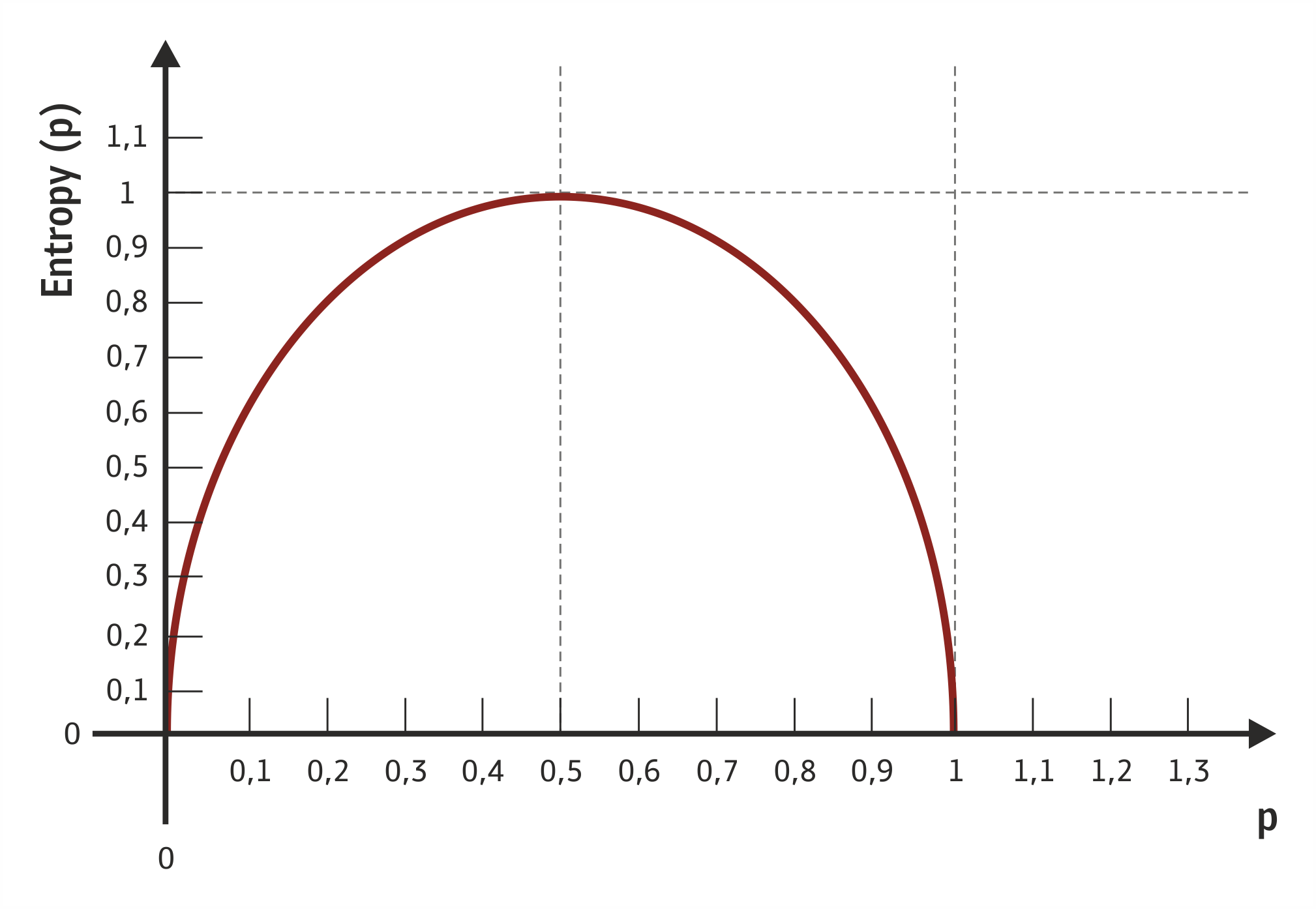
Σχήμα 4.3 Εντροπία σε μια δυαδική περίπτωση κατηγοριών

Εάν σε ένα σύνολο S 14 μπαλών υπήρχαν 5 άσπρες μπάλες και 9 μαύρες, τότε η εντροπία θα υπολογιζόταν ως εξής:

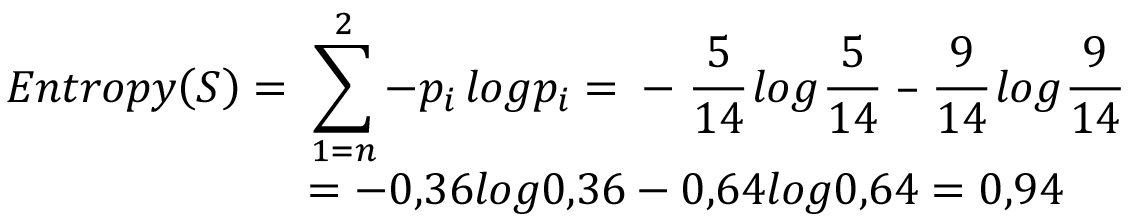
Σχήμα 4.4 Εύρεση εντροπίας με την χρήση πίνακα συχνοτήτων ενός χαρακτηριστικού

Έστω τώρα ότι μας ενδιαφέρει η εντροπία ενός χαρακτηριστικού Χ με n διαφορετικές τιμές c σε σχέση με την κατηγορία S. Τότε η εντροπία δίνεται με τη συνάρτηση:

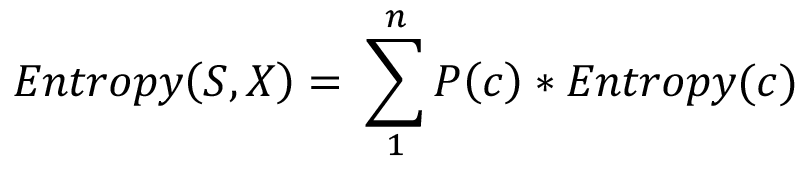
Στο σχήμα 4.5 δίνεται ένα παράδειγμα υπολογισμού της εντροπίας για το πρόβλημα της διαφήμισης αντηλιακού που παρουσιάστηκε παραπάνω, με βάση το σύνολο εκπαίδευσης που δόθηκε στον πίνακα 4.1:

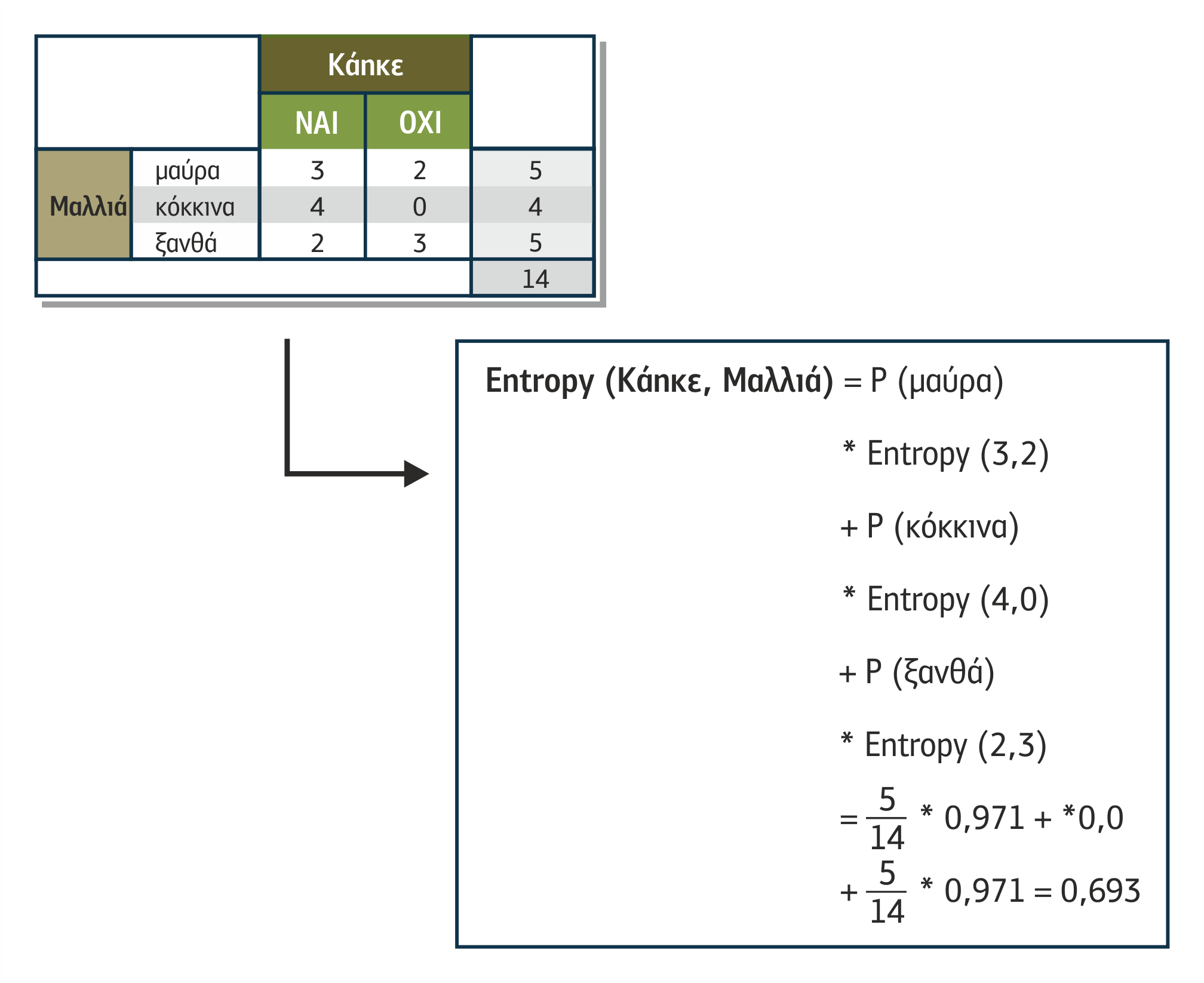
Σχήμα 4.5 Εύρεση εντροπίας με τη χρήση πίνακα συχνοτήτων δύο χαρακτηριστικών

Κέρδος Πληροφορίας

Εάν Α είναι χαρακτηριστικό σε ένα S σύνολο δειγμάτων από το σύνολο μάθησης, τότε το κέρδος πληροφορίας (information gain) χαρακτηρίζει το πόση πληροφορία «φέρει» το χαρακτηριστικό Α:

όπου

• E(...) η συνάρτηση εντροπίας
• m το πλήθος των τιμών Αi που παίρνει το A στο S
• fs(Αi) το ποσοστό των δειγμάτων στο S που παίρνουν την τιμή Ai
• SAi το υποσύνολο του S όπου η τιμή του Α είναι Αi

Ή πιο απλά:

Η γενική ιδέα του ID3, για να διαχωρίσει ένα μη ομοιογενές σύνολο δειγμάτων σε έναν κόμβο του δένδρου απόφασης που ανήκει σε ένα συγκεκριμένο κλαδί, είναι:

• Για όλα τα αχρησιμοποίητα στο συγκεκριμένο κλαδί χαρακτηριστικά υπολόγισε την εντροπία σε σχέση με τα δείγματα.
• Διάλεξε το χαρακτηριστικό που παρουσιάζει το μέγιστο κέρδος πληροφορίας.
• Κατασκεύασε κόμβο για το χαρακτηριστικό αυτό.

Παράδειγμα ID3

Αν χρησιμοποιήσουμε τον αλγόριθμο ID3 για το πρόβλημα της διαφήμισης αντηλιακού που παρουσιάσαμε προηγουμένως, τα χαρακτηριστικά (FS) που θα χρησιμοποιήσει ο αλγόριθμος θα είναι:

• Μαλλιά = {ξανθά, καστανά, κόκκινα}
• Μάτια = {καφέ, μπλε, πράσινα}
• Δέρμα = {ανοιχτό, σκούρο}
• Αντηλιακό = {ναι, όχι}

Οι κατηγορίες ταξινόμησης (C) είναι:

• Κάηκε = {ΝΑΙ, ΟΧΙ}

Το σύνολο δειγμάτων εκπαίδευσης είναι συγκεντρωμένο στον επόμενο πίνακα 4.2.

Πίνακας 4.2 Σύνολο εκπαίδευσης για το πρόβλημα της διαφήμισης αντηλιακού

Παράδειγμα δημιουργίας δένδρου απόφασης με χρήση εντροπίας και κέρδους πληροφορίας

Βήμα 1: Υπολογισμός εντροπίας της κατηγορίας του στόχου

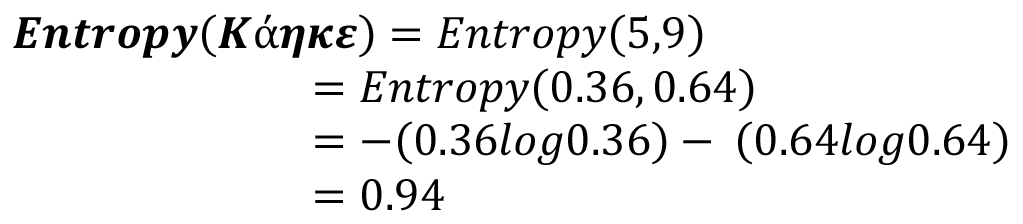
Βήμα 2: To σύνολο εκπαίδευσης διαχωρίζεται ως προς τα διαφορετικά χαρακτηριστικά.

Για κάθε διαφορετικό χαρακτηριστικό γίνεται ο ακόλουθος υπολογισμός: Υπολογίζεται η εντροπία για κάθε διαφορετική τιμή του χαρακτηριστικού και στη συνέχεια, αφού πολλαπλασιαστεί με το ποσοστό των δειγμάτων που διαθέτουν την αντίστοιχη τιμή, προστίθεται για να υπολογιστεί η συνολική εντροπία του διαχωρισμένου τμήματος.

Η εντροπία που προκύπτει ως αποτέλεσμα αφαιρείται από την εντροπία πριν από το διαχωρισμό. Το αποτέλεσμα είναι το κέρδος πληροφορίας (Gain).

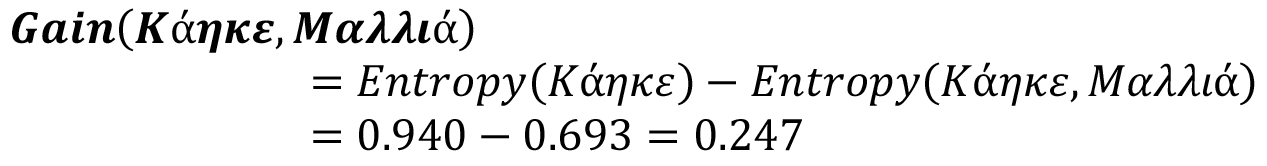
Το κέρδος πληροφορίας πρέπει να υπολογιστεί για κάθε διαφορετικό χαρακτηριστικό που μπορεί να εφαρμοστεί για να διαχωρίσει ένα συγκεκριμένο υποσύνολο μη πλήρως διαχωρισμένων δειγμάτων που είναι συγκεντρωμένα σε έναν κόμβο του δένδρου (βλέπε Σχήμα 4.6).

Σχήμα 4.6 Υπολογισμός κέρδους πληροφορίας για επιλογή χαρακτηριστικού

Βήμα 3: Επιλογή του χαρακτηριστικού με το μεγαλύτερο κέρδος.

Στον πρώτο κύκλο διαχωρισμού επιλέγεται το χαρακτηριστικό Μαλλιά για να διαχωρίσει το δείγμα, δεδομένου ότι έχει το μεγαλύτερο κέρδος πληροφορίας.

Παρατηρούμε ότι τα δείγματα που έχουν κόκκινα μαλλιά είναι ομοιογενή ως προς το αποτέλεσμα, δηλαδή έχουν όλα καεί.

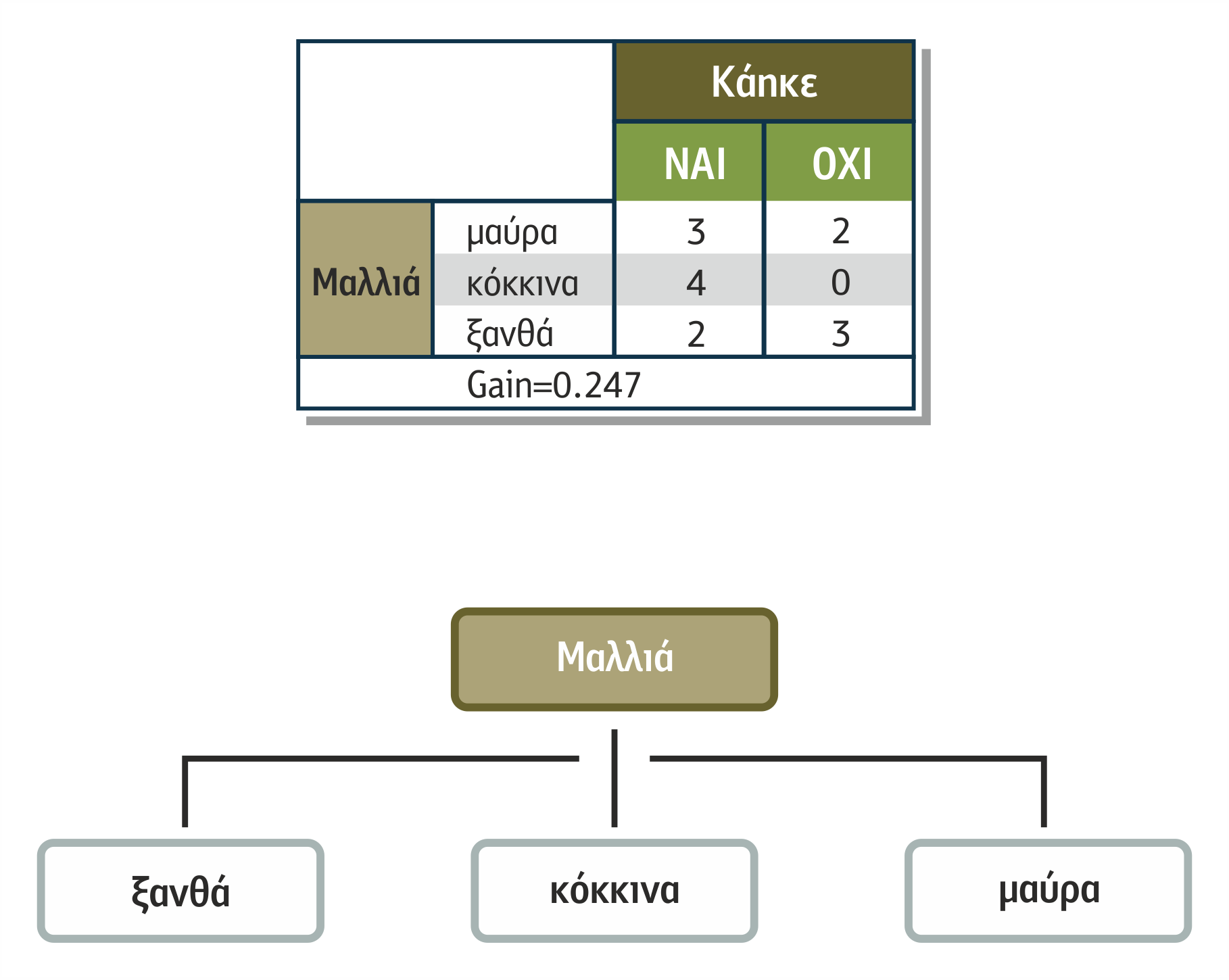
Σχήμα 4.7 Επιλογή του χαρακτηριστικού Μαλλιά για να διαχωρίσει το δείγμα

Βήμα 4Α: Ολοκλήρωση διαχωρισμού

Ένα κλαδί με εντοπία 0, δηλαδή όταν όλα τα δείγματα του κόμβου είναι ομοιογενή, θεωρείται φύλλο. Ένα κλαδί που ξεκινά από τη ρίζα του δένδρου και καταλήγει σε φύλλο, θεωρείται ολοκληρωμένο και μπορεί να εκφραστεί ως κανόνας.

Σχήμα 4.8 Ημιτελές δένδρο απόφασης με ένα πλήρως διαχωρισμένο κλαδί.

Βήμα 4Β: Συνέχιση διαχωρισμού

Ένα κλαδί με εντροπία μεγαλύτερη από το 0, δηλαδή όταν τα δείγματα του κόμβου δεν είναι ομοιογενή, χρειάζεται περαιτέρω διαχωρισμό. Το ημιτελές δένδρο απόφασης στο σχήμα 4.8 περιέχει ένα ολοκληρωμένο κλαδί και δύο που χρήζουν περαιτέρω διαχωρισμού.

Για να διαχωρίσομε τα ανομοιογενή δείγματα του τελευταίου κόμβου του αριστερού κλαδιού του δένδρου και επειδή χρησιμοποιήσαμε το χαρακτηριστικό Μαλλιά ήδη, πρέπει να αποφασίσουμε μόνο για το ποιο από τα υπόλοιπα τρία χαρακτηριστικά είναι καταλληλότερο να εφαρμοστεί: Μάτια, Δέρμα ή Αντηλιακό. Μελετώντας ξεχωριστά το κέρδος πληροφορίας για κάθε ένα από αυτά, έχουμε τα παρακάτω αποτελέσματα:

 

Μαλλιά ξανθά = {Τ1, Τ2, Τ8, Τ9, Τ11} = 5 δείγματα από τον πίνακα 1 με Μαλλιά = Ξανθά

Κέρδος πληροφορίας (Μαλλιά ξανθά, Δέρμα) = 0.970

Κέρδος πληροφορίας (Μαλλιά ξανθά, Μάτια) = 0.570

Κέρδος πληροφορίας (Μαλλιά ξανθά, Αντηλιακό) = 0.019

 

Παρατηρούμε ότι το χαρακτηριστικό Δέρμα έχει το υψηλότερο κέρδος πληροφορίας. Ως εκ τούτου, εφαρμόζεται ως χαρακτηριστικό διαχωρισμού των δειγμάτων του συγκεκριμένου κόμβου (Μαλλιά Ξανθά), όπως φαίνεται στο παρακάτω σχήμα 4.9.

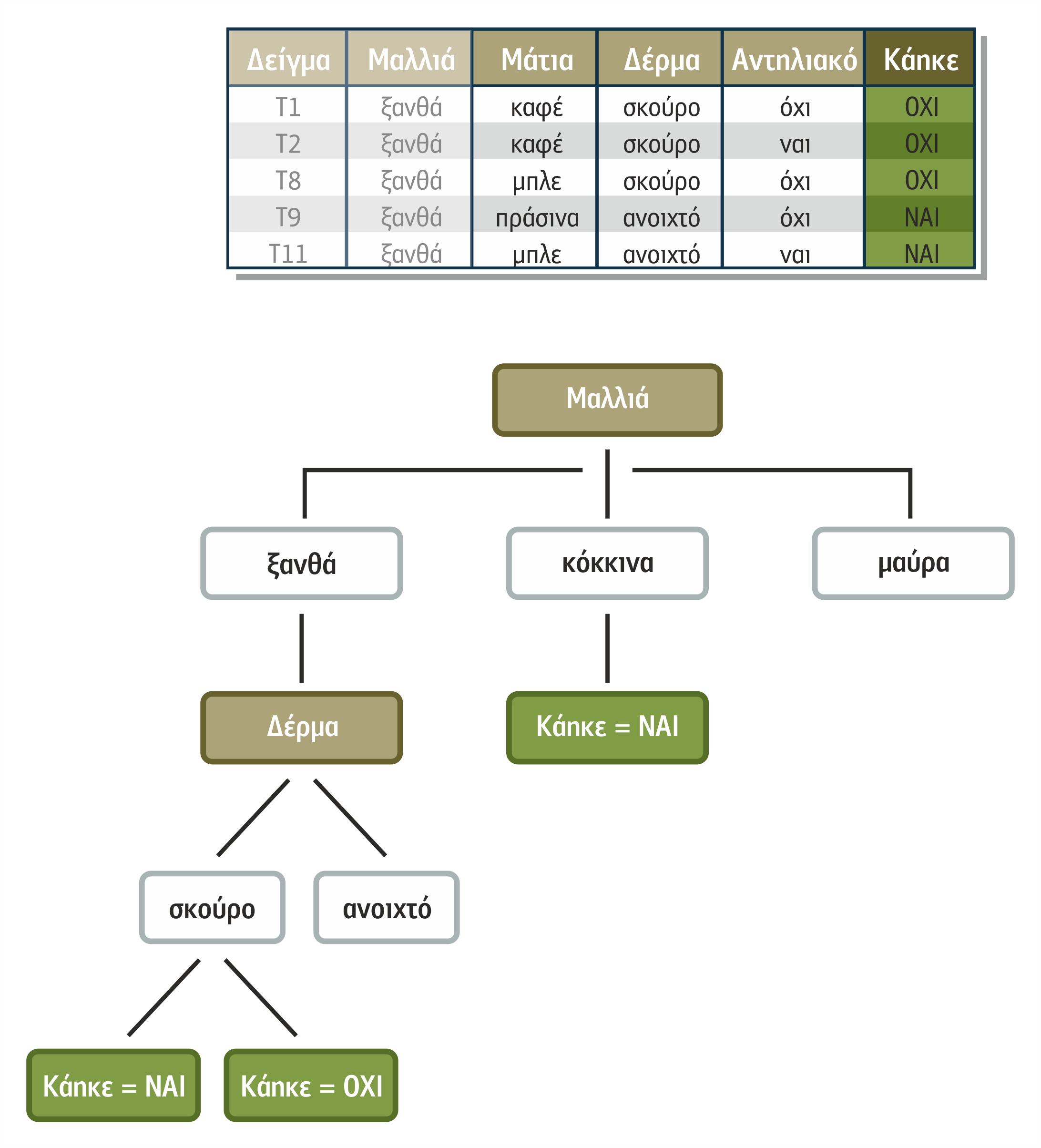
Σχήμα 4.9. Ημιτελές δένδρο απόφασης με δύο πλήρως διαχωρισμένα κλαδιά.

Βήμα 5: Ολοκλήρωση διαχωρισμού

Ο αλγόριθμος ID3 τρέχει αναδρομικά διαχωρίζοντας σε κάθε κύκλο έναν κόμβο του δένδρου που δεν είναι φύλλο, έως ότου όλα τα δείγματα κατηγοριοποιηθούν.

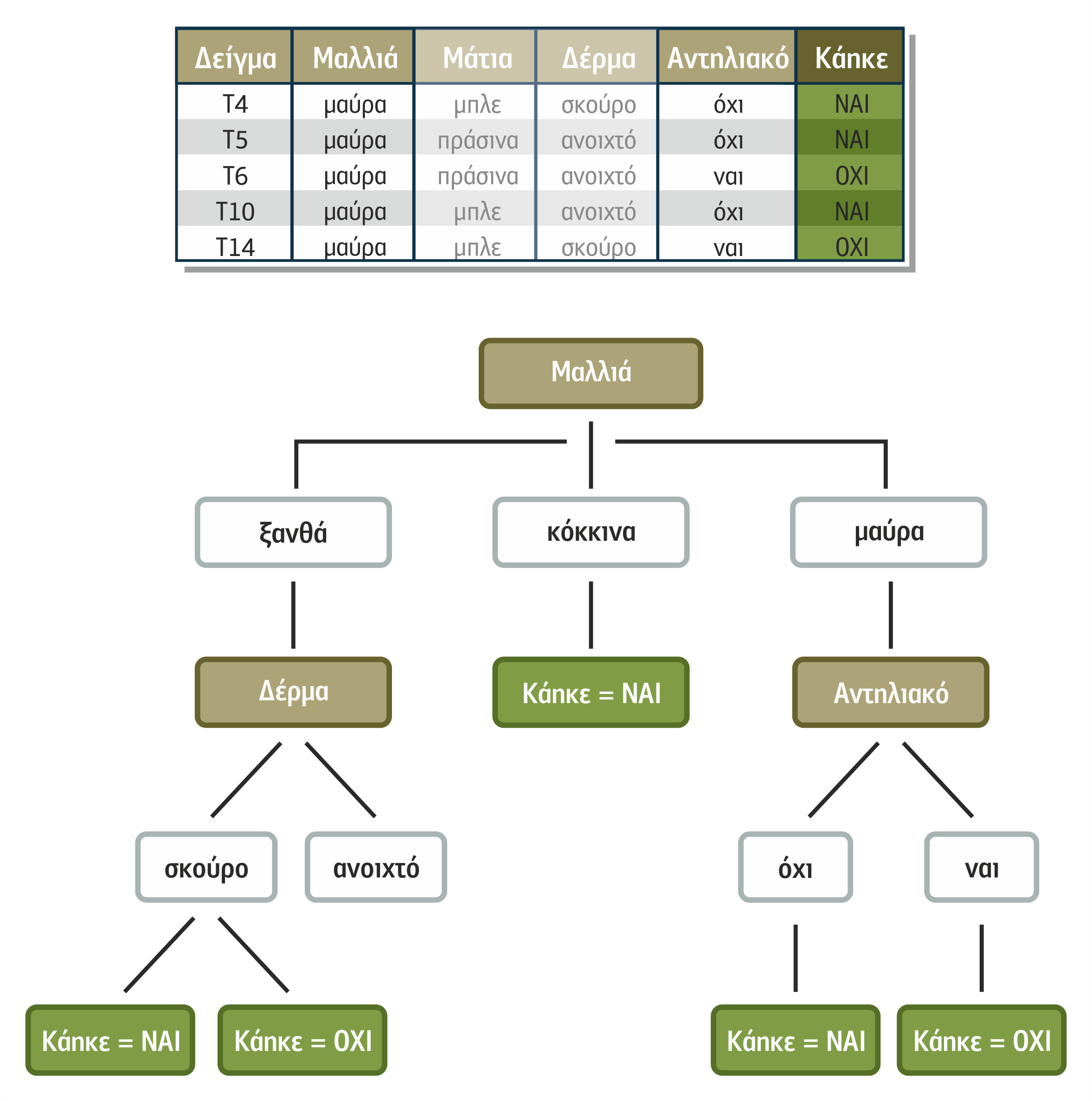
Σχήμα 4.10 Δένδρο απόφασης με όλα τα δείγματα κατηγοριοποιημένα

Δείτε κινούμενη εικόνα 4.1 - Βηματική ανάπτυξη Δένδρου Απόφασης

 

Αν δεν υπάρχουν άλλα χαρακτηριστικά για να διαχωρίσουν έναν κόμβο που δεν είναι φύλλο, αυτό σημαίνει αποτυχία διαχωρισμού ελλείψει επαρκών χαρακτηριστικών και η όλη μελέτη για τη λύση του προβλήματος πρέπει να επαναληφθεί από την αρχή.

 

Βήμα 6: Έλεγχος αποτελεσμάτων

Ο αλγόριθμος μπαίνει σε φάση πιστοποίησης (recall) ελέγχοντας την εγκυρότητα των αποτελεσμάτων του με τη βοήθεια των δειγμάτων του συνόλου ελέγχου, δηλαδή δειγμάτων που δεν είχαν περιληφθεί στο σύνολο εκπαίδευσης.

Σε περίπτωση που υπάρχουν εξαιρέσεις, τα εξαιρούμενα δείγματα προστίθενται στο σύνολο εκπαίδευσης και η εκπαίδευση επαναλαμβάνεται από την αρχή.

Αν δεν υπάρχουν εξαιρέσεις, τα αποτελέσματα θεωρούνται έγκυρα και δίνονται προς χρήση.

Άλλα παραδείγματα εφαρμογής ID3

Η εντροπία και το κέρδος πληροφορίας δεν είναι ο μόνος τρόπος επιλογής χαρακτηριστικών. Σε πολλά προβλήματα ως ευρετικοί μηχανισμοί χρησιμοποιούνται άλλες απλούστερες μέθοδοι, όπως για παράδειγμα ο δοκιμαστικός διαχωρισμός των δειγμάτων του συνόλου εκπαίδευσης σε υποσύνολα βάσει κάθε διαφορετικού χαρακτηριστικού και επιλογή εκείνου που (ιδανικά) θα αποδώσει υποσύνολα με δείγματα «όλα θετικά» ή «όλα αρνητικά» ή θα προσεγγίσει μια τέτοια κατάσταση.

Παράδειγμα όπου εφαρμόζεται μια τέτοια τακτική είναι το πρόβλημα της αναμονής σε εστιατόριο (Russel & Norvig, 2003).Το συγκεκριμένο πρόβλημα αφορά τη λήψη απόφασης ενός πελάτη να περιμένει ή όχι για να φάει σε ένα εστιατόριο.

Το σύνολο των χαρακτηριστικών (FS) περιλαμβάνει τα ακόλουθα χαρακτηριστικά:

 

Εναλλακτικό:	υπάρχει μια εναλλακτική λύση εστιατόριου κοντά (Ναι/Όχι);
Μπαρ	υπάρχει κοντά ένα άνετο μπαρ για να περιμένει κανείς εκεί(Ναι/Όχι)
Π/Σ	η ημέρα είναι Παρασκευή ή Σάββατο(Ναι/Όχι)
Πεινασμένος	ο πελάτης είναι πεινασμένος (Ναι/Όχι)
Πελάτες	ποιο το πλήθος των πελατών στο εστιατόριο (Κανείς, Μερικοί, Πλήρες)
Τιμή	εύρος τιμών ($, $$, $$$)
Βρέχει	έξω βρέχει (Ναι/Όχι)
Κράτηση	έχει γίνει κράτηση (Ναι/Όχι)
Τύπος	είδος του εστιατορίου (Γαλλικό-fre, Ιταλικό-ital, Ταϋλανδέζικο-thai, Ταχυφαγείο-fast)
Αναμονή	εκτιμώμενος χρόνος αναμονής σε λεπτά (0-10, 10-30, 30-60,> 60)

 

Το σύνολο εκπαίδευσης είναι καταχωρημένο στον ακόλουθο πίνακα 4.3.

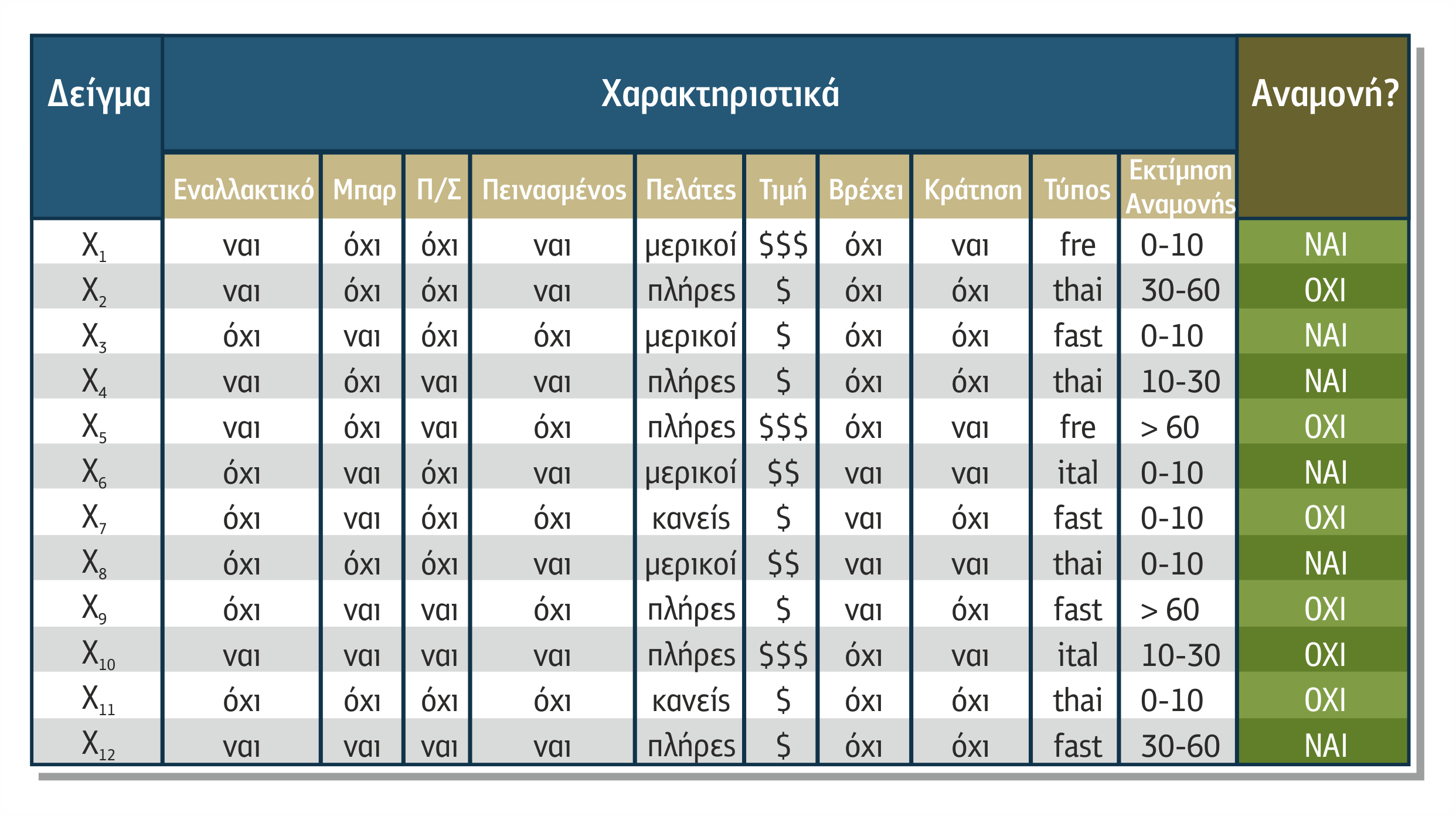
Πίνακας 4.3 Σύνολο εκπαίδευσης για το πρόβλημα της αναμονής στο εστιατόριο

Για την επιλογή του 1ου χαρακτηριστικoύ που θα διαχωρίσει το αρχικό σύνολο δειγμάτων του προβλήματος, έστω ότι συγκρίνονται τα χαρακτηριστικά Πελάτες και Τύπος. Από το αποτέλεσμα παρατηρούμε ότι το Πελάτες διαχωρίζει το σύνολο δημιουργώντας δυο φύλλα και ένα μη διαχωρισμένο κόμβο, ενώ το Ναι/Όχι δε δημιουργεί κανένα φύλλο (βλέπε Σχήμα 4.11).

Σχήμα 4.11 Σύγκριση χαρακτηριστικών για το πρόβλημα αναμονής σε εστιατόριο

Αν ως ευρετικό κριτήριο θεωρεί ότι το καλύτερο χαρακτηριστικό είναι αυτό με το οποίο ο διαχωρισμός οδηγεί στα περισσότερα φύλλα, τότε ο αλγόριθμος θα επιλέξει το Πελάτες έναντι του Τύπος. Προφανώς, η σύγκριση πρέπει να γίνει μεταξύ όλων των χαρακτηριστικών που μπορούν να εφαρμοστούν.

Έστω ότι το χαρακτηριστικό πελάτες είναι καλύτερο όλων και εφαρμόζεται στην κορυφή του δένδρου και στη συνέχεια το παραπάνω ευρετικό κριτήριο εφαρμόζεται σε κάθε κόμβο που πρέπει να διαχωριστεί.

Το δένδρο που θα προκύψει θα είναι αυτό του σχήματος 4.12.

Σχήμα 4.12 Δένδρο απόφασης για το πρόβλημα αναμονής σε εστιατόριο

Ανάλογα με το ευρετικό κριτήριο που έχει, ο ID3 θα δημιουργήσει και διαφορετικό ΔΑ. Αν, για παράδειγμα, το κριτήριο είναι να εφαρμοστούν όσο γίνεται περισσότερα χαρακτηριστικά, για να αποφευχθεί η πρόωρη σύγκλιση και να είναι πιο πλούσια η γνώση που θα προκύψει, πρέπει να επιλεγούν τα χαρακτηριστικά με διαφορετική σειρά.

Στο σχήμα 4.13 παρουσιάζεται ένα πιθανό ΔΑ για το πρόβλημα αναμονής σε εστιατόριο που λαμβάνει υπόψη του το συγκεκριμένο κριτήριο.

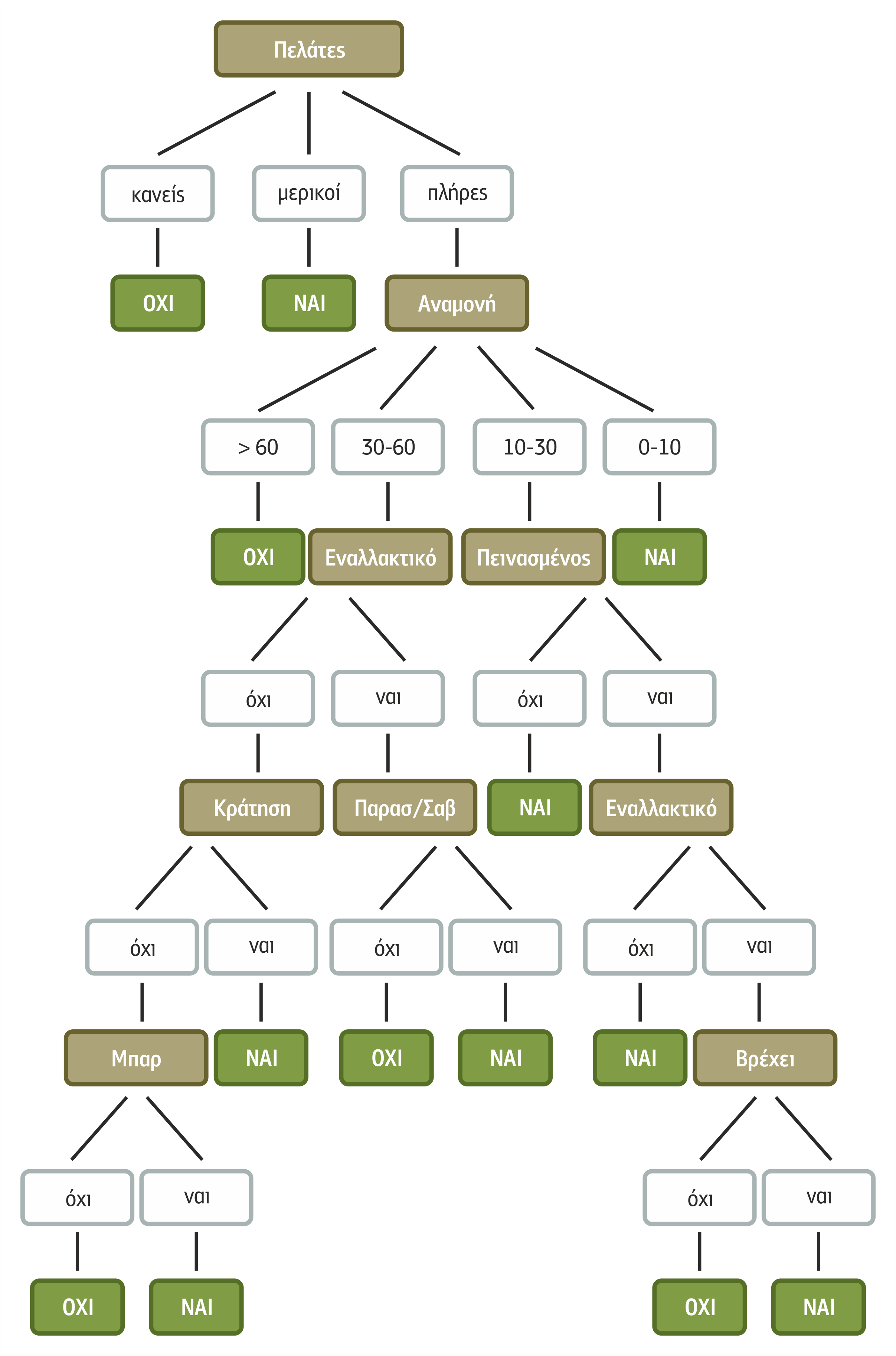
Σχήμα 4.13 Δένδρο απόφασης για το πρόβλημα αναμονής σε εστιατόριο που προσπαθεί να εξαντλήσει τα χαρακτηριστικά

Από δένδρα απόφασης σε κανόνες

Ένα δένδρο απόφασης μπορεί πολύ εύκολα να μετατραπεί σε ένα σύνολο κανόνων, απεικονίζοντας έναν προς έναν όλους τους κόμβους του δένδρου από τη ρίζα προς κάθε διαφορετικό κόμβο-φύλλο.

Για παράδειγμα, στο πρόβλημα της διαφήμισης αντηλιακού, το δένδρο απόφασης που δημιουργεί ο ID3 απεικονίζει 5 κανόνες (βλέπε Σχήμα.14).

Σχήμα 4.14 Δένδρο απόφασης για το πρόβλημα της διαφήμισης αντηλιακού

Πλεονεκτήματα και Μειονεκτήματα των ΔΑ

 

Πλεονεκτήματα

• Φυσικός και κατανοητός τρόπος αναπαράστασης της γνώσης για αποσαφήνιση,
• Παραγόμενος αυτόματα εκτελέσιμος κώδικας, εφόσον κάθε δέντρο μεταφράζεται σε μια ακολουθία if-then εντολών,
• Αποτελεί παραδοσιακό μοντέλο μηχανικής μάθησης.

Μειονεκτήματα

• Υπάρχει δυσκολία στη μετατροπή αριθμητικών τιμών χαρακτηριστικών σε αντίστοιχα κατηγορήματα (για παράδειγμα μια τιμή του χαρακτηριστικού Ηλικία σε κατηγορίες 20-39, 40-59, και 60-79).
• Προκύπτει ανάγκη κλαδέματος κλαδιών που αναπτύσσονται συνεχώς. Η υπερβολική ανάπτυξη μειώνει μεν το σφάλμα στο σύνολο εκπαίδευσης, αλλά με κόστος την αύξηση του πλήθους των απαιτούμενων ελέγχων σφάλματος.
• Υπάρχει δυσχέρεια στη διαχείριση χαρακτηριστικών με πολλές τιμές
• Δυσκολεύεται ο αλγόριθμος να λειτουργήσει σωστά, όταν στο σύνολο εκπαίδευσης υπάρχουν δείγματα χωρίς τιμές σε ορισμένα από τα χαρακτηριστικά τους, σύνηθες φαινόμενο κατά τη συγκέντρωση και καταγραφή δειγμάτων.

4.4 Μάθηση με Συλλογιστική Βασισμένη σε Περιπτώσεις

Η Συλλογιστική Βασισμένη σε Περιπτώσεις-ΣΒΠ (Case-Based Reasoning-CBR) βασίζεται στην αξιοποίηση καταγεγραμμένης εμπειρίας και στην έρευνα περιπτώσεων προβλημάτων (cases) που αντιμετωπίστηκαν επιτυχώς στο παρελθόν, για να επιλυθεί με παραπλήσιο τρόπο ένα νέο πρόβλημα. Η επιτυχής έρευνα για την επιλογή κατάλληλων παρελθοντικών περιπτώσεων βασίζεται στην ομοιότητά τους με την τρέχουσα περίπτωση. Η ΣΒΠ/CBR ονομάζεται και Συλλογιστική με Αναλογίες (Analogical Reasoning) και χρησιμοποιείται (ίσως υποσυνείδητα) από τους περισσότερους ανθρώπους τόσο για επίλυση προβλημάτων όσο και για απόκτηση εμπειρίας.

Η επίλυση μιας νέας περίπτωσης προκύπτει από την ανάκτηση της πλέον σχετικής περίπτωσης από τις επιλεγμένες παρελθοντικές περιπτώσεις και την προσαρμογή της λύσης της. Η ΣΒΠ/CBR βασίζεται σε δυο αρχές σχετικές με τη φύση του κόσμου:

• Ο κόσμος είναι κανονικός: όμοια προβλήματα έχουν όμοια λύση.
• Προβλήματα που κάποιος αντιμετωπίζει τείνουν να ξανασυμβούν. Άρα, μελλοντικά προβλήματα είναι πολύ πιθανόν να μοιάζουν με τρέχοντα προβλήματα.

Η ΣΒΠ/CBR είναι από τις μεθόδους Μηχανικής Μάθησης που βασίζονται κατά κύριο λόγο στις ειδικές γνώσεις που έχουν αποκτηθεί κατά την επιτυχή αντιμετώπιση παρελθοντικών περιπτώσεων και έχουν καταχωρηθεί μέσα σε βάσεις περιπτώσεων με τρόπο που επιτρέπει την αξιοποίησή τους για την αντιμετώπιση παρόμοιων νέων περιπτώσεων.

Η ΣΒΠ/CBR χρησιμοποιείται σε δύο περιπτώσεις: για διερμηνεία (interpretation) και για επίλυση προβλημάτων (problem-solving). Τα συστήματα ΣΒΠ/CBR βρίσκουν εφαρμογή σε ποικίλους τομείς, όπως είναι η Νομική, όπου οι αποφάσεις του δικαστή βασίζονται στο δικαστικό προηγούμενο, και η Εγκληματολογία, είτε πρόκειται για κοινό έγκλημα, όπου για παράδειγμα τα αποτυπώματα και το DNA που υπάρχουν σε βάσεις δεδομένων βοηθούν στην ανακριτική διαδικασία μέσω της ταυτοποίησης, είτε πρόκειται για ηλεκτρονικό έγκλημα. Επίσης, η ΣΒΠ/CBR βρίσκει εφαρμογή σε συστήματα διαχείρισης επιχειρήσεων, οικονομικής διαχείρισης, διάγνωση σφαλμάτων και πρόβλεψης.

Στην ΤΝ, οι ρίζες του ΣΒΠ/CBR βρίσκονται στα έργα του Roger Schank (1982) για τη δυναμική μνήμη, τον σημαντικό ρόλο που παίζει η απομνημόνευση παρελθοντικών καταστάσεων (episodes, cases), τον τρόπο ανάκλησή τους για την επίλυση των προβλημάτων και την καινούρια γνώση που αποκτάται. Άλλες γνώσεις στο πεδίο των συστημάτων ΣΒΠ/CBR προέρχονται από τη μελέτη της αναλογικής σκέψης.

Η Συλλογιστική Βασισμένη σε Περιπτώσεις είναι ένας τρόπος επίλυσης προβλημάτων που, από πολλές απόψεις, είναι θεμελιωδώς διαφορετική από άλλες σημαντικές προσεγγίσεις της ΤΝ (Leake, 1996). Αντί να στηρίζεται αποκλειστικά σε γενικές γνώσεις ενός τομέα προβλημάτων, όπως ένα έμπειρο σύστημα, ή στις ενώσεις διαφορετικών τομέων, εδράζεται στις γενικευμένες σχέσεις μεταξύ των περιγραφών του προβλήματος και των συμπερασμάτων του.

Με την πρώτη ματιά, η ΣΒΠ/CBR μπορεί να φαίνεται παρόμοια με τους υπόλοιπους αλγόριθμους Επαγωγικής Μάθησης που χρησιμοποιούνται στη Μηχανική Μάθηση.

Όπως και σε έναν επαγωγικό αλγόριθμο μάθησης κανόνων, η ΣΒΠ/CBR ξεκινά με ένα σύνολο περιπτώσεων ή παραδειγμάτων εκπαίδευσης και σχηματίζει γενικεύσεις από τα παραδείγματα αυτά, αν και το πραγματοποιεί έμμεσα, εντοπίζοντας τα κοινά σημεία μεταξύ μιας ανακτηθείσας περίπτωσης και του προβλήματος-στόχου.

Βασική διαφορά, όμως, μεταξύ της ρητής γενίκευσης σε ΣΒΠ/CBR και της γενίκευσης από παραδείγματα για την εξαγωγή ενός κανόνα έγκειται στο πότε γίνεται η γενίκευση αυτή. Ένας κλασικός αλγόριθμος επαγωγής, όπως για παράδειγμα τα ΔΑ, αντλεί τις γενικεύσεις του από ένα σύνολο παραδειγμάτων εκπαίδευσης. Δηλαδή, εκτελεί μια βιαστική γενίκευση. Για παράδειγμα, αν στον αλγόριθμο ID3 το σύνολο εκπαίδευσης περιέχει ως δείγματα τη μέθοδο παρασκευής μαρμελάδας νεράντζι, μαρμελάδας πορτοκάλι και μαρμελάδας λεμόνι, αναμένεται με τη λήξη της φάσης εκπαίδευσης να προκύψει ένα σύνολο γενικών κανόνων για την παραγωγή όλων των τύπων της παρασκευής μαρμελάδας, γενικεύοντας έτσι, σιωπηρά, το σύνολο των καταστάσεων στις οποίες μπορεί να χρησιμοποιηθεί η βασική μέθοδος παρασκευής μαρμελάδας. Μέχρι να χρησιμοποιηθεί ο κανόνας για έναν νέο τύπο μαρμελάδας, έστω μαρμελάδα φράουλα, δεν θα είναι γνωστό αν η γενίκευση που επιχειρήθηκε, για να παραχθεί ο κανόνας, ήταν η ορθή.

Αυτό έρχεται σε αντίθεση με την ΣΒΠ/CBR, η οποία καθυστερεί (σιωπηρά) τη γενίκευση των περιπτώσεών της μέχρι τη στιγμή οπότε θα δοθεί ο συγκεκριμένος στόχος. Αυτό αποκαλείται στρατηγική «ράθυμης γενίκευσης». Στο παράδειγμα των μαρμελάδων, στη ΣΒΠ/CBR έχει ήδη δοθεί ο στόχος του προβλήματος που είναι η παρασκευή μαρμελάδας φράουλας. Έτσι, η μέθοδος μπορεί να γενικεύσει τις τρεις υπάρχουσες περιπτώσεις της ακριβώς όσο χρειάζεται, για να καλυφθεί αυτή η νέα περίπτωση.

Ως εκ τούτου, η ΣΒΠ/CBR τείνει να είναι μια καλή προσέγγιση για τομείς στους οποίους υπάρχουν πολλοί εναλλακτικοί τρόποι για να γενικευθεί μια υπόθεση και μας ενδιαφέρει να επιλέξουμε τον καταλληλότερο, όταν είναι γνωστός ο στόχος του προβλήματος που θέλουμε να λύσουμε.

4.4.1 Χαρακτηριστικά της ΣΒΠ/CBR

Ένα σύστημα ΣΒΠ/CBR αποτελείται από τα εξής βασικά τμήματα:

• μια βιβλιοθήκη από παλιές περιπτώσεις (case library),
• μια μέθοδο για το ταίριασμα και την ανάκληση από τη βιβλιοθήκη της περίπτωσης που είναι περισσότερο όμοια με την τωρινή (case retrieval) ως προς τα κυριότερα χαρακτηριστικά του προβλήματος.
• μια μέθοδο για την προσαρμογή της λύσης που δόθηκε στο παρελθόν (case adaptation), ώστε αυτή, με κάποιες τροποποιήσεις, να επαναχρησιμοποιηθεί,
• μια μέθοδο για τη δοκιμή, επαλήθευση και επιδιόρθωση της προσαρμοσμένης λύσης (case verification),
• μια μέθοδο για την εκμάθηση της λύσης (case learning), η οποία θα κρίνει αν η νέα περίπτωση και η προσαρμοσμένη λύση της συνιστούν μια πολύ διαφορετική περίπτωση από αυτές που βρίσκονται στη βιβλιοθήκη και πρέπει να προστεθούν σε αυτήν. Η διαδικασία της εκμάθησης καθιστά τα συστήματα ΣΒΠ/CBR συστήματα μηχανικής μάθησης.

4.4.2 Ο Κύκλος ΣΒΠ/CBR

Ένας κύκλος ΣΒΠ/CBR μπορεί να περιγραφεί με βάση τις εξής 4 λειτουργίες:

• Ανάκτηση (retrieve) της πιο όμοιας περίπτωσης ή περιπτώσεων,
• Επαναχρησιμοποίηση (reuse) των πληροφοριών και της γνώσης, στη συγκεκριμένη περίπτωση για να λυθεί το πρόβλημα,
• Τροποποίηση (revise) της προτεινόμενης λύσης ,
• Διατήρηση (retain) των τμημάτων αυτών της εμπειρίας που ενδέχεται να φανούν χρήσιμα για μελλοντική επίλυση προβλημάτων.

Ένα νέο πρόβλημα θα έχει λυθεί με την ανάκτηση μίας ή περισσότερων προηγουμένων περιπτώσεων, την επαναχρησιμοποίηση της περίπτωσης με τον ένα ή με τον άλλο τρόπο, την τροποποίηση της λύσης, που βασίζεται στην επαναχρησιμοποίηση μιας προηγούμενης περίπτωσης και τη διατήρηση της νέας εμπειρίας με την ενσωμάτωσή της στην υπάρχουσα βάση των περιπτώσεων. Καθεμία από τις τέσσερις λειτουργίες περιλαμβάνει μια σειρά από πιο συγκεκριμένες ενέργειες (Aamodt &Plaza, 1994). Στο σχήμα 4.15 φαίνεται αυτός ο κύκλος.

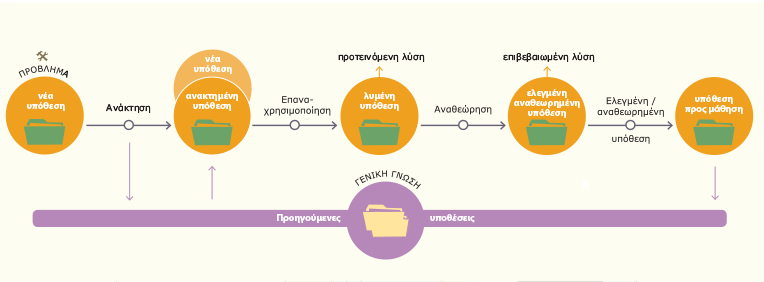
Σχήμα 4.15 Ο κύκλος των διεργασιών της Συλλογιστικής Βασισμένης σε Περιπτώσεις

Δείτε κινούμενη εικόνα 4.2 - Ο κύκλος των διεργασιών της CBR

 

Μια πρώτη περιγραφή του προβλήματος (αριστερά στο σχήμα 4.15) καθορίζει μια νέα περίπτωση (New Case). Η νέα περίπτωση χρησιμοποιείται για την ανάκτηση (RETRIEVE) μιας περίπτωσης από τη συλλογή των προηγούμενων περιπτώσεων (Previous Cases). Η ανακτημένη περίπτωση (Retrieved Case) συνδυάζεται με τη νέα περίπτωση-μέσω της επαναχρησιμοποίησης (REUSE)- ως προτεινόμενη λύση (Suggested Solution) στο υπό επίλυση πρόβλημα. Μέσω της διαδικασίας αναθεώρησης (REVISE), η λύση που προτείνεται (Solved Case) δοκιμάζεται στο πραγματικό περιβάλλον ή αξιολογείται από έναν ειδικό (Tested Case) και, εφόσον επιτύχει, γίνεται αποδεκτή (Confirmed Solution). Διαφορετικά, τροποποιείται κατάλληλα (Repaired Case). και επαναξιολογείται, έως ότου γίνει αποδεκτή Κατά τη διαδικασία διατήρησης (RETAIN), η χρήσιμη εμπειρία (Learned Case) διατηρείται για μελλοντική χρήση και η βάση των προηγούμενων περιπτώσεων ενημερώνεται είτε με τη νέα επιλυμένη περίπτωση είτε με τη μετατροπή της ανακτημένης περίπτωσης, για να αποτελέσει λύση.

Όπως παρουσιάζεται στο σχήμα 4.15, η γενική γνώση συνήθως επιτελεί σημαντικό ρόλο σε αυτό τον κύκλο, υποστηρίζοντας τις διαδικασίες της ΣΒΠ/CBR. Η υποστήριξη αυτή μπορεί να είναι πολύ αδύναμη (ή να μην υπάρχει) ή πολύ ισχυρή, ανάλογα με το είδος της μεθόδου ΣΒΠ/CBR. Με τον όρο γενική γνώση εννοείται η γνώση που εξαρτάται από το γενικό τομέα, σε αντίθεση με την ειδική γνώση που ενσωματώνεται από τις περιπτώσεις.

Ο γενικός αλγόριθμος της ΣΒΠ/CBR μπορεί να συνοψιστεί ως:

• ΑΡΧΗ
  • δέξου τις προδιαγραφές του νέου προβλήματος
  • προσδιόρισε τα χαρακτηριστικά αναζήτησης μέσα στη βάση περιπτώσεων,
  • ανάκτησε ένα σύνολο περιπτώσεων με χαρακτηριστικά που ταιριάζουν,
  • επίλεξε μια περίπτωση.
  • Επανάλαβε
    • τροποποίησε την περίπτωση,
    • αξιολόγηση τη λύση που δίνει.
  • Έως ότου η λύση είναι ικανοποιητική
• ΤΕΛΟΣ

Για τη δεικτοδότηση των περιπτώσεων στη μνήμη, οι προδιαγραφές ενός καινούριου προβλήματος μετατρέπονται σε πρότυπο προς αντιστοίχιση. Το πρότυπο στη συνέχεια μπορεί να χρησιμοποιηθεί ως έχει ή μπορεί να τροποποιηθεί από το χρήστη. Το πρότυπο μπορεί να συγκριθεί με κάθε περίπτωση στη μνήμη ή αυτό μπορεί να παρέχει ένα σύνολο από δείκτες, ώστε να περιοριστεί ο χώρος αναζήτησης και μόνο ένα υποσύνολο σχετικών περιπτώσεων να συγκριθούν μαζί του. Η ανάκτηση μπορεί να βασίζεται σε μια τέλεια αντιστοίχιση ή σε μερικές αντιστοιχίσεις.

Το πρότυπο αποτελείται από ένα σύνολο σταθμισμένων χαρακτηριστικών αντιστοίχισης και η κάθε περίπτωση που έχει ανακτηθεί είναι δεικτοδοτημένη σύμφωνα με αυτά, έτσι ώστε η επιλογή να βασίζεται στην ανακτηθείσα περίπτωση με την πιο ικανοποιητική ταύτιση. Δηλαδή, αν το πρότυπο αποτελείται από ένα σύνολο χαρακτηριστικών, η επιλογή βασίζεται στην περίπτωση που έχει τα περισσότερα κοινά χαρακτηριστικά με αυτό (Maher κ.ά. , 1995, σ.4).

Η διαδικασία της τροποποίησης προσαρμόζει μια προηγούμενη περίπτωση σε ένα νέο πρόβλημα συνδέοντας τύπους με τα χαρακτηριστικά ή τις παραμέτρους που μπορούν να αλλάξουν. Όταν προσδιορίζεται το περιεχόμενο της μνήμης, μερικά χαρακτηριστικά αναγνωρίζονται ως τροποποιήσιμα. Καθένα από τα χαρακτηριστικά έχει έναν τύπο ή μια διαδικασία που αξιολογείται κατά τη διάρκεια της τροποποίησης.

Όταν μια ανακτημένη περίπτωση επιλεχθεί ως βάση για τη νέα λύση, υπάρχουν περιορισμοί που παρέχουν τη γνώση που απαιτείται για τον έλεγχο των διαφορών μεταξύ της επιλεγμένης περίπτωσης και του νέου προβλήματος.

4.4.3 Κύριοι τύποι μεθόδων ΣΒΠ/CBR

Ο μηχανισμός της ΣΒΠ/CBR καλύπτει ένα εύρος διαφορετικών μεθόδων για την οργάνωση, την ανάκτηση, την αξιοποίηση και τη δεικτοδότηση των γνώσεων που διατηρούνται από παρελθοντικές περιπτώσεις. Οι περιπτώσεις διατηρούνται είτε ως συγκεκριμένες εμπειρίες είτε ως σύνολο παρόμοιων περιπτώσεων που μπορεί να αποτελέσουν μια γενικευμένη περίπτωση. Η λύση από μία προηγούμενη περίπτωση μπορεί να εφαρμοστεί άμεσα στο σημερινό πρόβλημα ή να τροποποιηθεί ανάλογα με τις διαφορές μεταξύ των δύο περιπτώσεων. Μερικές μέθοδοι ΣΒΠ/CBR χρησιμοποιούν ένα αρκετά μεγάλο μέρος των δεικτοδοτημένων περιπτώσεων μέσα στις βάσεις, παλαιών περιπτώσεων ενώ άλλες βασίζονται σε ένα πιο περιορισμένο σύνολο χαρακτηριστικών περιπτώσεων. Προηγούμενες περιπτώσεις μπορεί να ανακτηθούν και να αξιολογηθούν διαδοχικά ή παράλληλα. Οι μέθοδοι ΣΒΠ/CBR μπορούν να είναι καθαρά αυτόνομες και αυτόματες ή να αλληλεπιδρούν σε μεγάλο βαθμό με τον χρήστη για την υποστήριξη και την καθοδήγηση των επιλογών του.

Τρεις είναι οι χαρακτηριστικοί σχετικοί τύποι ΣΒΠ/CBR σε σχέση με τη δομή των περιπτώσεων μέσα στη βάση:

• Διαρθρωτικός (διαθέτει κοινό δομημένο λεξιλόγιο, δηλαδή μια οντολογία)
• Κειμένου (οι περιπτώσεις παρουσιάζονται ως ελεύθερο κείμενο, δηλαδή ως συμβολοσειρές)
• Διαλόγου (μια περίπτωση αντιπροσωπεύεται από μια λίστα ερωτήσεων που ποικίλλει από τη μια περίπτωση στην άλλη, η δε γνώση αποκτάται από συζητήσεις μεταξύ συστήματος και χρήστη.

Στην πραγματικότητα, ο όρος «Συλλογιστική Βασισμένη σε Περιπτώσεις –ΣΒΠ/CBR» είναι ένας μόνο από τους όρους που χρησιμοποιούνται όσον αφορά τα συστήματα αυτού του είδους.

Άλλοι όροι που σχετίζονται με την ΣΒΠ/CBR παρατίθεται στη συνέχεια (Aamodt&Plaza, 1994):

• Συλλογιστική Βασισμένη σε Υποδείγματα (Exemplar-based reasoning
• Συλλογιστική Βασισμένη σε Περιστατικά (Instance-based reasoning)
• Συλλογιστική Βασισμένη στη Μνήμη (Memory-based reasoning)
• Συλλογιστική Βασισμένη στη Αναλογική Σκέψη (Analogy-based reasoning)

Παρά το γεγονός ότι η ΣΒΠ/CBR χρησιμοποιείται ως γενικός όρος, η τυπική μέθοδος ΣΒΠ/CBR έχει κάποια χαρακτηριστικά που τη διακρίνει από τους άλλους τύπους που αναφέρονται εδώ. Πρώτον, μια τυπική περίπτωση συνήθως έχει κάποιο βαθμό πλούτου πληροφοριών που περιέχονται σε αυτήν, καθώς και μια σχετική πολυπλοκότητα όσον αφορά την οργάνωση του εσωτερικού της. Δηλαδή, ένα διάνυσμα χαρακτηριστικών γνωρισμάτων που κατέχουν κάποιες αξίες και μια αντίστοιχη κλάση δεν είναι αυτό που θα χαρακτηριζόταν ως μια τυπική περιγραφή της περίπτωσης. Η τυπική βασισμένη σε περιπτώσεις μέθοδος έχει ακόμα άλλο ένα χαρακτηριστικό: τη δυνατότητα να τροποποιήσει, να προσαρμόσει και να ανακτήσει μια λύση, όταν εφαρμόζεται σε ένα διαφορετικό πλαίσιο επίλυσης προβλημάτων.

4.4.4 Πλεονεκτήματα - Μειονεκτήματα

Τα πλεονεκτήματα της ΣΒΠ/CBR σε σχέση με τα κλασσικά συστήματα διαχείρισης γνώσης (π.χ. συστήματα κανόνων) μπορούν να συνοψιστούν στα ακόλουθα:

Η ΣΒΠ/CBR βρίσκεται πιο κοντά στον τρόπο με τον οποίο σκέφτονται οι άνθρωποι. Τα συστήματα κανόνων βασίζονται στην εμπειρία που εκμαιεύτηκε από κάποιον ειδικό, αλλά η γνώση του ειδικού αναπαρίσταται στον υπολογιστή πολύ διαφορετικά. Με άλλα λόγια, στα έμπειρα συστήματα η γνώση του ειδικού έχει υποστεί μετατροπές, είτε από τον ίδιο τον ειδικό που αναγκάζεται να ομαδοποιήσει τις εμπειρίες του ή από τον μηχανικό γνώσης ο οποίος πρέπει αφαιρετικά να βρει κοινά στοιχεία στις εμπειρίες του ειδικού και να τις μετατρέψει σε κανόνες, ενώ στη ΣΒΠ/CBR η εμπειρία του ειδικού αναπαρίσταται ευθέως με τη μορφή περιπτώσεων που αντιμετώπισε στο παρελθόν και ανακαλεί από τη μνήμη του. Τα προβλήματα που αντιμετωπίστηκαν στο παρελθόν συγκρίνονται με τις τωρινές καταστάσεις και οι λύσεις που υιοθετήθηκαν ξαναχρησιμοποιούνται με μικρές μετατροπές.

Η διαδικασία απόκτησης της γνώσης απλουστεύεται, γιατί τις περισσότερες φορές η γνώση των παρελθοντικών περιπτώσεων υπάρχει ήδη κάπου αποθηκευμένη, στην καλύτερη περίπτωση μέσα σε βάσεις δεδομένων που διατηρούν εταιρείες και οργανισμοί. Εάν δεν υπάρχει βιβλιοθήκη περιπτώσεων, τότε κάποιος ειδικός καλείται να τη δημιουργήσει από τις εμπειρίες που υπάρχουν διαθέσιμες για το πρόβλημα σε μια ποικιλία μορφών. Βέβαια, η περίπτωση αυτή απαιτεί πολύ μεγαλύτερο κόπο εκ μέρους του ειδικού από μια απλή συμμετοχή του στη διαδικασία εκμαίευσης γνώσης, όπως γίνεται στα έμπειρα συστήματα.

Το κυριότερο μειονέκτημα της συλλογιστικής των περιπτώσεων, όπως και κάθε άλλου πληροφορικού συστήματος, είναι η δυσχέρεια στην απόκτηση γνώσης για το πεδίο και το υπολογιστικό κόστος της αναζήτησης στη βιβλιοθήκη των περιπτώσεων. Επίσης, βασικό μειονέκτημα είναι οι δυσκολίες στην προσαρμογή της λύσης μιας ανακτηθείσας περίπτωσης στην τρέχουσα κατάσταση.

Στη συνέχεια, αναφέρονται συνοπτικά τα πλεονεκτήματα και τα μειονεκτήματα της ΣΒΠ/CBR:

 

Πλεονεκτήματα

• Επιτρέπει στο σύστημα να προτείνει λύσεις σε προβλήματα γρήγορα, αποφεύγοντας τον απαιτούμενο χρόνο της παραγωγής των απαντήσεων εξαρχής σε τομείς που δεν έχουν πλήρως αναλυθεί.
• Παρέχει στο σύστημα τα μέσα για να αξιολογεί τις λύσεις, όταν δεν υπάρχει διαθέσιμη αλγοριθμική μέθοδος.
• Βοηθάει στη διερμήνευση ορισμένων «ανοιχτών» και με λανθασμένο τρόπο διατυπωμένων προβλημάτων.
• Βοηθάει το σύστημα να εντοπίσει τα πιο σημαντικά χαρακτηριστικά του προβλήματος και να επικεντρώσει τη συλλογιστική του σε αυτά.
• Βοηθάει το σύστημα να αποφύγει την επανάληψη παρελθοντικών προβλημάτων τα οποία μπορεί να αναδείξουν οι περιπτώσεις.

Μειονεκτήματα

• Οι παρελθοντικές περιπτώσεις μπορεί να είναι «ελλιπείς».
• Η βιβλιοθήκη των περιπτώσεων μπορεί να αναφέρεται σε ένα επιλυμένο πρόβλημα χωρίς να έχει συγκεντρωθεί ένα ικανοποιητικός αριθμός παρελθοντικών περιπτώσεων.
• Υπάρχει δυσκολία στην ανάκτηση των πιο σχετικών περιπτώσεων.

Η ΣΒΠ/CBR βρίσκει εφαρμογή σε μια ευρεία ποικιλία έργων επίλυσης προβλημάτων, συμπεριλαμβανομένων του καθορισμού στόχων (planning), της διάγνωσης (diagnosis) και του σχεδιασμού (design) ενός προβλήματος. Σε καθένα από αυτά τα έργα, οι περιπτώσεις είναι χρήσιμες στο να προτείνουν λύσεις, καθώς και στην προειδοποίηση πιθανών προβλημάτων που μπορεί να προκύψουν. Η ΣΒΠ/CBR βρίσκει επιπλέον εφαρμογή σε προβλήματα που απαιτούν ικανότητες διερμηνείας της διατιθέμενης γνώσης, όπως είναι η κατάταξη μιας νέας κατάστασης ενός προβλήματος, η απόδειξη της ορθότητας ενός επιχειρήματος ή η πρόβλεψη των αποτελεσμάτων μιας λύσης. Στην περίπτωση αυτή, η ΣΒΠ/CBR καλείται Διερμηνευτική ΣΒΠ/CBR (Interpretive CBR).

4.4.5 Δυσχέρεια στην απόκτηση γνώσης

Η απόκτηση γνώσης είναι η μετατροπή της προϋπάρχουσας εμπειρίας σε μια μορφή αναγνωρίσιμη και επεξεργάσιμη από ένα Βασισμένο στη Γνώση Σύστημα (Knowledge-Based System-KBS). Το πρόβλημα της δυσχέρειας στην απόκτηση γνώσης στα συστήματα ΣΒΠ/CBR είναι άρρηκτα συνδεδεμένο με το μέγεθος της βιβλιοθήκης και με την ποικιλία των αποθηκευμένων περιπτώσεων σε αυτή.

Συγκεκριμένα, σε ένα σύστημα θα πρέπει να ελέγχονται τα νέα στιγμιότυπα, προτού αυτά αποθηκευτούν, και να μην επιτρέπεται να καταχωρούνται παρόμοια στιγμιότυπα, αλλά να τροποποιούνται σε ένα, το οποίο θα δίνει λύση σε όλες τις παραπλήσιες περιπτώσεις. Απώτερος σκοπός της παραπάνω διαδικασίας είναι να μη δημιουργούνται δαιδαλώδεις βιβλιοθήκες περιπτώσεων καθιστώντας τες μη λειτουργικές και κατ’ επέκταση επιβαρύνοντας το σύστημα.

Ένα άλλο πρόβλημα δημιουργείται, όταν μία περίπτωση αντιμετωπίζεται για πρώτη φορά από το σύστημα. Για παράδειγμα, όταν στο περιεχόμενο της βιβλιοθήκης δεν υπάρχει κάποια περίπτωση παρόμοια με την τρέχουσα, τότε η λύση πρέπει να δομηθεί από την αρχή. Για να αποκτήσει το σύστημα την απαιτούμενη γνώση, θα απαιτηθεί περισσότερος υπολογιστικός φόρτος και μια αρκετά χρονοβόρα διαδικασία. Εντούτοις, το κόστος είναι απαραίτητο, διότι διαφορετικά το σύστημα θα αναλώνεται στην τροποποίηση των ήδη υπαρχουσών περιπτώσεων, καταλήγοντας τελικά σε μια διαφορετική λύση από αυτήν που απαιτείται.

4.5 Νευρωνικά Δίκτυα

4.5.1 Γενικά

Ο όρος Νευρωνικά Δίκτυα (Neural Networks, Connectionist Networks, Parallel Distributed Processing Μodels) περιγράφει έναν αριθμό από διαφορετικά μαθηματικά μοντέλα, εμπνευσμένα από αντίστοιχα βιολογικά μοντέλα, δηλαδή μοντέλα που προσπαθούν να μιμηθούν τη συμπεριφορά των νευρώνων του ανθρώπινου εγκεφάλου.

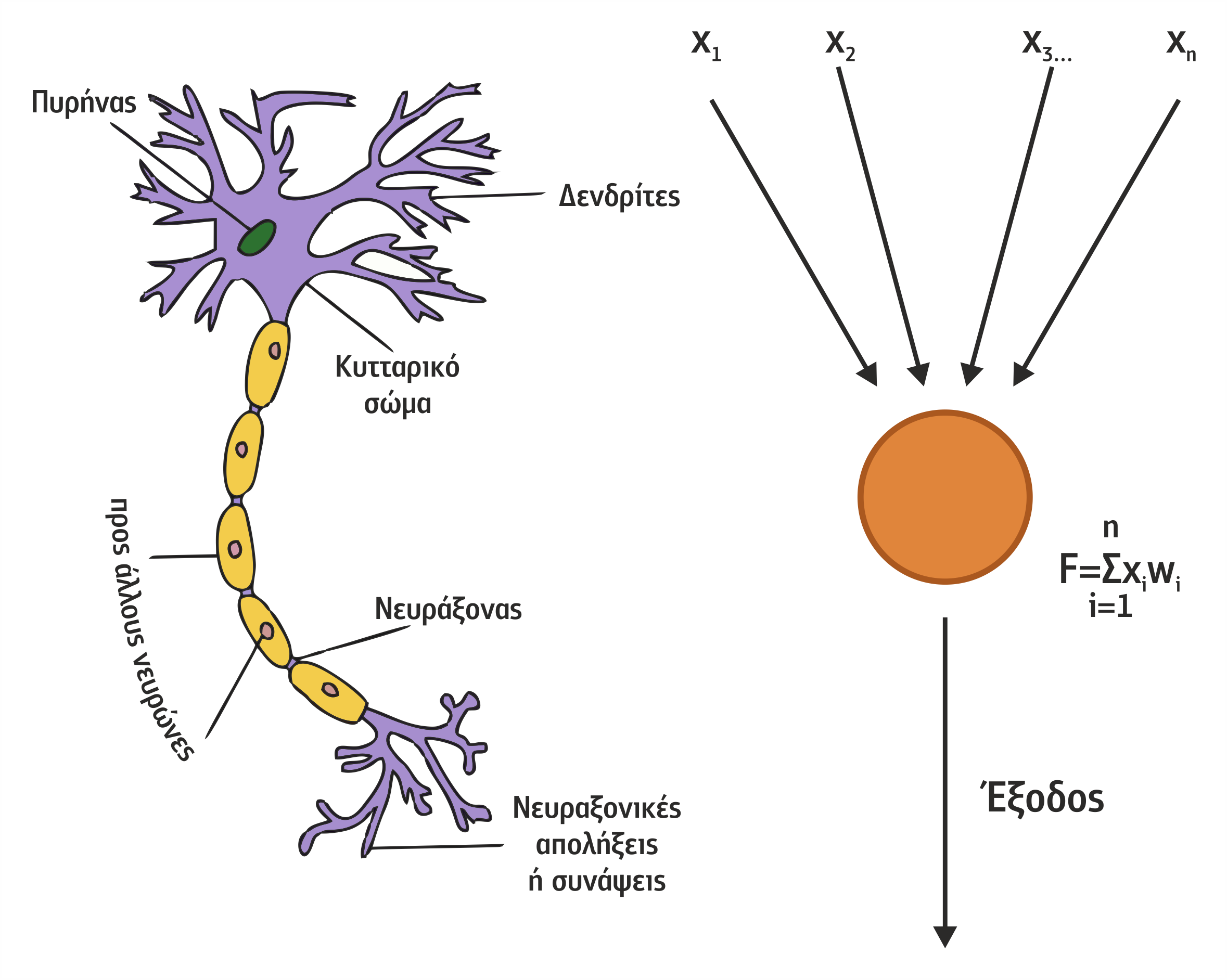
Ήδη από τον 19ο αιώνα οι επιστήμονες παραδέχονται ότι ο εγκέφαλος αποτελείται από διακριτά στοιχεία, τους νευρώνες (neurons), που επικοινωνούν το ένα με το άλλο. Οι νευρώνες συνιστούν το βασικό δομικό κομμάτι του ανθρώπινου εγκεφάλου. Υπολογίζεται ότι ο εγκέφαλος περιέχει 10 δισ. περίπου νευρώνες τοποθετημένους σε ομάδες, καθεμία από τις οποίες συνιστά ένα φυσικό νευρωνικό δίκτυο. Έτσι, ο ανθρώπινος εγκέφαλος περιέχει εκατοντάδες φυσικά νευρωνικά δίκτυα, καθένα από τα οποία περιέχει χιλιάδες διασυνδεδεμένους νευρώνες με μέσο αριθμό διασυνδέσεων ανά νευρώνα 1000 με 10.000.

Εικόνα 4.1 Μικροσκοπική φωτογραφία φυσικών νευρώνων

Ένας νευρώνας διαχωρίζεται από τα υπόλοιπα κύτταρα με μια μεμβράνη και έχει την ικανότητα να μεταφέρει ηλεκτρικά σήματα από το νευρώνα αυτόν προς τους υπόλοιπους νευρώνες με τους οποίους επικοινωνεί.

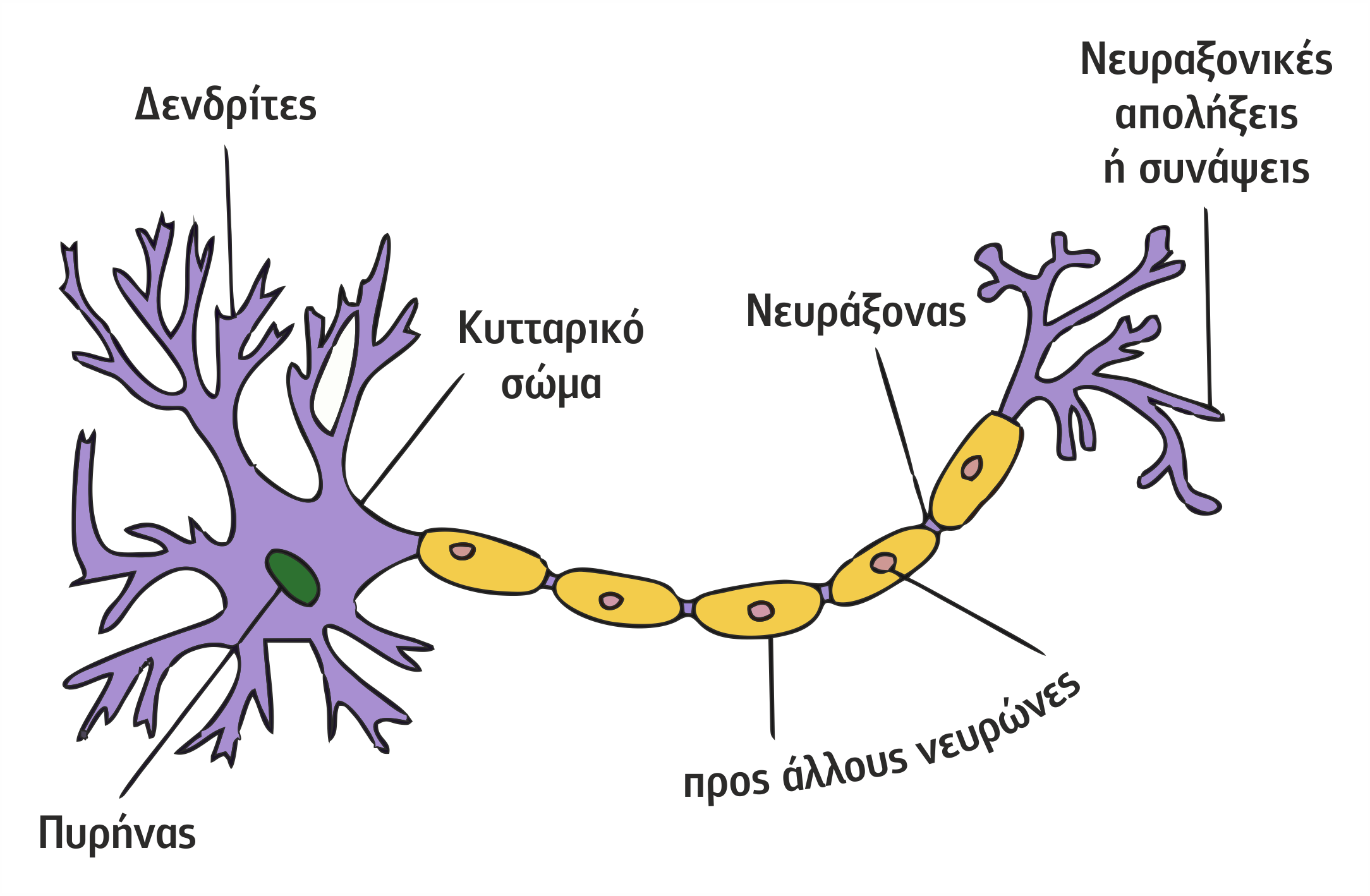
Σχήμα 4.16 Σχηματικό διάγραμμα ενός τυπικού νευρώνα

Κάθε νευρώνας αποτελείται από 3 κύρια τμήματα (βλέπε Σχήμα 4.16):

• τους δενδρίτες (dendrites),οι οποίοι λειτουργούν ως κανάλια εισόδου για το νευρώνα,
• το κυρίως κυτταρικό σώμα (cell body),
• τον άξονα του κυττάρου-νευροάξονα (axon), που συνδέει ένα νευρώνα με άλλους νευρώνες.

Ο άξονας του ενός νευρώνα μεταφέρει σήματα στους δενδρίτες γειτονικών νευρώνων μέσω του σημείου ένωσης που ονομάζεται νευροαξονική απόληξη ή σύναψη (synapse). Ένας νευρώνας μπορεί να λάβει σήματα από ένα σύνολο γειτονικών νευρώνων μέσω των δενδριτών, να τα επεξεργαστεί και να τροφοδοτήσει την έξοδό του μέσω του άξονα προς ένα άλλο σύνολο γειτονικών νευρώνων (βλέπε Σχήμα 4.17). Τα σήματα που έρχονται μέσω των δενδριτών «ζυγίζονται» και τα αποτελέσματα αθροίζονται. Όταν το άθροισμα ξεπεράσει το οριακό επίπεδο (τιμή κατωφλίου), ο νευρώνας δημιουργεί μια έξοδο (με τη μορφή νευρικής ώσης ή ηλεκτρικού σήματος) στον άξονά του, η οποία εν συνεχεία μέσω των συνάψεων θα μεταφερθεί στους γειτονικούς νευρώνες.

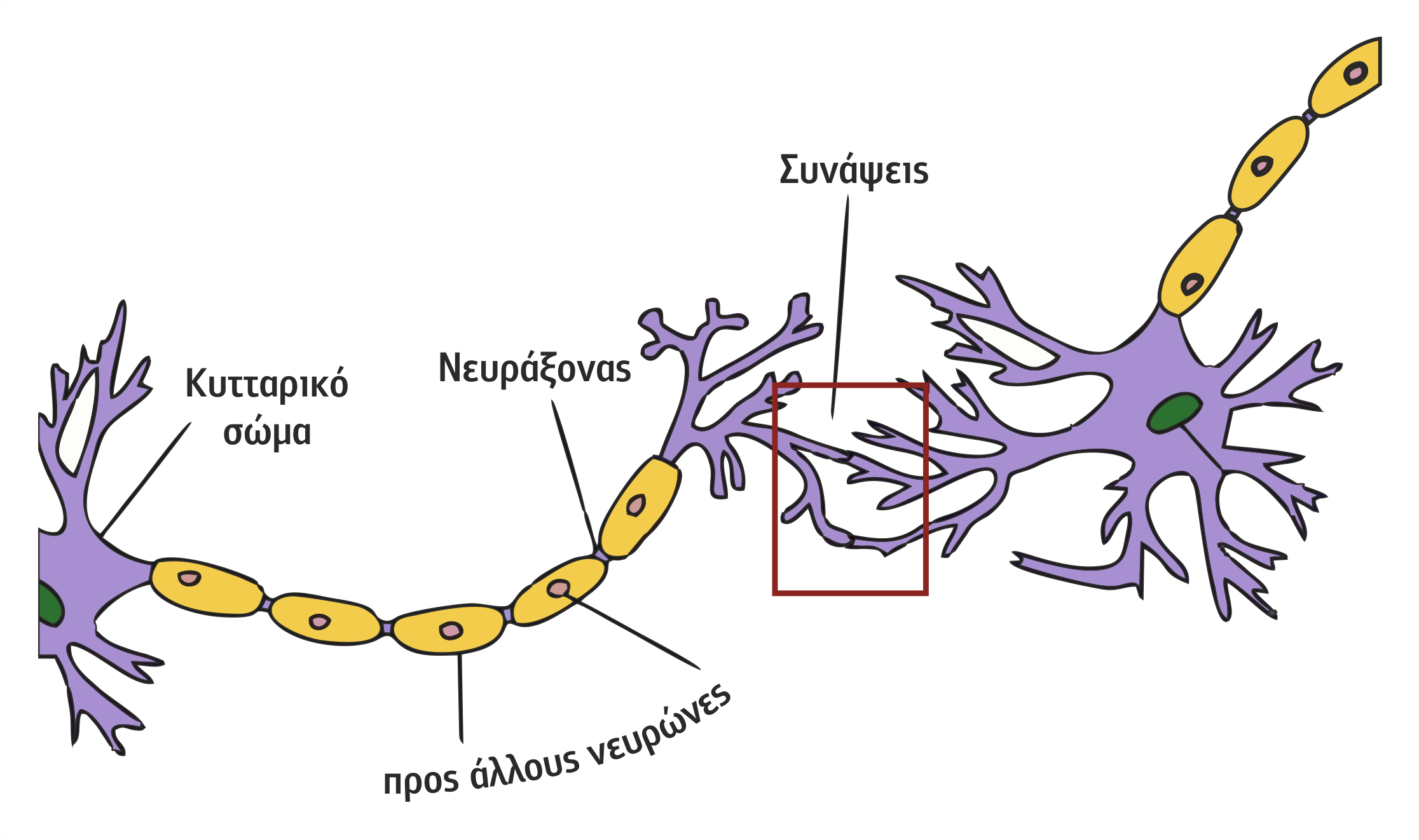
Σχήμα 4.17 Φυσικοί διασυνδεδεμένοι νευρώνες

Για την παραγωγή σήματος, ο νευρώνας δέχεται σήματα εισόδου που επιδρούν στο δυναμικό του αυξομειώνοντάς το. Όταν αθροιστικά το δυναμικό ξεπεράσει κάποιο όριο (ποικίλλει από κατηγορία σε κατηγορία κυττάρου μεταξύ – 40 mV και – 75 mV), τότε ο νευρώνας διεγείρεται και παράγει το ηλεκτρικό σήμα. Ο νευρώνας μεταφέρει το ηλεκτρικό σήμα πάντοτε προς μια προβλέψιμη και σταθερή κατεύθυνση. Υπάρχουν δυο διακριτές καταστάσεις σημάτων:

• Δυναμικό ηρεμίας
• Δυναμικό ενέργειας

Τα σήματα που λαμβάνονται από ένα νευρώνα μεταβάλλονται από τα ηλεκτρικά χαρακτηριστικά των επαφών των συνάψεων, ώστε να εμποδίζονται μερικά και να επιτρέπεται σε άλλα να διαδοθούν. Τα ηλεκτρικά χαρακτηριστικά των συνάψεων αποτελούν κάποιο είδος πληροφορίας μοναδικής σε κάθε νευρώνα. Με αυτό τον τρόπο οι πληροφορίες που κρατούνται από ένα δίκτυο κατανέμονται στους νευρώνες του.

Η μεταβίβαση πληροφορίας γίνεται με βάση το δυναμικό ενέργειας που καθορίζεται όχι από τον τύπο του σήματος, αλλά από την οδό του εγκεφάλου μέσα από διακριτά επικοινωνούντες νευρώνες από τους οποίους περνάει το σήμα.

Η έκφραση «διακριτά επικοινωνούντα στοιχεία» είναι η βάση του ορισμού των ψηφιακών κυκλωμάτων, αλλά σε καμία περίπτωση ο εγκέφαλος δεν είναι ένας ψηφιακός ηλεκτρονικός υπολογιστής ούτε ένας ηλεκτρονικός υπολογιστής μπορεί να αντικαταστήσει τον εγκέφαλο. Μία από τις βασικές αιτίες είναι ότι τα πολλαπλά φυσικά νευρωνικά δίκτυα του εγκεφάλου είναι οργανωμένα σε τμήματα που λειτουργούν παράλληλα· το καθένα από αυτά μπορεί να προκαλέσει ανεξάρτητες συμπεριφορές, εμφανίζοντας πλαστικότητα στην ανάληψη λειτουργιών (δηλαδή προσαρμόζονται σε αλλαγές που επιφέρει το εσωτερικό ή εξωτερικό περιβάλλον, ώστε να εξακολουθούν να λειτουργούν επιτυχώς στο μέτρο του δυνατού) και ως εκ τούτου δεν μπορούν να εξομοιωθούν με ηλεκτρονικά κυκλώματα που δε διαθέτουν παρόμοια χαρακτηριστικά.

4.5.2 Προσομοίωση φυσικών νευρωνικών δικτύων με τεχνητά νευρωνικά δίκτυα

Τα μαθηματικά μοντέλα των τεχνητών νευρωνικών δικτύων, σε πλήρη αντιστοιχία με τα βιολογικά, αποτελούνται από έναν αριθμό απλών και με υψηλό βαθμό εσωτερικής διασύνδεσης επεξεργαστικών μονάδων, οργανωμένων σε στρώματα. Τα Τεχνητά Νευρωνικά Δίκτυα-ΤΝΔ (Artificial Neural Networks-ANN) επεξεργάζονται πληροφορίες ανταποκρινόμενα δυναμικά σε εξωτερικά ερεθίσματα (εισόδους). Κάθε τεχνητός νευρώνας αποτελείται από πολλές εισόδους xi και μία μόνο έξοδο y. Κάθε είσοδος xi «ζυγίζεται» με ένα βάρος wi και τα αποτελέσματα αθροίζονται μέσω της συνάρτησης αθροίσματος (summation function) F:

Ο τεχνητός νευρώνας δίνει έξοδο μέσω της συνάρτησης μετάβασης (transfer function), μόνο όταν το ζυγισμένο άθροισμα των εισόδων είναι μεγαλύτερο μιας ορισμένης τιμής κατωφλίου (threshold value) θ, δηλαδή όταν:

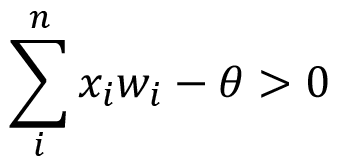
Ένας τεχνητός νευρώνας αποτελεί απλοποιημένο μοντέλο του φυσικού νευρώνα κατά το ότι τα βάρη διασύνδεσης σχηματίζουν τα ηλεκτρικά χαρακτηριστικά της επαφής της σύναψης και η τιμή κατωφλίου προσομοιώνει τη συμπεριφορά κορεσμού του φυσικού νευρώνα (βλέπε Σχήμα 4.18).

Σχήμα 4.18 Ο φυσικός νευρώνας σε σχέση με τον στοιχειώδη τεχνητό νευρώνα (Perceptron)

Ένα από τα απλούστερα ΤΝΔ που προσομοιώνουν τον φυσικό νευρώνα είναι ο στοιχειώδης Perceptron (basic Perceptron), δηλαδή ένα ΤΝΔ που αποτελείται από έναν μόνο νευρώνα Η έξοδος α του Perceptron για ένα διάνυσμα εισόδου x=(x1, x2,.., xn) δίνεται μέσω της συνάρτησης μετάβασης g ως ακολούθως:

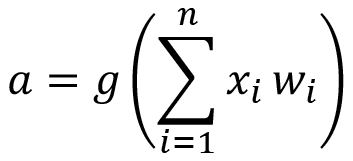
Συνοπτική περιγραφή ενός ΤΝΔ:

• Τα ΤΝΔ συνήθως οργανώνονται σε επίπεδα (layers) τα οποία καλούνται και στρώματα. Τα ενδιάμεσα επίπεδα καλούνται κρυμμένα επίπεδα (hidden layers) και δεν είναι απαραίτητο να υπάρχουν.
• Τα επίπεδα αποτελούνται από έναν αριθμό μονάδων (units) ή κόμβων (nodes) που είναι έτσι συνδεδεμένες μεταξύ τους, ώστε μία μονάδα να έχει συνδέσμους με πολλές άλλες μονάδες του ίδιου ή άλλου επιπέδου.
• Οι μονάδες επιδρούν σε άλλες μονάδες με το να τις διεγείρουν ή να αναστέλλουν την ενεργοποίησή τους. Για να επιτευχθεί αυτό η μονάδα λαμβάνει το σταθμισμένο άθροισμα όλων των εισόδων μέσω των συνδέσμων που καταλήγουν σε αυτήν και παράγει μέσω της συνάρτησης μετάβασης μία μοναδική έξοδο, εάν το άθροισμα υπερβαίνει μία τιμή κατωφλίου.
• Οι είσοδοι παρουσιάζονται στο δίκτυο μέσω του επιπέδου εισόδου (input layer) το οποίο επικοινωνεί με έναν ή περισσότερα κρυμμένα επίπεδα Τα κρυμμένα επίπεδα συνδέονται με το επίπεδο εξόδου (output layer) από το οποίο εξάγεται η απάντηση.

Βασικά στοιχεία της αρχιτεκτονικής των ΤΝΔ που πρέπει να καθοριστούν κατά τη δημιουργία τους είναι:

• Ο αριθμός των ενδιάμεσων κρυφών επιπέδων,
• Ο αριθμός των μονάδων (ή κόμβων) ανά επίπεδο,
• Ο τρόπος σύνδεσης των μονάδων μεταξύ τους,
• Η τιμή ενεργοποίησης (τιμή κατωφλίου),
• Η μορφή της συνάρτησης μετάβασης,
• Οι τιμές των αρχικών βαρών μεταξύ των μονάδων,
• Οι αλγόριθμοι (κανόνες εκπαίδευσης) που χρησιμοποιούνται, για να ενισχυθούν οι σύνδεσμοι μεταξύ των μονάδων κατά τη διαδικασία της εκπαίδευσης.

4.5.3 Ιστορική Αναδρομή

Τα ορόσημα στην εξέλιξη του χώρου των ΤΝΔ είναι τα ακόλουθα:

 

1943: McCulloch & Pitts – Δημιουργούν το πρώτο μοντέλο ΤΝΔ

1949: Ηebb – Δημιουργεί το μοντέλο μάθησης που πήρε το όνομά του στο οποίο κάθε φορά που ενεργοποιείται μια σύναψη αυτή ενισχύεται, με αποτέλεσμα το δίκτυο να μαθαίνει «λίγο περισσότερο» το πρότυπο που του παρουσιάζεται εκείνη τη στιγμή.

1957: Rosenblatt- Προτείνει το στοιχειώδες ΤΝΔ του απλού αισθητήρα που ονόμασε Perceptron.

1969: Minsky & Papert- Απoδεικνύουν μαθηματικά ότι τα ΤΝΔ ενός επιπέδου δεν μπορούν να λύσουν μη γραμμικά προβλήματα.

1982: Μαθηματική απόδειξη ότι ένα ΤΝΔ πολλών επιπέδων μπορεί να αποθηκεύσει οποιαδήποτε πληροφορία.

1986: Werbos & Rumelhart – Προτείνουν τη μέθοδο οπισθοδιάδοσης (backpropagation) για την εκπαίδευση ΤΝΔ.

4.5.4 Αρχιτεκτονική ΤΝΔ

Όσον αφορά το πώς είναι συνδεδεμένες οι μονάδες μεταξύ τους, υπάρχουν δυο βασικές κατηγορίες ΤΝΔ:

• πρόσθιας τροφοδότησης (feed forward) και
• οπίσθιας τροφοδότησης (feed backward)

Στα νευρωνικά δίκτυα πρόσθιας τροφοδότησης, οι μονάδες είναι οργανωμένες σε διαφορετικά επίπεδα, ώστε οι μονάδες του ενός επιπέδου να τροφοδοτούν τις μονάδες του επόμενου επιπέδου, έως ότου τροφοδοτηθούν και οι μονάδες του τελευταίου επιπέδου (βλέπε Σχήμα 4.19). Δηλαδή, δεν υπάρχει έξοδος μονάδας ενός επιπέδου που να αποτελεί είσοδο μονάδας του ίδιου ή προηγούμενων επιπέδου. Τέτοια ΤΝΔ είναι τα δίκτυα οπισθοδιάδοσης (backpropagation).

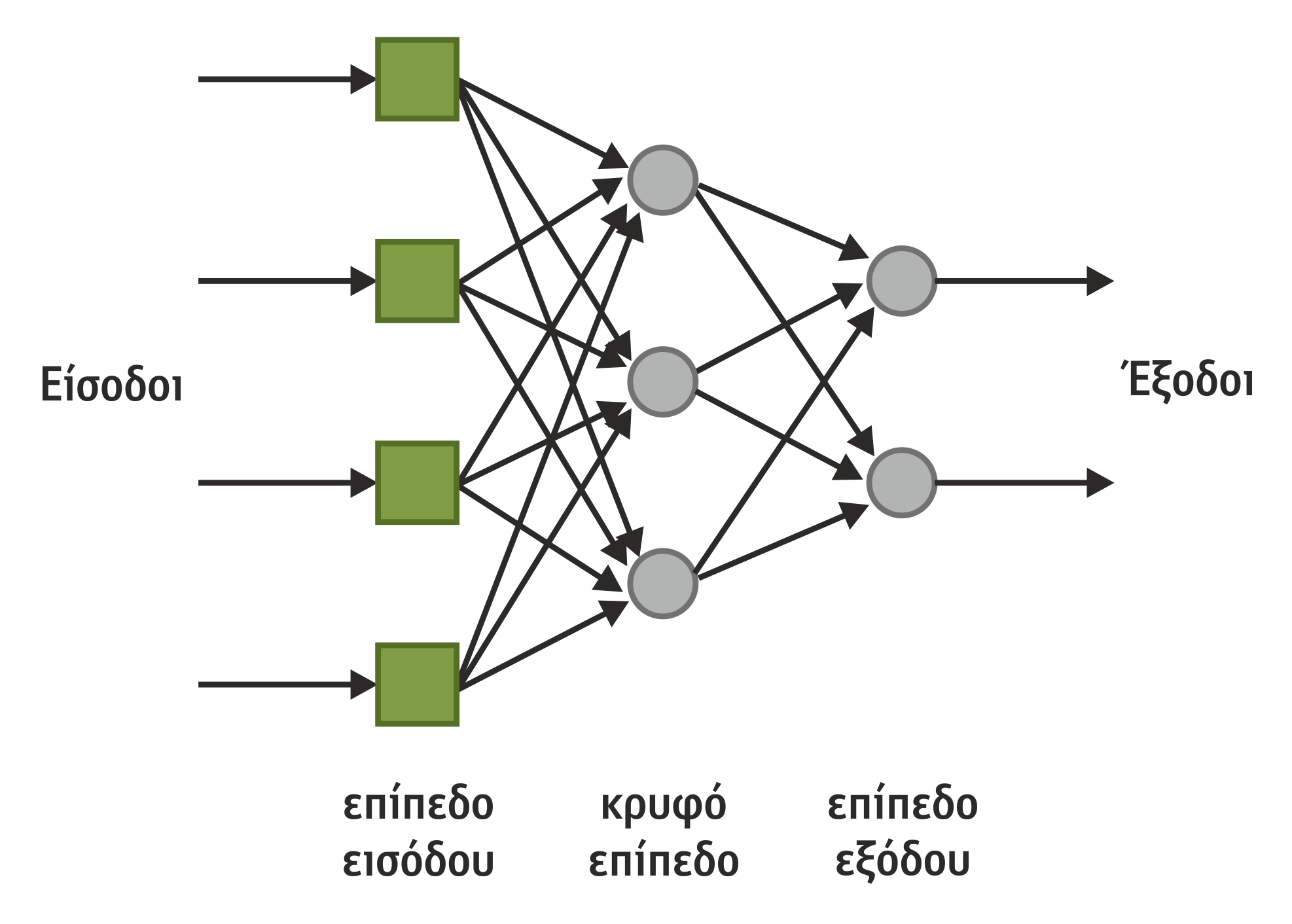
Σχήμα 4.19 Παράδειγμα ΤΝΔ πρόσθιας τροφοδότησης

Στα οπισθίως τροφοδοτούμενα δίκτυα, που καλούνται και ανατροφοδοτούμενα ΤΝΔ (recurrent ANN), επιτρέπεται στις μονάδες ενός επιπέδου να τροφοδοτούν και μονάδες του ιδίου επιπέδου ή και προηγούμενων επιπέδων. Αν η ανατροφοδότηση αφορά κόμβους στο ίδιο επίπεδο, τότε τα δίκτυα καλούνται αυτοσυσχετιζόμενες μνήμες (autoassociated memories) διαφορετικά, καλούνται ετεροσυσχετιζόμενες μνήμες (heteroassociated memories) (βλέπε Σχήμα 4.20) .

Σχήμα 4.20 Παράδειγμα ανατροφοδοτούμενων ΤΝΔ

Στα ανατροφοδοτούμενα ΤΝΔ δεν υπάρχουν συνήθως άνω του ενός ενδιάμεσα (κρυφά) επίπεδα. Αν και τα ανατροφοδοτούμενα δίκτυα είναι πολύ χρήσιμα, τα περισσότερα των νευρωνικών δικτύων είναι πρόσθιας τροφοδότησης.

Πολυεπίπεδα ΤΝΔ

Κοινό χαρακτηριστικό της δομής των πολυεπίπεδων ΤΝΔ είναι ότι διαθέτουν τουλάχιστον ένα κρυφό επίπεδο. Οι κόμβοι των διάφορων επιπέδων μπορεί να είναι πλήρως συνδεδεμένοι (fully connected), δηλαδή κάθε κόμβος του ενός επιπέδου συνδέεται με όλους τους κόμβους του επόμενου, όπως στο σχήμα 4.19, ή μερικώς συνδεδεμένοι (partially connected), όπως στο σχήμα 4.21.

Τα ΤΝΔ χαρακτηρίζονται, επιπλέον, με βάση τον τρόπο με τον οποίο είναι συνδεδεμένοι οι κόμβοι τους, όπως αναφέραμε στην προηγούμενη παράγραφο περί Αρχιτεκτονικής ΤΝΔ, δηλαδή αν είναι πρόσθιας τροφοδότησης (feed forward) ή οπίσθιας τροφοδότησης (feed backward ή recurrent).

Στην πλειοψηφία των εφαρμογών χρησιμοποιούνται δίκτυα πρόσθιας τροφοδότησης ενός κρυφού επιπέδου με πλήρως συνδεδεμένους κόμβους.

Σχήμα 4.21 Πολυεπίπεδο ΤΝΔ ενός κρυφού επιπέδου πρόσθιας τροφοδότησης 2 κρυμμένων επιπέδων με πλήρως συνδεδεμένους κόμβους

Συναρτήσεις μετάβασης

Όσον αφορά τις συναρτήσεις μετάβασης (transfer functions) οι πιο απλές είναι οι γραμμικές (βλέπε Σχήμα 4.22), όπως οι παρακάτω:

• βηματικές συναρτήσεις ή συναρτήσεις κατωφλίου (threshold functions),
• συναρτήσεις προσήμου (sign functions),
• συναρτήσεις βηματικής μεταβολής (hard limiter functions),
• συναρτήσεις αναρρίχησης (ramping functions).

  κ.ά.

Σχήμα 4.22 Γραμμικές συναρτήσεις μετάβασης

Ένα γνωστό ΤΝΔ που χρησιμοποιεί τη δυαδική γραμμική συνάρτηση είναι ο Perceptron (βλέπε Σχήμα 4.18). Συνηθέστερα, όμως, χρησιμοποιούνται μη γραμμικές συναρτήσεις, όπως οι σιγμοειδείς συναρτήσεις (sigmoid functions) και οι Γκαουσιανές συναρτήσεις (Gaussian functions) (βλέπε Σχήμα 4.23).

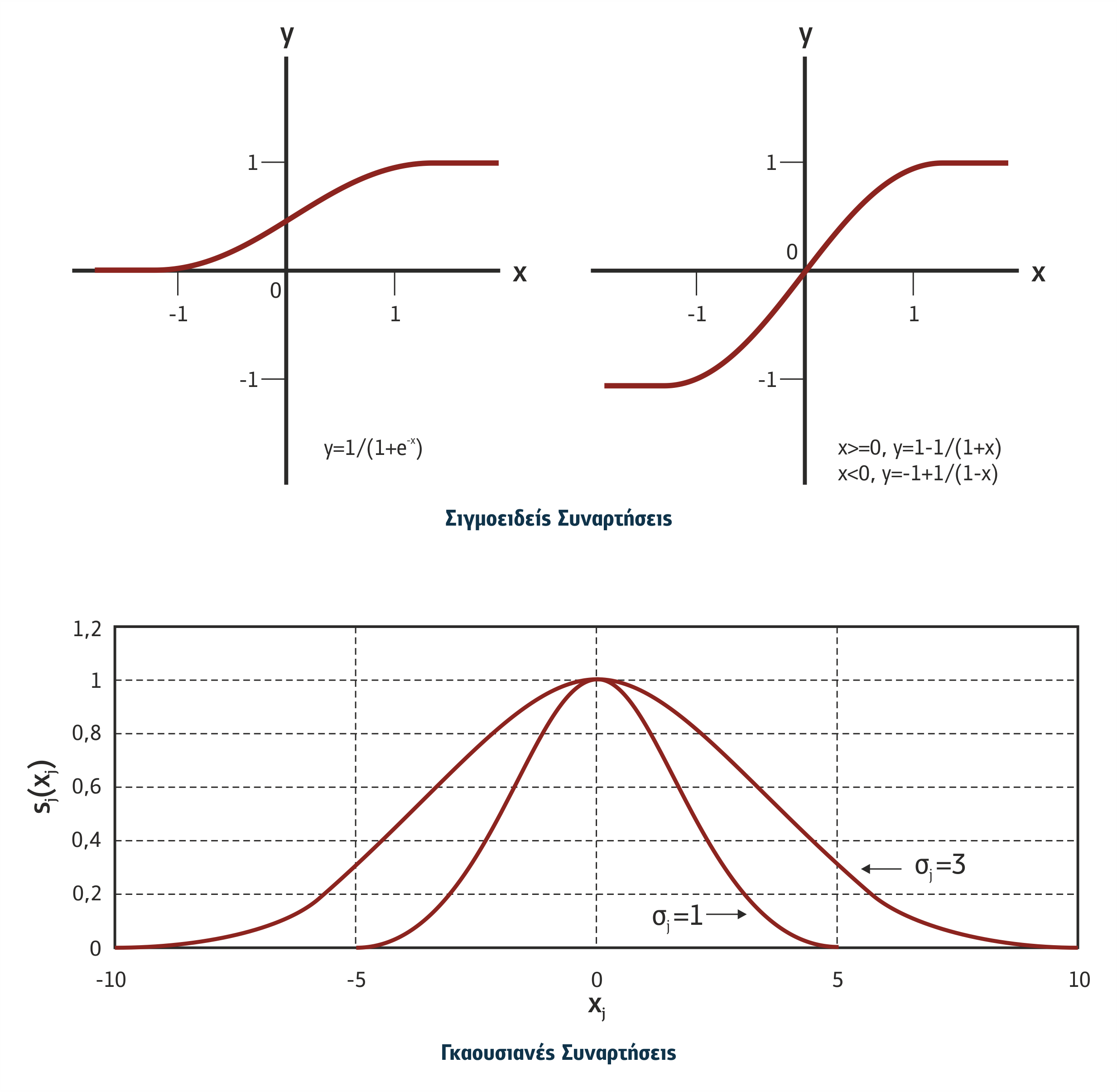
Σχήμα 4.23 Σιγμοειδείς και Γκαουσιανές συναρτήσεις μετάβασης

Στη Γκαουσιανή συνάρτηση που παρουσιάζεται στο σχήμα 4.23, σj είναι ο συντελεστής Γκαουσιανής διασποράς και cj είναι το κέντρο που στην περίπτωση του σχήματος 4.23 είναι το 0, το δε αποτέλεσμα της υπολογίζεται ως εξής:

4.5.5 ΤΝΔ Πρόσθιας Τροφοδότησης

Perceptrons

Αν και ο όρος Perceptron (Rosenblatt, 1962) χρησιμοποιήθηκε αρχικά για το στοιχειώδες ΤΝΔ πολλών εισόδων και μόνο μιας εξόδου, όπως αυτό του σχήματος 4.18, έχει επικρατήσει να χαρακτηρίζονται ως Perceptrons όλα τα ΤΝΔ πρόσθιας τροφοδότησης που δεν περιέχουν στην αρχιτεκτονική τους κρυφά επίπεδα. Αν διαθέτουν την κατάλληλη δομή, οι Perceptrons είναι ικανοί να επιλύουν οποιαδήποτε γραμμική συνάρτηση, όπως την κλασική συνάρτηση με διαχωρίσιμες τιμές ‘or’ (βλέπε Σχήμα 4.24 αριστερά).

Σχήμα 4.24 Διαχωρισμός τιμών συναρτήσεων

Στο σχήμα 4.25 παρουσιάζεται ένας Perceptron που επιλύει την or περιέχει. Ο Perceptron περιέχει στη δομή του δύο κόμβους εισόδου και διαθέτει έναν κόμβο εξόδου. Ως είσοδοι γίνονται δεκτές οι τιμές 0 και 1 και ως έξοδοι προκύπτει η τιμή 0 ή 1 σύμφωνα με τον πίνακα αληθείας.

Σχήμα 4.25 O Perceptron που επιλύει τη γραμμικά διαχωρίσιμη συνάρτηση or

Δείτε κινούμενη εικόνα 4.3 - Λειτουργία ΤΝΔ για την or

 

Το ότι οι Perceptrons δεν μπορούν να επιλύσουν προβλήματα με μη γραμμικά διαχωρίσιμες τιμές εξόδου, όπως η περίπτωση του xor (βλέπε Σχήμα 4.24 δεξιά), οδήγησε στην ανάγκη προσθήκης κρυφών επιπέδων στη δομή των Perceptrons και στη δημιουργία πολυεπίπεδων ΤΝΔ.

Παράδειγμα λειτουργίας πολυεπίπεδου ΤΝΔ για το xor

Κάποια από τα απλούστερα πολυεπίπεδα ΤΝΔ ενός κρυφού επιπέδου με πρόσθια τροφοδότηση και πλήρως συνδεδεμένους κόμβους είναι αυτά που προσομοιώνουν τη λειτουργία της μη γραμμικά διαχωρίσιμης συνάρτησης xor (βλέπε Σχήμα 4.24), όπως αυτό του σχήματος 4.26, που έχει προκύψει μετά από εκπαίδευση ενός ΤΝΔ πρόσθιας τροφοδότησης με πλήρως συνδεδεμένους κόμβους. Μέσα στους κόμβους φαίνονται οι τιμές κατωφλίου, ενώ στις ακμές τα βάρη. Ως συνάρτηση μετάβασης εφαρμόζεται η απλή βηματική. Ως είσοδοι γίνονται δεκτές οι τιμές 0 και 1 και η τιμή εξόδου είναι 0 ή 1 σύμφωνα με τον πίνακα αληθείας.

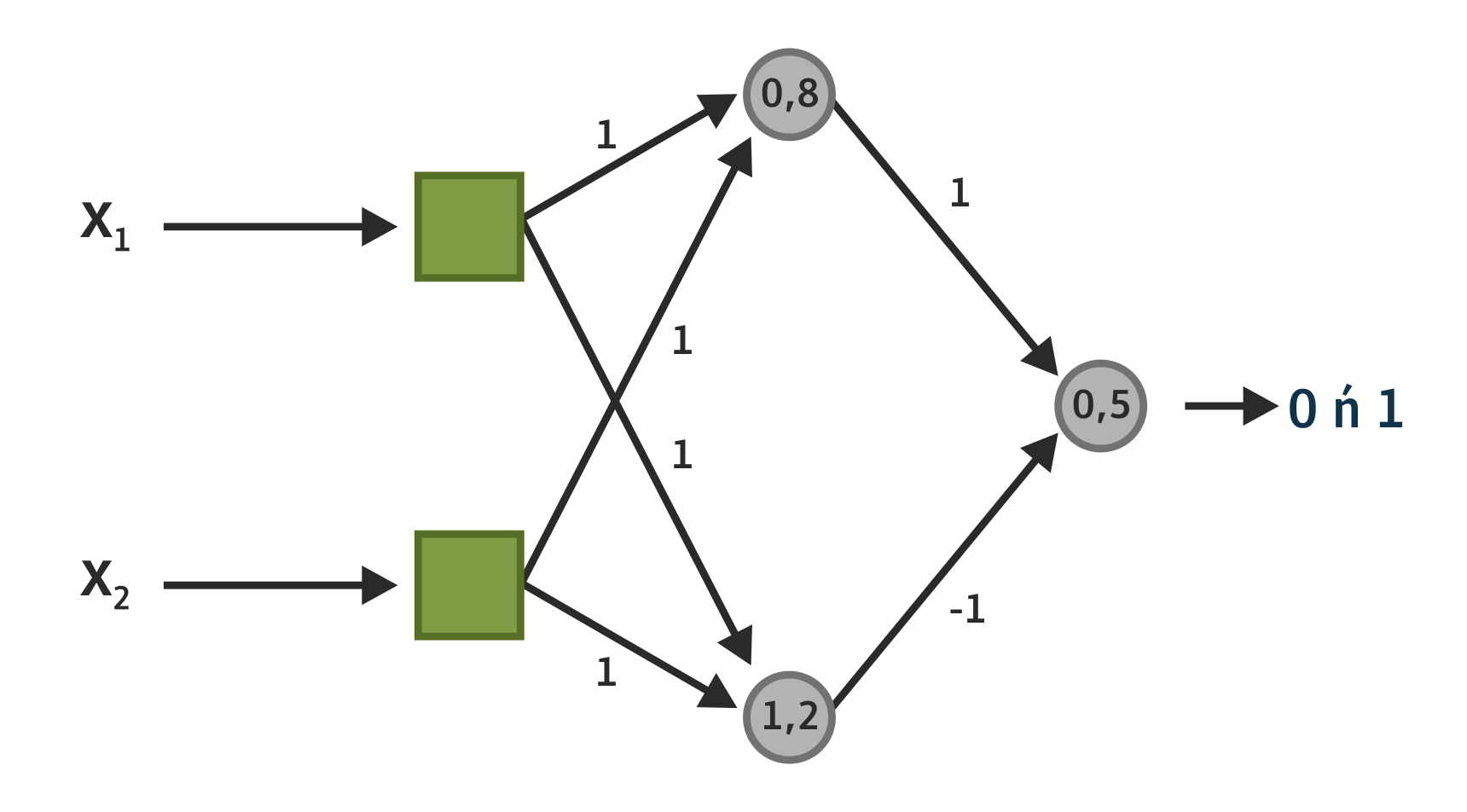
Σχήμα 4.26 Πολυεπίπεδο ΤΝΔ για το xor

Δείτε κινούμενη εικόνα 4.4 - Λειτουργία ΤΝΔ για την xor

Στάδια ολοκλήρωσης ΤΝΔ

Αφού καθοριστεί η αρχιτεκτονική ενός ΤΝΔ, όσον αφορά τον τύπο τροφοδότησης και την εσωτερική του δομή, ακολουθούν δυο στάδια κρίσιμα για την ολοκλήρωσή του: εκπαίδευση (training) και ανάκληση (recall) (βλέπε Σχήμα 4.27).

Κατά το στάδιο της εκπαίδευσης, τα συνδεσμικά βάρη του δικτύου «μαθαίνουν» προσαρμόζοντας τα βάρη τους.

Μετά την εκπαίδευση, ακολουθεί η φάση της ανάκλησης (δηλαδή του ελέγχου του δικτύου) με τη βοήθεια ενός νέου συνόλου δειγμάτων τα οποία δεν είχαν πάρει μέρος στη διαδικασία εκπαίδευσης.

Σχήμα 4.27 Στάδια ολοκλήρωσης ΤΝΔ

4.5.6 Εκπαίδευση ΤΝΔ

Ακριβώς για τη δυνατότητα που έχουν να μαθαίνουν μετά από εκπαίδευση, τα ΤΝΔ είναι τόσο δημοφιλή μέσα στο χώρο των συστημάτων Μηχανικής Μάθησης. Η εκπαίδευσή τους γίνεται βάσει αλγορίθμων που μπορεί να υιοθετούν μοντέλα μάθησης με επίβλεψη, χωρίς επίβλεψη ή ενισχυτικής μάθησης (βλέπε παράγραφο 4.2).

• Εκπαίδευση με επίβλεψη, όπου το νευρωνικό δίκτυο μαθαίνει να απεικονίζει δεδομένες εισόδους σε εξόδους εκ των προτέρων γνωστές (σύνολο εκπαίδευσης), με απώτερο στόχο τη γενίκευση της αναγνώρισης αυτής και για παρεμφερείς εισόδους στο μέλλον.
• Εκπαίδευση χωρίς επίβλεψη, όπου το νευρωνικό δίκτυο κατασκευάζει απεικονίσεις από μια αναπαράσταση σε μια άλλη.
• Ενισχυτική Εκπαίδευση, όπου ο αλγόριθμος μαθαίνει μια στρατηγική ενεργειών για δεδομένου τύπου παρατηρήσεις.

Η εκπαίδευση έχει ως βασικό στόχο να βρεθεί ένας τρόπος αλλαγής των συνδεσμικών βαρών που θα έχει ως αποτέλεσμα την αλλαγή της γενικής συμπεριφοράς του δικτύου με την αύξηση της ικανότητας του δικτύου να παρέχει στο μέλλον μία επιθυμητή έξοδο μετά από μία δεδομένη είσοδο. Όταν η επιθυμητή έξοδος είναι εκ των προτέρων γνωστή λέμε ότι το δίκτυο μαθαίνει με επίβλεψη (supervised learning), αλλιώς μαθαίνει χωρίς επίβλεψη (unsupervised learning). Τα ΤΝΔ με οπισθοδρόμηση ανήκουν στην πρώτη περίπτωση, ενώ στη δεύτερη ανήκει το δίκτυο Kohonen. Ο πίνακας 4.4 παρουσιάζει τα βασικότερα είδη δικτύων και τον τρόπο με τον οποίο μαθαίνουν.

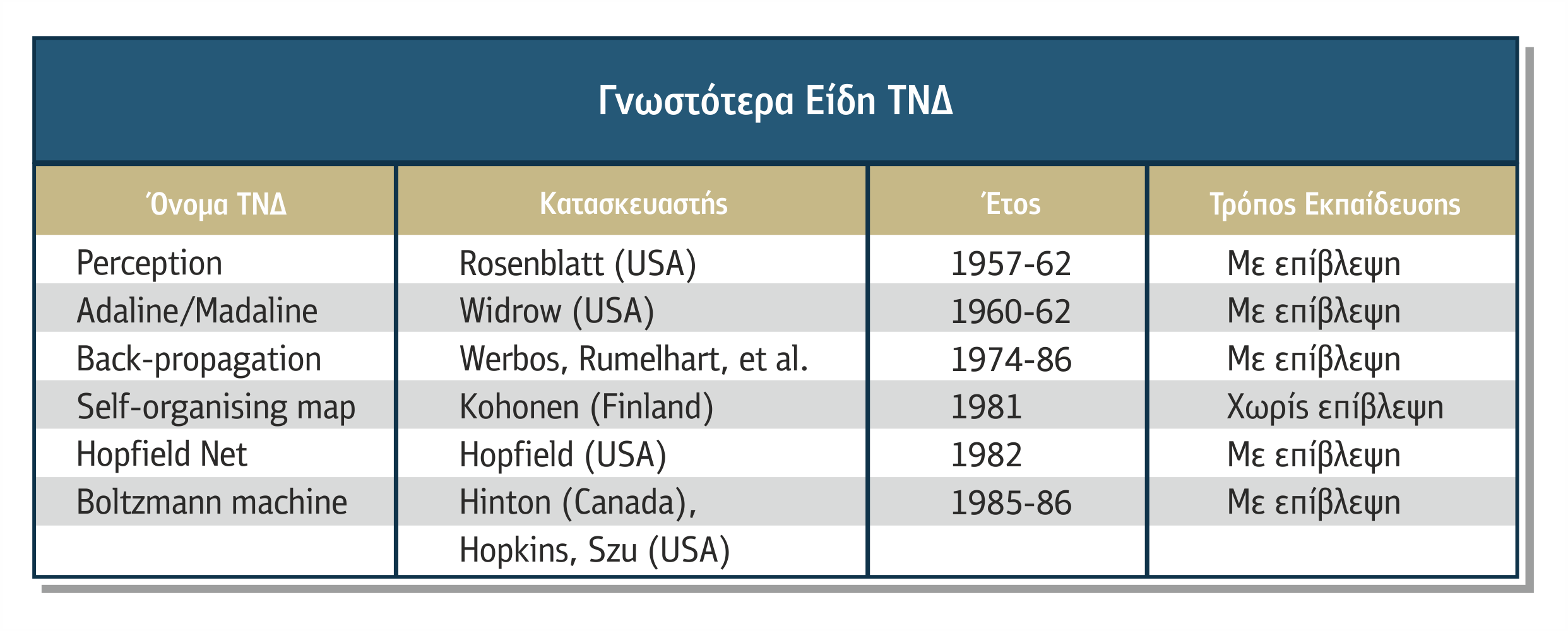
Πίνακας 4.4 Γνωστότερα είδη ΤΝΔ

Βασικό στοιχείο της αρχιτεκτονικής ενός ΤΝΔ είναι ο τρόπος ελέγχου της αλλαγής των βαρών κατά την εκπαίδευση, δηλαδή ο αλγόριθμος εκπαίδευσης (training algorithm) που υλοποιείται αποκλειστικά από το ίδιο το δίκτυο χωρίς εξωτερική επέμβαση. Γνωστότεροι αλγόριθμοι εκπαίδευσης είναι οι ακόλουθοι:

• Αλγόριθμος οπισθοδιάδοσης λάθους (backpropagation),
• Ανταγωνιστική μάθηση (competitive learning),
• Τυχαία μάθηση (random learning).

Κάθε αλγόριθμος εκπαίδευσης χρησιμοποιεί κάποιον κανόνα εκμάθησης, για να προσαρμόσει τα συνδεσμικά βάρη μεταξύ των νευρώνων του. Ο απλούστερος αλγόριθμος επιβλεπόμενης εκπαίδευσης είναι αυτός του στοιχειώδους perceptron, ο οποίος μπορεί να εφαρμοστεί και σε οποιονδήποτε απλό νευρώνα ενός ΤΝΔ.

Εκπαίδευση Perceptron

Η βασική ιδέα της εκπαίδευσης ενός Perceptron που γίνεται πάντα κάτω από επίβλεψη είναι να γίνει χρήση ενός συνόλου εκπαίδευσης (training set), όπου για κάθε ζεύγος (x, f(x)) ο αλγόριθμος εκπαίδευσης πραγματοποιεί τα ακόλουθα βήματα:

• Ελέγχει εάν η y που δίνει ο νευρώνας για το δείγμα x είναι η αναμενόμενη.  

• Εάν είναι, η διαδικασία εκπαίδευσης προχωρά στο επόμενο δείγμα.
• Εάν όχι, τότε:
  • εάν η σωστή έξοδος είναι μεγαλύτερη από αυτήν που υπολόγισε ο νευρώνας, ο κανόνας εκμάθησης αυξάνει τα βάρη των εισόδων που είναι θετικές και μειώνει τα βάρη των εισόδων που είναι αρνητικές.
  • εάν η σωστή έξοδος είναι μικρότερη από αυτήν που υπολόγισε ο νευρώνας, ο κανόνας εκμάθησης μειώνει τα βάρη των εισόδων που είναι θετικές και αυξάνει τα βάρη των εισόδων που είναι αρνητικές.

• Η διαδικασία αυτή εκτελείται, μέχρις ότου ο νευρώνας να απαντά σωστά σε όλα τα δείγματα ή να μη βελτιώνει πλέον σημαντικά την απόδοσή του.

Αλγόριθμος Εκπαίδευσης Perceptron με δυο κλάσεις ταξινόμησης, Α και Β

 

Βήμα1: Αρχικοποίηση

Θέσε w(0)=0.

 

Βήμα 2: Ενεργοποίηση

Στο χρόνο n, ενεργοποίησε τον Perceptron εφαρμόζοντας το συνεχές διάνυσμα εισόδου x(n) και το d(n).

 

Βήμα 3: Υπολογισμός πραγματικής απόκρισης

Υπολόγισε την πραγματική απόκριση του Perceptron:

Βήμα 4: Προσαρμογή διανύσματος βαρών

Προσάρμοσε τα βάρη του Perceptron.

Όπου:

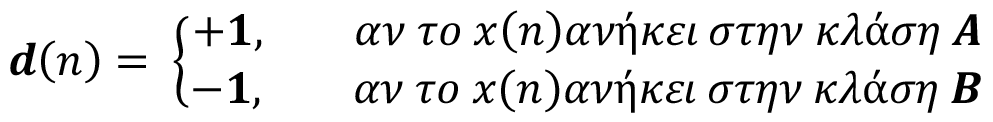
Βήμα 5: Αύξησε το χρόνο κατά μια μονάδα και πήγαινε στο βήμα 2.

Κάθε μονάδα μέσα σε ένα ΤΝΔ είναι ανεξάρτητη από τις υπόλοιπες και ομοίως είναι και η εκπαίδευσή της. Άρα, στα δίκτυα που μαθαίνουν υπό επίβλεψη κάθε μονάδα μπορεί να θεωρηθεί ως ένας στοιχειώδης Perceptron και να ακολουθήσει την περιγραφείσα διαδικασία εκπαίδευσης.

Κανόνες Εκμάθησης

Οι αλγόριθμοι εκπαίδευσης χαρακτηρίζονται από τους κανόνες εκμάθησης (learning rules) που χρησιμοποιούνται, για να υπολογίσουν τα σφάλματα και να διορθώσουν τα συνδεσμικά βάρη των εσωτερικών νευρώνων του δικτύου. Ένας από τους γνωστότερους κανόνες μάθησης που χρησιμοποιείται για εκπαίδευση είναι ο κανόνας Δέλτα (Delta rule), που χρησιμοποιεί τη βηματική συνάρτηση ενεργοποίησης και υπολογίζει τη μεταβολή βάρους ως ακολούθως:

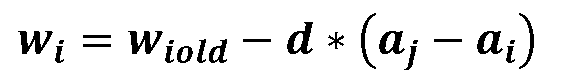
όπου:

• ai: η τρέχουσα έξοδος του νευρώνα i,
• aj: η επιθυμητή έξοδος του νευρώνα i για το τρέχον δείγμα,
• d: ο ρυθμός εκμάθησης (d>0) ,
• wi: το νέο βάρος εισόδου από τον νευρώνα i,
• wiold: το παλιό βάρος εισόδου από τον νευρώνα i.

Ο ρυθμός εκμάθησης d καθορίζει το πόσο γρήγορα συγκλίνει η μάθηση. Μεγάλος ρυθμός μάθησης μπορεί να οδηγήσει σε γρηγορότερη σύγκλιση και σε ταλάντωση γύρω από τις βέλτιστες τιμών βαρών. Μικρός ρυθμός μάθησης έχει ως αποτέλεσμα πιο αργή σύγκλιση, ενώ μπορεί να οδηγήσει σε παγίδευση σε τοπικά ακρότατα.

Άλλος Κανόνας Εκμάθησης είναι ο Κανόνας του Ηebb (Hebbian rule):

όπου

• Irate : σταθερά που καθορίζει το ρυθμό εκμάθησης,
• au, ai : τιμές ενεργοποίησης στις μονάδες u και i.

Εάν au.ai>0 (και οι δυο + ή -), τότε οι συνδέσεις μεταξύ τους ενισχύονται αναλογικά με το αποτέλεσμα των δυο ενεργοποιήσεων. Αλλιώς, μειώνονται αναλογικά.

Σφάλματα

Ως σφάλμα μιας εξόδου o ενός νευρώνα k από μια επιθυμητή του έξοδο α, αναφορικά με ένα δείγμα p, ορίζεται η ποσότητα:

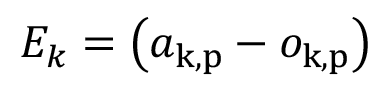
Το συνολικό σφάλμα για όλα τα παραδείγματα εκπαίδευσης για το νευρώνα k είναι το μέσο τετραγωνικό σφάλμα:

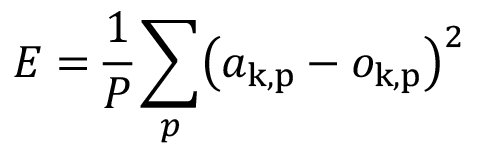
Με παρόμοιο τρόπο μπορούμε να ορίσουμε το μέσο τετραγωνικό σφάλμα για όλους τους νευρώνες εξόδου k και όλα τα παραδείγματα p:

Ο τερματισμός της διαδικασίας εκπαίδευσης πραγματοποιείται, όταν το συνολικό σφάλμα Ε για όλα τα παραδείγματα και για όλους τους νευρώνες εξόδου πέσει κάτω από μια μικρή τιμή.

Εκπαίδευση ΤΝΔ με τη μέθοδο οπισθοδιάδοσης σφάλματος

Στα πολυεπίπεδα ΤΝΔ, ο συνηθέστερος τρόπος επιβλεπόμενης μάθησης είναι η μάθηση με οπισθοδιάδοση σφάλματος (error back-propagation). Τα πολυεπίπεδα ΤΝΔ στα οποία ακολουθείται αυτή η μέθοδος εκπαίδευσης, καλούνται Backpropagation ΤΝΔ (Backpropagation ANN).

Κατά την εκπαίδευση των Backpropagation ΤΝΔ, για κάθε είσοδο που δίνεται στο δίκτυο υπολογίζονται οι έξοδοι με εφαρμογή των συναρτήσεων μετάβασης σε κάθε μονάδα κρυφού ή εξωτερικού επιπέδου (βλέπε Σχήμα 4.28). Για κάθε μονάδα εξωτερικού επιπέδου λαμβάνονται υπόψη οι διαφορές μεταξύ του υπολογιζόμενου και του επιθυμητού αποτελέσματος και διαδίδονται προς τα πίσω στις μονάδες του κρυφών επιπέδων, έτσι ώστε να καθορίσουν τις απαραίτητες αλλαγές στα βάρη σύνδεσης μεταξύ των μονάδων. Οι αλλαγές αυτές γίνονται βάσει του κανόνα εκμάθησης οπισθοδιάδοσης και ως σκοπό έχουν τη μείωση του εμφανιζόμενου στην έξοδο σφάλματος.

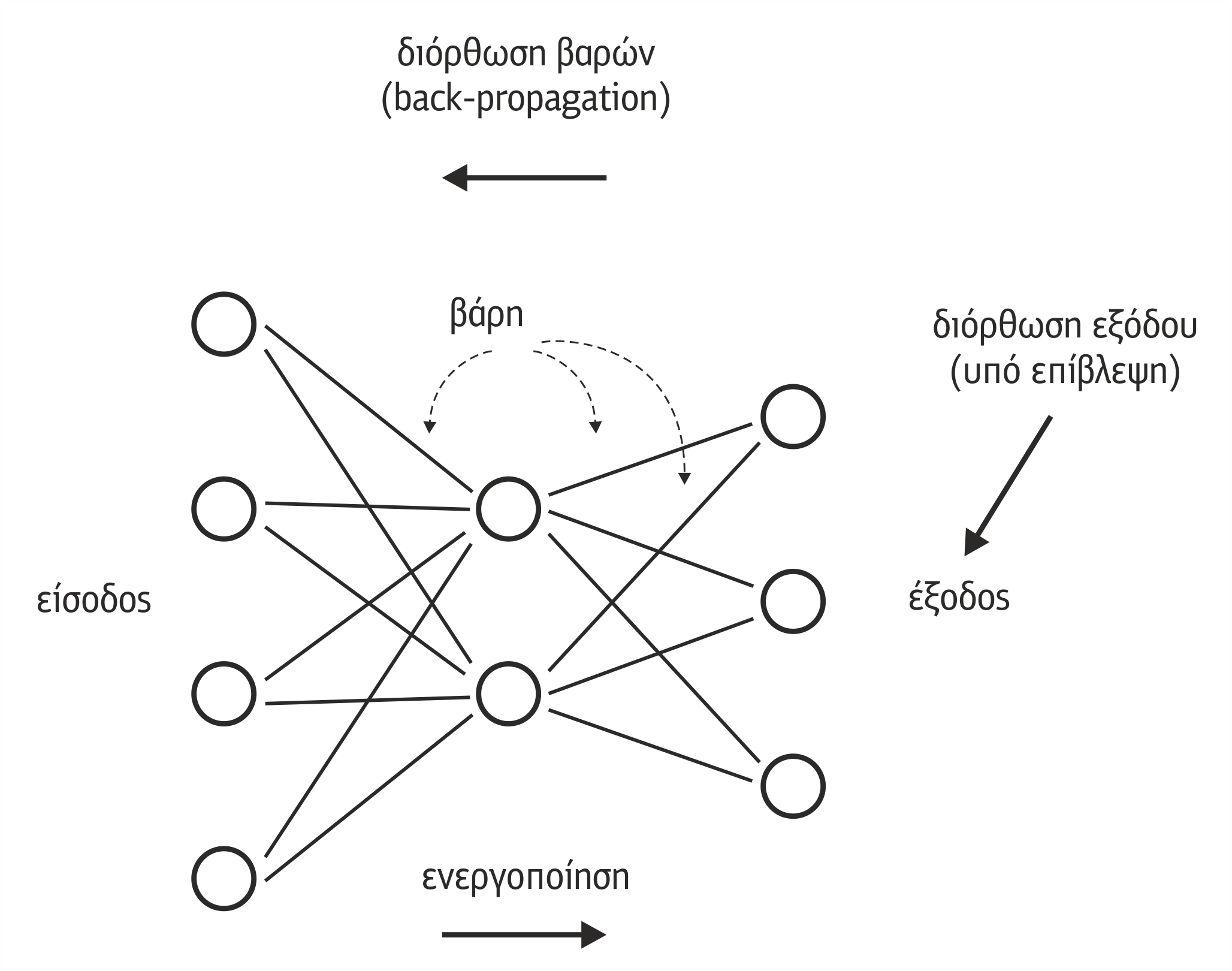
Σχήμα 4.28 Εκπαίδευση δικτύου με οπισθοδιάδοση

Η συμμετοχή μιας μονάδας στα σφάλματα των μονάδων του επόμενου επιπέδου της είναι ανάλογη της τρέχουσας εισόδου της και των συντελεστών βαρύτητας που τη συνδέουν με τις μονάδες του επόμενου επιπέδου. Το δίκτυο εν συνεχεία εφαρμόζει εκ νέου τις συναρτήσεις μετάβασης, για να υπολογίσει το νέο σφάλμα.

Το πραγματικό σφάλμα Εk μιας μονάδας εξόδου k ενός παραδείγματος p υπολογίζεται καταρχάς όπως και στον Perceptron, δηλαδή:

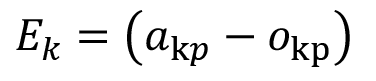
Στη συνέχεια πολλαπλασιάζεται επί την παράγωγο της συνάρτησης ενεργοποίησης στη μονάδα k (uk), σύμφωνα με τον γενικευμένο κανόνα δέλτα, για να υπολογιστεί το λεγόμενο προσαρμοσμένο σφάλμα νευρώνα:

To αντίστοιχο σφάλμα σε μια μονάδα κρυφού επιπέδου i υπολογίζεται από τα προσαρμοσμένα σφάλματα στις k μονάδες του επόμενου επιπέδου με τις οποίες η μονάδα συνδέεται με βάρη wik, ως εξής:

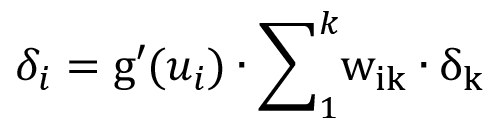
Η διαδικασία της εκπαίδευσης περιλαμβάνει πλήθος τέτοιων κύκλων διόρθωσης σφάλματος και λήγει με τη μείωση του σφάλματος κάτω από ένα επιθυμητό όριο. Εναλλακτικά, ως συνθήκη τερματισμού μπορεί να θεωρηθεί η πραγματοποίηση ενός συγκεκριμένου αριθμού κύκλων εκπαίδευσης ή η πάροδος ενός συγκεκριμένου χρονικού διαστήματος.

Αλλαγές στα βάρη

Αφού έχει υπολογισθεί για κάθε μονάδα i το σφάλμα δi, η αλλαγή στα βάρη εισόδου σε όλους τους νευρώνες γίνεται ως εξής:

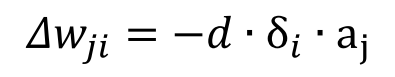
Δηλαδή, η αλλαγή στο βάρος από τον νευρώνα i στον νευρώνα j εξαρτάται από το σφάλμα του νευρώνα i, την έξοδο του νευρώνα j και τo ρυθμό μάθησης (learning rate) d.

 

Υπάρχουν 2 τρόποι αλλαγής των βαρών κατά την παρουσίαση των παραδειγμάτων εκπαίδευσης:

• Αυξητική εκπαίδευση (incremental training), όπου για κάθε δείγμα που παρουσιάζεται γίνονται άμεσα οι αλλαγές των βαρών
• Μαζική εκπαίδευση (batch training), όπου πρώτα παρουσιάζονται όλα τα παραδείγματα μια φορά, υπολογίζονται μόνο οι αλλαγές των βαρών για κάθε δείγμα και εφαρμόζονται ταυτόχρονα αφού παρουσιαστούν όλα τα παραδείγματα.

Η παρουσίαση όλων των παραδειγμάτων μια φορά (ανεξαρτήτως του τρόπου αλλαγής των βαρών) αντιστοιχεί σε έναν κύκλο εκπαίδευσης και ονομάζεται εποχή εκπαίδευσης (training epoch).

Μη Επιβλεπόμενη Μάθηση ΤΝΔ – Δίκτυα Kohonen

Αυτό το μοντέλο των δικτύων προτάθηκε το 1984 από τον Kοhonen και αφορά δίκτυα που ακολουθούν διαδικασία εκπαίδευσης χωρίς επίβλεψη δεν υπάρχει καμία εξωτερική επέμβαση ως προς το τι πρέπει να εκπαιδευθεί ένα δίκτυο να αναγνωρίζει. Το χαρακτηριστικό του προτύπου αυτού είναι ότι μπορεί να ταξινομεί διανύσματα με τη βοήθεια ενός αλγόριθμου μη επιβλεπόμενης μάθησης.

Το δίκτυο Kοhonen οργανώνει τον πίνακα των βαρών του με τέτοιον τρόπο, ώστε αναγνωρίζει όποια κανονικότητα υπάρχει στα διανύσματα εισόδου. Στο σημείο αυτό προσομοιώνει μία σημαντική αρχή της οργάνωσης των αισθητηρίων οργάνων του εγκεφάλου: η κατανομή των νευρώνων παρουσιάζει κανονικότητα που αντικατοπτρίζει κάποια ειδικά χαρακτηριστικά των εξωτερικών ερεθισμάτων που διαδίδονται σε αυτά.

Κάθε δίκτυο Kοhonen αποτελείται από δύο επίπεδα: το 1ο είναι το επίπεδο εισόδου και το 2ο καλείται επίπεδο Kοhonen (Kοhonen layer), με ιδιαίτερο χαρακτηριστικό ότι είναι οργανωμένο σε μορφή πλέγματος, το οποίο μπορεί να έχει οποιαδήποτε διάσταση: για παράδειγμα, μπορεί να έχουμε ένα δισδιάστατο πλέγμα, δηλαδή μία επιφάνεια που έχει επάνω της n x m μονάδες που αντιστοιχούν στους νευρώνες. Τα δύο αυτά επίπεδα έχουν πλήρη συνδεσμολογία, δηλαδή κάθε μονάδα εισόδου συνδέεται με όλες τις μονάδες του επιπέδου Kohonen. Αν το επίπεδο εισόδου αντιστοιχεί σε ένα διάνυσμα με k στοιχεία εισόδου, τελικά θα έχουμε k x n x m συνδέσεις. Το σχήμα 4.29 δείχνει την τυπική δομή ενός τέτοιου δικτύου.

Η εκπαίδευση ενός δικτύου Kohonen περιλαμβάνει την παρουσίαση στο δίκτυο ενός μοντέλου (pattern) και τελικώς την εύρεση στο επίπεδο Kohonen εκείνων των μονάδων για τις οποίες ισχύει ότι το άθροισμα των τιμών ενεργοποίησης που καταλήγουν σε αυτές έχουν τις υψηλότερες τιμές (δηλαδή μια μονάδα ξεχωρίζει από τις υπόλοιπες σε σχέση με τη συνολική ενέργεια που δέχεται). Τα βάρη της μονάδας που «κέρδισε» και όλων των μονάδων που αποτελούν τη γειτονιά ή συστάδα (cluster) ρυθμίζονται βάσει του νόμου εκμάθησης. Στην αρχή της περιόδου εκπαίδευσης, η γειτονιά είναι ένα μεγάλο μέρος του επιπέδου Kohonen, μέσα σε μια προκαθορισμένη ακτίνα από τη μονάδα που κερδίζει. Όμως, η ακτίνα αυτή μειώνεται προοδευτικά όσο προχωράει η εκπαίδευση. Η προσαρμογή των βαρών γίνεται με τέτοιον τρόπο, ώστε μετά την εκπαίδευση το δίκτυο να είναι σε θέση να διεγείρει την ίδια πάντα μονάδα εξόδου για διανύσματα εισόδου που ανήκουν στην ίδια κατηγορία.

Επειδή η εκπαίδευση γίνεται αυτόνομα (χωρίς στόχους), δεν μπορούμε να γνωρίζουμε εκ των προτέρων σε ποια από τις τάξεις θα αντιστοιχεί η καθεμία από τις μονάδες εξόδου, με αποτέλεσμα η αντιστοίχιση να γίνεται μόνο μετά την εκπαίδευσή τους με το σχηματισμό γειτονιών συσχετισμένων με τις επιδιωκόμενες τάξεις. Ο κανόνας εκμάθησης μπορεί να διαφέρει από μονάδα σε μονάδα της γειτονιάς, αλλά συνήθως ακολουθεί τη γνωστή συνάρτηση του μεξικάνικου καπέλου (mexican hat function).

Λόγω του τρόπου εκπαίδευσής τους, τα δίκτυα Kohonen καλούνται και αυτο-οργανωνόμενοι χάρτες (self-organizing maps).

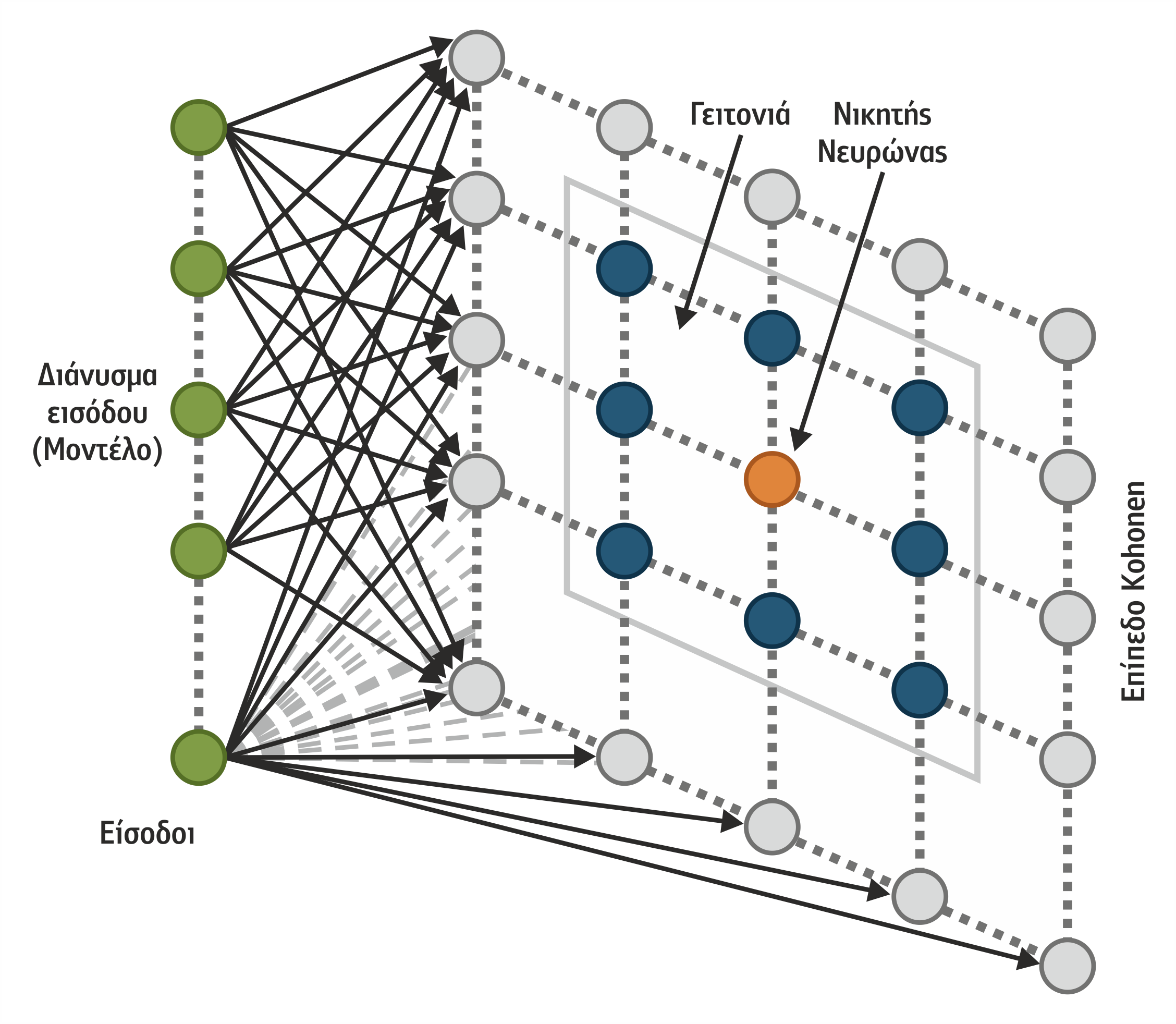
Σχήμα 4.29 Τυπικό δίκτυο Kohonen

Παράδειγμα εκπαίδευσης δικτύου Kohonen

Έστω το δίκτυο Kohonen του σχήματος 4.30 το οποίο θέλουμε να εκπαιδευτεί να αναγνωρίζει δυο τάξεις κατηγοριοποίησης, δηλαδή να «μάθει» 2 γειτονιές. Το επίπεδο εισόδου του δικτύου αποτελείται από 2 μονάδες, ενώ το επίπεδο Kohonen διαθέτει 9 νευρώνες.

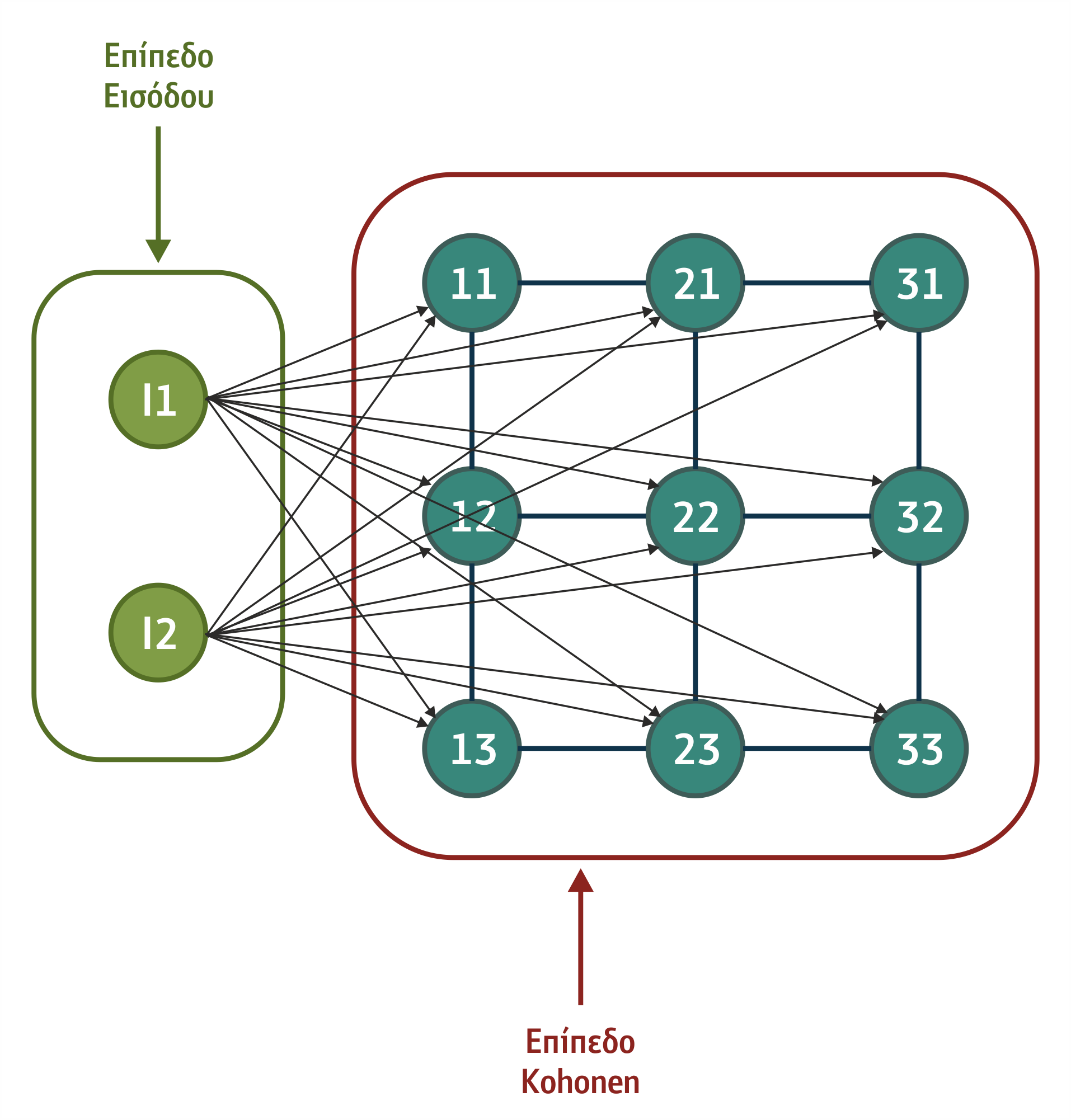
Σχήμα 4.30 Παράδειγμα δικτύου Kohonen

Η εκπαίδευση θα πραγματοποιηθεί σε 2 κύκλους εκπαίδευσης.

• 1ος : το δίκτυο θα μάθει να αναγνωρίζει την 1η τάξη διαχωρισμού
• 2ος : η εκπαίδευση θα επαναληφθεί για το ήδη εκπαιδευμένο δίκτυο, ώστε να μάθει και τη δεύτερη τάξη.

Στο παράδειγμά μας, κατά τον 1ο κύκλο το σύνολο εκπαίδευσης θα αποτελείται από δείγματα μοντέλων της 1ης τάξης διαχωρισμού. Στην αρχή, τα συνδεσμικά βάρη θα είναι τυχαία και, αφού υπολογιστεί η ενέργεια που δέχεται κάθε μονάδα του επιπέδου Kohonen, θα επιλεχθεί η νικήτρια μονάδα και η γειτονιά της. Στην περίπτωσή μας η νικήτρια μονάδα είναι η 11 και η γειτονιά της αποτελεί τις μονάδες 12 και 21. Οι 7 πιο αδύνατες μονάδες του επιπέδου θα εξαιρεθούν της διαδικασίας εκπαίδευσης και οι υπόλοιπες ως μια γειτονιά θα συμμετέχουν στη διαδικασία, ώστε να διαμορφωθούν τα τελικά βάρη τους (βλέπε Σχήμα 4.31). Στον 2ο κύκλο, θα διατηρηθούν τα βάρη της 1ης γειτονιάς και ο κύκλος θα επαναληφθεί με δείγματα μοντέλων που ανήκουν στη 2η τάξη διαχωρισμού.

Σχήμα 4.31 Γειτονιά μετά τον 1ο κύκλο εκπαίδευσης δικτύου Kohonen

Τα δίκτυα Kohonen έχουν μεγάλη εφαρμογή στην εξόρυξη δεδομένων (data mining) κυρίως μέσα από μεγάλες βάσεις δεδομένων στο διαδίκτυο.

Ανατροφοδοτούμενα ΤΝΔ - Δίκτυα Hopfield

Ένα δίκτυο Hopfield είναι μια μη-γραμμική συσχετιστική μνήμη (autoassociative memory) ή μνήμη διευθυνσιοδοτούμενη από τα περιεχόμενα. Η κύρια λειτουργία μιας τέτοιας μνήμης είναι η ανάκτηση ενός προτύπου, που έχει αποθηκευθεί σε αυτήν. Τα δίκτυα Hopfield ανήκουν στην κατηγορία των ανατροφοδοτούμενων (recurrent) ΤΝΔ.

Η δομή των δικτύων Hopfield έχει τα ακόλουθα χαρακτηριστικά:

• Υπάρχει μόνο ένα επίπεδο, αλλά με πολλές μονάδες (νευρώνες).
• Είναι δυαδικά συστήματα· κάθε μονάδα χαρακτηρίζεται από μία δυαδική κατάσταση, δηλαδή μπορεί να έχει μία από δύο δυνατές τιμές. Συνήθως οι τιμές αυτές είναι 0 και 1, αλλά αυτό δεν είναι απαραίτητο.
• Οι συνδέσεις μεταξύ των νευρώνων είναι πλήρεις, δηλαδή κάθε μονάδα συνδέεται με κάθε άλλη μονάδα στο δίκτυο.
• Όλοι οι νευρώνες λειτουργούν ταυτόχρονα ως είσοδοι και έξοδοι του δικτύου.

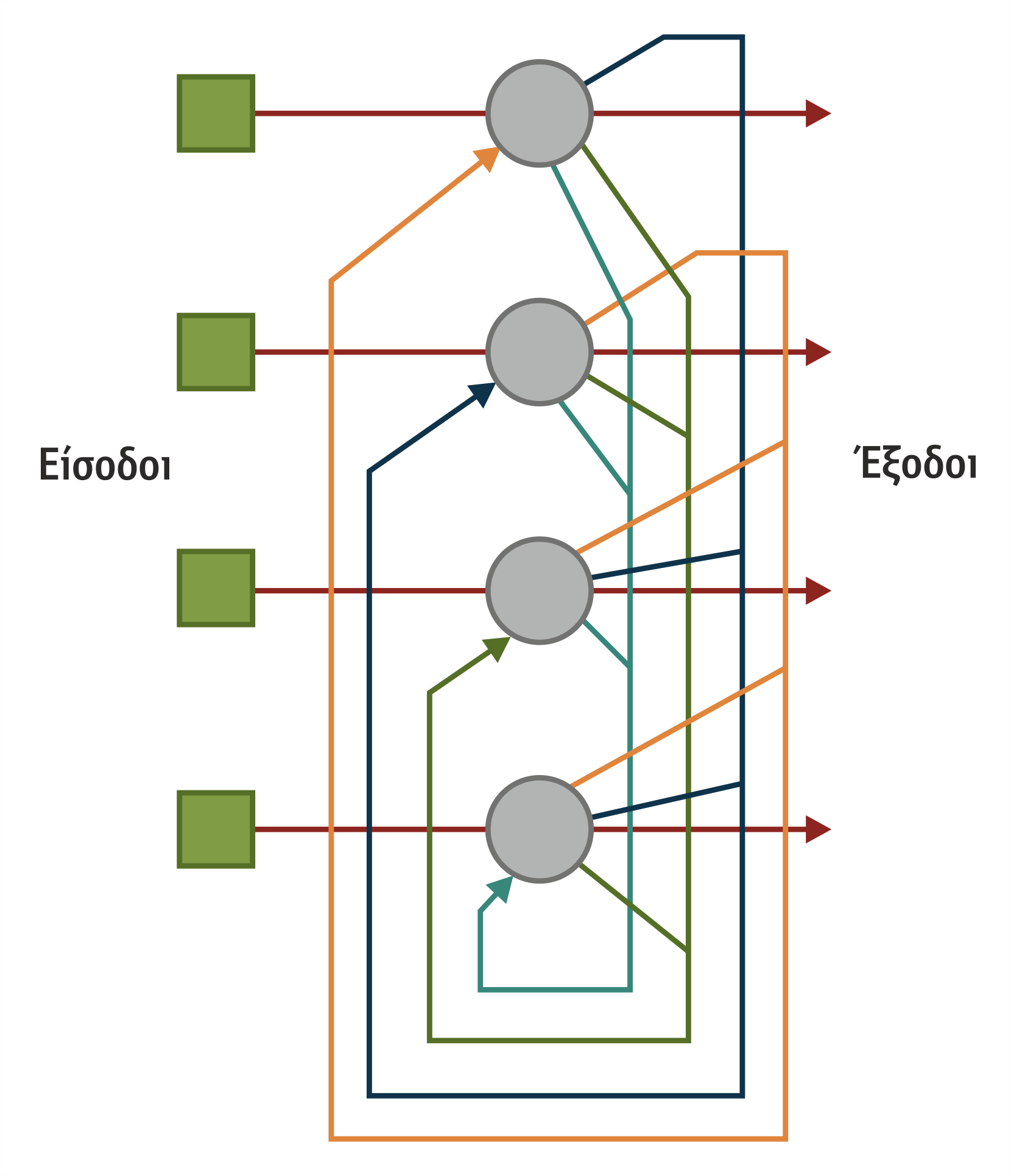
Σχήμα 4.32 Αρχιτεκτονική του Δικτύου Hopfield

Σε ένα δίκτυο Hopfield με n μονάδες και δομή όπως περιγράφηκε παραπάνω, θα έχουμε n x (n-1) συνδέσεις, διότι κάθε μονάδα συνδέεται με κάθε άλλη μονάδα, αλλά όχι με τον εαυτό της (βλέπε Σχήμα 4.32). Στη γενική περίπτωση, οι συνδέσεις έχουν και συγκεκριμένη κατεύθυνση. Έτσι, σε κάθε ζευγάρι μονάδων που συνδέονται υπάρχει σύνδεση και προς τις δύο κατευθύνσεις, δηλαδή μεταξύ των μονάδων i και j υπάρχουν η σύνδεση wij και η σύνδεση wji. Γενικά, στα δίκτυα Hopfield θα ισχύει πάντοτε ότι wij=wji, διότι τότε εξασφαλίζεται ότι το δίκτυο συγκλίνει και καταλήγει σε μία σταθερή κατάσταση.

Η μάθηση στα δίκτυα Hopfield είναι επιβλεπόμενη με συνάρτηση μετάβασης τη συνάρτηση προσήμου. Χαρακτηριστικό των δικτύων αυτών είναι ότι τα βάρη του δικτύου συνεχώς αναπροσαρμόζονται κατά τη φάση της εκπαίδευσης. Κατά την εκπαίδευση, η κατάσταση των μονάδων αλλάζει (από 0 σε 1 και αντίστροφα) ή παραμένει η ίδια. Η εκπαίδευση ολοκληρώνεται όταν δεν πραγματοποιούνται πλέον άλλες αλλαγές.

Τα δίκτυα Hopfield χρησιμοποιούνται σε προβλήματα βελτιστοποίησης.

4.5.7 Προτερήματα ΤΝΔ

Τα ΤΝΔ διαφέρουν αισθητά από άλλες τεχνικές υλοποίησης υπολογιστικών συστημάτων, που επιλύουν προβλήματα παρόμοια με αυτά που επιλύουν στα ΤΝΔ, στα παρακάτω:

• Δεν χρησιμοποιούν σύμβολα για αναπαράσταση εννοιών του μοντέλου.
• Δεν κάνουν (σαφή) προγραμματισμό της συμπεριφοράς του μοντέλου.
• Αυτοπρογραμματίζονται «μαθαίνοντας» να παράγουν συγκεκριμένες εξόδους, όταν δίνονται κάποιες είσοδοι.

Οι παραπάνω διαφορές χαρακτηρίζουν και τα προτερήματά τους που παραθέτονται στη συνέχεια:

 

Όσον αφορά το Σχεδιασμό:

• Ένα ΤΝΔ σχεδιάζεται σε αναλογία με τον ανθρώπινο εγκέφαλο. Οι μηχανικοί αντλούν από τη νευροβιολογία νέες ιδέες για την επίλυση πολύπλοκων προβλημάτων.
• Επίσης σχεδιάζεται για να παρέχει πληροφορίες όχι μόνο για το συγκεκριμένο σύνολο υποδειγμάτων με το οποίο εκπαιδεύεται αλλά και για όποιο καινούργιο υπόδειγμα παρουσιαστεί.
• Τα ΤΝΔ παρουσιάζουν ομοιομορφία ανάλυσης και σχεδιασμού, με την έννοια ότι ο ίδιος συμβολισμός χρησιμοποιείται σε όλα τα επιστημονικά πεδία που περιέχουν εφαρμογές των ΤΝΔ, επιτρέποντας λόγω αυτού τη διάχυση της σχετικής τεχνογνωσίας.

Όσον αφορά την Υλοποίηση:

• Ένα ΤΝΔ δομείται από τη σύνδεση νευρώνων, οι οποίοι θεωρούνται μη-γραμμικές συσκευές. Η μη-γραμμικότητα είναι πολύ σημαντική ιδιότητα, αν ο φυσικός μηχανισμός για την παραγωγή των σημάτων εισόδου είναι μη-γραμμικός.
• Η γνώση, κατά την είσοδο στο ΤΝΔ, αναπαρίσταται από μια διασκορπισμένη μορφή (ένα σύνολο από τιμές χαρακτηριστικών σε μορφή συμβολοσειράς) και όχι από μια τεχνικά κατασκευασμένη συμβολική μορφή (π.χ. δομημένη εγγραφή ενός αρχείου ή μιας βάσης δεδομένων).

Όσον αφορά τη Δομή:

• Τα ΤΝΔ έχουν τη δυνατότητα να προσαρμόζουν τα βάρη τους στις αλλαγές του περιβάλλοντός τους επαναλαμβάνοντας απλώς την εκπαίδευσή τους με νέο σύνολο παραδειγμάτων από το μεταβαλλόμενο περιβάλλον.
• Ένα ΤΝΔ υλοποιημένο σε υλικό (hardware) έχει τη σημαντική ιδιότητα να είναι «ανεκτικό σε σφάλματα». Για παράδειγμα, αν μια σύνδεση ενδιάμεσου επιπέδου διαγραφεί ή ένα βάρος αλλοιωθεί, η λειτουργία το δικτύου δε θα επηρεαστεί γιατί το συνολικό μέσο σφάλμα δε θα αλλάξει σημαντικά.
• Η δομή των ΤΝΔ σε επίπεδα τους δίνει δυνατότητες παράλληλων λειτουργιών και κάνει δυνατή την υλοποίησή τους σε VLSI (Very-Large-Scale Integration) τεχνολογία που τα καθιστά κατάλληλα, μεταξύ άλλων τεχνολογιών, να συμπεριληφθούν σε εφαρμογές πραγματικού χρόνου.

4.5.8 ΤΝΔ και Ανθρώπινος Εγκέφαλος

Υπάρχουν πολλά χαρακτηριστικά των ΤΝΔ κοινά με συμπεριφορές του ανθρώπινου εγκεφάλου. Πιο συγκεκριμένα μπορούν να παρατηρηθούν τα παρακάτω:

1. Η συμπεριφορά τους είναι βιολογικά ερμηνευόμενη.
2. Δίνουν συγκεκριμένες απαντήσεις σε συγκεκριμένα ερεθίσματα.
3. Μαθαίνουν με επαναληπτική παρουσίαση παραδειγμάτων.
4. Λειτουργούν ικανοποιητικά ακόμα και μετά από καταστροφή ορισμένων κόμβων ή με ελλιπείς εισόδους.
5. Αναγνωρίζουν και κατηγοριοποιούν νέες πληροφορίες παρόμοιες με ήδη κατηγοριοποιημένες.
6. Εξηγούν το φαινόμενο της αμνησίας λόγω του ότι η ορθή λειτουργία ενός εκπαιδευμένου δικτύου μπορεί να αλλοιωθεί αν καταστραφεί ένα σημαντικό μέρος της δομής του αλλά μόλις αποκατασταθεί η λειτουργία του θα επανέλθει κανονικά δεδομένου ότι τα βάρη που έχουν δημιουργηθεί μεταξύ των μονάδων κατά την εκπαίδευση εξακολουθούν να υφίστανται αναλλοίωτα.

4.5.9 Εφαρμογές ΤΝΔ

Τα ΤΝΔ είναι δημοφιλή σε προβλήματα τα οποία περιέχουν μη-προβλέψιμες λειτουργίες και δεν είναι πλήρως κατανοητά (κατηγοριοποίηση, αποτίμηση, πρόβλεψη):

• αναγνώριση εικόνας,
• επεξεργασία φωνής,
• σχεδιασμός ενεργειών (planning),
• εξόρυξη πληροφορίας,
• χρονοπρογραμματισμός (Scheduling),
• συστήματα ελέγχου και παραγωγής.

Όλα τα παραπάνω βρίσκουν εφαρμογή στη Ρομποτική, στην Άμυνα, στην Αεροπορία και Αυτοκίνηση, στην Ιατρική Διαγνωστική, σε γεωλογικές έρευνες, στην Οικονομία και σε τραπεζικές εφαρμογές, στη Βιομηχανία και σε πολλούς ακόμα χώρους παραγωγής.

4.6 Γενετικοί Αλγόριθμοι

4.6.1 Φυσική εξέλιξη: Η αρχική έμπνευση

Οι Γενετικοί Αλγόριθμοι–ΓΑ (Genetic Algorithms-GA) αποτελούν μία από τις μεθόδους που χρησιμοποιεί η ΤΝ, για να δημιουργήσει συστήματα Μηχανικής Μάθησης που βασίζονται στην Εξελικτική Μάθηση (Evolutionary Learning). Πιο συγκεκριμένα, οι Γενετικοί Αλγόριθμοι είναι γνωστικά συστήματα που μιμούνται την αναπαραγωγική διαδικασία πληθυσμών απλών βιολογικών οργανισμών κατά τη φάση της φυσικής εξέλιξης. Η διαδικασία λαμβάνει χώρα στα χρωμοσώματά τους (chromosomes), τα οποία με τη σειρά τους καταγράφουν τη δομή κάθε οργανισμού μέσω των γονιδίων τους (genes).

Εικόνα 4.2 Δομή φυσικού χρωμοσώματος

Μια ζωντανή ύπαρξη δημιουργείται μερικώς μέσω μιας διαδικασίας αποκωδικοποίησης των χρωμοσωμάτων. Οι ιδιαιτερότητες της κωδικοποίησης και αποκωδικοποίησης των χρωμοσωμάτων δεν έχουν κατανοηθεί πλήρως, αλλά μερικά από τα γενικά χαρακτηριστικά της θεωρίας είναι ευρέως αποδεκτά:

• Η φυσική επιλογή είναι ο σύνδεσμος μεταξύ των χρωμοσωμάτων και της απόδοσης των κωδικοποιημένων δομών. Διαδικασίες της φυσικής επιλογής επιτυγχάνουν την επικράτηση των χρωμοσωμάτων που περιέχουν τις πιο ισχυρές δομές και την αναπαραγωγή των πιο συχνά εμφανιζόμενων ισχυρών δομών.
• Κατά την αναπαραγωγή πραγματοποιείται η βιολογική εξέλιξη. Μεταλλάξεις μπορούν να κάνουν τα χρωμοσώματα των βιολογικών απογόνων να είναι διαφορετικά από αυτά των βιολογικών γονέων. Επίσης, και η διαδικασία του συνδυασμού χρωμοσωμάτων μπορεί να δημιουργήσει διαφορετικά χρωμοσώματα στους απογόνους, συνδυάζοντας «υλικά» από τα χρωμοσώματα των γονέων.
• Η βιολογική εξέλιξη δεν έχει μνήμη. Ό,τι γνωρίζει για την παραγωγή υπάρξεων που θα ταιριάζουν μέσα στο περιβάλλον τους εμπεριέχεται μέσα στον γενετικό χώρο, δηλαδή στο σύνολο των χρωμοσωμάτων από τις γονικές υπάρξεις, καθώς και στη δομή που τα χαρακτηρίζει.

H συνδυασμένη δράση της φυσικής επιλογής και ο ανασυνδυασμός του γενετικού υλικού (των γονιδίων) κατά τη διάρκεια της αναπαραγωγής αποτελούν την κινητήριο δύναμη της εξέλιξης.

Η μίμηση των φυσικών μεθόδων οδήγησε στην ανάπτυξη των επονομαζόμενων Εξελικτικών Αλγορίθμων (Evolutionary Algorithms) μια κατηγορία άμεσων, πιθανολογικών αλγορίθμων αναζήτησης και βελτιστοποίησης.

Τυπικά, ένας εξελικτικός αλγόριθμος αρχικοποιεί τον πληθυσμό του σε τυχαίες τιμές, αν και μπορεί να χρησιμοποιηθεί προηγούμενη γνώση του πεδίου εφαρμογής (εάν υπάρχει), για να επιδράσει στην αρχικοποίηση του πληθυσμού. Ακολουθεί η αξιολόγηση του πληθυσμού με απόδοση αντίστοιχων τιμών ποιότητας σε κάθε άτομο του πληθυσμού στο συγκεκριμένο περιβάλλον. H αξιολόγηση γίνεται µέσω της συνάρτησης ποιότητας (αντιπροσωπευτικής του συγκεκριμένου περιβάλλοντος), η οποία μπορεί να είναι πολύ απλή, όπως ο υπολογισµός µιας απλής συνάρτησης, ή εξαιρετικά πολύπλοκη, όπως η εκτέλεση μιας πολύπλοκης προσομοίωσης. Η επιλογή συνήθως υλοποιείται σε δύο βήματα: επιλογή γονέων και επιβίωση γονέων. Κατά την επιλογή των γονέων καθορίζεται ποια άτομα θα γίνουν γονείς και πόσους απογόνους/παιδιά (offsprings/children) θα αποκτήσουν.

Οι απόγονοι δημιουργούνται µέσω ανασυνδυασµού των γονέων, δηλαδή µε την ανταλλαγή πληροφορίας μεταξύ των γονέων και µέσω μετάλλαξης η οποία διαταράσσει περαιτέρω τους απογόνους. Ακολουθεί η χρήση της συνάρτησης ποιότητας για την αξιολόγηση των απογόνων και τελικά η επιλογή των ατόµων του πληθυσμού που θα επιβιώσουν στην επόμενη γενιά. Η διαδικασία αυτή ονομάζεται εξελικτικός κύκλος (evolutionary cycle). Το σχήμα 4.33 εμφανίζει τον συνήθη εξελικτικό κύκλο.

Σχήμα 4.33 Ο εξελικτικός κύκλος των Γενετικών Αλγορίθμων

4.6.2 Ιστορική Εξέλιξη

Ο όρος Γενετικός Αλγόριθμος (ΓΑ) χρησιμοποιήθηκε για πρώτη φορά από τον John Holland (1975) για έναν από τους βασικούς εκπροσώπους των εξελικτικών αλγορίθμων, ο οποίος θεωρείται και ως ο ευρύτατα γνωστός εξελικτικός αλγόριθμος των τελευταίων χρόνων. Όμως, πλέον, πολλοί ερευνητές χρησιμοποιούν κυρίως τον όρο Εξελικτική Υπολογιστική (Evolutionary Computation), προκειμένου να αναφερθούν στις εξελίξεις των τελευταίων ετών σε έναν τομέα που υπερβαίνει κατά πολύ τον αρχικό ΓΑ και ανήκει στις κατευθυνόμενες τεχνικές αναζήτησης εμπνευσμένες από τη φύση (βλέπε Σχήμα 4.34).

Σχήμα 4.34 Ο τομέας των μεθόδων αναζήτησης εμπνευσμένων από τη φύση

Αρκετοί επιστήμονες έχουν δραστηριοποιηθεί στην ανάπτυξη της Εξελικτικής Υπολογιστικής ήδη από τη δεκαετία του 1960. Το 1975, αφενός κυκλοφόρησε το βιβλίο του John Holland «Adaptation in Natural and Artificial Systems» και αφετέρου ο Kenneth DeJong, μεταπτυχιακός φοιτητής του Holland, ολοκλήρωσε τη διδακτορική του διατριβή με θέμα «Analysis of the behavior of a class of genetic adaptive systems». Θεωρείται ότι αμφότερα τα συγγράμματα έθεσαν τα θεμέλια των γενετικών αλγορίθμων. Ο DeJong ήταν, μάλιστα, ο πρώτος που παρέσχε μια ολοκληρωμένη παρουσίαση των δυνατοτήτων των ΓΑ στη βελτιστοποίηση και ακολούθησε μια σειρά από περαιτέρω μελέτες.

Η πρώτη διάσκεψη για αυτό το πρωτοεμφανισθέν ενδιαφέρον θέμα συγκλήθηκε το 1985. Ένας άλλος μεταπτυχιακός φοιτητής του Holland, ο David Goldberg, εκπόνησε τη βραβευμένη διδακτορική διατριβή του σχετικά με την εφαρμογή του ΓΑ στη βελτιστοποίηση αγωγού φυσικού αερίου. Κατόπιν, ο Goldberg εξέδωσε το 1989 το σημαντικό βιβλίο «Genetic Algorithms in Search, Optimization and Machine Learning», το οποίο λειτούργησε ως καταλύτης για την ανάπτυξη της θεωρίας και των εφαρμογών των ΓΑ, οι οποίες σήμερα εξακολουθούν να αυξάνονται με ταχείς ρυθμούς.

Σε αντίθεση με τους προηγούμενους εξελικτικούς αλγόριθμους, οι οποίοι επικεντρώνονταν στη μετάλλαξη των ατόμων του πληθυσμού και θα μπορούσαν να θεωρηθούν ως απλή εξέλιξη των μεθόδων αναρρίχησης λόφων, ο ΓΑ του Holland είχε ένα επιπλέον συστατικό, την ιδέα του ανασυνδυασµού των γονιδίων των γονέων.

4.6.3 Γενικά περί Γενετικών Αλγορίθμων

Η χρήση των Γενετικών Αλγορίθμων (ΓΑ) αποβλέπει στη δημιουργία απλών τρόπων αναζήτησης λύσεων σε προβλήματα, κυρίως βελτιστοποίησης και χρονοδρομολόγησης, τα οποία κατεξοχήν εξαρτώνται από μεγάλο πλήθος παραμέτρων, καθιστάμενα ελάχιστα κατανοητά, με πολλές αλληλεξαρτήσεις ή πολύ περίπλοκα ώστε δεν εφαρμόζονται η βελτιστοποίηση ή χρονοδρομολόγηση με άλλες πιο άμεσες μεθόδους.

Για να μπορέσει να τρέξει ένας ΓΑ, απαιτείται να έχουν ικανοποιηθεί 2 προϋποθέσεις επιτυχώς:

• μια κωδικοποίηση του χώρου επίλυσης και
• μια συνάρτηση καταλληλότητας που να αξιολογεί το χώρο επίλυσης.

Μόλις επιτευχθούν τα δυο παραπάνω, τότε μπορεί να εφαρμοστεί ο ΓΑ, για να δημιουργήσει και να αξιολογήσει τις υποψήφιες λύσεις μέσω μιας προσομοίωσης της εξελικτικής διαδικασίας. Οι συμβατικές μέθοδοι βελτιστοποίησης και οι μέθοδοι αναρρίχησης λόφου εντοπίζουν το πλησιέστερο τοπικό βέλτιστο μιας συνάρτησης, αλλά συνήθως αποτυγχάνουν στη εύρεση καθολικής λύσης. Από την άλλη, οι στατιστικές τεχνικές απαιτούν μεγάλο υπολογιστικό χρόνο, ενώ οι υπολογιστικές μέθοδοι απαιτούν την ύπαρξη παραγώγων, η χρήση των οποίων δεν συνιστάται σε μεγάλα πολυεπίπεδα συστήματα με αυξανόμενη πολυπλοκότητα και ασυνέχεια.

Αντίθετα, η χρήση των ΓΑ είναι αποτελεσματική τεχνική τυχαίας αναζήτησης για την εύρεση της βέλτιστης λύσης σε συγκεκριμένο χρόνο. Η τεχνική αυτή βασίζεται στην ανακάλυψη πρώτα πολλών τμηματικών λύσεων για τη δημιουργία του αρχικού πληθυσμού και μετά στο συνδυασμό των καλυτέρων λύσεων μέχρι την επίτευξη της βέλτιστης εξ αυτών. Η όλη δυσκολία εντοπίζεται στην ορθή εκτίμηση της απόδοσης των τμηματικών λύσεων, διότι λανθασμένη εκτίμηση μπορεί να οδηγήσει σε λύσεις που θα απέχουν πολύ από τη ζητούμενη βέλτιστη.

Η λειτουργία των ΓΑ βασίζεται στη δυνατότητά τους να αναπαράγουν τον πληθυσμό σε γενεές. Κάθε γενεά προκύπτει από την προηγούμενη, αφού επιλεγούν οι γονείς και εφαρμοστούν οι γενετικοί τελεστές της διασταύρωσης και της μετάλλαξης.

 

Τα κυριότερα χαρακτηριστικά των ΓΑ είναι τα ακόλουθα:

• Είναι ένας νέος τρόπος προγραμματισμού, κατάλληλος για επίλυση προβλημάτων σε χώρους αναζήτησης ιδιαίτερα πολύπλοκους, προσαρμόσιμος σε ποικίλα και ευμετάβλητα περιβάλλοντα.
• Περιλαμβάνουν ένα σύνολο μεθόδων εμπνευσμένων από τη θεωρία της εξέλιξης. Αρχίζουν από έναν συνήθως επιλεγμένο πληθυσμό και επιδιώκουν την παραγωγή ατόμων με υψηλή απόδοση.
• Η προοδευτική βελτίωση του πληθυσμού επιτυγχάνεται με τις ενέργειες των γενετικών τελεστών που επιδρούν στην αναπαραγωγή, σύμφωνα με την ικανότητα των ατόμων, με εφαρμογή των τεχνικών της διασταύρωσης και της μετάλλαξης.
• Οι είσοδοι και οι έξοδοι του προβλήματος αναπαρίστανται ως συμβολοσειρές (strings) σταθερού μήκους, ενός συγκεκριμένου αλφαβήτου (συνήθως δυαδικού), με ρόλο αντίστοιχο του χρωμοσώματος στη Γενετική.
• Κάθε σημείο του χώρου επίλυσης του προβλήματος αντιπροσωπεύεται από μια συμβολοσειρά ή δομή, όπως αναφέρθηκε παραπάνω.
• Κάθε θέση στη συμβολοσειρά καταλαμβάνεται από ένα ή περισσότερα σύμβολα του αλφαβήτου, αντιπροσωπεύοντας μια μεταβλητή του προβλήματος και έχοντας ρόλο αντίστοιχο με αυτόν του γενετικού υλικού στους βιολογικούς μηχανισμούς, δηλαδή γονιδίου μέσα σε χρωμόσωμα.
• Απαιτείται η δυνατότητα πληροφόρησης για την ικανότητα των διάφορων συμβολοσειρών του πληθυσμού, σύμφωνα με τη συνάρτηση καταλληλότητας (fitness function), που καλείται επίσης και συνάρτηση απόδοσης, συνάρτηση προσαρμογής ή αντικειμενική συνάρτηση.
• Ο χρόνος στην εξέλιξη της διαδικασίας υπολογίζεται σε διακριτά διαστήματα τα οποία καλούνται γενεές∙ παράδειγμα Ν(t): ο πληθυσμός κατά τη γενεά t.

4.6.4 Η Ανατομία ενός Γενετικού Αλγόριθμου

Τρία είναι τα βασικά λειτουργικά τμήματα ενός ΓΑ:

• Τμήμα πληθυσμού, με τις δομές και τεχνικές για τη δημιουργία και τη διαχείρισή του,
• Τμήμα εκτίμησης της απόδοσης, με τη συνάρτηση καταλληλότητας,
• Τμήμα αναπαραγωγής, με τεχνικές για τη δημιουργία νέων δομών με την εφαρμογή των γενετικών τελεστών.

Στα παραπάνω, οι βασικοί μηχανισμοί που συνδέουν τον ΓΑ με το πρόβλημα που επιλύει είναι ο τρόπος κωδικοποίησης της δομής που αναπαριστά μια λύση του προβλήματος, καθώς και η συνάρτηση καταλληλότητας που επιστρέφει τη μέτρηση της απόδοσης της δομής.

Επιπλέον, ο ΓΑ απαιτεί να οριστεί ένα όριο καταλληλότητας, το οποίο θα αντιστοιχεί στην επιθυμητή τιμή απόδοσης που πρέπει να επιτευχθεί από μια δομή, ώστε να τερματιστεί ο ΓΑ και 3 επιπλέον παράμετροι:

• το πλήθος Ν των δομών του αρχικού πληθυσμού,
• το ποσοστό r του πληθυσμού που θα αναπαραχθεί σε μια γενεά,
• το ποσοστό m των απογόνων που θα υποστούν μετάλλαξη.

Οι μηχανισμοί λειτουργίας του αλγορίθμου ποικίλλουν ως προς την εφαρμογή και τα αποτελέσματα.

Στο βιβλίο του «Genetic Algorithms in Search, Optimization and Machine Learning» (1989), ο Goldberg περιγράφει τι κάνει τους γενετικούς αλγόριθμους να λειτουργούν και εισάγει τον απλό γενετικό αλγόριθμο ή κανονικό γενετικό αλγόριθμο (canonical genetic algorithm): έναν εξελικτικό αλγόριθμο που εκτελεί ενέργειες σε μια συμβολοσειρά δυαδικών ψηφίων με τους ακόλουθους τρεις γενετικούς τελεστές:

• αναπαραγωγή
• διασταύρωση
• μετάλλαξη

Μια συνάρτηση καταλληλότητας αντιστοιχίζει τη δυαδική αναπαράσταση σε έναν πραγματικό αριθμό. Ο στόχος του κανονικού γενετικού αλγορίθμου είναι η βελτιστοποίηση της απόδοσης με την εξερεύνηση του δυαδικού χώρου αναζήτησης, ώστε ο πραγματικός αριθμός να ελαχιστοποιηθεί ή να μεγιστοποιηθεί.

 

Τα βήματα του Κανονικού Γενετικού Αλγόριθμου:

1. Δημιουργήστε έναν τυχαίο πληθυσμό με Ν δυαδικές συμβολοσειρές.
2. Αξιολογήστε την απόδοση της κάθε μεμονωμένης συμβολοσειράς μέσω της συνάρτησης καταλληλότητας g(x).
3. Εφαρμόστε την αναπαραγωγή, δηλαδή επιλέξτε ζεύγη γονέων από τον πληθυσμό βάσει της απόδοσής τους.
4. Για κάθε ζεύγος γονέων επαναλάβετε:
5. Με πιθανότητα r εφαρμόστε τον τελεστή διασταύρωσης στους γονείς, για να παραχθεί μια νέα συμβολοσειρά-απόγονος.
6. Με πιθανότητα m εφαρμόστε τη μετάλλαξη σε κάποιο δυαδικό ψηφίο της συμβολοσειράς κάθε απόγονου ξεχωριστά.
7. Τοποθετήστε τη συμβολοσειρά-απόγονο στον νέο πληθυσμό.
8. Αντικαταστήστε τον παλιό με τον νέο πληθυσμό.
9. Αν δεν έχει βρεθεί αποδεκτή λύση ούτε έχει εξαντληθεί ο προκαθορισμένος μέγιστος αριθμός γενεών, μεταβαίνετε ξανά στο ανωτέρω βήμα 2.

4.6.5 Κωδικοποίηση

Στο περιβάλλον ενός ΓΑ, οι είσοδοι του προβλήματος είναι στην ουσία τα Ν χρωμοσώματα του αρχικού πληθυσμού που αντιπροσωπεύουν μερικές λύσεις του προβλήματος. Κάθε χρωμόσωμα αναπαρίσταται με δομή συμβολοσειράς (string) σταθερού μήκους n, ενός συγκεκριμένου αλφαβήτου. Τα χρωμοσώματα πρέπει να έχουν μία αναπαράσταση τέτοια, ώστε να περιέχουν μέσα τους τα χαρακτηριστικά της λύσης που εκπροσωπούν. Τα χαρακτηριστικά ενός χρωμοσώματος καλούνται γονότυπος (genotype) του χρωμοσώματος. Πάνω στον γονότυπο εφαρμόζονται οι γενετικοί τελεστές και παράγονται οι απόγονοι.

Ο Holland κωδικοποίησε το γονότυπο ενός χρωμοσώματος ως μία σειρά δυαδικών ψηφίων{0,1}. Η επιλογή του δυαδικού αλφαβήτου για την κωδικοποίηση διαθέτει έναν αριθμό θετικών χαρακτηριστικών που επιτρέπουν τη δημιουργία απλών, αποδοτικών και κομψών ΓΑ. Όμως, υπάρχουν και άλλοι τρόποι για την κωδικοποίηση των χρωμοσωμάτων με δικά τους εγγενή πλεονεκτήματα. Για παράδειγμα, η κωδικοποίηση μέσα στο γονότυπο μπορεί να γίνει χρησιμοποιώντας ακέραιους ή πραγματικούς αριθμούς και άλλων αριθμητικών συστημάτων, όπως είναι το δεκαδικό, το οκταδικό, το δεκαεξαδικό κτλ.

Η συνάρτηση καταλληλότητας ενός χρωμοσώματος απαιτεί την αποκωδικοποίηση του γονότυπου στο δεκαδικό σύστημα. Η αποκωδικοποίηση αυτή οδηγεί στη δημιουργία του αντίστοιχου φαινότυπου (phenotype). Όταν η κωδικοποίηση γίνεται με το δυαδικό σύστημα αναπαράστασης, τότε για την αποκωδικοποίηση στο επίπεδο του φαινότυπου εφαρμόζεται μια απλή αντιστοίχιση της δυαδικής τιμής προς την ακέραια δεκαδική. Αντίστοιχα, αν η κωδικοποίηση γίνει με το δεκαδικό σύστημα, τότε υπάρχει συγχώνευση των επιπέδων του γονότυπου και του φαινότυπου.

 

Παράδειγμα δυαδικού γονότυπου και αντίστοιχου φαινότυπου:

 

Γονότυπος: 01101

Φαινότυπος: 13

 

Κάθε σημείο (λύση) του πεδίου του προβλήματος αποτελεί μια δομή (χρωμόσωμα ή άτομο) του πληθυσμού που έχει αναπαρασταθεί μέσω του επιλεγμένου αλφάβητου. Σε οποιαδήποτε χρονική στιγμή, το όλο σύστημα περιέχει έναν πληθυσμό από Ν άτομα που αναπαριστούν το σύνολο των μέχρι τότε εντοπισμένων λύσεων στο πρόβλημα.

4.6.6 Η αρχικοποίηση ενός πληθυσμού

Το πρώτο βήμα ενός ΓΑ είναι να αρχικοποιήσει έναν πληθυσμό από πιθανές λύσεις του προβλήματος σε μορφή συμβολοσειρών αποδεκτού γονότυπου κωδικοποιημένου βάσει ενός επιλεγμένου αλφαβήτου.

Η αρχικοποίηση ενός τυχαίου πληθυσμού είναι η πλέον συνηθισμένη τακτική. Ως τυχαίο πληθυσμό εννοούμε ένα πλήθος δομών των οποίων ο γονότυπος καθορίζεται από μια τυχαία διαδικασία. Ο αρχικός πληθυσμός χαρακτηρίζεται από το πλήθος Ν των συμβολοσειρών μέσα σε αυτόν και από το μήκος των συμβολοσειρών του που είναι πάντα σταθερό.

Το πλήθος Ν των συμβολοσειρών μέσα σε έναν πληθυσμό χαρακτηρίζεται ως μέγεθος του πληθυσμού και μπορεί να παραμένει σταθερό ή να μεταβάλλεται κατά την εξέλιξη του πληθυσμού. Το μέγεθος του αρχικού πληθυσμού ορίζεται από μια παράμετρο που δίνεται κατά την αρχικοποίηση του ΓΑ και η οποία πρέπει να επιλέγεται με προσοχή, γιατί ανάλογα με το κάθε πρόβλημα, το βέλτιστο μέγεθος διαφέρει. Όταν το μέγεθος του πληθυσμού είναι πολύ μικρό, τότε δεν γίνεται επαρκής εξερεύνηση του συνολικού χώρου αναζήτησης, δεδομένου ότι η σύγκλιση είναι ταχύτερη. Εάν το μέγεθος του πληθυσμού είναι πολύ μεγάλο, τότε ο χρόνος θα αναλωθεί με την επεξεργασία περισσότερων δεδομένων από όσα απαιτούνται και οι χρόνοι σύγκλισης θα είναι σημαντικά μεγαλύτεροι.

Παράδειγμα αρχικοποίησης πληθυσμού

Έστω το πρόβλημα του Μαύρου Κουτιού με τους 5 διακόπτες εισόδου, των οποίων την έξοδο επιθυμούμε να βελτιστοποιήσουμε. Ο κάθε διακόπτης μπορεί να βρίσκεται στην κατάσταση off ή on που αντιστοιχεί στην κατάσταση 0 ή 1 (βλέπε Σχήμα 4.35).

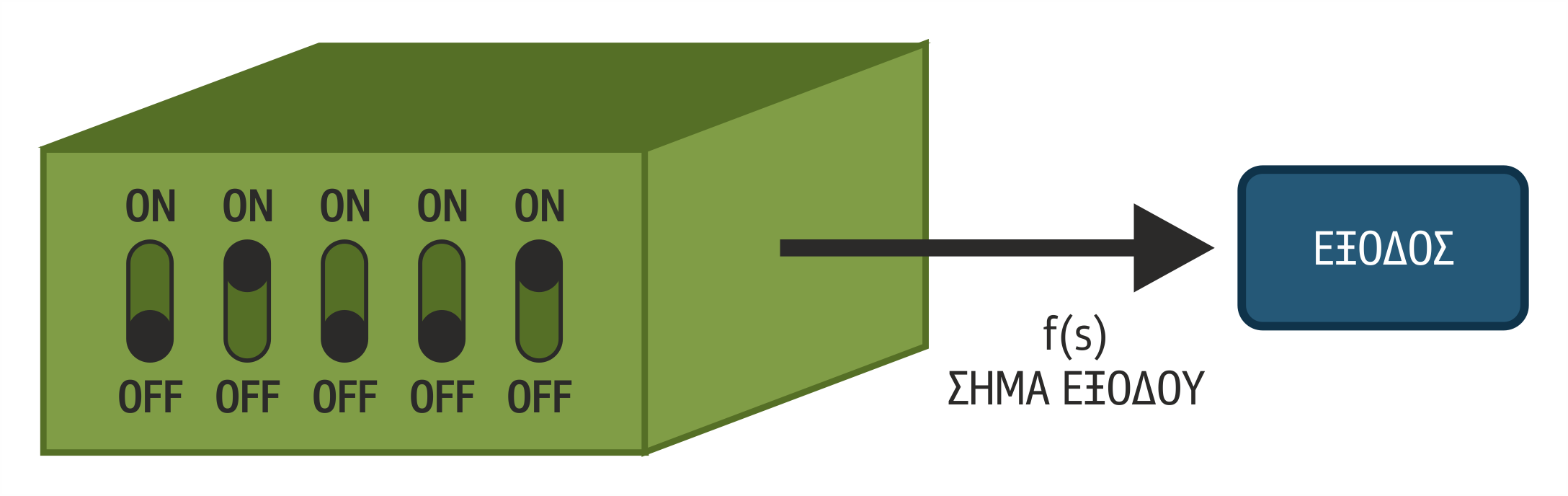
Σχήμα 4.35 Το πρόβλημα βελτιστοποίησης του Μαύρου Κουτιού µε τους 5 διακόπτες

Μια λύση του προβλήματος αναπαρίσταται ως ένα χρωμόσωμα με γονότυπο 5 γονιδίων, τα οποία παρουσιάζουν την κατάσταση στην οποία βρίσκεται καθένας από τους 5 διακόπτες τη δεδομένη στιγμή. Η κωδικοποίηση του γονότυπου γίνεται με το δυαδικό αλφάβητο και η συμβολοσειρά που προκύπτει είναι ένας 5ψήφιος δυαδικός αριθμός. Παρακάτω, δίνεται ένας τυχαία δημιουργημένος αρχικός πληθυσμός μεγέθους 4, όπου κάθε δομή αντιστοιχεί σε έναν συνδυασμό καταστάσεων των διακοπτών (όπου 0=κλειστός και 1=ανοιχτός):

 

01101

11000

01000

10011

 

Το παραπάνω παράδειγμα προέρχεται από το βιβλίο του Goldberg «Genetic Algorithms in Search, Optimization & Machine Learning» και θα χρησιμοποιηθεί και σε επόμενες παραγράφους του κεφαλαίου.

4.6.7 Θεωρία σχημάτων

Ένα λεπτό σημείο που πρέπει να προσεχθεί στην αναπαράσταση ενός χρωμοσώματος μέσω μιας δομής είναι τα δομικά της κομμάτια που ονομάζονται και δυνατά σχήματα της δομής του χρωμοσώματος.

Ένα σχήμα (schema) ή αλλιώς πρότυπο ομοιότητας (prototype resemblance) μπορεί ουσιαστικά να οριστεί ως ένα πρότυπο χρωμοσωμάτων.

Για παράδειγμα, ας σκεφτούμε έναν πληθυσμό χρωμοσωμάτων στον οποίο το καθένα από αυτά, δηλαδή η καθεμία υποψήφια λύση, έχει την κωδικοποίηση που παρουσιάστηκε στο παράδειγμα της προηγούμενης παραγράφου.

Έστω ότι 01101 και 01010 είναι δύο τέτοια χρωμοσώματα. Μια κοινή περιγραφή για αυτά τα χρωμοσώματα είναι «τα χρωμοσώματα των οποίων τα δύο πρώτα bits είναι 01». Έτσι, υποστηρίζουμε ότι το 01*** είναι ένα πρότυπο, δηλαδή ένα σχήμα καθορισμού αυτών των χρωμοσωμάτων. Οι αστερίσκοι αντιπροσωπεύουν «οποιαδήποτε τιμή», κάτι το οποίο σημαίνει ότι μπορεί να είναι είτε 0 είτε 1. Τα 0 και τα 1 ονομάζονται σταθερά bits. Ως εκ τούτου, ένα σχήμα στο δυαδικό αλφάβητο είναι ένα πρότυπο το οποίο χρησιμοποιεί τα σύμβολα {0, 1, *}, για να καθορίσει ένα σύνολο χρωμοσωμάτων. Εύκολα μπορούμε να συμπεράνουμε ότι ένα σχήμα αντιπροσωπεύει χρωμοσώματα στον πληθυσμό, όπου n είναι ο αριθμός των αστερίσκων στο σχήμα. Στο παράδειγμά μας, το 01*** αντιπροσωπεύει ένα σύνολο από 8 χρωμοσώματα, δεδομένου ότι υπάρχουν τρεις αστερίσκοι στο σχήμα, το [01100, 01000, 01110, 01111, 01001, 01010, 01011, 011101]. Προφανώς, το ***** αντιπροσωπεύει ολόκληρο τον πληθυσμό.

Σύμφωνα με τη Θεωρία Σχημάτων, ως μήκος ορισμού (defining length) ενός σχήματος ορίζεται η διαφορά των θέσεων του πρώτου και του τελευταίου καθορισμένου bit μέσα στο σχήμα. Για παράδειγμα, για το σχήμα 01***01***, το πρώτο καθορισμένο bit (το πρώτο 0) είναι στη θέση 1 και το τελευταίο καθορισμένο bit (το δεύτερο 1) είναι στη θέση 7. Έτσι, το σχήμα αυτό έχει μήκος 7 - 1 = 6. Η τάξη (order) ενός σχήματος είναι ο αριθμός των καθορισμένων του bits. Το 01***10*** έχει 4 σταθερά καθορισμένα ψηφία, δηλαδή έχει τάξη 4.

Η Θεωρία Σχημάτων εξηγεί ποιο συγκεκριμένο σχήμα είναι πιθανόν να διαδοθεί από γενεά σε γενεά:

• Τα σχήματα με μήκος κοντά στο μήκος του χρωμοσώματος έχουν λιγότερες πιθανότητες να επιβιώσουν λόγω της διασταύρωσης.
• Τα σχήματα υψηλής τάξης, δηλαδή με πολλά καθορισμένα bits, είναι επίσης πιο πιθανό να εξαφανιστούν ως αποτέλεσμα της μετάλλαξης.
• Συνάγεται το συμπέρασμα ότι τα μικρού μήκους, χαμηλής τάξης σχήματα που έχουν καταλληλότητα πάνω από τον μέσο όρο είναι πιο πιθανόν να υπάρχουν στις διάδοχες γενεές. Τέτοια σχήματα ονομάζονται δομικά στοιχεία και μπορούν να οριστούν ως επιμέρους λύσεις. Ένα χρωμόσωμα το οποίο έχει πολλά δομικά στοιχεία έχει μεγάλες πιθανότητες να προσεγγίζει μια σχεδόν βέλτιστη λύση και στη διαδικασία επιλογής πρέπει να του δίνονται περισσότερες ευκαιρίες διάδοσης στην επόμενη γενεά.

4.6.8 Αναπαραγωγή

Οι τυχαίοι αρχικοί πληθυσμοί είναι σχεδόν πάντα εξαιρετικά αποτυχημένοι στο να προσφέρουν ικανοποιητικές λύσεις. Οι λύσεις που περιέχονται σε μια γενεά και αποτελούν τα χρωμοσώματα του πληθυσμού της πρέπει να αξιολογηθούν, πριν τους επιτραπεί να συμμετέχουν στις διαδικασίες αναπαραγωγής της επόμενης γενεάς με στόχο τη βελτίωση του πληθυσμού. Αναπαραγωγή (Reproduction) σε ένα ΓΑ καλείται η αξιολόγηση των δομών του πληθυσμού μιας γενεάς με τη βοήθεια της συνάρτησης καταλληλότητας, για να τους δοθεί στη συνέχεια η ευκαιρία, μικρότερη ή μεγαλύτερη ανάλογα με την απόδοσή τους, να συμμετέχουν μέσω διαδικασιών αναπαραγωγής στη δημιουργία του πληθυσμού της επόμενης γενεάς.

Ανάλογα με τον τρόπο με τον οποίο δομούμε τη συνάρτηση καταλληλότητας, μπορούμε να στοχεύουμε στη δημιουργία είτε του λιγότερο δαπανηρού πληθυσμού είτε του περισσότερο κατάλληλου, θέτοντας κατ’ αντιστοιχία ένα ζήτημα ελαχιστοποίησης του κόστους ή μεγιστοποίησης της φυσικής καταλληλότητας. Στα προβλήματα βελτιστοποίησης, το κόστος δεν είναι μέτρο της αξίας (π.χ. χρηματικής), αλλά ένα μέτρο αποδοτικότητας. Φυσικά, η καταλληλότητα μπορεί να θεωρηθεί ως αντιστρόφως ανάλογη με το κόστος• ως εκ τούτου, μπορεί να γίνει εύκολα μετατροπή από το ένα μέγεθος στο άλλο. Ο σχεδιασμός μιας συνάρτησης καταλληλότητας που μπορεί να αποτιμήσει επιτυχώς την αξία ενός πληθυσμού βάσει της διαθέσιμης γνώσης για το πρόβλημα είναι βασική προϋπόθεση της επιτυχίας ενός ΓΑ και αποτελεί ένα από τα δυσκολότερα προβλήματα που έχει να αντιμετωπίσει ο δημιουργός του.

Στις τεχνικές βελτιστοποίησης, το εύρος των πιθανών λύσεων αναφέρεται συχνά ως o χώρος των λύσεων, ενώ η καταλληλότητα του κάθε σημείου στο χώρο λύσεων αναφέρεται ως το υψόμετρο (altitude) στο τοπίο του προβλήματος. Η αναζήτηση για το ολικό ελάχιστο (ή μέγιστο) του κόστους είναι το ίδιο με την αναζήτηση του χαμηλότερου σημείου στη χαμηλότερη κοιλάδα του τοπίου του κόστους. Ομοίως, η αναζήτηση για το ολικό μέγιστο της καταλληλότητας είναι το ίδιο με την αναζήτηση για το υψηλότερο σημείο του ψηλότερου όρους στο τοπίο της καταλληλότητας.

Γονική επιλογή

Σκοπός της γονικής επιλογής σε ένα ΓΑ είναι να δοθούν περισσότερες πιθανότητες αναπαραγωγής σε εκείνα τα μέλη του πληθυσμού που είναι ισχυρότερα βάσει της εκτίμησης της συνάρτησης καταλληλότητας. Τα μέλη που επιλέγονται ως κατάλληλα για αναπαραγωγή καλούνται γονείς.

Ο κλασικός μηχανισμός επιλογής γονέων είναι η ρουλέτα γονικής επιλογής (roullete wheel selection), η οποία επιλέγει μέλη ενός πληθυσμού με πιθανότητα ανάλογη προς την καταλληλότητά τους με βάση το μέτρο της απόδοσής τους.

 

Τα βήματα του αλγόριθμου της Ρουλέτας Γονικής Επιλογής

• Άθροισε την απόδοση όλων των μελών του πληθυσμού. Κάλεσε το άθροισμα συνολική απόδοση.
• Δημιούργησε έναν τυχαίο αριθμό n μεταξύ 0 και της συνολικής απόδοσης.
• Επίστρεψε το πρώτο μέλος του πληθυσμού του οποίου η απόδοση προστιθέμενη στην απόδοση των προηγούμενων μελών είναι ≥ n.
• Επανάλαβε τη διαδικασία τόσες φορές όσες ο πληθυσμός.

Ο αλγόριθμος αναφέρεται ως ρουλέτα γονικής επιλογής, γιατί μπορεί να παρομοιαστεί με την περιστροφή ενός τροχού ρουλέτας χωρισμένου σε τόσους κυκλικούς τομείς όσα τα μέλη του πληθυσμού, όπου κάθε τομέας αντιστοιχεί σε ένα διαφορετικό μέλος του πληθυσμού και είναι ανάλογος σε εμβαδόν με την απόδοση του μέλους. Η επιλογή ενός μέλους ως γονέα μπορεί να απεικονιστεί ως μια περιστροφή του τροχού με επιλεγμένο το γονέα στον τομέα του οποίου θα σταματήσει ο τροχός.

Παράδειγμα εφαρμογής ρουλέτας γονικής επιλογής

Στον πληθυσμό του προηγούμενου παραδείγματος της παραγράφου 4.6.6 εφαρμόζουμε τη συνάρτηση καταλληλότητας g, όπου g (x)=x2, η οποία δίνει για κάθε μέλος του πληθυσμού τις τιμές απόδοσης (πίνακας 4.5) και την αντίστοιχη πιθανότητα κάθε μέλους να επιλεγεί ως γονέας της νέας γενεάς.

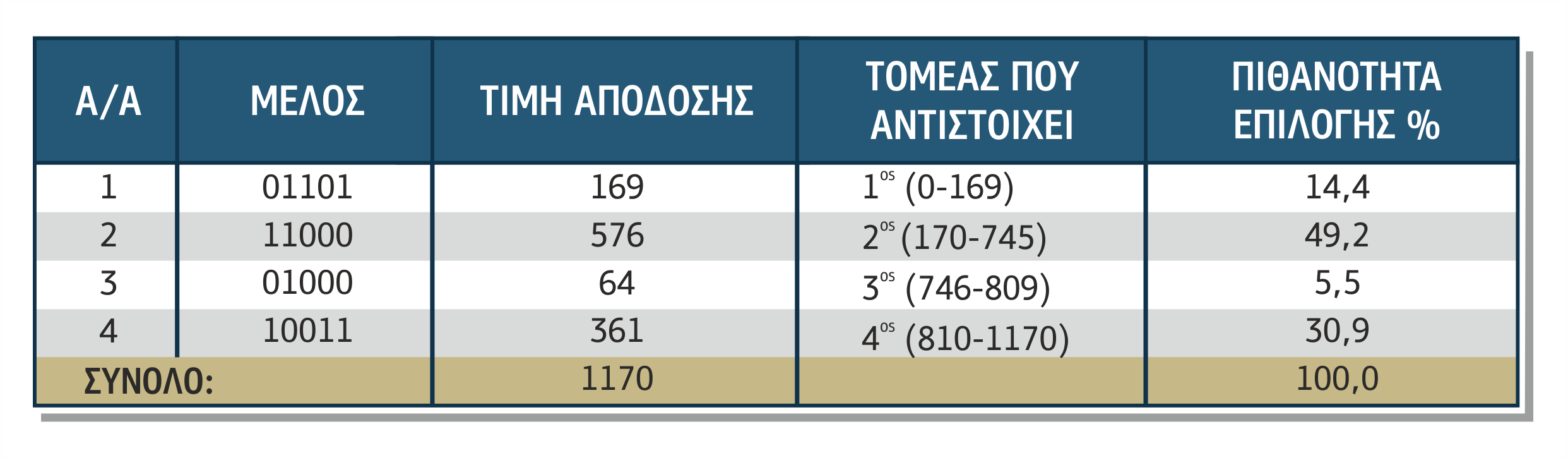
Πίνακας 4.5 Πληθυσμός προς αναπαραγωγή και οι αντίστοιχες τιμές απόδοσης των μελών του

Οι τιμές απόδοσης υπολογίστηκαν με την εφαρμογή της συνάρτησης g σε κάθε αποκωδικοποιημένη δυαδική συμβολοσειρά στο δεκαδικό σύστημα, δηλαδή στο φαινότυπο κάθε χρωμοσώματος του πληθυσμού.

 

Παράδειγμα υπολογισμού για το μέλος 01101:

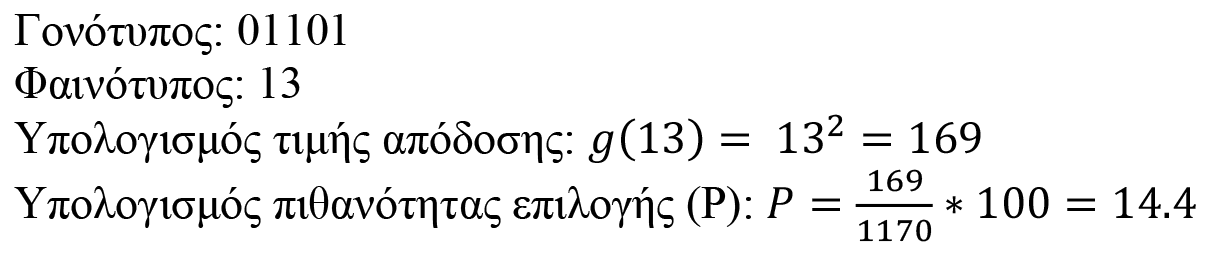
Ομοίως υπολογίζονται οι τιμές απόδοσης και οι πιθανότητες επιλογής για τα υπόλοιπα 3 μέλη του πληθυσμού.

Σύμφωνα με τα ποσοστά που εμφανίζονται στον παραπάνω πίνακα 4.5, προκύπτει η ρουλέτα του σχήματος 4.36, η οποία θα χρησιμοποιηθεί για την επιλογή των γονέων και την αναπαραγωγή της επόμενης γενεάς:

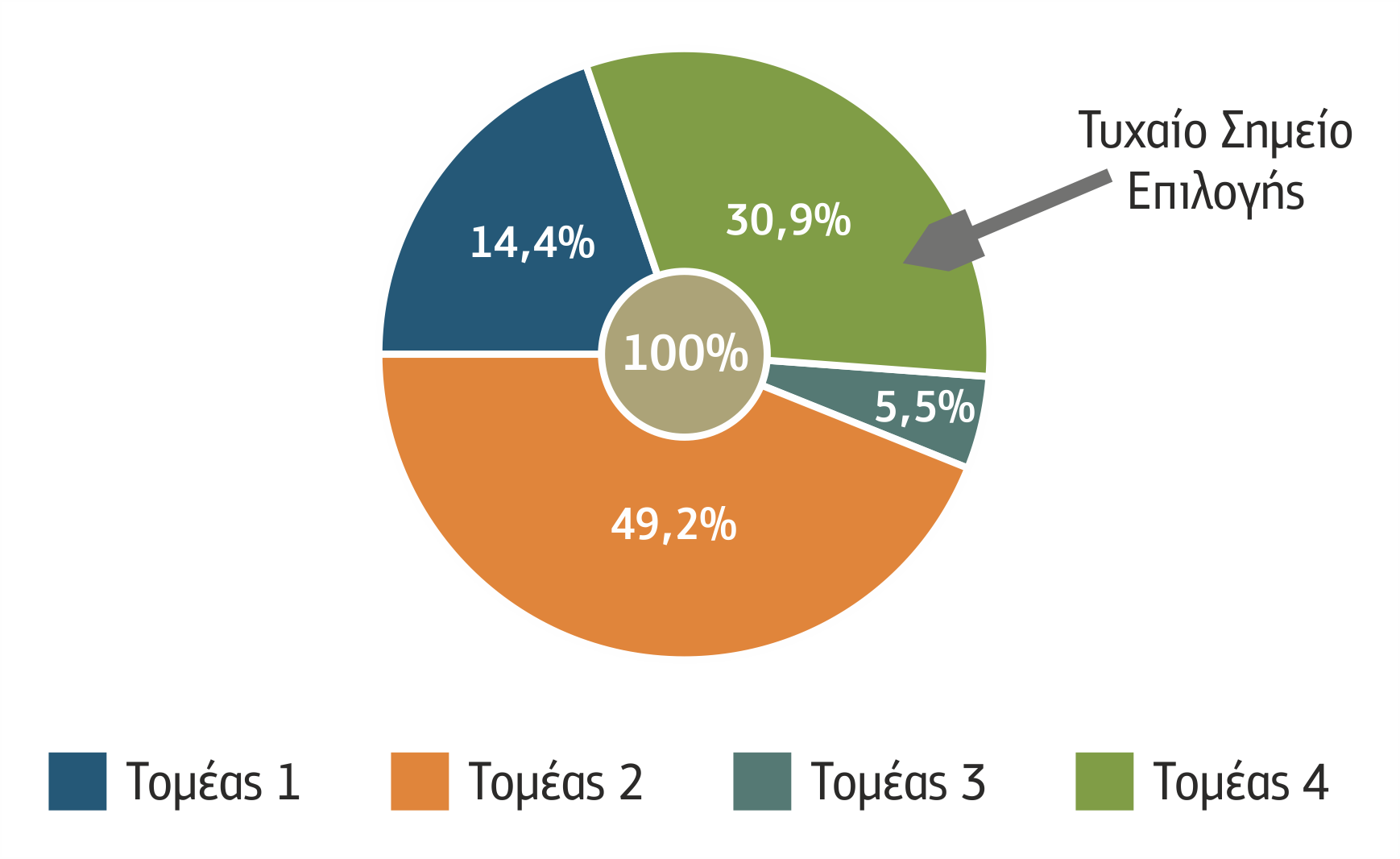
Σχήμα 4.36 Ρουλέτα γονικής επιλογής

Για να ενεργοποιηθεί η διαδικασία της αναπαραγωγής, απλώς τρέχουμε επαναληπτικά τα βήματα του αλγόριθμου της ρουλέτας 4 φορές (όσες και το μέγεθος του πληθυσμού).

 

Βήματα Αλγόριθμου Ρουλέτας Γονικής Επιλογής:

• Άθροισε την απόδοση όλων των μελών του πληθυσμού.
• Κάλεσε το άθροισμα συνολική απόδοση.
• Δημιούργησε έναν τυχαίο αριθμό n μεταξύ 0 και της συνολικής απόδοσης.
• Επίστρεψε το πρώτο μέλος του πληθυσμού του οποίου η απόδοση, προστιθέμενη στην απόδοση των προηγούμενων μελών, είναι ≥ n.
• Επανάλαβε τη διαδικασία τόσες φορές όσες ο πληθυσμός.

Στο συγκεκριμένο παράδειγμα, το πρώτο μέλος έχει τιμή απόδοσης ίση με 169, που αντιστοιχεί στο 14.4% της συνολικής απόδοσης. Ως αποτέλεσμα, στο συγκεκριμένο μέλος αποδίδεται το 14.4% του εμβαδού της ρουλέτας που αντιστοιχεί σε ένα διάστημα που αρχίζει από το 0 και τελειώνει στο 169. Κάθε περιστροφή της ρουλέτας θα επιλέξει το πρώτο μέλος του πληθυσμού, αν ο τροχός επιστρέψει μια τιμή από 0-169, με πιθανότητα να συμβεί 0.144. Το δεύτερο μέλος έχει τιμή απόδοσης ίση με 576, που αντιστοιχεί στο 49.2% της συνολικής απόδοσης. Ως αποτέλεσμα, στο συγκεκριμένο μέλος αποδίδεται το επόμενο διάστημα που αρχίζει από το 170 και τελειώνει στο 745 (170+ 576) που αντιστοιχεί στο 49.2% του εμβαδού της ρουλέτας. Μια περιστροφή της ρουλέτας θα επιλέξει το δεύτερο μέλος του πληθυσμού, αν ο τροχός επιστρέψει μια τιμή από 170-745, με πιθανότητα να συμβεί 0,492. Τα αντίστοιχα συμβαίνουν για τα υπόλοιπα δύο μέλη.

Εφαρμόζοντας τη ρουλέτα στον πληθυσμό του παραδείγματός μας έχουμε ως πιθανά αποτελέσματα αυτά που αποτυπώνονται στον Πίνακα 4.6.

Πίνακας 4.6 Αποτελέσματα ρουλέτας γονικής επιλογής

Δείτε κινούμενη εικόνα 4.5 - Ρουλέτα γονικής επιλογής

 

Στον παρακάτω πίνακα 4.7 παρουσιάζονται όλα τα μεγέθη που υπολογίστηκαν για την παραγωγή των γονέων του παραδείγματός μας με χρήση της ρουλέτας γονικής επιλογής

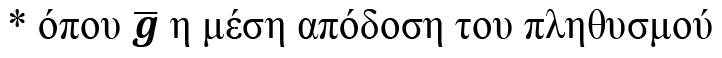
Πίνακας 4.7 Αποτύπωση όλων των στοιχείων για την επιλογή γονέων μέσω ρουλέτας γονικής επιλογής

Η μέθοδος της ρουλέτας ευνοεί την επιλογή μελών με τη μεγαλύτερη απόδοση, δίνοντάς τους μεγαλύτερη πιθανότητα επιλογής, δεδομένου ότι το εμβαδόν του κυκλικού τομέα τους είναι μεγαλύτερο και ως εκ τούτου ευνοείται η επιλογή του.

Μια ακόμη πολύ συχνά χρησιμοποιούμενη τεχνική είναι η επιλογή τουρνουά (tournament selection). Σε γενικές γραμμές, η διαδικασία επιλογής τουρνουά επιλέγει τυχαία μια ομάδα από μέλη του τρέχοντος πληθυσμού, συγκρίνει τις αποδόσεις τους και επιλέγει εκείνο το οποίο έχει την υψηλότερη απόδοση ως γονέας για την επόμενη γενεά. Η επιλογή τουρνουά θεωρείται ως μία από τις ταχύτερες μεθόδους επιλογής, είναι εύκολα υλοποιήσιμη και προσφέρει καλό έλεγχο της επιλεκτικής πίεσης (βλέπε παρακάτω).

Ανάλογα με τον ΓΑ, στη διαδικασία επιλογής γονέων μπορεί να συμμετέχει το σύνολο των μελών του πληθυσμού (Ν) ή μόνο ένα μέρος του (rN). Οι γονείς που θα επιστρέψει ο μηχανισμός επιλογής αποτελούν έναν προσωρινό πληθυσμό, στον οποίο θα επιδράσει ο γενετικός τελεστής της διασταύρωσης, για να παραχθεί ένας πληθυσμός rNαπογόνων από rN/2 ζεύγη γονέων. Ο προσωρινός πληθυσμός μπορεί να συμπληρωθεί με (1-r)N μέλη της παλαιάς γενεάς, κατάλληλα επιλεγμένα με βάση το μηχανισμό επιλογής του ΓΑ σε περίπτωση κατά την οποία το πλήθος του είναι μικρότερο από το μέγεθος του πληθυσμού (r≠1). Ο συμπληρωμένος προσωρινός πληθυσμός θα αποτελέσει τη νέα γενεά, αφού πρώτα επιδράσει σε αυτόν ο γενετικός τελεστής της μετάλλαξης (βλέπε Σχήμα 4.37).

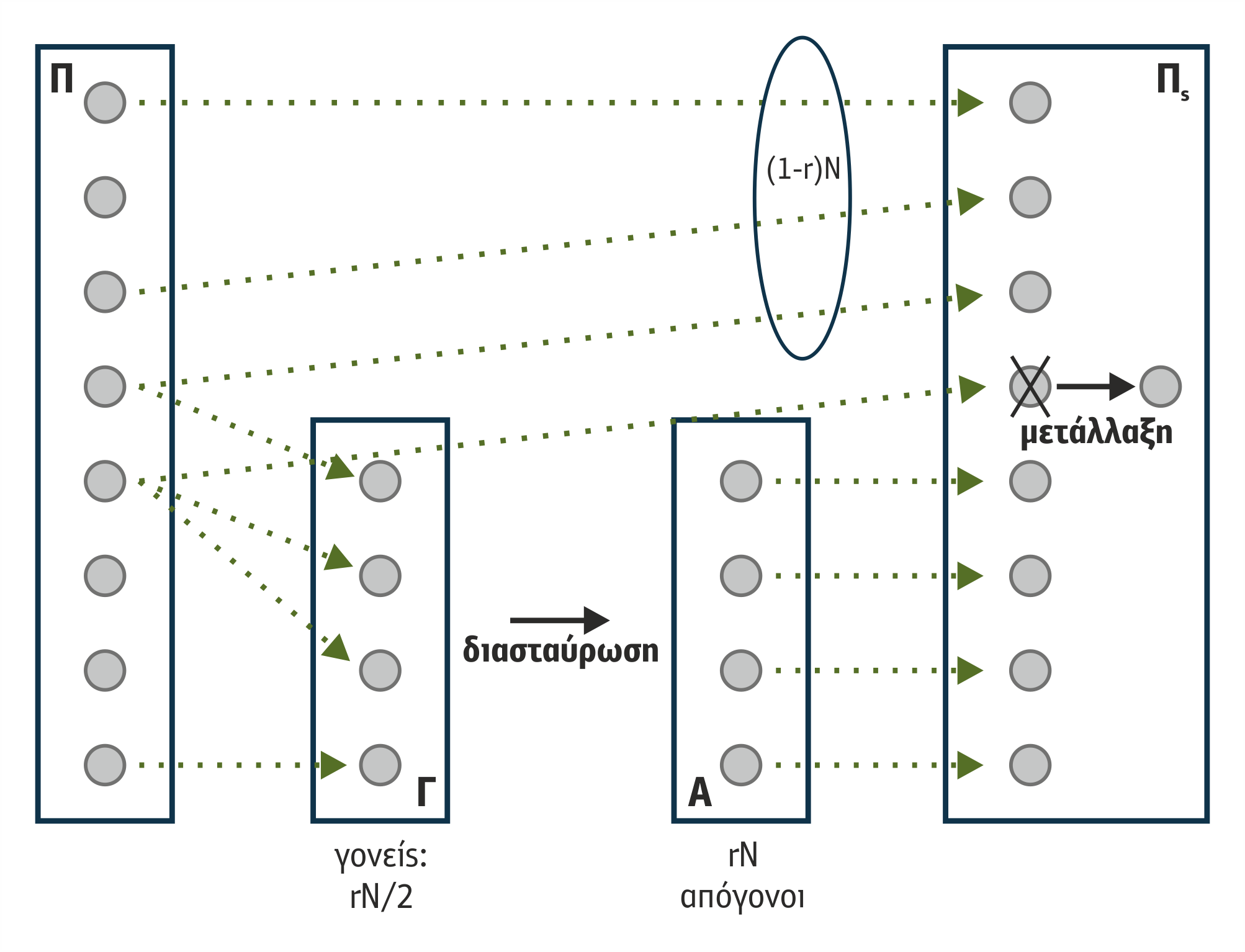
Σχήμα 4.37 Αναπαραγωγή πληθυσμού

4.6.9 Γενετικοί Τελεστές

Απαραίτητοι για την εξέλιξη του πληθυσμού είναι οι γενετικοί τελεστές (genetic operators), που επιδρούν στον πληθυσμό επαναληπτικά, με απώτερο σκοπό να περιληφθούν σε αυτόν οι βέλτιστες λύσεις ή δομές, δηλαδή οι συμβολοσειρές με την καλύτερη τιμή απόδοσης.

Ένας ΓΑ αποδίδει ικανοποιητικά αποτελέσματα βάσει δύο θεμελιωδών γενετικών τελεστών:

• Διασταύρωση
• Μετάλλαξη

Οι τελεστές υποστηρίζουν ο ένας τον άλλον κατά σημαντικό τρόπο. Η μετάλλαξη εισάγει τη διαφοροποίηση στον πληθυσμό και η διασταύρωση ενεργεί για το σχεδιασμό των καλών σχημάτων που ήδη υπάρχουν. Αν η μετάλλαξη καταργηθεί, ο αλγόριθμος συγκλίνει γρήγορα, ενώ λείπουν σημαντικά σχήματα. Όταν τα σχήματα δεν είναι πλήρη, η διασταύρωση δεν μπορεί να κάνει πραγματική διαφοροποίηση στον πληθυσμό. Αν αφαιρεθεί η διασταύρωση, το σύστημα χρησιμοποιεί τη μετάλλαξη για την ανίχνευση μιας συγκεκριμένης περιοχής χωρίς τη δυνατότητα σχεδιασμού καλύτερων χαρακτηριστικών των σημείων της περιοχής αυτής, που οδηγεί αυτονόητα το σύστημα σε μειωμένη απόδοση.

4.6.10 Διασταύρωση

Αφού επιλέγουν οι γονείς, η αναπαραγωγή αυτή καθεαυτή μπορεί να ξεκινήσει εφαρμόζοντας καταρχάς τον γενετικό τελεστή της Διασταύρωσης (Crossover) που στη βιολογία αναφέρεται και ως Γενετική Μείωση. Η αναπαραγωγή μέσω διασταύρωσης είναι συνδυασμένη πληροφορία από δυο γονείς για το σχηματισμό απογόνων. Πολλοί ερευνητές πιστεύουν πως η διασταύρωση είναι τόσο σημαντικό συστατικό ενός ΓΑ, ώστε, αν αφαιρεθεί από αυτόν, τότε παύει να είναι γενετικός αλγόριθμος. Ο μηχανισμός της αναπαραγωγής μαζί με τη διασταύρωση έχουν ως αποτέλεσμα τα καλύτερα σχήματα να επικρατούν στον πληθυσμό και ο συνδυασμός τους να παράγει νέα σχήματα υψηλής ποιότητας.

Μια νέα δομή παράγεται επιλέγοντας είτε από τον ένα γονέα είτε από τον άλλον ένα αλληλόμορφο (allele) για καθένα από τα γονίδια του χρωμοσώματος. Η διαδικασία συνδυασμού των γονιδίων μπορεί να πραγματοποιηθεί με διάφορους τρόπους που παρουσιάζονται στη συνέχεια.

Διασταύρωση Ενός Σημείου

Η απλούστερη μέθοδος συνδυασμού ονομάζεται διασταύρωση ενός σημείου (single point crossover), την οποία εδώ παρουσιάζουμε χρησιμοποιώντας γονίδια που κωδικοποιούνται δυαδικά (βλέπε Σχήμα 4.38), αν και η διαδικασία βρίσκει εφαρμογή σε σχεδόν οποιαδήποτε γονιδιακή αναπαράσταση (βλέπε Σχήμα 4.39). Το σημείο διασταύρωσης επιλέγεται τυχαία κάπου στη σειρά των γονιδίων. Όλο το γενετικό υλικό μετά από το σημείο διασταύρωσης λαμβάνεται από τον ένα γονέα και όλο το υλικό μετά το σημείο διασταύρωσης λαμβάνεται από τον άλλο.

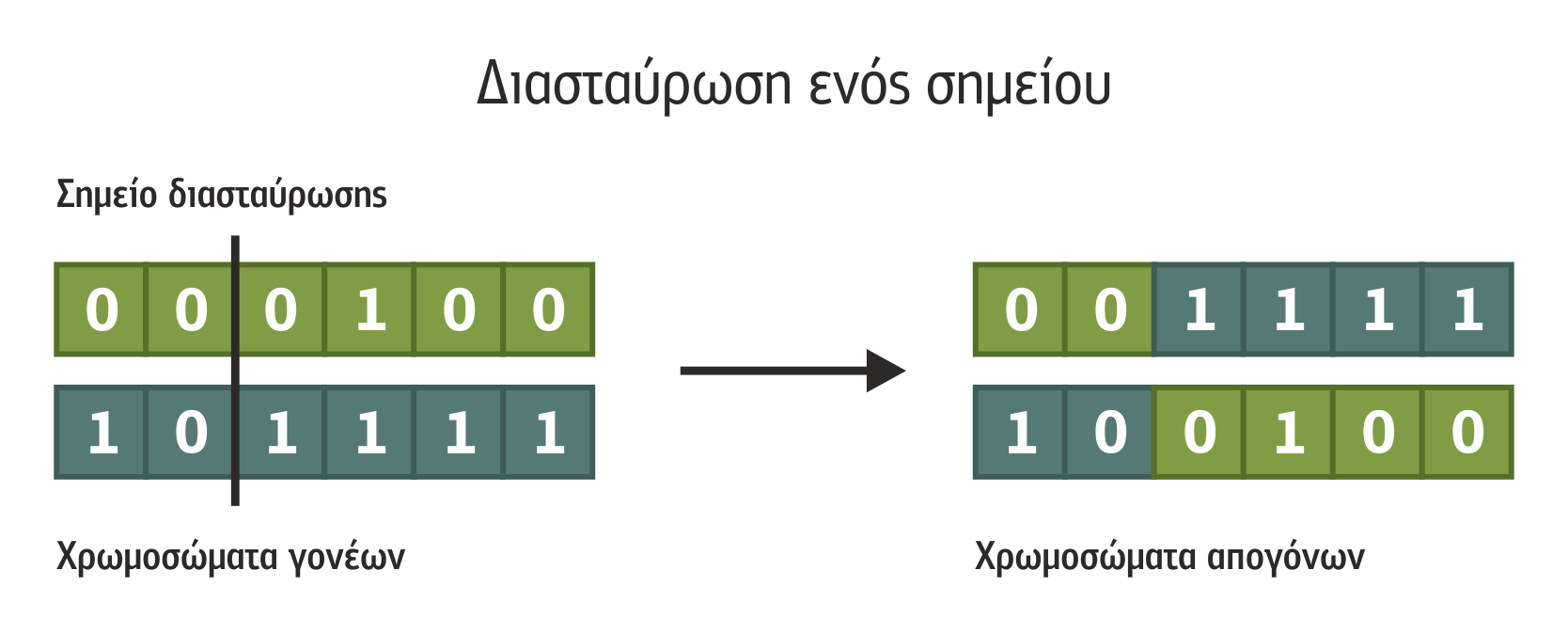
Σχήμα 4.38 Διασταύρωση ενός σημείου

Στην περίπτωση κωδικοποίησης με αλφάβητο φυσικών αριθμών, η διασταύρωση ενός σημείου θα μπορούσε να επιτευχθεί με μετάθεση των γονιδίων ενός γονέα με οδηγό τον άλλο γονέα, όπως στο παράδειγμα του σχήματος 4.39, όπου ο πληθυσμός έχει χρωμοσώματα μήκους 5 με γονίδια κωδικοποιημένα στο αλφάβητο {2 3 4 5 6}, με κάθε γονίδιό του να έχει διαφορετική τιμή από τα άλλα. Αν το σημείο διασταύρωσης είναι το 2 και ο 1ος γονέας είναι ο (5,3,4,6,2) και ο 2ος ο (3,4,2,6,4), τότε ο ένας απόγονος διαμορφώνεται από τα πρώτα δύο γονίδια του 1ου γονέα, δηλαδή τα 5 & 3, και τα υπόλοιπα 3 που υπολείπονται, δηλαδή τα 4,2 & 6, προέρχονται από τον 2ο γονέα και τοποθετούνται στη σειρά με την οποία εμφανίζονται στον 2ο γονέα. Το αντίστοιχο συμβαίνει για τον άλλο απόγονο.

Σχήμα 4.39 Διασταύρωση ενός σημείου για φυσικούς αριθμούς

Διασταύρωση Πολλαπλών Σημείων

Η διασταύρωση ενός σημείου έχει το μειονέκτημα ότι στην αναπαράσταση που χρησιμοποιείται στον αλγόριθμο τα αλληλόμορφα που βρίσκονται κοντά μεταξύ τους διατηρούνται μαζί με πολύ μεγαλύτερη πιθανότητα από εκείνα που είναι περισσότερο απομακρυσμένα.

Ένας απλός τρόπος για τη μείωση αυτού του προβλήματος είναι να χρησιμοποιηθεί μια διαδικασία διασταύρωσης δύο σημείων. Στη διασταύρωση δύο σημείων (two-points crossover) δημιουργούνται δύο τυχαίες θέσεις . Στους απογόνους αντιγράφονται από τον ένα γονέα τα αλληλόμορφα πριν και μετά τα σημεία διασταύρωσης, και από τον άλλο γονέα αυτά που είναι ανάμεσα στα σημεία διασταύρωσης.

Η διαδικασία της διασταύρωσης μπορεί να πραγματοποιηθεί με περισσότερα από δύο σημεία διασταύρωσης. Ακόμη και όλα τα σημεία μπορούν να επιλεγούν για διασταύρωση, αν το επιθυμούμε. Σε αυτή την περίπτωση, κάθε γονίδιο έχει ίση πιθανότητα να προέλθει από τον ένα ή τον άλλο γονέα και μπορεί να υπάρχει σημείο διασταύρωσης μετά από οποιοδήποτε γονίδιο. Αυτή η ιδέα οδηγεί στη γενίκευση ότι θα μπορούσε κανείς, για παράδειγμα, να χρησιμοποιήσει έναν τυχαίο αριθμό σημείων διασταύρωσης σε κάθε επανάληψη.

Σχήμα 4.40 Διασταύρωση δυο σημείων

Ομοιόμορφη Διασταύρωση

Μία μέθοδος διασταύρωσης, που χρησιμοποιείται συχνά, είναι η ομοιόμορφη διασταύρωση (uniform crossover), η οποία λειτουργεί ως εξής: Αρχικά επιλέγονται δύο γονείς με στόχο να δημιουργηθούν δύο απόγονοι. Για κάθε γονιδιακή θέση ενός απογόνου, αποφασίζεται τυχαία ποιος από τους γονείς θα συνεισφέρει το δικό του αλληλόμορφο που βρίσκεται στην αντίστοιχη θέση.

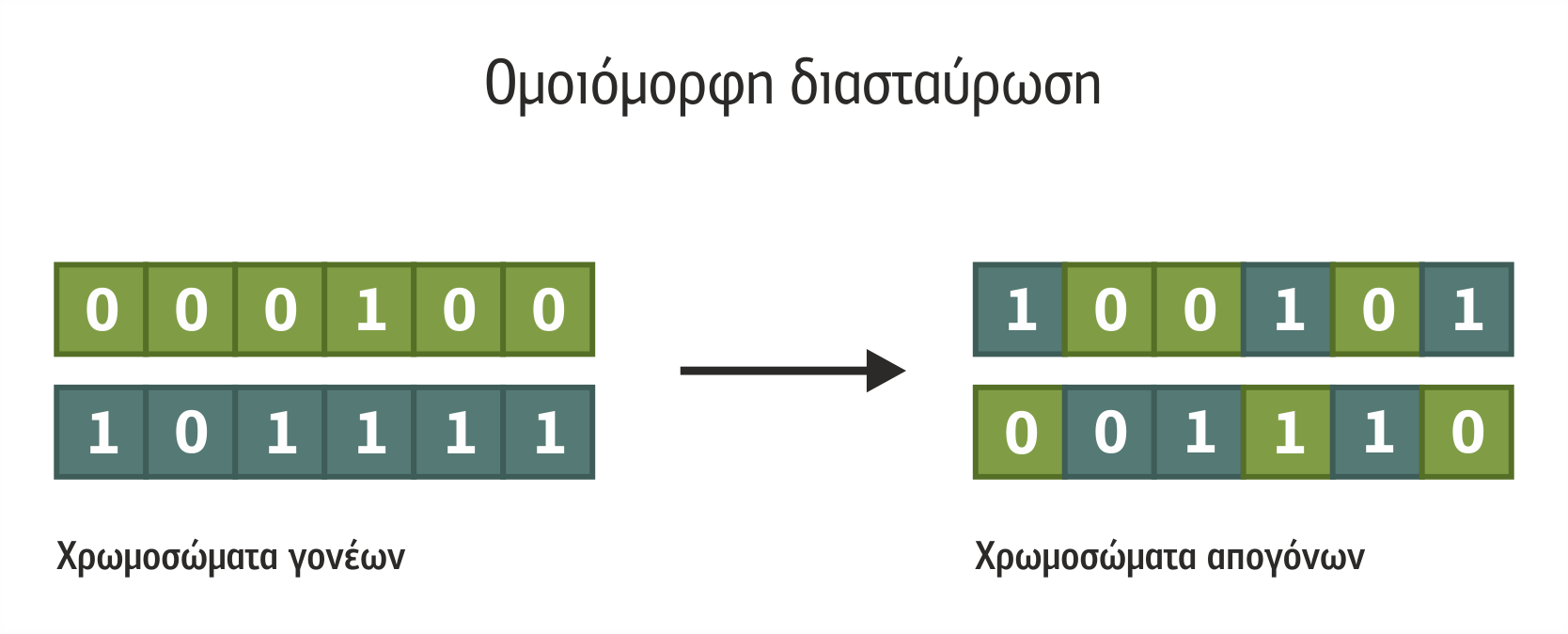
Σχήμα 4.41 Ομοιόμορφη τυχαία Διασταύρωση

Για την υλοποίηση αυτής της μεθόδου διασταύρωσης μπορούμε να χρησιμοποιήσουμε ως οδηγό μια τυχαία δημιουργημένη μάσκα σε μορφή μονοδιάστατου πίνακα με άσσους και μηδενικά, της οποίας οι μεν άσσοι ευνοούν τον πρώτο γονέα, ο οποίος δίνει την τιμή του γονιδίου του σε εκείνη τη θέση στον πρώτο απόγονο, τα δε μηδενικά ευνοούν το δεύτερο γονέα. Ο άλλος απόγονος παίρνει για κάθε γονιδιακή θέση το αλληλόμορφο του εκάστοτε μη ευνοημένου γονέα σε εκείνη τη θέση.

Σχήμα 4.42 Ομοιόμορφη Διασταύρωση με χρήση μάσκας

4.6.11 Μετάλλαξη (Mutation)

Στον φυσικό κόσμο, ο βιολογικός γονικός οργανισμός προωθεί αντίγραφα του γενετικού του κώδικα στους απογόνους του. Συνήθως όμως, κάποιο λάθος στην αντιγραφή μπορεί να προκαλέσει μια ωφέλιμη αλλαγή. Ο σκοπός της μετάλλαξης (mutation) είναι να εισαγάγει θόρυβο και, ειδικότερα, νέα αλληλόμορφα γονίδια εντός του πληθυσμού. Η μετάλλαξη είναι χρήσιμη, γιατί βοηθάει να βρεθούν τα τοπικά ακρότατα που δεν έχουν ανακαλυφθεί ακόμα, δεδομένου ότι βοηθά να εξερευνηθούν νέες περιοχές του πολυδιάστατου χώρου λύσεων. Εάν ο ρυθμός μετάλλαξης είναι πολύ υψηλός, μπορεί να οδηγήσει σε απώλεια καλών γονιδίων, με επακόλουθο να μειωθεί η εκμετάλλευση των περιοχών υψηλής καταλληλότητας του χώρου λύσεων. Για να πραγματοποιηθεί η μετάλλαξη, επιλέγεται πρώτα το ποσοστό m που θα καθορίσει το πλήθος των μελών στα οποία θα εφαρμοστεί η μετάλλαξη. Το ποσοστό m συνήθως είναι πολύ μικρό (< 10%) και πολλές φορές μηδενικό. Σε περίπτωση που το m είναι μηδενικό, δεν χρησιμοποιείται καθόλου ο τελεστής μετάλλαξης, με κίνδυνο ο ΓΑ να εγκλωβιστεί σε τοπικά ακρότατα ή να συγκλίνει πρόωρα.

Μόλις έχει επιλεγεί ένα γονίδιο για μετάλλαξη, η ίδια η μετάλλαξη μπορεί να λάβει διάφορες μορφές. Αυτό, πάλι, εξαρτάται από την υλοποίηση του γενετικού αλγόριθμου. Η μετάλλαξη στους ΓΑ υλοποιείται γενικά μέσω της τυχαίας αλλαγής κάποιων εκ των γονιδίων του χρωμοσώματος. Οι αλλαγές που επιφέρονται στα σχήματα από τη μετάλλαξη δεν έχουν σχέση με την απόδοσή τους.

Στην περίπτωση της κωδικοποίησης με δυαδικό αλφάβητο (βλέπε Σχήμα 4.43), η απλή μετάλλαξη ενός μόνο γονιδίου οδηγεί στο συμπλήρωμα της τιμής αυτού του γονιδίου, δηλαδή το ένα 1 γίνεται 0 και το αντίστροφο.

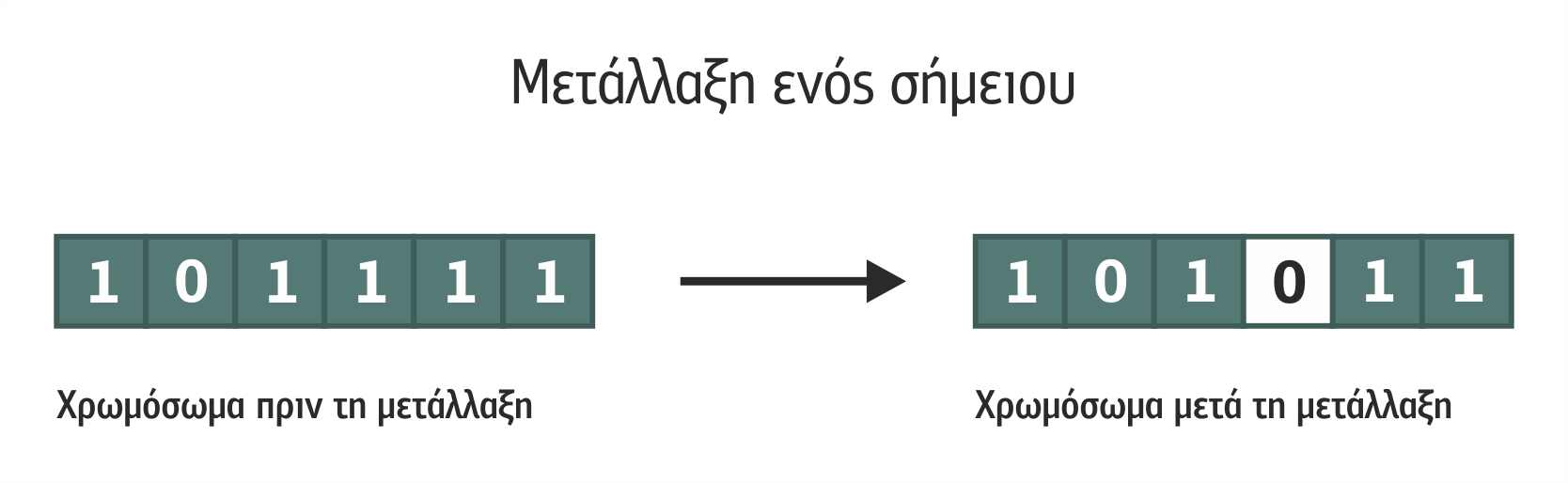
Σχήμα 4.43 Η διαδικασία της μετάλλαξης σε δυαδικές συμβολοσειρές

Συνήθως, το σημείο ή τα σημεία μετάλλαξης επιλέγονται τυχαία ή με τη βοήθεια μιας μήτρας σημείων μετάλλαξης (βλέπε Σχήμα 4.44).

Σχήμα 4.44 Η διαδικασία της μετάλλαξης 3 σημείων βάσει μήτρας

Στην περίπτωση της μη δυαδικής κωδικοποίησης του χρωμοσώματος, απαιτούνται πιο περίπλοκες μέθοδοι μετάλλαξης. Η πιο απλή από αυτές είναι η μετάλλαξη τυχαίας ανταλλαγής, όπου γίνεται τυχαία επιλογή δύο γονιδίων και ανταλλαγή των θέσεών τους μέσα στο ίδιο χρωμόσωμα, όπως αυτή φαίνεται στο σχήμα 4.45. Άλλη είναι η μετάλλαξη scrabble lists (scrabble lists mutation) κατά την οποία αποκόπτεται με τυχαία επιλογή μια υπολίστα γονιδίων μέσα στο χρωμόσωμα, τα οποία κατά τη μετάλλαξη αναδιατάσσονται επίσης με τυχαίο τρόπο. Τέλος, στην ομοιόμορφη μετάλλαξη (uniform mutation), επιλέγονται εκτός του χρωμοσώματος που θα υποστεί μετάλλαξη και ένα δεύτερο χρωμόσωμα που θα οδηγήσει τη μετάλλαξη. Από το πρώτο χρωμόσωμα κρατούνται τυχαία κάποια γονίδια στις θέσεις τους (έστω το 50%) και τα υπόλοιπα ταξινομούνται βάσει της θέσης τους στο δεύτερο χρωμόσωμα. Στο παράδειγμα του σχήματος 4.45, από το x1 κρατούνται τα 2,3,5,6 και τα υπόλοιπα ταξινομούνται βάσει της θέσης τους στο άλλο χρωμόσωμα, δηλαδή τοποθετούνται μέσα στις κενές θέσεις στο χρωμόσωμα με τη σειρά 8,4,7,1. Η ομοιόμορφη μετάλλαξη μπορεί να γίνει και σε ζεύγη χρωμοσωμάτων, κρατώντας κάποια γονίδια και από τα δυο χρωμοσώματα στη θέση τους και ταξινομώντας τα υπόλοιπα με βάση τη θέση τους στο άλλο χρωμόσωμα.

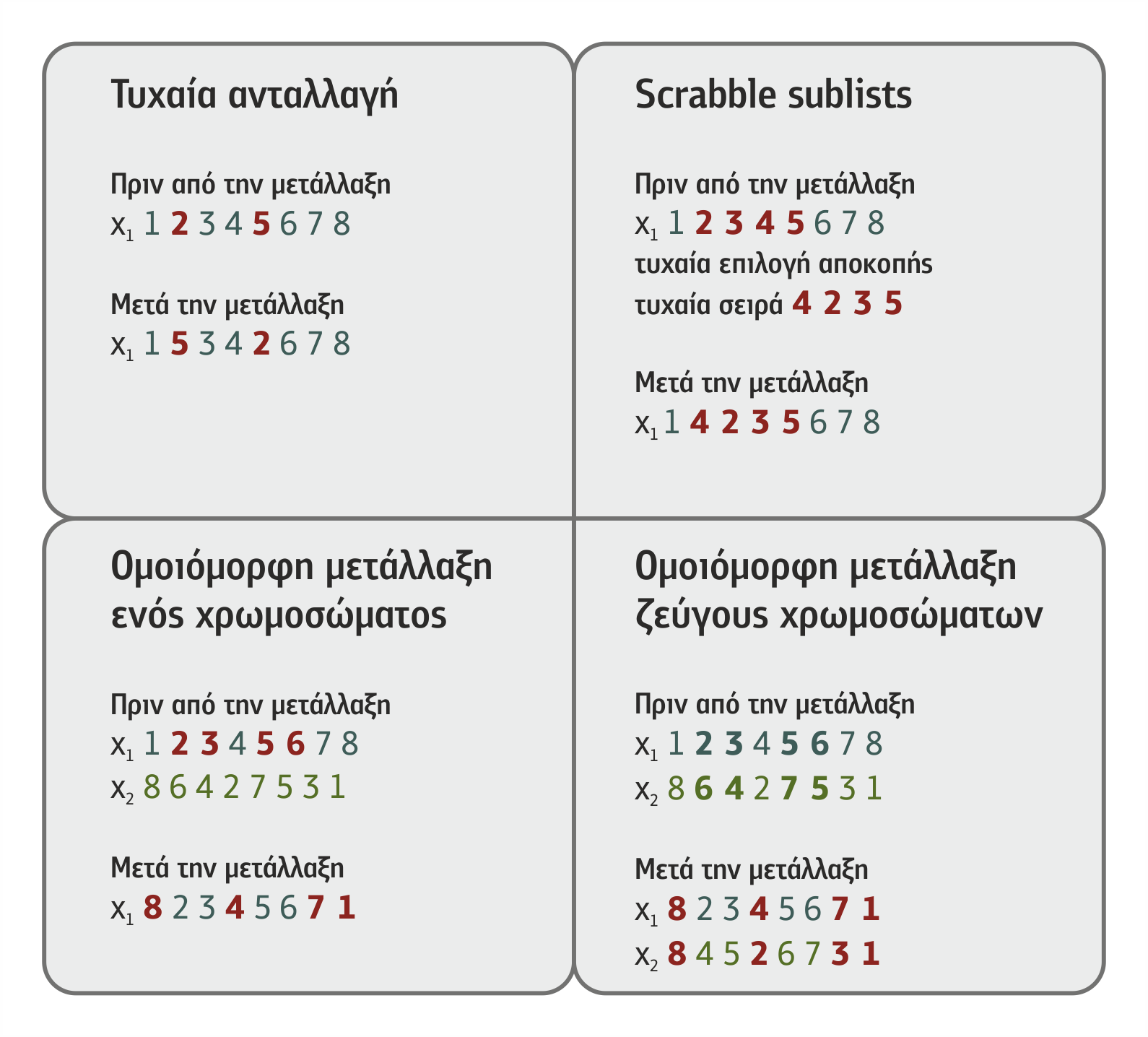
Σχήμα 4.45 Τεχνικές μετάλλαξης σε μη δυαδικές συμβολοσειρές

Σε πιο σύνθετους τύπους δεδομένων, μια τιμή μπορεί να επιλεγεί τυχαία από μια συλλογή με πιθανές τιμές. Σε γενετικές αναπαραστάσεις με υψηλότερο βαθμό αποκωδικοποίησης, η μετάλλαξη γίνεται όλο και πιο περίπλοκη. Σε κάθε περίπτωση, το μόνο που απαιτείται είναι να είναι η μέθοδος της μετάλλαξης αρκετά γενική, ώστε να μπορεί να προκαλέσει την εμφάνιση οποιουδήποτε πιθανού αλληλόμορφου εντός του πληθυσμού.

4.6.12 Γενεαλογική Αντικατάσταση

Μετά την εφαρμογή των γενετικών τελεστών, ακολουθεί η οριστικοποίηση της νέας γενεάς με την αντικατάσταση των γονέων από τους απόγονους τους, η οποία ονομάζεται γενεαλογική αντικατάσταση (generational replacement). Αξίζει να αναφέρουμε τις 3 κατηγορίες αντικατάστασης που έχουν επικρατήσει:

• Ολική αντικατάσταση (total replacement): ολόκληρος ο πληθυσμός των γονέων αντικαθίσταται από τους απόγονους.
• Μερική αντικατάσταση (partial replacement): ένα μέρος του νέου πληθυσμού των γονέων (συνήθως αυτοί με τη χαμηλότερη απόδοση) αντικαθίσταται από ένα ισοδύναμο πλήθος από απογόνους (συνήθως αυτούς με την υψηλότερη απόδοση).
• Αντικατάσταση σταθερής κατάστασης (steady state replacement): κάθε απόγονος που παράγεται αντικαθιστά έναν γονέα (συνήθως τον χειρότερο) και ταυτόχρονα μπορεί να πάρει μέρος στην παραγωγή του επόμενου απόγονου.

Υπάρχουν δύο ανταγωνιστικοί παράγοντες που πρέπει να εξισορροπούνται κατά τη διαδικασία αντικατάστασης, όταν αυτή δεν είναι ολική: η επιλεκτική πίεση και η γενετική ποικιλομορφία.

 

Επιλεκτική πίεση είναι η τάση να επιλέγονται μόνο τα καλύτερα μέλη της τρέχουσας γενεάς, για να διαδοθούν στην επόμενη. Είναι απολύτως απαραίτητη, για να κατευθύνει τον γενετικό αλγόριθμο σε ένα βέλτιστο.

Γενετική ποικιλομορφία είναι η διατήρηση ενός ποικιλόμορφου πληθυσμού λύσεων. Είναι επίσης απαραίτητη, για να εξασφαλιστεί ότι ο χώρος λύσεων έχει διερευνηθεί επαρκώς, ιδιαίτερα στα αρχικά στάδια της εκτέλεσης του αλγόριθμου.

 

Η υπερβολική επιλεκτική πίεση μπορεί να μειώσει τη γενετική ποικιλομορφία, ώστε το ολικό βέλτιστο να παραβλέπεται και ο γενετικός αλγόριθμος να συγκλίνει σε ένα κάποιο τοπικό βέλτιστο. Ωστόσο, με πολύ μικρή επιλεκτική πίεση ο αλγόριθμος δεν μπορεί να συγκλίνει σε μια βέλτιστη λύση σε εύλογο χρονικό διάστημα. Μια σωστή ισορροπία ανάμεσα στην επιλεκτική πίεση και τη γενετική ποικιλομορφία είναι απαραίτητη, για να συγκλίνει ο αλγόριθμος στο ολικό βέλτιστο σε ένα εύλογο χρονικό διάστημα.

4.6.13 Εκλεκτικές Στρατηγικές

Μια τεχνική που χρησιμοποιούμε, πριν οριστικοποιηθεί η κάθε γενεά, είναι ο Ελιτισμός (Elitism). Βασική αρχή του Ελιτισμού είναι η εύρεση του ατόμου με την υψηλότερη τιμή απόδοσης από την παλαιά γενεά και η αντιγραφή του στη νέα γενεά, ακόμα και αν οι εφαρμοζόμενες τεχνικές αναπαραγωγής απαιτήσουν την εξάλειψή του. Αυτό είναι μία εξασφάλιση ότι η καλύτερη λύση δεν θα χαθεί κατά τη γονική επιλογή ή κατά την εφαρμογή των γενετικών τελεστών και τελικά θα είναι η λύση στην οποία πρέπει να συγκλίνει όλος ο πληθυσμός.

Η αντιγραφή του τρέχοντος καλύτερου χρωμοσώματος στην επόμενη γενεά γίνεται με δύο διαφορετικούς τρόπους:

• Μόνο εάν δεν υπάρχει ήδη
• Ούτως ή άλλως

Υπάρχουν διάφορες εκδοχές για τη θέση μέσα στον πληθυσμό που θα καταλάβει:

• θέση ενός τυχαία επιλεγμένου χρωμοσώματος,
• θέση του χρωμοσώματος με τη μικρότερη απόδοση,
• χωρίς αντικατάσταση κάποιου άλλου χρωμοσώματος, οπότε προκαλείται μικρή σταδιακή αύξηση του μεγέθους του πληθυσμού.

4.6.14 Ολοκλήρωση ΓΑ

Το απλούστερο κριτήριο για να ολοκληρωθεί ένας ΓΑ είναι να βρεθεί στον πληθυσμό μιας γενεάς του μια λύση που να έχει τιμή απόδοσης πάνω από μια προκαθορισμένη ικανοποιητική τιμή, αν κάτι τέτοιο είναι εύκολο από το πρόβλημα να καθοριστεί.

Άλλο κριτήριο είναι η σύγκλιση του ΓΑ. Ένας ΓΑ συγκλίνει, όταν η συγκέντρωση των μελών του πληθυσμού βρίσκεται σε μία στενή περιοχή του συνολικού χώρου των λύσεων προσεγγίζοντας ένα τοπικό ή γενικό βέλτιστο. Αυτό φαίνεται, όταν οι γονότυποι των μελών του πληθυσμού είναι σχεδόν όλοι ίδιοι και ο ανασυνδυασμός τους δεν μπορεί να παράγει νέες λύσεις, με αποτέλεσμα τη στασιμότητα στην εξέλιξη του αλγόριθμου. Η μόνη πιθανότητα παραγωγής νέας βελτιωμένης λύσης σε μια τέτοια περίπτωση είναι μέσω της μετάλλαξης, αν και έχει μικρή πιθανότητα επιτυχίας.

Η σύγκλιση του ΓΑ μπορεί να αποτελέσει ένα κριτήριο τερματισμού του. Όμως, δεν είναι εύκολο να εντοπιστεί και για το λόγο αυτόν χρησιμοποιείται ως εναλλακτικό κριτήριο τερματισμού η ολοκλήρωση ενός μέγιστου αριθμού γενεών που έχει καθοριστεί από την έναρξη του ΓΑ.

 

Έτσι, ένας ΓΑ μπορεί να τερματιστεί:

• σε περίπτωση λύσης με ικανοποιητική τιμή απόδοσης,
• όταν επί μεγάλου αριθμού συνεχόμενων γενεών δεν παράγεται καλύτερη ή διαφορετική λύση,
• εάν το πλήθος των γενεών φτάσει σε έναν προκαθορισμένο αριθμό, π.χ. 500 γενεές.

4.6.15 Διαφορές από άλλες τεχνικές

Οι γενετικοί αλγόριθμοι διαφέρουν από άλλες τεχνικές αναζήτησης στα εξής σημεία:

• Εξισορροπούν την αναζήτηση νέων σημείων στο χώρο αναζήτησης με την εκμετάλλευση των ήδη γνωστών πληροφοριών.
• Είναι τυχαίοι αλγόριθμοι, δεδομένου ότι χρησιμοποιούν τελεστές των οποίων τα αποτελέσματα εξαρτώνται από τις πιθανότητες, με την έννοια ότι είναι βασισμένα στην τιμή ενός τυχαίου αριθμού. Δηλαδή, οι ΓΑ χρησιμοποιούν πιθανολογικούς κανόνες μετάβασης, όχι αιτιοκρατικούς.
• Λειτουργούν σε διάφορες λύσεις ταυτόχρονα, συγκεντρώνοντας πληροφορίες από τα τρέχοντα σημεία αναζήτησης για το αμέσως επόμενο επαναληπτικό βήμα. Η δυνατότητά τους να διατηρούν πολλαπλές λύσεις ταυτόχρονα τους καθιστά λιγότερο ευαίσθητους στο πρόβλημα των τοπικών μεγίστων και του θορύβου.
• Λειτουργούν με μια κωδικοποίηση του συνόλου των παραμέτρων, όχι με τις ίδιες τις παραμέτρους.
• Εκτελούν την αναζήτηση σε έναν πληθυσμό σημείων, όχι σε ένα μοναδικό σημείο.
• Χρησιμοποιούν τη συνάρτηση καταλληλότητας, για να στοχεύσουν σημεία στο χώρο λύσεων χωρίς άλλη βοηθητική γνώση.

4.6.16 Εφαρμογές Γενετικών Αλγορίθμων

Οι γενετικοί αλγόριθμοι έχουν εφαρμογή σε πολύπλοκα προβλήματα, κυρίως βελτιστοποίησης και χρονοδρομολόγησης. Προβλήματα με τέτοια χαρακτηριστικά που λύνονται πολύ αποτελεσματικά με την εφαρμογή ΓΑ είναι:

 

• εύρεση μέγιστης τιμής αριθμητικών συναρτήσεων,
• επεξεργασία εικόνων,
• συνδυαστική βελτιστοποίηση (καταμερισμός εργασιών, ωρολόγιο πρόγραμμα, πλανόδιος πωλητής κτλ),
• σχεδίαση (λύση+βελτιστοποίηση+νέες ιδέες κατασκευής),
• ανακάλυψη κανόνων.

 

Ειδική κατηγορία εφαρμογής ΓΑ είναι ο Γενετικός Προγραμματισμός (Genetic Programming), που έχει ως στόχο την αυτόματη κατασκευή κώδικα προγραμμάτων Η/Υ από τυπικές αλγοριθμικές δομές (IF-THEN-ELSE, WHILE κτλ.) που παίζουν το ρόλο των γονιδίων ενός χρωμοσώματος που αντιστοιχεί στον κώδικα που ζητείται να κατασκευαστεί.