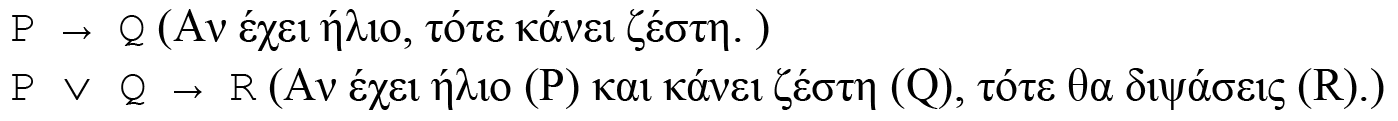ΚΕΦΑΛΑΙΟ 2 - Αναπαράσταση Γνώσης

Σύνοψη

Στο χώρο της επίλυσης προβλημάτων, κυρίως του πραγματικού κόσμου, η καταλληλότητα της επιλεγμένης μεθόδου για την αναπαράσταση της γνώσης που υπάρχει σχετικά με ένα πρόβλημα είναι θεμελιώδους σημασίας, όταν αυτό πρόκειται να επιλυθεί μέσω συστημάτων διαχείρισης της γνώσης, όπως είναι, για παράδειγμα, τα έμπειρα συστήματα. Στο συγκεκριμένο κεφάλαιο αναλύεται η έννοια της γνώσης και παρουσιάζονται οι βασικές λογικές και δομημένες μέθοδοι αναπαράστασης γνώσης, μεταξύ των οποίων συγκαταλέγονται ο κατηγορηματικός λογισμός πρώτης τάξης, τα σημασιολογικά δίκτυα, τα πλαίσια, τα σενάρια και οι κανόνες. Επίσης, ιδιαίτερη αναφορά γίνεται στους εννοιολογικούς χάρτες και στις οντολογίες.

Προαπαιτούμενη γνώση

Δεν υπάρχει προαπαιτούμενη γνώση.

2.1 Γνώση

Η γνώση αποτελεί ακρογωνιαίο λίθο της ανθρώπινης συμπεριφοράς, της οποίας τα ευφυή στοιχεία προσπαθεί ο άνθρωπος να μεταδώσει σε μια υπολογιστική μηχανή. Στο προηγούμενο κεφάλαιο, 1, αναφερθήκαμε πολλές φορές στον όρο ευφυΐα. Θα ήταν, λοιπόν, σκόπιμο να διευκρινίσουμε τι ακριβώς εννοούμε με αυτόν, γιατί, πριν επιχειρήσουμε να μεταδώσουμε ευφυΐα σε μια μηχανή, πρέπει να κατανοήσουμε τη φύση της δικής μας ευφυΐας.

Έχουν δοθεί πολλοί ορισμοί σχετικά με την ευφυΐα, αλλά θεωρείται σκοπιμότερο να περιγραφεί σύμφωνα με τα χαρακτηριστικά της:

 

Eυφυΐα (intelligence) είναι η συνεχής διαδικασία της συγκέντρωσης, εξέτασης, ταξινόμησης και διερμηνείας πληροφοριών.

 

Με τον όρο πληροφορία εννοούμε το σύνολο όλων των γεγονότων, των σχημάτων, των δεδομένων και των όρων που έχει κάποιος επινοήσει ή συγκεντρώσει, για να δημιουργήσει μία εσωτερική αναπαράσταση ή μοντέλο για τον κόσμο. Με τον όρο διερμηνεία, εννοούμε την επεξεργασία των πληροφοριών αυτών για επίλυση προβλημάτων, λήψη αποφάσεων και άντληση νέων πληροφοριών.

Για να οδηγήσει η πληροφορία σε μια ορθή διερμηνεία της, ο τρόπος με τον οποίο παρουσιάζεται μια πληροφορία πρέπει να καθιστά σαφές το νόημά της∙˙ για να το επιτύχει αυτό, συνήθως επιβάλλεται να παρουσιάζεται η πληροφορία τοποθετημένη μέσα στο εννοιολογικό της πλαίσιο. Για παράδειγμα, η παρακάτω αιγυπτιακή ιερογλυφική απεικόνιση έχει διερμηνευτεί από τους αρχαιολόγους, διότι τη συνέδεσαν εννοιολογικά με άλλα σύγχρονα ευρήματά της:

Εικόνα 2.1 Παράδειγμα πληροφορίας τοποθετημένης σε εννοιολογικό πλαίσιο

Αντίθετα, τα ευρήματα των μονολιθικών ανθρωπόμορφων στηλών moai στη Χιλιανή Πολυνησία, που απεικονίζονται στην παρακάτω φωτογραφία, δεν έχουν ακόμα διερμηνευτεί πλήρως, διότι δεν έχει καταστεί δυνατό να τοποθετηθούν σε κάποιο γνωστό εννοιολογικό πλαίσιο.

Εικόνα 2.2 Παράδειγμα πληροφορίας μη τοποθετημένης σε εννοιολογικό πλαίσιο

Πρόβλημα στη διερμηνεία της πληροφορίας μπορεί να δημιουργήσουν τα συμφραζόμενα, δηλαδή πόσες διαφορετικές ερμηνείες μπορεί να έχει αυτή∙ για παράδειγμα, η αγγλική λέξη ‘glass’ μπορεί να χρησιμοποιηθεί, για να εκφράσει το ποτήρι, το τζάμι, τα βιτρό ή τα γυαλιά όρασης ή ηλίου.

Σε μια τέτοια περίπτωση, το εννοιολογικό πλαίσιο θα μπορούσε να χρησιμοποιηθεί, για να οδηγήσει στη σωστή διερμηνεία, αλλά αυτό δεν είναι σίγουρο ότι θα είναι πάντα διαθέσιμο. Η ευκολότερη αντιμετώπιση της ύπαρξης συμφραζομένων είναι η πληροφορία να συνοδεύεται με περισσότερα στοιχεία που θα καθιστούν σαφές το νόημά της, π.χ. sun glasses.

Εικόνα 2.3 Συμφραζόμενα της έννοιας ‘glass’

Επειδή πληροφορίες που εμπεριέχουν ασάφειες, δηλαδή το νόημά τους είναι διφορούμενο, δεν μπορούν να οδηγήσουν σε μια συγκεκριμένη διερμηνεία, δεν μπορεί να ελεγχθεί η εγκυρότητά τους, ώστε να αποτελέσουν γνώση. Κλασικό παράδειγμα είναι ο διφορούμενος χρησμός της Πυθίας, όπου ανάλογα με το πού θα μπει το κόμμα κατά την εκφορά του προφορικού λόγου αλλάζει και το νόημα του χρησμού:

Τέλος, σημαντική είναι η αναπαράσταση μιας πληροφορίας για τη διερμηνεία της. Πρωταρχικός στόχος της έρευνας σχετικά με το τι είναι ευφυΐα και του πώς μπορεί να μεταδοθεί σε μια μηχανή είναι η κατανόηση του τρόπου αναπαράστασης των πιστοποιημένων πληροφοριών που κατέχουμε εσωτερικά στη μνήμη μας ως γνώσεις.

Γενικά, αναπαράσταση (representation) είναι το σύνολο των συντακτικών και σημασιολογικών παραδοχών που συγκροτούν μια οντολογία η οποία καθιστά δυνατή την περιγραφή ενός κόσμου ή μιας συγκεκριμένης κατηγορίας πραγμάτων με χρήση μιας συγκεκριμένης γλώσσας, η οποία διαθέτει το δικό της συντακτικό και τη δική της σημασιολογία.

Πρέπει, επίσης, να διευκρινιστεί ότι ο όρος αναπαράσταση διαφέρει από τον όρο περιγραφή με τον οποίο εννοούμε τη χρήση των παραδοχών για την αναπαράσταση ενός συγκεκριμένου στοιχείου μιας κατηγορίας. Η αναπαράσταση αντιστοιχεί στον προσδιορισμό μιας σύνταξης μέσω της οποίας περιγράφεται μια κατηγορία στοιχείων, ενώ η περιγραφή αφορά ένα αποτυπωμένο, μέσω αυτής της σύνταξης, στοιχείο της κατηγορίας σε κάποιο συγκεκριμένο στιγμιότυπο.

Η γνώση διαφέρει ως έννοια και από τα δεδομένα και από την πληροφορία (βλέπε Σχήμα 2.1).

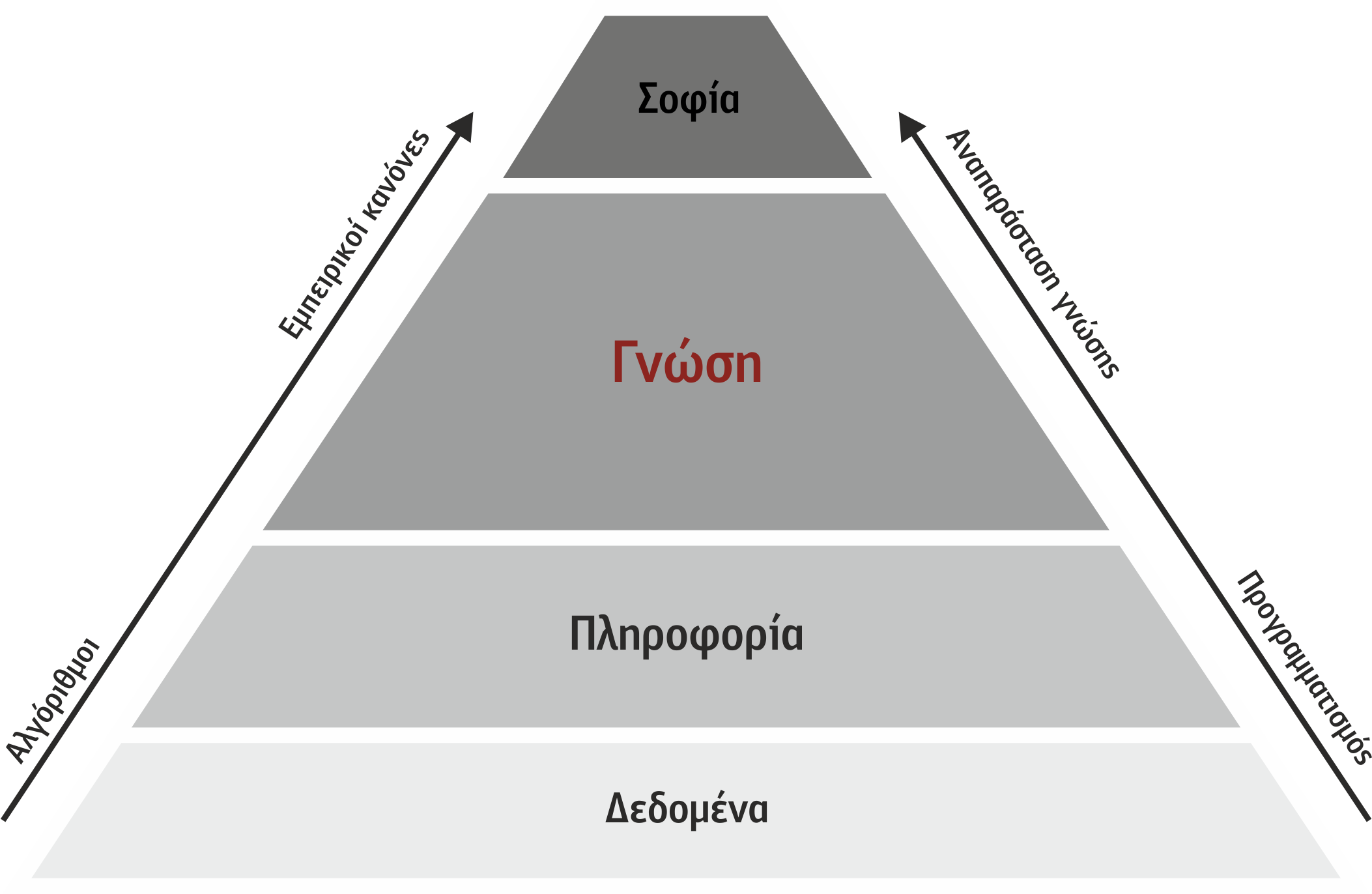
Σχήμα 2.1 Η πυραμίδα της γνώσης

2.1.1 Είδη Γνώσης

Η γνώση που κατέχουμε στη μνήμη μακράς διάρκειας είναι δύο ειδών:

Παραδείγματα διαδικαστικής γνώσης:

Η δηλωτική γνώση μπορεί περαιτέρω να διαχωριστεί σε

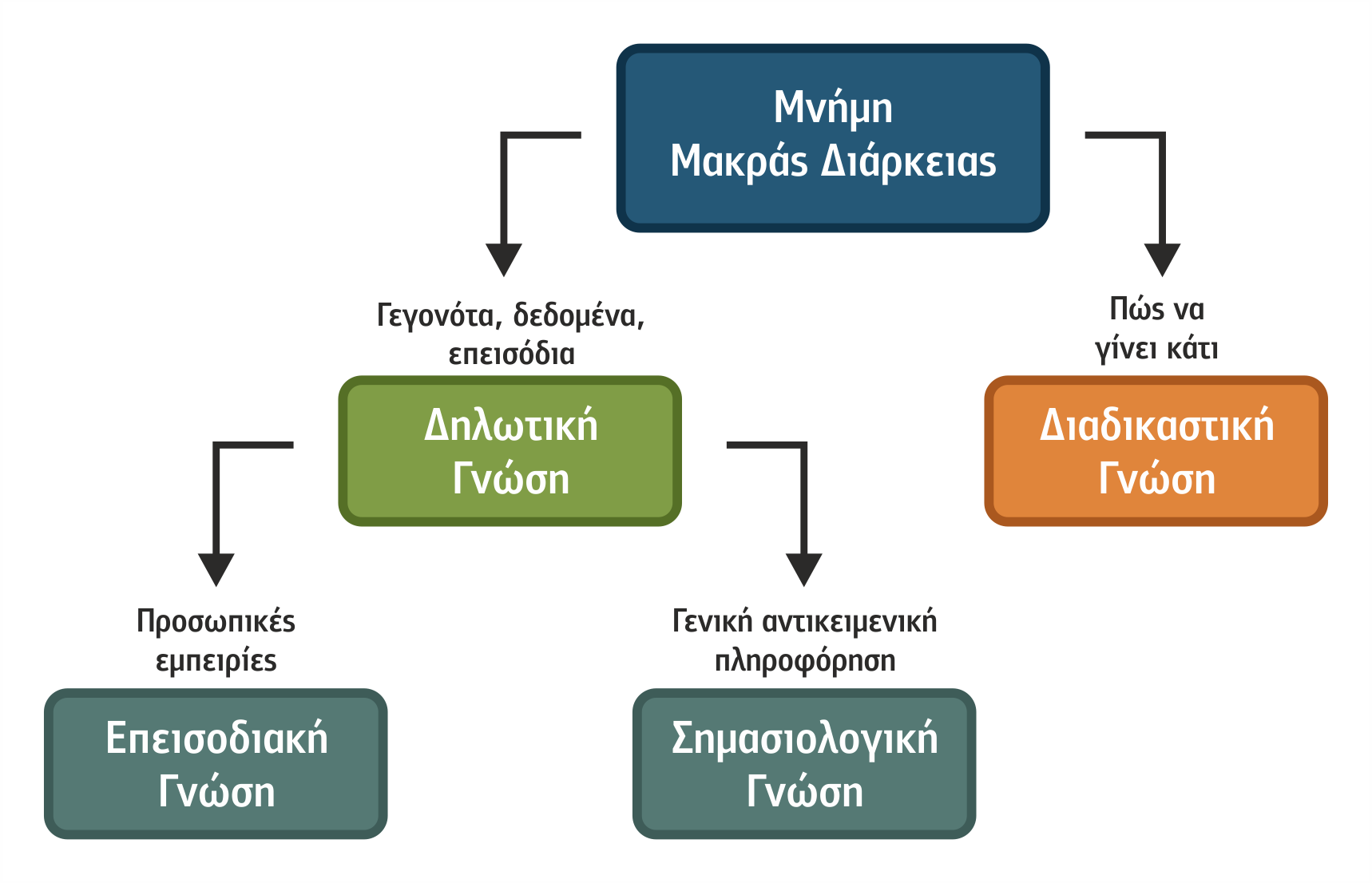
Σχήμα 2.2 Ανάλυση των ειδών γνώσης

Παραδείγματα επεισοδιακής γνώσης:

Παραδείγματα δηλωτικής σημασιολογικής γνώσης:

Η γνώση, δηλωτική ή διαδικαστική, διακρίνεται σε γενική γνώση (general knowledge, common sense) και ειδική γνώση (domain-specific knowledge) για ένα συγκεκριμένο θέμα που κατέχουμε. Π.χ. ξέρουμε γενικά ότι τα λεωφορεία μεταφέρουν επιβάτες από μέρος σε μέρος ή ότι ο πατέρας είναι μεγαλύτερος σε ηλικία από τον γιο του όμως ότι «το λεωφορείο Α8 πηγαίνει στο Μαρούσι» αποτελεί ειδική γνώση την οποία διαθέτουν κάποιοι που μετακινούνται προς το Μαρούσι, αλλά όχι απαραίτητα κάποιοι άλλοι που δεν έχουν επισκεφτεί ποτέ το Μαρούσι και ούτε ενδιαφέρονται να το κάνουν.

 

Παραδείγματα δηλωτικής γνώσης:

Γενική:

Ειδική:

Παραδείγματα διαδικαστικής γνώσης:

Γενική:

Ειδική:

2.2 Αναπαράσταση Γνώσης

Ο καλύτερος τρόπος να εκφράσουμε τη γνώση είναι η φυσική γλώσσα. Για να γίνει, όμως, επεξεργάσιμη από έναν υπολογιστή, χρειάζεται να επιλεγεί πρώτα κατάλληλος τρόπος αποτύπωσής της μέσω κάποιου είδους αναπαράστασης και ακολούθως ένας φορμαλισμός, δηλαδή μιας τεχνητή γλώσσα με το δικό της συντακτικό και τη δική της σημασιολογία, προκειμένου η αναπαράσταση αυτή να καταστεί κατανοητή από τον υπολογιστή.

Δεδομένης της διαφοράς μεταξύ γνώσης, δεδομένων και πληροφοριών, είναι ευνόητο ότι οι μέθοδοι αναπαράστασης της γνώσης πρέπει να διαφέρουν από τις μεθόδους μορφοποίησης των δεδομένων και των πληροφοριών.

Η αναπαράσταση της γνώσης (knowledge representation) που χρησιμοποιείται για την επίλυση ενός προβλήματος μέσα στο χώρο της ΤΝ πρέπει να διαθέτει ένα μονοσήμαντο και τυποποιημένο συμβολισμό που:

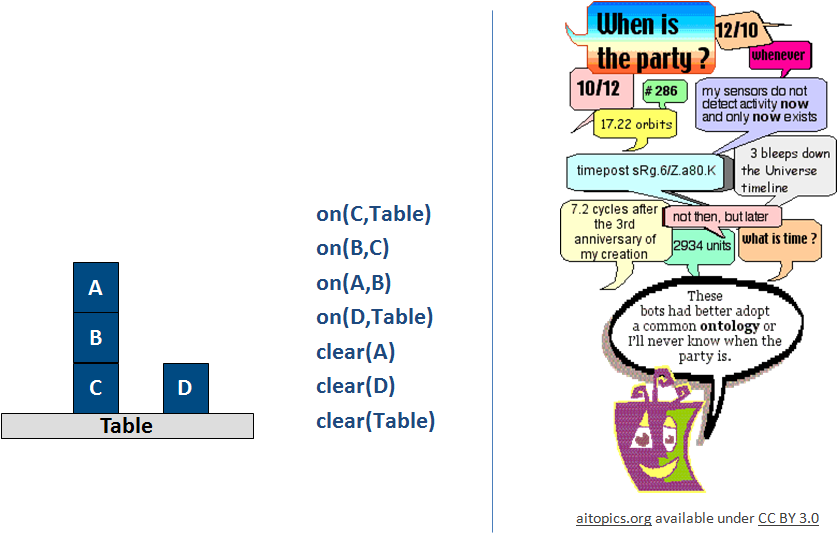
Εικόνα 2.4 Δυο διαφορετικές προσεγγίσεις έκφρασης της γνώσης, (πήγη εικόνας στα δεξιά)

Στην περίπτωση των παραδειγμάτων της εικόνας 2.4, στο δεξί παράδειγμα, που αφορά διαθέσιμη γνώση για την ώρα διεξαγωγής ενός πάρτι, υπάρχουν πολλοί διαφορετικοί τρόποι αναπαράστασης∙ ωστόσο, όλοι είναι ακατάλληλοι προς χρήση, καθώς άλλοι είναι ασαφείς (10/12, not the but later) ) και άλλων η σύνταξη δε διευκολύνει τους μηχανισμούς εξαγωγής συμπερασμάτων. Στο αριστερό παράδειγμα της εικόνας, αυτό της γραφικής αναπαράστασης του κόσμου των κύβων, η αναπαράσταση δεν είναι κατάλληλη, δεδομένου ότι μια αναπαράσταση πρέπει να είναι συμβολική, για να μπορεί να συνδυαστεί κατάλληλα με μηχανισμούς εξαγωγής συμπερασμάτων. Η μεσαία αναπαράσταση είναι αντιθέτως κατάλληλη, διότι είναι συμβολική και παράλληλα, ορίζει σαφώς τις σχέσεις μεταξύ των κύβων, παρέχοντας τη δυνατότητα μιας μονοσήμαντης διερμηνείας της γνώσης που αναπαρίσταται.

2.2.1 Χαρακτηριστικά μιας «καλής» αναπαράστασης γνώσης

Για να γίνει σαφής μία μεταβολή του κόσμου ενός προβλήματος, πρέπει η επιλεγμένη αναπαράσταση της γνώσης να διαθέτει ένα σύνολο χαρακτηριστικών που θα την κάνουν αξιοποιήσιμη από έναν υπολογιστή. Θεωρητικά, από τη στιγμή κατά την οποία ένα πρόβλημα έχει αναπαρασταθεί κατάλληλα, τότε έχει σχεδόν λυθεί!

Αυτά τα χαρακτηριστικά αφορούν τη σύνταξή της, που πρέπει

2.2.2 Μέθοδοι Αναπαράστασης Γνώσης

Για την αναπαράσταση της γνώσης, είναι απαραίτητο να χρησιμοποιείται μία μονοσήμαντη και τυποποιημένη σύνταξη, ένας φορμαλισμός που, όπως προείπαμε, πρέπει να δίνει μια ακριβή αναπαράσταση με νόημα (κατανόηση εννοιολογικού πλαισίου), χωρίς συμφραζόμενα, με κατανοητή πρόθεση, χωρίς ασάφειες, με δυνατότητα να συνδυαστεί κατάλληλα με μηχανισμούς εξαγωγής συμπερασμάτων (στρατηγική αναζήτησης - συλλογιστική).

Σημαντικότερες μέθοδοι αναπαράστασης που έχουν αναπτυχθεί στο πλαίσιο της ΤΝ είναι:

Ο διαχωρισμός των παραπάνω μεθόδων αναπαράστασης γνώσης σε μεθόδους κατάλληλες για σημασιολογική, δηλωτική και διαδικαστική γνώση αποτυπώνεται στο σχήμα 2.3.

Σχήμα 2.3 Είδη γνώσης και μέθοδοι αναπαράστασής τους

Όλοι οι τρόποι αναπαράστασης της γνώσης αποτελούν μοντέλα θεωριών από το χώρο της Γνωσιακής ή Γνωστικής Επιστήμης. Η ΤΝ παρέχει τα εργαλεία για την υλοποίηση, τη μελέτη και την εξέλιξη των μοντέλων αυτών, αλλά τα χρησιμοποιεί επίσης προσαρμόζοντάς τα στις δικές της ανάγκες για το σχεδιασμό ευφυών συστημάτων.

2.2.3 Σχήματα Λογικής Αναπαράστασης

Για την αναπαράσταση γνώσης οι λογικές αναπαραστάσεις χρησιμοποιούν εκφράσεις της τυπικής λογικής, η οποία είναι μια γλώσσα αναπαράστασης γνώσης που βασίζεται σε λογικά προτασιακά σχήματα και μπορεί να κατηγοριοποιηθεί στα εξής:

Προτασιακός Λογισμός

Στην προτασιακή λογική ή προτασιακό λογισμό (propositional calculus) ενδιαφερόμαστε για δηλωτικές προτάσεις (declarative sentences) που μπορούν να είναι αληθείς (true) ή ψευδείς (false), αλλά όχι και τα δύο.

 

Παραδείγματα προτάσεων που εκφράζουν δηλώσεις:

 

Έχει ήλιο.

Κάνει ζέστη.

Θα διψάσεις.

 

Η αλήθεια ή το ψεύδος που αποδίδεται σε μία πρόταση καλείται τιμή αλήθειας (truth value) της πρότασης.

Από απλές δηλωτικές προτάσεις μπορούμε να δομήσουμε σύνθετες προτάσεις (compound propositions), χρησιμοποιώντας τους 5 λογικούς συνδέσμους (logical connectives):

 

 

Παραδείγματα σύνθετων δηλωτικών προτάσεων είναι:

 

Έχει ήλιο και κάνει ζέστη. (δήλωση)

Αν κάνει ζέστη, τότε θα διψάσεις. (συνεπαγωγή)

 

Λογικοί σύνδεσμοι στις παραπάνω δύο σύνθετες προτάσεις είναι τα «και» και «εάν ... τότε».

Στην προτασιακή λογική χρησιμοποιούνται σύμβολα (π.χ.. P, Q, R) που ονομάζονται άτομα (atoms) και παριστάνουν δηλώσεις υπό μορφή προτάσεων είτε αληθείς είτε ψευδείς σε δεδομένη κατάσταση του περιβάλλοντος κόσμου, π.χ.:

 

P: Έχει ήλιο.

Q: Κάνει ζέστη.

R: Θα διψάσεις.

 

Οι καλοσχηματισμένοι τύποι (well-formed formulas) στην προτασιακή λογική είναι είτε απλά άτομα είτε

σύνθετοι τύποι που προκύπτουν από το συνδυασμό απλών ατόμων μέσω των λογικών συνδέσμων:

 

 

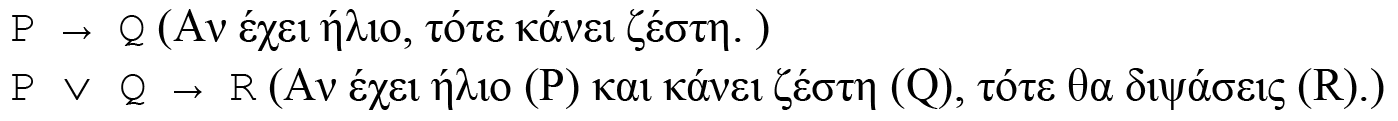
Η τιμή αλήθειας ενός καλοσχηματισμένου τύπου προκύπτει από τις επιμέρους τιμές αλήθειας των ατόμων που συμμετέχουν σ’ αυτόν σύμφωνα με τον παρακάτω πίνακα αληθείας:

Πίνακας 2.1 Πίνακας Αληθείας

Κατηγορηματικός Λογισμός

Ο κατηγορηματικός λογισμός (predicate calculus) διαθέτει, επιπλέον των ανωτέρω, την ικανότητα να καθορίζει σχέσεις και να κάνει γενικεύσεις σχετικά με τις προτάσεις. Οι λογικές εκφράσεις χρησιμοποιούν τον κατηγορηματικό λογισμό για την εξαγωγή συμπερασμάτων εξετάζοντας το αληθές ή ψευδές των προτασιακών δηλώσεων.

Για την αναπαράσταση γνώσεων στον κατηγορηματικό λογισμό χρησιμοποιούμε:

Π.χ. το κατηγόρημα ‘on’ μπορεί να χρησιμοποιηθεί, για να εκφραστεί ότι ένα αντικείμενο είναι επάνω σε ένα άλλο δηλαδή, η πρόταση ότι το βάζο είναι πάνω στο τραπέζι μπορεί να γραφεί στον κατηγορηματικό λογισμό ως οn(βάζο,τραπέζι).

Τα κατηγορήματα συνδυάζονται και με παραμέτρους, για να εκφραστούν σχέσεις των συμβόλων και παραμέτρων μέσα στις προτάσεις, π.χ. αν δηλωθεί on(x, τραπέζι) σημαίνει ότι η παράμετρος x πρέπει να ταυτιστεί με κάποιο από τα αντικείμενα που βρίσκονται πάνω στο τραπέζι.

Αν το κατηγόρημα ‘father’ χρησιμοποιείται, για να δηλώσει το όνομα του πατέρα ενός ατόμου, π.χ. father(Maria, Jim), τότε από τις κατηγορηματικές προτάσεις father(Maria, x) και father(George, x) προκύπτει ο λογικός συνειρμός ότι η Ann και ο George έχουν τον ίδιο πατέρα, χωρίς να μας ενδιαφέρει το όνομά του.

Οι καλοσχηματισμένοι τύποι στην κατηγορηματική λογική, όπως και στην προτασιακή λογική, είναι είτε απλά άτομα είτε σύνθετοι τύποι που προκύπτουν από το συνδυασμό απλών ατόμων μέσω των λογικών συνδέσμων (logical connectives):

Κατηγορηματικός Λογισμός Πρώτης Τάξης

Ο κατηγορηματικός λογισμός βασίζεται στην αλήθεια των προτάσεων και στους συμπερασματικούς μηχανισμούς που ακολουθούν λογικούς συνειρμούς. Ως επέκταση, με την προσθήκη συναρτήσεων σε αυτόν δημιουργείται ο κατηγορηματικός λογισμός πρώτης τάξης (first-order predicate calculus). Μια συνάρτηση είναι μία λογική κατασκευή που παράγει μια αξία.

Για παράδειγμα, βάσει της δήλωσης ποιος είναι γονέας των x και y μπορούμε να συναγάγουμε μέσω συναρτήσεων διάφορα συμπεράσματα μεταξύ των οποίων αν οι x και y είναι αδέλφια. Κάτι τέτοιο θα γραφόταν ως ακολούθως σε περιβάλλον PROLOG , όπου οι μεταβλητές πρέπει να γράφονται με κεφαλαίους χαρακτήρες:

 

 

Τα προτερήματα αυτού του είδους της αναπαράστασης είναι η απλότητα της σημειολογίας της, το ότι επιτρέπει τόσο την άμεση αντίληψη αυτών που αναπαριστά όσο και την προσθήκη νέων δηλώσεων, χωρίς να επηρεάζονται οι ήδη καταχωρισμένες.

Ο κατηγορηματικός λογισμός είναι κατάλληλος τρόπος αναπαράστασης για χώρους ολοκληρωμένων θεωριών, όπου μπορούν να εφαρμοστούν τεχνικές απόδειξης θεωρημάτων, ώστε να προκύψουν νέα θεωρήματα από παλαιά. Αντίθετα, είναι ακατάλληλος για αναπαράσταση διαδικαστικής και ευρετικής γνώσης, όπως, επίσης, για το χειρισμό μεγάλων βάσεων δεδομένων. Η πιο γνωστή γλώσσα που υλοποιεί τον κατηγορηματικό λογισμό είναι η PROLOG .

Σχήμα 2.4 Γραφική αναπαράσταση του προβλήματος των 6 κύβων

Η αναπαράσταση του κόσμου του προβλήματος στο συγκεκριμένο στιγμιότυπο, σε PROLOG, θα έχει ως ακολούθως:

 

Δηλώσεις για τις σχετικές θέσεις των 6 κύβων:

Δηλώσεις για τα χρώματα των 6 κύβων:

Καλοσχηματισμένος τύπος που περιγράφει πότε ένας κύβος είναι επάνω από κάποιον άλλον σε μια στήλη κύβων:

Ερωτήσεις που μπορούν να τεθούν και αντίστοιχες λογικές απαντήσεις:

Δηλαδή, η μεταβλητή Χ μπορεί να δεσμευτεί με εναλλακτικά με τις τιμές b1, b2, b3 που αντιστοιχούν στα ονόματα των τριών μαύρων κύβων.

2.2.4 Δομημένες Μορφές Αναπαράστασης Γνώσης

Οι λογικές αναπαραστάσεις δεν μπορούν εύκολα να αναπαραστήσουν κλάσεις αντικειμένων και είναι πολύ αυστηρές στο φορμαλισμό τους. Αντίθετα, οι δομημένες μορφές αναπαράστασης δίνουν αρκετή ελευθερία στον τρόπο αναπαράστασης, επιτρέποντας με αυτόν τον τρόπο μία περισσότερο διαισθητική προσέγγιση απ’ όσο οι λογικές.

Δομημένες μορφές αναπαράστασης είναι τα σημασιολογικά δίκτυα, τα σχήματα, τα πλαίσια και τα σενάρια.

 

Όλες οι δομημένες μορφές αναπαράστασης περιλαμβάνουν:

Περισσότερα για τα παραπάνω θα αναφερθούν στη συνέχεια.

Σημασιολογικά Δίκτυα

Πρώτοι οι Collins & Quillian (1969, 1970) ανέπτυξαν τα σημασιολογικά δίκτυα ως υπολογιστικά μοντέλα αναπαράστασης της γνώσης στο πλαίσιο των πρώτων ερευνών στο χώρο της Γνωστικής Επιστήμης.

Με τα σημασιολογικά δίκτυα (semantic networks) αποτυπώνεται γραφικά η υποκείμενη οργάνωση των ιδεών για έναν τομέα του επιστητού (π.χ. ποδόσφαιρο, Κοινωνιολογία).

Ένα σημασιολογικό δίκτυο είναι μία προσέγγιση των ιδιοτήτων και των σχέσεων των αντικειμένων, γεγονότων, στοιχείων, καταστάσεων και ενεργειών που το αποτελούν. Οι σχέσεις μπορεί να είναι γενικού ή ειδικού τύπου. Χαρακτηριστικό τους είναι η δυνατότητα που έχουν να υποστηρίζουν κληρονόμηση ιδιοτήτων, η οποία με τη σειρά της επιτρέπει την εξαγωγή συμπερασμάτων.

Σε ένα σημασιολογικό δίκτυο υπάρχουν κόμβοι, συνδέσεις και χαρακτηρισμοί συνδέσεων. Κάθε σύνδεση συνδέει ένα κόμβο-ουρά με έναν κόμβο-κεφαλή. Οι κόμβοι και οι συνδέσεις υποδεικνύουν οντότητες που αφορούν ένα συγκεκριμένο κόσμο προβλήματος.

Τα σημασιολογικά δίκτυα είναι ένα είδος αναπαράστασης που διαθέτει ιδιότητες για κατασκευή ενός κόμβου ή μιας νέας σύνδεσης δεδομένων δύο κόμβων, για απόδοση χαρακτηρισμού σε μια νέα σύνδεση και για δημιουργία: :

Κάθε κόμβος ενός σημασιολογικού δικτύου θεωρείται ως στοιχείο και μπορεί να διακριθεί σε τέσσερα είδη:

Τα σημασιολογικά δίκτυα έχουν τη μορφή δένδρου με τα εξής χαρακτηριστικά:

Οι κόμβοι-παιδιά μπορούν να οργανωθούν σε κλάσεις και οι δε κλάσεις σε ιεραρχίες με σχέσεις της μορφής:

Ένα σημασιολογικό δίκτυο μπορεί να είναι ιεραρχικό (βλέπε Σχήμα 2.5) ή ετεροαρχικό (βλέπε Σχήμα 2.6).

Τα ιεραρχικά σημασιολογικά δίκτυα (hierarchical semantic networks) έχουν όλα τα χαρακτηριστικά των σημασιολογικών δικτύων μόνο που όλοι οι άλλοι κόμβοι έχουν ακριβώς έναν γονέα.

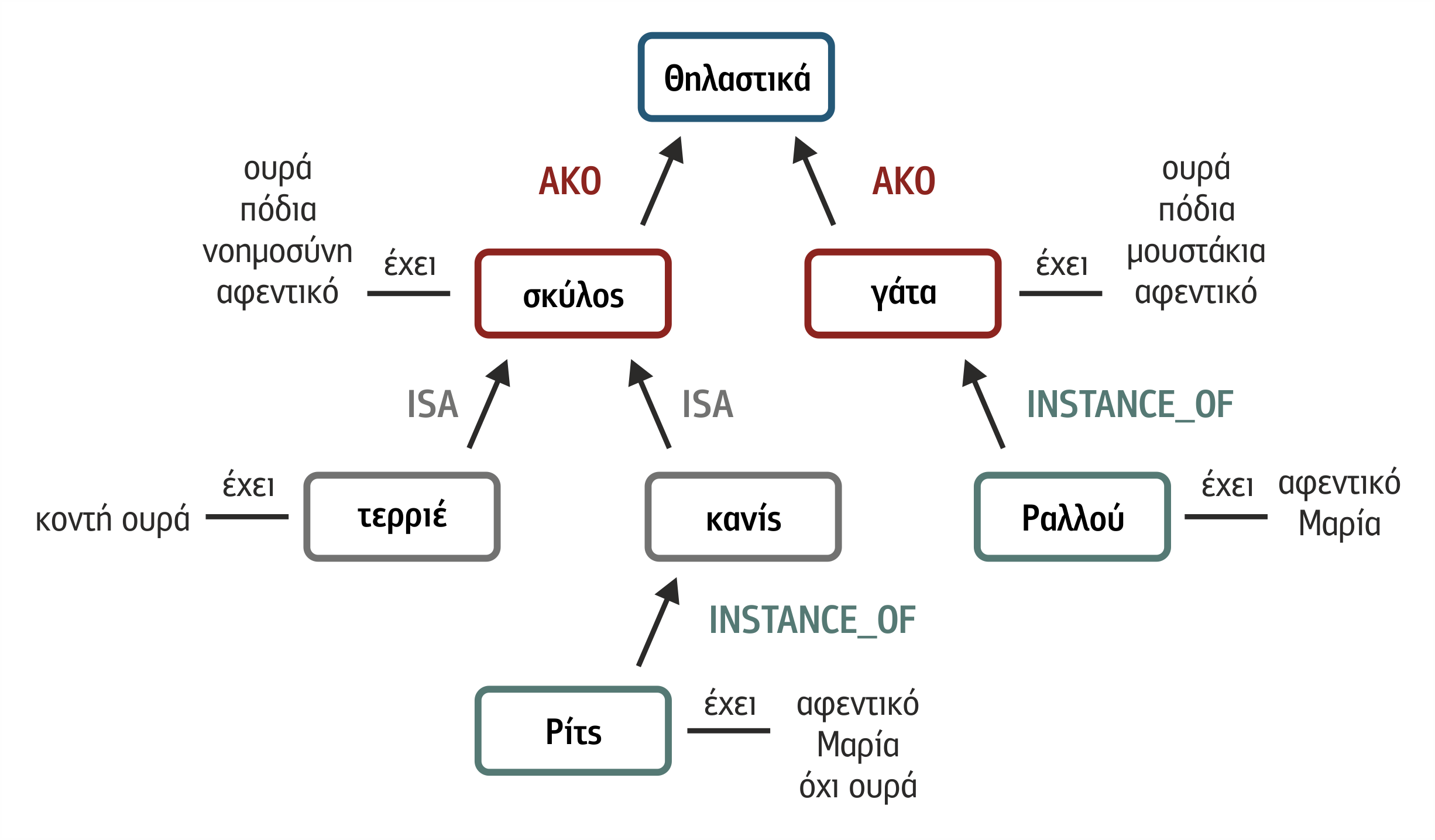
Σχήμα 2.5 Παράδειγμα ιεραρχικού σημασιολογικού δικτύου

Στο ιεραρχικό σημασιολογικό δίκτυο του σχήματος 2.5,

Η σχέση ΑΚΟ μεταξύ Μορφής Ζωής και Θηλαστικού δηλώνει ότι τα θηλαστικά ανήκουν μεν στις μορφές ζωής και κληρονομούν τα χαρακτηριστικά τους, αλλά είναι κλάση που διαθέτει και δικά της χαρακτηριστικά, όπως ότι γεννά ζωντανά παιδιά, που τη διαφοροποιούν από άλλες κλάσεις που ανήκουν στις μορφές ζωής, όπως για παράδειγμα τα πτηνά. Κάτι ανάλογο συμβαίνει και μεταξύ θηλαστικών και τίγρεων. Με σχέση ISA ή is_a συνδέονται οι ινδικές τίγρεις και οι τίγρεις , διότι οι ινδικές τίγρεις αποτελούν υπο-τάξη της μεγαλύτερης τάξης των τίγρεων και, ως εκ τούτου, κληρονομούν όλα τα χαρακτηριστικά τους, χωρίς να διαθέτουν άλλα επιπλέον και μόνο τιμές αυτών των χαρακτηριστικών μπορούν να διαφοροποιήσουν, όπως για παράδειγμα την τιμή του χαρακτηριστικού χρώματος που έχει τιμή καφέ αντί της τιμής κίτρινο που είχε η κλάση των τίγρεων.

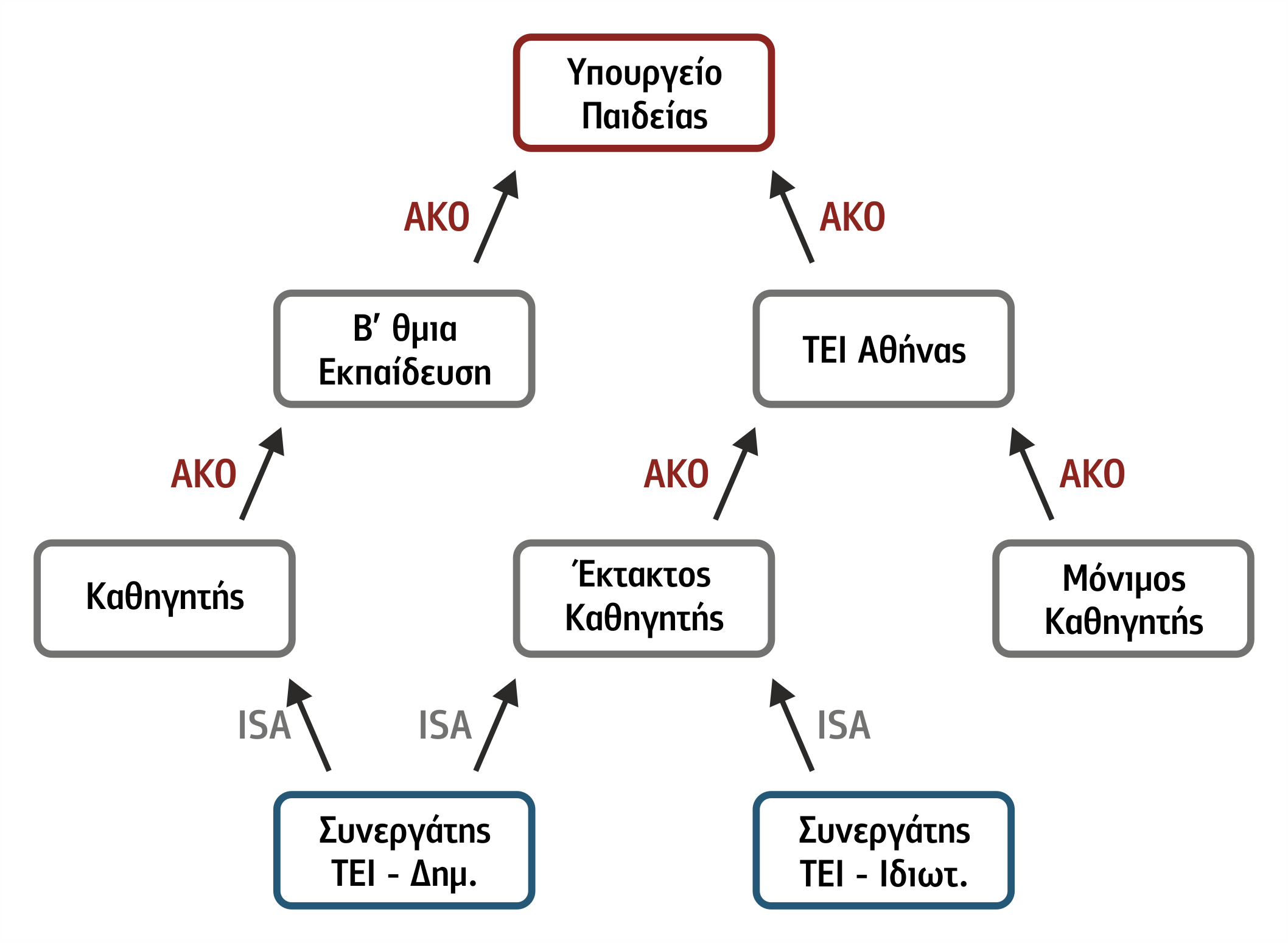
Σχήμα 2.6 Παράδειγμα ιεραρχικού σημασιολογικού δικτύου

Τα ετεροαρχικά σημασιολογικά δίκτυα (non-hierarchical neural network) έχουν όλα τα χαρακτηριστικά των ιεραρχικών σημασιολογικών δικτύων, με τη μόνη διαφορά ότι υπάρχει τουλάχιστον ένας ενδιάμεσος κόμβος που έχει παραπάνω από ένα γονέα.

Το σημασιολογικό δίκτυο του σχήματος 2.6 αναπαριστά γνώση για τους καθηγητές του ΤΕΙ Αθήνας,

Τα σημασιολογικά δίκτυα αποτυπώνονται εύκολα μέσα σε δομές συνδεδεμένων λιστών στον Η/Υ, με κόμβους που αποτελούνται από δύο μέρη: το πρώτο περιέχει το όνομα και τις ιδιότητες της οντότητας που απεικονίζει ο κόμβος και το δεύτερο τη διεύθυνση του επόμενου λογικά κόμβου. Το δεδομένο του πρώτου κόμβου καλείται κεφαλή, ενώ τα δεδομένα όλων των υπόλοιπων κόμβων καλούνται ουρά. Ο δείκτης του τελευταίου κόμβου της αλυσίδας που σχηματίζεται περιέχει ένα ειδικό σύμβολο ένδειξης τέλους, που συνήθως ονομάζεται κενός δείκτης (null pointer ή NIL).

Το παρακάτω παράδειγμα παρουσιάζει την υλοποίηση σε λίστα συνάφειας του ιεραρχικού σημασιολογικού δικτύου του αποτυπώνεται στο σχήμα 2.5:

Στο σχήμα 2.7 παρουσιάζεται η γενικότερη δομή συνδεδεμένης λίστας, στην οποία μπορεί να αποτυπωθεί ένα σημασιολογικό δίκτυο και οι τρόποι επεξεργασίας της από διάφορες γλώσσες ΤΝ, όπως PROLOG και LISP.

Σχήμα 2.7 Παράδειγμα υλοποίησης και επεξεργασίας σημασιολογικού δικτύου σε μορφή συνδεδεμένης λίστας

Παρακάτω παρουσιάζεται η αποτύπωση του ιεραρχικού σημασιολογικού δικτύου του σχήματος 2.5 υπό μορφή συνδεδεμένης λίστας σε γλώσσα Lisp.

 

(defun *mammal* ()

'((dog  (kind_of mammal)

               (tail YES)

               (feet YES)

               (intelligence YES)

               (boss YES))

   (cat ((kind_of mammal)

               (tail YES)

               (feet YES)

               (moustaches YES)

               (boss YES))

   (terrier    (is-a dog)

               (tail short))

   (canis      (is-a dog))

   (Rits       (instance canis)

               (tail no)

               (boss Costas))

   (Rallou     (instance cat)

               (boss Maria))))

 

Για μια τέτοια αναπαράσταση σε Lisp χρησιμοποιείται η συνάρτηση assoc για να εντοπιστεί μια οντότητα.

Τα προτερήματα των σημασιολογικών δικτύων είναι η ευχέρειά τους στην προσθήκη, αλλαγή και διαγραφή κόμβων, η ικανότητα των κόμβων να κληρονομούν χαρακτηριστικά και ιδιότητες από άλλους κόμβους και η ευκολία με την οποία συνάγονται συμπεράσματα σχετικά με την κληρονομούμενη ιεραρχία. Το μειονέκτημά τους είναι ότι μόνο απλές άλλες αναπαραστάσεις, όπως προτασιακές και τα πλαίσια που παρουσιάζονται παρακάτω, μπορούν να προκύψουν από αυτά.

Τα σημασιολογικά δίκτυα ως εννοιολογικοί χάρτες

Καρπός της προσπάθειας να λειτουργήσουν τα σημασιολογικά δίκτυα ως γνωστικά εργαλεία που εμπλέκουν τους μαθητές στην ανάλυση των διαρθρωτικών σχέσεων εντός του υπό μελέτη γνωστικού περιεχομένου είναι οι εννοιολογικοί χάρτες. . Αν παραδεχτούμε ότι ουσιαστικά η μνήμη μας είναι ένα σημασιολογικό δίκτυο, με τις γνώσεις μας να αποθηκεύονται στους νευρώνες του εγκεφάλου μας, τότε η μάθηση μπορεί να θεωρηθεί ως μια αναδιοργάνωση της σημασιολογικής μας μνήμης. Η παραγωγή νέων εννοιών ή ιδιοτήτων τους μέσα σε ένα σημασιολογικό δίκτυo αντανακλά αλλαγές που έχουν πραγματοποιηθεί στη σημασιολογική μνήμη, δεδομένου ότι τα σημασιολογικά δίκτυα περιγράφουν την υπάρχουσα γνώση. Με τον τρόπο αυτό, προγράμματα σημασιολογικής δικτύωσης μπορούν να χρησιμοποιηθούν για να απεικονίσουν την απόκτηση γνώσεων.

Ένας εννοιολογικός χάρτης- ΕΧ (concept map) συνδυάζει την έκφραση των εννοιών (με μορφή εικόνων, σχημάτων ή λέξεων) με τη σύνδεση αυτών ως κόμβων, προσδιορίζοντας την ιεραρχία μεταξύ τους.

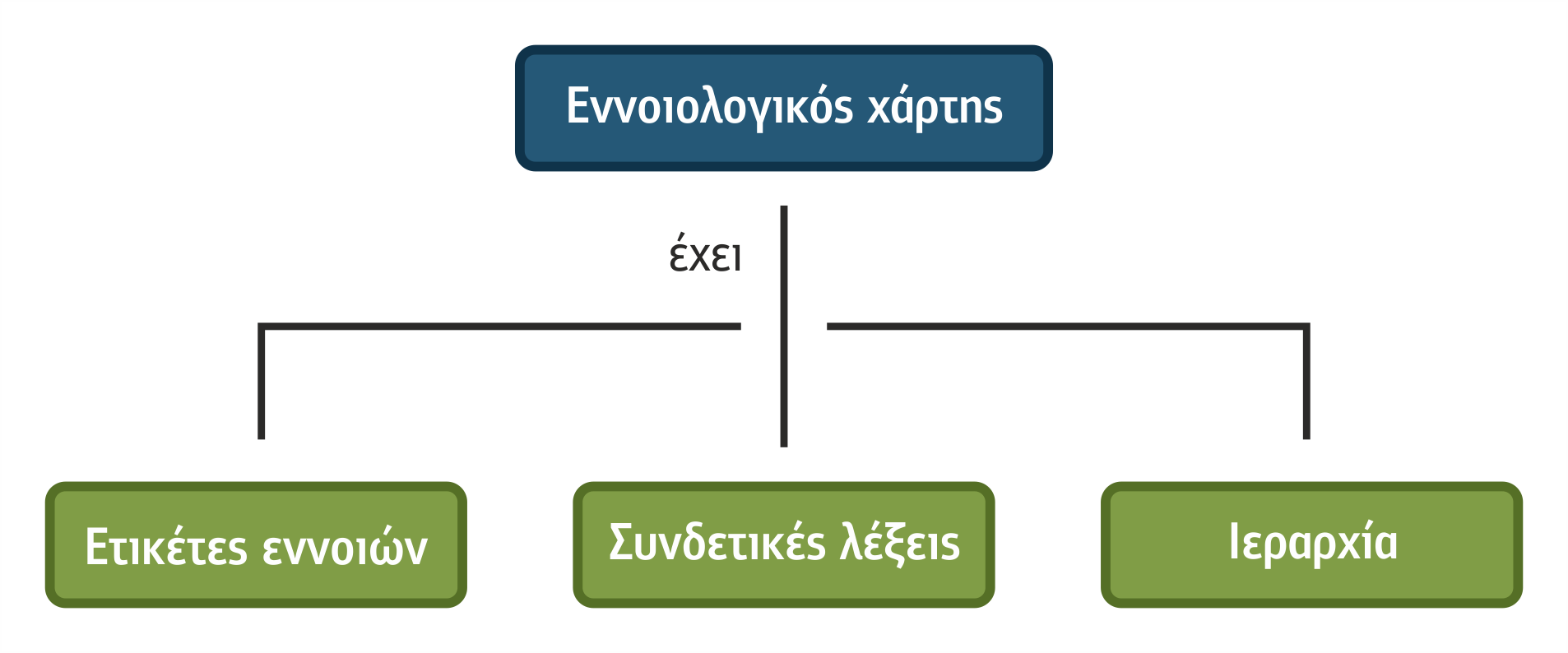
Σχήμα 2.8 Τμήματα από τα οποία δομείται ένας εννοιολογικός χάρτης

Η σύνδεση γίνεται μεταξύ κόμβων οι οποίοι αφορούν διαφορετικές ομάδες εννοιών (κλάσεις) που ανήκουν σε διάφορους τομείς με τρόπο παρόμοιο με αυτόν με τον οποίο σχεδιάζεται ένα περίγραμμα, αλλά λιγότερο γραμμικά και περισσότερα χωρικά.

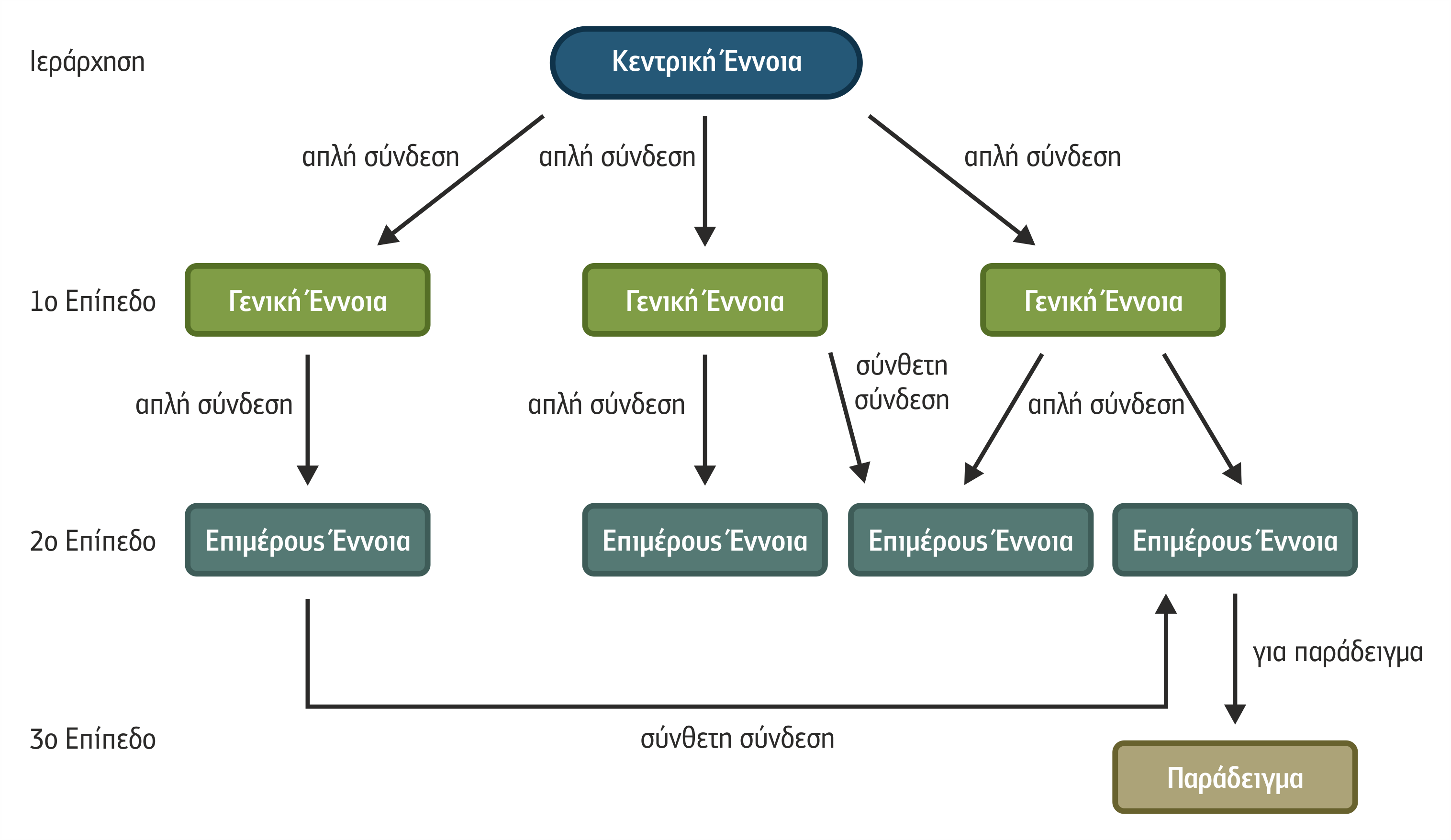
Σχήμα 2.9 Η Δομή ενός Εννοιολογικού Χάρτη

Παρεμφερώς, ο νοητικός χάρτης (mind map) αναφέρεται σε έναν εννοιολογικό χάρτη που καταγράφει γνώση για μία μόνη έννοια. Μπορεί να θεωρηθεί ως ένα διάγραμμα οπτικοποίησης πληροφοριών, στο οποίο μια κεντρική έννοια αναλύεται σε ένα αραχνοειδές διάγραμμα (spider diagram - tree like diagram) και περιμετρικά της κεντρικής έννοιας συνδέονται άλλες προτάσεις που αναλύουν την κεντρική έννοια. Οι σύνδεσμοι σε ένα νοητικό χάρτη είναι «παθητικοί» Δείχνουν απλώς μια σχέση ιεραρχική ανάμεσα στα δύο άκρα.

Σχήμα 2.10 Παράδειγμα δομής νοητικού χάρτη

Η τεχνική της εννοιολογικής χαρτογράφησης αναπτύχθηκε από τον J. D. Novak (Novak & Gowin, 1984, Novak, 1991) βάσει της θεωρίας του D. Ausubel (1968). Στην πράξη, αντικατοπτρίζεται πώς ο εγκέφαλός μας κάνει πραγματικά συνδέσεις μεταξύ των γνώσεων που προσλαμβάνει. Οι εννοιολογικοί χάρτες μπορούν να συνδεθούν μεταξύ τους, ώστε να δομήσουν μοντέλα γνώσης (knowledge models), όπως το παρακάτω ολοκληρωμένο μοντέλο γνώσης.

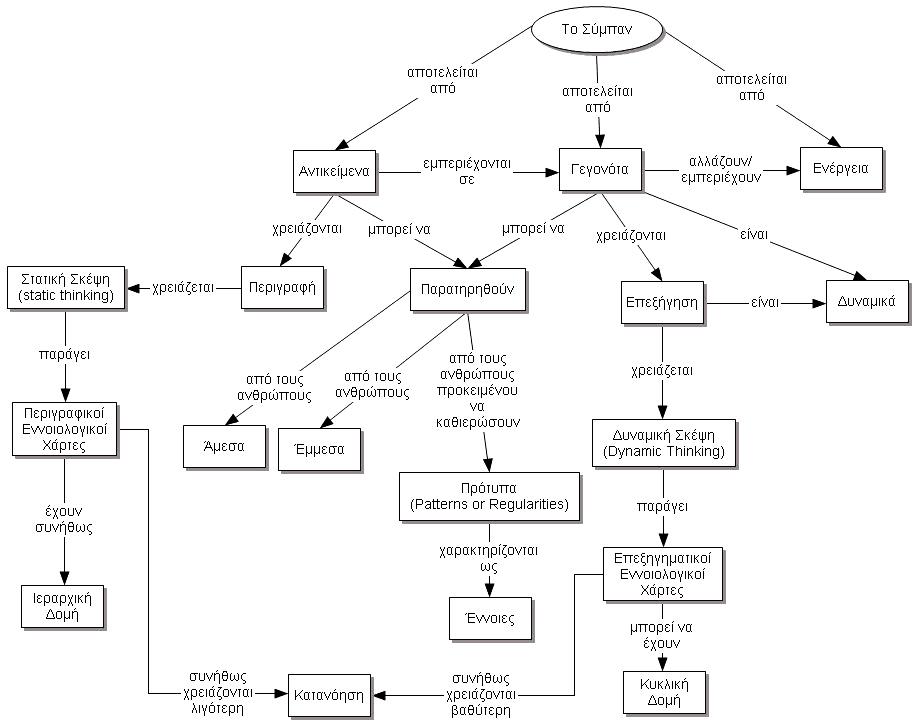
Σχήμα 2.11 Ολοκληρωμένο μοντέλο γνώσης αποτυπωμένο ως σύνθετος εννοιολογικός χάρτης7

Βήματα κατασκευής ενός εννοιολογικού χάρτη:

  1. Επιλέξτε το κείμενο και απαριθμήστε τη λίστα των βασικών εννοιών.
  2. Οργανώστε τις έννοιες (ιεραρχία).
  3. Κατασκευάστε χάρτη χρησιμοποιώντας μία αξιολογική σειρά για τις έννοιες.
  4. Συμπεριλάβετε έγκυρες συνδέσεις (προτάσεις), διασυνδέσεις μεταξύ εννοιών και παραδείγματα (γεγονότα ή αντικείμενα).
  5. Αξιολογήστε.

Στο πλαίσιο ενός εκπαιδευτικού σχεδιασμού ένας εννοιολογικός χάρτης μπορεί να αξιοποιηθεί ως:

Τα παραπάνω μπορούν να υλοποιηθούν μέσω εκπαιδευτικών δραστηριοτήτων, όπως:

Σχήματα

Ένα σχήμα (schema) είναι μία δομημένη κλάση εννοιών που περιέχει συνήθως γενική γνώση και η οποία μπορεί να χρησιμοποιηθεί για να αναπαραστήσει γεγονότα, σειρά γεγονότων, καταστάσεις, σχέσεις και αντικείμενα.

Τα σχήματα ήταν μία από τις πρώτες προτάσεις των ερευνητών στη προσπάθειά τους να δώσουν μία ερμηνεία για την οργάνωση των σύνθετων πληροφοριών στη μνήμη του ανθρώπου, με τρόπο που να ερμηνεύει την ανθρώπινη συμπεριφορά.

Η θεωρία περί σχημάτων απορρέει από μία σειρά φιλοσοφικών θεωριών που ξεκινούν από αυτές του E. Kant (1724-1804), συνεχίζουν με αυτές του J. Piaget (1896-1980) και καταλήγουν με πιο σύγχρονες προτάσεις στα τέλη της δεκαετίας του 1970 και στις αρχές της δεκαετίας του 1980 ( Rumelhart & Ortony 1977, Rumelhart, 1980), των οποίων το οντολογικό επιχείρημα είναι ότι υπάρχουν μοριακά φαινόμενα (π.χ. εκδηλώσεις, σκηνές σε χώρο, δομή λόγου) στον (ψυχολογικό) κόσμο, και ότι τα σχήματα είναι οι κατάλληλες μορφές αναπαράστασης γνώσης γι’ αυτά τα φαινόμενα. Παρόμοιες θεωρίες που αναφέρονται ως «θεωρίες σεναρίων ή ιστοριών» παρουσιάζονται από πολλούς ερευνητές από τους οποίους οι πιο γνωστοί είναι οι R. Schank και R.P. Abelson (1977), καθώς και ο D.E. Rumelhart (1975). Στο χώρο της ΤΝ ο Marvin Minsky (1975) προτείνει παρόμοιες δομές που καλούνται πλαίσια και μέχρι σήμερα χρησιμοποιούνται ευρέως για αναπαράσταση της γνώσης, κυρίως στα έμπειρα συστήματα.

Πλαίσια

Τα πλαίσια (frames) αποτυπώνουν κυρίως δηλωτική γνώση και είναι δύο κατηγοριών:

Ως προς τη δομή τους, τα πλαίσια είναι πιο κοντά από τα άλλα είδη αναπαράστασης στην έννοια της εγγραφής (record) στην πληροφορική.

Πίνακας 2.2 Παράδειγμα πλαισίου στιγμιότυπου

Τα πλαίσια αποτελούνται από σχισμές (slots) που περιέχουν έννοιες ή παραπέμπουν σε άλλα πλαίσια.

Οι σχισμές μπορούν να περιέχουν όλα τα είδη των στοιχείων:

Για παράδειγμα, η γενική δηλωτική γνώση που έχουμε για τα φρούτα θα μπορούσε να αναπαρασταθεί ιεραρχικά με πλαίσια ως εξής:

 

Πλαίσιο κλάσης: φρούτο (κλάση)

Σχισμή 1: φαγώσιμο (default yes)

Σχισμή 2: βασική διατροφή (default yes)

Σχισμή 3: εύπεπτο (default no)

 

Πλαίσιο κλάσης: μήλο (κλάση)

ΕΙΔΟΣ: φρούτο

Σχισμή εποχή: χειμερινό

Σχισμή γεύση: εύγευστο

 

Πλαίσιο στιγμιότυπο: GOLDEN (στιγμιότυπο)

EINAI: μήλο

Σχισμή χρώμα: κίτρινο

Σχισμή οσμή: αρωματική

Σχισμή εύπεπτο: yes

 

Στην παραπάνω αναπαράσταση,

Τα πλαίσια είναι ένας εύκολος τρόπος να δει κανείς ένα σημασιολογικό δίκτυο σε ανώτερο επίπεδο από εκείνο όπου κάποιος βλέπει μόνο κόμβους και συνδέσεις. Κάθε κόμβος και όλες οι συνδέσεις που ξεκινούν από αυτόν μπορούν να συγκεντρωθούν και να απεικονιστούν ως ένα πλαίσιο. Το όνομα του πλαισίου αντιστοιχεί στο όνομα του κόμβου και τα ονόματα των θέσεων αντιστοιχούν στα ονόματα των συνδέσεων. Οι έννοιες ή αξίες που περιέχονται στις θέσεις αντιστοιχούν στις έννοιες ή αξίες που απεικονίζουν οι κόμβοι στους οποίους καταλήγουν οι συνδέσεις. Για παράδειγμα, το ιεραρχικό σημασιολογικό δίκτυο του σχήματος 2.5 θα μπορούσε να γραφεί με μορφή συστήματος πλαισίων (και με εμπλουτισμένες ιδιότητες στο πλαίσιο θηλαστικά) ως εξής:

 

Πλαίσιο: θηλαστικά

Σχισμή 1: έμψυχο

Σχισμή 2: γεννά μωρά1

 

Πλαίσιο: σκύλος

ΕΙΔΟΣ: θηλαστικό

Σχισμή ουρά: ΝΑΙ

Σχισμή πόδια: NAI

Σχισμή νοημοσύνη: ΝΑΙ

Σχισμή αφεντικό: ΝΑΙ

 

Πλαίσιο: γάτα

ΕΙΔΟΣ: θηλαστικό

Σχισμή ουρά: ΝΑΙ

Σχισμή πόδια: ΝΑΙ

Σχισμή μουστάκια: ΝΑΙ

Σχισμή αφεντικό: ΝΑΙ

 

Πλαίσιο: κανίς

ΕΙΔΟΣ: σκύλος

 

Πλαίσιο: τερριέ

ΕΙΔΟΣ: σκύλος

Σχισμή ουρά: ΚΟΝΤΗ

 

Πλαίσιο στιγμιότυπου: Ριτς

ΕΙΝΑΙ: κανίς

Σχισμή ουρά: ΟΧΙ

Σχισμή αφεντικό: ΚΩΣΤΑΣ

 

Πλαίσιο στιγμιότυπου: Ραλλού

ΕΙΝΑΙ: γάτα

Σχισμή αφεντικό: ΜΑΡΙΑ

 

Ένα πλαίσιο στιγμιότυπου κληρονομεί όλες τις θέσεις που έχουν οι ανώτερες κλάσεις του και έχει επιπλέον θέσεις που το χαρακτηρίζουν. Ορισμένες κληρονομούμενες θέσεις ανώτερων κλάσεων επιτρέπεται να αλλάζουν τις προκαθορισμένες (default) αξίες τους και άλλες όχι. Θα μπορούσε, δηλαδή, η σχισμή πόδια να τοποθετηθεί στο πλαίσιο θηλαστικό με προκαθορισμένη αξία 4, να το κληρονομούν τα πλαίσια γάτα και σκύλος, αλλά σε ένα νέο πλαίσιο άνθρωπος να μπορεί να διαφοροποιηθεί η αξία της θέσης σε 2 και στο πλαίσιο φάλαινα να έχει αξία 0. Τα δεδομένα των θέσεων μπορούν να υπάρχουν κατά τη φάση της δημιουργίας ενός πλαισίου ή να προκύπτουν μετά απ’ αυτήν.

Επομένως, ένα σύστημα πλαισίων είναι μία αναπαράσταση αντίστοιχη με ένα σημασιολογικό δίκτυο όπου:

Διαθέτει επίσης δυνατότητες, όπως να δημιουργεί :

Η αναζήτηση σε ένα σύστημα πλαισίων μπορεί να γίνει με τις κλασικές μεθόδους αναζήτησης σε δίκτυα που αναφέρονται στο κεφάλαιο 1 με μεθόδους βασισμένες σε κανόνες που αναφέρονται στο κεφάλαιο συστημάτων κανόνων.

 

Παράδειγμα χρήσης πλαισίων στη PROLOG:

 

Έστω ότι θέλουμε να περιγράψουμε τη γενική κατηγορία φρούτων με όνομα fruit, ένα συγκεκριμένο είδος φρούτου το apple και τέλος το συγκεκριμένο τύπο φρούτου το golden. Τότε θα είχαμε:

 

όπου: fruit το όνομα του πλαισίου και τα [edible,[default,yes]], [nutrition,[default.yes]], [digestible,[default,yes]], [essential,[value,yes]], αποτελούν σχισμές του πλαισίου food όπου το πρώτο λεκτικό είναι το όνομα της σχισμής (π.χ. edible) και ακολουθεί η συνήθης τιμή (default) ή η τιμή που ισχύει σε κάθε περίπτωση (value).

Για να δηλωθούν οι μεταξύ τους σχέσεις, τα πλαίσια στη Prolog , συνδέονται με συναρτήσεις του τύπου:

 

frame(apple,[[link,[value,fruit]]])

 

Παράδειγμα χρήσης πλαισίων στη Common LISP:

 

Για την ίδια κατηγορία φρούτων, όπως παραπάνω, θα είχαμε:

Παράδειγμα χρήσης αντικειμενοστραφούς περιβάλλοντος στη LISP:

 

Κλάση με όνομα fruit που ανήκει στην κλάση food:

Συγκρίνοντας τα πλαίσια με τα σημασιολογικά δίκτυα μπορούμε να σημειώσουμε τα παρακάτω:

Το ποιο είναι προτιμότερο για την αναπαράσταση της γνώσης ενός προβλήματος εξαρτάται από το είδος του προβλήματος και από τον επιστημονικό τομέα στον οποίο αυτό ανήκει.

Σενάρια

Τα σενάρια (scripts) είναι μία τεχνική που προτάθηκε από τον R. Schank (1975) στο πλαίσιο της σχετικής θεωρία του περί πλαισίων (script theory) που εστιάζεται στη δόμηση της γνώσης στο πλαίσιο της κατανόησης της γλώσσας. Ο Schank υποστηρίζει ότι ένα σενάριο προορίζεται, κυρίως, για να εξηγήσει την επεξεργασία της γλώσσας και τις υψηλού επιπέδου δεξιότητες σκέψης. Τα σενάρια αποτελούν μία ειδική περίπτωση σχημάτων για την αναπαράσταση επεισοδιακής κυρίως γνώσης μέσω της παράθεσης πλαισίων σε χρονική σειρά.

Προκειμένου η θεωρία να αποδειχθεί, έχει αναπτυχθεί μια ποικιλία προγραμμάτων ηλεκτρονικών υπολογιστών. Ο Schank (1991) εφαρμόζει το θεωρητικό του πλαίσιο στην αφήγηση ιστοριών και στην ανάπτυξη ευφυών εκπαιδευτικών προγραμμάτων. Ένα σενάριο περιγράφει μία στερεότυπη, αναμενόμενη ακολουθία γεγονότων με ειδικό περιεχόμενο και τις σχετικές με αυτά πληροφορίες χρησιμοποιώντας μία χρονική σειρά από πλαίσια και ειδικότερα:

 

Παράδειγμα σεναρίου: Σενάριο Εστιατορίου (παρεμφερές: σενάριο καφετέριας)

 

Η είσοδος στο σενάριο απαιτεί ο πελάτης να πεινάει και να έχει χρήματα, για να πληρώσει το γεύμα του. Το σενάριο ολοκληρώνεται, όταν ο πελάτης δεν πεινάει πλέον, δηλαδή έχει φάει όσο επιθυμεί, και έχει πληρώσει τον ιδιοκτήτη του εστιατορίου. Ως αντικείμενα δηλώνονται εκείνα τα αντικείμενα του εστιατορίου που πρόκειται να χρησιμοποιήσει ο πελάτης, καθώς και τα χρήματα που διαθέτει:

 

Σενάριο: Εστιατόριο

 

Παραπομπή: Καφετέρια, Μαγείρεμα

 

Συνθήκες Εισόδου:

Πελάτης πεινάει

Πελάτης έχει χρήματα

 

Συνθήκες Εξόδου:

Πελάτης δεν πεινάει

Πελάτης έχει λιγότερα χρήματα

Ταμίας έχει περισσότερα χρήματα

 

Ιδιότητες / Αντικείμενα:

τραπέζι

κατάλογος φαγητών (Μενού)

παραγγελία

φαγητό

λογαριασμός

φιλοδώρημα

χρήματα

 

Ρόλοι:

Πελάτης

Σερβιτόρος

Μάγειρας

Ταμίας

 

Κανάλια:

PTRANS: Μετακίνηση

ATTENDS: Στρέψη προσοχής

MBUILD: Αλλαγή στάσης

ΜTRANS: Κίνηση μέλους

ATRANS: Παράδοση αντικειμένου

INGEST: Κατανάλωση τροφής

COMPUTE: Υπολογισμός λογαριασμού

 

Σκηνή 1: Είσοδος

Πελάτης PTRANS Πελάτη στο εστιατόριο

Πελάτης ATTENDS μάτια στα τραπέζια

Πελάτης MBUILD που θα καθίσει

Πελάτης PTRANS στο τραπέζι

 

Σκηνή 2: Παραγγελία

(Μενού στο Τραπέζι)

Πελάτης ΜTRANS (Πελάτη παίρνει Μενού)

Πελάτης MBUILD επιλογή Φαγητού

Πελάτης ΜTRANS σήμα στο Σερβιτόρο

Σερβιτόρος PTRANS Σερβιτόρο στο Τραπέζι

Πελάτης ΜTRANS παραγγελία στο Σερβιτόρο

Σερβιτόρος PTRANS Σερβιτόρος στην κουζίνα

Σερβιτόρος ΑTRANS παραγγελία στο Μάγειρα

Μάγειρας Μαγείρεμα παραγγελίας (Σενάριο προετοιμασίας φαγητού)

 

Σκηνή 3: Φαγητό

Μάγειρας ΑTRANS φαγητό στο Σερβιτόρο

Σερβιτόρος ΑTRANS φαγητό στον Πελάτη

Πελάτης INGEST Φαγητό

(Επιλογή: Σκηνή 2 για επόμενη παραγγελία ή αλλιώς Σκηνή 4)

 

Σκηνή 4: Έξοδος

Σερβιτόρος COMPUTE (ετοιμάζει λογαριασμό)

Σερβιτόρος PTRANS λογαριασμό στο Τραπέζι

Σερβιτόρος ATRANS λογαριασμό στον Πελάτη

Πελάτης ATRANS φιλοδώρημα στο Σερβιτόρο

Πελάτης PTRANS Πελάτης στην έξοδο

Πελάτης ATRANS χρήματα στον Ταμία

Πελάτης PTRANS Πελάτης έξω από το εστιατόριο

Κανόνες

Οι κανόνες (rules) αποτελούν μία μέθοδο αναπαράστασης διαδικαστικής γνώσης που αντιστοιχεί σε έγκυρους συλλογισμούς και έχει τη μορφή ΑΝ-ΤΟΤΕ. Η δήλωση ή το σύνολο των δηλώσεων μετά τον όρο ΑΝ αντιπροσωπεύει κάποιο παρατηρήσιμο πρότυπο. Η δήλωση ή το σύνολο των δηλώσεων μετά τον όρο ΤΟΤΕ αντιπροσωπεύει κάποιο εξαγώγιμο συμπέρασμα ή κάποια εκτελεστέα ενέργεια.

 

Επομένως, ένα κανόνας:

Υπάρχουν αρκετοί διαφορετικοί όροι για τις δηλώσεις που έρχονται μετά το ΑΝ και όσα ακολουθούν μετά το ΤΟΤΕ. Οι δηλώσεις μετά το ΑΝ μπορεί να ονομάζονται συνθήκες, ισχυρισμοί, προϋποθέσεις, πρόγονοι, ενώ αυτά που ακολουθούν μετά το ΤΟΤΕ μπορούν να ονομάζονται συμπεράσματα, συνεπαγόμενα ή ενέργειες. Τα παραπάνω αποτυπώνονται στην τυπική μορφή ενός κανόνα που ακολουθεί:

 

Μορφή ΑΝ/IF-ΤΟΤΕ/THEN κανόνων:

 

IF A                  premises (ισχυρισμοί)

and Β    antecedents (πρόγονοι,προηγούμενα)

and ...    preconditions (προϋποθέσεις)

THEN X           conclusions (συμπεράσματα)

and Y    consequents (συνεπαγόμενα)

and ...    actions (ενέργειες)

 

Οι κανόνες είναι τριών μορφών

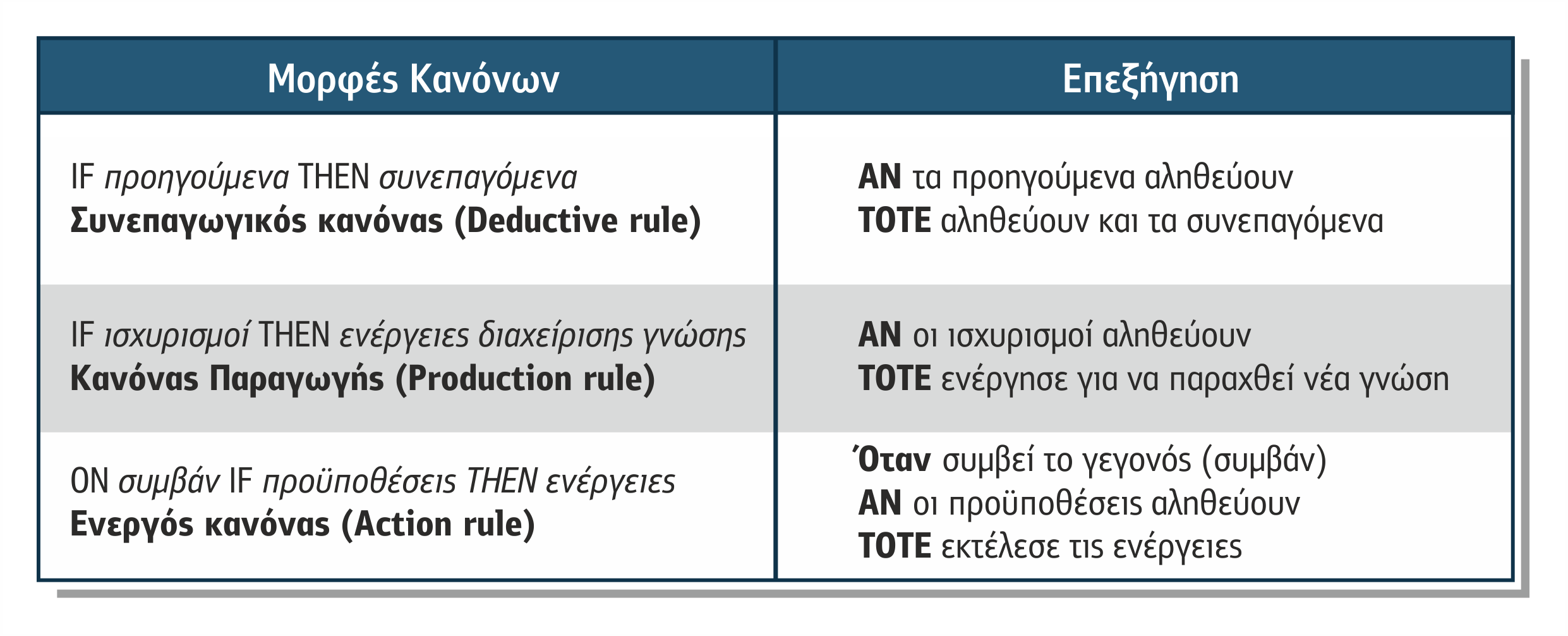
Πίνακας 2.3 Μορφές Κανόνων

Παράδειγμα συνεπαγωγικού κανόνα:

 

ΑΝ ο εκτυπωτής τυπώνει σωστά

και τα χρώματα δεν τυπώνονται σωστά

ΤΟΤΕ έχει τελειώσει το έγχρωμο μελάνι

 

Παράδειγμα Κανόνα Παραγωγής:

 

ΑΝ ο εκτυπωτής τυπώνει σωστά

και τα χρώματα δεν τυπώνονται σωστά

ΤΟΤΕ αλλάξτε την κεφαλή με το έγχρωμο μελάνι

 

Παράδειγμα Ενεργού κανόνα:

 

Όταν φέρει ο πελάτης έναν εκτυπωτή για έλεγχο

ΑΝ ο πελάτης είναι νέος

ΤΟΤΕ ενημέρωσέ τον για το κοστολόγιο του ελέγχου

 

Τα συστήματα που βασίζονται σε κανόνες ή συστήματα κανόνων (rule-based systems) είναι πολύ δημοφιλή, διότι:

Το κυριότερο μειονέκτημα των συστημάτων κανόνων είναι η απαίτηση ύπαρξης ενός πολύ αποτελεσματικού μηχανισμού αναζήτησης για την εύρεση του κατάλληλου κανόνα προς εκτέλεση σε κάθε κύκλο λειτουργίας τους. Άλλο μειονέκτημα είναι η μη ευέλικτη σύνταξη των κανόνων, που καθιστά δύσκολη την αναπαράσταση γεγονότων και αλγοριθμικών πληροφοριών.

Οντολογίες

Μια οντολογία (ontology) είναι μια τυπική αναπαράσταση ενός συνόλου εννοιών εντός ενός τομέα και των σχέσεων μεταξύ των εννοιών αυτών. Σε περιπτώσεις όπου η γνώση χρειάζεται να μοντελοποιηθεί, να δομηθεί και να διασυνδεθεί, οι οντολογίες παρέχουν έναν ικανοποιητικό μηχανισμό αναπαράστασης και διαμοίρασής της σε ομάδες ανθρώπων.

Η χρήση οντολογιών βοηθά στην ανάπτυξη του Παγκόσμιου Σημασιολογικού Ιστού (Semantic Web) ως το επόμενο στάδιο μετά τον Παγκόσμιο Ιστό (World Wide Web - WWW), δεδομένου ότι η ταξινόμηση που διαθέτει με τη βοήθεια απλών μηχανισμών συλλογιστικής καθιστά εφικτή την αναζήτηση με βάση έννοιες αντί λέξεις-κλειδιά που επιτρέπουν τη σημασιολογική εστίαση/διεύρυνση των ερωτήσεων, τις ερωταποκρίσεις ως προς περισσότερους του ενός όρους και τη χρήση τελεστών μετασχηματισμού των κειμένων. Τα παραπάνω επιτυγχάνονται, διότι οι οντολογίες ορίζουν δύο ουσιώδη συστατικά τα οποία συμβάλλουν στην πλήρη ανάπτυξη του Παγκόσμιου Ιστού:

Η έννοια της οντολογίας έχει υιοθετηθεί από την Τεχνητή Νοημοσύνη και σημαίνει:

 

«μια διαμοιρασμένη και κοινή κατανόηση κάποιου τομέα, η οποία μπορεί να ανταλλαγεί μεταξύ ανθρώπων και συστημάτων εφαρμογών» (Gruber, 2009)

 

Για να αποτυπωθεί μια οντολογία, μπορούν να υιοθετηθούν και λογικές αναπαραστάσεις και δομημένες αναπαραστάσεις από αυτές που παρουσιάστηκαν στις προηγούμενες παραγράφους.

Σήμερα η τεχνολογία των οντολογιών χρησιμοποιείται από την ΤΝ για αναπαράσταση σφαιρικής γνώσης και αποτελεί γενική αναπαράσταση της γνώσης για τον κόσμο ως σύνολο μέσω αναπαράστασης όλων των γενικών εννοιών, π.χ. φυσικά-αφηρημένα-σύνθετα αντικείμενα, ιδιότητες, ιεραρχία, δομή, καταστάσεις, πεποιθήσεις, ενέργειες, προϋποθέσεις, επακόλουθα, χώρος, χρόνος, αλλαγές, διαδικασίες, συναρτήσεις, σχέσεις κτλ. (βλέπε Σχήμα 2.12)

Σχήμα 2.12 Γραφική αναπαράσταση σφαιρικής οντολογίας

Μπορεί, όμως, να χρησιμοποιηθεί και για αναπαράσταση ειδικής γνώσης, οπότε καλείται οντολογία ειδικού σκοπού που είναι εφαρμόσιμη σε κάθε δυνατό πεδίο του πραγματικού κόσμου με την προσθήκη κατάλληλων αξιωμάτων πεδίου (βλέπε Σχήμα 2.13).

Σχήμα 2.13 Παράδειγμα γραφικής αναπαράστασης οντολογίας ειδικού σκοπού

Μια οντολογία διαθέτει κατηγορίες (π.χ. η κατηγορία cube) που μπορούν να αναπαρασταθούν με προτασιακή λογική ως ιδιότητες αντικειμένων, π.χ. cube (b1), ή ως συγκεκριμένο αντικείμενο του κόσμου του προβλήματος, π.χ. is (b1 cube). Υποστηρίζει την ταξινόμηση (taxonomy) για την αντιμετώπιση του μεγάλου όγκου αντικειμένων ορίζοντας υποκατηγορίες, ιεραρχική δομή κατηγοριών και υποκατηγοριών και κληρονομικότητα (inheritance), όπου τα στιγμιότυπα μιας υποκατηγορίας κληρονομούν τις ιδιότητες της γονικής κατηγορίας και πιθανόν να έχουν και επιπλέον ιδιότητες, δομώντας με τον τρόπο αυτόν ένα σημασιολογικό δίκτυο με σχέσεις AKO και ISA .

Μία οντολογία μπορεί να διατυπωθεί με κατηγορηματική λογική πρώτης τάξης, για να ορίσει κατηγορίες, αντικείμενα ως μέλη κατηγοριών, υποκατηγορίες μιας κατηγορίας, ιδιότητες κοινές στα μέλη μιας κατηγορίας και αναγνώριση μελών μιας κατηγορίας βάσει των κοινών χαρακτηριστικών τους.

Τα βασικά συστατικά μίας οντολογίας είναι πέντε: