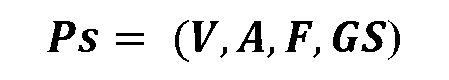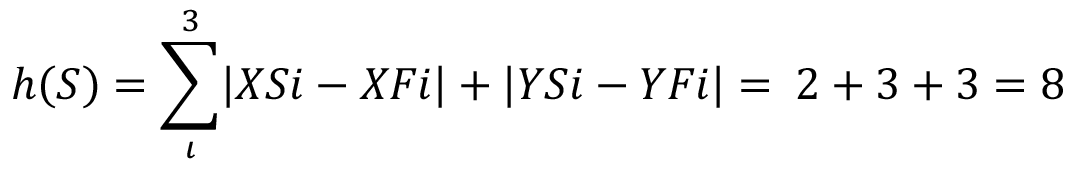ΚΕΦΑΛΑΙΟ 1 - Επίλυση Προβλημάτων

Σύνοψη

Στο κεφάλαιο αυτό θα παρουσιαστούν με παραδειγματικές περιπτώσεις οι θεμελιώδεις έννοιες για τον ορισμό ενός προβλήματος και η επίλυσή του μέσω αλγόριθμων αναζήτησης, κατά την οποία μπορεί ένα πρόγραμμα να βρει με εναλλακτικούς τρόπους μια ακολουθία ενεργειών που επιτυγχάνει τους στόχους του προβλήματος. Στη συνέχεια, θα περιγραφούν οι εναλλακτικοί τρόποι αναζήτησης με εμβάθυνση στην αναζήτηση με χώρο καταστάσεων. Τέλος, θα παρουσιαστεί η γενική αλγοριθμική προσέγγιση για τους αλγόριθμους αναζήτησης, θα παρουσιαστούν αναλυτικά οι πιο γνωστοί από αυτούς και θα συγκριθούν τα πλεονεκτήματά και τα μειονεκτήματά τους.

Προαπαιτούμενη γνώση

Δεν υπάρχει προαπαιτούμενη γνώση.

1.1 Προβλήματα και αναζήτηση λύσης

Όταν επιχειρούμε να λύσουμε ένα πρόβλημα, πρέπει πρώτα να το ορίσουμε και ακολούθως να σχεδιάσουμε έναν αλγόριθμο ο οποίος θα το επιλύει έχοντας στη διάθεσή του πολλές άμεσες επιλογές ενεργειών σε κάθε βήμα του και αποφασίζοντας ποια να επιλέξει ή στα τυφλά ή βάσει ενός ποιοτικού κριτηρίου.

Αναζήτηση (search) ονομάζεται η διαδικασία εύρεσης μιας ακολουθίας επιλεγμένων ενεργειών που οδηγεί σε ένα στόχο. Ένας αλγόριθμος αναζήτησης (search algorithm) δέχεται ως είσοδο ένα πρόβλημα και επιστρέφει μια λύση με τη μορφή ακολουθίας ενεργειών. Για να δοθεί ένα πρόβλημα ως είσοδος σε έναν αλγόριθμο αναζήτησης, πρέπει να έχει προηγηθεί μια σαφής διατύπωσή του και βάσει αυτής να γίνει ο ορισμός του με τρόπο κατάλληλο, ώστε να αποτελέσει είσοδο στον αλγόριθμο.

Τα συστήματα της ΤΝ αναζητούν λύσεις μέσα από εναλλακτικές αλγοριθμικές προσεγγίσεις και το κεφάλαιο που ακολουθεί αναφέρεται σε κάποιες από τις ευρέως χρησιμοποιούμενες για το σκοπό αυτόν. Πριν, όμως, αναφερθούμε σε συγκεκριμένους αλγόριθμους, θα πρέπει να μελετήσουμε τους διαφορετικούς τύπους των προς επίλυση προβλημάτων, δεδομένου ότι από αυτούς εξαρτάται άμεσα η καταλληλότητα ενός αλγόριθμου.

1.1.1 Τύποι προβλημάτων

Σε ορισμένα προβλήματα, ο στόχος προς επίτευξη είναι ήδη γνωστός και τα επιμέρους βήματα που θα οδηγήσουν σε αυτόν είτε δεν μας απασχολούν (παράδειγμα: στο τάβλι ο στόχος είναι να κερδίσει ένας από τους δύο παίκτες χωρίς να μας ενδιαφέρει να αποτυπωθεί το πώς το πέτυχε) είτε αποτελούν καίριο ζητούμενο (παράδειγμα: στο πρόβλημα του περιοδεύοντος πωλητή δε μας αρκεί απλώς να καταφέρει να φτάσει ο πωλητής στην πόλη που αποτελεί το στόχο του προβλήματος αλλά μας ενδιαφέρει μετακινούμενος από πόλη σε πόλη μέχρι να φτάσει στη πόλη-στόχο να διανύσει την μικρότερη δυνατή απόσταση). Σε άλλη κατηγορία προβλημάτων, ο στόχος δεν είναι γνωστός και μας ενδιαφέρει το πού μπορεί να καταλήξει η αναζήτηση (σχετικό παράδειγμα είναι το πρόβλημα της διάγνωσης ασθένειας βάσει των συμπτωμάτων του ασθενούς).

Οι αλγόριθμοι με συγκεκριμένη στόχευση έχουν μεγαλύτερες δυνατότητες μεγιστοποίησης της απόδοσής τους από αλγόριθμους χωρίς στόχευση. Ο στόχος ενός προβλήματος μπορεί να αντιστοιχεί είτε σε μία μόνη τελική κατάστασή του (για παράδειγμα, στο πρόβλημα του περιοδεύοντος πωλητή η τελική κατάσταση είναι μια συγκεκριμένη πόλη) είτε σε εναλλακτικές τελικές καταστάσεις του προβλήματος (στο τάβλι ο στόχος είναι το να πάρει όλα του τα πούλια στο χέρι ο ένας από τους δύο παίκτες, αλλά, όταν ο στόχος επιτευχθεί, τα πιόνια του άλλου παίκτη που έχουν απομείνει μπορεί να βρίσκονται σε πολλές εναλλακτικές θέσεις, κάθε πιθανός συνδυασμός των οποίων αποτελεί και μια δεκτή κατάσταση ως τελική).

Οι διαφορετικοί τύποι προβλημάτων είναι εν γένει οι ακόλουθοι:

  1. Προβλήματα στα οποία είναι πλήρως γνωστά ο στόχος και οι αντίστοιχες εναλλακτικές τελικές καταστάσεις τους και επιδιώκεται να βρει ο αλγόριθμος μία από αυτές: π.χ. προβλήματα σχεδιασμού ενεργειών και προβλήματα πλοήγησης.
  2. Προβλήματα στα οποία είναι γνωστά ο στόχος και οι αντίστοιχες εναλλακτικές τελικές καταστάσεις τους και επιδιώκεται να βρει ο αλγόριθμος τη βέλτιστη από αυτές: π.χ. προβλήματα βελτιστοποίησης.
  3. Προβλήματα στα οποία είναι γνωστές μόνο κάποιες ιδιότητες των τελικών καταστάσεων και επιδιώκεται η εύρεση ενός πλήρους στιγμιότυπου τελικής κατάστασης: π.χ. προβλήματα χρονοπρογραμματισμού, γνωστά ως προβλήματα ικανοποίησης περιορισμών.
  4. Προβλήματα στα οποία ο στόχος δεν είναι γνωστός και επιδιώκεται να βρεθεί μια έγκυρη τελική κατάσταση: π.χ. προβλήματα εξαγωγής συμπερασμάτων.

Στο κεφάλαιο αυτό θα εστιάσουμε μόνο στον τύπο προβλημάτων που ανήκουν στην πρώτη κατηγορία. Ως στόχος προβλήματος (problem goal) μπορεί να οριστεί το σύνολο των καταστάσεων του προβλήματος στις οποίες το ζητούμενο εκπληρώνεται και οι οποίες χαρακτηρίζονται ως τελικές καταστάσεις του προβλήματος. Η διατύπωση του στόχου είναι το πρώτο βήμα για την επίλυση ενός προβλήματος αυτής της κατηγορίας.

Συνήθως, προβλήματα του παραπάνω τύπου μπορούν να επιλυθούν με οποιαδήποτε αλγοριθμική προσέγγιση∙ παράδειγμα, το πρόβλημα των Πύργων του Ανόι (βλέπε Σχήμα 1.8) επιλύεται εύκολα με αναδρομή, χωρίς να μας απασχολούν τα βήματα επίλυσης που οδηγούν στο στόχο. Το μειονέκτημα της προσέγγισης που βασίζεται σε αναδρομή παρόμοιων αλγοριθμικών προσεγγίσεων είναι ότι αφενός δεν αποτυπώνει ρητά την ακολουθία των ενεργειών που κάνει ο αλγόριθμος και αφετέρου δεν έχει δυνατότητες αναζήτησης βάσει ποιοτικών κριτηρίων. Η αντίστοιχη αλγοριθμική προσέγγιση στο χώρο της ΤΝ είναι οι αλγόριθμοι αναζήτησης που, όπως προαναφέραμε, αποτυπώνουν ρητά την ακολουθία των ενεργειών που εκτελούνται κατά την επίλυση.

1.1.2 Προβλήματα που επιλύονται με αναζήτηση

Στην περίπτωση ενός προβλήματος που επιλύεται με αναζήτηση, ο αλγόριθμος αναζήτησης βασίζεται πάντα στην κατάσταση στην οποία βρίσκεται το πρόβλημα∙ στο πρόβλημα του περιοδεύοντος πωλητή όταν γίνεται μια συγκεκριμένη ενέργεια, το αποτέλεσμα μιας ενέργειας μετακίνησης εξαρτάται άμεσα από την τρέχουσα κατάσταση του προβλήματος, δηλαδή από το σε ποια πόλη βρίσκεται ο πωλητής.

Πρωταρχικής σημασίας είναι η έννοια της κατάστασης ενός προβλήματος (problem state) και η έννοια του χώρου καταστάσεων (state space) ο οποίος είναι το σύνολο των έγκυρων καταστάσεων στις οποίες μπορεί να βρεθεί ένα πρόβλημα, συμπεριλαμβανομένων της αρχικής και των πιθανών τελικών καταστάσεών του. Τα προβλήματα που επιλύονται με αναζήτηση χαρακτηρίζονται και ως προβλήματα που επιλύονται με χώρο καταστάσεων.

Σε πολλά από τα προβλήματα που επιλύονται με αναζήτηση μας ενδιαφέρει η εύρεση της καλύτερης ποιοτικά λύσης, δηλαδή η αναζήτηση διαμορφώνεται ως πρόβλημα βελτιστοποίησης∙ στο πρόβλημα του περιοδεύοντος πωλητή απαιτείται να βρεθεί ο συντομότερος δρόμος που οδηγεί στο στόχο του προβλήματος. Η έννοια της καλύτερης λύσης εξαρτάται από το πρόβλημα. Πιθανόν να υπονοείται η μεγιστοποίηση μιας μέτρησης (π.χ. κέρδος) ή η ελαχιστοποίηση κάποιου μεγέθους (π.χ. κόστος). Πολλές φορές, η έννοια του καλύτερου είναι σύνθετη και προκύπτει θετικά από την ποιότητα της τελικής κατάστασης που βρέθηκε και αρνητικά από το κόστος των ενεργειών που έγιναν (κόστος διαδρομής).

 

Συνολικό κόστος = κόστος (διαδρομής) - κέρδος(κατάστασης στόχου)

 

Τα προβλήματα που θα ερευνήσουμε ακολούθως ως υποδείγματα θα είναι προσδιοριστικά, δηλαδή οι ενέργειες που καλείται ο αλγόριθμος να κάνει σε κάθε βήμα του προσδιορίζονται επακριβώς από τους εγγενείς περιορισμούς του προβλήματος και όχι από εξωτερικούς παράγοντες. Υπάρχουν ωστόσο και προβλήματα στο πεδίο εφαρμογών της ΤΝ που σχετίζονται με παίξιμο παιχνιδιών (game playing) και στα οποία ο εξωτερικός κόσμος, μέσω των επιλογών του, επιδρά στη διαμόρφωση της τρέχουσας κατάστασης του προβλήματος∙ παράδειγμα είναι τα παιχνίδια δύο παικτών (σκάκι, τάβλι, τρίλιζα κτλ.) όπου ο 1ος παίκτης είναι ο υπολογιστής, αλλά ο 2ος παίκτης είναι φυσικό πρόσωπο. Η παρουσία ενός παίκτη-αντιπάλου αλλάζει δραστικά την αναζήτηση, καθώς τώρα υπάρχει ο ρόλος του ενός παίκτη (του υπολογιστή) υπέρ του οποίου ο αλγόριθμος προσπαθεί να βρει την καλύτερη λύση, δηλαδή να κερδίσει, ενώ ο αντίπαλος προσπαθεί να τον σταματήσει. Στο τάβλι, επιπλέον εξωτερικός παράγοντας είναι η τύχη, η οποία μέσω του τυχαίου αποτελέσματος του ριξίματος των ζαριών διαμορφώνει με μη προσδιοριστικό τρόπο την επόμενη κατάσταση στην οποία θα βρεθεί το πρόβλημα. Όμως, σε κάθε περίπτωση τον αλγόριθμο αναζήτησης απασχολεί η τρέχουσα κατάσταση του προβλήματος. Σε ορισμένα άλλα προβλήματα, για παράδειγμα σε παιχνίδια τράπουλας όπως το μπριτζ, ο παίκτης πρέπει, επιπλέον, να «θυμάται» όλες τις προηγούμενες κινήσεις, είτε δικές του είτε των αντιπάλων του, ώστε να επιλέξει την επόμενη κίνησή του.

Η αλληλεπίδραση με το φυσικό περιβάλλον μπορεί να θεωρηθεί, επίσης, ως μια μορφή παιξίματος παιχνιδιού όπου οι εξωγενείς παράγοντες πολλές φορές δεν είναι καν γνωστοί εκ των προτέρων. Καθώς ο αλγόριθμος προσπαθεί να ενεργήσει στον πραγματικό κόσμο, ανακαλύπτει νέα γνώση και προκύπτουν συνθήκες που μπορούν να υποστηρίξουν ή να εμποδίσουν την προγραμματισμένη διαδικασία.

Το παρόν κεφάλαιο θα αφιερωθεί μόνο στην προσδιοριστική αναζήτηση λύσεων σε χώρο καταστάσεων σε μικρά υποδειγματικά προβλήματα, όπως τα προβλήματα περιορισμένου φυσικού κόσμου, παιγνίων ενός παίκτη και τα κουίζ. Απαραίτητο επόμενο βήμα, για να μπορέσουν να επιλυθούν παρόμοια προβλήματα, είναι να έχουν γίνει κατανοητά, δηλαδή να διατυπωθούν με σαφή τρόπο. Διατύπωση ενός προβλήματος (problem formulation) είναι η διαδικασία με την οποία αποφασίζεται ποιες ενέργειες και καταστάσεις θα πρέπει να εξετάζονται με δεδομένο ένα στόχο.

Στο χώρο της ΤΝ, η αναζήτηση απαιτεί η διατύπωση του προβλήματος να αποτυπώνεται σε έναν σαφή και τυποποιημένο ορισμό.

1.1.3 Ορισμός Προβλήματος

Για να οριστεί ένα πρόβλημα, πρέπει πρώτα να περιγραφεί ο κόσμος του προβλήματος. Ο κόσμος του προβλήματος (problem world) είναι ένα υποσύνολο του πραγματικού κόσμου και περιέχει μόνο τα αντικείμενα που έχουν άμεση σχέση με το πρόβλημα, τις ιδιότητές τους και τις σχέσεις που τα συνδέουν. Για παράδειγμα, στον κόσμο του προβλήματος του περιοδεύοντος πωλητή σε 6 πόλεις, που φαίνεται στο παρακάτω σχήμα 1.1, περιέχονται οι 6 πόλεις που μπορεί να επισκεφτεί ο πωλητής, οι ιδιότητες που έχουν, όσον αφορά την απόσταση κάθε πόλης από καθεμία από τις υπόλοιπες πόλεις και τις σχέσεις που τις συνδέουν, δηλαδή τους υπάρχοντες δρόμους, που σημειώνονται με κόκκινη γραμμή.

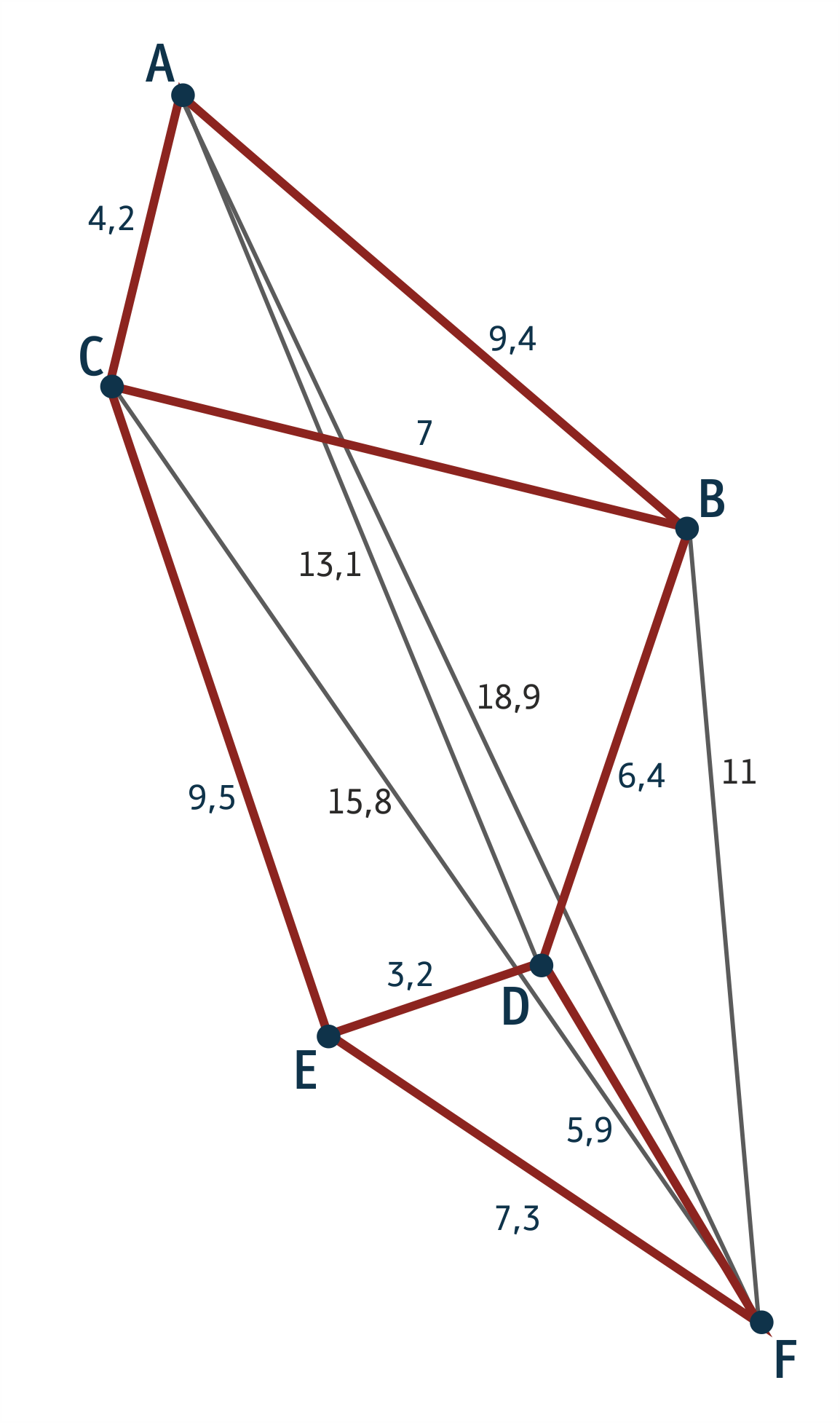
Σχήμα 1.1 Γραφική αναπαράσταση του κόσμου του προβλήματος του περιοδεύοντος πωλητή σε 6 πόλεις

Ο κόσμος ενός προβλήματος χαρακτηρίζεται ως:

Τα 4 χαρακτηριστικά στοιχεία που προκύπτουν από τη διατύπωση ενός προβλήματος και μπορούν να το ορίσουν τυπικά είναι:

  1. η αρχική κατάσταση (start state ή input state), από την οποία θα αρχίσει η αναζήτηση.
  2. ο στόχος (goal), ο οποίος περιλαμβάνει έγκυρες καταστάσεις με συγκεκριμένα επιθυμητά χαρακτηριστικά τις οποίες θέλει να εντοπίσει η αναζήτηση. Μια τέτοια κατάσταση χαρακτηρίζεται ως κατάσταση-στόχος (goal state) του προβλήματος.
  3. η περιγραφή των ενεργειών που έχει στη διάθεσή του ο αλγόριθμος. Αν δώσουμε το όνομα συνάρτηση διαδόχων (successor function) στη συνάρτηση που καλεί ένα σύνολο ενεργειών οι οποίες εφαρμόζονται σε μια κατάσταση, για να παράγουν διάδοχες καταστάσεις, τότε με δεδομένη μια συγκεκριμένη κατάσταση x του προβλήματος, η συνάρτηση διαδόχων θα επιστρέφει ένα σύνολο διατεταγμένων ζευγών (ενέργεια, διάδοχος), όπου κάθε ενέργεια είναι μία από τις επιτρεπτές ενέργειες στην κατάσταση x και διάδοχος (successor) είναι μια κατάσταση στην οποία μπορούμε να φτάσουμε από την κατάσταση x με την εκτέλεση αυτής της ενέργειας. Οι ενέργειες καλούνται και τελεστές μετάβασης (transition operators) του προβλήματος.
  4. ο χώρος καταστάσεων (state space) που ορίζεται έμμεσα από την αρχική κατάσταση και τη συνάρτηση διαδόχων. Ο χώρος καταστάσεων απεικονίζεται με ένα γράφημα του οποίου οι κόμβοι είναι καταστάσεις και τα τόξα μεταξύ καταστάσεων είναι ενέργειες (βλέπε Σχήμα 1.3). Σε προβλήματα διάσχισης δρόμου το γράφημα του χώρου καταστάσεων ταυτίζεται με τη γραφική αναπαράσταση του κόσμου του προβλήματος (βλέπε Σχήμα 1.1).

 

Με βάση τα παραπάνω, μπορούμε να πούμε ότι ένα πρόβλημα (Ρ) ορίζεται ως P=(I,G,T,S), όπου:

 

Ι: η αρχική κατάσταση,

G: το σύνολο των καταστάσεων που περιλαμβάνει ο στόχος,

T: το σύνολο των τελεστών μετάβασης,

S: ο χώρος των καταστάσεων.

 

Στα τα προβλήματα όπου μας ενδιαφέρει η ποιότητα της λύσης, επιπλέον στοιχείο αποτελεί η συνάρτηση κόστους διαδρομής (function of path cost), όπως αυτή περιγράφηκε στην προηγούμενη παράγραφο 1.1.2.

Στη συνέχεια, θα παρουσιάσουμε τη λεκτική περιγραφή των κλειστών κόσμων υποδειγματικών προβλημάτων, όπως του προβλήματος των 3 κύβων, του αγρότη με τη βάρκα, των 8 πλακιδίων, των 2 δοχείων κ.ά. Οι τεχνικές αναπαράστασης της γνώσης για ένα πρόβλημα, όπως αυτή προκύπτει μέσω της λεκτικής περιγραφής του, θα εκτεθούν για μερικά από τα παραπάνω προβλήματα στο κεφάλαιο της Αναπαράστασης της Γνώσης (Κεφάλαιο 2).

1.1.4 Παραδείγματα προβλημάτων

Εδώ θα παρουσιάσουμε μερικά από τα γνωστότερα προβλήματα που χρησιμοποιούνται ως παραδείγματα σε εκπαιδευτικά εγχειρίδια, κάνοντας διάκριση μεταξύ των προβλημάτων-παιχνιδιών και των προβλημάτων του πραγματικού κόσμου.

Προβλήματα-παιχνίδια

Το πρώτο παράδειγμα που θα εξετάσουμε είναι αυτό του προβλήματος των 3 κύβων.

 

Διατύπωση του προβλήματος των 3 κύβων: Τρεις κύβοι βρίσκονται σε μια τυχαία διάταξη πάνω σε ένα τραπέζι. Σκοπός του προβλήματος είναι να μετακινηθούν οι κύβοι, ώστε να σχηματιστεί μια νέα επιθυμητή διάταξη. Ένας κύβος μπορεί να μετακινηθεί, εφόσον έχει ελεύθερη την επάνω έδρα του.

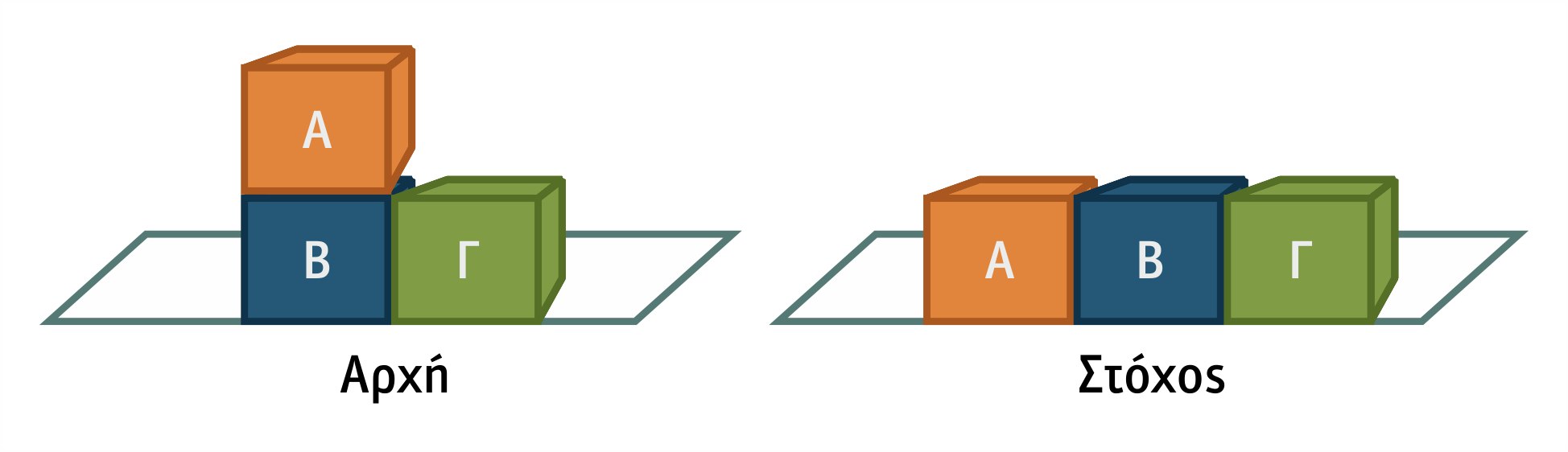
Σχήμα 1.2 Γραφική περιγραφή του κόσμου του προβλήματος των 3 κύβων

Το πρόβλημα των 3 κύβων, σε ένα στιγμιότυπό του, θα μπορούσε να περιγραφεί με τη βοήθεια του παρακάτω πίνακα:

Πίνακας 1.1 Η καταγραφή ενός στιγμιότυπου του προβλήματος των 3 κύβων

Οι τελεστές μετάβασης του προβλήματος μπορούν να περιγραφούν ως εξής:

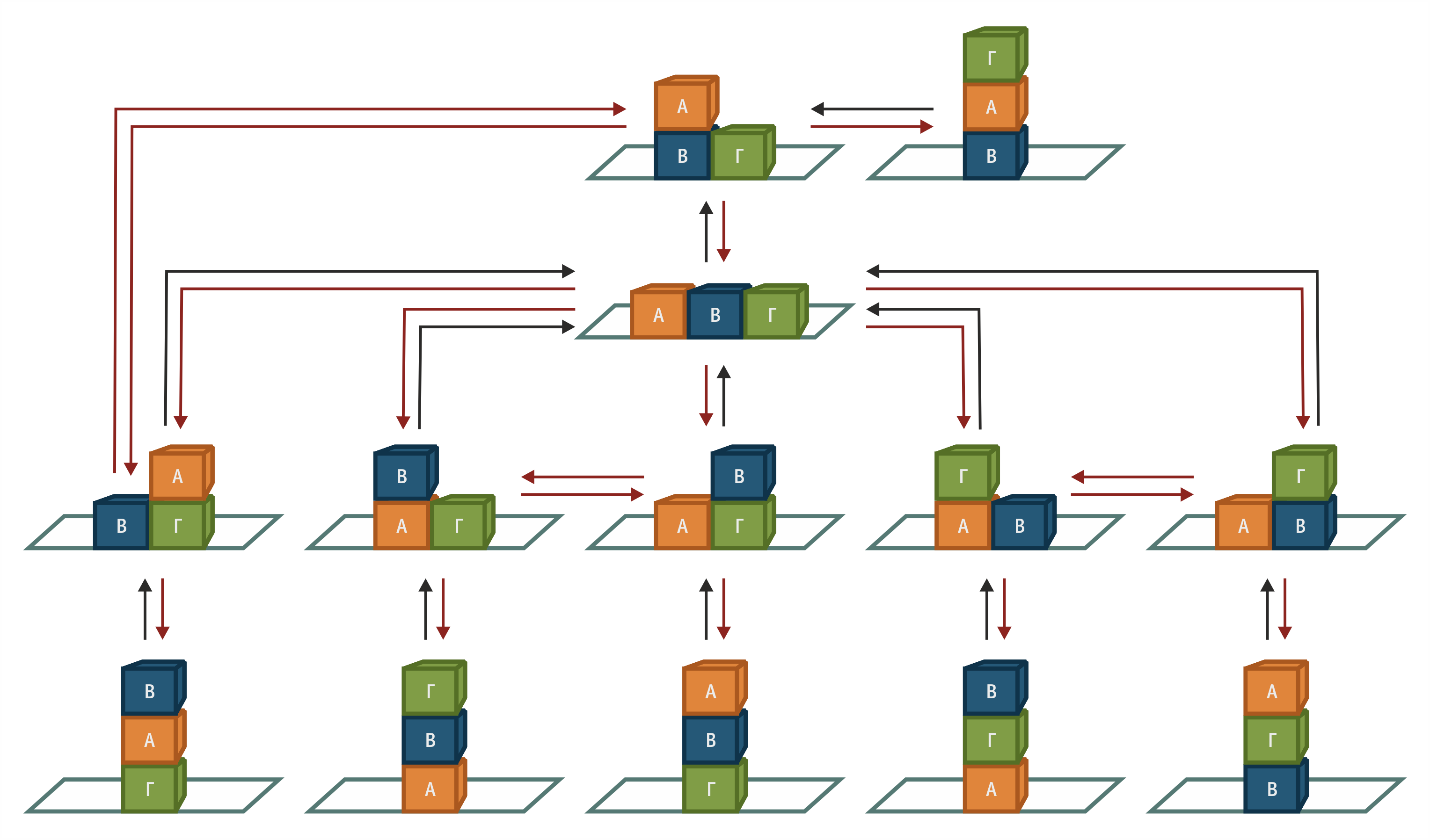
Σχήμα 1.3 Ο χώρος καταστάσεων του προβλήματος των 3 κύβων

Στο σχήμα 1.3 απεικονίζεται ο χώρος καταστάσεων του προβλήματος των 3 κύβων, όπου με κόκκινα βέλη απεικονίζεται ο τελεστής move-to-cube και με μαύρα ο τελεστής move-to-table.

 

Άλλο πρόβλημα-παιχνίδι είναι ο αγρότης με τη βάρκα.

 

Διατύπωση του προβλήματος του αγρότη με τη βάρκα: Ένας αγρότης (farmer) θέλει να περάσει μια χήνα (goose), ένα σακί σπόρων (seeds) και ένα λύκο (wolf) από τη μία όχθη ενός ποταμιού στην άλλη με τη βοήθεια μιας βάρκας. Η βάρκα μπορεί να μεταφέρει τον αγρότη ή μόνο του ή με κάποιο από τους άλλους 3 συντελεστές του προβλήματος, δηλαδή τη χήνα ή το σακί με τους σπόρους ή το λύκο. Ταυτόχρονα, σε καθεμία από τις όχθες δεν μπορούν να μείνουν μόνα τους τα ζεύγη χήνα-σπόροι και λύκος-χήνα, γιατί το ένα τρώει το άλλο.

Εικόνα 1.1 Γραφική αναπαράσταση ενός στιγμιότυπου του προβλήματος του αγρότη με τη βάρκα

Σε ένα στιγμιότυπό του όπου όλοι βρίσκονται στην αριστερή όχθη, το πρόβλημα του αγρότη με τη βάρκα θα μπορούσε να περιγραφεί με τη βοήθεια του παρακάτω πίνακα:

Πίνακας 1.2 Περιγραφή μιας κατάστασης του κόσμου του προβλήματος του αγρότη με τη βάρκα

Οι τελεστές μετάβασης του προβλήματος μπορούν να περιγραφούν ως εξής:

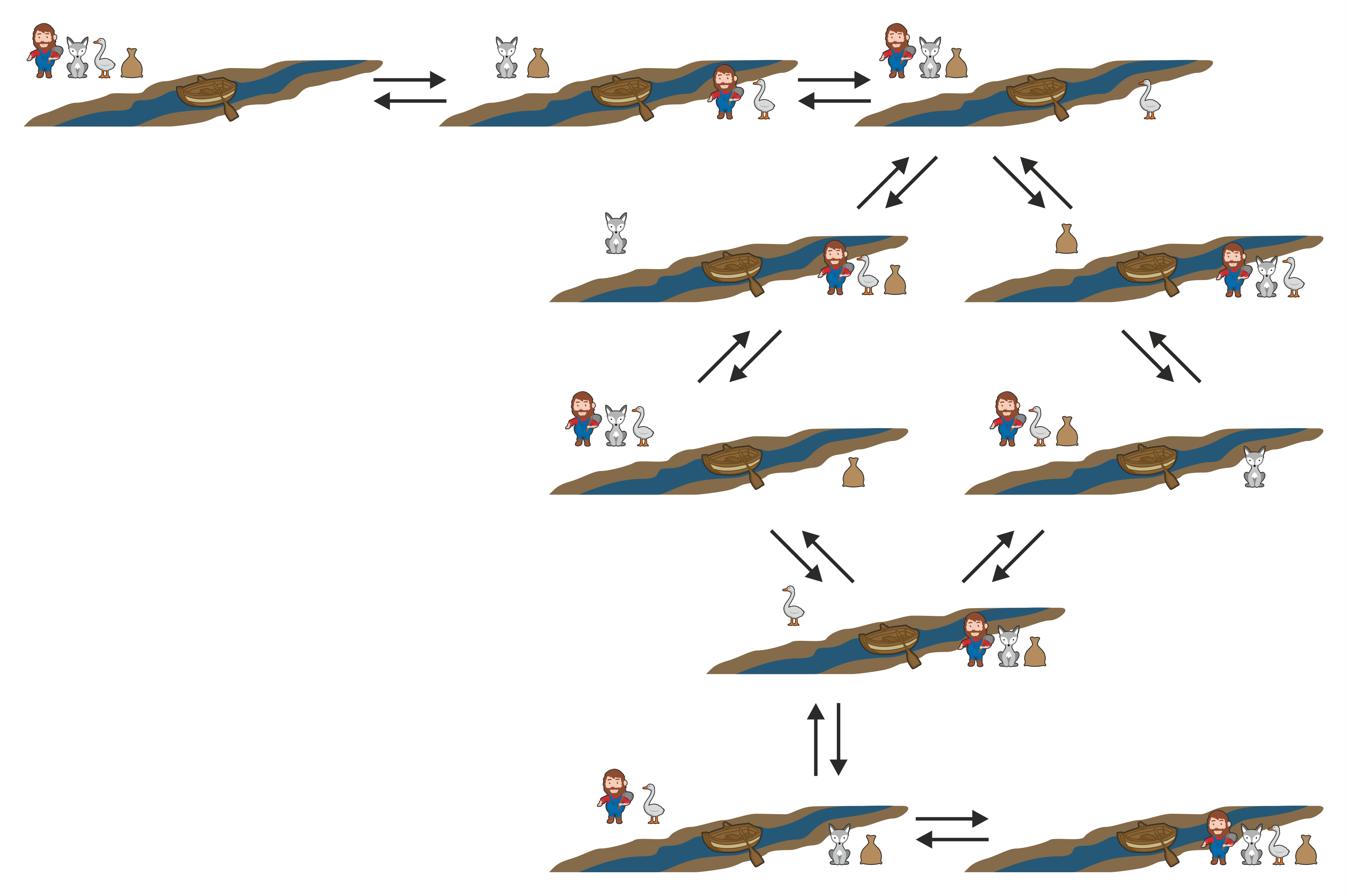
Σχήμα 1.4 Ο χώρος καταστάσεων του προβλήματος του αγρότη με τη βάρκα

Επίσης, πολύ γνωστά προβλήματα-παιχνίδια είναι αυτά των 8 πλακιδίων (8 Puzzles), των 2 δοχείων, των 8 Βασιλισσών, των Πύργων του Ανόι κ.ά.

 

Διατύπωση του προβλήματος των 8 πλακιδίων (8 Puzzles): Ένα πλαίσιο 3x3 περιέχει 8 πλακίδια, αριθμημένα από το 1 έως το 8, και μία θέση κενή χωρίς πλακίδιο. Τα πλακίδια μπορούν να μετακινηθούν σε μια γειτονική θέση, εφόσον αυτή η θέση είναι κενή. Σκοπός είναι να βρεθούν τα πλακίδια αυτά σε μια επιθυμητή διάταξη. Το πρόβλημα μπορεί να γενικευτεί για N πλακίδια.

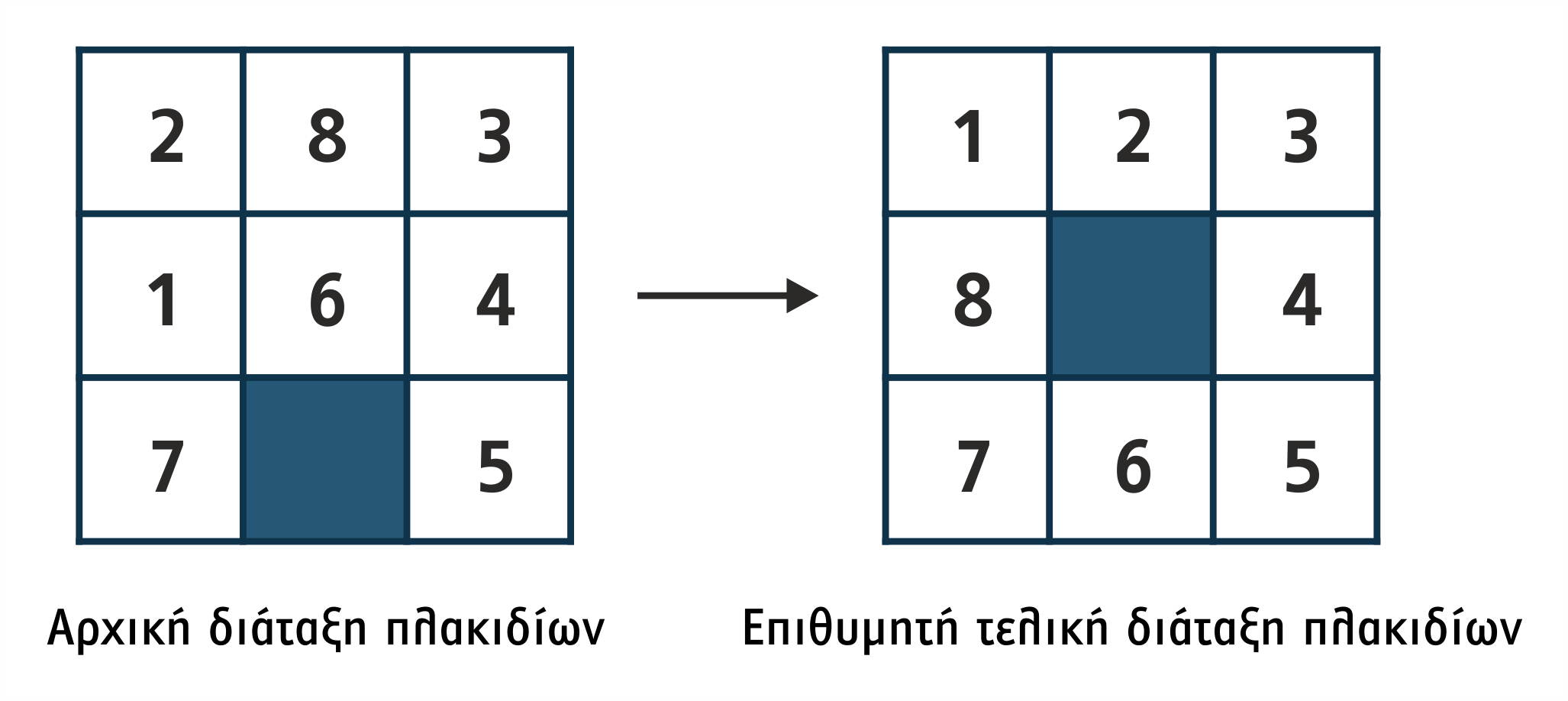
Σχήμα 1.5 Το πρόβλημα των 8 πλακιδίων

Διατύπωση του προβλήματος των 2 δοχείων: Στο πρόβλημα υπάρχουν δυο δοχεία, που χωράνε 4 λίτρα και 3 λίτρα νερού αντίστοιχα, και μια βρύση που μπορεί να τα γεμίσει πλήρως είτε είναι άδεια είτε μισογεμάτα. Το ζητούμενο είναι να βρεθούν μέσα στο μικρό δοχείο ακριβώς 2 λίτρα νερό. Επιτρεπτές ενέργειες είναι να γεμίσει ένα δοχείο πλήρως από τη βρύση, να αδειάσει τελείως ένα δοχείο από το περιεχόμενό του και να μεταγγιστεί το περιεχόμενο του ενός δοχείου στο άλλο, αν χωράει όλο, αλλιώς το μέρος που χωράει.

Σχήμα 1.6 Το πρόβλημα των 2 δοχείων

Διατύπωση του προβλήματος των 8 βασιλισσών: Το πρόβλημα των 8 βασιλισσών είναι παιχνίδι στρατηγικής, όπου σε μια σκακιέρα πρέπει να τοποθετηθούν 8 βασίλισσες έτσι, ώστε να μην απειλεί η μια την άλλη, δηλαδή καμιά να μη μοιράζεται την ίδια γραμμή, στήλη ή διαγώνιο με τις υπόλοιπες. Μπορεί να λυθεί με αναδρομή και άλλες κλασικές προσεγγίσεις, με αλγόριθμους αναζήτησης, αλλά και με μη παραδοσιακές προσεγγίσεις, όπως οι γενετικοί αλγόριθμοι.

Σχήμα 1.7 Το πρόβλημα των 8 βασιλισσών

Διατύπωση του προβλήματος των Πύργων του Ανόι: Δίνεται ένας αριθμός κρίκων διαφορετικού μεγέθους και τρεις στύλοι. Οι κρίκοι είναι τοποθετημένοι στον πρώτο στύλο με διάταξη από τον μεγαλύτερο χαμηλότερα προς τον μικρότερο στην κορυφή. Από το στύλο όπου βρίσκονται οι κρίκοι πρέπει να μεταφερθούν ένας με ίδια τελική διάταξη στον τρίτο στύλο, με τη βοήθεια του μεσαίου στύλου, χωρίς ποτέ ένας μεγαλύτερος κρίκος να τοποθετηθεί πάνω από έναν μικρότερο. Συνήθως λύνεται με αναδρομή αλλά και με κλασσικές μεθόδους αναζήτησης

Σχήμα 1.8 Σχηματική περιγραφή των Πύργων του Ανόι

Διατύπωση του προβλήματος του ρομπότ: Ένα ρομπότ κινείται κατά μία θέση οριζοντίως ή καθέτως σε ένα χώρο με εμπόδια. Σε διάφορες θέσεις υπάρχουν αντικείμενα τα οποία προσπαθεί να εντοπίσει το ρομπότ. Στόχος είναι το ρομπότ να καταφέρει να εντοπίσει όλα τα αντικείμενα ή κάποια από αυτά. Στην κατηγορία αυτή ανήκει το παιχνίδι του πάκμαν και γενικότερα παιχνίδια που χαρακτηρίζονται ως λαβύρινθοι.

Σχήμα 1.9 Το πρόβλημα του ρομπότ

Προβλήματα πραγματικού κόσμου

Τα προβλήματα πραγματικού κόσμου είναι κατά κανόνα δύσκολο να οριστούν. Κλασικότεροι εκπρόσωποί τους είναι τα προβλήματα περιήγησης, μεταξύ των οποίων συγκαταλέγεται το γνωστό πρόβλημα του περιοδεύοντος πωλητή (travelling salesperson problem-TSP), στο οποίο έχουμε αναφερθεί στην αρχή του Κεφαλαίου (βλέπε Σχήμα 1.1). Άλλα προβλήματα είναι τα προβλήματα διάταξης κυκλώματος, σχεδίασης πρωτεϊνών, κίνησης ρομπότ, αναζήτησης στο διαδίκτυο κτλ.

1.1.5 Λύση προβλήματος

Λύση ενός προβλήματος Ρ, όπου P=(I,G,T,S), είναι μια ακολουθία από τελεστές μετάβασης t1, t1, t2, …, tn, με την ιδιότητα:

 

G= tn(…(t2(t1(I)))..)

 

Παράδειγμα: Αν το πρόβλημα του αγρότη οριστεί τυπικά ως ακολούθως:

 

Ι (input)= Αγρότης-Λύκος-Χήνα-Σακί με σπόρους στην αριστερή όχθη

G (goal)=Αγρότης-Λύκος-Χήνα-Σακί στη δεξιά όχθη

Τ (transitions)={

Αν ο χώρος καταστάσεων S του προβλήματος είναι αυτός του σχήματος 1.4, τότε, υπάρχουν δύο εναλλακτικές λύσεις που είναι οι ακόλουθες:

 

G → F → S → G → W → F → G

G → F → W → G → S → F → G

 

Εναλλακτικός ορισμός είναι ο ακόλουθος:

Λύση ενός προβλήματος είναι μια ακολουθία από καταστάσεις στις οποίες μπορεί να βρεθεί διαδοχικά το πρόβλημα, με αρχή από την αρχική κατάσταση και κατάληξη σε μία από τις επιθυμητές τελικές καταστάσεις.

Ως μερική λύση (partial solution) εννοούμε μια ακολουθία βημάτων επίλυσης που δεν έχουν καταλήξει ακόμα σε επιτυχία ή αποτυχία∙ παράδειγμα, στο πρόβλημα του αγρότη τρεις χρονικά διαδοχικές μερικές λύσεις θεωρούνται οι:

 

G → F → S        

G → F → S → G    

G → F → S → G → W

 

Ένα πρόβλημα μπορεί να έχει πολλές λύσεις που προκύπτουν κατά την αναζήτηση μέσα στο χώρο καταστάσεων. Δοθέντος ενός προβλήματος P = (I, G, T, S), ο χώρος αναζήτησης (search space) είναι το σύνολο όλων των καταστάσεων που είναι προσβάσιμες από την αρχική κατάσταση K. Μια κατάσταση Κi χαρακτηρίζεται ως προσβάσιμη, αν υπάρχει μια ακολουθία τελεστών μετάβασης που οδηγεί από την αρχική κατάσταση K στην κατάσταση Κi.

Ο χώρος αναζήτησης ενός προβλήματος άλλοτε ταυτίζεται με το χώρο καταστάσεων και άλλοτε, για πολύ μεγάλους χώρους καταστάσεων ή για συγκεκριμένου τύπου προβλήματα, περιορίζεται ως υποσύνολό του σε ένα μικρότερο ή μεγαλύτερο μέρος του. Για παράδειγμα, στο πρόβλημα του αγρότη οι δύο χώροι ταυτίζονται, ενώ στην περίπτωση του προβλήματος του πάκμαν, που μπορεί να θεωρηθεί ως παραλλαγή του προβλήματος του ρομπότ, διαφοροποιούνται, αν ο κόσμος του προβλήματος στο αρχικό του στιγμιότυπο είναι αυτός που δίνεται στο σχήμα 1.10 (με γκρι σημειώνονται οι καταστάσεις του χώρου καταστάσεων στις οποίες δεν μπορεί να βρεθεί το πάκμαν κατά την αναζήτηση, δεδομένου ότι δεν μπορεί να τις προσεγγίσει λόγω των εμποδίων).

Σχήμα 1.10 Γραφική απεικόνιση του χώρου αναζήτησης του προβλήματος του πάκμαν

Ένας χώρος αναζήτησης μπορεί να αναπαρασταθεί ως γράφημα με κόμβους τις προσβάσιμες καταστάσεις του γράφου του χώρου καταστάσεων.

1.2 Αναζήτηση λύσης

Όταν ο χώρος καταστάσεων ενός προβλήματος είναι πολύ μεγάλος, τότε κρίνεται αναγκαία η ύπαρξη μιας συστηματικής μεθόδου έρευνάς του, δηλαδή ενός αλγόριθμου αναζήτησης (search algorithm). Με συνδυασμό και επέκταση των κλασικών αλγορίθμων αναζήτησης, τους οποίους και θα παρουσιάσουμε στις επόμενες παραγράφους, μπορούν να προκύψουν πολλοί ακόμα αλγόριθμοι κατάλληλοι για την επίλυση προβλημάτων συγκεκριμένων τύπων. Οι αλγόριθμοι αναζήτησης περιορίζονται στο χώρο αναζήτησης και χαρακτηρίζονται από την πολυπλοκότητα και την αποδοτικότητά τους.

Η αναζήτηση λύσης επιτυγχάνεται σε κύκλους αναζήτησης. Σε κάθε κύκλο επεκτείνεται το σύνολο των μερικών λύσεων που έχουν σχηματιστεί κατά τον προηγούμενο κύκλο. Η επιλογή του τρόπου επέκτασης εξαρτάται από τη στρατηγική αναζήτησης που έχει υιοθετήσει ο αλγόριθμος αναζήτησης.

Κατά τη διαδικασία αναζήτησης, αναπτύσσεται το δέντρο αναζήτησης που περιλαμβάνει μέρος ή το σύνολο των καταστάσεων του χώρου αναζήτησης.

1.2.1 Δένδρο Αναζήτησης

Βασικό εργαλείο για την εφαρμογή ενός αλγορίθμου αναζήτησης μέσα στο χώρο καταστάσεων είναι το δένδρο αναζήτησης (search tree). Το δένδρο αναζήτησης σχηματίζεται δυναμικά, καθώς ο αλγόριθμος ανιχνεύει όλες τις δυνατές να σχηματιστούν ακολουθίες διαδοχικών καταστάσεων που μπορεί να οδηγήσουν σε λύση. Κάθε τέτοια ακολουθία καταστάσεων, η οποία ξεκινά από την αρχική κατάσταση και καταλήγει σε ένα φύλλο του μέχρι εκείνου του σημείου ανεπτυγμένου δένδρου, καλείται μονοπάτι αναζήτησης (search path). Το σύνολο των αποτυπωμένων πάνω σε ένα δένδρο αναζήτησης εναλλακτικών μονοπατιών σε μια συγκεκριμένη στιγμή της εξέλιξης του κόσμου του προβλήματος καλείται ουρά αναζήτησης (search queue ή fringe). Τα μονοπάτια που αποτυπώνονται σε ένα δένδρο μιας μη ολοκληρωμένης αναζήτησης μπορούν να θεωρηθούν μερικές λύσεις του προβλήματος.

Σε ένα δένδρο αναζήτησης που αντιστοιχεί σε ένα λυμένο πρόβλημα, μια λύση του αποτελεί ένα ολοκληρωμένο μονοπάτι που αποδίδεται ως μια ακολουθία διαδοχικών καταστάσεων αρχίζοντας από την αρχική κατάσταση και καταλήγοντας σε μια τελική. Είναι σημαντικό να διαφοροποιηθούν οι έννοιες δέντρο αναζήτησης, χώρος αναζήτησης και χώρος καταστάσεων.

Ένα από τα γνωστότερα προβλήματα στο χώρο της ΤΝ, όπως προαναφέραμε, είναι το πρόβλημα του περιοδεύοντος πωλητή, το οποίο στο κεφάλαιο αυτό θα απλοποιήσουμε, για να καταστεί πρόβλημα-υπόδειγμα για την παρουσίαση των διαφορετικών αλγορίθμων αναζήτησης. Στην απλουστευμένη αυτή εκδοχή, ο πωλητής δεν έχει ως στόχο να επιστρέψει απαραίτητα στην αρχική πόλη, αλλά σε κάποια οποιαδήποτε από τις πόλεις του προβλήματος, χωρίς να απαιτείται να έχει επισκεφθεί όλες τις υπόλοιπες. Το πρόβλημα θεωρείται λυμένο, όταν βρεθεί ένα οποιοδήποτε μονοπάτι που να οδηγεί από την αρχική πόλη στην πόλη-στόχο. Στο παρακάτω σχήμα δίνεται η περιγραφή μιας εκδοχής του χώρου αναζήτησης του περιοδεύοντος πωλητή, όταν στο πρόβλημα υπάρχουν 10 πόλεις που συνδέονται μεταξύ τους με δρόμους διαφορετικού μήκους. Στην περιγραφή αυτή ο κάθε κόμβος αντιστοιχεί σε μια πόλη του προβλήματος και κάθε ακμή μεταξύ των κόμβων στους υπάρχοντες δρόμους. Επιπλέον, σε κάθε ακμή σημειώνεται η απόσταση μεταξύ των πόλεων που συνδέει.

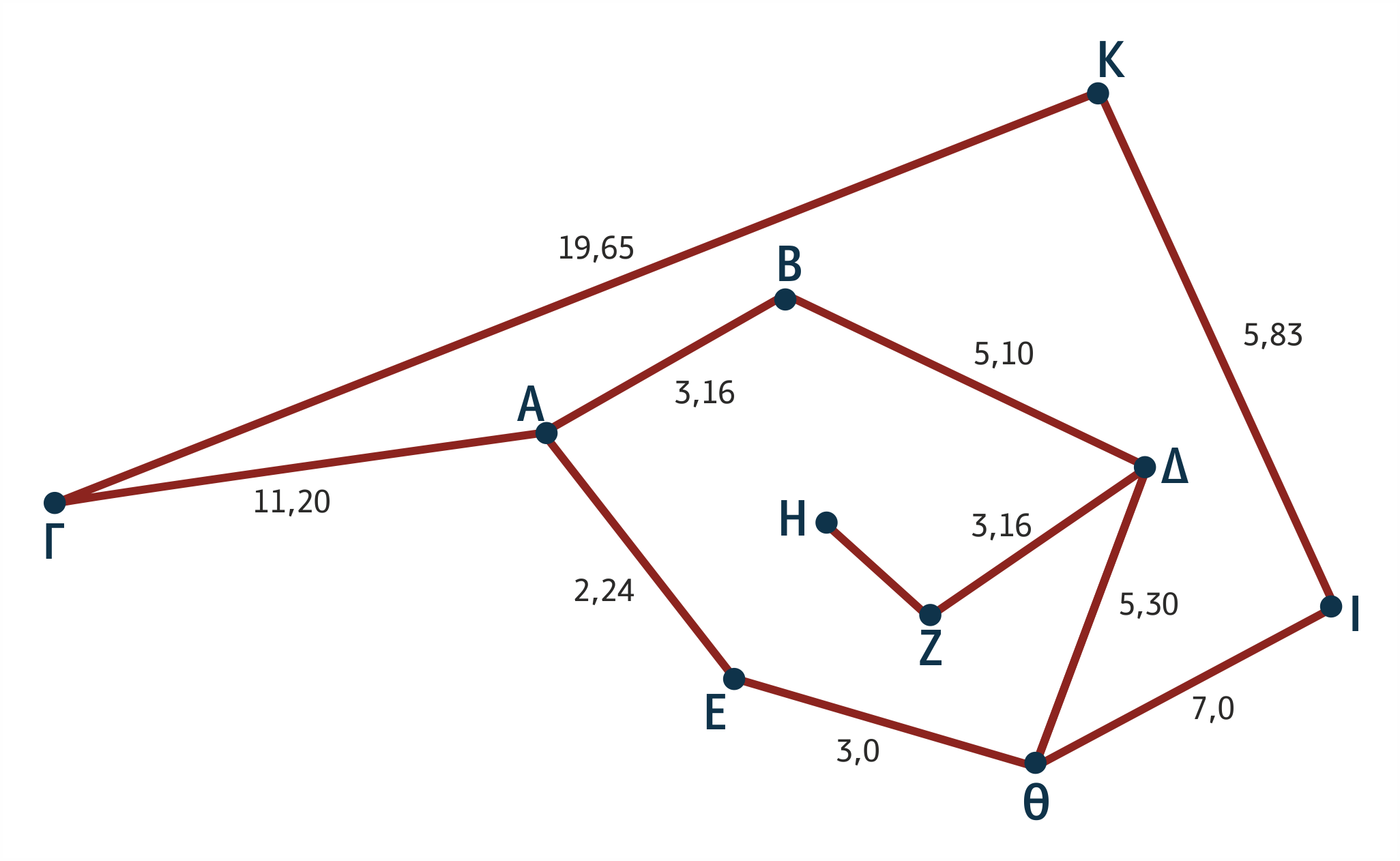
Σχήμα 1.11 Μια εκδοχή του χώρου αναζήτησης του προβλήματος του περιοδεύοντος πωλητή, όταν επισκέπτεται 10 πόλεις

Ο ορισμός του συγκεκριμένου προβλήματος έχει ως εξής:

 

Ι= Πωλητής σε πόλη Α

G= Πωλητής σε πόλη Κ

Τ={

S= κόμβοι του γραφήματος του σχήματος 1.11

 

Οι αλγόριθμοι αναζήτησης εξερευνούν γραφήματα όπως αυτόν στο σχήμα 1.11 χρησιμοποιώντας και εμπλουτίζοντας κατά την πορεία προς εύρεση λύσης τις γνώσεις σχετικά με τη δυνατότητα σύνδεσης απομακρυσμένων κόμβων μεταξύ τους και το μήκος των εναλλακτικών μονοπατιών που τις συνδέουν. Στην προκειμένη περίπτωση, ένας τύπος γνώσης που παράγεται βήμα-βήμα είναι αυτή που αφορά την απόσταση κάθε κόμβου από τον κόμβο-ρίζα. Για παράδειγμα, σε ένα στιγμιότυπο της επίλυσης του προβλήματος του πωλητή, όταν αυτός ξεκινά από την πόλη Α, ο αλγόριθμος θα μπορούσε να έχει διανύσει το μονοπάτι Α-Β-Δ-Θ και να έχει αποκτήσει τη γνώση ότι η πόλη Α συνδέεται με τη Θ με μεταξύ τους απόσταση 12,73 χιλ. (βλέπε Σχήμα 1.12).

Σχήμα 1.12 Απόσταση απομακρυσμένων κόμβων ενός γραφήματος

Όταν εκτελείται εξαντλητική αναζήτηση (exhaustive search), δηλαδή ο αλγόριθμος προσπαθεί να βρει όλες τις δυνατές λύσεις του προβλήματος, τότε στο δένδρο που σχηματίζεται αποτυπώνονται όλα τα μονοπάτια που είναι δυνατόν να διανυθούν (μερικά από τα οποία θα αποδειχθούν λύσεις), καθώς και όλη η γνώση που αποκτάται κατά τη διάνυση αυτή (βλέπε Σχήμα 1.13).

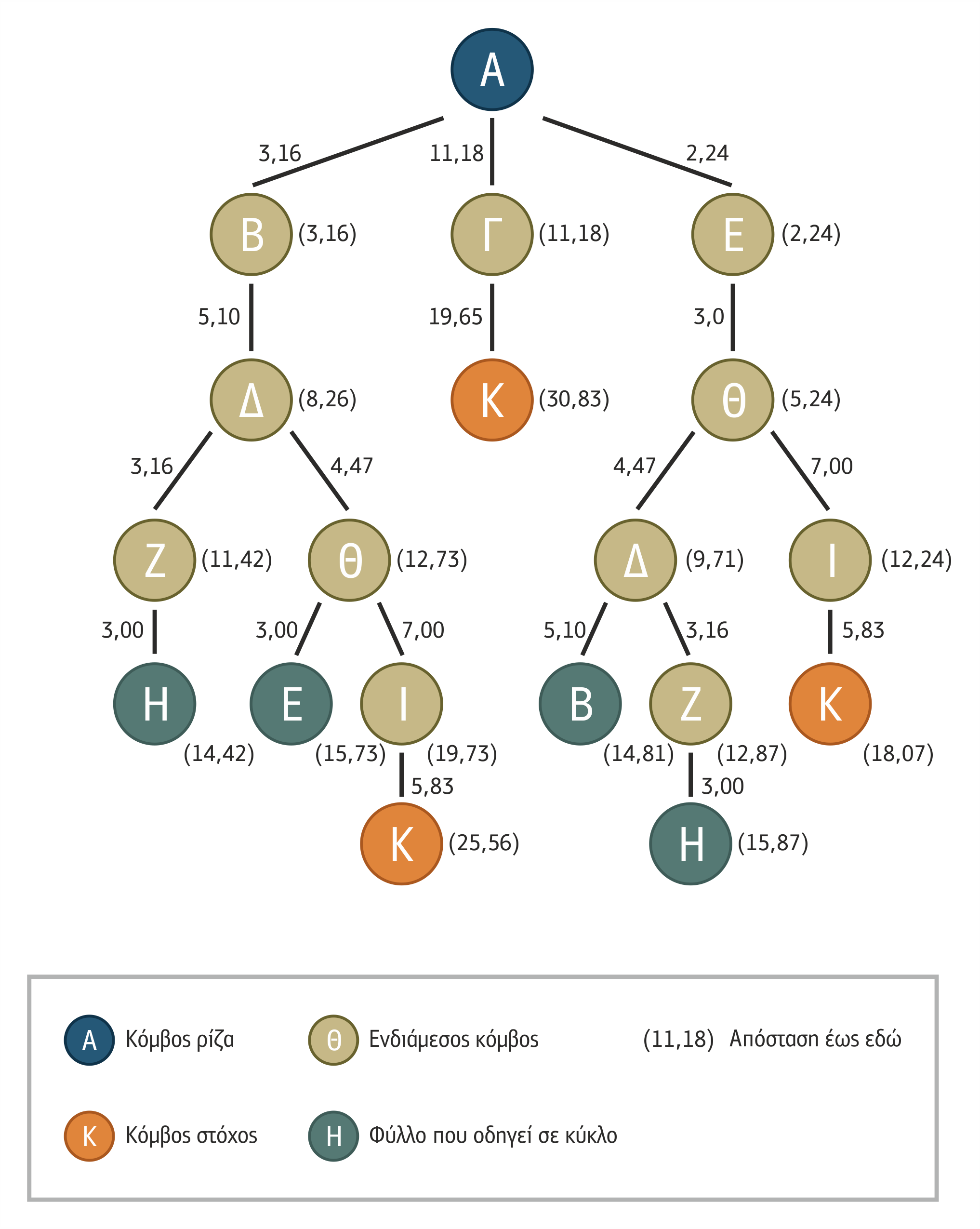
Σχήμα 1.13 Το δένδρο της εξαντλητικής αναζήτησης του προβλήματος του περιοδεύοντος πωλητή

1.2.2 Περιγραφή Δένδρων Αναζήτησης

Κάθε κόμβος του δέντρου αναζήτησης αντιστοιχεί σε μια κατάσταση του χώρου καταστάσεων του προβλήματος. Η ρίζα του δένδρου αντιστοιχεί στην αρχική κατάσταση. Ο κόμβος που δημιουργεί ένα συγκεκριμένο κόμβο καλείται πατρικός ή γονικός κόμβος (parent node). Οι κόμβοι που δημιουργούνται από ένα γονικό κόμβο καλούνται διάδοχοι κόμβοι (successor nodes). Η ενέργεια που εφαρμόζεται σε έναν κόμβο, για να καταστεί γονικός κόμβος, προκαλείται από κάποιον από τους τελεστές του προβλήματος και παριστάνεται ως ακμή ή κλαδί του δένδρου που ενώνει το γονικό κόμβο με καθέναν από τους διάδοχους κόμβους που δημιουργεί. Κάθε κόμβος του δένδρου αντιστοιχεί στην κατάσταση στην οποία καταλήγει το μονοπάτι που προκύπτει από την κατά ένα βήμα επέκταση του μονοπατιού που έχει ήδη καθορίσει ο γονικός του κόμβος. Το κόστος του αλγόριθμου, για να διανύσει ένα μονοπάτι, καλείται κόστος μονοπατιού (path cost). Το πλήθος των κόμβων μέσα σε ένα μονοπάτι καλείται βάθος μονοπατιού (path depth). Για παράδειγμα, στο μονοπάτι του σχήματος 1.14 το κόστος είναι 12,73 και το βάθος είναι 4.

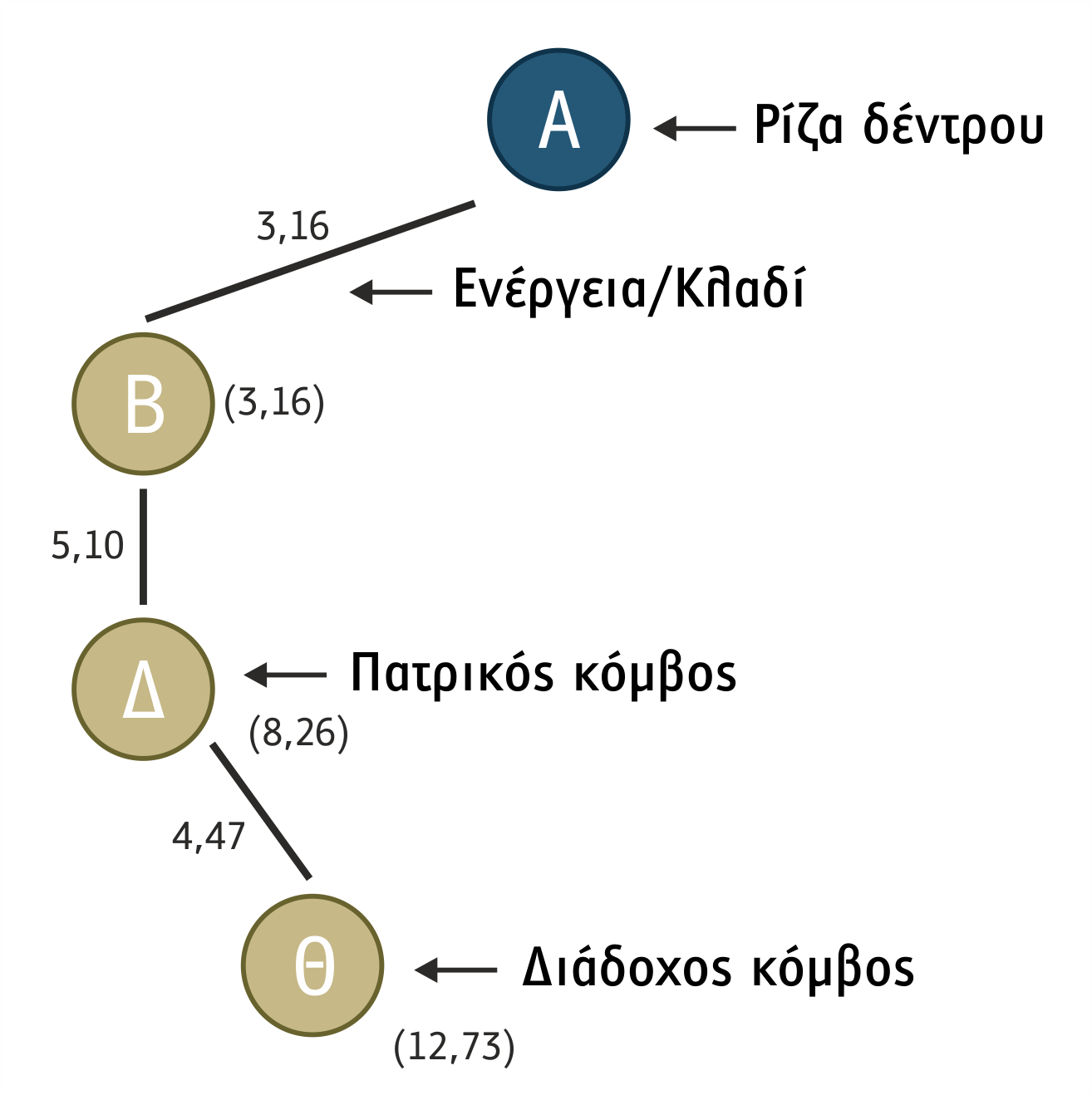
Σχήμα 1.14 Μονοπάτι βάθους 4 και κόστους 12,73 για το πρόβλημα του περιοδεύοντος πωλητή

Μέτωπο (fringe ή front) καλείται το διατεταγμένο σύνολο των κόμβων που ο αλγόριθμος έχει αναρτήσει στο δένδρο, αλλά δεν έχει ακόμα επεκτείνει προς διάδοχους κόμβους, δηλαδή τα φύλλα του δένδρου σε κάποιο στιγμιότυπο της εκτέλεσης του αλγόριθμου. Στο μέτωπο δεν περιλαμβάνονται οι κόμβοι που έχουν ήδη γίνει γονικοί κόμβοι, ακόμα και αν αυτοί αποτελούν φύλλα του δένδρου (περίπτωση μονοπατιών των οποίων η επέκταση θα δημιουργούσε κύκλους)∙ για παράδειγμα, η περίπτωση του κόμβου Η στο δένδρο του σχήματος 1.15 καλείται και κατάσταση αδιεξόδου. Στο ίδιο σχήμα, το μέτωπο περιλαμβάνει τους κόμβους Θ, Γ και Ε.

Το σύνολο των κόμβων ενός δένδρου αναζήτησης που ο αλγόριθμος έχει ήδη καταστήσει γονικούς καλείται κλειστό σύνολο (closed set). Στο σχήμα 1.15, το κλειστό σύνολο περιλαμβάνει τους κόμβους Α, Β, Δ, Ζ, Η, δηλαδή όλους τους κόμβους που δεν ανήκουν στο μέτωπο.

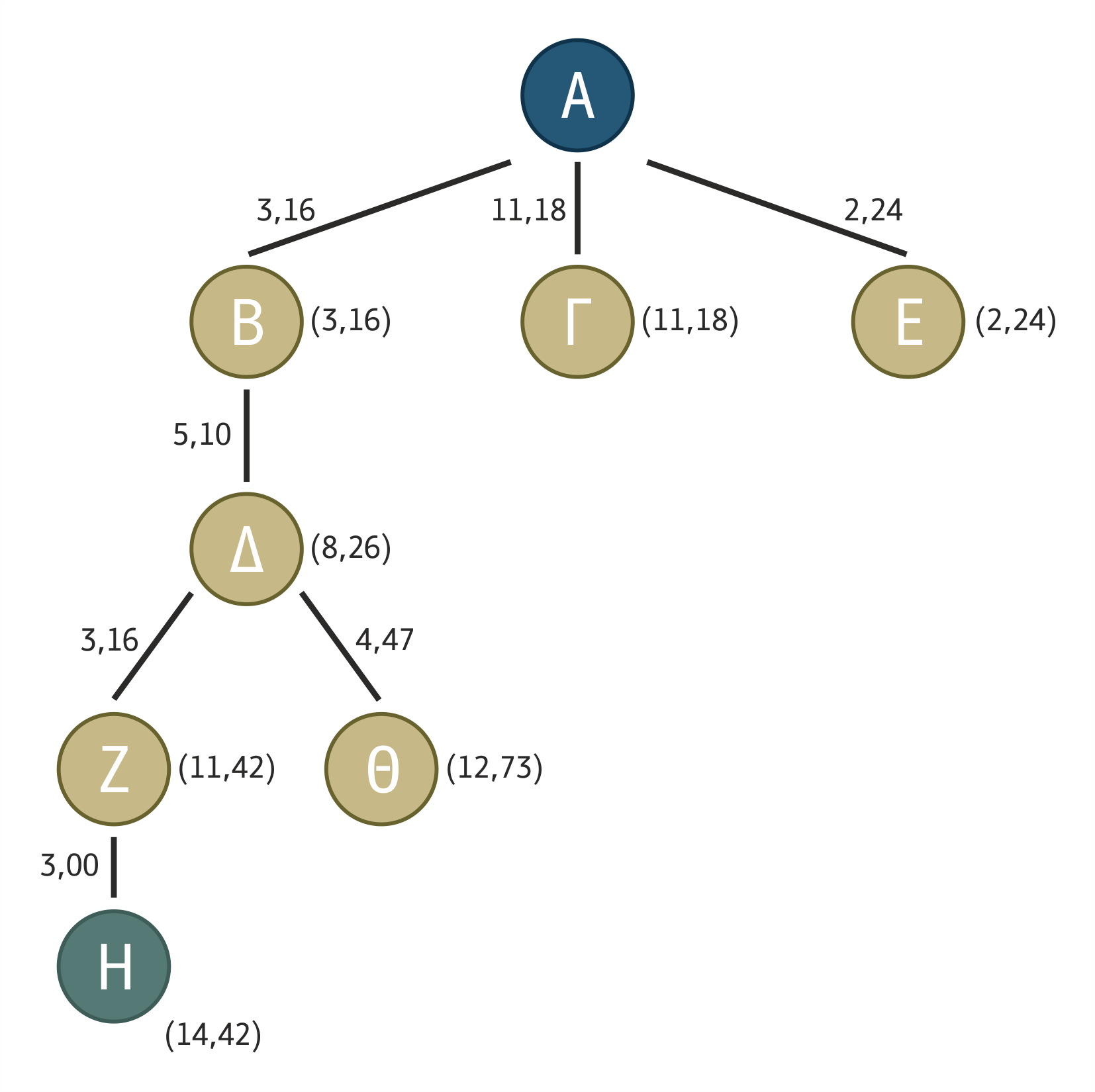
Σχήμα 1.15 Το δένδρο αναζήτησης του προβλήματος του περιοδεύοντος πωλητή σε ένα στιγμιότυπο της εξέλιξής του

Όλα όσα αναφέραμε σχετικά με τα δένδρα αναζήτησης έως τώρα αποτυπώνονται συγκεντρωτικά στο σχήμα 1.16:

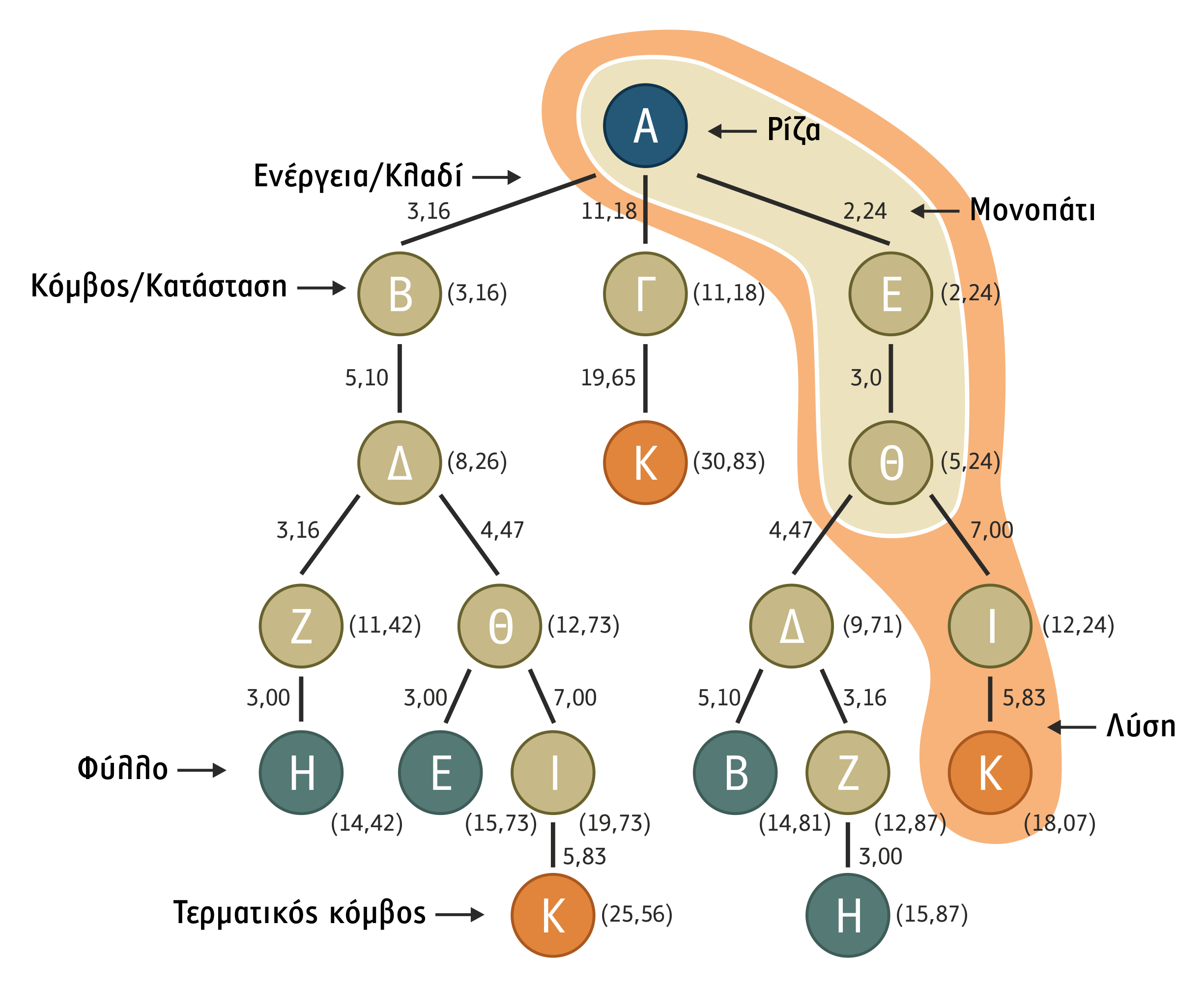
Σχήμα 1.16 Ανάλυση δένδρου αναζήτησης

1.3 Αλγόριθμοι Αναζήτησης

Για την επίλυση ενός προβλήματος πρέπει να αποφασιστεί ποιος από τους υπάρχοντες αλγόριθμους θα επιλεγεί. Αυτή η απόφαση θα χαρακτηρίσει την πορεία επίλυσης και θα καθορίσει αποφασιστικά την ποιότητα της λύσης ή των λύσεων που θα βρεθούν.

Τα βασικά στοιχεία που χαρακτηρίζουν μια αναζήτηση είναι τα παρακάτω:

Βάσει των παραπάνω, η επίλυση ενός προβλήματος Ps (problem solution) μέσω ενός αλγόριθμου αναζήτησης Α μπορεί να παρουσιαστεί αναλυτικά ως ακολούθως:

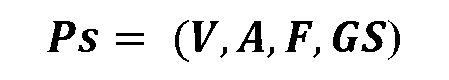
Ένας αλγόριθμος δεν είναι βέβαιο ότι θα βρει πάντα τη λύση σε ένα πρόβλημα, ακόμα και αν αυτή υπάρχει. Ένας αλγόριθμος καλείται πλήρης (complete), όταν εγγυάται την εύρεση λύσης σε περίπτωση κατά την οποία αυτή υπάρχει. Σε αντίθετη περίπτωση καλείται ατελής (incomplete).

Τα κριτήρια επιλογής ενός αλγορίθμου αναζήτησης είναι τα ακόλουθα:

Για να εκτιμήσουμε την αποδοτικότητα ενός αλγορίθμου αναζήτησης, εξετάζουμε:

Σε περίπτωση κατά την οποία μας ενδιαφέρουν και τα δύο, εξετάζουμε το ολικό κόστος. Η βαρύτητα που προσδίδουμε στο κάθε κόστος εξαρτάται από την εφαρμογή. Άλλοτε θέλουμε μια πολύ καλή (ή και τη βέλτιστη) λύση, χωρίς να μας απασχολεί ο χρόνος που θα αφιερώσουμε, για να τη βρούμε, και άλλοτε θέλουμε μια (οποιαδήποτε) λύση που θα βρεθεί γρήγορα.

1.3.1 Γενικός αλγόριθμος αναζήτησης

Για τη γενική διαδικασία αναζήτησης λύσης που εφαρμόζει κάθε αλγόριθμος μπορούμε να σημειώσουμε ότι η αναζήτηση:

Πιο αναλυτικά, ο γενικός αλγόριθμος αναζήτησης δομεί το δένδρο αναζήτησης ξεκινώντας από την αρχική κατάσταση του προβλήματος, που αποτελεί τη ρίζα του δένδρου, και καταλήγοντας σε κόμβους-φύλλα, μερικά από τα οποία μπορεί να είναι αδιέξοδα και άλλα να είναι στόχοι.

Καταρχάς, δημιουργείται το αρχικό μονοπάτι ως ένα μονοπάτι μηδενικού μήκους που περιέχει μόνο τη ρίζα του δένδρου (αρχική κατάσταση) και, παράλληλα, δημιουργείται η αρχική ουρά, που περιέχει μόνο το αρχικό μονοπάτι. Στη συνέχεια, δημιουργούνται νέα μονοπάτια στην ουρά, καθώς οι υπάρχοντες κόμβοι γίνονται γονικοί κόμβοι. Το σύνολο των κόμβων στους οποίους καταλήγουν τα μονοπάτια της ουράς, σε ένα δεδομένο στιγμιότυπο της αναζήτησης, δημιουργούν το τρέχον μέτωπο αναζήτησης.

Για να γίνουν πιο κατανοητά τα παραπάνω, θα παρουσιάσουμε πώς θα τα υλοποιούσε οποιοσδήποτε αλγόριθμος αναζήτησης στον πρώτο κύκλο λειτουργίας του κατά την επίλυση του προβλήματος του αγρότη με τις 10 πόλεις (βλέπε Σχήμα 1.11).


Αρχικοποίηση δένδρου αναζήτησης:

Αρχικό μέτωπο: <Α>

Αρχικό μονοπάτι: (Α)

Αρχική ουρά: <(Α)>

Αρχικό κλειστό σύνολο: {}


1ος κύκλος λειτουργίας:

Μέτωπο: <Β, Γ, Ε>

Ουρά: <(Α Β), (Α Γ), (Α Ε)>

Κλειστό: {Α}

 

όπου τα σύμβολα `<` και `>` χρησιμοποιούνται, για να περιγραφεί ένα διατεταγμένο σύνολο από καταστάσεις ή μονοπάτια και τα `(` και `)` χρησιμοποιούνται, για να περιγραφεί μια ακολουθία από καταστάσεις που περιγράφει ένα μονοπάτι.

Ο τρόπος επέκτασης στον επόμενο 2ο κύκλο διαφέρει από αλγόριθμο σε αλγόριθμο, ανάλογα με τον κόμβο του μετώπου που ο κάθε αλγόριθμος θα επιλέξει ως γονικό κόμβο. Αν η αναζήτηση χρησιμοποιούσε την πρώτα σε βάθος αναζήτηση που θα περιγραφεί σε επόμενη παράγραφο, τότε θα επιλέγετο ως γονικός κόμβος ο Β με διάδοχο κόμβο τον Δ και θα ίσχυαν τα επόμενα:


2ος κύκλος λειτουργίας:

Μέτωπο: <Δ, Γ, Ε>

Ουρά: <(Α Β Δ), (Α Γ), (Α Ε)>

Κλειστό: {Α, Β}

 

Τα παραπάνω αποτυπώνονται στο σχήμα 1.17 που ακολουθεί.

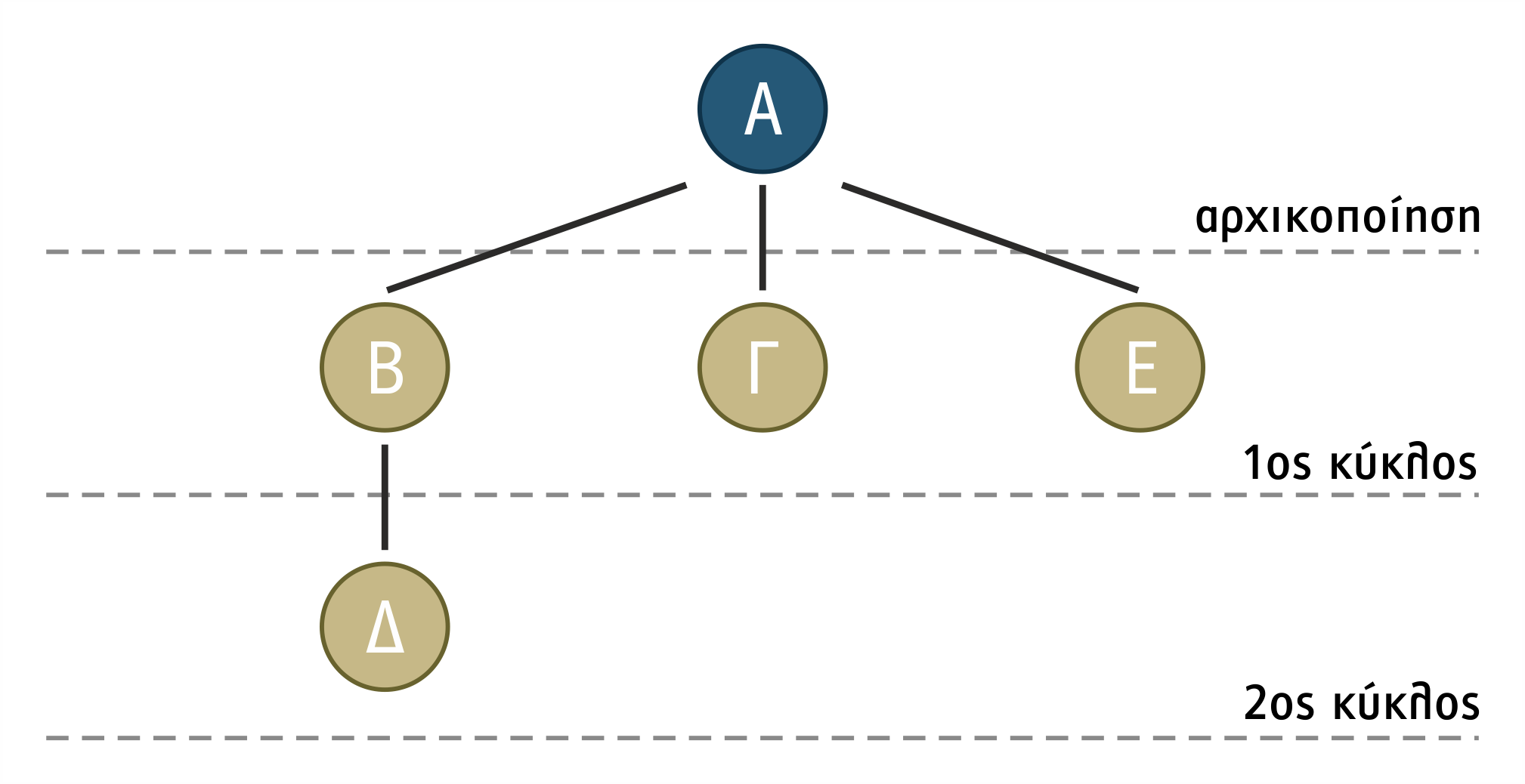
Σχήμα 1.17 Ανάπτυξη δένδρου αναζήτησης για το πρόβλημα του αγρότη έως τον 2ο κύκλο λειτουργίας

Δείτε κινούμενη εικόνα 1.1 - Ανάπτυξη δένδρου Αναζήτησης σε κύκλους

 

Η διαδικασία αναζήτησης θα μπορούσε να παρουσιαστεί και ως μια διαδικασία επιλογής γονικού κόμβου από το μέτωπο αναζήτησης και επέκτασης του μονοπατιού που καταλήγει σε αυτόν προς τους διάδοχους κόμβους ή κόμβους-παιδιά. Οι αλγόριθμοι αναζήτησης χαρακτηρίζονται από τις στρατηγικές που εφαρμόζουν, για να επιλέξουν έναν από τους κόμβους του μετώπου ως γονικό κόμβο, αλλά όλοι ακολουθούν ορισμένα κοινά βήματα που συγκροτούν έναν γενικό αλγόριθμο αναζήτησης.

Τα βήματα του γενικού αλγόριθμου αναζήτησης είναι τα ακόλουθα:

 

Βήματα Γενικού Αλγόριθμου Αναζήτησης

  1. Βάλε την αρχική κατάσταση στο κενό μέτωπο αναζήτησης.
  2. Αν το μέτωπο είναι κενό, τότε η αναζήτηση ολοκληρώθηκε ανεπιτυχώς, χωρίς να βρεθεί λύση, ΤΕΛΟΣ.
  3. Αν ο πρώτος σε σειρά κόμβος του μετώπου είναι στόχος, τότε βρέθηκε λύση, TEΛOΣ.
  4. Αν ο πρώτος σε σειρά κόμβος του μετώπου ανήκει στο κλειστό σύνολο, τότε Πήγαινε στο βήμα 2.
  5. Εφάρμοσε τους τελεστές στον πρώτο σε σειρά κόμβο του μετώπου, για να γίνει γονικός κόμβος και να παραχθούν οι διάδοχοι κόμβοι.
  6. Πρόσθεσε τους διάδοχους κόμβους στο μέτωπο, αφού αφαιρέσεις το γονικό κόμβο, και δημιούργησε το νέο μέτωπο.
  7. Αν το απαιτεί ο αλγόριθμος αναζήτησης, αναδιάταξε τους κόμβους του μετώπου σύμφωνα με το ποιοτικό κριτήριο που ορίζει η στρατηγική του αλγόριθμου.
  8. Βάλε το γονικό κόμβο στο κλειστό σύνολο.
  9. Πήγαινε στο βήμα 2.

Σε κάθε κύκλο λειτουργίας ενός αλγόριθμου αναζήτησης, το βήμα 5 ορίζει τον πρώτο κόμβο του μετώπου ως γονικό, αλλά τα βήματα 6 και 7 όρισαν το ποιος κόμβος θα βρεθεί στην πρώτη θέση .

Ο αλγόριθμος αναζήτησης αναπτύσσεται ως μια συνάρτηση που καλεί επαναληπτικά άλλες συναρτήσεις, για να υλοποιήσει τα παραπάνω βήματα.

 

Δείτε popup 1.1 - Ψευδοκώδικας Γενικού Αλγόριθμου Αναζήτησης με παρακολούθηση μετώπου

 

Αν θέλαμε να παρουσιάσουμε πιο αναλυτικά τα βήματα του γενικού αλγόριθμου, παρακολουθώντας τη διαμόρφωση του μετώπου ταυτόχρονα με τη διαμόρφωση της ουράς και χρησιμοποιώντας τον όρο κατάσταση αντί κόμβου, θα είχαμε την ακόλουθη περιγραφή βημάτων:

  1. Βάλε την αρχική κατάσταση στο κενό μέτωπο αναζήτησης. Βάλε το αρχικό μονοπάτι που περιέχει την αρχική κατάσταση μέσα στην κενή ουρά
  2. Αν το μέτωπο είναι κενό, τότε η αναζήτηση ολοκληρώθηκε ανεπιτυχώς, χωρίς να βρεθεί λύση, ΤΕΛΟΣ.
  3. Αν η πρώτη σε σειρά κατάσταση του μετώπου είναι στόχος, τότε επίστρεψε το πρώτο μονοπάτι της ουράς ως λύση, TEΛOΣ.
  4. Αν η πρώτη σε σειρά κατάσταση του μετώπου ανήκει στο κλειστό σύνολο, τότε Πήγαινε στο βήμα 2.
  5. Εφάρμοσε τους τελεστές μετάβασης στην πρώτη στη σειρά κατάσταση του μετώπου, για να γίνει κατάσταση-γονέας και να παραχθούν οι διάδοχες καταστάσεις. Δημιούργησε τα αντίστοιχα επεκεκταμένα μονοπάτια που καταλήγουν σε αυτές.
  6. Πρόσθεσε τις διάδοχες καταστάσεις στο μέτωπο, αφού αφαιρέσεις την κατάσταση-γονέα, και δημιούργησε το νέο μέτωπο. Πρόσθεσε τα επεκεκταμένα μονοπάτια στην ουρά, αφού αφαιρέσεις το μονοπάτι που οδηγούσε στον κόμβο-γονέα, και δημιούργησε τη νέα ουρά.
  7. Αν το απαιτεί ο αλγόριθμος αναζήτησης, αναδιάταξε τις καταστάσεις του μετώπου σύμφωνα με το ποιοτικό κριτήριο που ορίζει η στρατηγική του αλγόριθμου και πραγματοποίησε την αντίστοιχη αναδιάταξη στα μονοπάτια της ουράς.
  8. Βάλε την κατάσταση-γονέα στο κλειστό σύνολο.
  9. Πήγαινε στο βήμα 2.

Η δεύτερη εκδοχή παρουσίασης των βημάτων της διαδικασίας αναζήτησης με παρακολούθηση του μετώπου και ταυτόχρονα της ουράς βασίζεται στην περιγραφή της επέκτασης των μερικών λύσεων που αντιπροσωπεύει η ουρά μονοπατιών.

 

Δείτε popup 1.2 - Ψευδοκώδικας Γενικού Αλγόριθμου Αναζήτησης με παρακολούθηση μετώπου και ουράς

 

Οι μέθοδοι αναζήτησης χωρίζονται σε δύο μεγάλες κατηγορίες: στις τυφλές μεθόδους και τις ευρετικές. Οι αλγόριθμοι αναζήτησης των τυφλών μεθόδων τοποθετούν τα μονοπάτια στην ουρά βάσει του χρόνου δημιουργίας τους. Αντίθετα, στους ευρετικούς αλγόριθμους τα μονοπάτια της ουράς αναδιατάσσονται βάσει των ποιοτικών κριτηρίων που τα χαρακτηρίζουν.

Με απλές προσαρμογές, ο γενικός αλγόριθμος αναζήτησης μετατρέπεται εύκολα σε συγκεκριμένο τυφλό ή ευρετικό αλγόριθμο.

1.4 Τυφλές μέθοδοι αναζήτησης

Οι τυφλές μέθοδοι αναζήτησης (blind search methods) εφαρμόζονται σε προβλήματα στα οποία είτε δεν μας ενδιαφέρει να βρεθεί μια ποιοτική λύση είτε δε διαθέτουν πληροφορίες που να επιτρέπουν στον αλγόριθμο αναζήτησης την επιλογή του ποιοτικά καλύτερου κόμβου μέσα από το μέτωπο αναζήτησης, όταν αυτός επιχειρεί να αναπτύξει το δένδρο αναζήτησης.

Με τις τυφλές μεθόδους αναζήτησης, αν υπάρχει λύση, τότε η μέθοδος εγγυάται την εύρεσή της. Η διαφορά τους έγκειται στον τρόπο (τη χρονική σειρά) με τον οποίο αναπτύσσουν τα μονοπάτια μέσα στο δένδρο αναζήτησης.

Γνωστές τυφλές μέθοδοι αναζήτησης είναι οι:

1.4.1. Πρώτα σε Βάθος Αναζήτηση

Δεδομένου ότι σε μια τυφλή μέθοδο αναζήτησης ένα μονοπάτι είναι εξίσου καλό με οποιοδήποτε άλλο, η Πρώτα σε Βάθος Αναζήτηση (Depth-First Search - DFS) επεκτείνει κάθε φορά το αριστερότερο από τα υπάρχοντα μονοπάτια του δένδρου, αρχίζοντας από το μονοπάτι που περιέχει τη ρίζα του δένδρου. Ουσιαστικά, επεκτείνει το μέτωπο αναζήτησης προς αριστερά και προς το βάθος του δένδρου αναζήτησης. Η διαδικασία ολοκληρώνεται, όταν εντοπιστεί ένας κόμβος που αντιστοιχεί σε μια επιθυμητή τελική κατάσταση ή όταν εξαντληθεί η αναζήτηση, δηλαδή όταν όλα τα μονοπάτια καταλήξουν σε κόμβους που δεν μπορούν να επιλεγούν ως γονικοί κόμβοι, γιατί οδηγούν σε κύκλους.

Στο σχήμα 1.18 παρουσιάζεται η πορεία που ακολουθεί η Πρώτα σε Βάθος Αναζήτηση, καθώς σχηματίζει βήμα προς βήμα το δένδρο αναζήτησης του προβλήματος του περιοδεύοντος πωλητή, στην προσπάθειά της να οδηγήσει τον πωλητή από την πόλη Α στην πόλη Κ. Η λύση που βρίσκει ο αλγόριθμος είναι το μονοπάτι Α Β Δ Θ Ι Κ.

Σχήμα 1.18 Η πορεία σχηματισμού του δένδρου αναζήτησης που ακολουθεί η DFS κατά την επίλυση του προβλήματος του περιοδεύοντος πωλητή

Δείτε κινούμενη εικόνα 1.2 - Ανάπτυξη Δένδρου Αναζήτησης με DFS και παράλληλη παρακολούθηση μετώπου

 

Τα βήματα της Πρώτα σε Βάθος Αναζήτησης με παρακολούθηση μετώπου είναι τα ακόλουθα:

  1. Βάλε την αρχική κατάσταση στο κενό μέτωπο αναζήτησης.
  2. Αν το μέτωπο είναι κενό, τότε η αναζήτηση ολοκληρώθηκε ανεπιτυχώς, χωρίς να βρεθεί λύση, ΤΕΛΟΣ.
  3. Αν ο πρώτος σε σειρά κόμβος του μετώπου είναι στόχος, τότε βρέθηκε λύση, TEΛOΣ.
  4. Αν ο πρώτος σε σειρά κόμβος του μετώπου ανήκει στο κλειστό σύνολο, τότε Πήγαινε στο βήμα 2.
  5. Εφάρμοσε τους τελεστές στον πρώτο σε σειρά κόμβο του μετώπου, για να γίνει γονικός κόμβος και να παραχθούν οι διάδοχοι κόμβοι.
  6. Πρόσθεσε τους διάδοχους κόμβους

Στον παρακάτω πίνακα 1.3 παρουσιάζονται οι πρώτοι έξι κύκλοι ανάπτυξης του δένδρου αναζήτησης της DFS για το πρόβλημα του περιοδεύοντος πωλητή με παρακολούθηση του μετώπου αναζήτησης.

Πίνακας 1.3 Οι έξι πρώτοι κύκλοι λειτουργίας της DFS για το πρόβλημα του περιοδεύοντος πωλητή με μέτωπο αναζήτησης

Η διαφοροποίηση της λειτουργίας της DFS από άλλες τυφλές μεθόδους αναζήτησης βρίσκεται στο βήμα 7, όπου προσδιορίζεται η θέση του μετώπου στην οποία θα τοποθετηθούν οι κόμβοι-παιδιά. Η εξέταση αμέσως προηγουμένων (χρονικά) καταστάσεων, όπως υλοποιείται στο βήμα 4, ονομάζεται χρονική οπισθοδρόμηση (chronological backtracking).

Ακολουθεί ο ψευδοκώδικας του αλγόριθμου της DFS με παρακολούθηση μετώπου και ουράς.

Δείτε κινούμενη εικόνα 1.3 - Ανάπτυξη Δένδρου Αναζήτησης με DFS και παράλληλη παρακολούθηση ουράς

 

Στον παρακάτω πίνακα 1.4 παρουσιάζονται οι πρώτοι έξι κύκλοι ανάπτυξης του δένδρου αναζήτησης της DFS για το πρόβλημα του περιοδεύοντος πωλητή με παρακολούθηση ουράς αναζήτησης.

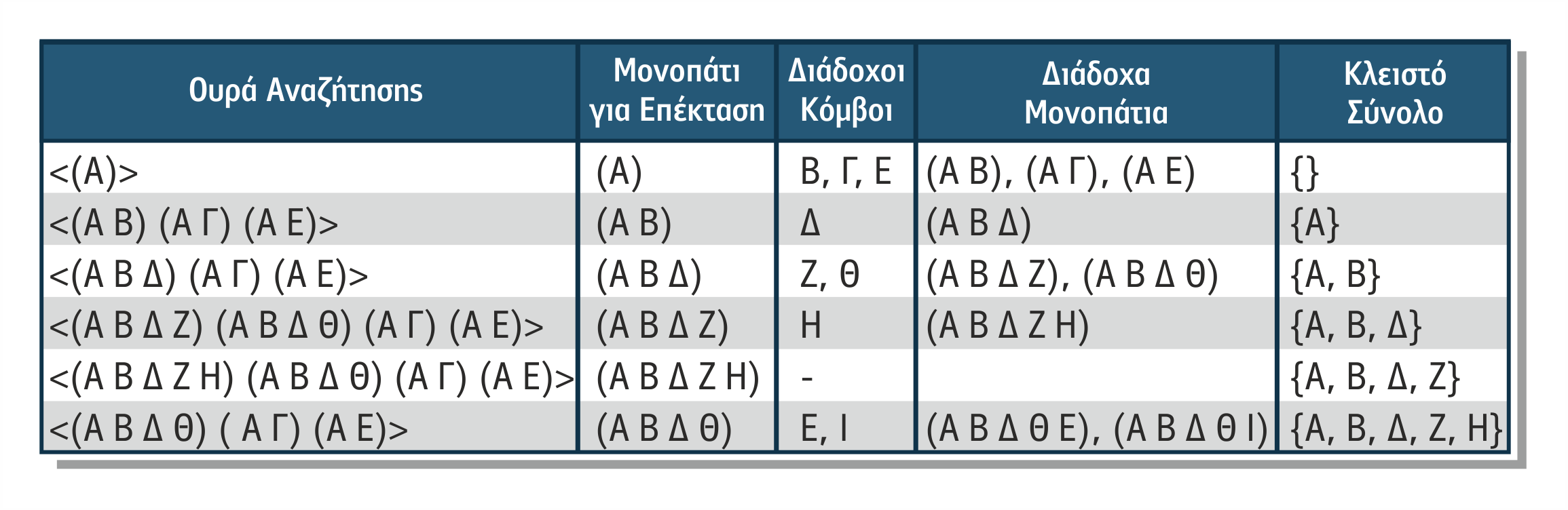
Πίνακας 1.4 Οι έξι πρώτοι κύκλοι λειτουργίας της DFS για το πρόβλημα του περιοδεύοντος πωλητή με ουρά αναζήτησης

Πλεονεκτήματα της DFS

Μειονεκτήματα της DFS

1.4.2 Η Πρώτα σε Πλάτος Αναζήτηση

Η Πρώτα σε Πλάτος Αναζήτηση (Breadth-First Search - BFS) εξετάζει πρώτα τα μονοπάτια που βρίσκονται στο ίδιο βάθος του δένδρου αναζήτησης. Μόνο όταν τα εξετάσει όλα, αρχίζει την επέκτασή τους στο αμέσως επόμενο επίπεδο. Ουσιαστικά, επεκτείνει το μέτωπο αναζήτησης ανά επίπεδο του δένδρου αναζήτησης. Η διαδικασία ολοκληρώνεται, όταν εντοπιστεί ένας κόμβος που αντιστοιχεί σε μια επιθυμητή τελική κατάσταση ή όταν εξαντληθεί η αναζήτηση, δηλαδή όταν όλα τα μονοπάτια καταλήξουν σε κόμβους που δεν μπορούν να επιλεγούν ως γονικοί κόμβοι, γιατί οδηγούν σε κύκλους.

Στο σχήμα 1.19 παρουσιάζεται η πορεία που ακολουθεί η Πρώτα σε Πλάτος Αναζήτηση, καθώς σχηματίζει βήμα-βήμα το δένδρο αναζήτησης στην προσπάθειά της να επιλύσει το πρόβλημα του περιοδεύοντος πωλητή, δηλαδή να οδηγήσει τον πωλητή από την πόλη Α στην πόλη Κ. Η λύση που θα βρεθεί είναι το μονοπάτι Α Γ Κ.

Σχήμα 1.19 Η πορεία σχηματισμού του δένδρου αναζήτησης που ακολουθεί η Πρώτα σε Πλάτος Αναζήτηση κατά την επίλυση του προβλήματος του περιοδεύοντος πωλητή

Τα βήματα της BFS με παρακολούθηση μετώπου είναι τα ακόλουθα:

  1. Βάλε την αρχική κατάσταση στο κενό μέτωπο αναζήτησης.
  2. Αν το μέτωπο είναι κενό, τότε η αναζήτηση ολοκληρώθηκε ανεπιτυχώς, χωρίς να βρεθεί λύση, ΤΕΛΟΣ.
  3. Αν ο πρώτος σε σειρά κόμβος του μετώπου είναι στόχος, τότε βρέθηκε λύση, TEΛOΣ.
  4. Αν ο πρώτος σε σειρά κόμβος του μετώπου ανήκει στο κλειστό σύνολο, τότε Πήγαινε στο βήμα 2.
  5. Εφάρμοσε τους τελεστές στον πρώτο σε σειρά κόμβο του μετώπου, για να γίνει γονικός κόμβος και να παραχθούν οι διάδοχοι κόμβοι.
  6. Πρόσθεσε τους διάδοχους κόμβους στο τέλος του μετώπου, αφού αφαιρέσεις το γονικό κόμβο, και δημιούργησε το νέο μέτωπο.
  7. Βάλε το γονικό κόμβο στο κλειστό σύνολο.
  8. Πήγαινε στο βήμα 2.

Δείτε κινούμενη εικόνα 1.4 - Ανάπτυξη Δένδρου Αναζήτησης με BFS και παράλληλη παρακολούθηση μετώπου

 

Στον παρακάτω πίνακα 1.5 παρουσιάζεται η ανάπτυξη του δένδρου αναζήτησης της BFS με παρακολούθηση μετώπου αναζήτησης για το πρόβλημα του περιοδεύοντος πωλητή μέχρι την εύρεση στόχου.

Πίνακας 1.5 Οι κύκλοι λειτουργίας της ΒFS για το πρόβλημα του περιοδεύοντος πωλητή με μέτωπο αναζήτησης

Ακολουθεί ο ψευδοκώδικας του αλγόριθμου της BFS με παρακολούθηση μετώπου και ουράς.

Δείτε κινούμενη εικόνα 1.5 - Ανάπτυξη Δένδρου Αναζήτησης με ΒFS και παράλληλη παρακολούθηση ουράς

 

Στον παρακάτω πίνακα 1.6 παρουσιάζεται η ανάπτυξη του δένδρου αναζήτησης της BFS με παρακολούθηση ουράς για το πρόβλημα του περιοδεύοντος πωλητή μέχρι την εύρεση λύσης.

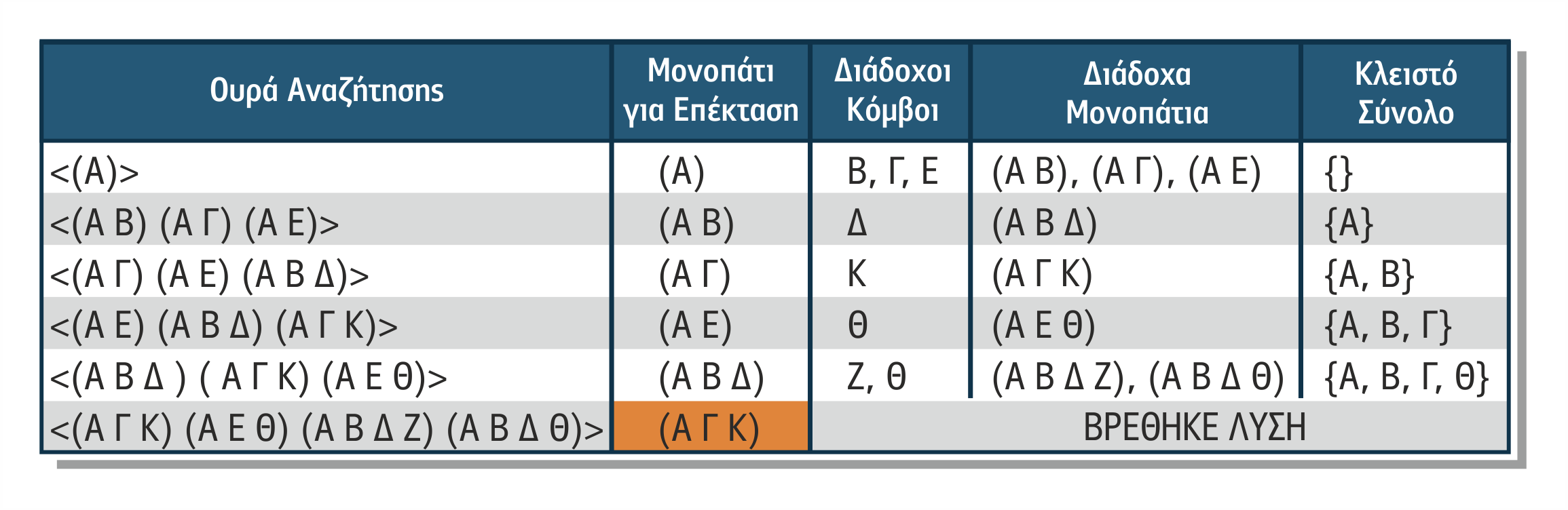
Πίνακας 1.6 Οι κύκλοι λειτουργίας της BFS για το πρόβλημα του περιοδεύοντος πωλητή με ουρά αναζήτησης

Πλεονεκτήματα της ΒFS

Μειονεκτήματα της BFS

Το να κρίνουμε ποια από τις 2 τυφλές μεθόδους, DFS και BFS, είναι προσφορότερη εξαρτάται άμεσα από το πρόβλημα προς επίλυση. Γενικά, πρέπει να αποφεύγεται η BFS, όταν είναι γνωστό ότι οι υπάρχουσες λύσεις βρίσκονται σε μεγάλο βάθος. Αντίστοιχα, η χρήση της DFS είναι προτιμότερη, όταν ο στόχος βρίσκεται σε μονοπάτια μεγάλου μήκους.

1.4.3 Αλγόριθμος Αναζήτησης Επαναληπτικής Εμβάθυνσης

Η μέθοδος Αναζήτησης Επαναληπτικής Εμβάθυνσης (Iterative Deepening Search - IDS) αναζητά τη λύση με τη λογική της DFS, αλλά περιορίζει το βάθος της αναζήτησης θέτοντας ένα μικρό βάθος στην αρχή ως όριο, το οποίο σταδιακά αυξάνεται με εμβάθυνση. Αυτό αποτελεί έναν τρόπο αντιμετώπισης του προβλήματος εύρεσης σωστού ορίου για το βάθος αναζήτησης. Συνήθως, η μέθοδος δοκιμάζει όλα τα πιθανά βάθη, αυξάνοντας προοδευτικά το βάθος κατά 1 αρχίζοντας από το βάθος 0, π.χ. 0, 1, 2, κτλ.

 

Βήματα αλγόριθμου Επαναληπτικής εκβάθυνσης:

  1. Όρισε το αρχικό βάθος αναζήτησης (συνήθως 0).
  2. Εφάρμοσε τον αλγόριθμο DFS μέχρι αυτό το βάθος αναζήτησης.
  3. Αν έχεις βρει λύση, σταμάτησε.
  4. Αύξησε το βάθος αναζήτησης (συνήθως κατά 1).
  5. Πήγαινε στο βήμα 2.

Στο παράδειγμα του σχήματος 1.20, ο αλγόριθμος επαναληπτικής εμβάθυνσης θα δημιουργήσει το δένδρο αναζήτησης σε 3 κύκλους.

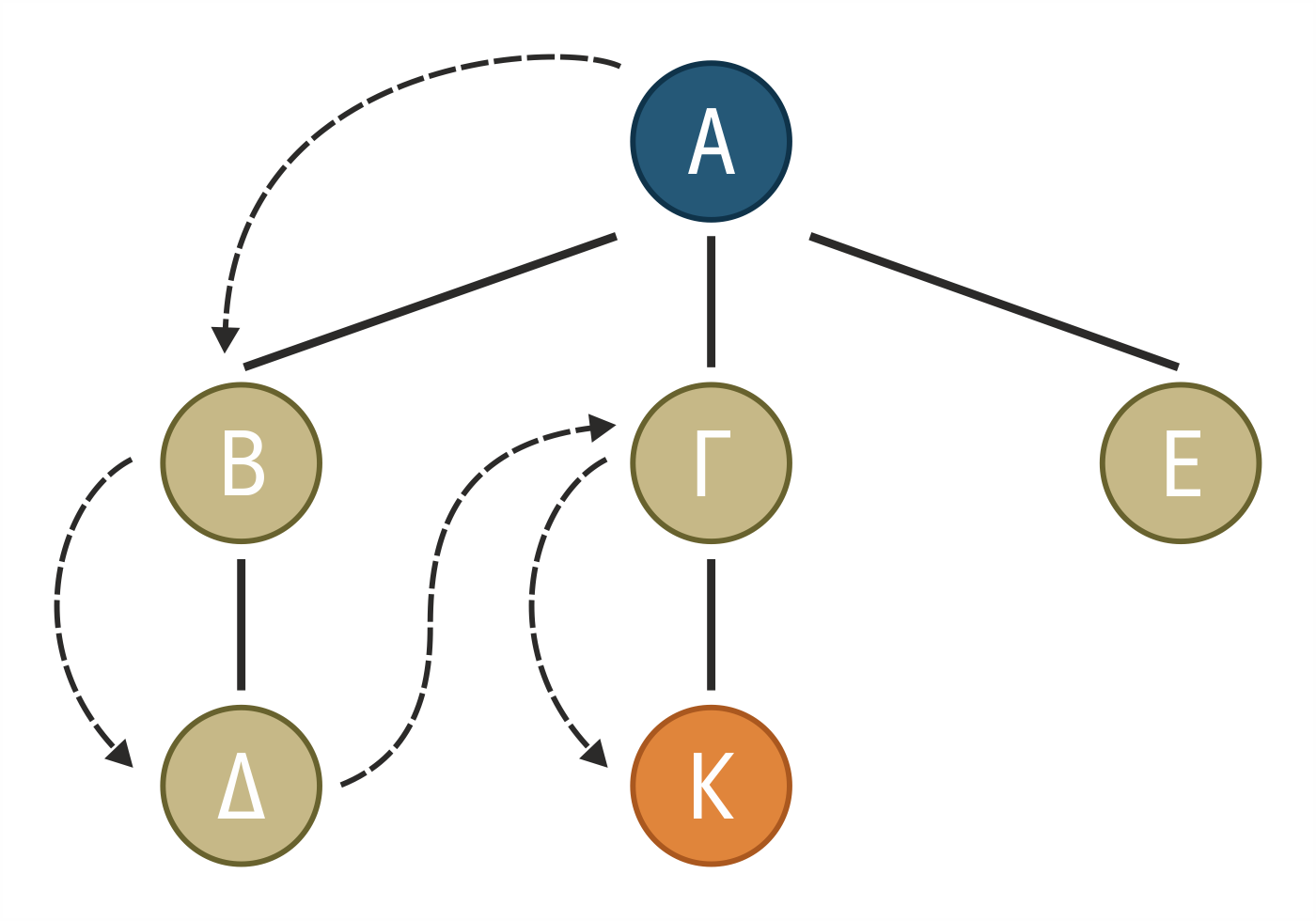
Σχήμα 1.20 Η πορεία σχηματισμού δένδρου αναζήτησης που ακολουθεί η επαναληπτική εμβάθυνση σε βάθος αναζήτησης n=2

Δείτε κινούμενη εικόνα 1.6 - Υποδειγματική Ανάπτυξη Δένδρου Αναζήτησης με την IDS για το πρόβλημα των 8 πλακιδίων μέχρι βάθους n=2

 

Πλεονεκτήματα της IDS

Μειονεκτήματα της IDS

1.4.4 Μέθοδος Αναζήτησης Διπλής Κατεύθυνσης

Η μέθοδος Αναζήτησης Διπλής Κατεύθυνσης (Βidirectional Search) πραγματοποιεί αναζήτηση ταυτόχρονα από την αρχική κατάσταση προς το στόχο και από το στόχο προς την αρχική κατάσταση. Για να εφαρμοστεί, θα πρέπει οι ενέργειες που πραγματοποιούν οι τελεστές μετάβασης του προβλήματος να είναι αναστρέψιμες (reversible) και να είναι πλήρως γνωστός ο στόχος του προβλήματος. Η αναζήτηση σταματά, όταν οι δύο επιμέρους αναζητήσεις συναντηθούν.

 

Βασικά βήματα Αλγόριθμου Διπλής Κατεύθυνσης

 

Άρχισε την αναζήτηση από την αρχική και τελική κατάσταση ταυτόχρονα.

Αν κάποια κατάσταση που επεκτείνεται είναι κοινή, τότε βρέθηκε λύση.

 

Λύση στην περίπτωση της αναζήτησης του σχήματος 1.21 είναι η ένωση του μονοπατιού που ξεκινά από τον κόμβο Α και καταλήγει στον κοινό κόμβο των δύο αναζητήσεων, δηλαδή το F, και του μονοπατιού που ξεκινά από τον κόμβο-στόχο K και καταλήγει επίσης στο F, δηλαδή λύση είναι το μονοπάτι A, C, F, J, K.

Σχήμα 1.21 Παράδειγμα δένδρων αναζήτησης διπλής κατεύθυνσης

Παρά το ότι η εφαρμογή του αλγόριθμου υπόσχεται σημαντική μείωση του χρόνου αναζήτησης, ένα σύνολο από προβλήματα μπορούν να προκύψουν, όπως τα ακόλουθα:

Η εφαρμογή ταυτόχρονα της DFS και της BFS αναζήτησης απαντά σε μερικά από τα παραπάνω ερωτήματα και εγγυάται ότι σίγουρα οι δυο αναζητήσεις θα συναντηθούν, αλλά παραμένει πρόβλημα σε ποια κατεύθυνση να εφαρμοστεί η καθεμία από αυτές, ώστε να συναντηθούν πιο αποδοτικά.

Μειονέκτημα της αναζήτησης διπλής κατεύθυνσης είναι ότι υπάρχει επιπλέον κόστος επικοινωνίας μεταξύ των δύο αναζητήσεων.

1.5 Ευρετικές μέθοδοι αναζήτησης

Η εκθετική πολυπλοκότητα του χρόνου που απαιτούν οι μέθοδοι τυφλής αναζήτησης είναι ασύμφορη για την επιλογή τους, όταν τα προβλήματα προς επίλυση είναι προβλήματα του πραγματικού κόσμου. Η πρόταση στην περίπτωση αυτή είναι η χρήση ενός ευρετικού μηχανισμού με τέτοιο τρόπο, ώστε η επιλογή κόμβων για επίσκεψη να γίνεται σύμφωνα με κάποιο ποιοτικό κριτήριο και όχι τυφλά. Ο ευρετικός μηχανισμός (heuristic) συνήθως χρησιμοποιεί την κοινή λογική, για να εκφράσει το κριτήριο που θα αποτελέσει κατευθυντήρια ιδέα για τη χάραξη πορείας κατά την αναζήτηση. Η κατευθυντήρια ιδέα στοχεύει στο να επιλέγεται κάθε φορά η περισσότερα υποσχόμενη πορεία. Για παράδειγμα, στο πρόβλημα του περιοδεύοντος πωλητή, κατευθυντήρια ιδέα θα μπορούσε να είναι ότι «προσφορότερη πόλη, για να γίνει γονικός κόμβος, είναι εκείνη της οποίας η απόσταση από την πόλη-στόχο σε ευθεία γραμμή είναι η μικρότερη».

Η ευρετική αναζήτηση (heuristic search) είναι η μέθοδος αναζήτησης που υποστηρίζεται από κάποιον ευρετικό μηχανισμό. Βασίζεται στη γνώση για το συγκεκριμένο πρόβλημα προς επίλυση και στην κοινή λογική∙ συνήθως χρησιμοποιείται για εύρεση μίας «καλής» λύσης και όχι απαραίτητα της άριστης. Στην πράξη, σχηματίζει το δένδρο αναζήτησης αναδιατάσσοντας σε κάθε κύκλο λειτουργίας το μέτωπο αναζήτησης σύμφωνα με το κριτήριο που χρησιμοποιεί, χωρίς να ερευνά αν είναι ορθό ή λανθασμένο. Το κριτήριο προκύπτει μέσω μιας ευρετικής συνάρτησης. Μια ευρετική αναζήτηση δεν εγγυάται πάντα την εύρεση λύσης, αν αυτή υπάρχει.

Γνωστές ευρετικές μέθοδοι αναζήτησης είναι οι παρακάτω καθώς και πολλές ακόμα που αποτελούν παραλλαγές ή και συνδυασμούς τους:

Επίσης, γνωστές ευρετικές μέθοδοι αναζήτησης για προβλήματα παιχνιδιών 2 ατόμων είναι οι:

Στο εγχειρίδιο αυτό δεν θα ασχοληθούμε με αλγόριθμους επίλυσης παιχνιδιών δύο ατόμων ή άλλων παρόμοιων προβλημάτων φυσικού κόσμου.

1.5.1 Ευρετικές Συναρτήσεις

Ευρετική συνάρτηση (heuristic function) είναι η υλοποίηση ενός ευρετικού μηχανισμού. Έχει πεδίο ορισμού το χώρο καταστάσεων ενός προβλήματος και πεδίο τιμών το σύνολο των τιμών που αντιστοιχούν σε αυτές. Επιστρέφει ευρετικές τιμές που προκύπτουν ως αποτέλεσμα υπολογισμών βασισμένων στη γνώση που διατίθεται για το πρόβλημα και την κατάσταση που εξετάζεται.

Ευρετική τιμή (heuristic value) είναι η τιμή της ευρετικής συνάρτησης και εκφράζει το κόστος αναζήτησης. Μπορεί σε μια απλή προσέγγιση να εκφράζει απλώς το κόστος μετάβασης από τον τρέχοντα κόμβο σε έναν κόμβο-στόχο, αλλά για εύρεση άριστων λύσεων πρέπει να εκφράζει μια συν-εκτίμηση του κόστους της διαδρομής έως τον τρέχοντα κόμβο και του εκτιμώμενου κόστους από το σημείο αυτό έως τον κόμβο-στόχο.

Η επιλογή μιας ευρετικής συνάρτησης πρέπει να βασίζεται στο:

Γνωστοί ευρετικοί μηχανισμοί είναι η Ευκλείδεια απόσταση και η απόσταση Manhattan που υπολογίζονται, όπως φαίνεται στο παρακάτω σχήμα 1.22.

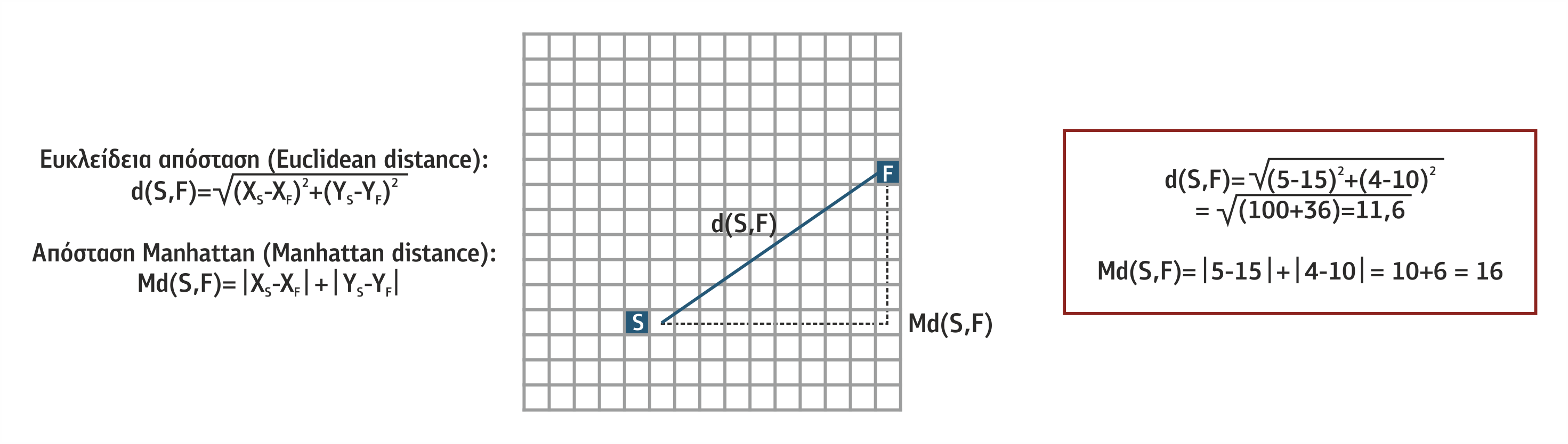
Σχήμα 1.22 Υπολογισμός Ευκλείδειας απόστασης και απόστασης Manhattan

Για παράδειγμα, στο πρόβλημα των 8 πλακιδίων μπορούμε να θεωρήσουμε ως ευρετικό μηχανισμό τη διαφορά των θέσεων των πλακιδίων της τρέχουσας κατάστασης από τις αντίστοιχες θέσεις των ίδιων πλακιδίων στην τελική θέση και ευρετική συνάρτηση το άθροισμα των αποστάσεων Manhattan κάθε πλακιδίου από την τελική του θέση.

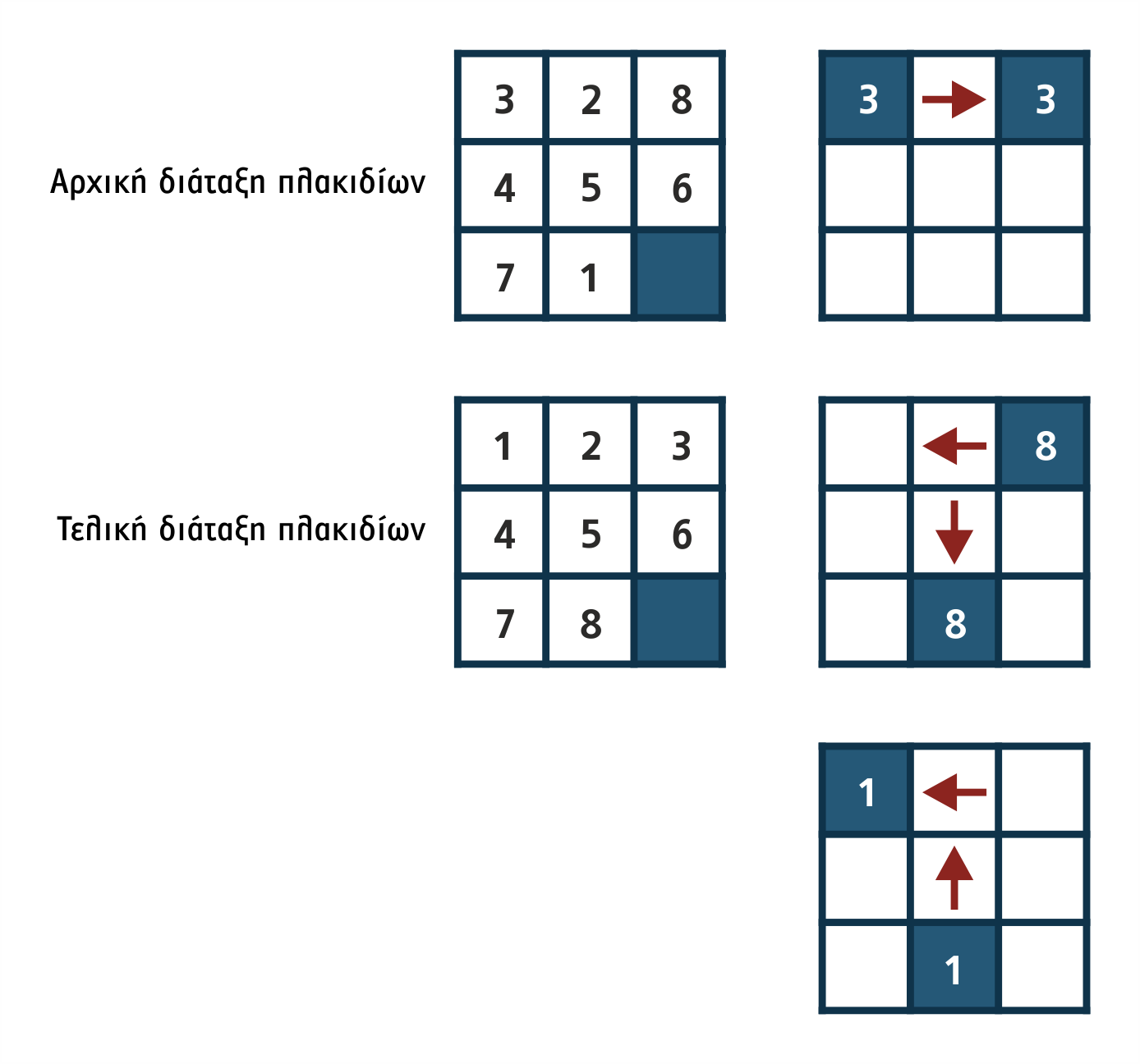
Σχήμα 1.23 Αποστάσεις Manhattan για το πρόβλημα των 8 πλακιδίων

Στην περίπτωση του σχήματος 1.23, στην αρχική κατάσταση μόνο τα πλακίδια “3”, “8” και “1” είναι τοποθετημένα με λανθασμένο τρόπο σε σχέση με τον επιδιωκόμενο στόχο. Η απόσταση Manhattan αυτών από την τελική τους θέση είναι 2, 3, και 3 αντίστοιχα, ενώ των υπολοίπων η αντίστοιχη απόσταση είναι 0. Έτσι, αν ως Si χαρακτηρίσουμε ένα πλακίδιο της κατάστασης S που είναι σε λάθος θέση, η ευρετική συνάρτηση θα επιστρέψει 8, που είναι το άθροισμα των επιμέρους αποστάσεων Manhattan.

 

Manhattan Distance κατάστασης S:

 

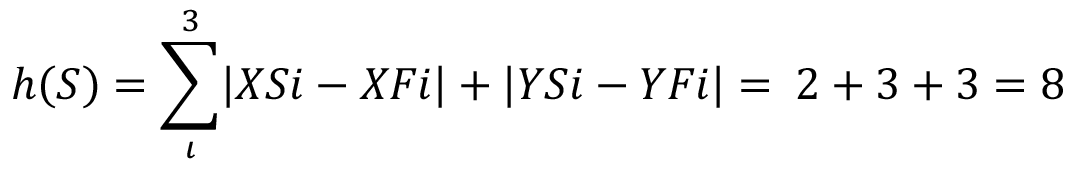
Ένα εναλλακτικό ευρετικό κριτήριο για το πρόβλημα των 8 πλακιδίων είναι ο υπολογισμός του πλήθους των πλακιδίων που είναι σε λάθος θέση. Για την κατάσταση S του σχήματος 1.23, επειδή υπάρχουν μόνο 3 πλακίδια σε λάθος θέση, τα “3”, “8” και “1”, η ευρετική συνάρτηση θα επιστρέψει 3: h(S)=3

1.5.2 Αναζήτηση Καλύτερης-Πρώτης

Η μέθοδος αναζήτησης Πρώτα στο Καλύτερο ή Καλύτερη-Πρώτη (Best First Search - BestFS) σε κάθε κύκλο λειτουργίας της επισκέπτεται την κατάσταση του μετώπου αναζήτησης την οποία το κριτήριο θεωρεί «καλύτερη» βάσει ενός ευρετικού κριτηρίου άμεσα εξαρτώμενου από το πρόβλημα προς επίλυση. Χαρακτηριστικό της μεθόδου είναι ότι σε κάθε βήμα αναζήτησης η μέθοδος επιλέγει προς επέκταση το πιο πολλά υποσχόμενο μονοπάτι μεταξύ των μονοπατιών που βρίσκονται στην ουρά.

 

Ψευδοκώδικας αλγόριθμου BestFS

Στο σχήμα 1.24 δίνουμε μια μικρή περιγραφή της εφαρμογής της μεθόδου αναζήτησης BestFS για το πρόβλημα του πωλητή με τις 6 πόλεις (βλέπε Σχήμα 1.1), όταν αρχική κατάσταση είναι η πόλη Α, στόχος η πόλη F και ευρετικό κριτήριο η Ευκλείδεια απόσταση. Δίπλα στους κόμβους του γραφήματος και του δένδρου αναζήτησης παρουσιάζονται οι Ευκλείδειες αποστάσεις των πόλεων του δικτύου από την πόλη-στόχο F.

Στην αρχή, ο αλγόριθμος δημιουργεί το αρχικό μέτωπο τοποθετώντας μέσα την κατάσταση Α και την αντίστοιχη αρχική ουρά. Στη συνέχεια, υπολογίζεται η Ευκλείδεια απόσταση της πόλης Α από την F και, δεδομένου ότι είναι η μοναδική κατάσταση στο μέτωπο, επιλέγεται ως η «καλύτερη», για να αποτελέσει γονικό κόμβο. Δημιουργούνται οι διάδοχοι κόμβοι, δηλαδή οι κόμβοι Β και C, και τοποθετούνται μέσα στο μέτωπο στη θέση του γονικού κόμβου. Ακολουθεί ταξινόμηση των κόμβων του μετώπου και τα αντίστοιχα συμβαίνουν για την ουρά. Τέλος ενημερώνεται το κλειστό σύνολο. Στον επόμενο βήμα το μέτωπο περιέχει τις καταστάσεις Β και C, οι οποίες ταξινομούνται βάσει των αποστάσεων αυτών από την F. Η πλησιέστερη είναι η Β∙ άρα, επιλέγεται ως γονικός κόμβος δίνοντας τους διάδοχους κόμβους C και D. Τώρα το μέτωπο περιέχει τους κόμβους C, που ανήκει στη μερική λύση (A C), C, που ανήκει στη μερική λύση (A B C), και τον D. Ο D έχει τη μικρότερη απόσταση έναντι των δύο άλλων ισοτίμων C και, επομένως, επιλέγεται ως γονικός κόμβος. Η αναζήτηση συνεχίζεται με αυτήν τη λογική, μέχρι να βρει το στόχο και να επιστρέψει ως λύση το μονοπάτι (A B D F).

Σχήμα 1.24 Παράδειγμα εφαρμογής της BestFS για το πρόβλημα του περιοδεύοντος πωλητή, όπως παρουσιάζεται στο σχήμα 1.1

Δείτε κινούμενη εικόνα 1.7 - Ανάπτυξη Δένδρου Αναζήτησης με την BestFS για το πρόβλημα του περιοδεύοντος πωλητή

Δείτε κινούμενη εικόνα 1.8 - Ανάπτυξη Δένδρου Αναζήτησης με την BestFS για το πρόβλημα των 8 πλακιδίων

 

Προτερήματα της BestFS

Μειονεκτήματα της BestFS

1.5.3. Αναζήτηση με αναρρίχηση λόφων

Η μέθοδος της αναζήτησης με Αναρρίχηση Λόφων (Hill-Climbing - HC) αποτελεί μια εξειδίκευση της BestFS μεθόδου. Η πιο κλασική τεχνική που χρησιμοποιούν οι αλγόριθμοι αναρρίχησης λόφων είναι αυτή της πλέον απότομης ανάβασης (steepest ascent), βάσει της οποίας ο αλγόριθμος σε κάθε βήμα του αντικαθιστά τον τρέχοντα κόμβο με τον καλύτερο γειτονικό του. Η αναρρίχηση λόφων με απότομη ανάβαση έχει τα ακόλουθα χαρακτηριστικά:

Προφανώς ο αλγόριθμος αναρρίχησης λόφων με απότομη ανάβαση δεν είναι πλήρης, αλλά είναι πολύ γρήγορος και απαιτεί ελάχιστη μνήμη. Η διαφορά του με την αναζήτηση Καλύτερης-Πρώτης είναι ότι στην αναρρίχηση λόφων η ταξινόμηση και επιλογή γίνονται μεταξύ των διάδοχων κόμβων, ενώ στην Καλύτερη-Πρώτη η ταξινόμηση και επιλογή γίνονται σε όλους τους κόμβους του μετώπου.

 

Αλγόριθμος μεθόδου αναζήτησης με Αναρρίχηση Λόφων

Στο σχήμα 1.25 φαίνεται το δένδρο αναζήτησης λύσης του προβλήματος του πωλητή με τις 6 πόλεις (βλέπε Σχήμα 1.1), όπως προκύπτει από την αναρρίχηση λόφων, όταν αρχική κατάσταση είναι η πόλη Α, στόχος η πόλη Β και ευρετικό κριτήριο είναι η απόσταση Manhattan κάθε κόμβου από τον κόμβο στόχο. Οι αποστάσεις Manhattan αποτυπώνονται δίπλα σε κάθε κόμβο.

Σχήμα 1.25 Αναζήτηση λύσης με τη μέθοδο Αναρρίχησης Λόφων για το πρόβλημα του περιοδεύοντος πωλητή, όπως παρουσιάζεται στο σχήμα 1.1

Δείτε κινούμενη εικόνα 1.9 - Ανάπτυξη Δένδρου Αναζήτησης με την HC για το πρόβλημα του περιοδεύοντος πωλητή

 

Η αναρρίχηση λόφων λέγεται και άπληστη τοπική αναζήτηση (greedy local search), επειδή επιλέγει μια καλή γειτονική κατάσταση, χωρίς να σκέφτεται πού θα πάει στη συνέχεια. Όπως όλοι οι αλγόριθμοι άπληστης αναζήτησης, αποδίδει αρκετά καλά, κάνοντας συχνά πολύ γρήγορη πρόοδο προς μια λύση, επειδή συνήθως είναι πολύ εύκολο να βελτιώσει μια κακή κατάσταση. Δυστυχώς, συχνά η αναρρίχηση λόφων παγιδεύεται για τους εξής λόγους:

Η παγίδευση παρουσιάζεται, όταν υπάρχει μια θέση που δεν είναι στόχος, αλλά από εκεί καμία κίνηση δεν βελτιώνει την τρέχουσα κατάσταση ή η θέση οδηγεί σε πρώιμη σύγκλιση, δηλαδή εύρεση λύσης που δεν αποτελεί τη βέλτιστη λύση. Αυτό θα συμβεί, αν έχουμε φτάσει σε ένα τοπικό μέγιστο, ένα οροπέδιο ή μια κορυφογραμμή (βλέπε Σχήμα 1.26).

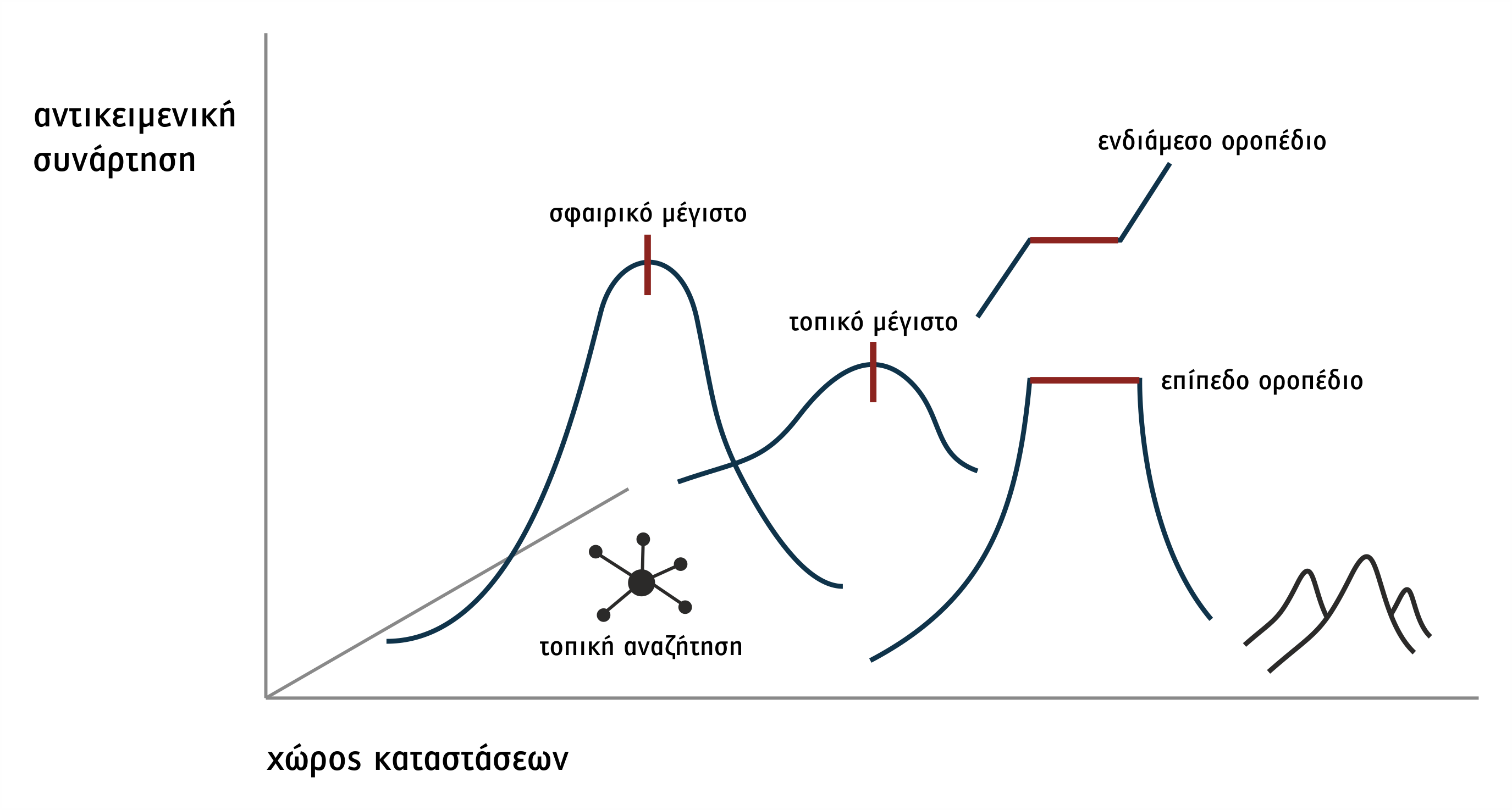
Σχήμα 1.26 Προβλήματα που μπορούν να δημιουργηθούν κατά την αναρρίχηση λόφων

Τοπικό μέγιστο: Είναι μια κατάσταση που είναι καλύτερη από όλες τις γείτονές της, αλλά δεν είναι καλύτερη από όσο κάποιες άλλες πιο μακριά που δεν μπορούν να προσεγγιστούν από την πορεία που έχει ακολουθηθεί. Όλες οι πιθανές επόμενες κινήσεις φαίνεται να οδηγούν σε χειρότερες καταστάσεις. Λύση σε αυτό είναι η οπισθοδρόμηση σε κάποια προηγούμενη κατάσταση και η συνέχιση της αναζήτησης σε διαφορετική κατεύθυνση∙ όμως, ο κλασικός αλγόριθμος αναρρίχησης λόφων δεν το επιτρέπει.

 

Οροπέδιο: Είναι μια επίπεδη έκταση του χώρου αναζήτησης στην οποία ένα σύνολο γειτονικών καταστάσεων έχουν την ίδια ευρετική τιμή. Ως εκ τούτου, δεν είναι δυνατόν να καθοριστεί η καλύτερη κατεύθυνση προς την οποία πρέπει να συνεχιστεί η αναζήτηση. Λύση είναι να διαμορφωθεί έτσι ο αλγόριθμος, ώστε να μπορεί να κάνει ένα μεγάλο άλμα προς κάποια κατεύθυνση και να προσπαθήσει να προσεγγίσει ένα νέο τμήμα του χώρου αναζήτησης.

 

Κορυφογραμμές: Είναι μια περιοχή του χώρου αναζήτησης υψηλότερη από τις γύρω περιοχές (τοπική κορυφή), αλλά, αν η αναζήτηση βρίσκεται σε μια γειτονική κορυφογραμμή, δεν μπορεί να την προσεγγίσει με μια μοναδική κίνηση (ειδική περίπτωση τοπικών μεγίστων). Εδώ η εφαρμογή δύο ή περισσότερων βημάτων μετάβασης προς πολλές κατευθύνσεις ταυτόχρονα πρέπει να προηγηθεί του ευρετικού μηχανισμού για τον έλεγχο της καλύτερης πορείας.

Γενικές ενέργειες για την αντιμετώπιση παγιδεύσεων, όπως αυτές που αναφέραμε παραπάνω, είναι οι ακόλουθες:

Διάφορες παραλλαγές του αλγόριθμου αναρρίχησης λόφων χρησιμοποιούν τους παραπάνω τρόπους αποφυγής παγιδεύσεων, θυσιάζοντας λίγη από την ταχύτητα της αναζήτησης, για να αυξήσουν την πιθανότητα να βρεθεί λύση. Μία παραλλαγή είναι η Εξαναγκασμένη Αναρρίχηση Λόφων (Enforced Hill Climbing – EHC). Μια από τις πιο απλές είναι αυτή της EHC που καθιστά τον αλγόριθμο πλήρη. Στην EHC επιτρέπεται η οπισθοδρόμηση, με διατήρηση στο μέτωπο και των καταστάσεων του ακριβώς προηγούμενου βήματος. Στο σχήμα 1.27 το παράδειγμα εφαρμογής είναι παραλλαγή του παραδείγματος του σχήματος 1.25, όπου σε κάθε βήμα κρατούνται όλα τα παιδιά του συγκεκριμένου βήματος για τις ανάγκες της οπισθοδρόμησης, που είναι επιτρεπτή μόνο κατά ένα βήμα, και στο επόμενο βήμα διαγράφονται για να αντικατασταθούν με τα παιδιά του επόμενου βήματος.

Σχήμα 1.27 Αναζήτηση λύσης με EHC για το πρόβλημα του περιοδεύοντος πωλητή

Επίσης δημοφιλής είναι και ο αλγόριθμος προσομοιωμένης ανόπτησης (Simulated Annealing Algorithm) ο οποίος δίνει μία πιθανότητα μετάβασης σε χειρότερες καταστάσεις, αφήνοντας έτσι περιθώριο στην αναζήτηση να ξεφύγει από τοπικά βέλτιστα. Άλλος αλγόριθμος αναρρίχησης λόφων είναι ο αλγόριθμος αναζήτησης με απαγορεύσεις (Taboo Search Algorithm), όπου σε κάθε βήμα επέκτασης γίνεται πάντα μετάβαση στη καλύτερη διάδοχη κατάσταση, ακόμα και αν είναι χειρότερη από τη γονική, ενώ ταυτόχρονα η αναζήτηση αποφεύγει απαγορευμένες καταστάσεις αποθηκευμένες σε λίστα από την αρχή της αναζήτησης (παρόμοιας λειτουργικότητας με το κλειστό σύνολο, αλλά σταθερού μεγέθους).

1.5.4 Αναζήτηση Βασικής Επέκτασης και Οριοθέτησης

Η μέθοδος αναζήτησης Βασικής Επέκτασης και Οριοθέτησης (Basic Branch & Bound search - Β&Β) εφαρμόζεται σε προβλήματα όπου αναζητείται η λύση με το ελάχιστο κόστος. Η αναζήτηση δεν επισκέπτεται κόμβους του δένδρου αναζήτησης που οδηγούν σε λύσεις που υπερβαίνουν το μέγιστο επιτρεπόμενο κόστος.

 

Αλγόριθμος αναζήτησης B&B

 

Στο σχήμα 1.28 δίνεται παράδειγμα εφαρμογής της μεθόδου αναζήτησης B&B κατά την εξαντλητική αναζήτηση λύσεων στο πρόβλημα του περιοδεύοντος πωλητή σε 10 πόλεις. Ως κριτήριο είναι το κόστος του μονοπατιού μέχρι τον τρέχοντα κόμβο. Από τα δύο υπο-δένδρα που σχηματίζονται κάτω από τους κόμβους Θ, η μέθοδος θα αποκόψει το αριστερό, γιατί το κόστος του μονοπατιού Α-Β-Δ-Θ είναι 12,73, ενώ του A-E-Θ είναι μόνο 5,24.

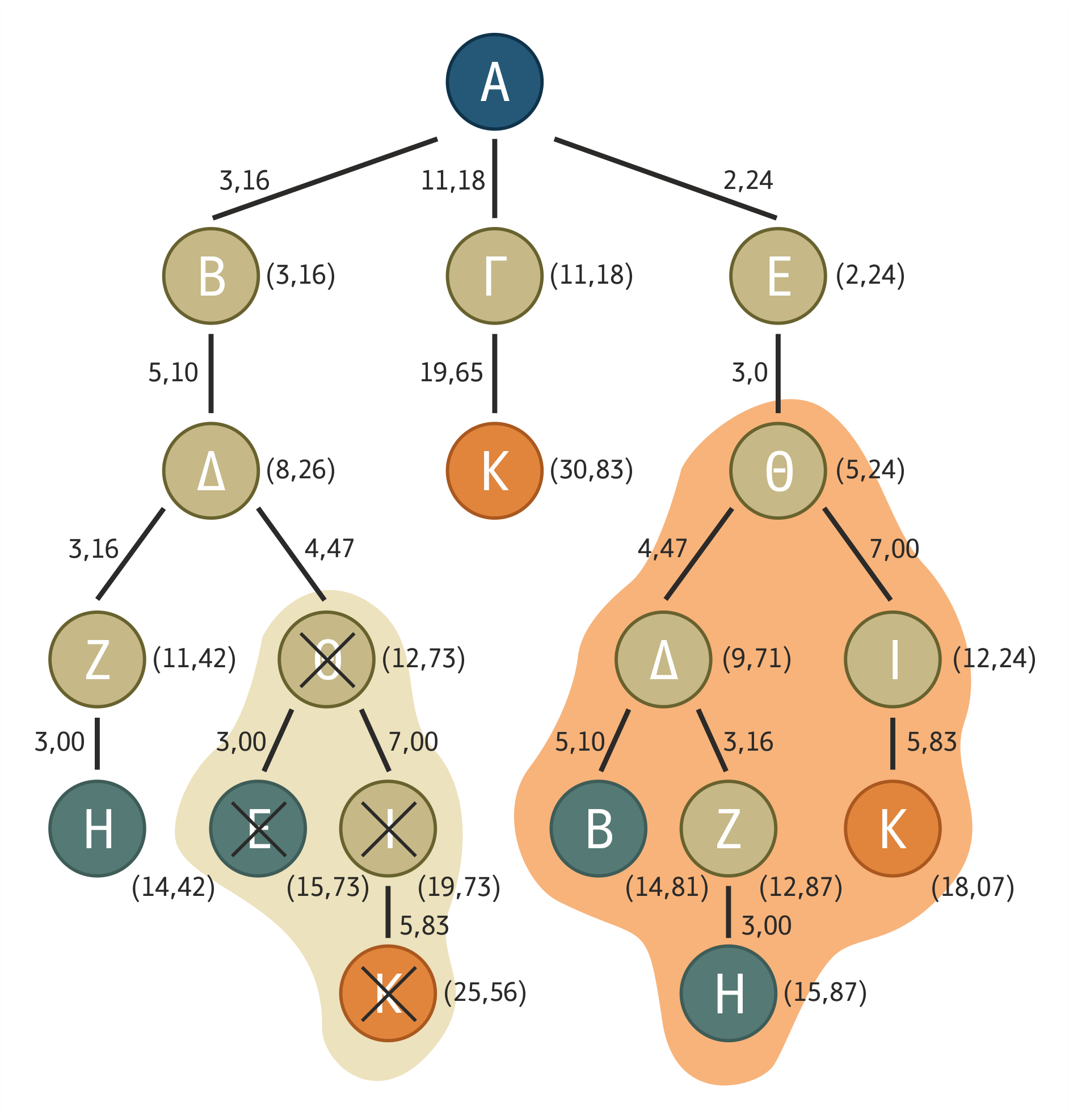
Σχήμα 1.28 Εξαντλητική αναζήτηση Β&B για το πρόβλημα του περιοδεύοντος πωλητή

1.5.5 Ακτινωτή μέθοδος αναζήτησης

Η Ακτινωτή μέθοδος αναζήτησης (Βeam search) μπορεί να θεωρηθεί βελτίωση των μεθόδων αναζήτησης Αναρρίχησης Λόφου και Καλύτερης-Πρώτης.

Διαφέρει αφενός από την Αναρρίχηση Λόφων στο ότι προχωρά ανά επίπεδο και όχι σε ένα μονοπάτι με ολοένα καλύτερες καταστάσεις και αφετέρου από την αναζήτηση Καλύτερης-Πρώτης στο ότι, καθώς προχωρά σε βάθος, βασίζεται στην ποιότητα των κόμβων κάθε επιπέδου επισκεπτόμενη μόνο τον καλύτερο κόμβο κάθε επιπέδου που εντοπίζει η ευρετική συνάρτηση, αγνοώντας τους υπόλοιπους κόμβους. Με αυτόν τον τρόπο μειώνεται σημαντικά ο αριθμός των κόμβων που επισκέπτεται.

 

Τα χαρακτηριστικά της μεθόδου είναι τα ακόλουθα:

Αλγόριθμος ακτινωτής μεθόδου αναζήτησης

 

 

Στο σχήμα 1.29, έχει αποτυπωθεί η ανά επίπεδο πορεία της ακτινωτής αναζήτησης για το πρόβλημα του περιοδεύοντος σε 10 πόλεις πωλητή, όταν το κριτήριο είναι το μήκος του μονοπατιού μέχρι τον τρέχοντα κόμβο. Το πλάτος της αναζήτησης είναι 2 και ξεκινά από το επίπεδο 0 όπου το μέτωπο περιέχει μόνο τον κόμβο της αρχικής κατάστασης.

Στο επίπεδο 1 που διαμορφώνεται από τον επόμενο κύκλο λειτουργίας δημιουργούνται όλοι οι διάδοχοι κόμβοι του προηγούμενου επιπέδου και παραμένουν στο μέτωπο οι Ε και Β ως οι δύο καλύτεροι.

Στο επίπεδο 2 δημιουργούνται οι διάδοχοι κόμβοι των Ε και Β και παραμένουν στο μέτωπο όλοι, γιατί είναι μόνο δύο, οι Δ και Θ.

Στο επίπεδο 3 δημιουργούνται οι διάδοχοι κόμβοι Ζ, Θ, Ι, Δ και παραμένουν οι Ζ και Δ ως οι δύο καλύτεροι.

Στο επίπεδο 4 δημιουργούνται οι διάδοχοι κόμβοι Η, Β, Ζ και παραμένουν οι H, Ζ ως οι δύο καλύτεροι.

Στο επίπεδο 5 ο κόμβος H δεν έχει διάδοχο κόμβο, γιατί θα δημιουργείτο κύκλος, ενώ ο Ζ έχει διάδοχο κόμβο τον Η που μπαίνει στο μέτωπο. Ο Η αυτός δεν έχει διάδοχο κόμβο, γιατί θα οδηγείτο σε κύκλο και έτσι η αναζήτηση ολοκληρώνεται χωρίς λύση, παρότι το πρόβλημα έχει τρεις λύσεις.

Σχήμα 1.29 Αποτυχημένη αναζήτηση με ακτινωτή μέθοδο και κριτήριο το μήκος του μονοπατιού μέχρι τον τρέχοντα κόμβο

1.5.6 Μέθοδος αναζήτησης Άλφα-Άστρο

Η μέθοδος αναζήτησης Άλφα-Άστρο (Α*) είναι κατά βάσει BestFS, αλλά με ευρετική συνάρτηση:

 

F(S) = g(S) + h(S)

 

Όπου:

Για την Α* ισχύει ότι, αν για κάθε κατάσταση η τιμή είναι μικρότερη ή το πολύ ίση με την πραγματική απόσταση της από την τελική κατάσταση, τότε η Α* βρίσκει πάντα τη βέλτιστη λύση.

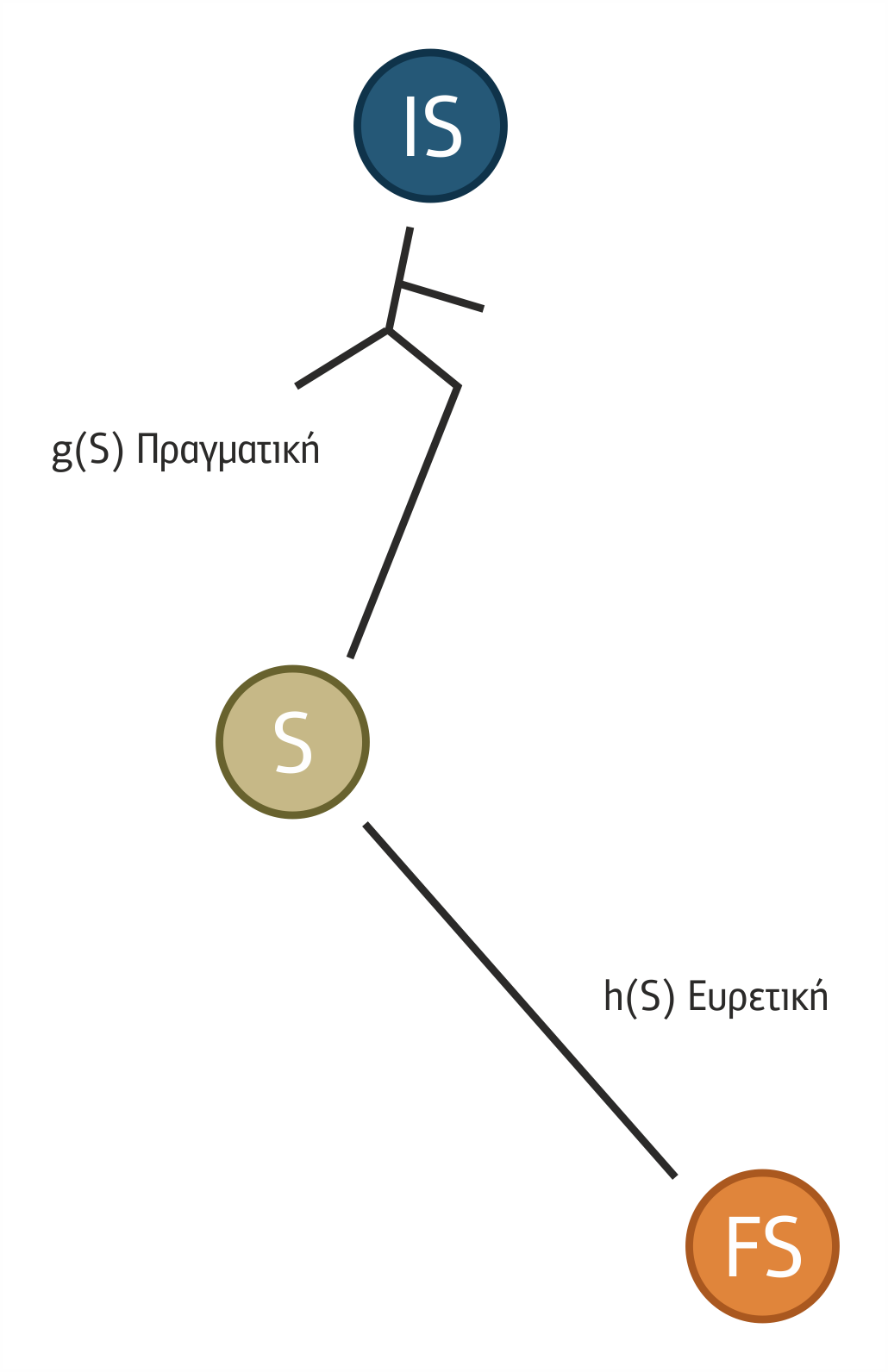
Σχήμα 1.30 Η πορεία της Α* από μια αρχική κατάσταση IS μέχρι μια τελική κατάσταση FS, όταν η αναζήτηση βρίσκεται στην κατάσταση S

Ακολουθεί ο αλγόριθμος της Α*

 

 

Για παράδειγμα, αν στο πρόβλημα των 8 πλακιδίων η Α* εφαρμόσει την ευρετική συνάρτηση:

 

f(S) = g(S) + h(S)

 

όπου:

 

g(S) = το βάθος του κόμβου της κατάστασης S στο δένδρο αναζήτησης

h(S) = ο αριθμός των κόμβων εκτός θέσης στη δεδομένη κατάσταση S,

 

και μια τρέχουσα κατάσταση S με αριθμό κόμβων εκτός θέσης 4 όπως παρακάτω:

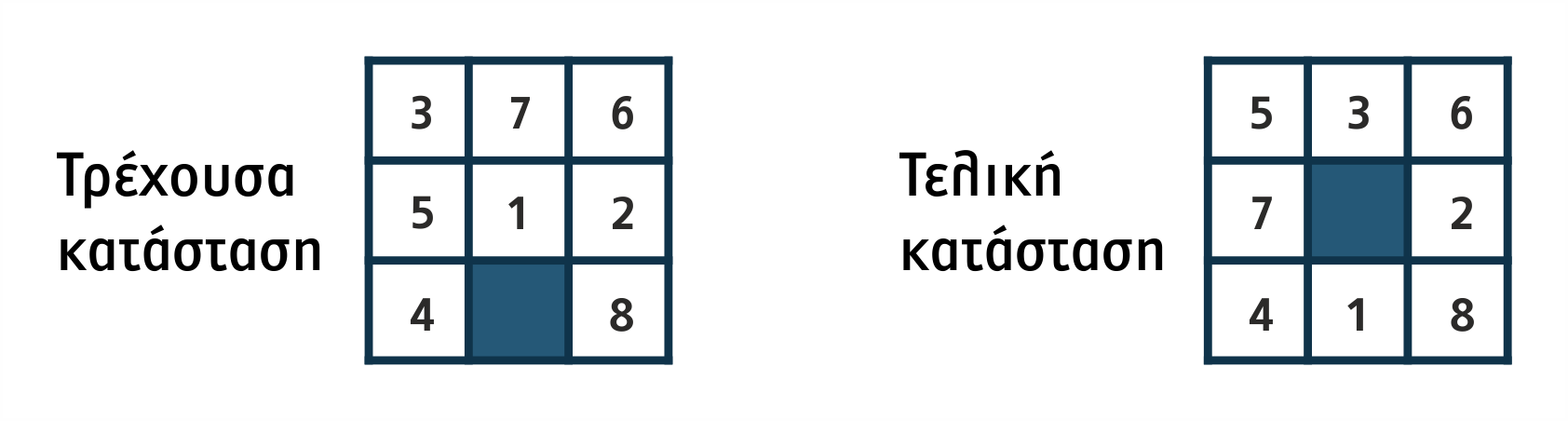
τότε, αν η τρέχουσα κατάσταση S είναι η αρχική (με βάθος 0), ο κόμβος που αντιστοιχεί θα έχει ευρετική τιμή:

 

f(initial_node) = 0 + 4 = 4

 

και το δένδρο που θα σχηματίσει η Α* δίνεται στο επόμενο σχήμα 1.31 όπου με κόκκινα βέλη αποτυπώνεται το μονοπάτι-λύση.

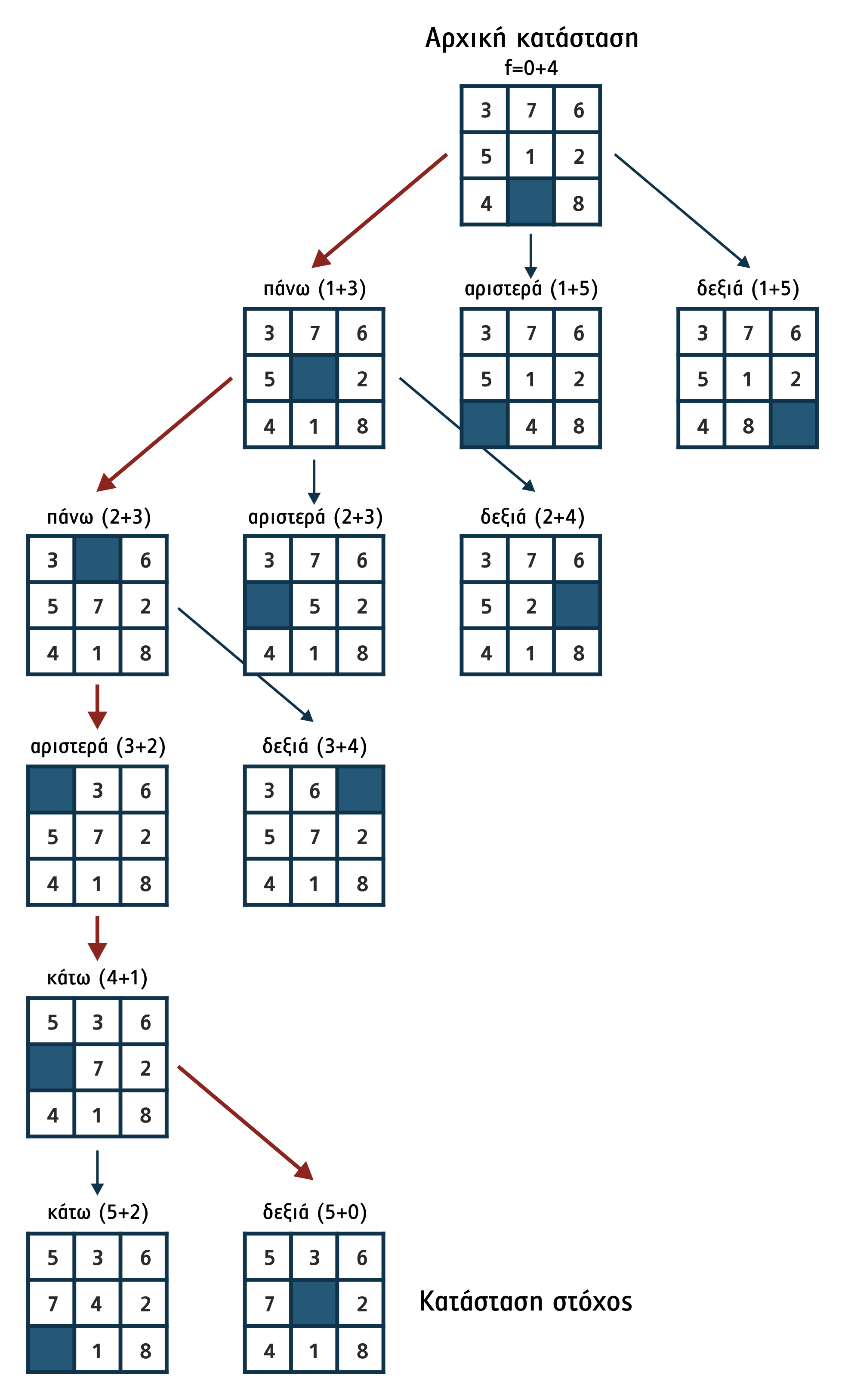
Σχήμα 1.31 Δένδρο αναζήτησης της Α* για τα το πρόβλημα των 8 πλακιδίων

Δείτε κινούμενη εικόνα 1.10 - Ανάπτυξη Δένδρου Αναζήτησης με την Α* για το πρόβλημα των 8-puzzles