ΚΕΦΑΛΑΙΟ 3 - Συστήματα Κανόνων

Σύνοψη

Στο κεφάλαιο αυτό παρουσιάζεται ο χώρος των συστημάτων κανόνων με επικέντρωση στα συστήματα παραγωγής. Η χρήση κανόνων για την αναπαράσταση της διαδικαστικής και επεισοδιακής γνώσης ενός προβλήματος είναι μία από τις βασικές προσεγγίσεις για την επίλυση προβλημάτων βασισμένων στη γνώση στο πλαίσιο της Τεχνητής Νοημοσύνης. Αναλύονται εν συντομία τα διαφορετικά μοντέλα λογικής σκέψης στο χώρο της συλλογιστικής, παρουσιάζονται τα χαρακτηριστικά των συστημάτων κανόνων και περιγράφεται αναλυτικά ο τρόπος λειτουργίας των συστημάτων παραγωγής. Μεγάλη σημασία δίνεται στη διεξοδική παρουσίαση παραδειγμάτων λειτουργίας της προς τα εμπρός και προς τα πίσω αλυσιδωτής εκτέλεσης κανόνων.

Προαπαιτούμενη γνώση

Αναπαράσταση γνώσης

3.1 Συλλογιστική

Συλλογισμός είναι η ικανότητα του ανθρώπου να χρησιμοποιεί τις γνώσεις του για την εξαγωγή συμπερασμάτων σχετικά με τον κόσμο μέσα στον οποίο υπάρχει, ακολουθώντας διαφορετικά μοντέλα λογικής σκέψης. Η ικανότητα συλλογισμού αποτελεί ένα βασικό χαρακτηριστικό αυτού που αποκαλούμε «νοημοσύνη» στον άνθρωπο.

Η συλλογιστική (reasoning), ως επιστημονικός χώρος, περιλαμβάνει τους διαφορετικούς τρόπους συλλογισμού (μοντέλα λογικής σκέψης) με τους οποίους χρησιμοποιούμε την προϋπάρχουσα γνώση για τη δημιουργία νέας γνώσης.

Υπάρχουν τρία διαφορετικά μοντέλα λογικής:

3.1.1 Επαγωγή

Κατά την επαγωγή (induction) καταλήγουμε σε νέα γνώση από προϋπάρχουσα γνώση που έχει προκύψει από την εμπειρία μας σε παρόμοιες καταστάσεις. Η επαγωγή ορίζεται ως η γενίκευση από περιπτώσεις που είναι ήδη γνωστές, για να συναχθούν συμπεράσματα για περιπτώσεις που δεν έχουν ακόμα βιωθεί.

 

Επαγωγή: Κοινές ιδιότητες μελών => συμπεράσματα για κλάση

 

Για παράδειγμα, ένας επί πτυχίω φοιτητής γνωρίζει πολύ καλά πώς θα διεξαχθούν οι γραπτές εξετάσεις στα μαθήματα στα οποία εξετάζεται, βάσει της εμπειρίας που έχει αποκτήσει από αντίστοιχες εξετάσεις κατά τη φοίτησή του.

Ανάλογα, θα μπορούσαμε να κάνουμε τον παρακάτω συλλογισμό:

 

Κάθε ημέρα έως σήμερα ο ήλιος ανατέλλει από την ανατολή.

=>

Πάντα ο ήλιος θα ανατέλλει από την ανατολή.

 

Ο παραπάνω συλλογισμός δείχνει αληθοφανής, αλλά σε παρόμοιους συλλογισμούς εμπεριέχεται ο κίνδυνος λανθασμένου συμπεράσματος, γιατί η εμπειρία μας δεν είναι ποτέ πλήρης. Στο επόμενο παράδειγμα, ο αντίστοιχος συλλογισμός ότι:

 

Όσα κοράκια έχω δει μέχρι τώρα στη ζωή μου είναι μαύρα.

=>

Όλα τα κοράκια του κόσμου είναι μαύρα.

 

δεν είναι βέβαιο ότι είναι ορθός, δεδομένου ότι είναι πολύ πιθανό να υπάρχει κάπου στον κόσμο ένα είδος κορακιών διαφορετικού χρώματος που δεν έτυχε ποτέ να δω.

Παρόλα αυτά, η δυνατότητα επαγωγικών συλλογισμών αποτελεί βασικό τρόπο εκδήλωσης της νοημοσύνης του ανθρώπου που τον καθιστά ικανό να μαθαίνει από τις εμπειρίες του, ακόμα και αν σε ορισμένες περιπτώσεις καταλήξει σε λανθασμένα συμπεράσματα.

Στο χώρο της Τεχνητής Νοημοσύνης, η επαγωγή χρησιμοποιείται επιτυχώς από συστήματα μηχανικής μάθησης, στα οποία θα αναφερθούμε στο επόμενο κεφάλαιο, 4. Στο χώρο της μηχανικής μάθησης, ένας μηχανισμός εξαγωγής συμπερασμάτων που χρησιμοποιεί επαγωγικό συλλογισμό βασίζεται πάντα στη συλλογή παραδειγματικών περιπτώσεων και η εξαγωγή συμπερασμάτων προκύπτει από συγκέντρωση παρατηρήσεων που αφορούν κοινά χαρακτηριστικά των παραδειγματικών περιπτώσεων. Τα συμπεράσματα αυτά μπορεί να εξαχθούν ως νέα διαδικαστική γνώση υπό μορφή κανόνων.

 

Για παράδειγμα:

Παρατηρήσεις: Έχω καλές βαθμολογίες στα μαθήματα των οποίων παρακολούθησα τις παραδόσεις.

Κανόνας: Όταν παρακολουθώ τις παραδόσεις ενός μαθήματος, το περνώ με καλό βαθμό.

3.1.2 Απαγωγή

Η απαγωγή (abduction) συνάγει λογικά συμπεράσματα βασιζόμενη σε σχετικές μέχρι τώρα μαρτυρίες και χρησιμοποιείται όταν δεν διαθέτουμε ολοκληρωμένες πληροφορίες για το πρόβλημα που επιχειρούμε να επιλύσουμε. Στην ουσία είναι ένας τρόπος να κάνουμε την «καλύτερη λογική υπόθεση» με βάση σχετικές διαθέσιμες μαρτυρίες, όταν οι γνώσεις που διαθέτουμε είναι ελλιπείς.

 

Απαγωγή: Μη πλήρης γνώση => εικασίες

 

Για παράδειγμα:

 

Οι άντρες πάντα θυμώνουν, όταν κάποιος τους καθυστερεί. (διαθέσιμες μαρτυρίες)

Ο φίλος μου είναι θυμωμένος. (μη πλήρης γνώση, λείπει η αιτία)

Πιθανώς το ότι ο φίλος μου θύμωσε να οφείλεται στο ότι τον καθυστέρησα. (καλύτερη λογική υπόθεση-εικασία)

 

Ένας μηχανισμός εξαγωγής συμπερασμάτων που χρησιμοποιεί απαγωγικούς συλλογισμούς βασίζεται αφενός σε υπάρχοντα δεδομένα και σε γεγονότα που συνθέτουν το πρόβλημα και αφετέρου σε σχετικές διαθέσιμες μαρτυρίες. Για παράδειγμα, ο παραπάνω συλλογισμός μπορεί να παρουσιαστεί δομημένα και ως ακολούθως:

 

Διαθέσιμες μαρτυρίες: Οι άντρες πάντα θυμώνουν, όταν κάποιος αργεί να πάει σε μια συνάντηση.

Γεγονός: Ο φίλος μου είναι θυμωμένος.

Δεδομένο: Άργησα να πάω στη συνάντησή μας.

Συμπέρασμα: Ο φίλος μου είναι θυμωμένος, επειδή άργησα να πάω στη συνάντησή μας.

 

Γνωστά συστήματα ΤΝ που εξάγουν λογικά συμπεράσματα για ένα πρόβλημα χρησιμοποιώντας την προϋπάρχουσα εμπειρία από παρόμοιες περιπτώσεις είναι τα λεγόμενα συστήματα Συλλογιστικής Βασισμένης σε Περιπτώσεις (Case-Based Reasoning - ΣΒΠ/CBR) που αναλύονται στο κεφάλαιο της μηχανικής μάθησης.

3.1.3 Παραγωγή

Το τρίτο είδος συλλογισμού, η παραγωγή (deduction), βασίζεται στην τυπική λογική, όπως αυτή έχει παρουσιαστεί στο προηγούμενο κεφάλαιο περί αναπαράστασης γνώσης.

 

Παραγωγή:

 

Γνώση για την κλάση => συμπεράσματα για το μέλος

 

Για παράδειγμα:

 

Αν βρέχει και κάθομαι κάτω από τη βροχή, θα βραχούν τα μαλλιά μου. (κανόνας)

Βρέχει και κάθομαι κάτω από τη βροχή.(γεγονότα)

=>

Θα βραχούν τα μαλλιά μου. (λογικό συμπέρασμα που προκύπτει από τον κανόνα)

 

Η παραγωγή αποτελεί τον μόνο έγκυρο συλλογισμό, αλλά η εφαρμογή της δεν είναι απαραίτητο να οδηγήσει σε σωστά συμπεράσματα, αν ο συλλογισμός δεν είναι σωστά σχεδιασμένος. Λόγου χάρη, στο προηγούμενο παράδειγμα δεν είναι πάντα αληθές το συμπέρασμα, γιατί ο συλλογισμός έχει «κενά». Δηλαδή, δεν έχει προβλεφθεί από το σχεδιαστή του να περιληφθεί στους ισχυρισμούς ότι απαιτείται, επίσης, να μην κρατώ ομπρέλα, γιατί, αν κρατώ ομπρέλα, τα μαλλιά μου δε θα βραχούν, οπότε το συμπέρασμα καθίστανται λανθασμένο και ο κανόνας προβληματικός. Για το λόγο αυτόν, παρότι η παραγωγή είναι πάντα έγκυρος μηχανισμός εξαγωγής συμπεράσματος, πρέπει παράλληλα να γίνει σαφές ότι είναι μια τεχνική εξαγωγής συμπερασμάτων που δεν οδηγεί απαραίτητα σε σωστά συμπεράσματα, αν η γνώση που αποτυπώνει είναι ελλιπής ή λανθασμένη.

Γνωστά στο χώρο της συλλογιστικής είναι τα δύο μοντέλα λογικής σκέψης και έγκυροι παραγωγικοί συλλογισμοί τα Modus Ponens και Modus Tollens. Στο μεν πρώτο μοντέλο η αλήθεια των ισχυρισμών οδηγεί στην παραδοχή των συμπερασμάτων – έχουμε ήδη παρουσιάσει αρκετά σχετικά παραδείγματα παραπάνω. Στο δεύτερο μοντέλο, η άρνηση των συμπερασμάτων οδηγεί στην άρνηση των ισχυρισμών.

 

Για παράδειγμα:

 

Αν βρέχει και κάθομαι κάτω από τη βροχή, θα βραχούν τα μαλλιά μου. (κανόνας)

ΔΕΝ έχουν βραχεί τα μαλλιά μου. (άρνηση συμπεράσματος)

=>

Ή ΔΕΝ βρέχει ή ΔΕΝ κάθομαι κάτω από τη βροχή ή και τα δύο. (άρνηση ισχυρισμών ως λογικό συμπέρασμα)

 

Η εξαγωγή συμπερασμάτων σε κάθε ένα από τα δύο μοντέλα υλοποιείται ως ακολούθως:

 

Modus Ponens:

ΑΝ Α αληθές ΤΟΤΕ Β αληθές

Α αληθές => Β αληθές

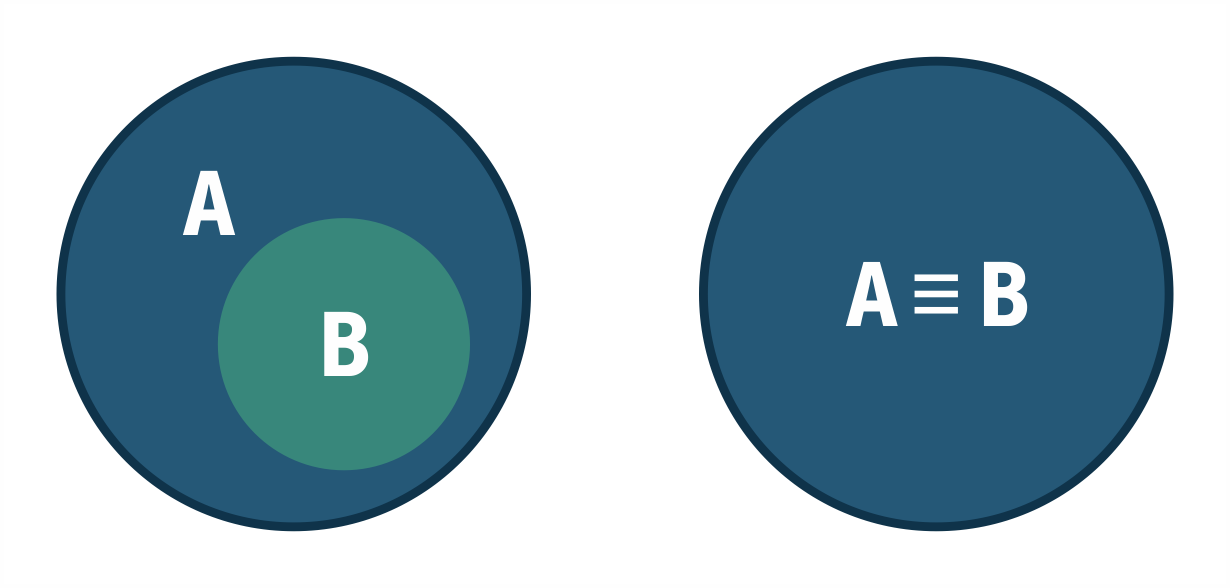
Σχήμα 3.1 Κύκλοι του Euler για το Modus Ponens

Δείτε κινούμενη εικόνα 3.1 - Κύκλοι του Euler (Modus Ponens)

 

Modus Tollens:

ΑΝ Α αληθές, ΤΟΤΕ Β αληθές

Β όχι αληθές => Α όχι αληθές

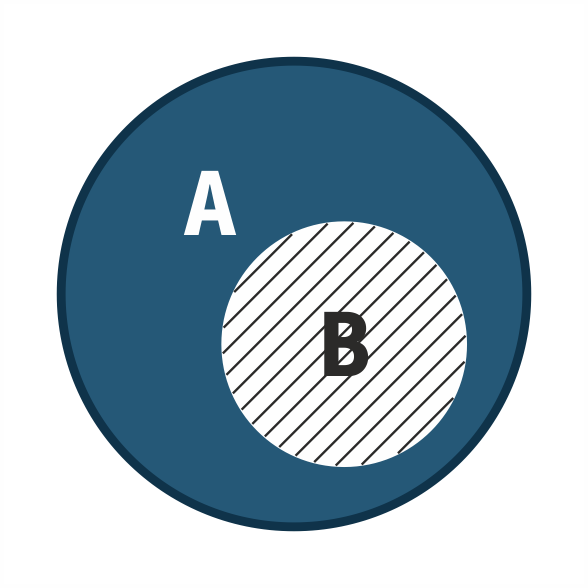
Σχήμα 3.2 Κύκλοι του Euler για το Modus Tollens

Δείτε κινούμενη εικόνα 3.2 - Κύκλοι του Euler (Modus Tollens)

 

Βάσει όλων των παραπάνω, η υλοποίηση συγκεκριμένων συλλογιστικών μέσα στα συστήματα κανόνων προϋποθέτει την υιοθέτηση αντίστοιχων μηχανισμών εξαγωγής συμπερασμάτων (inference mechanisms) που βασίζονται σε:

Εκτενέστερη αναφορά στους μηχανισμούς αυτούς θα γίνει στην παράγραφο περί συστημάτων παραγωγής (ανατρέξτε στην παράγραφο 3.4 παρακάτω).

3.2 Συστήματα Κανόνων

Τα συστήματα κανόνων ανήκουν στο γενικότερο χώρο των Συστημάτων Βασισμένων στη Γνώση - ΣΒΓ (Knowledge-Based Systems - KBS), όπου είναι απαραίτητη η επιλογή κατάλληλης αναπαράστασης της διαδικαστικής γνώσης εκφρασμένης υπό μορφή έγκυρων συλλογισμών. Τα ΣΒΓ/KBS που χρησιμοποιούν κανόνες για την αναπαράσταση της διαδικαστικής γνώσης του προς επίλυση προβλήματος καλούνται Συστήματα Βασισμένα σε Κανόνες (Rule-Based Systems-ΣΒΚ/RBS) ή απλώς Συστήματα Κανόνων.

3.2.1 Υλοποίηση κανόνων

Η δομή ενός κανόνα αποτελείται από δύο τμήματα, το τμήμα των ισχυρισμών (τμήμα ΑΝ/IF) και το τμήμα των ενεργειών ή συμπερασμάτων (τμήμα ΤΟΤΕ/THEN):

 

ΑΝ <ισχυρισμοί>

ΤΟΤΕ <ενέργειες>/<συμπεράσματα>

 

Γενικά, υπάρχουν δύο μεγάλες κατηγορίες εξειδικεύσεων αυτής της γενικής μορφής. Στην πρώτη κατηγορία, οι σχέσεις μεταξύ ισχυρισμών και γεγονότων δηλώνονται ρητά, οπότε μια βάση κανόνων μπορεί να παρασταθεί ως δίκτυο που παριστάνει τις αλληλεξαρτήσεις μεταξύ κανόνων και γεγονότων, όπως αυτό του σχήματος 3.6. Στην κωδικοποίηση των κανόνων της πρώτης αυτής κατηγορίας στις συνθήκες τα γεγονότα ορίζονται ρητά.

Ένα παράδειγμα κανόνα που ακολουθεί την παραπάνω σύνταξη είναι το εξής:

 

ΑΝ ισχύει <Ελένη πληροφορικός>

ΤΟΤΕ πρόσθεσε το συμπέρασμα <είναι Ελένη νοήμων>

 

Η δεύτερη κατηγορία στηρίζεται στην έννοια του ταιριάσματος προτύπων (pattern matching), του οποίου ένας ορισμός είναι ο ακόλουθος:

Οι σχέσεις μεταξύ ισχυρισμών και γεγονότων σ’ αυτές τις εξειδικεύσεις δε δηλώνονται ρητά, αλλά σχηματοποιούνται κατά τη διαδικασία εξαγωγής συμπερασμάτων. Μπορούμε να έχουμε χρήση μεταβλητών στους ισχυρισμούς αλλά και στα συμπεράσματα.

Ένα παράδειγμα κανόνα που ακολουθεί την παραπάνω σύνταξη είναι το εξής:

 

ΑΝ ισχύει <είναι ?X πληροφορικός>

ΤΟΤΕ εμφάνισε ”Βρέθηκε ένας πληροφορικός“

 

Παρατηρήστε ότι η μεταβλητή στο συγκεκριμένο παράδειγμα, για να διασαφηνιστεί ως τέτοια, έχει όνομα που ο πρώτος χαρακτήρας είναι συμβατικά ο χαρακτήρας «?». Μια τέτοια προσέγγιση ακολουθεί το προγραμματιστικό περιβάλλον της Lisp. Σε άλλα περιβάλλοντα, όπως αυτό της Prolog ακολουθούνται άλλες συμβατικές προσεγγίσεις.

Επίσης, μεταβλητές μέσα σε πρότυπα μπορούν να παρουσιάζονται και στο then μέρος ενός κανόνα, αλλά μόνο αν αυτές έχουν ήδη ταυτοποιηθεί στο if μέρος του ίδιου κανόνα. Για τη μεταβλητή στο μέρος then δεν ακολουθείται εκ νέου η διαδικασία ταυτοποίησης, διότι η διαδικασία που έχει ήδη γίνει για την ίδια μεταβλητή στο if μέρος μεταδίδεται και στην αντίστοιχη μεταβλητή του then μέρους. Η διεργασία αυτή καλείται ενοποίηση (unification). Ακολουθεί σχετικό παράδειγμα:

 

Δήλωση:

<είναι Κώστας πληροφορικός>

Κανόνας:

AN ισχύει <είναι ?X πληροφορικός>

TOTE πρόσθεσε το συμπέρασμα <είναι ?Χ νοήμων>

 

Στο παραπάνω παράδειγμα, όταν εκτελεστεί ο κανόνας, η μεταβλητή ?Χ στο if μέρος θα ταυτιστεί με τη λέξη Κώστας, ταύτιση που μεταδίδεται στην ?Χ του then μέρους μέσω της ενοποίησης και έτσι παράγεται το συμπέρασμα <είναι Κώστας νοήμων>. Ενοποιήσεις μπορούν να γίνουν και στο if μέρος ενός κανόνα όταν η ίδια μεταβλητή αναφέρεται μέσα σε δυο ή περισσότερες διαδοχικές υποθέσεις. Για παράδειγμα, στον επόμενο κανόνα, η ταύτιση του πρώτου ?Χ με το Κώστας θα μεταδοθεί και στο δεύτερο ?Χ και για να είναι αληθείς οι υποθέσεις του κανόνα θα πρέπει να υπάρχει εκτός της δήλωσης <είναι Κώστας πληροφορικός> και η δήλωση <έχει Κώστας δουλειά>.

 

Κανόνας:

AN ισχύει <είναι ?X πληροφορικός>

Και <έχει ?Χ δουλειά>

TOTE πρόσθεσε το συμπέρασμα <είναι ?Χ νοήμων>

 

Όταν οι ισχυρισμοί είναι παραπάνω του ενός, τότε συνδέονται με τα λογικά συνδετικά AND και OR. Επίσης, οι σχέσεις μεταξύ ισχυρισμών και γεγονότων μπορεί να δηλώνονται ρητά για κάποιους από αυτούς και για άλλους να χρησιμοποιούνται μεταβλητές. Για παράδειγμα, ένας κανόνας που υλοποιεί στο πρόβλημα του αγρότη τον τελεστή μετάβασης του αγρότη με τη χήνα από τη μία όχθη στην απέναντι, χρησιμοποιώντας μεταβλητή, για να δηλωθεί άρρητα η έννοια της όχθης αφετηρίας και της απέναντι όχθης, θα μπορούσε να συνταχθεί ως ακολούθως:

 

ΑΝ <is Farmer ?side>

και <is Goose ?side>

και <opposite ?side ?otherside>

ΤΟΤΕ αφαίρεσε τα γεγονότα <is Farmer ?side>, <is Goose ?side>

πρόσθεσε τα γεγονότα <is Farmer ?otherside> <is Goose ?otherside>

 

Στο παράδειγμα αυτό, αν υπάρχουν τα γεγονότα <is Farmer left> και <opposite left right> στη μνήμη εργασίας, η μεταβλητή ?side θα ταυτιστεί με το left και η μεταβλητή ?otherside θα ταυτιστεί με το right, σε όποιο σημείο του κανόνα και αν παρουσιάζονται αυτά. Συνεπώς, ο κανόνας μετά το ταίριασμα προτύπων και την ενοποίηση θα έχει μια μορφή που αντιστοιχεί σε αυτήν ενός κανόνα γραμμένου με ρητές αναφορές σε γεγονότα, όπως ο επόμενος:

 

ΑΝ <is Farmer left>

και <is Goose left>

και <opposite left right>

ΤΟΤΕ αφαίρεσε τα γεγονότα <is Farmer left>, <is Goose left>

πρόσθεσε τα γεγονότα <is Farmer right>, <is Goose right>

3.2.2 Περιγραφή Συστημάτων Κανόνων

Τα συστήματα κανόνων διακρίνονται σε 2 κατηγορίες, ανάλογα με το αν ο σκοπός για τον οποίο χρησιμοποιούν την υπάρχουσα γνώση για ένα πρόβλημα είναι:

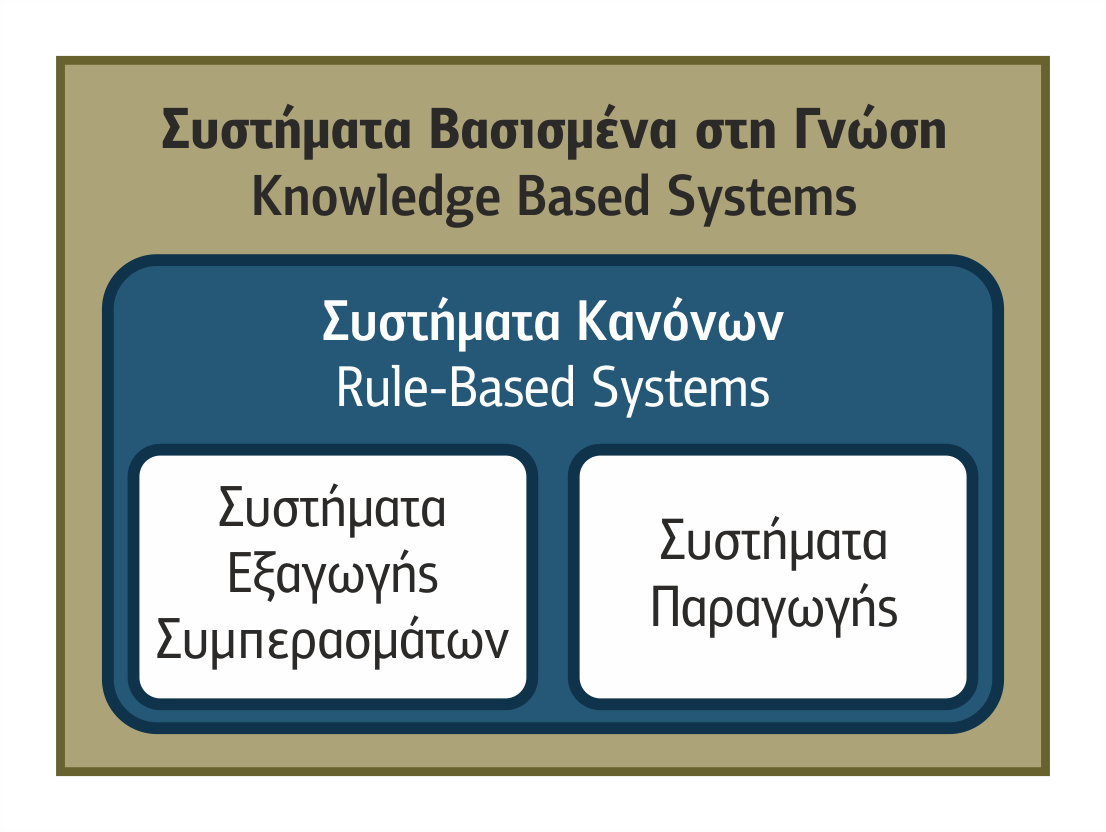
Σχήμα 3.3 Συστήματα Βασισμένα στη Γνώση

Τα συστήματα κανόνων αποτελούνται από τρία κύρια μέρη :

Η συλλογή γεγονότων περιγράφει τη δηλωτική γνώση για ένα πρόβλημα. Γεγονός (fact) είναι μία δήλωση ότι κάποιος ισχυρισμός είναι αληθής, όπως π.χ. «πέφτει χιόνι», «ο ασθενής έχει υψηλό πυρετό», «η γάτα μου είναι καλή σύντροφος». Η δηλωτική γνώση για το πρόβλημα προκύπτει από παρατηρήσεις που αφορούν τα αντικείμενα του κόσμου του προβλήματος και αποτυπώνεται κωδικοποιημένη σε μια συλλογή γεγονότων (facts) που καλείται ενεργός μνήμη (active memory) ή μνήμη εργασίας (working memory). Η μνήμη εργασίας περιέχει γεγονότα, τόσο αυτά που ορίζονται κατά την εκκίνηση του συστήματος όσο και αυτά που δημιουργούνται κατά την εκτέλεσή του.

Οι κανόνες αποτυπώνουν γνώση που προκύπτει από προϋπάρχουσα εμπειρία σε σχέση με το πρόβλημα. Σε έναν κανόνα στον οποίο υπάρχουν περισσότεροι του ενός ισχυρισμού στο IF μέρος, συνδεδεμένοι με AND και OR, η αλήθεια ή όχι αυτού του σύνθετου ισχυρισμού προκύπτει από τους νόμους της λογικής, όπως αυτοί αναπαριστώνται σε προηγούμενη παράγραφο (βλέπε Σχήμα 3.1 και Σχήμα 3.2) ή πίνακες αληθείας ή άλλες μεθόδους.

Όταν το AN μέρος ενός κανόνα περιέχει έναν ή περισσότερους ισχυρισμούς, αυτοί πρέπει να είναι αληθείς, δηλαδή να περιέχονται στη συλλογή των γεγονότων, ώστε να μπορεί ο κανόνας να λειτουργήσει ως παραγωγικός συλλογισμός με αληθείς ισχυρισμούς και να δώσει έγκυρα αποτελέσματα ακολουθώντας το μοντέλο modus ponens. Το TOTE μέρος περιέχει αποτελέσματα/συμπεράσματα που επιδρούν ή όχι στον κόσμο του προβλήματος, επιφέροντας ή όχι αλλαγές στην υπάρχουσα δηλωτική γνώση. Η συλλογή των κωδικοποιημένων κανόνων καλείται Βάση Κανόνων (Rules Base) και αποτελεί τη Βάση Γνώσης (Knowledge Base) του συστήματος.

Ο μηχανισμός εξαγωγής συμπερασμάτων (inference mechanism) ή συμπερασματική μηχανή (inference engine) είναι υπεύθυνος, αφού ελέγξει την αλήθεια των ισχυρισμών ενός κανόνα, να τον θέτει ως υποψήφιο προς εκτέλεση και να εξάγει τα συμπεράσματα μέσα στη μνήμη εργασίας, αν ο κανόνας επιλεγεί προς εκτέλεση. Η εκτέλεση ενός κανόνα καλείται πυροδότηση κανόνα (rule firing).

Η συμπερασματική μηχανή ελέγχει τη λειτουργία ολόκληρου του συστήματος και ενεργεί σε κύκλους λειτουργίας, όπου σε κάθε κύκλο πυροδοτείται μόνο ένας κανόνας.

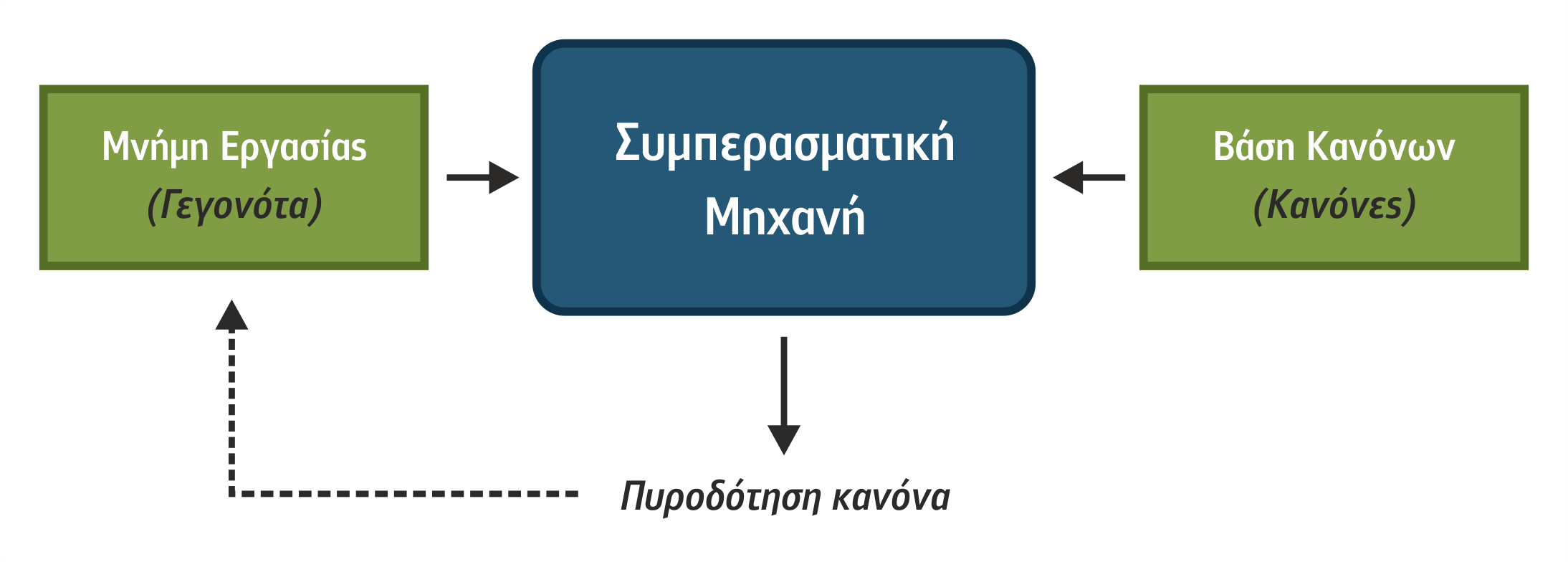
Σχήμα 3.4 Τυπική Δομή και λειτουργία Συστημάτων Κανόνων

3.3 Συστήματα Εξαγωγής Συμπερασμάτων

Τα συστήματα εξαγωγής συμπερασμάτων (deduction systems) περιέχουν μη παραγωγική διαδικαστική γνώση, δηλαδή κανόνες που οδηγούν σε λογικά συμπεράσματα, αλλά δε διαφοροποιούν τον κόσμο του προβλήματος.

Οι κανόνες στα συστήματα εξαγωγής συμπερασμάτων καλούνται συμπερασματικοί κανόνες (inference rules) και εκφράζουν κυρίως δηλωτική γνώση:

 

ΑΝ οι ισχυρισμοί αληθεύουν

ΤΟΤΕ αληθεύει και το συμπέρασμα

 

Χαρακτηριστικό παράδειγμα είναι αυτό του γενεαλογικού δένδρου, όπου συνάγονται συμπεράσματα για τις συγγενικές σχέσεις μεταξύ των προσώπων που το απαρτίζουν, χωρίς αυτό να σημαίνει ότι υπάρχει κανόνας με την εκτέλεση του οποίου θα αλλάξει κάποια από τις σχέσεις μεταξύ των προσώπων αυτών.

Για παράδειγμα, έστω ότι σε ένα σύστημα εξαγωγής συμπερασμάτων έχουμε:

 

Μνήμη Εργασίας:

 

{<Χ γονέας του Υ>, <Υ γονέας του Ζ>}

 

Βάση Κανόνων:

 

{R1:ΕΑΝ <Χ γονέας του Υ> και <Υ γονέας του Ζ>

ΤΟΤΕ <Χ παππούς του Ζ>}

 

Όταν το παραπάνω σύστημα εκτελεστεί, η συμπερασματική μηχανή θα καλέσει τη δομή ελέγχου να εκτελέσει τον κανόνα R1, επειδή έχει αληθείς ισχυρισμούς. Η εκτέλεση θα προσθέσει το γεγονός <Χ παππούς του Ζ> στη μνήμη εργασίας, αλλά αυτό δε διαφοροποιεί τις υπάρχουσες συγγενικές σχέσεις μεταξύ των Χ, Υ και Ζ∙ απλώς εξάγει κάποια συμπεράσματα που δεν είχαν συμπεριληφθεί ως γεγονότα στην αρχική μνήμη εργασίας.

 

Άλλα παραδείγματα συμπερασματικών κανόνων:

 

ΑΝ ένα ζώο διαθέτει τρίχωμα και το ζώο δίνει γάλα

ΤΟΤΕ το ζώο είναι θηλαστικό

 

ΑΝ τα φώτα του δρόμου είναι αναμμένα

ΤΟΤΕ υπάρχει ασφάλεια

 

Οι παρακάτω συμπερασματικοί κανόνες αποτυπώνουν δηλωτική γνώση από το ζωικό βασίλειο σε σχέση με τις ιδιότητες που χαρακτηρίζουν κάποια θηλαστικά και πτηνά. Η δομή τους περιέχει ισχυρισμούς και συμπεράσματα σε κατηγορηματική μορφή.

Σχήμα 3.5 Σύστημα κανόνων μέρους ζωικού βασιλείου

Για τους παραπάνω κανόνες ισχύουν οι εξής συσχετισμοί που μπορούν να οδηγήσουν σε λογικά συμπεράσματα:

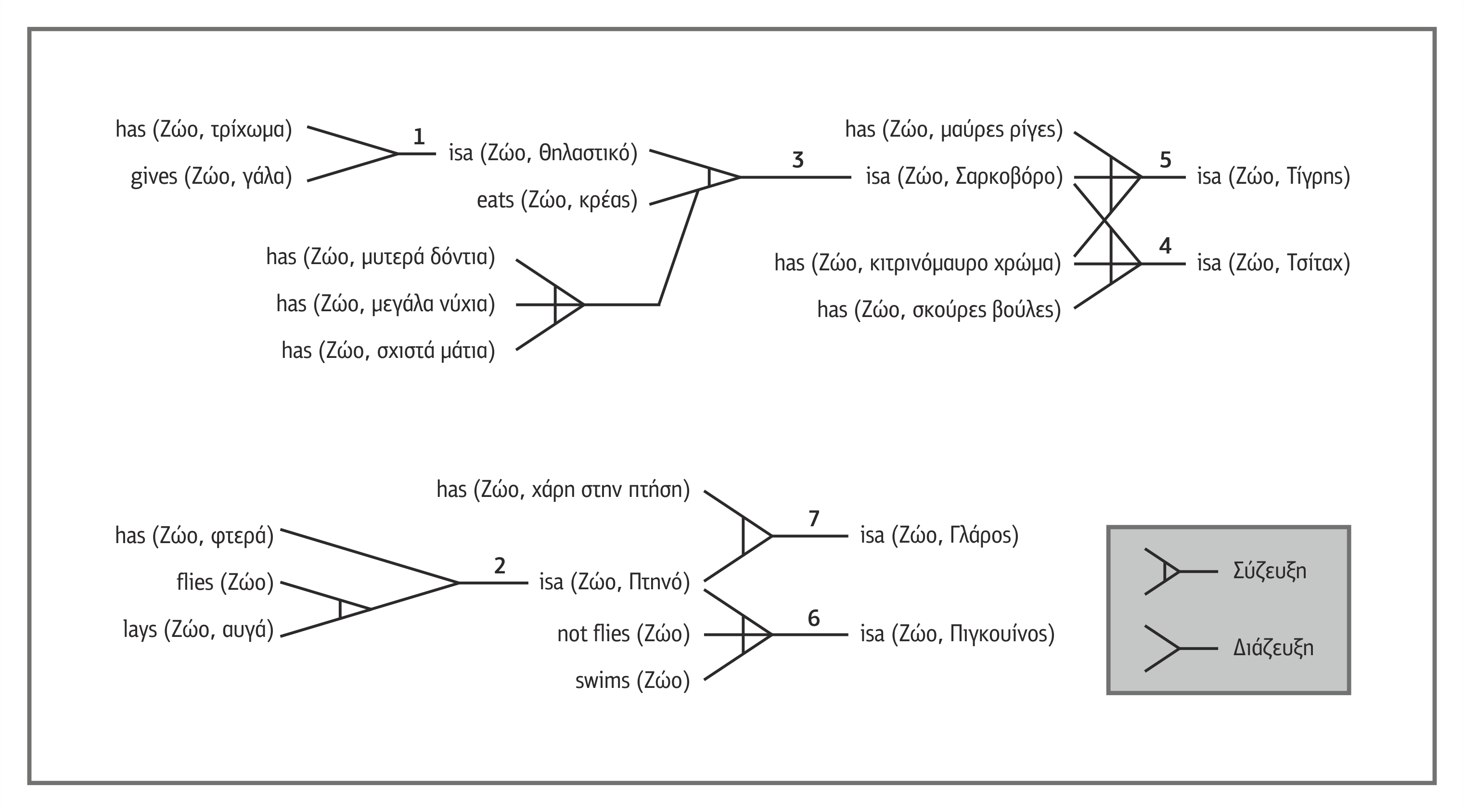
Σχήμα 3.6 Συσχετισμός κανόνων μέσα στη βάση γνώσης

Βάσει των συσχετισμών του σχήματος 3.6, αν υπάρχουν στη μνήμη εργασίας τα γεγονότα που ακολουθούν (καθιστώντας τους αντίστοιχους ισχυρισμούς των κανόνων αληθείς):

 

flies(Ιωνάθαν),

lays(Ιωνάθαν,αυγά),

has(Ιωνάθαν,χάρη στην πτήση)

 

τότε θα εξαχθούν λογικά τα παρακάτω συμπεράσματα:

 

isa(Ιωνάθαν,Πτηνό) και

isa(Ιωνάθαν,Γλάρος)

 

ακολουθώντας την εξής σειρά εξαγωγής λογικών συμπερασμάτων:

 

flies(Ιωνάθαν) lays(Ιωνάθαν,αυγά) → isa(Ιωνάθαν,Πτηνό)

isa(Ιωνάθαν,Πτηνό) has(Ιωνάθαν,χάρη στην πτήση)

→ isa(Ιωνάθαν,Γλάρος)

 

Κατά τα λοιπά, τα συστήματα εξαγωγής συμπερασμάτων λειτουργούν ακριβώς όπως και τα συστήματα παραγωγής που παρουσιάζονται στη συνέχεια.

3.4 Συστήματα παραγωγής

Στα συστήματα παραγωγής (production systems), η διαδικαστική γνώση για το πρόβλημα που επιχειρείται να επιλυθεί μέσω του συστήματος εκφράζεται με κανόνες της μορφής:

 

ΑΝ οι ισχυρισμοί αληθεύουν

ΤΟΤΕ εκτέλεσε τις ενέργειες που αλλάζουν τον κόσμο

 

Δηλαδή, το ΑΝ μέρος του κανόνα αναφέρεται σε ενέργειες των οποίων τα αποτελέσματα, αφού ο κανόνας εκτελεστεί, θα επιδράσουν, στην τρέχουσα κατάσταση του προβλήματος με τον ακόλουθο τρόπο: οι ενέργειες θα επιφέρουν αλλαγές στη μνήμη εργασίας και ιδιαίτερα στα γεγονότα που περιγράφουν τον κόσμο του προβλήματος είτε προσθέτοντας νέα γεγονότα είτε μεταβάλλοντας χαρακτηριστικά υπαρχόντων γεγονότων είτε διαγράφοντας υπάρχοντα γεγονότα, παράγοντας με τον τρόπο αυτό ένα νέο στιγμιότυπο του κόσμου του προβλήματος. Κανόνες με τέτοια χαρακτηριστικά καλούνται κανόνες παραγωγής ή παραγωγικοί κανόνες (production rules).

 

Παραδείγματα παραγωγικών κανόνων:

 

ΑΝ ο αγρότης βρίσκεται σε μια όχθη

ΤΟΤΕ μετάφερε τον αγρότη στην απέναντι όχθη

 

ΑΝ το ζάρι φέρει 3

ΤΟΤΕ προχώρησε το πούλι 3 θέσεις μπροστά

 

Ουσιαστικά τα συστήματα παραγωγής είναι συστήματα κανόνων που περιέχουν τουλάχιστον έναν παραγωγικό κανόνα. Η βάση κανόνων τους καλείται παραγωγική μνήμη (production memory). Τα συστήματα παραγωγής ακολουθούν τη δομή και τον τρόπο λειτουργίας των συστημάτων κανόνων και δουλεύουν, όπως αυτοί, σε κύκλους.

Σχήμα 3.7 Δομή και λειτουργία Συστημάτων Παραγωγής

3.4.1 Κύκλοι Λειτουργίας

Σε κάθε κύκλο λειτουργίας ενός συστήματος κανόνων επιλέγεται ένας κανόνας από το σύνολο των κανόνων που μπορούν να πυροδοτηθούν και ως συνέπεια:

Ένας παραγωγικός κανόνας πρέπει να περιέχει τουλάχιστον μια παραγωγική ενέργεια και πιθανώς επιπλέον παραγωγικές και μη παραγωγικές ενέργειες. Η περιγραφή ενός κύκλου λειτουργίας σε βήματα είναι η ακόλουθη:

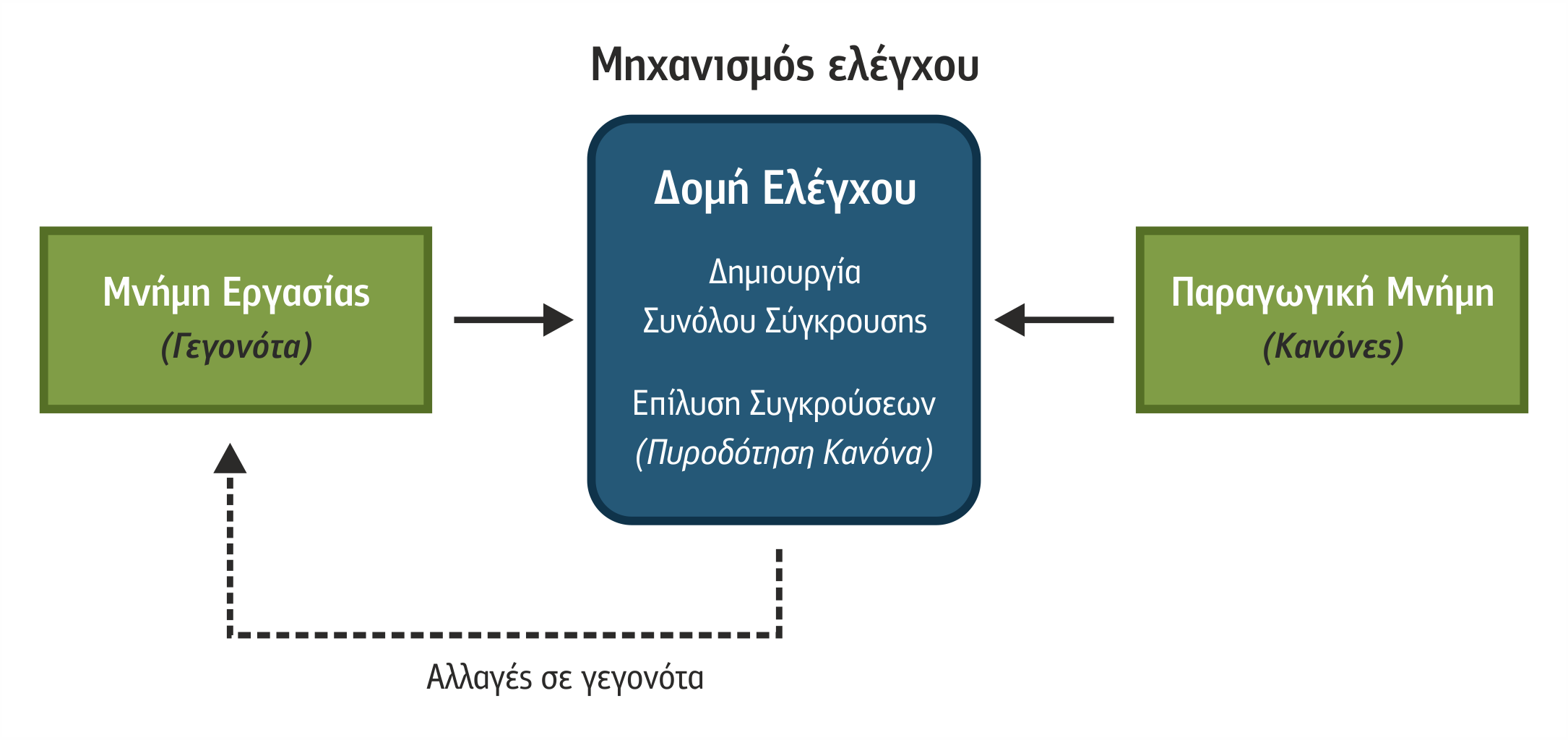
Σχήμα 3.8 Τα βήματα ενός κύκλου λειτουργίας

Δείτε κινούμενη εικόνα 3.3 - Κύκλοι Λειτουργίας ενός Συστήματος Κανόνων

3.4.2 Δομή Ελέγχου

Η δομή ελέγχου, σε κάθε κύκλο λειτουργίας, αναζητεί κανόνες των οποίων οι ισχυρισμοί είναι αληθείς, δηλαδή υπάρχουν ως γεγονότα στη μνήμη εργασίας. Οι κανόνες που έχουν εντοπιστεί να έχουν ικανοποιημένους ισχυρισμούς καταχωρίζονται σε ένα χώρο που καλείται σύνολο σύγκρουσης ή ατζέντα (conflict set).

 

Σε ένα σύνολο σύγκρουσης:

Η εκλογή ενός από τους κανόνες του συνόλου σύγκρουσης προς πυροδότηση καλείται επίλυση σύγκρουσης (conflict resolution) και γίνεται βάσει της ισχύουσας στρατηγικής επίλυσης συγκρούσεων . Μια τέτοια στρατηγική μπορεί να έχει διαφορετικά κριτήρια για την επιλογή κανόνα προς εκτέλεση, μερικά από τα οποία μπορεί να είναι:

Πρέπει να σημειωθεί ότι όλοι οι τρόποι επιλογής μπορεί να θεωρηθούν ευρετικοί, αφού δεν εγγυώνται την ορθότητα της επιλογής.

Βασικά θέματα σχεδιασμού συστημάτων εξαγωγής συμπερασμάτων είναι:

Η δομή ελέγχου μπορεί να βασίζεται στην προς τα εμπρός αλυσιδωτή εκτέλεση (forward chaining) ή στην προς τα πίσω αλυσιδωτή εκτέλεση (backward chaining) κανόνων. Για την εξαγωγή συμπερασμάτων στα συστήματα που ακολουθούν την προς τα εμπρός αλυσιδωτή πυροδότηση κανόνων χρησιμοποιείται το μοντέλο Modus Ponens, ενώ για αυτά που ακολουθούν την προς τα πίσω αλυσιδωτή πυροδότηση κανόνων χρησιμοποιείται το μοντέλο Modus Tollens (ανατρέξτε στην παράγραφο περί συλλογιστικής).

3.4.3 Προς τα εμπρός αλυσιδωτή εκτέλεση κανόνων

Η προς τα εμπρός αλυσιδωτή εκτέλεση κανόνων (forward chaining) είναι μια παραγωγική διαδικασία εξαγωγής συμπερασμάτων από κανόνες σύμφωνα με το μοντέλο έγκυρων συλλογισμών modus ponens, μίας από τις δυο μορφές έγκυρων συλλογισμών του προτασιακού λογισμού που χρησιμοποιεί την παραγωγή (deduction) για την εξαγωγή συμπερασμάτων.

 

Παράδειγμα συλλογισμού με modus ponens:

 

ΑΝ Α ΤΟΤΕ Β

Ισχύει το Α επομένως ισχύει το Β

 

Η προς τα εμπρός αλυσιδωτή εκτέλεση κανόνων πραγματοποιείται σε κύκλους λειτουργίας οδηγούμενη από τη συμπερασματική μηχανή και έχει τα παρακάτω χαρακτηριστικά:

Ο ψευδοκώδικας της προς τα εμπρός αλυσιδωτής εκτέλεσης είναι ο ακόλουθος:

Παράδειγμα προς τα εμπρός αλυσιδωτής εκτέλεσης :

Στο παράδειγμά μας, στη μνήμη εργασίας βρίσκονται τα παρακάτω δυο γεγονότα:

 

Ελένη πληροφορικός

Νίκος πληροφορικός

 

Επίσης, στη βάση γνώσης βρίσκονται οι παρακάτω δύο κανόνες:

 

R1:

IF ?X πληροφορικός

THEN ?Χ είναι νοήμων

 

R2:

IF ?X είναι νοήμων

THEN εμφάνισε «Μπράβο» ?Χ

 

Στον πρώτο κύκλο λειτουργίας του συστήματος, η συμπερασματική μηχανή θα πραγματοποιήσει ταίριασμα προτύπων (pattern matching) μεταξύ των γεγονότων της μνήμης εργασίας και των ισχυρισμών των κανόνων και θα εντοπίσει δύο κανόνες με ικανοποιημένους ισχυρισμούς τους οποίους και θα τοποθετήσει στο σύνολο σύγκρουσης.

Αυτοί είναι:

Ως αποτέλεσμα, το σύνολο σύγκρουσης θα διαμορφωθεί ως εξής:

 

Σύνολο σύγκρουσης: {R1(?Χ=Ελένη), R1(?Χ=Νίκος)}

 

Στη συνέχεια θα επιχειρηθεί να επιλυθεί η σύγκρουση (conflict resolution) με την επιλογή ενός κανόνα από το σύνολο σύγκρουσης βάσει μιας στρατηγικής επίλυσης συγκρούσεων. Στο παράδειγμά μας, αυτή είναι η τυχαία επιλογή. Στον πρώτο κύκλο λειτουργίας, κατά την εφαρμογή του μηχανισμού τυχαίας επιλογής, επιλέγεται τυχαία προς πυροδότηση ο R1(?Χ=Ελένη), ο οποίος και πυροδοτείται παράγοντας μέσα στη μνήμη εργασίας το νέο γεγονός «Ελένη είναι νοήμων» (βλέπε επόμενο πίνακα 3.1).

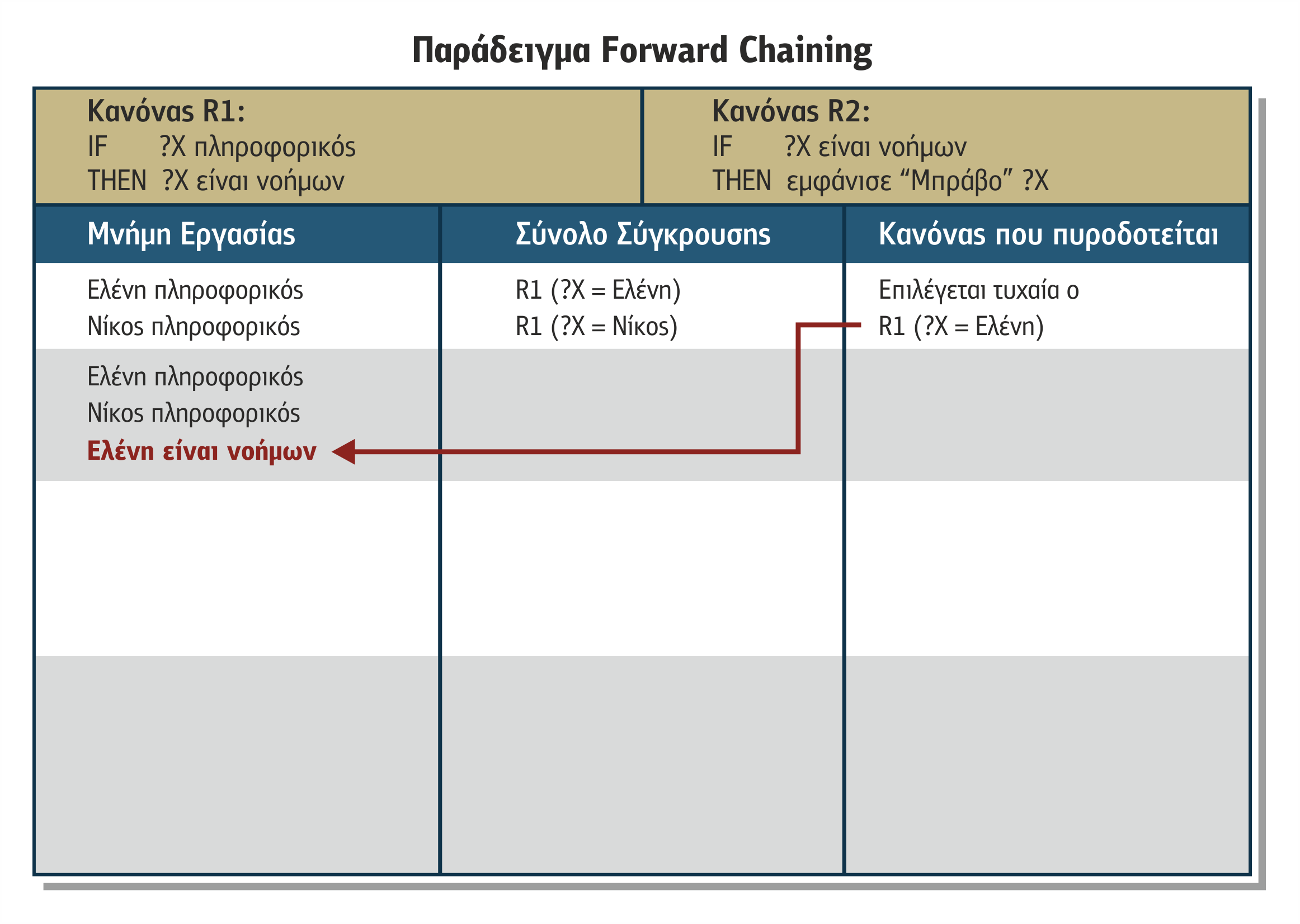
Πίνακας 3.1 Πρώτος κύκλος λειτουργίας παραδείγματος προς τα εμπρός αλυσιδωτής εκτέλεσης

Στη συνέχεια, παρουσιάζονται όλοι οι κύκλοι εκτέλεσης του συστήματος μέχρι την ολοκλήρωσή του, δηλαδή μέχρι να εξαχθούν όλα τα δυνατά συμπεράσματα και να εκτελεστούν οι πιθανές ενέργειες, έως ότου το σύνολο σύγκρουσης βρεθεί κενό:

 

1ος Κύκλος

2ος Κύκλος

3ος Κύκλος

4ος Κύκλος

Κατάσταση συστήματος κατά την έξοδο:

Πίνακας 3.2 Κατάσταση του συστήματος μετά τον τελευταίο κύκλο λειτουργίας παραδείγματος προς τα εμπρός αλυσιδωτής εκτέλεσης

Δείτε κινούμενη εικόνα 3.4 - Λειτουργία της προς τα εμπρός αλυσιδωτής εκτέλεσης κανόνων

 

Άλλο ενδιαφέρον παράδειγμα είναι αυτό του Ρομπότ (Βλαχάβας κ.ά, 2011).

Το πρόβλημα έχει ως εξής: Σε ένα πλαίσιο 10x10 θέσεων που περιέχει εμπόδια και αντικείμενα είναι τοποθετημένο ένα ρομπότ σε μια αρχική θέση (βλέπε Σχήμα 1.9) με μια συγκεκριμένη κατεύθυνση προς τα δυτικά, ανατολικά, βόρεια ή νότια. Το ρομπότ μπορεί να μετακινηθεί προς την κατεύθυνσή του σε μια γειτονική θέση, με την προϋπόθεση ότι η θέση αυτή δεν περιέχει εμπόδιο. Στόχος του προβλήματος είναι το ρομπότ να μετακινηθεί προς θέση, αποφεύγοντας τα εμπόδια, έως ότου βρεθεί σε κάποια θέση με αντικείμενο, οπότε να στείλει ένα μήνυμα και να σταματήσει.

Η μνήμη εργασίας για την αρχική κατάσταση του προβλήματος του ρομπότ, όπως αυτή αποτυπώνεται στο σχήμα 1.9, είναι η ακόλουθη:

 

Μνήμη Εργασίας:

robot_at(6,4)

direction(e)

choice(w) choice(e) choice(n) choice(s)

obstacle_at(2,3) obstacle_at(3,8) obstacle_at(4,2)

obstacle_at(5,2) obstacle_at(5,6) obstacle_at(6,8)

obstacle_at(7,4) obstacle_at(7,7) obstacle_at(9,2)

object_at(4,4) object_at(4,7) object_at(7,2)

object_at(8,5) object_at(10,6)

 

όπου δηλώνουν:

Οι αντίστοιχοι κανόνες της βάσης γνώσης είναι οι ακόλουθοι:

 

1: detect_object:      if robot_at(X,Y) and object_at(X,Y)

                   then output(‘object is found’), exit

2: move_west:      if robot_at(X,Y) and direction(w)

                   then delwm(robot_at(X,Y)), NX=X-1,

                        addwm(robot_at(NX,Y))

3: move_east:       if robot_at(X,Y) and direction(e)

                   then delwm(robot_at(X,Y)), NX=X+1

                        addwm(robot_at(NX,Y))

4: move_north:        if robot_at(X,Y) and direction(n)

                   then delwm(robot_at(X,Y)), NY=Y+1

                        addwm(robot_at(X,NY))

5: move_south:     if robot_at(X,Y) and direction(s)

                   then delwm(robot_at(X,Y)), NY=Y-1

                        addwm(robot_at(X,NY))

6: avoid_obstacle_south: if robot_at(X,Y) and NY=Y-1

                            and obstacle_at(X,NY) and direction(s)

                            and choice(ND)

                         then delwm(direction(s))

                         addwm(direction(ND))

7: avoid_obstacle_west:  if robot_at(X,Y) and NX=X-1

                            and obstacle_at(NX,Y) and direction(w)

                            and choice(ND)

                         then delwm(direction(w))

                              addwm(direction(ND))

8:avoid_obstacle_north:  if robot_at(X,Y) and NY=Y+1

                            and obstacle_at(X,NY) and direction(n)

                            and choice(ND)

                         then delwm(direction(n))

                              addwm(direction(ND))

9:avoid_obstacle_east:   if robot_at(X,Y) and NX=X+1

                            and obstacle_at(NX,Y) and direction(e)

                            and choice(ND)

                         then delwm(direction(e))

                            addwm(direction(ND))

 

Στον 1ο κύκλο λειτουργίας, το σύνολο σύγκρουσης θα περιέχει 5 κανόνες, τον κανόνα 3 μετακίνησης ανατολικά move_east και τέσσερεις διαφορετικές εκδοχές του κανόνα 9 avoid_obstacle_east, μία για κάθε ταύτιση των ισχυρισμών του με τα γεγονότα robot_at(6 4) και choice(w), robot_at(6 4) και choice(e), robot_at(6 4) και choice(n) και, τέλος, robot_at(6 4) και choice(s) αντίστοιχα:

 

Σύνολο σύγκρουσης:

{3: move_east (X=6 και Υ=4)

9:avoid_obstacle_east (X=6 και Υ=4 ND=w),

9:avoid_obstacle_east (X=6 και Υ=4 ND=n),

9:avoid_obstacle_east (X=6 και Υ=4 ND=s),

9:avoid_obstacle_east (X=6 και Υ=4 ND=e) }

 

Αν στον πρώτο κύκλο εκτέλεσης ως στρατηγική επίλυσης συγκρούσεων επιλεγεί η επιλογή του πιο ειδικού κανόνα (ΕΕ) και ως ειδικός κριθεί ο κανόνας avoid_obstacle_east έναντι του move_east, διότι η αποφυγή του εμποδίου έχει μεγαλύτερη σημασία από την κίνηση προς θέση με εμπόδιο, η επιλογή αυτή δε θα επιλύσει οριστικά τη σύγκρουση, δεδομένου ότι θα παραμένει προς επίλυση η σύγκρουση των τεσσάρων διαφορετικών εκδοχών του κανόνα avoid_obstacle_east. Εφόσον η επίλυση αφορά τέσσερεις κανόνες με ίδια προτεραιότητα, επιβάλλεται η επιλογή νέας στρατηγικής για την επίλυση της σύγκρουσης. Θεωρούμε ότι ως νέα στρατηγική εφαρμόζεται αυτή της τυχαίας επιλογής (ΤΕ) που επιστρέφει τον κανόνα 9 avoid_obstacle_east (ND=n), ο οποίος, όταν πυροδοτηθεί, θα διαγράψει από τη μνήμη εργασίας την τρέχουσα κατεύθυνση (delwm(direction(e)) και θα προσθέσει τη νέα (addwm(direction(n)).

Η λειτουργία του συστήματος ολοκληρώνεται, όταν το ρομπότ βρεθεί σε μία θέση όπου υπάρχει ένα αντικείμενο και πυροδοτηθεί ο κανόνας 1 detect_object. Οι κύκλοι λειτουργίας της εκτέλεσης του συστήματος παραγωγής που θα επιλύσει το πρόβλημα του ρομπότ παρουσιάζονται στον παρακάτω πίνακα.

Πίνακας 3.3 Κύκλοι εκτέλεσης του προβλήματος του Ρομπότ

3.4.4 Προς τα πίσω αλυσιδωτή εκτέλεση κανόνων

Για να μπορέσει να εφαρμοστεί η προς τα πίσω αλυσιδωτή εκτέλεση κανόνων (backward chaining) απαιτείται να είναι από την αρχή γνωστός ο σκοπός της αναζήτησης.

Τα χαρακτηριστικά της προς τα πίσω αλυσιδωτής εκτέλεσης είναι:

Περιληπτικά, ο τρόπος με τον οποίο λειτουργεί η προς τα πίσω αλυσιδωτή πυροδότηση των κανόνων είναι ο εξής: Αναζητούνται κανόνες που περιέχουν τον επιθυμητό στόχο στα συμπεράσματά τους. Αν βρεθούν ένας ή περισσότεροι μεταξύ αυτών με αληθείς ισχυρισμούς, συγκεντρώνονται στο σύνολο σύγκρουσης και πυροδοτείται αυτός που θα επιλεγεί με βάση την ισχύουσα στρατηγική επίλυσης σύγκρουσης, ολοκληρώνοντας με τον τρόπο αυτό την εκτέλεση του συστήματος.

Άλλως, αρχίζει ένας νέος κύκλος όπου σημειώνονται οι διαφορές του τρέχοντος κόσμου του προβλήματος από τον επιδιωκόμενο στόχο και κάθε διαφορά ορίζεται ως νέος υπο-στόχος. Στη συνέχεια, αναζητούνται κανόνες που μπορούν να ικανοποιήσουν τους υπο-στόχους και αυτοί που έχουν αληθείς ισχυρισμούς συγκεντρώνονται στο σύνολο σύγκρουσης. Ο μηχανισμός επίλυσης σύγκρουσης επιλέγει και πυροδοτεί έναν από αυτούς βάσει της ισχύουσας στρατηγικής και ο κύκλος ολοκληρώνεται με τη μείωση της διαφοράς που επέφερε ο κανόνας. Αν σε κάποιον κύκλο δε βρεθεί κανόνας που μειώνει τις εναπομείνασες διαφορές, αυτό σημαίνει ότι δεν υπάρχει αλυσίδα κανόνων που οδηγεί στο στόχο, δηλαδή το πρόβλημα δεν έχει λύση.

 

Ψευδοκώδικας της προς τα πίσω αλυσιδωτής εκτέλεσης

Παράδειγμα προς τα πίσω αλυσιδωτής εκτέλεσης κανόνα

 

Το πρόβλημα που έχουμε να λύσουμε με τη βοήθεια του συστήματός μας είναι η κατασκευή ενός κέικ. Τα απαραίτητα υλικά είναι το αλεύρι, τα αυγά, η ζάχαρη και το γάλα. Όταν υπάρχουν όλα, τότε η κατασκευή είναι δυνατή, αλλιώς πρέπει να αγοράσουμε όσα λείπουν πληρώνοντας ανάλογα χρήματα.

Σε κάθε κύκλο λειτουργίας του συστήματος, όσα υλικά είναι διαθέσιμα στην κουζίνα αποτελούν τα γεγονότα του προβλήματος μέσα στην τρέχουσα ενεργό μνήμη. Η γνώση σχετικά με το ποια υλικά είναι απαραίτητα για την κατασκευή του κέικ και πώς πρέπει να ενεργήσει κάποιος, όταν του λείπουν κάποια από αυτά, είναι η υπάρχουσα διαδικαστική γνώση για το πρόβλημα, η οποία αποτυπώνεται μέσα στους κανόνες. Στην αρχή του προβλήματος, στην κουζίνα υπάρχει μόνο ζάχαρη, αλλά υπάρχουν διαθέσιμα χρήματα – σε ρευστό και σε λογαριασμό μέσα στην τράπεζα. Βάσει αυτού, ως πρωταρχικός στόχος τίθεται η ικανοποίηση των μη ικανοποιημένων ισχυρισμών του κανόνα που θα μας δώσει την κατασκευή του κέικ, του R1, όπως θα δούμε αμέσως μετά.

 

Μνήμη Εργασίας (γεγονότα)

Υπάρχει ζάχαρη

Υπάρχει χρήμα

Υπάρχει λογαριασμός στην τράπεζα

 

Κανόνες

R1:

IF   Υπάρχει αλεύρι AND Υπάρχει ζάχαρη AND Υπάρχει αυγά AND Υπάρχει γάλα

THEN εμφάνισε "Το κέικ μπορεί να κατασκευαστεί"

R2:

IF   Υπάρχει χρήμα AND NOT Υπάρχει αλεύρι

THEN ΠΡΟΣΘΕΣΕ Υπάρχει αλεύρι, ΑΦΑΙΡΕΣΕ Υπάρχει χρήμα

R3:

IF   Υπάρχει χρήμα AND NOT Υπάρχει ζάχαρη

THEN ΠΡΟΣΘΕΣΕ Υπάρχει ζάχαρη, ΑΦΑΙΡΕΣΕ Υπάρχει χρήμα

R4:

IF   Υπάρχει χρήμα AND NOT Υπάρχουν αυγά

THEN ΠΡΟΣΘΕΣΕ Υπάρχουν αυγά, ΑΦΑΙΡΕΣΕ Υπάρχει χρήμα

R5:

IF   Υπάρχει χρήμα AND NOT Υπάρχει γάλα

THEN ΠΡΟΣΘΕΣΕ Υπάρχει γάλα, ΑΦΑΙΡΕΣΕ Υπάρχει χρήμα

R6:

IF   Υπάρχει λογαριασμός στην τράπεζα AND NOT Υπάρχει χρήμα

THEN ΠΡΟΣΘΕΣΕ Υπάρχει χρήμα

 

Στόχος (ικανοποίηση των ανικανοποίητων ισχυρισμών του R1) η απόκτηση των:

Υπάρχει αλεύρι, Υπάρχουν αυγά, Υπάρχει γάλα

 

 

Το ζητούμενο του προβλήματος, δηλαδή η δυνατότητα κατασκευής κέικ, θα επιτευχθεί, όταν εκτελεστεί ο κανόνας R1, δηλαδή όταν ικανοποιηθούν όλοι οι ισχυρισμοί του. Σε κάθε κύκλο εργασίας, στο σύνολο σύγκρουσης συγκεντρώνονται οι κανόνες που περιέχουν στα συμπεράσματά τους τουλάχιστον ένα γεγονός που ταυτίζεται με ανικανοποίητο ισχυρισμό. Η εκτέλεση σε κύκλους, μέχρι να βρεθεί το ζητούμενο, έχει ως εξής:

 

1ος Κύκλος

Μνήμη εργασίας: Υπάρχει ζάχαρη, Υπάρχει χρήμα, Υπάρχει λογαριασμός στην τράπεζα

Ενδιάμεσος στόχος: Υπάρχει αλεύρι, Υπάρχουν αυγά, Υπάρχει γάλα

Σύνολο σύγκρουσης :

R2 (δίνει ως συμπέρασμα το Υπάρχει αλεύρι)

R4 (δίνει ως συμπέρασμα το Υπάρχουν αυγά)

R5 (δίνει ως συμπέρασμα το Υπάρχει γάλα)

Επιλέγεται ο R2 και πυροδοτείται.

Νέο γεγονός: Υπάρχει αλεύρι

 

2ος Κύκλος

Μνήμη εργασίας: Υπάρχει ζάχαρη, Υπάρχει αλεύρι, Υπάρχει λογαριασμός στην τράπεζα

Ενδιάμεσος στόχος: Υπάρχουν αυγά, Υπάρχει γάλα

Σύνολο σύγκρουσης :

R4 (δίνει ως συμπέρασμα το Υπάρχουν αυγά)

R5 (δίνει ως συμπέρασμα το Υπάρχει γάλα)

Επιλέγεται ο R4, αλλά έχει μη ικανοποιημένους ισχυρισμούς και δεν μπορεί να πυροδοτηθεί.

Νέος ενδιάμεσος στόχος ο ανικανοποίητος ισχυρισμός του R4: Υπάρχει χρήμα

Νέο σύνολο σύγκρουσης :

R6 (δίνει ως συμπέρασμα το Υπάρχει χρήμα), R4, R5

Επιλέγεται ο R6 και πυροδοτείται.

Νέο γεγονός στη μνήμη εργασίας: Υπάρχει χρήμα

 

3ος Κύκλος

Μνήμη εργασίας: Υπάρχει ζάχαρη, Υπάρχει αλεύρι, Υπάρχει χρήμα, Υπάρχει λογαριασμός στην τράπεζα

Ενδιάμεσος στόχος: Υπάρχουν αυγά, Υπάρχει γάλα

Σύνολο σύγκρουσης :

R4 (δίνει ως συμπέρασμα το Υπάρχουν αυγά)

R5 (δίνει ως συμπέρασμα το Υπάρχει γάλα)

Επιλέγεται ο R4 και πυροδοτείται.

Νέο γεγονός στη μνήμη εργασίας: Υπάρχουν αυγά

 

4ος Κύκλος

Μνήμη εργασίας: Υπάρχει ζάχαρη, Υπάρχει αλεύρι, Υπάρχουν αυγά, Υπάρχει λογαριασμός στην τράπεζα

Ενδιάμεσος στόχος: Υπάρχει γάλα

Σύνολο σύγκρουσης :

R5 (δίνει ως συμπέρασμα το Υπάρχει γάλα)

Επιλέγεται ο R5, αλλά έχει μη ικανοποιημένους ισχυρισμούς και δεν μπορεί να πυροδοτηθεί.

Νέος ενδιάμεσος στόχος ο ανικανοποίητος ισχυρισμός του R5: Υπάρχει γάλα

Νέο σύνολο σύγκρουσης :

R6 (δίνει ως συμπέρασμα το Υπάρχει χρήμα), R5

Επιλέγεται ο R6 και πυροδοτείται.

Νέο γεγονός στη μνήμη εργασίας: Υπάρχει χρήμα

 

5ος Κύκλος

Μνήμη εργασίας: Υπάρχει ζάχαρη, Υπάρχει αλεύρι, Υπάρχουν αυγά, Υπάρχει λογαριασμός στην τράπεζα, Υπάρχει χρήμα

Ενδιάμεσος στόχος: Υπάρχει γάλα

Σύνολο σύγκρουσης :

R5 (δίνει ως συμπέρασμα το Υπάρχει γάλα)

Επιλέγεται ο R5 και πυροδοτείται.

Νέο γεγονός στη μνήμη εργασίας: Υπάρχει γάλα

 

6ος Κύκλος

Μνήμη εργασίας: Υπάρχει ζάχαρη, Υπάρχει αλεύρι, Υπάρχουν αυγά, Υπάρχει λογαριασμός στην τράπεζα, υπάρχει γάλα

Ενδιάμεσος στόχος: -

Σύνολο σύγκρουσης :

R1 (στόχος της αναζήτησης)

Πυροδοτείται ο R1

Εμφανίζεται: "Το κέικ μπορεί να κατασκευαστεί"

 

Δείτε κινούμενη εικόνα 3.5 - Λειτουργία της προς τα πίσω αλυσιδωτής εκτέλεσης κανόνων

3.4.5 Ο Γενικός Επιλυτής Προβλημάτων (General Problem Solver)

Ο αλγόριθμος της προς τα πίσω αλυσιδωτής εκτέλεσης βασίζεται στη θεωρία των Newell & Simon (1972) σχετικά με το χώρο επίλυσης προβλημάτων, η οποία αναπτύχθηκε στο πλαίσιο της Γνωστικής Επιστήμης και που συνοπτικά αναφέρει τα εξής:

 

Η ανθρώπινη συμπεριφορά στην επίλυση προβλημάτων μπορεί να θεωρηθεί ως η δημιουργία καταστάσεων γνώσης, με εφαρμογή νοητικών τελεστών και μετάβαση από μια αρχική κατάσταση σε μία τελική. Οι τελεστές αυτοί υπαγορεύουν τις επιτρεπόμενες κινήσεις στο χώρο ή ποιες κινήσεις απαγορεύονται, όταν κάποιες ειδικές συνθήκες ισχύουν.

 

Για κάθε δεδομένο πρόβλημα υπάρχει ένα μεγάλο πλήθος εναλλακτικών δρόμων που οδηγούν στο στόχο του. Το σύνολο των καταστάσεων που δημιουργούν οι τελεστές κατά την αναζήτηση λύσης αποκαλείται βασικός χώρος επίλυσης προβλήματος (basic problem solution space).

Οι άνθρωποι χρησιμοποιούν τις γνώσεις τους και διάφορες ευρετικές μεθόδους, για να δημιουργήσουν το βασικό χώρο επίλυσης των προβλημάτων και να αναζητήσουν τη συντομότερη λύση.

Όλα αυτά λειτουργούν με τους περιορισμούς του ανθρώπινου γνωσιακού συστήματος, δηλαδή λαμβανομένων υπόψη των ορίων του χώρου της μνήμης μικρής διάρκειας και των ορίων στην ταχύτητα με την οποία μπορούν να μεταφέρονται οι πληροφορίες από και προς τη μνήμη μακράς διάρκειας.

Ήδη το 1959 οι προαναφερθέντες ερευνητές είχαν δημιουργήσει την πρώτη εκδοχή του Γενικού Επιλυτή Προβλημάτων - ΓΕΠ (General Problem Solver - GPS) ως γενικού συστήματος επίλυσης προβλημάτων (Newell κ.ά., 1959).

Ο ΓΕΠ/GPS είναι ένας μηχανισμός για επίλυση προβλημάτων μέσω ηλεκτρονικού υπολογιστή που αποτελεί μοντέλο του ανθρώπινου τρόπου επίλυσης προβλημάτων με βάση τη συλλογιστική. Το σύστημα χρησιμοποιεί στοίβα αποθήκευσης ενδιάμεσων στόχων και βασίζεται στην Means-Ends Analysis (MEA), μια μέθοδο επίλυσης προβλημάτων στο χώρο της ΤΝ για τον περιορισμό του χώρου αναζήτησης .

Η ΜΕΑ υλοποιεί τη θεωρία των ερευνητών για το χώρο επίλυσης προβλημάτων με τα εξής βήματα:

  1. Σημείωσε τις διαφορές μεταξύ της τρέχουσας κατάστασης και του στόχου.
  2. Δημιούργησε έναν ενδιάμεσο στόχο, για να μειώσεις αυτές τις διαφορές.
  3. Διάλεξε έναν τελεστή που εφαρμοζόμενος θα ικανοποιήσει τον τεθέντα ενδιάμεσο στόχο.
  4. Αν ο τελεστής έχει ανικανοποίητες προϋποθέσεις, για να εφαρμοστεί, θέσε μία από αυτές τις προϋποθέσεις ως νέο ενδιάμεσο στόχο και συνέχισε.

Ο αλγόριθμος του ΓΕΠ/GPS είναι ο εξής:

Κλασικό παράδειγμα κατάλληλο, για να παρουσιάσει τον τρόπο υλοποίησης του ΓΕΠ/GPS, είναι η επίλυση του προβλήματος των πύργων του Ανόι με αναδρομή.

Γενικά, η επίλυση ενός προβλήματος με συλλογιστική που βασίζεται στην προς τα πίσω αλυσιδωτή πυροδότηση κανόνων μπορεί να προσομοιωθεί με τον τρόπο συλλογισμού ενός γιατρού, ο οποίος προσπαθώντας να επιβεβαιώσει τις υποψίες του για την αιτία μιας ασθένειας κάνει στον ασθενή συγκεκριμένες ερωτήσεις για τα συμπτώματα που θα επιβεβαιώσουν την υπόθεσή του. Ένας επιστήμων στα Μαθηματικά σκέφτεται πολλές φορές με παρόμοιο τρόπο, για να καταλήξει στην απόδειξη ενός θεωρήματος που ισχυρίζεται ότι ισχύει.

Στο κεφάλαιο περί εμπείρων συστημάτων θα αναλύσουμε βαθύτερα τις μεθόδους πυροδότησης κανόνων καθώς και τις στρατηγικές επίλυσης συγκρούσεων σε καθεμία, θα συγκρίνουμε τα προτερήματα και μειονεκτήματά τους στο πλαίσιο της επίλυσης προβλημάτων του πραγματικού κόσμου και θα παρουσιάσουμε το τεχνολογικό πλαίσιο μέσα στο οποίο πρέπει να σχεδιάζονται.