6.4 Σύγκλιση κατά $L^2$

Από τη θεωρία $L^2$ που έχουμε δει εύκολα προκύπτει ότι στην περίπτωση του χώρου $L^2({\mathbb{T}})$ η απάντηση είναι καταφατική: ${\left\Vert{S_N(f)-f}\right\Vert}_2 \to 0$ για κάθε $f \in L^2({\mathbb{T}})$. Αυτό αποδεικνύεται πολύ εύκολα χρησιμοποιώντας το θεώρημα του Parseval (Θεώρημα 5.2):

$${\left\Vert{S_N(f)-f}\right\Vert}_2^2 = \sum_k {\left\vert{(S_N(f)-f)^\wedge(k)}\right\vert}^2$$

$$= \sum_{{\left\vert{k}\right\vert}>N} {\left\vert{\widehat{f}(k)}\right\vert}^2$$

$$\to 0 \gamma\iota\alpha N\to\infty$$

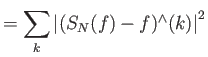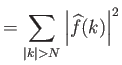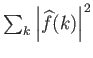αφού η σειρά $\sum_k {\left\vert{\widehat{f}(k)}\right\vert}^2$ είναι συγκλίνουσα.

Αναφέρουμε χωρίς απόδειξη το γεγονός ότι έχουμε σύγκλιση κατά νόρμα και στην περίπτωση των χώρων $L^p({\mathbb{T}})$ με $1<p<+\infty$. Με αυτά που έχουμε δείξει μέχρι στιγμής δε μπορούμε να δείξουμε αυτό το αποτέλεσμα.