4.4 Ο πυρήνας του Dirichlet και τα μερικά αθροίσματα της σειράς Fourier

Κεντρικό αντικείμενο για τη μελέτη της κατά σημείο σύγκλισης

$$S_N(f)(x) \to f(x)$$

είναι ο λεγόμενος πυρήνας του Dirichlet τάξης $N$, το τριγωνομετρικό πολυώνυμο δηλ. που ορίζεται ως

$$D_N(x) = \sum_{k=-N}^N e^{ikx}.$$ (4.13)

Δεν είναι δύσκολο να βρει κανείς ένα κλειστό τύπο για το $D_N(x)$:

$$D_N(x) = \frac{\sin{(N+\frac12)x}}{\sin{\frac{x}{2}}}.$$ (4.14)

Για να δείξουμε την (4.14) χρησιμοποιούμε τον τύπο για το άθροισμα της πεπερασμένης γεωμετρικής σειράς

$$1+z+z^2+\cdots+z^n = \frac{1-z^{n+1}}{1-z}, (z \neq 1),$$ (4.15)

(με $e^{ix}$ στη θέση του $z$) και τον τύπο για τη διαφορά συνημιτόνων

$$\cos A - \cos B = 2 \sin\frac{A+B}{2} \sin\frac{B-A}{2}.$$ (4.16)

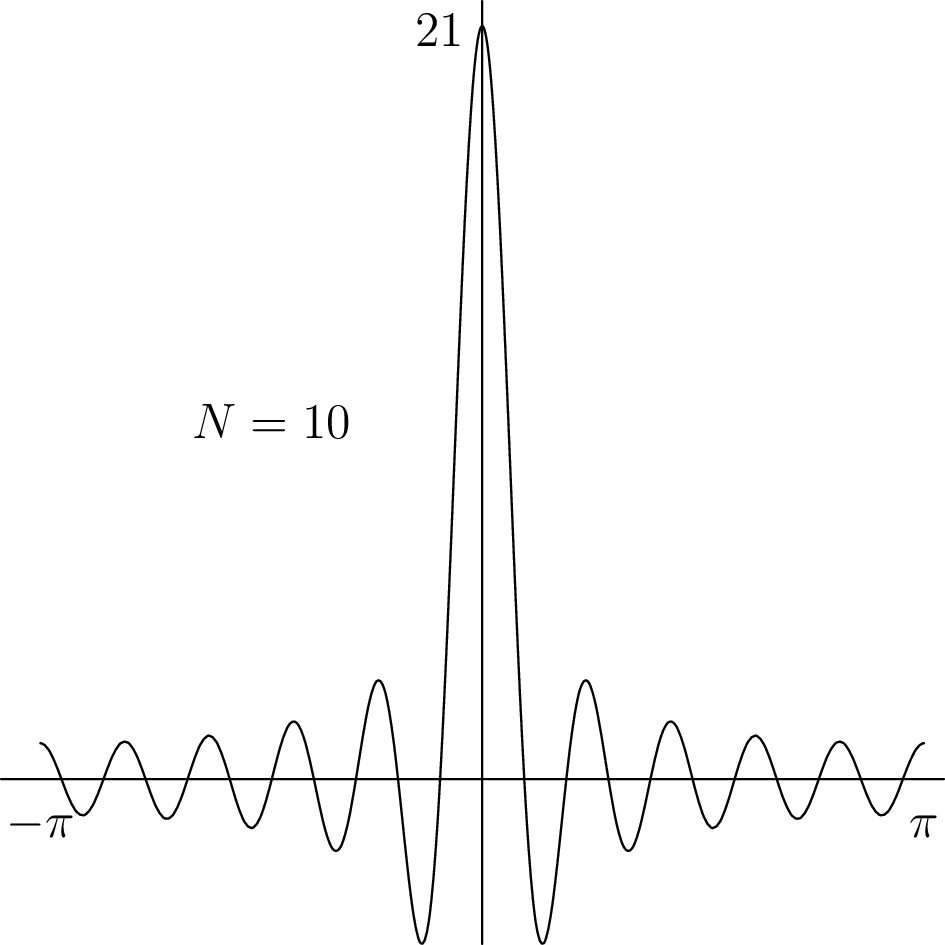
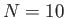
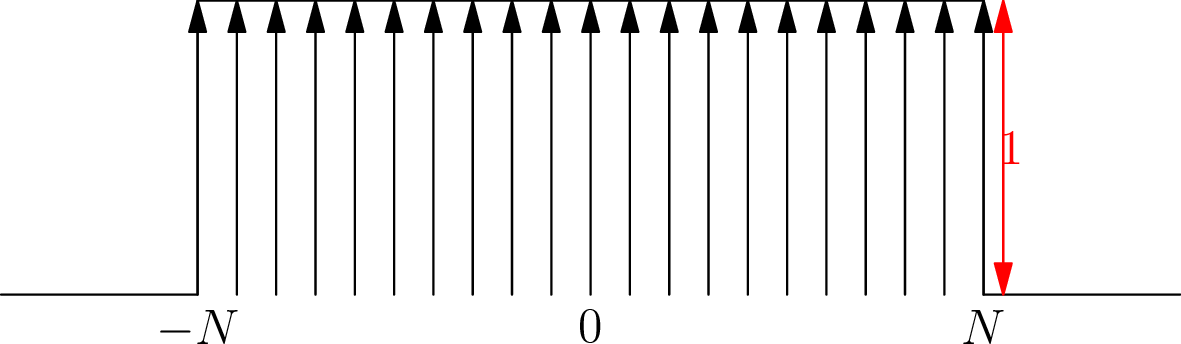
Σχήμα 4.3: Ο πυρήνας του Dirichlet για $N=10$

Σχήμα 4.4: Οι συντελεστές Fourier του πυρήνα του Dirichlet $D_N(x)$ για $N=10$

Άσκηση 4.4   Αποδείξτε τις (4.15) και (4.16).

Άσκηση 4.5   Κάντε τις πράξεις μόνοι σας για εξάσκηση και αποδείξτε την (4.14). Θυμηθείτε ότι μια εν γένει καλή στρατηγική όταν έχετε ένα κλάσμα με μιγαδικό παρανομαστή είναι να πολλαπλασιάζετε αριθμητή και παρανομαστή με το συζυγή του παρανομαστή ώστε να γίνεται πραγματικός ο παρανομαστής.

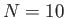
Ποια είναι όμως η σχέση του πυρήνα του Dirichlet με τα μερικά αθροίσματα της σειράς Fourier μιας ολοκληρώσιμης συνάρτησης $f$; Η απάντηση είναι εύκολη αν παρατηρήσουμε ότι οι δύο συναρτήσεις

$$S_N(f)(x) \kappa\alpha\iota f*D_N(x)$$

έχουν ίδιους συντελεστές Fourier.

Πραγματικά, όσον αφορά την $S_N(f)(x)$, η συνάρτηση αυτή είναι ένα τριγωνομετρικό πολυώνυμο βαθμού $N$ με συντελεστές Fourier ίδιους με τους συντελεστές Fourier της $f$ μέχρι και τάξης $N$, και οι υπόλοιποι συντελεστές Fourier μηδενίζονται.

Όσον αφορά τη συνάρτηση $f*D_N$ έπεται από το Πρόβλημα 4.3 ότι και αυτή είναι τριγωνομετρικό πολυώνυμο βαθμού $\le N$ και από το Θεώρημα 4.5 έπεται ότι έχει τους ίδιους συντελεστές Fourier με την $S_N(f)(x)$.

Αφού και οι δύο αυτές συναρτήσεις είναι παντού συνεχείς (ως τριγωνομετρικά πολυώνυμα) έπεται ότι είναι παντού ίδιες από το Θεώρημα Μοναδικότητας για συνεχείς συναρτήσεις (Θεώρημα 4.1).

Άσκηση 4.6   Αποδείξτε τη σχέση

$$S_N(f)(x) = f*D_N(x)$$

χωρίς χρήση του θεωρήματος Μοναδικότητας (θεώρημα 4.1).

Υπόδειξη: Υπολογίστε το δεξί μέλος και εμφανίστε τους συντελεστές Fourier της $f$.

Από την ταυτότητα

$$S_N(f)(x) = f*D_N(x)$$

βλέπουμε ότι η μελέτη των μερικών αθροισμάτων μιας σειράς Fourier είναι άρρηκτα συνδεδεμένη με τη μελέτη του πυρήνα Dirichlet και ειδικότερα με το μέγεθος του πυρήνα για μεγάλες τιμές του $N$.