5.2 Εφαρμογή: Η ισοπεριμετρική ανισότητα

Σε αυτή την παράγραφο θα δώσουμε μια απόδειξη που βασίζεται σε σειρές Fourier της «ισοπεριμετρικής ανισότητας»

$$A \le \frac{\ell^2}{4\pi}.$$ (5.6)

Εδώ $\ell$ είναι το μήκος μιας απλής κλειστής καμπύλης $\gamma$ στο επίπεδο και $A$ είναι το εμβαδό που περικλείει αυτή η καμπύλη. Ένας άλλος τρόπος να διατυπώσει κανείς την ισοπεριμετρική ανισότητα είναι να πει ότι από όλες τις απλές κλειστές καμπύλες του επιπέδου με δεδομένο μήκος ο κύκλος είναι αυτός που περικλείει το μεγαλύτερο εμβαδό. Με αυτό τον τρόπο είχε διατυπωθεί το πρόβλημα από την αρχαιότητα. Η λύση που θα περιγράψουμε δεν είναι η πρώτη χρονικά. Oφείλεται στον Hurwitz και δόθηκε το 1901, ενώ η πρώτη αυστηρή απόδειξη οφείλεται στον Steiner στα μέσα του 19ου αιώνα, ο οποίος χρησιμοποίησε αυτό που σήμερα ονομάζουμε «συμμετρικοποίηση Steiner».

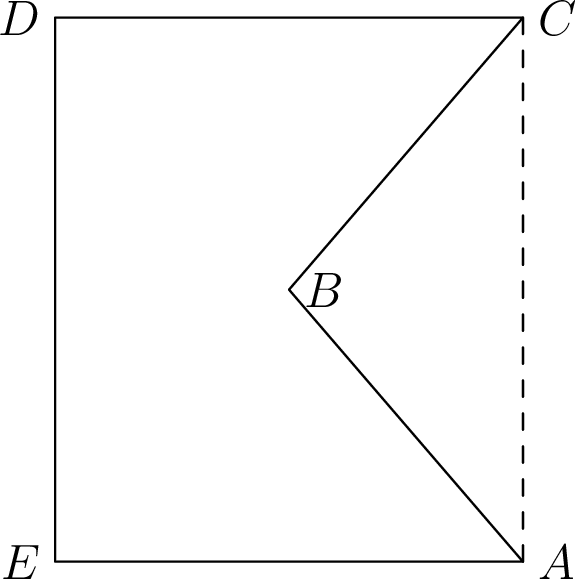
Σχήμα 5.2: Το $ABCDE$ είναι ένα μη κυρτό πολύγωνο

Άσκηση 5.10   Ένα πολύγωνο ονομάζεται κυρτό αν για κάθε πλευρά του η ευθεία που αυτή ορίζει χωρίζει το επίπεδο σε δύο ανοιχτά ημιεπίπεδα ένα από τα οποία δεν τέμνει το πολύγωνο.

Δείξτε ότι αν ένα πολύγωνο με μήκος $\ell$ δεν είναι κυρτό τότε υπάρχει ένα άλλο κυρτό πολύγωνο με το ίδιο μήκος και με μεγαλύτερο εμβαδό.

Υπόδειξη: Δείτε το παράδειγμα που δίνεται στο Σχήμα 5.2 και τροποποιήστε κατάλληλα το πολύγωνο $ABCDE$ χρησιμοποιώντας μια συμμετρία γύρω από τη διακεκομμένη γραμμή $AC$.

Η λύση αυτού του προβλήματος στη μέγιστη γενικότητα προϋποθέτει ότι έχουμε πρώτα ξεκαθαρίσει τις έννοιες του μήκους και του περικλειόμενου εμβαδού για μια καμπύλη στο επίπεδο. Αλλά, και μόνο το γεγονός ότι μια απλή (όχι αυτοτεμνόμενη δηλαδή) κλειστή καμπύλη, μια συνεχής δηλ. συνάρτηση

$$\gamma:[a,b] \to {\mathbb{R}}^2, \gamma(a)=\gamma(b),$$

χωρίζει το επίπεδο σε δύο συνεκτικά κομμάτια, το εσωτερικό της καμπύλης (το φραγμένο κομμάτι) και το εξωτερικό της, αποτελεί το Θεώρημα του Jordan το οποίο δεν είναι καθόλου απλό στην απόδειξή του, και πρόκειται να το πάρουμε ως δεδομένο. Επίσης το ποιες καμπύλες «έχουν μήκος» δεν είναι καθόλου φανερό γενικά, είναι όμως ξεκάθαρο αν υποθέσουμε, όπως θα κάνουμε από δω και πέρα, ότι η $\gamma$ είναι κατά τμήματα $C^\infty$. Σε αυτή την περίπτωση το μήκος $L$ της καμπύλης $\gamma(t) = (x(t), y(t))$ δίδεται από τον τύπο

$$\int_a^b \sqrt{x'(t)^2 + y'(t)^2} dt$$

όπως μαθαίνουμε στα μαθήματα Απειροστικού Λογισμού. Το διάνυσμα $\gamma'(t) = (x'(t), y'(t))$ είναι το διάνυσμα της ταχύτητας τη χρονική στιγμή $t$ όταν κινούμαστε πάνω στην καμπύλη με τρόπο ώστε η θέση μας στο χρόνο $t$ να είναι η $\gamma(t) = (x(t), y(t))$. Το μέτρο της ταχύτητας ${\left\vert{\gamma'(t)}\right\vert} = \sqrt{x'(t)^2 + y'(t)^2}$ είναι η ποσότητα που ολοκληρώνουμε ως προς το χρόνο για να βρούμε το μήκος που διανύσαμε.

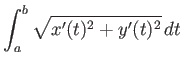
Ένα άλλο πολύ βασικό θεώρημα Απειροστικού Λογισμού το οποίο θα χρησιμοποιήσουμε είναι το θεώρημα του Green για τη μετατροπή διπλών ολοκληρωμάτων σε επικαμπύλια.

Θεώρημα 5.3 (Green)   Αν η κατά τμήματα $C^\infty$, απλή, κλειστή καμπύλη $\gamma$ περικλείει το χωρίο $\Omega \in {\mathbb{R}}^2$ και $P(x,y), Q(x,y)$ είναι $C^1$ συναρτήσεις ορισμένες σε ένα ανοιχτό σύνολο του επιπέδου που περιέχει το $\Omega$, τότε ισχύει

$$\iint_{\Omega} Q_x-P_y dx dy = \oint_\gamma Pdx+Qdy.$$

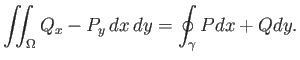
Οι ποσότητες $Q_x$ και $P_y$ είναι οι μερικές παράγωγοι των συναρτήσεων ως προς τις αντίστοιχες μεταβλητές και το ολοκήρωμα δεξιά είναι επικαμπύλιο ολοκλήρωμα το οποίο δίνεται από τον τύπο

$$\oint_\gamma Pdx+Qdy = \int_a^b [P(x(t),y(t))x'(t)+Q(x(t),y(t))y'(t)] dt.$$

Υποθέτουμε πάντα ότι η καμπύλη διανύεται κατά την θετική (αριστερόστροφη) φορά. Όταν κινούμαστε δηλ. πάνω στην καμπύλη $\gamma$ σύμφωνα με την παραμέτριση $(x(t), y(t))$, με το $t$ να αυξάνει, τότε έχουμε το χωρίο $\Omega$ στα αριστερά μας (δείτε το Σχήμα 5.3).

Με $Q(x,y)=x, P(x,y) = 0$ παίρνουμε από το Θεώρημα 5.3

$$A = \iint_\Omega 1 dx dy = \oint_\gamma x dy = \int_a^b x(t)y'(t) dt.$$

Ομοίως παίρνοντας $Q(x,y)=0, P(x,y)=-y$ παίρνουμε

$$A = \iint_\Omega 1 dx dy = -\oint_\gamma y dx = -\int_a^b y(t)x'(t) dt.$$

Συνδυάζοντας τα δύο παραπάνω παίρνουμε την πιο συμμετρική έκφραση για το εμβαδό

$$A = \frac{1}{2}\oint_\gamma x dy-y dx = \frac{1}{2} \int_a^b x(t)y'(t) - y(t)x'(t) dt.$$ (5.7)

Άσκηση 5.11   Δίδεται ένα πολυγωνικό χωρίο στο επίπεδο μέσω των συντεταγμένων των κορυφών του

$$(x_0, y_0), (x_1, y_1), \ldots, (x_{N-1}, y_{N-1}),$$

όπου η κορυφή $(x_j, y_j)$ έπεται της $(x_{j-1},y_{j-1})$ και προηγείται της $(x_{j+1}, y_{j+1})$ όταν διανύουμε αριστερόστροφα την πολυγωνική γραμμή που αποτελεί το σύνορο του χωρίου (τα $j\pm 1$ τα ερμηνεύουμε $\bmod N$).

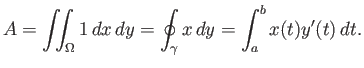
Δώστε ένα (όσο γίνεται πιο απλό) τύπο για το εμβαδό του χωρίου μέσω των αριθμών $x_j, y_j$, $j=0,1,\ldots,N-1$.

Υπόδειξη: Χρησιμοποιήστε το Θεώρημα 5.3 και υπολογίστε το επικαμπύλιο ολοκλήρωμα χρησιμοποιώντας μια απλή παραμέτριση για καθένα από τα ευθύγραμμα τμήματα $(x_j, y_j)$- $(x_{j+1}, y_{j+1})$ που απαρτίζουν το σύνορο.

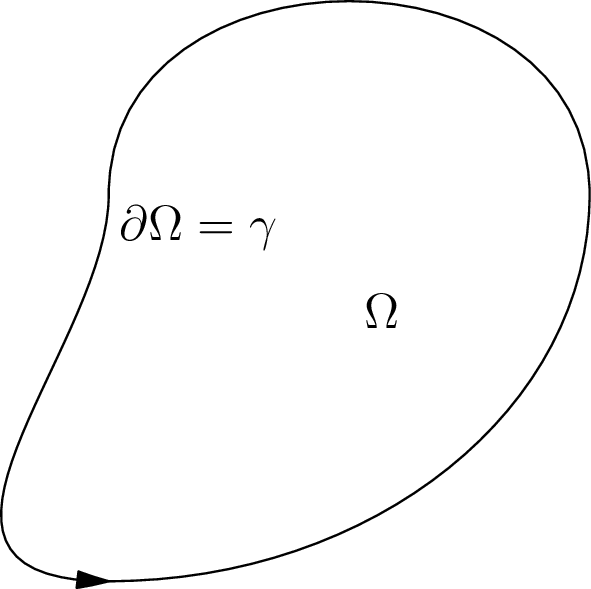
Σχήμα 5.3: Η καμπύλη $\gamma$ περικλείει το χωρίο $\Omega$, του οποίου είναι το σύνορο $\gamma=\partial\Omega$

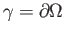
Τώρα πλέον έχουμε μια αναλυτική έκφραση για το μήκος της καμπύλης και μια για το εμβαδό που αυτή περικλείει. Κάνουμε τώρα την επιπλέον υπόθεση ότι χρονικό διάστημα κίνησης είναι το $[a,b]=[0, 2\pi]$ και ότι η ταχύτητα κίνησης έχει σταθερό μέτρο ίσο με $1$ καθόλη τη διάρκεια της κίνησης. Η δεύτερη αυτή υπόθεση μαζί με την πρώτη έχουν ως συνέπεια ότι το συνολικό μήκος της καμπυλης είναι

$$L = \int_0^{2\pi}{\left\vert{\gamma'(t)}\right\vert} dt = 2\pi.$$ (5.8)

Οι δύο αυτές υποθέσεις που κάνουμε δεν περιορίζουν την ισχύ της απόδειξης που θα ακολουθήσει. Ο λόγος είναι ότι ούτε το μήκος μιας καμπύλης ούτε το εμβαδό του χωρίου που αυτή περικλείει εξαρτώνται από το ποια είναι η παραμέτριση της καμπύλης, άρα είμαστε ελεύθεροι να επιλέξουμε την παραμέτριση που μας βολεύει.

Παίρνουμε λοιπόν την καμπύλη μας να έχει συνολικό μήκος $L=2\pi$ και την ταχύτητά μας να έχει μέτρο $1$ για κάθε $t \in [0,2\pi]$. Η ισοπεριμετρική ανισότητα παίρνει τώρα τη μορφή

$$A \le \pi.$$

Υπό αυτές τις (αβλαβείς) υποθέσεις οι συναρτήσεις $x(t), y(t)$ που καθορίζουν την καμπύλη μας είναι $2\pi$-περιοδικές συναρτήσεις που είναι τμηματικά $C^\infty$, και άρα είναι και στο $L^2({\mathbb{T}})$ όπως και οι παράγωγοί τους $x'(t), y'(t)$. Στις συναρτήσεις αυτές και στις παραγώγους τους αντιστοιχούν οι σειρές Fourier

$$x(t) \sim \sum_n \widehat{x}(n) e^{int}, y(t) \sim \sum_n \widehat{y}(n) e^{int},$$

και

$$x'(t) \sim \sum_n in\widehat{x}(n) e^{int}, y'(t) \sim \sum_n in\widehat{y}(n) e^{int}.$$

Η υπόθεση ${\left\vert{\gamma'(t)}\right\vert}=1$ συνεπάγεται ότι ${\left\vert{\gamma'(t)}\right\vert}^2 = {\left\vert{\gamma'(t)}\right\vert}$, οπότε

$$\int_0^{2\pi} x'(t)^2 + y'(t)^2 dt = 2\pi,$$

και χρησιμοποιώντας την ισομετρία του Parseval (Θεώρημα 5.2) παίρνουμε

$$\sum_n {\left\vert{n}\right\vert}^2 ({\left\vert{\widehat{x}(n)}\right\vert}^2 + {\left\vert{\widehat{y}(n)}\right\vert}^2) = 1.$$ (5.9)

Το ολοκλήρωμα (5.7), επίσης χρησιμοποιώντας την ισομετρία του Parseval, γράφεται

$$A = -i \pi \sum_n n(\widehat{x}(n)\overline{\widehat{y}(n)} - \widehat{y}(n)\overline{\widehat{x}(n)}).$$ (5.10)

Παρατηρούμε τώρα την ανισότητα

$${\left\vert{ \widehat{x}(n)\overline{\widehat{y}(n)} - \widehat{y... ...vert{\widehat{x}(n)}\right\vert}^2 + {\left\vert{\widehat{y}(n)}\right\vert}^2$$

και, χρησιμοποιώντας ότι ${\left\vert{n}\right\vert} \le {\left\vert{n}\right\vert}^2$, παίρνουμε

$$A \le \pi \sum_n {\left\vert{n}\right\vert}^2 ({\left\vert{\widehat{x}(n)}\right\vert}^2 + {\left\vert{\widehat{y}(n)}\right\vert}^2) \le \pi,$$

λόγω της (5.9), το οποίο συμπληρώνει την απόδειξη της ισοπεριμετρικής ανισότητας.

Άσκηση 5.12   Αποδείξτε ότι αν για μια κατά τμήματα $C^\infty$ καμπύλη ισχύει $A = \ell^2/(4\pi)$ τότε η καμπύλη είναι κύκλος.

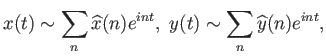
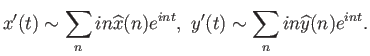
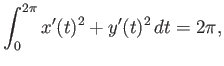
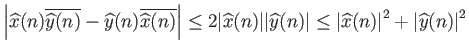
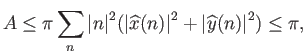
Υπόδειξη: Στην προηγούμενη απόδειξη της ισοπεριμετρικής ανισότητας δείτε που χρησιμοποιήσαμε κάποιες ανισότητες και τι συμπέρασμα βγαίνει αν αυτές ισχύουν ως ισότητες. Αρχίστε από την ανισότητα ${\left\vert{n}\right\vert} \le {\left\vert{n}\right\vert}^2$, $n\in{\mathbb{Z}}$.