2.4 Εσωτερικό γινόμενο και ορθογωνιότητα
Αν
![$ f, g \in C([0,2\pi])$](img442.png) (ο χώρος των συνεχών συναρτήσεων στο διάστημα
(ο χώρος των συνεχών συναρτήσεων στο διάστημα ![$ [0,2\pi]$](img394.png) )
ορίζουμε το εσωτερικό τους γινόμενο να είναι η ποσότητα
)
ορίζουμε το εσωτερικό τους γινόμενο να είναι η ποσότητα
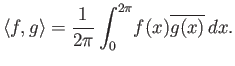
Παρατήρηση 2.3
Δεν είναι απαραίτητο οι δύο συναρτήσεις να είναι συνεχείς για να οριστεί το εσωτερικό τους γινόμενο.
Για παράδειγμα, και αυτή είναι μια περίπτωση που θα τη χρησιμοποιήσουμε πολύ,
μπορεί η μία συνάρτηση να είναι απλά ολοκληρώσιμη (στο
![$ L^1([0,2\pi])$](img448.png) δηλ.) και η άλλη να είναι φραγμένη.
Σε αυτή την περίπτωση το ολοκλήρωμα που δίνει το εσωτερικό γινόμενο ορίζεται αφού ο ολοκληρωτέος είναι ολοκληρώσιμη συνάρτηση.
δηλ.) και η άλλη να είναι φραγμένη.
Σε αυτή την περίπτωση το ολοκλήρωμα που δίνει το εσωτερικό γινόμενο ορίζεται αφού ο ολοκληρωτέος είναι ολοκληρώσιμη συνάρτηση.
Μια άλλη σημαντική περίπτωση είναι όταν και οι δύο συναρτήσεις είναι συναρτήσεις στο
![$ L^2([0,2\pi])$](img449.png) . Σε αυτή την περίπτωση εύκολα βλέπει κανείς ότι ο ολοκληρωτέος είναι ολοκληρώσιμη συνάρτηση και πάλι, από την ανισότητα Cauchy-Schwartz (Θεώρημα 1.7).
. Σε αυτή την περίπτωση εύκολα βλέπει κανείς ότι ο ολοκληρωτέος είναι ολοκληρώσιμη συνάρτηση και πάλι, από την ανισότητα Cauchy-Schwartz (Θεώρημα 1.7).
Τέλος, από την ανισότητα Hölder (Θεώρημα 1.6) βλέπει κανείς ότι το εσωτερικό γινόμενο μιας 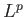 και μιας
και μιας 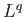 συνάρτησης με
συνάρτησης με
επίσης ορίζεται.
Στην περίπτωση που οι δύο συναρτήσεις  και
και 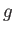 είναι από διαφορετικούς χώρους τότε η ποσότητα
είναι από διαφορετικούς χώρους τότε η ποσότητα
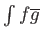 συνήθως
δεν ονομάζεται εσωτερικό γινόμενο αλλά «δράση» της μιας συνάρτησης πάνω στην άλλη.
συνήθως
δεν ονομάζεται εσωτερικό γινόμενο αλλά «δράση» της μιας συνάρτησης πάνω στην άλλη.
Άσκηση 2.8 (Αλγεβρικές ιδιότητες του εσωτερικού γινομένου)
Το εσωτερικό γινόμενο είναι ουσιαστικά γραμμικό στους δύο παράγοντες,
αν εξαιρέσουμε την μικρή επιπλοκή που δημιουργεί η ύπαρξη του μιγαδικού συζυγούς στο
δεύτερο παράγοντα.
Αποδείξτε τις παρακάτω ιδιότητες (
![$ f, g, h \in C([0,2\pi])$](img453.png) ):
(παραλλαγή ορισμού της
):
(παραλλαγή ορισμού της 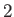 -νόρμας).
-νόρμας).
Δύο συναρτήσεις
![$ f, g \in C([0,2\pi])$](img442.png) ονομάζονται ορθογώνιες αν
ονομάζονται ορθογώνιες αν
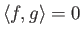 .
.
Άσκηση 2.9 (Πυθαγόρειο Θεώρημα)
Αν
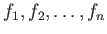 είναι ανά δύο ορθογώνιες τότε
είναι ανά δύο ορθογώνιες τότε
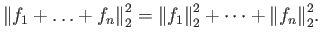 |
(2.4) |
Υπόδειξη: Χρησιμοποιήστε επαγωγή ως προς 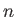 . Για
. Για  γράψτε
γράψτε
και χρησιμοποιήστε την ορθογωνιότητα.
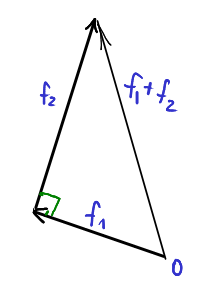
Σχήμα 2.3: Το άθροισμα δύο ορθογώνιων συναρτήσεων 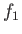 και
και 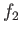 και το Πυθαγόρειο θεώρημα
και το Πυθαγόρειο θεώρημα
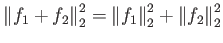
Είναι πολύ βασικό και πολύ χρήσιμο ότι οι μιγαδικές εκθετικές συναρτήσεις
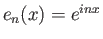 ,
,
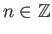 ,
είναι ανά δύο ορθογώνιες. Αν
,
είναι ανά δύο ορθογώνιες. Αν 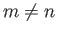 και θέτοντας
και θέτοντας
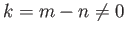 έχουμε
έχουμε
Ισχύει επίσης
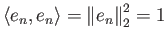 για
για
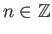 .
Γι' αυτό το λόγο οι συναρτήσεις
.
Γι' αυτό το λόγο οι συναρτήσεις 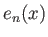 λέμε ότι αποτελούν ένα ορθοκανονικό σύστημα.
λέμε ότι αποτελούν ένα ορθοκανονικό σύστημα.
Άσκηση 2.10
(Ορθογωνιότητα των τριγωνομετρικών συναρτήσεων)
Αποδείξτε ότι οι συναρτήσεις
είναι ανά δύο ορθογώνιες. Αν τις διαιρέσουμε όλες (εκτός από τη σταθερή συνάρτηση) με 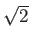 τότε εκτός από ορθογώνιο σύστημα συναρτήσεων είναι και ορθοκανονικό.
τότε εκτός από ορθογώνιο σύστημα συναρτήσεων είναι και ορθοκανονικό.
Υπόδειξη: Γενικά οι υπολογισμοί ολοκληρωμάτων με τις τριγωνομετρικές συναρτήσεις δεν είναι
από τις πιο απολαυστικές ασχολίες. Είναι πολύ καλύτερο να τις μετατρέψουμε σε μιγαδικές εκθετικές
συναρτήσεις και να κάνουμε εκεί τις πράξεις μας μια και οι εκθετικές συναρτήσεις είναι
φτιαγμένες για να πολλαπλασιάζονται.
Για παράδειγμα, για να δείξετε την ορθογωνιότητα των 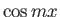 και
και 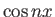 υπολογίστε το
ολοκλήρωμα αφού πρώτα γράψετε
υπολογίστε το
ολοκλήρωμα αφού πρώτα γράψετε
Θυμίζουμε τον ορισμό της γραμμικής ανεξαρτησίας διανυσμάτων
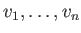 σε ένα
διανυσματικό χώρο
σε ένα
διανυσματικό χώρο 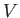 : θεωρούνται αυτά γραμμικώς ανεξάρτητα αν για κάθε επιλογή των συντελεστών
: θεωρούνται αυτά γραμμικώς ανεξάρτητα αν για κάθε επιλογή των συντελεστών
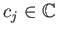 ισχύει η συνεπαγωγή
ισχύει η συνεπαγωγή
Οι διανυσματικοί χώροι που μας απασχολούν σε αυτό το μάθημα είναι κατά κανόνα χώροι συναρτήσεων
όπως ο
![$ C([0,2\pi])$](img489.png) με τον οποίο ασχολούμαστε εδώ. Είναι πολύ βασικό ότι η ορθογωνιότητα
συνεπάγεται τη γραμμική ανεξαρτησία. Αν οι μη μηδενικές
με τον οποίο ασχολούμαστε εδώ. Είναι πολύ βασικό ότι η ορθογωνιότητα
συνεπάγεται τη γραμμική ανεξαρτησία. Αν οι μη μηδενικές
![$ f_1, f_2, \ldots, f_n \in C([0,2\pi])$](img490.png) είναι ανά δύο
ορθογώνιες τότε, υποθέτοντας ότι έχουμε ένα μηδενιζόμενο γραμμικό συνδυασμό τους
είναι ανά δύο
ορθογώνιες τότε, υποθέτοντας ότι έχουμε ένα μηδενιζόμενο γραμμικό συνδυασμό τους
και παίρνοντας το εσωτερικό γινόμενο και τον δύο μελών με την 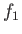 , έχουμε
, έχουμε
πράγμα που συνεπάγεται 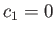 αφού
αφού
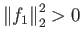 αρκεί η
αρκεί η 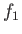 να μην είναι η μηδενική
συνάρτηση. Ομοίως αποδεικνύουμε ότι όλα τα
να μην είναι η μηδενική
συνάρτηση. Ομοίως αποδεικνύουμε ότι όλα τα 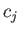 είναι μηδέν και άρα τα
είναι μηδέν και άρα τα
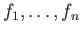 είναι γραμμικώς ανεξάρτητα.
είναι γραμμικώς ανεξάρτητα.
Άσκηση 2.11
(Η 2-νόρμα ενός τριγωνομετρικού πολυωνύμου)
Αν
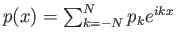 δείξτε ότι
δείξτε ότι
Υπόδειξη: Χρησιμοποιήστε την ορθογωνιότητα των εκθετικών συναρτήσεων και το Πυθαγόρειο Θεώρημα.
Άσκηση 2.12
Αποδείξτε ξανά τη μοναδικότητα των συντελεστών
των τριγωνομετρικών πολυωνύμων χωρίς τον πίνακα Vandermonde
(δείτε το Πρόβλημα 2.7).
Αν
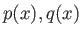 είναι δύο τριγωνομετρικά πολυώνυμα που ταυτίζονται σε ολόκληρο το
διάστημα
είναι δύο τριγωνομετρικά πολυώνυμα που ταυτίζονται σε ολόκληρο το
διάστημα ![$ [0,2\pi]$](img394.png) τότε έχουν τους ίδιους συντελεστές.
τότε έχουν τους ίδιους συντελεστές.
Υπόδειξη: Αποδείξτε ότι οι συντελεστές ενός τριγωνομετρικού πολυωνύμου δίδονται από τον τύπο
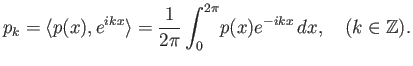 |
(2.5) |
Άσκηση 2.13
Αποδείξτε ότι το τριγωνομετρικό πολυώνυμο 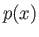 παίρνει μόνο πραγματικές τιμές αν και μόνο αν για κάθε
παίρνει μόνο πραγματικές τιμές αν και μόνο αν για κάθε
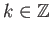 με
με
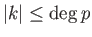 ισχύει
ισχύει
Παρατήρηση 2.4
Το δεξί μέλος της (2.5) μπορεί να εφαρμοστεί σε οποιαδήποτε συνεχή
συνάρτηση 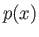 στο διάστημα
στο διάστημα ![$ [0,2\pi]$](img394.png) . Η ποσότητα αυτή ονομάζεται συντελεστής Fourier
. Η ποσότητα αυτή ονομάζεται συντελεστής Fourier
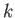 τάξης της συνάρτησης
τάξης της συνάρτησης 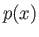 .
.
Έστω
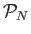 το σύνολο όλων των τριγωνομετρικών πολυωνύμων βαθμού
το σύνολο όλων των τριγωνομετρικών πολυωνύμων βαθμού 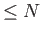
Αφού το άθροισμα δυο τέτοιων πολυωνύμων παραμένει στοιχείο του
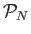 και
γινόμενο ενός μιγαδικού αριθμού με στοιχείο του
και
γινόμενο ενός μιγαδικού αριθμού με στοιχείο του
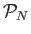 παραμένει στοιχείο του
παραμένει στοιχείο του
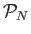 προκύπτει ότι το σύνολο αυτό είναι ένας μιγαδικός διανυσματικός χώρος.
Μάλιστα με την αντιστοίχιση
προκύπτει ότι το σύνολο αυτό είναι ένας μιγαδικός διανυσματικός χώρος.
Μάλιστα με την αντιστοίχιση
που είναι καλώς ορισμένη (μοναδικότητα των συντελεστών πολυωνύμου), γραμμική και αντιστρέψιμη
είναι φανερό πως ο χώρος
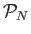 είναι ισομορφικός, ως γραμμικός χώρος, με το χώρο
είναι ισομορφικός, ως γραμμικός χώρος, με το χώρο
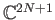 .
Μια βάση του χώρου
.
Μια βάση του χώρου
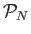 αποτελείται από τα
αποτελείται από τα 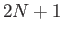 τριγωνομετρικά πολυώνυμα
τριγωνομετρικά πολυώνυμα
Αυτή μάλιστα η βάση έχουμε αποδείξει ότι είναι και ορθοκανονική, είναι δηλαδή τα στοιχεία της ανά δύο
ορθογώνια και κάθε στοιχείο της έχει 2-νόρμα ίση με 1.
Υπάρχει μια ακόμη ορθοκανονική βάση του
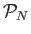 η οποία είναι χρήσιμη στις εφαρμογές, ειδικά όταν
πρόκειται για τριγωνομετρικά πολυώνυμα που παίρνουν πραγματικές τιμές.
η οποία είναι χρήσιμη στις εφαρμογές, ειδικά όταν
πρόκειται για τριγωνομετρικά πολυώνυμα που παίρνουν πραγματικές τιμές.
Θεώρημα 2.1
Οι συναρτήσεις
είναι μια ορθοκανονική βάση του
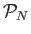 .
Επιπλέον, αν μια συνάρτηση
.
Επιπλέον, αν μια συνάρτηση
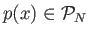 παίρνει πραγματικές τιμές τότε οι συντελεστές
της ως προς αυτή τη βάση είναι πραγματικοί.
παίρνει πραγματικές τιμές τότε οι συντελεστές
της ως προς αυτή τη βάση είναι πραγματικοί.
Από το Πρόβλημα 2.10 έχουμε την ορθογωνιότητα των συναρτήσεων ανά δύο.
Το ότι κάθε μια από αυτές έχει 2-νόρμα ίση με το 1 είναι ένας απλός υπολογισμός που στην περίπτωση
της σταθερής συνάρτησης είναι προφανής και σε όλες τις άλλες περιπτώσεις ανάγεται στον τύπο
Για να αποδείξουμε το δεύτερο μέρος του Θεωρήματος θα υπολογίσουμε ακριβώς τους συντελεστές
του πολυωνύμου
ως πρός τη βάση (2.6).
Έστω λοιπόν ότι
Εξισώνοντας (από τη μοναδικότητα των συντελεστών των τριγωνομετρικών πολυωνύμων) τους συντελεστές
των δύο μελών, και παρατηρώντας ότι οι συναρτήσεις 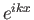 και
και 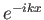 εμφανίζονται μόνο στον
εμφανίζονται μόνο στον
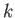 προσθετέο του αθροίσματος (2.8),
παίρνουμε ότι
προσθετέο του αθροίσματος (2.8),
παίρνουμε ότι 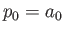 και για
και για
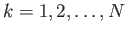 ότι
ότι
Κάνοντας πράξεις αυτό γράφεται
Από τη μοναδικότητα παίρνουμε τις δύο εξισώσεις
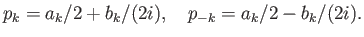 |
(2.9) |
Λύνοντας ως προς τις ποσότητες 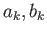 παίρνουμε
παίρνουμε
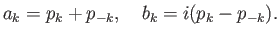 |
(2.10) |
Οι τύποι (2.9) και (2.10), μαζί με τον 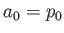 , μας λένε το πώς
γράφουμε μια συνάρτηση
, μας λένε το πώς
γράφουμε μια συνάρτηση 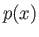 στην τριγωνομετρική βάση (2.6) αν την έχουμε
γραμμένη ως προς την εκθετική βάση και το αντίστροφο.
στην τριγωνομετρική βάση (2.6) αν την έχουμε
γραμμένη ως προς την εκθετική βάση και το αντίστροφο.
Τέλος, ας υποθέσουμε ότι η συνάρτηση 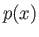 παίρνει πραγματικές τιμές. Έχουμε τότε
παίρνει πραγματικές τιμές. Έχουμε τότε
Όλα τα εσωτερικά γινόμενα που εμφανίζονται παραπάνω έχουν και τους δύο παράγοντες πραγματικές συναρτήσεις,
άρα είναι πραγματικά.
Mihalis Kolountzakis
2015-11-28
![]() (ο χώρος των συνεχών συναρτήσεων στο διάστημα
(ο χώρος των συνεχών συναρτήσεων στο διάστημα ![]() )
ορίζουμε το εσωτερικό τους γινόμενο να είναι η ποσότητα
)
ορίζουμε το εσωτερικό τους γινόμενο να είναι η ποσότητα
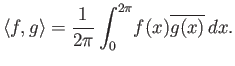
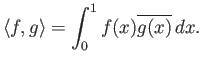
![]() . Σε αυτή την περίπτωση εύκολα βλέπει κανείς ότι ο ολοκληρωτέος είναι ολοκληρώσιμη συνάρτηση και πάλι, από την ανισότητα Cauchy-Schwartz (Θεώρημα 1.7).
. Σε αυτή την περίπτωση εύκολα βλέπει κανείς ότι ο ολοκληρωτέος είναι ολοκληρώσιμη συνάρτηση και πάλι, από την ανισότητα Cauchy-Schwartz (Θεώρημα 1.7).
![]() και μιας
και μιας ![]() συνάρτησης με
συνάρτησης με
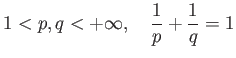
![]() και
και ![]() είναι από διαφορετικούς χώρους τότε η ποσότητα
είναι από διαφορετικούς χώρους τότε η ποσότητα
![]() συνήθως
δεν ονομάζεται εσωτερικό γινόμενο αλλά «δράση» της μιας συνάρτησης πάνω στην άλλη.
συνήθως
δεν ονομάζεται εσωτερικό γινόμενο αλλά «δράση» της μιας συνάρτησης πάνω στην άλλη.
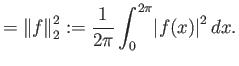
![]() ονομάζονται ορθογώνιες αν
ονομάζονται ορθογώνιες αν
![]() .
.
![]() . Για
. Για ![]() γράψτε
γράψτε

και
και το Πυθαγόρειο θεώρημα
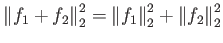
![]() ,
,
![]() ,
είναι ανά δύο ορθογώνιες. Αν
,
είναι ανά δύο ορθογώνιες. Αν ![]() και θέτοντας
και θέτοντας
![]() έχουμε
έχουμε
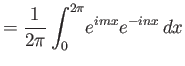
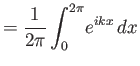
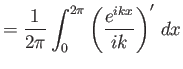
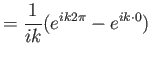
![]() και
και ![]() υπολογίστε το
ολοκλήρωμα αφού πρώτα γράψετε
υπολογίστε το
ολοκλήρωμα αφού πρώτα γράψετε
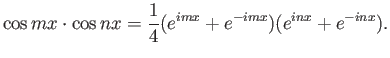
![]() σε ένα
διανυσματικό χώρο
σε ένα
διανυσματικό χώρο ![]() : θεωρούνται αυτά γραμμικώς ανεξάρτητα αν για κάθε επιλογή των συντελεστών
: θεωρούνται αυτά γραμμικώς ανεξάρτητα αν για κάθε επιλογή των συντελεστών
![]() ισχύει η συνεπαγωγή
ισχύει η συνεπαγωγή
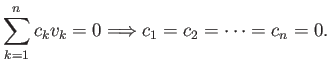
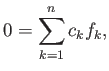
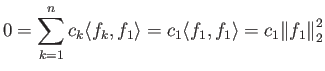
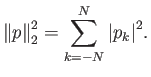
![]() το σύνολο όλων των τριγωνομετρικών πολυωνύμων βαθμού
το σύνολο όλων των τριγωνομετρικών πολυωνύμων βαθμού ![]()
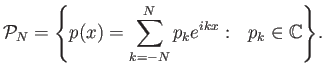
![]() η οποία είναι χρήσιμη στις εφαρμογές, ειδικά όταν
πρόκειται για τριγωνομετρικά πολυώνυμα που παίρνουν πραγματικές τιμές.
η οποία είναι χρήσιμη στις εφαρμογές, ειδικά όταν
πρόκειται για τριγωνομετρικά πολυώνυμα που παίρνουν πραγματικές τιμές.
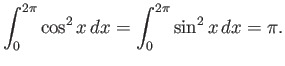
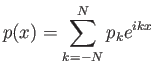
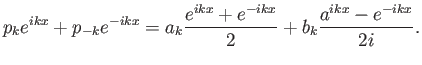
![]() , μας λένε το πώς
γράφουμε μια συνάρτηση
, μας λένε το πώς
γράφουμε μια συνάρτηση ![]() στην τριγωνομετρική βάση (2.6) αν την έχουμε
γραμμένη ως προς την εκθετική βάση και το αντίστροφο.
στην τριγωνομετρική βάση (2.6) αν την έχουμε
γραμμένη ως προς την εκθετική βάση και το αντίστροφο.
![]() παίρνει πραγματικές τιμές. Έχουμε τότε
παίρνει πραγματικές τιμές. Έχουμε τότε