Next: 4.2 Συνέλιξη στην ευθεία Up: 4. Αθροισιμότητα σειρών Fourier Previous: 4. Αθροισιμότητα σειρών Fourier Contents Index
Μπορούν δύο διαφορετικές ολοκληρώσιμες ![]() -περιοδικές συναρτήσεις να
έχουν τους ίδιους συντελεστές Fourier; Θα δούμε ότι
η απάντηση σε αυτό το ερώτημα είναι όχι, αν και θα χρειαστεί σε αυτή τη
φάση με επιβάλλουμε και κάποιες συνθήκες στις συναρτήσεις.
Κατ' αρχήν είναι φανερό ότι κάποια συνθήκη πρέπει να επιβληθεί αφού μπορούμε να πάρουμε
μια συνάρτηση
-περιοδικές συναρτήσεις να
έχουν τους ίδιους συντελεστές Fourier; Θα δούμε ότι
η απάντηση σε αυτό το ερώτημα είναι όχι, αν και θα χρειαστεί σε αυτή τη
φάση με επιβάλλουμε και κάποιες συνθήκες στις συναρτήσεις.
Κατ' αρχήν είναι φανερό ότι κάποια συνθήκη πρέπει να επιβληθεί αφού μπορούμε να πάρουμε
μια συνάρτηση ![]() και να την αλλάξουμε σε ένα σημείο (ή σε ένα πεπερασμένο πλήθος σημείων)
πράξη η οποία δεν αλλάζει κανένα συντελεστή Fourier, αλλάζει όμως τη συνάρτηση, καταστρέφοντας
τη μοναδικότητα.
και να την αλλάξουμε σε ένα σημείο (ή σε ένα πεπερασμένο πλήθος σημείων)
πράξη η οποία δεν αλλάζει κανένα συντελεστή Fourier, αλλάζει όμως τη συνάρτηση, καταστρέφοντας
τη μοναδικότητα.
Πριν δώσουμε την απόδειξη του Θεωρήματος 4.1 ας δώσουμε το σημαντικότερο πόρισμά του από το οποίο φαίνεται καθαρά γιατί το ονομάζουμε θεώρημα μοναδικότητας.
Το κεντρικό ερώτημα στο οποίο η Ανάλυση Fourier οφείλει την ύπαρξή της είναι το πότε
μια συνάρτηση ![]() μπορεί να «παρασταθεί» από τη σειρά Fourier της. Το επόμενο πόρισμα
των Θεωρημάτων 4.1 και 3.2 είναι το πρώτο αποτέλεσμα
που βλέπουμε που λέει ότι υπό κάποιες ευρείες συνθήκες αυτό όντως ισχύει.
μπορεί να «παρασταθεί» από τη σειρά Fourier της. Το επόμενο πόρισμα
των Θεωρημάτων 4.1 και 3.2 είναι το πρώτο αποτέλεσμα
που βλέπουμε που λέει ότι υπό κάποιες ευρείες συνθήκες αυτό όντως ισχύει.
Οι προϋποθέσεις του προηγούμενου Πορίσματος ισχύουν αν υποθέσουμε κάποια ομαλότητα για την ![]() .
.
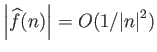 το οποίο
συνεπάγεται ότι
το οποίο
συνεπάγεται ότι
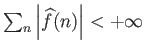 και το αποτέλεσμα προκύπτει από το Πόρισμα
4.2.
και το αποτέλεσμα προκύπτει από το Πόρισμα
4.2.
Απόδειξη του Θεωρήματος 4.1.
Μπορούμε κατ' αρχήν να υποθέσουμε ότι ![]() (αυτό θα απλουστεύσει λίγο τους συμβολισμούς στην απόδειξη που ακολουθεί) αντικαθιστώντας
τη συνάρτηση
(αυτό θα απλουστεύσει λίγο τους συμβολισμούς στην απόδειξη που ακολουθεί) αντικαθιστώντας
τη συνάρτηση ![]() με τη συνάρτηση
με τη συνάρτηση ![]() στην οποία τώρα το 0 είναι σημείο συνέχειας.
Επειδή
στην οποία τώρα το 0 είναι σημείο συνέχειας.
Επειδή
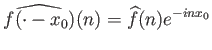
Αρνούμαστε τώρα το συμπέρασμά μας και υποθέτουμε ότι
![]() , και χωρίς βλάβη της
γενικότητας υποθέτουμε
, και χωρίς βλάβη της
γενικότητας υποθέτουμε ![]() . Λόγω της συνέχειας της
. Λόγω της συνέχειας της ![]() στο 0 προκύπτει ότι υπάρχει
στο 0 προκύπτει ότι υπάρχει ![]() τέτοιο ώστε
τέτοιο ώστε
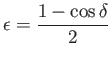
Σχήμα 4.1: Η συνάρτηση
Ορίζουμε τώρα το τριγωνομετρικό πολυώνυμο
![]() όπου
όπου ![]() ένας μεγάλος φυσικός αριθμός
που μένει ακόμη να προσδιορισθεί (αφού γινόμενο τριγωνομετρικών πολυωνύμων είναι επίσης τριγωνομετρικό πολυώνυμο προκύπτει ότι και το
ένας μεγάλος φυσικός αριθμός
που μένει ακόμη να προσδιορισθεί (αφού γινόμενο τριγωνομετρικών πολυωνύμων είναι επίσης τριγωνομετρικό πολυώνυμο προκύπτει ότι και το ![]() είναι τριγωνομετρικό πολυώνυμο).
Ο λόγος που υψώσαμε το
είναι τριγωνομετρικό πολυώνυμο).
Ο λόγος που υψώσαμε το ![]() σε μια μεγάλη δύναμη είναι ότι θέλουμε να το κάνουμε πολύ μικρό
στα δύο διαστήματα
σε μια μεγάλη δύναμη είναι ότι θέλουμε να το κάνουμε πολύ μικρό
στα δύο διαστήματα
![]() και
και
![]() , ή, με άλλα λόγια,
στο σύνολο
, ή, με άλλα λόγια,
στο σύνολο
![]() .
Αυτό το επιτυγχάνουμε επειδή ισχύει η (4.2):
.
Αυτό το επιτυγχάνουμε επειδή ισχύει η (4.2):
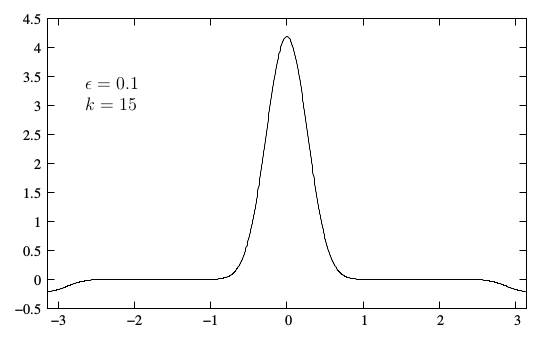
Σχήμα 4.2: Το πολυώνυμο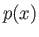
Σπάμε τώρα το εσωτερικό γινόμενο
![]() σε τρία κομμάτια:
σε τρία κομμάτια:
| 0 | 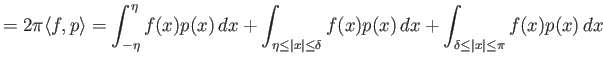 |
|
Κάνουμε τώρα την παρατήρηση ότι λόγω της (4.1) και επειδή ![]() στο
στο
![]() θα έχουμε ότι
θα έχουμε ότι ![]() .
Επίσης λόγω της (4.1) και της (4.3) ισχύει
.
Επίσης λόγω της (4.1) και της (4.3) ισχύει
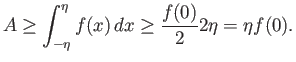
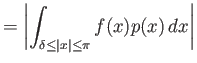 |
||
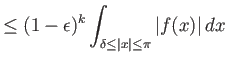 |
||
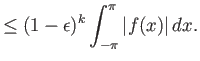 |
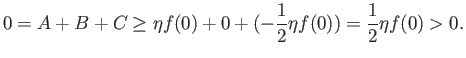
Mihalis Kolountzakis 2015-11-28