4.2 Συνέλιξη στην ευθεία

Ας είναι $R>0$ και $f,g:{\mathbb{R}}\to{\mathbb{C}}$ δύο συνεχείς συναρτήσεις που είναι 0 έξω από το διάστημα $[-R,R]$. Σε αυτή την περίπτωση η συνέλιξη των δύο συναρτήσεων

$$f*g(x) = \int_{-\infty}^\infty f(y)g(x-y) dy$$ (4.5)

είναι χωρίς αμφιβολία καλώς ορισμένη αφού ο ολοκληρωτέος $f(y)g(x-y)$ είναι, για κάθε σταθερό $x$, μια συνεχής συνάρτηση του $y$ που μηδενίζεται έξω από το διάστημα $[-R,R]$, και άρα το ολοκλήρωμα στον ορισμό (4.5) είναι το ίδιο με το $\int_{-R}^R f(y)g(x-y) dy$.

Εύκολα βλέπουμε σε αυτή την περίπτωση ότι η συνάρτηση $f*g(x)$ μηδενίζεται για ${\left\vert{x}\right\vert}>2R$ αφού σε αυτή την περίπτωση δεν γίνεται ταυτόχρονα να έχουμε $y \in [-R,R]$ και $x-y \in [-R,R]$, και άρα ο ολοκληρωτέος μηδενίζεται ταυτοτικά.

Με την αλλαγή μεταβλητής $u = x-y$ στο ολοκλήρωμα (4.5) βλέπουμε ότι η συνέλιξη είναι αντιμεταθετική πράξη

$$f*g(x) = g*f(x).$$

Η συνέχεια των $f$ και $g$ που ζητήσαμε εδώ να έχουμε είναι κάπως περιοριστική. Μήπως θα μπορούσαν οι $f$ και $g$ να είναι απλώς ολοκληρώσιμες; Το απλό παράδειγμα των ολοκληρωσίμων συναρτήσεων

$$f(x) = g(x) = \begin{cases}0 & \alpha\nu x=0 \eta {\left\v... ...}\right\vert}}} & \gamma\iota\alpha 0<{\left\vert{x}\right\vert}<1\end{cases}$$

μας δείχνει ότι τα πράγματα δεν είναι τόσο απλά αφού ο υπολογισμός του $f*g(0)$ καταλήγει στο ολοκλήρωμα της $1/{\left\vert{x}\right\vert}$ στο $(-1,1)$ το οποίο είναι $+\infty$.

Άσκηση 4.1   Δείξτε παρ' όλα αυτά ότι, για τις συναρτήσεις $f$ και $g$ που ορίσαμε παραπάνω ότι, η ποσότητα $f*g(x)$ είναι καλώς ορισμένη (η υπό ολοκλήρωση συνάρτηση είναι ολοκληρώσιμη) για κάθε $x \neq 0$.

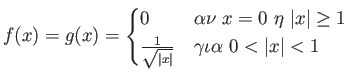
Αν θέλουμε το ολοκλήρωμα στην (4.5) πάντα να συγκλίνει μια φυσιολογική συνθήκη για τις $f$ και $g$ είναι να έχουμε την μια από αυτές ολοκληρώσιμη και την άλλη φραγμένη. Αν για παράδειγμα η $f$ είναι μια ολοκληρώσιμη συνάρτηση στο ${\mathbb{R}}$ (δεν υποθέτουμε ότι μηδενίζεται έξω από κάποιο διάστημα) και ${\left\vert{g(x)}\right\vert} \le M < +\infty$ για κάθε $x \in {\mathbb{R}}$ τότε εύκολα βλέπουμε ότι η $f*g$ ορίζεται παντού και είναι μια φραγμένη συνάρτηση

$${\left\vert{f*g(x)}\right\vert} = {\left\vert{\int_{-\infty}^\inf... ...\right\vert} dy \le M \int_{-\infty}^\infty{\left\vert{f(y)}\right\vert} dy$$

και το δεξί μέλος της ανισότητας είναι μια πεπερασμένη σταθερά αφού η $f$ έχει υποτεθεί ολοκληρώσιμη.

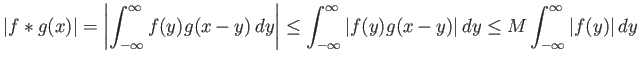
Αν όμως είμαστε διατεθειμένοι να αποδεχτούμε η συνάρτηση $f*g$ να ορίζεται σχεδόν παντού τότε αρκεί $f,g \in L^1({\mathbb{R}})$.

Θεώρημα 4.2   Αν $f,g \in L^1({\mathbb{R}})$ τότε σχεδόν για κάθε $x \in {\mathbb{R}}$ η συνάρτηση $F(x, y)=f(y)g(x-y)$ είναι ολοκληρώσιμη ως προς $y$, άρα η συνάρτηση $f*g(x)$ ορίζεται σχεδόν για κάθε $x \in {\mathbb{R}}$ και

$${\left\Vert{f*g}\right\Vert _{1}} \le {\left\Vert{f}\right\Vert _{1}} {\left\Vert{g}\right\Vert _{1}}.$$

Απόδειξη.
Έχουμε

$$\int\int{\left\vert{F(x, y)}\right\vert} dy dx = \int\int {\left\vert{f(y)}\right\vert} {\left\vert{g(x-y)}\right\vert} dx dy$$

$$= \int {\left\vert{f(y)}\right\vert}\int{\left\vert{g(x-y)}\right\vert} dx dy$$

$$= \int {\left\vert{f(y)}\right\vert} dy \int{\left\vert{g(x)}\right\vert} dx$$

$$= {\left\Vert{f}\right\Vert _{1}}{\left\Vert{g}\right\Vert _{1}}.$$

Για την εναλλαγή της σειράς ολοκλήρωσης χρησιμοποιήσαμε το θεώρημα του Fubini (Θεώρημα 1.4).

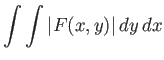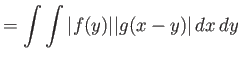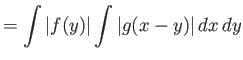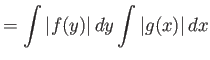Άρα η ποσότητα $\int F(x, y) dy$ είναι πεπερασμένη σχεδόν για κάθε $x \in {\mathbb{R}}$, όπως θέλαμε να αποδείξουμε.