Next: 1.3 Οι χώροι Up: 1. Μέτρο και ολοκλήρωμα Previous: 1.1 Μέτρο Lebesgue στο Contents Index
Το μεγάλο μειονέκτημα του ολοκληρώματος Riemann είναι ότι είναι πολύ ευαίσθητο σε μικρές αλλαγές
στη συνάρτηση. Πράγματι, το ολοκλήρωμα Riemann ορίζεται ως το όριο των λεγόμενων Riemann αθροισμάτων
τα οποία χρησιμοποιούν τις τιμές της υπό ολοκλήρωση συνάρτησης σε σημεία του διαστήματος. Μπορούμε εύκολα λοιπόν
να «καταστρέψουμε» αυτά τα Riemann αθροίσματα πειράζοντας τη συνάρτηση στα κατάλληλα σημεία, πράγμα που
σίγουρα δε θα έπρεπε να έχει επίπτωση στο εμβαδό του αθροίσματος κάτω από το γράφημα της συνάρτησης.
Αυτός είναι και ο λόγος που συναρτήσεις που είναι πολύ εύκολο να οριστούν δεν έχουν ολοκλήρωμα Riemann.
Το πιο απλό ίσως παράδειγμα είναι η χαρακτηριστική συνάρτηση των ρητών (όπως και αυτή των αρρήτων) της οποίας
όλα τα κάτω Riemann αθροίσματα είναι 0 και όλα τα άνω Riemann αθροίσματα είναι 1 (στο διάστημα ![]() για παράδειγμα), και άρα δεν είναι Riemann ολοκληρώσιμη.
για παράδειγμα), και άρα δεν είναι Riemann ολοκληρώσιμη.
Αν αλλάξουμε μια Riemann ολοκληρώσιμη συνάρτηση, για παράδειγμα την μηδενική, σε πεπερασμένα σημεία τότε η συνάρτηση θα παραμείνει Riemann ολοκληρώσιμη και δεν θα αλλάξει το ολοκλήρωμα Riemann της. Αν, όμως, την αλλάξουμε σε άπειρα σημεία και από την μηδενική δημιουργήσουμε την συγκεκριμένη χαρακτηριστική συνάρτηση των ρητών, τότε η συνάρτηση παύει να είναι Riemann ολοκληρώσιμη. Αυτό δεν ισχύει για το ολοκλήρωμα Lebesgue που θα περιγράψουμε στη συνέχεια. Και η μηδενική αλλά και η χαρακτηριστική συνάρτηση των ρητών είναι Lebesgue ολοκληρώσιμες και έχουν ολοκλήρωμα Lebesgue ίσο με 0.
Ιδού άλλη μία ένδειξη του πόσο πιο εύχρηστο
είναι το ολοκλήρωμα Lebesgue σε σχέση με τις τιμές της συνάρτησης σε μεμονωμένα σημεία.
Θα επιτρέπουμε από δω και πέρα στις συναρτήσεις να παίρνουν και τις τιμές ![]() ή
ή ![]() και αυτό δε θα μας εμποδίσει, ως επί το πλείστον, να βρίσκουμε το ολοκλήρωμά τους.
Ας είναι λοιπόν
και αυτό δε θα μας εμποδίσει, ως επί το πλείστον, να βρίσκουμε το ολοκλήρωμά τους.
Ας είναι λοιπόν
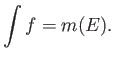
Σχήμα 1.4: Η χαρακτηριστική συνάρτηση του συνόλουκαι το ολοκληρωμά της (εμβαδό κάτω από το γράφημά της).
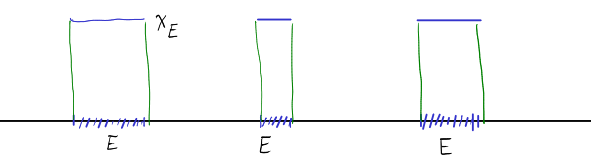
Αν επίσης θέλουμε το ολοκλήρωμα να είναι γραμμικό, να ισχύει δηλ.
Πρέπει φυσικά να είμαστε λίγο προσεκτικοί με την προσθαφαίρεση αριθμών του
![]() και να θυμόμαστε
ότι δεν προσθέτουμε ποτέ το
και να θυμόμαστε
ότι δεν προσθέτουμε ποτέ το ![]() με το
με το ![]() .
Μια άλλη διαφορά με την ανάλυση όπως την ξέραμε ως τώρα είναι ότι στον παραπάνω τύπο ένα γινόμενο του
τύπου
.
Μια άλλη διαφορά με την ανάλυση όπως την ξέραμε ως τώρα είναι ότι στον παραπάνω τύπο ένα γινόμενο του
τύπου
![]() είναι πάντα ίσο με 0.
είναι πάντα ίσο με 0.
Σχήμα 1.5: Η απλή συνάρτηση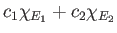
Υπόδειξη:
Το ότι η συνάρτηση, ας την πούμε ![]() , είναι απλή σημαίνει ότι το σύνολο των τιμών της,
, είναι απλή σημαίνει ότι το σύνολο των τιμών της, ![]() , είναι
ένα πεπερασμένο σύνολο
, είναι
ένα πεπερασμένο σύνολο
![]() .
Χρησιμοποιήστε τα σύνολα
.
Χρησιμοποιήστε τα σύνολα
![]() όπου
όπου
![]() .
.
Υπόδειξη: Η
![]() είναι απλή συνάρτηση.
είναι απλή συνάρτηση.
Ο ορισμός του ολοκληρώματος Lebesgue για μια οποιαδήποτε μη αρνητική συνάρτηση
![]() γίνεται χρησιμοποιώντας όλες τις μη αρνητικές απλές συναρτήσεις που είναι κάτω από την
γίνεται χρησιμοποιώντας όλες τις μη αρνητικές απλές συναρτήσεις που είναι κάτω από την ![]() (Σχήμα 1.6):
(Σχήμα 1.6):
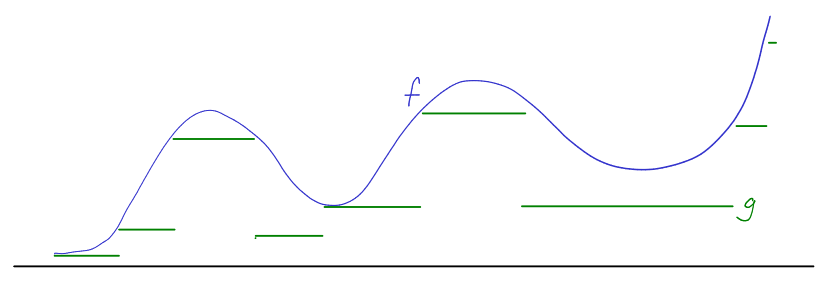
Σχήμα 1.6: Μια μη αρνητική συνάρτησηκαι μια απλή συνάρτηση
με
παντού
Τέλος, αν
![]() είναι οποιαδήποτε συνάρτηση μπορούμε να γράψουμε την
είναι οποιαδήποτε συνάρτηση μπορούμε να γράψουμε την ![]() ως διαφορά
δύο μη αρνητικών συναρτήσεων (Σχήμα 1.7)
ως διαφορά
δύο μη αρνητικών συναρτήσεων (Σχήμα 1.7)
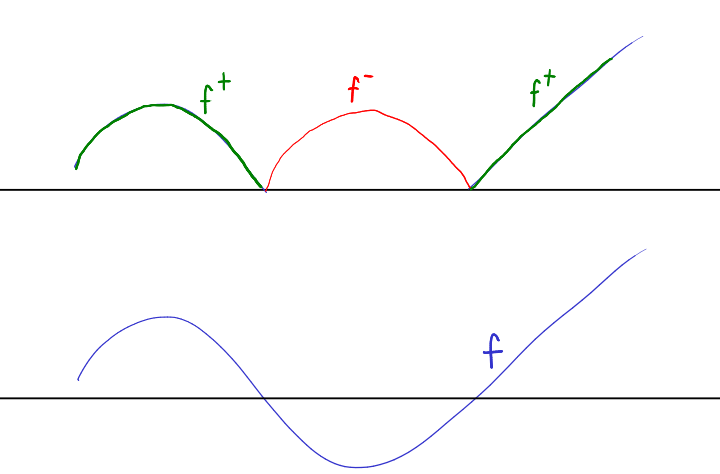
Σχήμα 1.7: Μια προσημασμένη συνάρτησημαζί με το θετικό και αρνητικό μέρος της
και
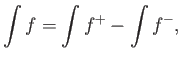
Αν τώρα η ![]() είναι μιγαδική συνάρτηση,
είναι μιγαδική συνάρτηση, ![]() , όπου
, όπου ![]() είναι πραγματικές συναρτήσεις,
ορίζουμε το ολοκλήρωμα της
είναι πραγματικές συναρτήσεις,
ορίζουμε το ολοκλήρωμα της ![]() (και πάλι λόγω της επιθυμητής γραμμικότητας) να είναι
(και πάλι λόγω της επιθυμητής γραμμικότητας) να είναι
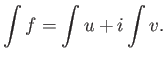
Μέχρι τώρα έχουμε ορίσει μόνο το ολοκλήρωμα μιας συνάρτησης πάνω σε όλη την πραγματική ευθεία. Πώς μπορούμε
να ορίσουμε το ολοκλήρωμα μιας συνάρτησης πάνω σε ένα υποσύνολο
![]() ; Πολύ απλά
; Πολύ απλά
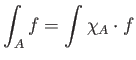
Αξίζει εδώ να αναφέρουμε ότι η κατάσταση με το ολοκλήρωμα Riemann είναι πολύ διαφορετική: μια συνάρτηση είναι Riemann ολοκληρώσιμη αν και μόνο αν το σύνολο των σημείων όπου είναι ασυνεχής έχει μέτρο 0.
Υπόδειξη: Αν
![]() μπορεί το μέτρο του συνόλου όπου
μπορεί το μέτρο του συνόλου όπου ![]() να είναι θετικό;
Παρατηρήστε ότι
να είναι θετικό;
Παρατηρήστε ότι
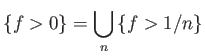
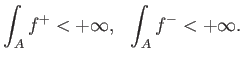
Γράφουμε ![]() για το χώρο όλων των συναρτήσεων
για το χώρο όλων των συναρτήσεων
![]() που είναι ολοκληρώσιμες στο
που είναι ολοκληρώσιμες στο ![]() .
.
Υπόδειξη: Συγκρίνετε την ![]() με την απλή συνάρτηση
με την απλή συνάρτηση ![]() που είναι 0 εκεί όπου η
που είναι 0 εκεί όπου η ![]() είναι πεπερασμένη
και
είναι πεπερασμένη
και ![]() όπου και η
όπου και η ![]() . Ποιο το
. Ποιο το ![]() και ποια η σχέση του με το
και ποια η σχέση του με το ![]() ;
;
Πόσο καλύτερη μπορεί να γίνει η ανισότητα αυτή αν γνωρίζετε όχι απλά ότι
![]() αλλά ότι
αλλά ότι
![]() ;
;
Μπορείτε να βάλετε πιο γενικές συναρτήσεις της ![]() στη θέση της εκθετικής εδώ;
στη θέση της εκθετικής εδώ;
Υπόδειξη: Αν
![]() τότε
τότε
![]() .
.
Επίσης ισχύει ο γνωστός μας τύπος για την αλλαγή μεταβλητής. Αν
![]() είναι συνεχώς παραγωγίσιμη και αύξουσα τότε
είναι συνεχώς παραγωγίσιμη και αύξουσα τότε
Το ολοκλήρωμα Lebesgue είναι πολύ εύχρηστο κυρίως λόγω των θεωρημάτων σύγκλισης, τα οποία μας λένε ουσιαστικά πότε μπορούμε να αλλάξουμε τη σειρά δύο οριακών διαδικασιών.
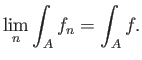
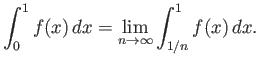
Υπόδειξη: Γράψτε
Χρησιμοποιήστε το αυτό για να υπολογίσετε τα ολοκληρώματα
![]() για όλες τις
τιμές του
για όλες τις
τιμές του
![]() . Για ποιες τιμές του
. Για ποιες τιμές του ![]() είναι η
είναι η ![]() στο
στο
![]() ;
Με παρόμοιο τρόπο εργαζόμενοι αλλά στο διάστημα
;
Με παρόμοιο τρόπο εργαζόμενοι αλλά στο διάστημα
![]() βρείτε για ποιες τιμές είναι
η συνάρτηση
βρείτε για ποιες τιμές είναι
η συνάρτηση ![]() στο
στο
![]() ;
;
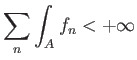
Υπόδειξη: Ποιο το ολοκλήρωμα της ![]() ; Χρησιμοποιήστε και το Πρόβλημα 1.12.
; Χρησιμοποιήστε και το Πρόβλημα 1.12.
![$\displaystyle \sum_n \chi_{[x_n, x_n+\ell_n]}(x)
$](img171.png)
Τι συμπεραίνετε για την ποσότητα ![]() σε πόσα από τα διαστήματα
σε πόσα από τα διαστήματα
![]() ανήκει
ο αριθμός
ανήκει
ο αριθμός
![]() ;
;
Υπόδειξη: Χρησιμοποιήστε το Πρόβλημα 1.15.
Το σημαντικότερο ίσως οριακό θεώρημα για το μέτρο Lebesgue είναι το επόμενο.
Λέμε ότι οι ![]() «κυριαρχούνται» από την
«κυριαρχούνται» από την ![]() .
.
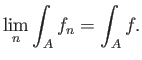
Σχήμα 1.8: Η συνάρτησηείναι μεγαλύτερη και από την
και από τις
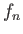
Υπόδειξη: Από την τριγωνική ανισότητα έχουμε
![]() .
.
Υπόδειξη:
Δε θα πρέπει φυσικά να ισχύουν οι υποθέσεις του Θεωρήματος 1.3
για να τα καταφέρετε.
Είναι καλή ιδέα να μη ψάχνετε για μια φόρμουλα για την ακολουθία ![]() αλλά να προσπαθήσετε
να σχεδιάσετε το πώς μοιάζουν τα γραφήματά τους και να θυμάστε ότι το ολοκλήρωμα είναι το εμβαδό κάτω από
το γράφημα.
Μια ιδέα είναι να προχωρήσετε όπως στο Σχήμα 1.9.
αλλά να προσπαθήσετε
να σχεδιάσετε το πώς μοιάζουν τα γραφήματά τους και να θυμάστε ότι το ολοκλήρωμα είναι το εμβαδό κάτω από
το γράφημα.
Μια ιδέα είναι να προχωρήσετε όπως στο Σχήμα 1.9.
Σχήμα 1.9: Ακολουθία συναρτήσεωνπου τείνει στο 0 κατά σημείο αλλά που τα ολοκληρώματά της τείνουν στο
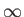
![$\displaystyle F(x) = \int_a^x f(t) dt (x \in [a,b])
$](img188.png)
Υπόδειξη: Αν ![]() δείξτε ότι η ποσότητα
δείξτε ότι η ποσότητα
![]() τείνει στο 0 χρησιμοποιώντας το
Θεώρημα 1.3 για τις συναρτήσεις
τείνει στο 0 χρησιμοποιώντας το
Θεώρημα 1.3 για τις συναρτήσεις
![]() οι οποίες
κυριαρχούνται από την
οι οποίες
κυριαρχούνται από την ![]() .
.
Υπόδειξη: Γράψτε την ![]() σαν άθροισμα των συναρτήσεων
σαν άθροισμα των συναρτήσεων
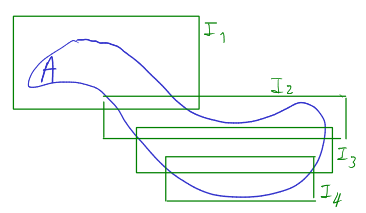
Όπως ορίζει κανείς το μέτρο ενός συνόλου στο
![]() έτσι ορίζει και το μέτρο ενός συνόλου στο
έτσι ορίζει και το μέτρο ενός συνόλου στο
![]() για
για
![]() . Υπάρχουν κάποιες λίγες διαφορές και επιπλέον τεχνικές δυσκολίες αλλά η ουσία είναι η ίδια.
Η στρατηγική που ακολουθείται για να οριστεί το μέτρο στο
. Υπάρχουν κάποιες λίγες διαφορές και επιπλέον τεχνικές δυσκολίες αλλά η ουσία είναι η ίδια.
Η στρατηγική που ακολουθείται για να οριστεί το μέτρο στο
![]() είναι και πάλι ότι πρώτα ορίζει κανείς
το μέτρο ενός διαστήματος (διάστημα στο
είναι και πάλι ότι πρώτα ορίζει κανείς
το μέτρο ενός διαστήματος (διάστημα στο
![]() είναι η ορολογία που χρησιμοποιείται για να περιγράψουμε ένα ορθογώνιο
με πλευρές παράλληλους με τους άξονες)
είναι η ορολογία που χρησιμοποιείται για να περιγράψουμε ένα ορθογώνιο
με πλευρές παράλληλους με τους άξονες)
Σχήμα 1.10: Κάλυψη συνόλουαπό τέσσερα διαστήματα
.
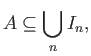
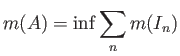
Για το μέτρο Lebesgue στο
![]() ισχύουν και πάλι όλες οι ιδιότητες του Θεωρήματος
1.1 με μόνη διαφορά στο 1.1.11 που ισχύει ως εξής:
ισχύουν και πάλι όλες οι ιδιότητες του Θεωρήματος
1.1 με μόνη διαφορά στο 1.1.11 που ισχύει ως εξής:
Το ολοκλήρωμα Lebesgue συναρτήσεων στο
![]() ορίζεται με την ίδια διαδικασία. Πρώτα ορίζουμε
το ολοκλήρωμα κάθε απλής συνάρτησης
ορίζεται με την ίδια διαδικασία. Πρώτα ορίζουμε
το ολοκλήρωμα κάθε απλής συνάρτησης
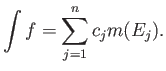
Έπειτα ορίζει κανείς το ολοκλήρωμα μη αρνητικών συναρτήσεων προσεγγίζοντας τις από κάτω από απλές συναρτήσεις
όπως ακριβώς στη μια διάσταση και τέλος ορίζει το ολοκλήρωμα προσημασμένων συναρτήσεων γράφοντάς τις
ως διαφορά δύο μη αρνητικών συναρτήσεων. Η ολοκληρωσιμότητα και οι χώροι ![]() ορίζονται ακριβώς
το ίδιο και το Θεώρημα Μονότονης Σύγκλισης 1.2
όπως και το Θεώρημα Κυριαρχημένης Σύγκλισης 1.3 ισχύουν και σε αυτή την περίπτωση.
ορίζονται ακριβώς
το ίδιο και το Θεώρημα Μονότονης Σύγκλισης 1.2
όπως και το Θεώρημα Κυριαρχημένης Σύγκλισης 1.3 ισχύουν και σε αυτή την περίπτωση.
Το θεώρημα του Fubini 1.4
μας επιτρέπει να υπολογίσουμε ένα ολοκλήρωμα (ένα διπλό ολοκλήρωμα όπως λέμε)
στο
![]() (ή σε μεγαλύτερη διάσταση
αλλά ας περιοριστούμε προς το παρόν στο
(ή σε μεγαλύτερη διάσταση
αλλά ας περιοριστούμε προς το παρόν στο
![]() ) ως ένα επαναλαμβανόμενο ολοκλήρωμα.
) ως ένα επαναλαμβανόμενο ολοκλήρωμα.
Συνέπεια της τελευταίας πρότασης είναι ότι αν ισχύει
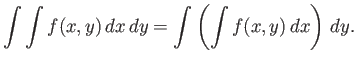
Υπόδειξη: Χρησιμοποιήστε το Θεώρημα Fubini 1.4 για μη αρνητικές συναρτήσεις και δείξτε ότι
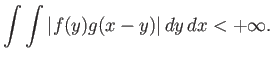
Υπόδειξη: Χρησιμοποιήστε τον τύπο (1.4) για μια κατάλληλη αλλαγή μεταβλητής και το Θεώρημα 1.4.
Mihalis Kolountzakis 2015-11-28