Subsections
Όταν μιλάμε για μια σειρά του τύπου
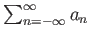 , με
, με
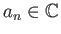 , μια σειρά δηλαδή
διπλής κατεύθυνσης, θα εννοούμε πάντα τη σύγκλισή της ως σύγκλιση των συμμετρικών μερικών αθροισμάτων
της
, μια σειρά δηλαδή
διπλής κατεύθυνσης, θα εννοούμε πάντα τη σύγκλισή της ως σύγκλιση των συμμετρικών μερικών αθροισμάτων
της
όταν
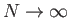 .
Όταν μιλάμε για τριγωνομετρική σειρά εννοούμε μια σειρά συναρτήσεων του τύπου
.
Όταν μιλάμε για τριγωνομετρική σειρά εννοούμε μια σειρά συναρτήσεων του τύπου
Οι σειρές Fourier ολοκληρώσιμων συναρτήσεων είναι λοιπόν ειδικές περιπτώσεις τριγωνομετρικών
σειρών, όπου οι συντελεστές της σειράς ταυτίζονται με τους συντελεστές Fourier κάποιας ολοκληρώσιμης
συνάρτησης. Το γενικό ερώτημα του πότε μια τριγωνομετρική σειρά είναι σειρά Fourier είναι ένα δύσκολο
ερώτημα που δεν έχει ουσιαστικά απαντηθεί. Η θεωρία των τριγωνομετρικών σειρών έχει αναπτυχθεί ιδιαίτερα
σε σχέση με ερωτήματα τύπου συνόλων μοναδικότητας
(sets of uniqueness),
ερωτήματα που έχουν συμβάλλει
πάρα πολύ στην ανάπτυξη της Μαθηματικής Ανάλυσης και όχι μόνο. Για παράδειγμα, η Θεωρία Συνόλων οφείλει
τη δημιουργία της στον G. Cantor
ο οποίος τη θεμελίωσε για να απαντήσει ερωτήματα
πάνω σε σύνολα μοναδικότητας τριγωνομετρικών σειρών.
Σε αυτό το μάθημα δε θα ασχοληθούμε σχεδόν καθόλου με τριγωνομετρικές σειρές που δεν είναι
σειρές Fourier.
Στην περίπτωση που οι συντελεστές μιας τριγωνομετρικής σειράς φθίνουν αρκετά γρήγορα η σειρά αυτή
αναμένεται να έχει κάποιες καλές ιδιότητες. Το ακόλουθο είναι ένα τυπικό (και εύκολο) παράδειγμα
ενός τέτοιου θεωρήματος (μικροί συντελεστές
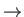 ομαλή συνάρτηση).
ομαλή συνάρτηση).
Θεώρημα 3.1
Αν
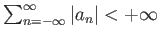 τότε η τριγωνομετρική σειρά
τότε η τριγωνομετρική σειρά
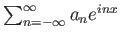 συγκλίνει ομοιόμορφα σε μια συνεχή
συγκλίνει ομοιόμορφα σε μια συνεχή  -περιοδική συνάρτηση.
-περιοδική συνάρτηση.
Απόδειξη.
Κατ' αρχήν η σειρά συγκλίνει σε μια συνάρτηση 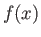 επειδή συγκλίνει απόλυτα, λόγω της υπόθεσής μας.
Το ότι η συνάρτηση
επειδή συγκλίνει απόλυτα, λόγω της υπόθεσής μας.
Το ότι η συνάρτηση 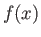 είναι
είναι  -περιοδική είναι προφανές. Ας είναι
-περιοδική είναι προφανές. Ας είναι 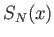 τα μερικά αθροίσματα.
Τότε
τα μερικά αθροίσματα.
Τότε
Όμως η ποσότητα 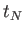 δεν εξαρτάται από το
δεν εξαρτάται από το 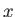 και
τείνει στο 0 αφού είναι η (διπλής κατεύθυνσης) ουρά μιας συγκλίνουσας σειράς.
Έχουμε συνεπώς δείξει ότι
και
τείνει στο 0 αφού είναι η (διπλής κατεύθυνσης) ουρά μιας συγκλίνουσας σειράς.
Έχουμε συνεπώς δείξει ότι
δηλαδή ότι η σύγκλιση είναι ομοιόμορφη σε όλο το
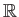 . Τέλος, επειδή οι
. Τέλος, επειδή οι 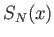 είναι συνεχείς συναρτήσεις
(αφού η καθεμία τους είναι πεπερασμένο άθροισμα συνεχών) έπεται από την ομοιόμορφη
σύγκλιση ότι και η
είναι συνεχείς συναρτήσεις
(αφού η καθεμία τους είναι πεπερασμένο άθροισμα συνεχών) έπεται από την ομοιόμορφη
σύγκλιση ότι και η 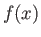 είναι συνεχής.
είναι συνεχής.
Έστω
 . Τότε, από το Θεώρημα 3.1, η τριγωνομετρική σειρά
. Τότε, από το Θεώρημα 3.1, η τριγωνομετρική σειρά
συγκλίνει ομοιόμορφα σε μια συνεχή συνάρτηση 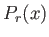 την οποία ονομάζουμε
πυρήνα Poisson
και η οποία είναι πάρα πολύ σημαντική στη θεωρία των αρμονικών και αναλυτικών συναρτήσεων.
Μπορούμε εύκολα να βρούμε ένα κλειστό τύπο για τον πυρήνα του Poisson
αν γράψουμε τη σειρά στη μορφή
την οποία ονομάζουμε
πυρήνα Poisson
και η οποία είναι πάρα πολύ σημαντική στη θεωρία των αρμονικών και αναλυτικών συναρτήσεων.
Μπορούμε εύκολα να βρούμε ένα κλειστό τύπο για τον πυρήνα του Poisson
αν γράψουμε τη σειρά στη μορφή
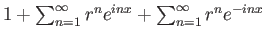 και εφαρμόσουμε τον τύπο για την άθροιση της άπειρης γεωμετρικής σειράς
και εφαρμόσουμε τον τύπο για την άθροιση της άπειρης γεωμετρικής σειράς
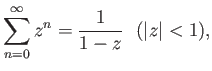 |
(3.4) |
ο οποίος είναι άμεση συνέπεια του (4.15).
Καταλήγουμε στον τύπο
Τι σχέση έχει η συνάρτηση που ορίζει η σειρά Fourier μιας συνάρτησης  με την ίδια την
με την ίδια την  ;
Ένα πρώτο βήμα για να το απαντήσουμε αυτό είναι το επόμενο Θεώρημα που αφορά και πάλι την περίπτωση
που οι συντελεστές Fourier της
;
Ένα πρώτο βήμα για να το απαντήσουμε αυτό είναι το επόμενο Θεώρημα που αφορά και πάλι την περίπτωση
που οι συντελεστές Fourier της  φθίνουν τόσο γρήγορα ώστε να είναι μια αθροίσιμη ακολουθία (το
άθροισμα των απολύτων τιμών τους να είναι πεπερασμένο).
φθίνουν τόσο γρήγορα ώστε να είναι μια αθροίσιμη ακολουθία (το
άθροισμα των απολύτων τιμών τους να είναι πεπερασμένο).
Θεώρημα 3.2
Αν  είναι ολοκληρώσιμη συνάρτηση και
είναι ολοκληρώσιμη συνάρτηση και
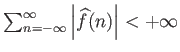 τότε
η σειρά Fourier της
τότε
η σειρά Fourier της  συγκλίνει ομοιόμορφα
σε μια συνάρτηση που έχει τους ίδιους συντελεστές Fourier με την
συγκλίνει ομοιόμορφα
σε μια συνάρτηση που έχει τους ίδιους συντελεστές Fourier με την  .
.
Απόδειξη.
Από το Θεώρημα 3.1 προκύπτει ότι η σειρά Fourier της  συγκλίνει ομοιόμορφα
σε μια συνεχή συνάρτηση
συγκλίνει ομοιόμορφα
σε μια συνεχή συνάρτηση  , ισχύει δηλ.
, ισχύει δηλ.
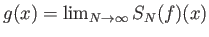 και το όριο είναι ομοιόμορφο.
Από την ομοιόμορφη σύγκλιση προκύπτει ότι για κάθε
και το όριο είναι ομοιόμορφο.
Από την ομοιόμορφη σύγκλιση προκύπτει ότι για κάθε
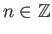
αφού
(από την ομοιόμορφη σύγκλιση).
Αλλά οι συναρτήσεις 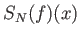 είναι τριγωνομετρικά πολυώνυμα άρα
είναι τριγωνομετρικά πολυώνυμα άρα
άρα, για 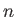 σταθερό, η ακολουθία
σταθερό, η ακολουθία
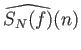 είναι τελικά σταθερή αν το
είναι τελικά σταθερή αν το 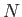 είναι αρκετά μεγάλο και συνεπώς
είναι αρκετά μεγάλο και συνεπώς
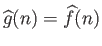 .
.
Mihalis Kolountzakis
2015-11-28
![]() , με
, με
![]() , μια σειρά δηλαδή
διπλής κατεύθυνσης, θα εννοούμε πάντα τη σύγκλισή της ως σύγκλιση των συμμετρικών μερικών αθροισμάτων
της
, μια σειρά δηλαδή
διπλής κατεύθυνσης, θα εννοούμε πάντα τη σύγκλισή της ως σύγκλιση των συμμετρικών μερικών αθροισμάτων
της
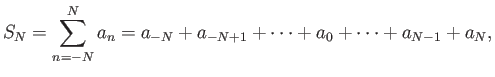
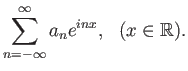
![]() ομαλή συνάρτηση).
ομαλή συνάρτηση).
![]() επειδή συγκλίνει απόλυτα, λόγω της υπόθεσής μας.
Το ότι η συνάρτηση
επειδή συγκλίνει απόλυτα, λόγω της υπόθεσής μας.
Το ότι η συνάρτηση ![]() είναι
είναι ![]() -περιοδική είναι προφανές. Ας είναι
-περιοδική είναι προφανές. Ας είναι ![]() τα μερικά αθροίσματα.
Τότε
τα μερικά αθροίσματα.
Τότε
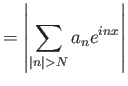
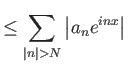
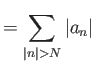
![]() . Τότε, από το Θεώρημα 3.1, η τριγωνομετρική σειρά
. Τότε, από το Θεώρημα 3.1, η τριγωνομετρική σειρά
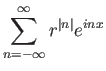
![]() με την ίδια την
με την ίδια την ![]() ;
Ένα πρώτο βήμα για να το απαντήσουμε αυτό είναι το επόμενο Θεώρημα που αφορά και πάλι την περίπτωση
που οι συντελεστές Fourier της
;
Ένα πρώτο βήμα για να το απαντήσουμε αυτό είναι το επόμενο Θεώρημα που αφορά και πάλι την περίπτωση
που οι συντελεστές Fourier της ![]() φθίνουν τόσο γρήγορα ώστε να είναι μια αθροίσιμη ακολουθία (το
άθροισμα των απολύτων τιμών τους να είναι πεπερασμένο).
φθίνουν τόσο γρήγορα ώστε να είναι μια αθροίσιμη ακολουθία (το
άθροισμα των απολύτων τιμών τους να είναι πεπερασμένο).
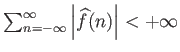 τότε
η σειρά Fourier της
τότε
η σειρά Fourier της ![]() συγκλίνει ομοιόμορφα
σε μια συνεχή συνάρτηση
συγκλίνει ομοιόμορφα
σε μια συνεχή συνάρτηση ![]() , ισχύει δηλ.
, ισχύει δηλ.
![]() και το όριο είναι ομοιόμορφο.
Από την ομοιόμορφη σύγκλιση προκύπτει ότι για κάθε
και το όριο είναι ομοιόμορφο.
Από την ομοιόμορφη σύγκλιση προκύπτει ότι για κάθε
![]()
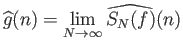
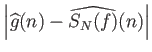
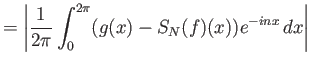
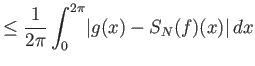
![$\displaystyle \le \sup_{x\in[0,2\pi]} {\left\vert{g(x)-S_N(f)(x)}\right\vert}$](img666.png)
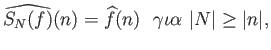
 είναι τελικά σταθερή αν το
είναι τελικά σταθερή αν το