3.5 Ασυμπτωτικές σχέσεις ανάμεσα σε ποσότητες και συμβολισμός

Οι συμβολισμοί $O(\cdot)$ και $o(\cdot)$ που ορίζονται παρακάτω είναι πάρα πολύ κοινοί στην Ανάλυση αλλά και στα Εφαρμοσμένα Μαθηματικά και η χρησιμότητά τους έγκειται ότι καταφέρνουν να δηλώσουν κάτι για την «τάξη μεγέθους» μιας ακολουθίας κρύβοντας ταυτόχρονα πληροφορία που δεν ενδιαφέρει και η παρουσία της οποίας θα έκανε αυτή τη δήλωση μεγέθους δυσανάγνωστη.

Ορισμός 3.2   Αν $a_n, b_n\ge 0$ τότε γράφουμε $a_n = O(b_n)$ αν υπάρχει μια θετική σταθερά $C$ και δείκτης $n_0$ ώστε να ισχύει

$$a_n \le C b_n, (\forall n\ge n_0).$$

Ομοίως γράφουμε $a_n = o(b_n)$ αν η ακολουθία $a_n/b_n$ τείνει στο 0. (Εδώ υποθέτουμε ότι η $b_n$ τελικά δεν παίρνει την τιμή 0.)

Άσκηση 3.17  

1. Τι σημαίνουν: $a_n = O(1)$, $a_n = o(1)$;
2. Δείξτε, χωρίς να υπολογίσετε το άθροισμα, ότι για κάθε $k=0,1,2,\ldots$ ισχύει
   $$1^k + 2^k + 3^k + \cdots n^k = O(n^{k+1}).$$

3. Δείξτε
   $$\sum_{k=1}^n \frac{1}{k} = O(\log n).$$

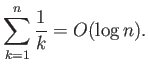
Οι συμβολισμοί αυτοί έχουν νόημα ακόμη και όταν η παράμετρος δεν είναι ένας ακέραιος που τείνει στο άπειρο ( $n \to \infty$ στον ορισμό 3.2) αλλά και μια πραγματική παράμετρος που συγκλίνει σε πεπερασμένο ή άπειρο όριο.

Ορισμός 3.3   Αν $x_0 \in {\mathbb{R}}\cup{\left\{{-\infty, +\infty}\right\}}$ και οι συναρτήσεις $f(x)\ge 0, g(x) > 0$ είναι ορισμένες σε μια γειτονιά του $x_0$ τότε λέμε $f(x) = O(g(x))$ και $f(x) = o(g(x))$ για $x \to x_0$ αν συνάρτηση $f(x)/g(x)$ είναι φραγμένη σε μια γειτονιά του $x_0$ ή συγκλίνει στο 0 για $x \to x_0$ αντίστοιχα.

Άσκηση 3.18   Δείξτε ότι ${\left\vert{\sin{x}}\right\vert} = O({\left\vert{x}\right\vert})$ για $x\to 0$ και επίσης ότι ${\left\vert{x}\right\vert} = O({\left\vert{\sin x}\right\vert})$ στο ίδιο όριο.

Καμιά φορά γράφουμε και $A = O(B)$ ή $A = o(B)$ και για προσημασμένες ποσότητες $A, B$ και εννοούμε ${\left\vert{A}\right\vert} = O({\left\vert{B}\right\vert})$ και ${\left\vert{A}\right\vert} = o({\left\vert{B}\right\vert})$ αντίστοιχα.