3.3 Απλές πράξεις πάνω σε μια συνάρτηση και πώς επηρεάζονται οι συντελεστές Fourier

Ας είναι $f:{\mathbb{R}}\to{\mathbb{C}}$ μια $2\pi$-περιοδική συνάρτηση που είναι ολοκληρώσιμη στο $[0,2\pi]$. Αν $\alpha\in{\mathbb{R}}$ τότε και η συνάρτηση

$$(\tau_\alpha f) (x) = f(x-\alpha)$$

είναι επίσης $2\pi$-περιοδική και ολοκληρώσιμη στο $[0,2\pi]$. Ένας εύκολος υπολογισμός (ορισμός ακολουθούμενος από μια αλλαγή μεταβλητής) μας δίνει την εξής σχέση ανάμεσα στους συντελεστές Fourier της $\tau_\alpha f$ και της $f$:

$$\widehat{\tau_\alpha f}(n) = e^{-in\alpha}\widehat{f}(n).$$ (3.6)

Άσκηση 3.9   Αποδείξτε τη σχέση (3.6).

Η απεικόνιση $f \to \tau_\alpha f$ ονομάζεται τελεστής μετατόπισης (παραδοσιακά στα μαθηματικά ονομάζουμε συναρτήσεις τις απεικονίσεις που στέλνουν «σημεία» σε αριθμούς ενώ χρησιμοποιούμε τη λέξη τελεστής για μια απεικόνιση που στέλνει συναρτήσεις, ή άλλα «πολύπλοκα» αντικείμενα, σε συναρτήσεις) και είναι μάλιστα γραμμικός τελεστής, ικανοποιεί δηλ. τη σχέση

$$\tau_\alpha (\lambda f + \mu g) = \lambda \tau_\alpha f + \mu \tau_\alpha g, (\lambda,\mu \in {\mathbb{C}}).$$

Για να είμαστε ακριβείς θα πρέπει να καθορίσουμε και σε ποιο χώρο ανήκουν οι διάφορες συναρτήσεις στις οποίες αναφερόμαστε. Αυτό δεν έχει και τόση μεγάλη σημασία όταν πρόκειται να μιλήσουμε για ιδιότητες συναρτήσεων που αποδεικνύονται κυρίως με αλγεβρικά ή φορμαλιστικά επιχειρήματα (κοινώς: με πράξεις) οπότε ας πούμε ότι όλες οι συναρτήσεις στις οποίες αναφερόμαστε ανήκουν στο χώρο $X$ των συναρτήσεων ${\mathbb{R}}\to{\mathbb{C}}$ που είναι $2\pi$-περιοδικές και συνεχείς.

Αν συμβολίσουμε και με $Y$ το χώρο όλων των μιγαδικών ακολουθιών (με δείκτες $n\in{\mathbb{Z}}$) τότε μπορούμε να δούμε την απεικόνιση

$$f \to (f(n))_{n \in {\mathbb{Z}}}$$

ως ένα τελεστή από το χώρο $X$ στο χώρο $Y$, τον οποίο συμβολίζουμε με ${\mathcal F}$:

$$({\mathcal F}f)(n) = \widehat{f}(n).$$

Ορίζουμε τέλος τον τελεστή $m_\alpha:Y\to Y$ να είναι ο «πολλαπλασιαστής»

$$(m_\alpha a)_n = e^{-in\alpha} a_n.$$

Και οι τρεις αυτοί τελεστές που ορίσαμε είναι γραμμικοί.

Έχοντας ορίσει τους τελεστές και τους χώρους που εμφανίζονται στην (3.6) μπορούμε τώρα να ξαναγράψουμε τη σχέση αυτή ως μια σχέση αντιμετάθεσης τελεστών

$${\mathcal F} \tau_\alpha = m_\alpha {\mathcal F}.$$ (3.7)

ή ως ένα αντιμεταθετικό διάγραμμα

$$\begin{CD}X @>{\mathcal F}» Y @VV{\tau_\alpha}V @VV{m_\alpha}V X @>{\mathcal F}» Y \end{CD}$$ (3.8)

Ο τρόπος που ερμηνεύουμε τη σχέση (3.7) καθώς και το διάγραμμα (3.8) είναι ότι το να εφαρμόσουμε σε μια συνάρτηση πρώτα τον τελεστή $\tau_\alpha$ και μετά τον τελεστή Fourier ${\mathcal F}$ (αριστερό μέλος της (3.7) ή κάτω-και-μετά-δεξιά κίνηση στο διάγραμμα (3.8)) είναι το ίδιο με πρώτα να εφαρμόσουμε τον τελεστή Fourier ${\mathcal F}$ και μετά τον πολλαπλασιαστή $m_\alpha$ (δεξί μέλος της (3.7) ή δεξιά-και-μετά-κάτω κίνηση στο διάγραμμα (3.8)).

Μπορούμε να ορίσουμε τους τελεστές μετατόπισης $\tau$ πάνω στο χώρο $Y$ και τους πολλαπλασιαστές $m$ πάνω στο χώρο $X$:

$$(\tau_k a)_n = a_{n-k},$$

για κάθε ακολουθία $a \in Y$ και

$$(m_k f)(x) = e^{-i k x}f(x),$$

για κάθε συνάρτηση $f \in X$.

Παρατηρήστε ότι για να έχουν νόημα αυτοί οι τελεστές πρέπει η παράμετρος της μετατόπισης να είναι ακέραια και η συχνότητα του εκθετικού με το οποίο πολλαπλασιάζουμε να είναι επίσης ακέραια (ώστε να μη χαλάει η περιοδικότητα της συνάρτησης).

Άσκηση 3.10   Δείξτε ότι ${\mathcal F} m_k = \tau_{-k} {\mathcal F}$ αφού πρώτα γράψετε αυτή την ισότητα τελεστών σε μορφή παρόμοια με την σχέση (3.6).

Δύο άλλοι γραμμικοί τελεστές που είναι ιδιαίτερα χρήσιμοι, και οι οποίοι επίσης ορίζονται και πάνω σε συναρτήσεις και πάνω σε ακολουθίες (στους χώρους $X$ και $Y$ δηλαδή) είναι οι τελεστές της ανάκλασης $A$ και συζυγίας $C$:

$$(A f)(x) = f(-x), (A a)_n = a_{-n},$$

για $f \in X, a \in Y$, και

$$(C f)(x) = \overline{f(x)}, (C a)_n = \overline{a_n},$$

για $f \in X, a \in Y$.

Άσκηση 3.11   Δείξτε τις ισότητες

$${\mathcal F} A = A {\mathcal F} \kappa\alpha\iota {\mathcal F}C = C A {\mathcal F},$$

αφού πρώτα τις γράψετε στη μορφή (3.6).

Άσκηση 3.12   Αν $f$ είναι άρτια συνάρτηση ( $f(-x)=f(x)$) δείξτε ότι η σειρά Fourier της $f$ μπορεί να γραφεί ως σειρά συνημιτόνων $a_0+\sum_{n=1}^\infty a_n \cos{nx}$. Ποια η σχέση των $a_n$ με τους συντελεστές Fourier της $f$;

Ομοίως αν η $f$ είναι περιττή ( $f(-x) =-f(x)$) δείξτε ότι η σειρά Fourier της $f$ μπορεί να γραφεί ως σειρά συνημιτόνων $\sum_{n=1}^\infty a_n \sin{nx}$. Ποια η σχέση των $a_n$ με τους συντελεστές Fourier της $f$;

Άσκηση 3.13   Αν η $f$ είναι $\pi$-περιοδική τότε $\widehat{f}(n) = 0$ για κάθε περιττό $n$.

Άσκηση 3.14   Δείξτε ότι αν η $f$ παίρνει πραγματικές τιμές τότε $\widehat{f}(-n) = \overline{\widehat{f}(n)}$.

Άσκηση 3.15   Αν $f$ είναι $2\pi$-περιοδική συνάρτηση και $k \in {\mathbb{N}}$ τι σχέση έχει το γράφημα της $g(x) = f(kx)$ με το γράφημα της $f$; Ποια η περίοδος της $g(x)$;

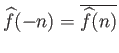Ποιο το ολοκλήρωμα $\int_0^{2\pi} g(x) dx$ σε σχέση με αυτό της $f$;

Ποιοι οι συντελεστές Fourier της $g(x)$ σε σχέση με τους συντελεσες Fourier της $f$;