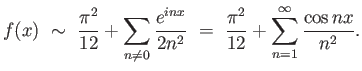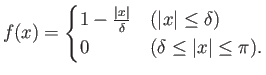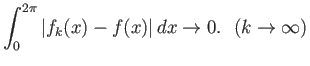3.1 Συντελεστές Fourier μιας ολοκληρώσιμης συνάρτησης και σειρά Fourier
Ας είναι τώρα
![$ f:[0,2\pi]\to{\mathbb{C}}$](img392.png) μια ολοκληρώσιμη συνάρτηση. Τότε
και η συνάρτηση
μια ολοκληρώσιμη συνάρτηση. Τότε
και η συνάρτηση
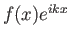 είναι ολοκληρώσιμη (αφού έχει το ίδιο μέτρο με την
είναι ολοκληρώσιμη (αφού έχει το ίδιο μέτρο με την  )
όποιο και να είναι το
)
όποιο και να είναι το
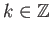 ,
και άρα μπορούμε να ορίσουμε το
,
και άρα μπορούμε να ορίσουμε το 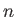 -οστό συντελεστή Fourier της
-οστό συντελεστή Fourier της  από τον τύπο
από τον τύπο
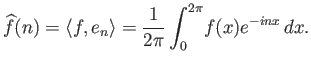 |
(3.1) |
Από την τριγωνική ανισότητα για το ολοκλήρωμα
προκύπτει άμεσα η ανισότητα
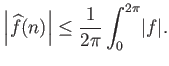 |
(3.2) |
Άσκηση 3.1
Αν 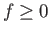 δείξτε ότι
δείξτε ότι
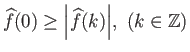 .
.
Για κάθε ολοκληρώσιμη συνάρτηση  μπορεί κανείς να δείξει ότι
μπορεί κανείς να δείξει ότι
για
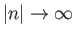 .
Αυτό είναι το λεγόμενο Λήμμα Riemann-Lebesgue (δείτε Πρόβλημα 1.38).
.
Αυτό είναι το λεγόμενο Λήμμα Riemann-Lebesgue (δείτε Πρόβλημα 1.38).
Έχοντας ορίσει τους συντελεστές Fourier της  ορίζουμε τώρα και τη σειρά Fourier
ως τη σειρά
ορίζουμε τώρα και τη σειρά Fourier
ως τη σειρά
Στη σειρά αυτή το 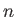 απειρίζεται και προς τα δεξιά (το συνηθισμένο) και προς τα αριστερά. Τι σημαίνει για μια
σειρά μιγαδικών αριθμών
απειρίζεται και προς τα δεξιά (το συνηθισμένο) και προς τα αριστερά. Τι σημαίνει για μια
σειρά μιγαδικών αριθμών
ότι το άθροισμά της είναι ο αριθμός
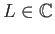 ;
Πολύ απλά ότι το
;
Πολύ απλά ότι το 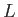 είναι το όριο των συμμετρικών μερικών αθροισμάτων της σειράς
είναι το όριο των συμμετρικών μερικών αθροισμάτων της σειράς
Για να υποδηλώσουμε ότι μια σειρά είναι η σειρά Fourier της  γράφουμε συνήθως
γράφουμε συνήθως
Δε χρησιμοποιούμε το σύμβολο  ακριβώς για να τονίσουμε ότι κατ' αρχήν δεν κάνουμε κανένα
ισχυρισμό όσον αφορά τη σύγκλιση της σειράς και μάλιστα στην
ακριβώς για να τονίσουμε ότι κατ' αρχήν δεν κάνουμε κανένα
ισχυρισμό όσον αφορά τη σύγκλιση της σειράς και μάλιστα στην 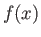 .
Το μεγαλύτερο μέρος της κλασικής Αρμονικής Ανάλυσης αφορά ακριβώς το να ξεκαθαρίσουμε υπό ποιες
συνθήκες (για την
.
Το μεγαλύτερο μέρος της κλασικής Αρμονικής Ανάλυσης αφορά ακριβώς το να ξεκαθαρίσουμε υπό ποιες
συνθήκες (για την  ) ισχύει μια τέτοια σύγκλιση ή σύγκλιση κάποιου άλλου είδους (π.χ. ομοιόμορφη
σύγκλιση των μερικών αθροισμάτων της σειράς Fourier).
) ισχύει μια τέτοια σύγκλιση ή σύγκλιση κάποιου άλλου είδους (π.χ. ομοιόμορφη
σύγκλιση των μερικών αθροισμάτων της σειράς Fourier).
Τα συμμετρικά μερικά αθροίσματα της σειράς Fourier της  όμως είναι τριγ. πολυώνυμα και άρα είναι
ταυτόχρονα και συναρτήσεις (δεν τίθεται εδώ θέμα σύγκλισης):
όμως είναι τριγ. πολυώνυμα και άρα είναι
ταυτόχρονα και συναρτήσεις (δεν τίθεται εδώ θέμα σύγκλισης):
(Προσέξτε ότι το όνομα της συνάρτησης είναι 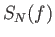 και
και 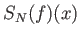 είναι η τιμή της συνάρτησης
αυτής στο
είναι η τιμή της συνάρτησης
αυτής στο 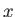 . Σε άλλα βιβλία μπορεί να δείτε αντί για τον παραπάνω συμβολισμό να χρησιμοποιείται το
. Σε άλλα βιβλία μπορεί να δείτε αντί για τον παραπάνω συμβολισμό να χρησιμοποιείται το
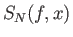 ή και κάτι σαν
ή και κάτι σαν 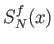 .)
.)
Ένα κεντρικό πρόβλημα της Αρμονικής Ανάλυσης είναι λοιπόν το κατά πόσο τα μερικά αθροίσματα 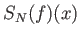 συγκλίνουν στη συνάρτηση
συγκλίνουν στη συνάρτηση 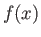 όταν
όταν
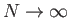 και με ποια έννοια συγκλίνουν (κατά σημείο, ομοιόμορφα,
σε κάποια ολοκληρωτική νόρμα όπως θα δούμε αργότερα).
και με ποια έννοια συγκλίνουν (κατά σημείο, ομοιόμορφα,
σε κάποια ολοκληρωτική νόρμα όπως θα δούμε αργότερα).
Άσκηση 3.2
Ποιοι οι συντελεστές Fourier της συνάρτησης 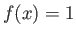 ;
;
Άσκηση 3.4
Η συνάρτηση
![$ f:[0,2\pi]\to{\mathbb{C}}$](img392.png) δίνεται από τον τύπο
δίνεται από τον τύπο
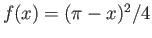 .
Δείξτε ότι η σειρά Fourier της
.
Δείξτε ότι η σειρά Fourier της  είναι η
είναι η
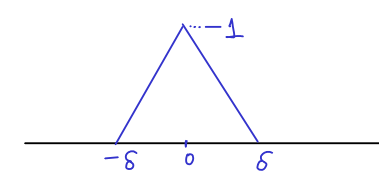
Σχήμα 3.1: Η συνάρτηση του προβλήματος 3.5
Άσκηση 3.5
Αν
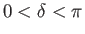 υπολογίστε τους συντελεστές Fourier της συνάρτησης
υπολογίστε τους συντελεστές Fourier της συνάρτησης
![$ f:[-\pi,\pi]\to{\mathbb{R}}$](img625.png) με τριγωνικό γράφημα που δίνεται από τον τύπο
με τριγωνικό γράφημα που δίνεται από τον τύπο
Άσκηση 3.6
Αν
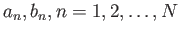 είναι μιγαδικοί αριθμοί και
είναι μιγαδικοί αριθμοί και
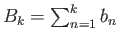 δείξτε τον πολύ χρήσιμο τύπο της άθροισης κατά μέρη (που είναι το ανάλογο για αθροίσματα
του τύπου της ολοκλήρωσης κατά μέρη)
δείξτε τον πολύ χρήσιμο τύπο της άθροισης κατά μέρη (που είναι το ανάλογο για αθροίσματα
του τύπου της ολοκλήρωσης κατά μέρη)
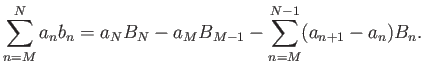 |
(3.3) |
Άσκηση 3.7
Αν 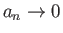 είναι φθίνουσα ακολουθία και τα μερικά αθροίσματα της σειράς
είναι φθίνουσα ακολουθία και τα μερικά αθροίσματα της σειράς
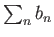 είναι φραγμένα
τότε η σειρά
είναι φραγμένα
τότε η σειρά
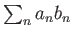 συγκλίνει.
συγκλίνει.
Υπόδειξη: Χρησιμοποιήστε το Πρόβλημα 3.6.
Άσκηση 3.8
Αν 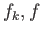 είναι
είναι  -περιοδικές και ολοκληρώσιμες στο
-περιοδικές και ολοκληρώσιμες στο ![$ [0,2\pi]$](img394.png) και
(σύγκλιση στο
και
(σύγκλιση στο
![$ L^1([0,2\pi])$](img448.png) )
)
τότε έχουμε
ομοιόμορφα για όλα τα
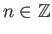 .
.
Mihalis Kolountzakis
2015-11-28
![]() μια ολοκληρώσιμη συνάρτηση. Τότε
και η συνάρτηση
μια ολοκληρώσιμη συνάρτηση. Τότε
και η συνάρτηση
![]() είναι ολοκληρώσιμη (αφού έχει το ίδιο μέτρο με την
είναι ολοκληρώσιμη (αφού έχει το ίδιο μέτρο με την ![]() )
όποιο και να είναι το
)
όποιο και να είναι το
![]() ,
και άρα μπορούμε να ορίσουμε το
,
και άρα μπορούμε να ορίσουμε το ![]() -οστό συντελεστή Fourier της
-οστό συντελεστή Fourier της ![]() από τον τύπο
από τον τύπο
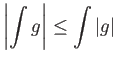
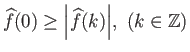 .
.![]() μπορεί κανείς να δείξει ότι
μπορεί κανείς να δείξει ότι
![]() ορίζουμε τώρα και τη σειρά Fourier
ως τη σειρά
ορίζουμε τώρα και τη σειρά Fourier
ως τη σειρά
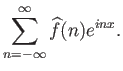
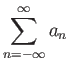
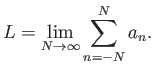
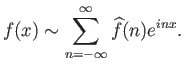
![]() όμως είναι τριγ. πολυώνυμα και άρα είναι
ταυτόχρονα και συναρτήσεις (δεν τίθεται εδώ θέμα σύγκλισης):
όμως είναι τριγ. πολυώνυμα και άρα είναι
ταυτόχρονα και συναρτήσεις (δεν τίθεται εδώ θέμα σύγκλισης):
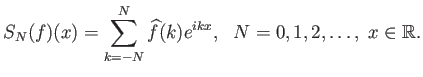
![]() συγκλίνουν στη συνάρτηση
συγκλίνουν στη συνάρτηση ![]() όταν
όταν
![]() και με ποια έννοια συγκλίνουν (κατά σημείο, ομοιόμορφα,
σε κάποια ολοκληρωτική νόρμα όπως θα δούμε αργότερα).
και με ποια έννοια συγκλίνουν (κατά σημείο, ομοιόμορφα,
σε κάποια ολοκληρωτική νόρμα όπως θα δούμε αργότερα).
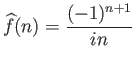
![]() στα άκρα του διαστήματος
στα άκρα του διαστήματος
![]() αφού όπως και να οριστεί εκεί τα ολοκληρώματα που ορίζουν τα
αφού όπως και να οριστεί εκεί τα ολοκληρώματα που ορίζουν τα
![]() δεν
επηρεάζονται.
δεν
επηρεάζονται.