5 Εξίσωση θερμότητας: Πεπερασμένες διαφορές 5.2 Πεπλεγμένη μέθοδος του Euler 5.4 Άλλες μέθοδοι και προβλήματα

5.3 Μέθοδος των Crank-Nicolson

Μια άλλη μέθοδος προκύπτει αν αντί για τις προσεγγίσεις $\delta^{+}_{k}$ ή $\delta^{-}_{k}$ της $u_{t}$ που θεωρήσαμε προηγουμένως, θεωρήσουμε τη $\delta^{c}_{k}$ . Όπως και πριν θα θέσουμε $U_{0}^{j}=U_{N+1}^{j}=0$ για $j=0,\dots,M$ , και $U_{i}^{0}=g(x_{i})$ και θα κατασκευάσουμε τώρα προσεγγίσεις $U_{i}^{j}$ , $i=1,\dots,N$ , $j=1,\dots,M$ , των τιμών $u(x_{i},t^{j})$ της ακριβούς λύσης του (5.1), μεγαλύτερης τάξης ακρίβειας.

Λόγω του Λήμματος 2.1 και της εξίσωσης (5.1) έχουμε για $x=1,\dots,N$ ,

\begin{split}\displaystyle\dfrac{u(x_{i},t^{j})-u(x_{i},t^{j-1})}{k}&% \displaystyle=u_{t}(x_{i},t^{j}-\frac{k}{2})+\hat{\eta}_{i}^{j}\\ &\displaystyle=u_{xx}(x_{i},t^{j}-\frac{k}{2})+\hat{\eta}_{i}^{j},\quad j=1,% \dots,M,\end{split}

(5.37)

όπου

|\hat{\eta}_{i}^{j}|\leq\dfrac{k^{2}}{6}\max_{t\in[0,T]}|u_{ttt}(x_{i},t)|

(5.38)

Επειδή τα σημεία $(x_{i},t^{j}-\frac{k}{2})$ δεν αποτελούν μέρος του διαμερισμού που έχουμε θεωρήσει, προσεγγίζουμε την $u_{xx}(x_{i},t^{j}-\frac{k}{2})$ , $i=1,\dots,N$ , $j=1,\dots,M$ , στην (5.37) με τον μέσο όρο της $u_{xx}$ στα $(x_{i},t^{j})$ και $(x_{i},t^{j-1})$ . Έτσι, είναι απλό να δούμε με τη βοήθεια αναπτυγμάτων Taylor ότι

u_{xx}(x_{i},t^{j}-\frac{k}{2})=\dfrac{1}{2}(u_{xx}(x_{i},t^{j})+u_{xx}(x_{i},% t^{j-1}))-\dfrac{k^{2}}{2}u_{xxtt}(x_{i},\xi^{j}),

(5.39)

με $\xi^{j}\in(t^{j-1},t^{j})$ . Επομένως, συνδυάζοντας αυτή τη σχέση με την (5.37), έχουμε για $j=1,\dots,M$ ,

\begin{split}\displaystyle\dfrac{u(x_{i},t^{j})-u(x_{i},t^{j-1})}{k}&% \displaystyle=\dfrac{1}{2}(u_{xx}(x_{i},t^{j})+u_{xx}(x_{i},t^{j-1}))+\bar{% \eta}_{i}^{j}+\hat{\eta}_{i}^{j},\end{split}

(5.40)

με

|\bar{\eta}_{i}^{j}|\leq\dfrac{k^{2}}{6}\max_{t\in[0,T]}|u_{xxtt}(x_{i},t)|.

(5.41)

Στη συνέχεια, για την προσέγγιση των $u_{xx}(x_{i},t^{j})$ , $j=1,\dots,M$ , στην (5.40) εφαρμόζουμε τη $\delta^{c}_{h,2}u(x_{i},t^{j})$ που θεωρήσαμε στην (2.8). Έτσι, αν υποθέσουμε ότι $\allowbreak\frac{\partial^{4}}{\partial x^{4}}u(x,t)\in C([a,b]\times[0,T])$ , λόγω της (2.9), η (5.40) γίνεται για $i=1,\dots,N,$ και $j=1,\dots,M,$

\begin{split}&\displaystyle\dfrac{u(x_{i},t^{j})-u(x_{i},t^{j-1})}{k}=\frac{1}% {2}\frac{u(x_{i+1},t^{j})-2u(x_{i},t^{j})+u(x_{i-1},t^{j})}{h^{2}}\\ &\displaystyle\qquad+\frac{1}{2}\frac{u(x_{i+1},t^{j-1})-2u(x_{i},t^{j-1})+u(x% _{i-1},t^{j-1})}{h^{2}}\\ &\displaystyle\qquad+\hat{\eta}_{i}^{j}+\bar{\eta}_{i}^{j}+\tilde{\eta}_{i}^{j% },\end{split}

(5.42)

όπου η $\tilde{\eta}_{i}^{j}$ φράσσεται όπως στην (5.7). Συνεπώς, για $\eta_{i}^{j}=\hat{\eta}_{i}^{j}+\bar{\eta}_{i}^{j}+\tilde{\eta}_{i}^{j}$ , η (5.42) δίνει για $i=1,\dots,N,$ και $j=1,\dots,M,$

\delta^{c}_{h}u(x_{i},t^{j}-\dfrac{k}{2})-\dfrac{1}{2}(\delta^{c}_{h,2}u(x_{i}% ,t^{j})+\delta^{c}_{h,2}u(x_{i},t^{j-1}))=\eta_{i}^{j},

(5.43)

και λόγω των (5.38), (5.41) και (5.7) εύκολα βλέπουμε ότι ισχύει το ακόλουθο λήμμα.

Λήμμα 5.3.

Έστω $u$ η λύση του (5.1) με $\frac{\partial^{4}}{\partial x^{4}}u,u_{tt},u_{ttxx}\in C([0,L]\times[0,T])$ . Τότε για την $\eta_{i}^{j}$ που δίνεται στην (5.43) έχουμε ότι υπάρχει σταθερά $C$ ανεξάρτητη των $k$ και $h$ , τέτοια ώστε

\max_{1\leq j\leq M}\max_{1\leq i\leq N}|\eta_{i}^{j}|\leq C(k^{2}+h^{2}).

(5.44)

Για να κατασκευάσουμε, λοιπόν, προσεγγίσεις $U_{i}^{j}$ των $u(x_{i},t^{j})$ , $i=1,\dots,N$ , $j=0,\dots,M$ , θεωρούμε την ακόλουθη μέθοδο

		$\displaystyle\begin{aligned}\displaystyle\dfrac{U_{i}^{j}-U_{i}^{j-1}}{k}=&% \displaystyle\dfrac{1}{2}\dfrac{U_{i+1}^{j}-2U_{i}^{j}+U_{i-1}^{j}}{h^{2}}+% \dfrac{1}{2}\dfrac{U_{i+1}^{j-1}-2U_{i}^{j-1}+U_{i-1}^{j-1}}{h^{2}},\\ &\displaystyle\text{ για}\quad i=1,\dots,N,\ j=1,\dots,M,\end{aligned}$		(5.45)
		$\displaystyle\left\{\begin{aligned}\displaystyle U_{0}^{j}&\displaystyle=U_{N+% 1}^{j}=0,\quad j=0,\dots,M,\\ \displaystyle U_{i}^{0}&\displaystyle=g(x_{i}),\quad i=1,\dots,N.\end{aligned}\right.$		(5.46)

Το τοπικό σφάλμα διακριτοποίησης $\eta_{i}^{j}$ της (5.45)–(5.46) δίνεται από την (5.43). Επίσης από το Λήμμα 5.3–(5.46) έχουμε ότι η $\eta_{i}^{j}$ τείνει στο μηδέν, καθώς $k$ και $h$ τείνουν στο μηδέν. Επομένως, η μέθοδος (5.45)–(5.46) είναι συνεπής.

Αν συμβολίσουμε και πάλι με $\lambda$ τον λόγο $\dfrac{k}{h^{2}}$ , η (5.45) γράφεται ως

-\dfrac{1}{2}\lambda U_{i+1}^{j}+(1+\lambda)U_{i}^{j}-\dfrac{1}{2}\lambda U_{i% -1}^{j}=\dfrac{1}{2}\lambda U_{i+1}^{j-1}+(1-\lambda)U_{i}^{j-1}+\dfrac{1}{2}% \lambda U_{i-1}^{j-1},

(5.47)

με $i=1,\dots,N$ , $j=1,\dots,M$ . Όμοια όπως και στην πεπλεγμένη μέθοδο του Euler, (5.32), αν ξεκινήσουμε από το χρονικό επίπεδο $t^{0}=0$ , δεν μπορούμε άμεσα να υπολογίσουμε την προσέγγιση στο χρονικό επίπεδο $t^{1}$ από την (5.47). Στο Σχήμα 5.6 φαίνεται ένα παράδειγμα πλέγματος όπου σημειώνουμε τις γνωστές ή άγνωστες τιμές της προσέγγισης σε κάθε βήμα με τη μέθοδο (5.47).

Επομένως, αν $U^{j}\in\mathbb{R}^{N}$ το διάνυσμα με συνιστώσες $U_{1}^{j},\dots,U_{N}^{j}$ , $U=(U_{1}^{j}$ , $\dots$ , $U_{N}^{j})^{T}$ , το σύστημα των εξισώσεων (5.47) μπορούμε να το γράψουμε ως

BU^{j}=AU^{j-1},\quad j=1,\dots,M,\quad\text{ με }U^{0}=G,

(5.48)

όπου $B$ και $A$ είναι οι $N\times N$ πίνακες

B=\left(\begin{array}[]{ccccc}1+\lambda&-\lambda/2&0&&0\\ -\lambda/2&1+\lambda&-\lambda/2&0&\\ 0&\ddots&\ddots&\ddots&0\\ &&-\lambda/2&1+\lambda&-\lambda/2\\ &&&-\lambda/2&1+\lambda\\ \end{array}\right),

A=\left(\begin{array}[]{ccccc}1-\lambda&\lambda/2&0&&0\\ \lambda/2&1-\lambda&\lambda/2&0&\\ 0&\ddots&\ddots&\ddots&0\\ &&\lambda/2&1-\lambda&\lambda/2\\ &&&\lambda/2&1-\lambda\\ \end{array}\right),

και $G=(g(x_{1}),\dots,g(x_{N}))^{T}$ .

Σχήμα 5.6: Σημεία ενός πλέγματος για τον υπολογισμό της λύσης με τη μέθοδο των Crank-Nicolson. Με άσπρο σημειώνουμε τα σημεία που αντιστοιχούν σε άγνωστες τιμές της προσέγγισης και με μαύρο αυτά που αντιστοιχούν σε γνωστές τιμές.

Από την (5.45) έχουμε ότι η προσέγγιση $U^{0}$ στο χρονικό επίπεδο $t^{0}$ είναι γνωστή, οπότε για να υπολογίσουμε τη λύση στο χρονικό επίπεδο $t^{1}$ αρκεί να λύσουμε το γραμμικό σύστημα $BU^{1}=AU^{0}$ . Εύκολα βλέπουμε ότι ο $B$ έχει αυστηρά κυριαρχική διαγώνιο, επομένως είναι αντιστρέψιμος και επειδή είναι τριδιαγώνιος μπορούμε να εφαρμόσουμε τον αλγόριθμο της Παραγράφου 3.2 για τον υπολογισμό της $U^{1}$ . Συνεχίζουμε με αυτό τον τρόπο και αν στο χρονικό επίπεδο $t^{j-1}$ γνωρίζουμε την προσέγγιση $U^{j-1}$ , λύνοντας το γραμμικό σύστημα (5.48), βρίσκουμε την προσέγγιση $U^{j}$ στο χρονικό επίπεδο $t^{j}$ . Για τον ίδιο λόγο, όπως και για την πεπλεγμένη μέθοδο του Euler, η μέθοδος (5.45) είναι πεπλεγμένη ή έμμεση και καλείται μέθοδος των Crank–Nicolson.

Για την ευστάθεια της μεθόδου μπορούμε να δείξουμε το ακόλουθο θεώρημα.

Θεώρημα 5.5.

Έστω $U^{j}\in\mathbb{R}^{N}$ , $j=0,\dots,M$ , η λύση του προβλήματος (5.47), με $U_{0}^{j}=U_{N+1}^{j}=0$ , $j=0,\dots,M$ . Τότε, αν $\lambda\leq 1$ , ισχύει η ακόλουθη ανισότητα

\max_{0\leq i\leq N+1}|U_{i}^{j}|\leq\max_{0\leq i\leq N+1}|U_{i}^{0}|,\quad% \text{για }j=0,1,2,\dots,M.

(5.49)

Proof.

Από τη σχέση (5.47) εύκολα παίρνουμε για $i=1,\dots,N$ , $j=1,\dots,M$ ,

(1+\lambda)|U_{i}^{j}|\leq\dfrac{\lambda}{2}(|U_{i+1}^{j}|+|U_{i-1}^{j}|)+(1-% \lambda)|U_{i}^{j-1}|+\dfrac{\lambda}{2}(|U_{i+1}^{j-1}|+|U_{i-1}^{j-1}|).

Αν θέσουμε λοιπόν $\bar{U}^{j}=\max_{0\leq i\leq N+1}|U_{i}^{j}|$ , $j=0,\dots,M$ , έχουμε

(1+\lambda)|U_{i}^{j}|\leq\lambda\bar{U}^{j}+\bar{U}^{j-1},

και άρα

\bar{U}^{j}\leq\bar{U}^{j-1}\leq\dots\leq\bar{U}^{0},

από όπου προκύπτει η ζητούμενη ανισότητα. ∎

Παρατηρούμε ότι για να δείξουμε το Θεώρημα 5.5, υποθέσαμε ότι $\lambda\leq 1$ . Θα δούμε παρακάτω ότι αυτή η υπόθεση δεν είναι απαραίτητη για να δείξουμε την ευστάθεια von Neumann για τη μέθοδο των Crank-Nicolson, επομένως η υπόθεση $\lambda\leq 1$ στο Θεώρημα 5.5 δεν είναι ουσιαστική και γίνεται μόνο για να μπορέσουμε να αποδείξουμε το θεώρημα, ακολουθώντας τα βήματα που χρησιμοποιήσαμε στην αντίστοιχη απόδειξη.

Θεωρούμε και πάλι ότι οι $U_{i}^{j}=w_{j}e^{rx_{i}I}$ ικανοποιούν την (5.47), οπότε

\begin{split}&\displaystyle-\dfrac{\lambda}{2}w_{j}e^{rx_{i+1}I}+(1+\lambda)w_% {j}e^{rx_{i}I}-\dfrac{\lambda}{2}w_{j}e^{rx_{i-1}I}\\ &\displaystyle=\dfrac{\lambda}{2}w_{j-1}e^{rx_{i+1}I}+(1-\lambda)w_{j-1}e^{rx_% {i}I}+\dfrac{\lambda}{2}w_{j-1}e^{rx_{i-1}I},\end{split}

(5.50)

για $i=1,\dots,N,j=1,\dots,M$ . Χρησιμοποιούμε τώρα και πάλι τις ιδιότητες (5.23) και (5.20) και έχουμε

\begin{split}&\displaystyle-2\lambda w_{j}e^{rx_{i}I}\cos(rh)+(1+\lambda)w_{j}% e^{rx_{i}I}=2\lambda w_{j-1}e^{rx_{i}I}\cos(rh)+(1-\lambda)w_{j-1}e^{rx_{i}I},% \end{split}

από την οποία προκύπτει

\begin{split}&\displaystyle(1+4\lambda\sin^{2}(\frac{rh}{2}))w_{j}=(1-4\lambda% \sin^{2}(\frac{rh}{2}))w_{j-1}.\end{split}

Συνεπώς

\begin{split}\displaystyle w_{j}=\dfrac{1-4\lambda\sin^{2}(\frac{rh}{2})}{1+4% \lambda\sin^{2}(\frac{rh}{2})}w_{j-1}=\kappa w_{j-1}=\dots=\kappa^{j}w_{0}.% \end{split}

(5.51)

Είναι απλό να δούμε ότι σε αυτήν την περίπτωση ισχύει $|\kappa|\leq 1$ για κάθε $\lambda$ και $r$ . Συνεπώς, η απόλυτη τιμή της $U_{i}^{j}$ είναι φραγμένη ανεξάρτητα της τιμής του $\lambda$ , οπότε δεν είναι αναγκαία καμιά συνθήκη για στις παραμέτρους της διαμέρισης $h$ και $k$ , ώστε να είναι ευσταθής η μέθοδος Crank–Nicolson.

Θεώρημα 5.6.

Έστω ότι η λύση $u$ του προβλήματος (5.1) είναι αρκετά ομαλή και $U_{i}^{j}$ , $i=0,\dots,N+1$ , $j=0,\dots,M$ , η λύση της μεθόδου (5.47). Τότε, υπάρχει μια σταθερά $C$ , ανεξάρτητη των $k, h$ , τέτοια ώστε

\max_{0\leq j\leq M}\max_{0\leq i\leq N+1}|U_{i}^{j}-u(x_{i},t^{j})|\leq C(k^{% 2}+h^{2}).

(5.52)

Proof.

Θέτουμε $E_{i}^{j}=U_{i}^{j}-u(x_{i},t^{j})$ , $i=0,\dots,N+1$ , $j=0,\dots,M$ , όπου λόγω των σχέσεων $U_{0}^{j}=u(0,t^{j})=0$ και $U_{N+1}^{j}=u(L,t^{j})=0$ , έχουμε $E_{0}^{j}=E_{N+1}^{j}=0$ . Αφαιρούμε τώρα κατά μέλη τις (5.45) και (5.42), οπότε παίρνουμε για $i=1,\dots,N$ , $j=1,\dots,M$ ,

(1+\lambda)E_{i}^{j}=\dfrac{\lambda}{2}(E_{i+1}^{j}+E_{i-1}^{j})+(1-\lambda)E_% {i}^{j-1}+\dfrac{\lambda}{2}(E_{i+1}^{j-1}+E_{i-1}^{j-1})+k\eta_{i}^{j}.

Θέτουμε, στη συνέχεια, $\bar{E}^{j}=\max_{1\leq i\leq N}|E_{i}^{j}|$ , $\bar{\eta}=\max_{1\leq i\leq N,1\leq j\leq M}|\eta_{i}^{j}|$ και έχουμε

(1+\lambda)E_{i}^{j}\leq{\lambda}\bar{E}^{j}+(1-\lambda)\bar{E}^{j-1}+{\lambda% }\bar{E}^{j-1}+k\bar{\eta},

οπότε

\bar{E}^{j}\leq\bar{E}^{j-1}+k\bar{\eta}\leq\dots\leq\bar{E}^{0}+jk\bar{\eta}.

Από εδώ, επειδή $jk\leq T$ και λόγω του Λήμματος 5.3, προκύπτει η ζητούμενη εκτίμηση. ∎

Παράδειγμα 5.3.

Επαναλαμβάνουμε και εδώ το Παράδειγμα 5.1 όπου χρησιμοποιούμε τώρα τη μέθοδο των Crank-Nicolson. Στο Σχήμα 5.7 απεικονίζονται οι γραφικές παραστάσεις της $u$ για $t=0$ , καθώς και οι προσεγγίσεις για $\allowbreak t=0.025$ , $0.05$ , $0.0625$ , με $M=24,32,128$ . Επίσης, στον Πίνακα 5.3 βλέπουμε το μέγιστο σφάλμα στα χρονικά επίπεδα $t=0.025,0.05,0.0625,0.075$ .

Σχήμα 5.7: Η ακριβής λύση $u(x,t)=e^{-4\pi^{2}t}\sin(2\pi x)$ του Παραδείγματος 5.1 και οι προσεγγίσεις της για $N=23$ και $M=24,32,128$ , με τη μέθοδο των Crank-Nicolson για $\allowbreak t=0,0.025,0.05$ και $0.0625$ .

	$t=0.025$		$t=0.05$		$t=0.0625$		$t=0.075$
$M$	$j$	$\bar{E}^{j}$	$j$	$\bar{E}^{j}$	$j$	$\bar{E}^{j}$	$j$	$\bar{E}^{j}$
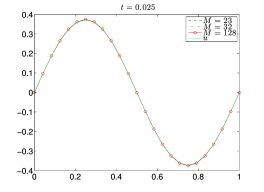24	6	0.0013	12	0.0010	15	0.0007	18	0.0005
32	8	0.0016	16	0.0012	20	0.0008	24	0.0007
128	32	0.0021	64	0.0015	80	0.0012	96	0.0009

Πίνακας 5.3: Το σφάλμα

\bar{E}^{j}=\max_{1\leq i\leq N}|U_{i}^{j}-u(x_{i},t^{j})|

στα χρονικά επίπεδα

t=0.025,0.05

και

0.0625

0.075

του Παραδείγματος 5.3 για

N=23

και

M=24,32,128

. Στη στήλη αριστερά του κάθε σφάλματος δίνεται το χρονικό βήμα

j

, τέτοιο ώστε

t=jk

, με

k=1/M

Παρατηρούμε από τα Παραδείγματα 5.2 και 5.3, ότι το σφάλμα σε κάθε χρονικό επίπεδο είναι μικρότερο στη μέθοδο Crank–Nicolson από ότι στη πεπλεγμένη μέθοδο του Euler. Αυτό οφείλεται στη μεγαλύτερη τάξη ως προς $k$ που έχει το σφάλμα για τη μέθοδο Crank–Nicolson από το αντίστοιχο σφάλμα για τη πεπλεγμένη μέθοδο του Euler, βλ. Θεωρήματα 5.4 και 5.6. Στο επόμενο παράδειγμα παραθέτουμε ορισμένα αριθμητικά αποτελέσματα, όπου φαίνεται ότι τα σφάλματα που προκύπτουν με τη μέθοδο Crank–Nicolson έχουν τάξη ακρίβειας $k^{2}$ .

Παράδειγμα 5.4.

Αν οι παράμετροι $k, h$ της διαμέρισης των $[0,L]\times[0,T]$ είναι ίσες, τότε το σφάλμα για την πεπλεγμένη μέθοδο του Euler σύμφωνα με το Θεώρημα 5.4, θα ικανοποιεί

\max_{0\leq j\leq M}\max_{0\leq i\leq N+1}|U_{i}^{j}-u(x_{i},t^{j})|\leq Ck,% \quad\text{ για }k=h,\text{ και }k\text{ μικρό},

και το σφάλμα για τη μέθοδο των Crank–Nicolson σύμφωνα με το Θεώρημα 5.6, θα ικανοποιεί

\max_{0\leq j\leq M}\max_{0\leq i\leq N+1}|U_{i}^{j}-u(x_{i},t^{j})|\leq Ck^{2% },\quad\text{ για }k=h,\text{ και }k\text{ μικρό}.

Αν υποθέσουμε λοιπόν ότι το μέγιστο σφάλμα $\bar{E}=\max_{0\leq i\leq N+1}|U_{i}^{M}-u(x_{i},t^{M})|\approx Ck^{p}$ , στο χρονικό επίπεδο $t^{M}=T$ , μπορούμε να προσδιορίσουμε πειραματικά, με τη χρήση Η/Υ, τη δύναμη $p$ , από τον λόγο $p\approx(\log(E_{1}/E_{2})/\log(k_{1}/k_{2}))$ , όπου $E_{1}$ είναι το σφάλμα που αντιστοιχεί στη διαμέριση με βήμα $k_{1}$ και $E_{2}$ το σφάλμα για τη διαμέριση με βήμα $k_{2}$ .

Αν θεωρήσουμε και πάλι το πρόβλημα των Παραδείγματων 5.1 και 5.2, μπορούμε να υπολογίσουμε κατά προσέγγιση την τάξη σύγκλισης για την πεπλεγμένη μέθοδο του Euler και τη μέθοδο των Crank–Nicolson για $t=T=0.1$ . Στον Πίνακα 5.4, εμφανίζεται η κατά προσέγγιση δύναμη $p$ και παρατηρούμε ότι για τη μέθοδο Euler είναι κατά προσέγγιση ένα, ενώ για τη μέθοδο Crank–Nicolson είναι δύο.

	BE		CN
$k=h$	$\bar{E}_{BE}$	$p$	$\bar{E}_{CN}$	$p$
1/20	0.095012		0.01918
1/40	0.045123	1.074	0.00592	1.69539
1/80	0.021160	1.092	0.00150	1.97976
1/160	0.010064	1.072	0.00037	1.99623
1/250	0.004876	1.045	0.00009	1.99912

Πίνακας 5.4: Τα σφάλματα των μεθόδων Euler και Crank–Nicolson στο χρονικό επίπεδo

t=T=0.1

\bar{E}_{BE}

και

\bar{E}_{CN}

, αντίστοιχα, στο Παράδειγμα 5.4 και η κατά προσέγγιση τάξη ακρίβειάς τους

p

, αν θεωρήσουμε

k=h