5.1 Άμεση μέθοδος του Euler
Θεωρούμε το ακόλουθο πρόβλημα: Ζητείται μια συνάρτηση , τέτοια ώστε
| (5.1) |
όπου , . Όπως είπαμε στην Παραγράφο 1.2.2 η λύση του (5.1) δίνεται από τη
| (5.2) |
με και .
Όπως και στην προηγούμενη παράγραφο θα θεωρήσουμε ορισμένα σημεία στο χωρίο και θα κατασκευάσουμε προσεγγίσεις της ακριβούς λύσης του (5.1) σε αυτά τα σημεία. Θεωρούμε λοιπόν έναν φυσικό αριθμό και τη διαμέριση του διαστήματος από ισαπέχοντα σημεία , όπου , . Επίσης, θεωρούμε και έναν φυσικό αριθμό και τη διαμέριση του από ισαπέχοντα σημεία , όπου , , βλ. Σχήμα 5.1. Τότε σε κάθε σημείο του διαμερισμού του , θα ισχύει:
| (5.3) |
Θα θεωρήσουμε λοιπόν προσεγγίσεις των τιμών της στα παραπάνω σημεία τις οποίες θα συμβολίσουμε με , , . Λόγω των συνοριακών συνθηκών , , θέτουμε , , και επειδή η λύση της (5.1) είναι γνωστή για , θέτουμε , . Οι υπόλοιπες τιμες , , , είναι άγνωστες και θα τις προσεγγίσουμε.

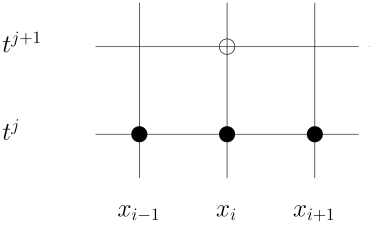
Στο Σχήμα 5.1, για ένα παράδειγμα πλέγματος σημείων, σημειώνουμε με άσπρο κύκλο τα σημεία που αναζητούμε στις τιμές και με έντονο μαύρο τα σημεία που αντιστοιχούν στις γνωστές συνοριακές τιμές της . Τις άγνωστες τιμές τις προσεγγίζουμε με τις τιμές , , , οι οποίες προκύπτουν με τον ακόλουθο τρόπο.
Για να προσεγγίσουμε τις , , , στην (5.3) χρησιμοποιούμε τη που θεωρήσαμε στην (2.1). Έτσι, αν υποθέσουμε ότι , λόγω της (2.3), η (5.3) γίνεται για ,
| (5.4) |
όπου
| (5.5) |
Στη συνέχεια, για να προσεγγίσουμε τις , , , στην (5.4) χρησιμοποιούμε την προσέγγιση που θεωρήσαμε στην (2.8). Έτσι, αν υποθέσουμε ότι , λόγω της (2.9), η (5.4) γίνεται για και
| (5.6) |
και
| (5.7) |
Αν θέσουμε τώρα , η (5.6) δίνει για και
| (5.8) |
και λόγω των (5.5) και (5.7) εύκολα βλέπουμε ότι ισχύει το ακόλουθο λήμμα.
Λήμμα 5.1.
Θα κατασκευάσουμε λοιπόν προσεγγίσεις της λύσης του προβλήματος (5.1) στα σημεία , , , θεωρώντας τις ακόλουθες εξισώσεις,
| (5.10) | ||||
| (5.11) |
Κατ’ αναλογία με το Κεφάλαιο 3, το σφάλμα που δίνεται στις (5.8) καλείται τοπικό σφάλμα διακριτοποίησης για τη μέθοδο (5.10)–(5.11).
Έστω τώρα ότι έχουμε θεωρήσει έναν διαμερισμό σημείων του , με βήμα και του , με βήμα , τότε προκύπτει ένας διαμερισμός σημείων του . Αν το τοπικό σφάλμα διακριτοποίησης , ενός αριθμητικού σχήματος σε ένα σημείο ενός διαμερισμού , φράσσεται κατά απόλυτη τιμή από το γινόμενο μιας θετικής σταθεράς, που δεν εξαρτάται από τα και , επί και , τότε λέμε ότι έχει τάξη ακρίβειας ως προς και ως προς .
Επομένως, λόγω των (5.5) και (5.7), το τοπικό σφάλμα διακριτοποίησης της μεθόδου (5.10)-(5.11) έχει τάξη ακρίβειας δύο ως προς και ένα ως προς .
Επίσης, κατ’αναλογία του Oρισμού 3.1, αν το τοπικό σφάλμα διακριτοποίησης μιας μεθόδου, , τείνει στο μηδέν, καθώς τα βήματα και του διαμερισμού τείνουν στο μηδέν, τότε η μέθοδος λέγεται συνεπής.
Συνεπώς σύμφωνα με το Λήμμα 5.1, το τοπικό σφάλμα διακριτοποίησης τείνει στο μηδέν, καθώς τα και τείνουν στο μηδέν, οπότε η (5.10)-(5.11) είναι μια συνεπής μέθοδος.
Αν συμβολίσουμε τώρα με τον λόγο , τότε η (5.10) γράφεται ως
| (5.12) |
για , . Ξεκινώντας από το χρονικό επίπεδο , χρησιμοποιώντας δηλαδή τις αρχικές συνθήκες (5.11), από την (5.12) μπορούμε να υπολογίσουμε άμεσα την προσέγγιση στο χρονικό επίπεδο . Συνεχίζοντας με αυτό τον τρόπο, λαμβάνουμε, με άμεσο τρόπο μέσω της (5.12), την προσέγγιση στο χρονικό επίπεδο , από τις ήδη γνωστές τιμές στο χρονικό επίπεδο .
Η μέθοδος (5.10)-(5.11) καλείται άμεση μέθοδος του Euler. Στο Σχήμα 5.2 φαίνεται ένα παράδειγμα πλέγματος, κοντά στο , όπου σημειώνουμε με άσπρο κύκλο το σημείο του χρονικού επιπέδου , όπου σύμφωνα με την (5.12), αντιστοιχεί σε άγνωστη τιμή της προσέγγισης και με μαύρο αυτά του χρονικού επιπέδου που αντιστοιχούν σε γνωστές τιμές της προσέγγισης.
Αν συμβολίσουμε με το διάνυσμα με συνιστώσες, , , , μπορούμε να γράψουμε το σύστημα των εξισώσεων (5.12) ισοδύναμα ως
| (5.13) |
όπου είναι ο πίνακας
και .
Επομένως, για να υπολογίσουμε την προσέγγιση στο χρονικό επίπεδο , απλώς πολλαπλασιάζουμε τον πίνακα με τη γνωστή, από το προηγούμενο βήμα, . Επειδή για να υπολογίσουμε την προσέγγιση σε κάθε χρονικό βήμα δεν χρειάζεται να αντιστρέψουμε κάποιον πίνακα, δηλαδή να λύσουμε κάποιο γραμμικό σύστημα με αριθμητικές μεθόδους, η μέθοδος καλείται άμεση.
Η ύπαρξη και η μοναδικότητα της προσεγγιστικής λύσης σε κάθε χρονικό βήμα είναι δεδομένη, διότι για να την υπολογίσουμε αρκεί να πολλαπλασιάζουμε έναν γνωστό πίνακα με τη γνωστή από το προηγούμενο χρονικό βήμα προσεγγιστική λύση.
Στη συνέχεια, θα δείξουμε το ακόλουθο θεώρημα για την ευστάθεια της άμεσης μεθόδου του Euler.
Θεώρημα 5.1.
Έστω , , τα διανύσματα που προκύπτουν από την (5.13), με , . Τότε, αν , ισχύει η ακόλουθη ανισότητα,
Απόδειξη.
Από τη σχέση (5.12) και το γεγονός , εύκολα παίρνουμε
Αν θέσουμε λοιπόν , , έχουμε
από όπου προκύπτει η ζητούμενη εκτίμηση. ∎
Για να αποδείξουμε την ευστάθεια της μεθόδου στο Θεώρημα 5.1 υποθέσαμε ότι . Λόγω της ύπαρξης μιας συνθήκης ανάμεσα στις παραμέτρους διακριτοποίησης και , λέμε ότι η μέθοδος είναι ευσταθής υπό συνθήκες. Το γεγονός ότι αυτή η συνθήκη είναι αναγκαία και δεν οφείλεται σε τυχόν αδυναμία της απόδειξης του Θεώρηματος 5.1 που δώσαμε φαίνεται από το ακόλουθο παράδειγμα.
Είναι απλό να δούμε ότι αν και , τότε το πρόβλημα (5.1) γίνεται
| (5.14) | ||||||
| (5.15) | ||||||
| (5.16) |
και η ακριβής λύση είναι η , μια δηλαδή από τις θεμελιώδεις συναρτήσεις που εμφανίζονται στην έκφραση (5.2). Παρατηρούμε λοιπόν ότι σε κάθε χρονικό επίπεδο καθεμιά από αυτές τις θεμελιώδεις συναρτήσεις είναι μια ημιτονοειδής συνάρτηση, της οποίας το πλάτος μειώνεται συνεχώς με εκθετικό τρόπο, καθώς το χρονικό επίπεδο αυξάνει. Είναι προφανές ότι, αν θεωρήσουμε για αρχική συνθήκη μια από τις , και η προσεγγιστική λύση που λαμβάνουμε με τη μέθοδο (5.10), δεν αποτυπώνει αυτήν την ιδιότητα, ή τουλάχιστον το πλάτος δεν παραμένει φραγμένο, δεν θα προσεγγίζει “καλά” την αντίστοιχη θεμελιώδη συνάρτηση.
Επειδή η ακριβής λύση του (5.14)–(5.16) αποτελείται από το γινόμενο της , που εξαρτάται μόνο από τον χρόνο , και της , υποθέτουμε ότι η λύση της (5.10) έχει τη μορφή . Δηλαδή αποτελείται από δύο παράγοντες, ο ένας από τους οποίους εξαρτάται μόνο από τον χρόνο και ο άλλος είναι ακριβώς η ημιτονοειδής συνάρτηση που βρίσκεται στην έκφραση της ακριβούς λύσης του (5.14). Αντικαθιστούμε λοιπόν την παραπάνω μορφή της στην εξίσωση (5.12), οπότε παίρνουμε για ,
| (5.17) |
Στη συνέχεια, εφαρμόζοντας την τριγωνομετρική ταυτότητα
| (5.18) |
η (5.17) γίνεται
| (5.19) |
Επίσης, λόγω της τριγωνομετρικής ιδιότητας
| (5.20) |
η (5.19) δίνει
| (5.21) |
Συνεπώς, , με Άρα, η μέγιστη τιμή της είναι φραγμένη, αν και μόνο αν . Θα πρέπει, λοιπόν,
Επομένως, επειδή , για , αρκεί . Βλέπουμε ότι η συνθήκη ευστάθειας στο Θεώρημα 5.1 είναι αναγκαία για να έχουμε “καλές” προσεγγίσεις με την άμεση μέθοδο του Euler.
Μπορούμε να γενικεύσουμε την παραπάνω απόδειξη θεωρώντας τώρα ότι
με τη φανταστική μονάδα, ικανοποιούν την εξίσωση (5.12). Αν οι τιμές παραμένουν φραγμένες για κάθε , θα καλούμε αυτή την ιδιότητα ευστάθεια von Neumann. Είναι φανερό ότι για να είναι φραγμένες οι , αρκεί να φράσσονται οι για κάθε . Μια πιο διεξοδική μελέτη της ευστάθειας von Neumann ο ενδιαφερόμενος αναγνώστης μπορεί να βρεί στο (Strikwerda, (2004)).
Μπορεί να αποδειχθεί ότι για την εξίσωση της θερμότητας η ευστάθεια von Neumann συνεπάγεται την ευστάθεια μιας μεθόδου, βλ. π.χ. (Morton and Mayers, (2005)). Στη συνέχεια, θα δείξουμε ότι για να είναι η άμεση μέθοδος του Euler von Neumann ευσταθής πρέπει και πάλι να ισχύει .
Υποθέτουμε λοιπόν ότι οι
με τη φανταστική μονάδα, ικανοποιούν την εξίσωση (5.12) και, άρα,
| (5.22) |
Λόγω τώρα της ταυτότητας
έχουμε
| (5.23) |
Οπότε η (5.22) λόγω της (5.20) γίνεται
Συνεπώς , με . Για να παραμένει η λύση φραγμένη κατ’απόλυτη τιμή θα πρέπει , για κάθε . Καταλήγουμε δηλαδή στο ίδιο αποτέλεσμα όπως και παραπάνω, δηλαδή ότι .
Στη συνέχεια, δείχνουμε το ακόλουθο για τη σύγκλιση της μεθόδου.
Θεώρημα 5.2.
Απόδειξη.
Παράδειγμα 5.1.
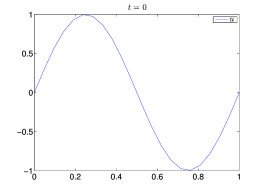
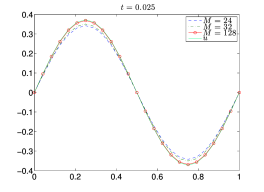
Ας θεωρήσουμε το πρόβλημα (5.14) με και , όπου η ακριβής λύση είναι . Θεωρούμε έναν διαμερισμό του με , και ισαπέχοντα σημεία του , με , και υπολογίζουμε τη λύση για καθέναν από τους τρεις αυτούς διαμερισμούς χρησιμοποιώντας το αριθμητικό σχήμα (5.10). Για μπορούμε να βρούμε τις αντίστοιχες προσέγγισεις της , με τέτοιο ώστε και . Στο Σχήμα 5.3 απεικονίζονται οι γραφικές παραστάσεις της για , καθώς και οι προσεγγίσεις για , με . Επίσης, στον Πίνακα 5.1 βλέπουμε το μέγιστο σφάλμα στα χρονικά επίπεδα . Στο Σχήμα 5.3 παρατηρούμε ότι η προσεγγιστική λύση για δεν φαίνεται να προσεγγίζει την ακριβή λύση, καθώς το χρονικό επίπεδο μεγαλώνει, το οποίο φαίνεται και στα αποτελέσματα του Πίνακα 5.1. Αυτό όμως δεν συμβαίνει στην περίπτωση . Αυτή η συμπεριφορά των προσεγγιστικών λύσεων οφείλεται στην αστάθεια της λύσης για και της ευστάθειας για , διότι η παράμετρος είναι για , αντίστοιχα.
 |
 |
 |
 |
| 24 | 6 | 0.0302 | 12 | 0.0216 | 15 | 0.0181 | 18 | 2.2244 |
| 32 | 8 | 0.0217 | 16 | 0.0157 | 20 | 0.1358 | 24 | 174.6062 |
| 128 | 32 | 0.0036 | 64 | 0.0027 | 80 | 0.0020 | 96 | 0.0015 |