1 Εισαγωγή 1.1 Διαφορικές εξισώσεις 1.3 Σειρές Fourier

1.2 Επίλυση προβλημάτων συνοριακών τιμών και αρχικών και συνοριακών τιμών

Σε αυτή την παράγραφο θα δούμε ορισμένες ιδιότητες των διαφορικών εξισώσεων που θα συναντήσουμε, καθώς και των λύσεων τους.

1.2.1 Πρόβλημα δύο σημείων

Θα ασχοληθούμε πρώτα με μια απλή διαφορική εξίσωση σε μία διάσταση, το πρόβλημα δύο σημείων. Έστω $u$ τέτοια, ώστε

$$ -u^{\prime\prime}(x)+q(x)u(x)=f(x),\quad\text{για }x\in[a,b].$$

(1.16)

Είναι γνωστό, βλ. π.χ. (Logan, (2014)), ότι η γενική λύση $u$ της (1.16) προκύπτει ως γραμμικός συνδυασμός δύο γραμμικώς ανεξαρτήτων λύσων της αντίστοιχης ομογενούς, $u_{1}$ και $u_{2}$ , και μιας λύσης $u_{p}$ της μη ομογενούς (1.16),

u=c_{1}u_{1}+c_{2}u_{2}+u_{p},

όπου $c_{1},c_{2}$ πραγματικές σταθερές. Αν θεωρήσουμε τώρα ότι η λύση $u$ του (1.16) ικανοποιεί, επιπλέον, τις συνθήκες

u(a)=a_{0},\quad u^{\prime}(a)=a_{1},

(1.17)

όπου $a_{0},a_{1}$ δοσμένες σταθερές, τότε έχουμε ένα πρόβλημα αρχικών τιμών, το οποίο έχει μία ακριβώς λύση, σύμφωνα με το ακόλουθο θέωρημα, [βλ. π.χ. (Logan, (2014), Κεφάλαιο 3.4)].

Θεώρημα 1.1.

Αν οι συναρτήσεις $f, q$ είναι συνεχείς στο διάστημα $[a,b]$ , τότε το πρόβλημα αρχικών τιμών (1.16)–(1.17) έχει μοναδική λύση στο $[a,b]$ .

Αν τώρα, αντί για τις αρχικές συνθήκες (1.17), θεωρήσουμε ότι η $u$ ικανοποιεί τις ομογενείς συνοριακές συνθήκες Dirichlet,

u(a)=u(b)=0,

(1.18)

τότε δεν είναι σίγουρο ότι υπάρχει μοναδική λύση $u$ του προβλήματος (1.16) και (1.18), για κάθε συνεχή συνάρτηση $f$ και $q$ . Όμως, μπορούμε να δείξουμε το ακόλουθο θεώρημα, βλ. π.χ. (Brezis, (1997), Κεφάλαιο VIII).

Θεώρημα 1.2.

Αν οι συναρτήσεις $f, q$ είναι συνεχείς στο διάστημα $[a,b]$ και $q\geq 0$ , τότε έχει μοναδική λύση ακόλουθο πρόβλημα: Ζητείται $u:[a,b]\to\mathbb{R}$ , τέτοια ώστε

$$-u^{\prime\prime}+qu=f,\quad\text{ στο }[a,b],\ \text{ με }u(a)=u(b)=0,$$

(1.19)

Η υπόθεση ότι $q\geq 0$ είναι σημαντική για την ύπαρξη και μοναδικότητα της λύσης του (1.19). Αν θεωρήσουμε, για παράδειγμα, την

$$-u^{\prime\prime}-\pi u=0,\quad\text{ στο }[0,1],\ \text{ με }u(0)=u(1)=0,$$

(1.20)

μπορούμε να δούμε ότι οι συναρτήσεις $c\sin(\pi x)$ , $c\in\mathbb{R}$ αποτελούν λύσεις του (1.20) και επομένως, το πρόβλημα (1.20) έχει άπειρες λύσεις. Στη συνέχεια, αν τροποποιήσουμε το (1.20) και θεωρήσουμε το πρόβλημα

$$-u^{\prime\prime}-\pi u=\pi,\quad\text{ στο }[0,1],\ \text{ με }u(0)=u(1)=0$$

(1.21)

από τη θεωρία των Σ.Δ.Ε., βλ. (Logan, (2014)), έχουμε ότι η γενική λύση αυτής της Δ.Ε. είναι η $c_{1}\sin(\pi x)+c_{2}\cos(\pi x)−1$ , με $c_{1},c_{2}\in\mathbb{R}$ . Όμως για καμία επιλογή των $c_{1},c_{2}$ δεν προκύπτει λύση του (1.21). Συνεπώς, το (1.21) δεν έχει καμμία λύση.

Αν τροποποιήσουμε τώρα τις συνοριακές συνθήκες Dirichlet στο πρόβλημα (1.19) και θεωρήσουμε το αντίστοιχο πρόβλημα με ομογενείς συνοριακές συνθήκες Neumann, δηλαδή: Ζητείται, $u$ τέτοια ώστε

$$-u^{\prime\prime}+qu=f,\quad\text{ στο }[a,b],\ \text{ με }u^{\prime}(a)=u^{\prime}(b)=0,$$

(1.22)

τότε, όπως και στο Θεώρημα 1.2 μπορούμε να δείξουμε μοναδικότητα της λύσης αν $q, f$ είναι συνεχείς συναρτήσεις στο $[a,b]$ και $q>0$ . Διαφορετικά, αν π.χ. $q=f=0$ , τότε το (1.22) γίνεται

$$-u^{\prime\prime}=0,\quad\text{ στο }[a,b],\ \text{ με }u^{\prime}(a)=u^{% \prime}(b)=0.$$

(1.23)

Είναι προφανές ότι όλες οι συναρτήσεις της μορφής $u(x)=c$ , με $c\in\mathbb{R}$ αποτελούν λύση και, άρα, έχουμε άπειρες λύσεις του προβλήματος.

1.2.2 Εξίσωση της θερμότητας

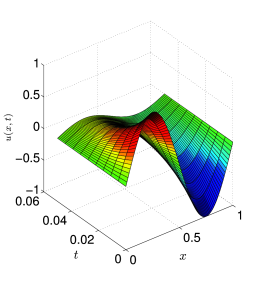
Θα θεωρήσουμε τώρα μια απλή παραβολική διαφορική εξίσωση και συγκεκριμένα την εξίσωση της θερμότητας (1.4), όπου η χωρική μεταβλητή $x$ ανήκει στο διάστημα $[0,L]$ , με $L>0$ και θα θεωρήσουμε, επιπλέον, αρχικές και ομογενείς συνοριακές συνθήκες Dirichlet. Έτσι, έχουμε το ακόλουθο πρόβλημα: Ζητείται $u:[0,L]\times[0,+\infty)\to\mathbb{R}$ , τέτοια ώστε

$\displaystyle u_{t}$	$\displaystyle=u_{xx},$	$\displaystyle\text{στο }[0,L]\times[0,+\infty)$	(1.24)
$\displaystyle u(0,t)$	$\displaystyle=u(L,t)=0,$	$\displaystyle\text{για }t\geq 0,$	(1.25)
$\displaystyle u(x,0)$	$\displaystyle=g(x),$	$\displaystyle\text{στο }[0,L],$	(1.26)

με $g$ μια συνεχή συνάρτηση.

Ένας τρόπος για να λύσουμε την (1.24) είναι να υποθέσουμε ότι $u(x,t)=X(x)T(t)$ , δηλαδή να θεωρήσουμε τη μέθοδο των χωριζομένων μεταβλητών. Σύμφωνα με αυτή τη μέθοδο, βλ. π.χ. (Logan, (2014)), οι συναρτήσεις $u_{n}$ , με $u_{n}=X_{n}T_{n}$ , $n=1,2,\dots$ , όπου

\begin{split}\displaystyle u_{n}&\displaystyle=X_{n}T_{n},\quad\text{ με }\\ \displaystyle X_{n}(x)&\displaystyle=c\sin{(\lambda_{n}x)},\ \text{ και }T_{n}% (t)=de^{-\lambda_{n}^{2}t}\text{ με }\lambda_{n}={\frac{n\pi}{L}},\ c,d\in% \mathbb{R},\end{split}

(1.27)

ικανοποιούν την εξίσωση (1.24) και τις συνοριακές συνθήκες (1.25). Λόγω της αρχής της υπέρθεσης, κάθε γραμμικός συνδυασμός λύσεων της μορφής (1.27) ικανοποιεί τις (1.24)-(1.25). Επομένως, αν θεωρήσουμε μια άπειρη σειρά συναρτήσεων της μορφής

u(x,t)=\sum_{n=1}^{\infty}c_{n}e^{-\lambda_{n}^{2}t}\sin(\lambda_{n}x),\quad% \text{με }c_{n}\in\mathbb{R},

(1.28)

η οποία συγκλίνει για κάθε σημείο $x\in[0,L]$ και $t\geq 0$ , τότε αποτελεί και λύση του προβλήματος (1.24)-(1.25). Μια λύση $u$ της μορφής (1.28) θα ικανοποιεί και την αρχική συνθήκη (1.26), μόνο αν

u(x,0)=\sum_{n=1}^{\infty}c_{n}\sin(\lambda_{n}x)=g(x),\quad\text{με }c_{n}\in% \mathbb{R}.

(1.29)

Ένα ανάπτυγμα της μορφής (1.29) καλείται σειρά Fourier ημιτόνων της $g$ , βλ. π.χ. την Παράγραφο 1.3.

Είναι γνωστό ότι το προβλήμα (1.24)-(1.26) έχει μοναδική λύση, βλ. π.χ. (Logan, (2014)).

Θεώρημα 1.3.

Αν η συνάρτηση $g$ είναι συνεχής στο $[0,L]$ , τότε υπάρχει μοναδική λύση $u$ του προβλήματος (1.24)–(1.26).

Έστω τώρα ότι γνωρίζουμε το ανάπτυγμα στη μορφή (1.29) της συνάρτησης $g(x)$ , της αρχικής συνθήκης (1.26), δηλαδή είναι γνωστές οι σταθερές $c_{n}$ , $n=1,2,\dots$ , στην (1.29). Τότε, η λύση $u$ του προβλήματος (1.24)–(1.26) δίνεται από την (1.28), με σταθερές $c_{n}$ αυτές της (1.29).

Παρόμοια αποτελέσματα ισχύουν αν αντί για τις συνοριακές συνθήκες Dirichlet (1.25), θεωρήσουμε ομογενείς συνοριακές συνθήκες Neumann, δηλαδή αν αναζητήσουμε $u$ , τέτοια ώστε

$\displaystyle u_{t}$	$\displaystyle=u_{xx},$	$\displaystyle\text{στο }[0,L]\times[0,+\infty)$	(1.30)
$\displaystyle u_{x}(0,t)$	$\displaystyle=u_{x}(L,t)=0,$	$\displaystyle\text{για }t\geq 0,$	(1.31)
$\displaystyle u(x,0)$	$\displaystyle=g(x),$	$\displaystyle\text{στο }[0,L],$	(1.32)

τότε οι συναρτήσεις

u_{n}(x,t)=e^{-\lambda_{n}^{2}t}\cos(\lambda_{n}x),\quad\lambda_{n}={\frac{n% \pi}{L}},\ n=0,1,2,\dots,

ικανοποιούν τις (1.30)–(1.31). Έστω τώρα ότι υπάρχουν σταθερές $c_{n}\in\mathbb{R}$ , τέτοιες ώστε

u(x,0)=g(x)=\sum_{n=0}^{\infty}c_{n}\cos(\lambda_{n}x),

(1.33)

όπου η σειρά συγκλίνει για κάθε $x\in[0,L]$ . Αν επιπλέον για κάθε $x\in[0,L]$ και $t\geq 0$ η σειρά $\sum_{n=1}^{\infty}c_{n}e^{-\lambda_{n}^{2}t}\cos(\lambda_{n}x)$ συγκλίνει, τότε η

u(x,t)=\sum_{n=1}^{\infty}c_{n}e^{-\lambda_{n}^{2}t}\cos(\lambda_{n}x),\quad% \text{με }c_{n}\in\mathbb{R},

(1.34)

είναι η μοναδική λύση του προβλήματος αρχικών και συνοριακών τιμών (1.30)–(1.32). Από τη μορφή της λύσης (1.28) ή (1.34), μπορούμε να παρατηρήσουμε ότι η $u$ φθίνει κατά απόλυτη τιμή, καθώς το $t$ τείνει στο άπειρο.

Παράδειγμα 1.1.

Αν $u(x,t)=e^{-4\pi^{2}t}\sin(2\pi x)$ , τότε εύκολα βλέπουμε ότι η $u$ είναι λύση του προβλήματος (1.24)–(1.26), με $L=1$ και $g(x)=\sin(2\pi x)$ . Στο Σχήμα 1.1 απεικονίζεται η $u$ στο $[0,1]\times[0,T]$ , με $T=0.05$ .

Σχήμα 1.1: Η ακριβής λύση $u$ του Παραδείγματος 1.1.

1.2.3 Εξίσωση μεταφοράς

Θα θεωρήσουμε τώρα μια απλή μερική διαφορική εξίσωση πρώτης τάξης, την εξίσωση μεταφοράς και το αντίστοιχο πρόβλημα αρχικών τιμών: Ζητείται μια συνάρτηση $u$ $\in C^{1}(\mathbb{R}\times[0,T])$ , $T>0$ , τέτοια ώστε

	$\displaystyle u_{t}(x,t)+\alpha u_{x}(x,t)$	$\displaystyle=0,$		$\displaystyle\quad x\in\mathbb{R},\ t\in[0,T],$		(1.35)
	$\displaystyle u(x,0)$	$\displaystyle=g(x),$		$\displaystyle\quad x\in\mathbb{R},$		(1.36)

όπου $\alpha\in\mathbb{R}$ και $g$ μια δοσμένη συνάρτηση. Αν θεωρήσουμε την ακόλουθη αλλαγή μεταβλητών

x=\alpha r+s,\quad t=r,

τότε εύκολα μπορούμε να δούμε ότι αν η $u$ είναι λύση του (1.35), τότε

\dfrac{\partial u}{\partial r}=\dfrac{\partial x}{\partial r}\dfrac{\partial u% }{\partial x}+\dfrac{\partial t}{\partial r}\dfrac{\partial u}{\partial t}=% \alpha u_{x}+u_{t}=0.

Επομένως, αν θεωρήσουμε ότι

z(s,r):=u(x-\alpha t,t),

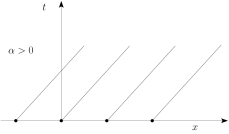
έχουμε $\dfrac{\partial z}{\partial r}=0$ , δηλαδή η $z$ δεν εξαρτάται από το $r$ και είναι σταθερή ως προς $r$ . Συνεπώς, η $u$ πάνω σε όλες τις ευθείες $x-\alpha t=c$ , με $c$ σταθερά, δεν μεταβάλλει την τιμή της και, έτσι, $u(x,t)=z(s,r)=z(s,0)=u(x-\alpha t,0)=g(x-\alpha t)$ . Λόγω αυτού του γεγονότος, οι ευθείες $x-\alpha t=c$ καλούνται χαρακτηριστικές για τη διαφορική εξίσωση (1.35), βλ. Σχήμα 1.2.

Σχήμα 1.2: Οι χαρακτηριστικές ευθείες $x-\alpha t=c$ πάνω στις οποίες είναι σταθερή η λύση $u$ της διαφορικής εξίσωσης (1.35).

Παράδειγμα 1.2.

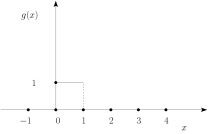
Ας θεωρήσουμε το πρόβλημα (1.35) και ότι η λύση $u$ για $t=0$ δίνεται από τη συνάρτηση

g(x)=\begin{cases}1&\text{ αν }0\leq x\leq 1\\ 0&\text{ διαφορετικά}.\end{cases}

Τότε η λύση είναι

u(x,t)=\begin{cases}1&\text{ αν }0\leq x-\alpha t\leq 1\\ 0&\text{ διαφορετικά},\end{cases}

ή ισοδύναμμα

u(x,t)=\begin{cases}1&\text{ αν }\alpha t\leq x\leq 1+\alpha t\\ 0&\text{ διαφορετικά},\end{cases}

Σχήμα 1.3: Η αρχική συνθήκη $g$ και η ακριβής λύση $u$ του Παραδείγματος 1.2 στην περίπτωση που $\alpha>0$ ή $\alpha<0$ .

Παρατηρούμε ότι για να προσδιορίσουμε με μοναδικό τρόπο τη λύση της διαφορικής εξίσωσης (1.35), αρκεί να γνωρίζουμε την αρχική συνθήκη $u(x,0)=g(x)$ . Επίσης, αν $\alpha>0$ , μπορούμε να διατυπώσουμε το πρόβλημα (1.35) ως πρόβλημα αρχικών και συνοριακών τιμών ως εξής: Ζητείται μια συνάρτηση $u$ $\in C^{1}([a,b]\times[0,T])$ , $a<b$ , $T>0$ , τέτοια ώστε

\begin{split}\displaystyle u_{t}(x,t)+\alpha u_{x}(x,t)&\displaystyle=0,\quad x% \in[a,b],\ t\in[0,T],\\ \displaystyle u(x,0)&\displaystyle=g(x),\quad x\in[a,b],\\ \displaystyle u(a,t)&\displaystyle=\phi_{0}(t),\quad t\in[a,b],\end{split}

(1.37)

όπου $\phi_{0}(t)=g(a-\alpha t)$ . Συνεπώς, σε αντίθεση με τα προβλήματα που είδαμε στις Παραγράφους 1.2.1 και 1.2.2, αρκεί μια συνοριακή συνθήκη για το σημείο $x=a$ για να προσδιορίσουμε μοναδικά τη λύση του προβλήματος (1.37). Όμως, στην περίπτωση τώρα που $\alpha<0$ , οι χαρακτηριστικές θα έχουν διαφορετική κατεύθυνση και διατυπώνουμε το πρόβλημα (1.35) ως πρόβλημα συνοριακών τιμών ως εξής: Ζητείται μια συνάρτηση $u$ $\in C^{1}([a,b]\times[0,T])$ , $a<b$ , $T>0$ , τέτοια ώστε

\begin{split}\displaystyle u_{t}(x,t)+\alpha u_{x}(x,t)&\displaystyle=0,\quad x% \in[a,b],\ t\in[0,T],\\ \displaystyle u(x,0)&\displaystyle=g(x),\quad x\in[a,b],\\ \displaystyle u(b,t)&\displaystyle=\phi_{1}(t),\quad t\in[a,b],\end{split}

(1.38)

όπου $\phi_{1}(t)=g(a-\alpha t)$ . Και σε αυτή την περίπτωση αρκεί μια συνοριακή συνθήκη για $x=b$ για να προσδιορίσουμε μοναδικά τη λύση του προβλήματος (1.38).

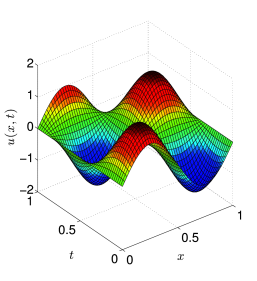
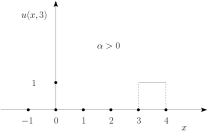
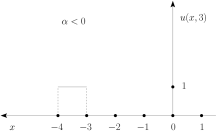
Είναι προφανές ότι η λύση $u$ του προβλήματος (1.35) διατηρεί τη μορφή της αρχικής συνάρτησης, καθώς ο χρόνος $t$ αυξάνει και ιδιαίτερα η μέγιστη κατά απόλυτο τιμή παραμένει σταθερή. Στο Σχήμα 1.3 βλέπουμε τη λύση του Παραδείγματος 1.2, για $t=3$ , αν η σταθερά $\alpha$ είναι θετική ή αρνητική.

1.2.4 Εξίσωση κύματος

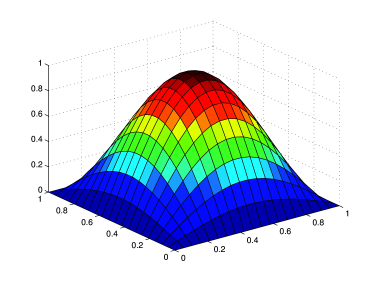
Θα θεωρήσουμε τώρα μια απλή υπερβολική διαφορική εξίσωση και συγκεκριμένα την εξίσωση του κύματος (1.6), όπου η χωρική μεταβλητή $x$ ανήκει στο διάστημα $[0,L]$ , με $L>0$ και θα θεωρήσουμε, επιπλέον, αρχικές και ομογενείς συνοριακές συνθήκες Dirichlet. Έτσι, έχουμε το ακόλουθο πρόβλημα: Ζητείται $u:[0,L]\times[0,+\infty)\to\mathbb{R}$ , τέτοια ώστε

$\displaystyle u_{tt}$	$\displaystyle=\alpha^{2}u_{xx},$	$\displaystyle\text{στο }[0,L]\times[0,+\infty)$	(1.39)
$\displaystyle u(0,t)$	$\displaystyle=u(L,t)=0,$	$\displaystyle\text{για }t\geq 0,$	(1.40)
$\displaystyle u(x,0)$	$\displaystyle=g(x),\ \text{ και }\ u_{t}(x,0)=g_{1}(x),$	$\displaystyle\text{στο }[0,L],$	(1.41)

με $\alpha>0$ και $g,g_{1}$ συνεχείς συναρτήσεις.

Χρησιμοποιώντας τη μέθοδο των χωριζομένων μεταβλητών, βλ. π.χ. (Logan, (2014)), οι συναρτήσεις $u_{n}$ , με $u_{n}=X_{n}T_{n}$ , $n=1,2,\dots$ , όπου

$\displaystyle u_{n}$	$\displaystyle=X_{n}T_{n},$	(1.42)
$\displaystyle X_{n}(x)$	$\displaystyle=c\sin{(\lambda_{n}x)},\text{ και }$	(1.43)
$\displaystyle T_{n}(t)$	$\displaystyle=d_{1}\sin(\lambda_{n}\alpha t)+d_{2}\cos(\lambda_{n}\alpha t)% \text{ με }\lambda_{n}={\frac{n\pi}{L}},\ c,d_{1},d_{2}\in\mathbb{R},$	(1.44)

ικανοποιούν την εξίσωση (1.39) και τις συνοριακές συνθήκες (1.40). Λόγω της αρχής της υπέρθεσης, κάθε γραμμικός συνδυασμός λύσεων της μορφής (1.42) ικανοποιεί τις (1.39)-(1.40). Επομένως, αν θεωρήσουμε μια άπειρη σειρά συναρτήσεων της μορφής

u(x,t)=\sum_{n=1}^{\infty}\sin(\lambda_{n}x)(c_{n}\sin(\lambda_{n}\alpha t)+d_% {n}\cos(\lambda_{n}\alpha t)),\quad\text{με }c_{n},d_{n}\in\mathbb{R},

(1.45)

η οποία συγκλίνει για κάθε $x\in[0,L]$ και $t\geq 0$ , τότε αυτή αποτελεί και λύση του προβλήματος (1.39)-(1.41). Μια λύση $u$ της μορφής (1.45) θα ικανοποιεί και την αρχική συνθήκη (1.41), αν

	$\displaystyle u(x,0)$	$\displaystyle=\sum_{n=1}^{\infty}d_{n}\sin(\lambda_{n}x)=g(x),\quad\text{με }d% _{n}\in\mathbb{R},$		(1.46)
	$\displaystyle u_{t}(x,0)$	$\displaystyle=\sum_{n=1}^{\infty}c_{n}\lambda_{n}\alpha\sin(\lambda_{n}x)=g_{1% }(x),\quad\text{με }c_{n}\in\mathbb{R}.$		(1.47)

Ένας διαφορετικός τρόπος για την περιγραφή της λύσης του προβλήματος (1.39)– (1.41) είναι η αναπαράσταση d’Alembert της λύσης, η οποία οδηγεί στην

u(x,t)=\Phi(x-\alpha t)+\Psi(x+\alpha t),

(1.48)

όπου $\Phi,\Psi$ είναι συνεχείς συναρτήσεις που εξαρτώνται από τις αρχικές συνθήκες (1.41). Μάλιστα, εύκολα μπορούμε να δούμε ότι στην περίπτωση που στην αρχική συνθήκη (1.41) η συνάρτηση $g_{1}$ μηδενίζεται στο $[0,L]$ , τότε η ακριβής λύση $u$ του προβλήματος (1.39)–(1.41) δίνεται από

u(x,t)=\dfrac{1}{2}(g(x-\alpha t)+g(x-\alpha t)).

(1.49)

Παράδειγμα 1.3.

Αν $u(x,t)=\sin(2\pi x)(\sin(2\pi t)+\cos(2\pi t))$ , τότε εύκολα βλέπουμε ότι η $u$ είναι λύση του προβλήματος (1.24)–(1.26), με $L=\alpha=1$ , $g(x)=\sin(2\pi x)$ και $g_{1}(x)=2\pi\sin(2\pi x)$ . Στο Σχήμα 1.4, απεικονίζεται η $u$ στο $[0,1]\times[0,T]$ , με $T=1$ .

Σχήμα 1.4: Η ακριβής λύση $u$ του Παραδείγματος 1.3.

1.2.5 Ελλειπτική εξίσωση

Θεωρούμε το ακόλουθο πρόβλημα: Ζητείται μια συνάρτηση $u:\Omega=(0,1)\times(0,1)\to\mathbb{R}$ , τέτοια ώστε

\begin{split}\displaystyle-(u_{xx}(x,y)+u_{yy}(x,y))+q(x,y)u(x,y)&% \displaystyle=f(x,y),\quad(x,y)\in\Omega,\\ \displaystyle u(x,y)&\displaystyle=g(x,y),\quad(x,y)\in\partial\Omega,\end{split}

(1.50)

όπου $\partial\Omega$ είναι το σύνορο του $\Omega$ , $q,f\in C(\Omega)$ , $g\in C(\partial\Omega)$ και $q(x,y)\geq 0$ , για κάθε $(x,y)\in\Omega$ . Στη συνέχεια, θα συμβολίζουμε με $q_{\min}=\min_{(x,y)\in\Omega}q(x,y)$ και $\bar{\Omega}=[0,1]\times[0,1]$ .

Η υπόθεση $q\geq 0$ είναι σημαντική για την ύπαρξη και μοναδικότητα της λύσης του προβλήματος (1.50). Παραδείγματος χάριν, αν θεωρήσουμε την

\begin{split}\displaystyle-(u_{xx}(x,y)+u_{yy}(x,y))-2\pi^{2}u(x,y)&% \displaystyle=0,\quad(x,y)\in\Omega,\\ \displaystyle u(x,y)&\displaystyle=g(x,y),\quad(x,y)\in\partial\Omega,\end{split}

(1.51)

τότε οι συναρτήσεις $u(x,y)=c\sin(\pi x)\sin(\pi y)$ , $c\in\mathbb{R}$ , αποτελούν λύσεις και, επομένως, το πρόβλημα (1.51) έχει άπειρες λύσεις.

Για τη διαφορική εξίσωση (1.50) ισχύει η αρχή του μεγίστου, η οποία δίνεται από το ακόλουθο θεώρημα, βλ. π.χ. (Larsson and V. Thomée, (2009)).

Θεώρημα 1.4.

Έστω ότι η λύση $u$ του (1.50) είναι τέτοια, ώστε $u\in C^{2}(\bar{\Omega})$ . Τότε

1.

Αν

$f(x,y)\leq 0,\quad\text{για κάθε}(x,y)\in\Omega,$

έχουμε ότι

$\max_{(x,y)\in\bar{\Omega}}u(x,y)\leq\begin{cases}\displaystyle\max_{(x,y)\in% \partial\Omega}g(x,y),&\text{αν }q\equiv 0,\\ \displaystyle\max\{\max_{(x,y)\in\partial\Omega}g(x,y),0\},&\text{αν }q\geq 0.% \end{cases}$ (1.52)
2.

Αν

$f(x,y)\geq 0,\quad\text{για κάθε}(x,y)\in\Omega,$

έχουμε ότι

$\min_{(x,y)\in\bar{\Omega}}u(x,y)\geq\begin{cases}\displaystyle\min_{(x,y)\in% \partial\Omega}g(x,y),&\text{αν }q\equiv 0,\\ \displaystyle\min\{\min_{(x,y)\in\partial\Omega}g(x,y),0\},&\text{αν }q\geq 0.% \end{cases}$ (1.53)

Παράδειγμα 1.4.

Αν $u(x,t)=\sin(\pi x)\sin(\pi y)$ , τότε εύκολα βλέπουμε ότι η $u$ είναι λύση του προβλήματος (1.50), με $g=0$ , $q=1$ και $f(x,y)=(2\pi^{2}+1)\sin(\pi x)\sin(\pi y)$ . Στο Σχήμα 1.5, απεικονίζεται η $u$ στο $[0,1]\times[0,1]$ .