2 Αναλυτική Μηχανική 2.3 Παράρτημα: Λογισμός μεταβολών 3 Δυναμικά συστήματα

2.4 Μελέτη

2.4.1 Ασκήσεις

Άσκηση 2.1.

Ταχύτητα και επιτάχυνση σε κυλινδρικές συντεταγμένες
Βρείτε τις συντεταγμένες της ταχύτητας σωματίου ( $v_{\rho},v_{\phi},v_{z}$ ) και της επιτάχυνσής του ( $a_{\rho},a_{\phi},a_{z}$ ) σε κυλινδρικές συντεταγμένες ( $\rho,\phi,z$ ), όπου $\bm{v}=v_{\rho}\bm{\hat{e}}_{\rho}+v_{\phi}\bm{\hat{e}}_{\phi}+v_{z}\bm{\hat{e% }}_{z}$ και $\bm{a}=a_{\rho}\bm{\hat{e}}_{\rho}+a_{\phi}\bm{\hat{e}}_{\phi}+a_{z}\bm{\hat{e% }}_{z}$ . Γράψτε τη Λαγκρανζιανή και τις εξισώσεις Euler-Lagrange για ένα γενικό δυναμικό $V=V(\rho,\phi,z)$ .

Άσκηση 2.2.

Ενέργεια και εξίσωση κίνησης
Aπό την εξίσωση διατήρησης της ενέργειας (2.15) να παραχθεί μία διαφορική εξίσωση δεύτερης τάξης.

Άσκηση 2.3.

Κίνηση σε παραβολικό δυναμικό σε μία διάσταση Έστω ένα σώμα το οποίο βρίσκεται σε δυναμικό $V(x)=\textstyle{\frac{1}{2}}kx^{2}$ . Δίνεται ότι η θέση του σωματίου κατά τη χρονική στιγμή $t=0$ είναι $x(t=0)=0$ και η ταχύτητά του είναι $\upsilon(t=0)=1$ . Βρείτε τη θέση του σαν συνάρτηση του χρόνου.

Άσκηση 2.4.

Μάζα εξαρτώμενη από ελατήριο
Έστω ότι ένα σωμάτιο μάζας $m$ εξαρτάται από ελατήριο σταθεράς $k$ και φυσικού μήκους $\ell$ και είναι ελεύθερο να κινείται κατακόρυφα. Η δύναμη που ασκείται στο σώμα είναι η δύναμη του ελατηρίου συν την βαρυτική δύναμη.

(α) Γράψτε τη δύναμη που ασκείται στο σώμα.
(β) Ποιά είναι η δυναμική ενέργεια που δίνει αυτή τη δύναμη;
(γ) Βρείτε την εξίσωση κίνησης και δώστε τη λύση της.

[Υπόδειξη: βρείτε τη θέση ισορροπίας του συστήματος. Ορίστε την μεταβλητή που δίνει την απόκλιση από τη θέση ισορροπίας και γράψτε την εξίσωση κίνησης με βάση την νέα αυτή μεταβλητή.]

Άσκηση 2.5.

Σώμα εξαρτώμενο από ελαστική ράβδο
Έστω ένα σωμάτιο μάζας $m$ το οποίο εξαρτάται από ελαστική ράβδο. Η ράβδος έχει φυσικό μήκος $\ell$ αλλά το μήκος της μπορεί να μεταβάλλεται όπως ένα ελατήριο σταθεράς $k$ . (α) Βρείτε γενικευμένες συντεταγμένες οι οποίες περιγράφουν το σύστημα. (β) Γράψτε τη δυναμική ενέργεια. (γ) Γράψτε τις εξισώσεις κίνησης.

Άσκηση 2.6.

Σημεία ισορροπίας εκκρεμούς
Βρείτε όλα τα σημεία ισορροπίας του απλού εκκρεμούς. Κάνετε για όλα τα σημεία την αρμονική προσέγγιση.

Άσκηση 2.7.

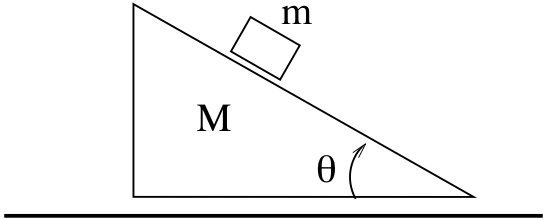
Σώμα σε κεκλιμένο επίπεδο
Σωμάτιο μάζας $m$ είναι ελεύθερο να ολισθαίνει επάνω σε κεκλιμένο επίπεδο. Το κεκλιμένο επίπεδο έχει μάζα $M$ και είναι ελεύθερο να ολισθαίνει επάνω σε επίπεδη οριζόντια βάση. (α) Γράψτε κατάλληλες γενικευμένες συντεταγμένες γιά το σύστημα, (β) γράψτε την Λαγκρανζιανή του συστήματος, (γ) γράψτε και λύστε τις εξισώσεις κίνησης.

Άσκηση 2.8.

Δυναμικό με εκθετικό
Σώμα μάζας $m$ κινείται στον άξονα $x$ σε δυναμική ενέργεια

V(x)=-Ax\,e^{-\alpha x},

όπου $A,\alpha$ είναι θετικές σταθερές. Βρείτε τη θέση ισορροπίας της μάζας. Επίσης, κάνετε την αρμονική προσέγγιση για κινήσεις κοντά στη θέση ισορροπίας και βρείτε την περίοδο αρμονικών ταλάντωσεων γύρω από αυτήν.

Άσκηση 2.9.

Κίνηση σε κύκλο
Έστω σώμα μάζας $m$ το οποίο κινείται σε κύκλο ακτίνας $a$ . (α) Θεωρήστε ότι στο σώμα δεν ασκούνται δυνάμεις και (i) γράψτε τη Λαγκρανζιανή, (ii) γράψτε την εξίσωση κίνησης και (iii) βρείτε μία διατηρήσιμη ποσότητα της κίνησης. (β) Θεωρήστε τώρα ότι το ίδιο σώμα δέχεται δύναμη τριβής ανάλογη της ταχύτητάς του $\bm{f}=-\lambda\,\bm{\upsilon}$ . Γράψτε την εξίσωση κίνησής του.

Άσκηση 2.10.

Κεντρικό δυναμικό
Ένα σώμα μάζας $m$ βρίσκεται σε βαρυτικό δυναμικό $V=V(r)$ όπου $r,\theta$ είναι πολικές συντεταγμένες.
(α) Γράψτε τη Λαγκρανζιανή και τις εξισώσεις κίνησης του συστήματος σε πολικές συντεταγμένες.
(β) Βρείτε τη στροφορμή (η οποία είναι διατηρήσιμη ποσότητα).
(γ) Θεωρήστε τώρα ότι στο σώμα ασκείται μία επιπλέον δύναμη τριβής $\bm{f}=-\lambda\,\bm{v}$ όπου $\lambda$ είναι μία σταθερά και $\bm{v}$ είναι η ταχύτητά του. Γράψτε τις εξισώσεις κίνησης του συστήματος. [Υπόδειξη: η γενικευμένη δύναμη τριβής που αντιστοιχεί στην συντεταγμένη $r$ είναι $(\bm{f}\cdot\bm{\hat{e}}_{r})$ και η γενικευμένη δύναμη για την $\theta$ είναι $(r\bm{f}\cdot\bm{\hat{e}}_{\theta})$ .]
(δ) Εάν δίνεται η αρχική στροφορμή του συστήματος (έστω $J_{0}$ για χρόνο $t=0$ ), βρείτε τη στροφορμή για τους χρόνους $t\geq 0$ .

Άσκηση 2.11.

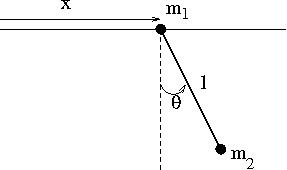
Εκκρεμές με ολισθαίνον σημείο εξάρτησης
΄Εστω ένα σωμάτιο μάζας $m_{2}$ το οποίο εξαρτάται από αβαρή ράβδο μήκους $\ell$ και η οποία μπορεί να ταλαντώνεται στο επίπεδο $(x,y)$ , όπου $x$ είναι η οριζόντια διεύθυνση και $y$ είναι η κάθετη διεύθυνση. Στο σημείο εξάρτησης της ράβδου υπάρχει μάζα $m_{1}$ η οποία μπορεί να ολισθαίνει επάνω σε οριζόντιο νήμα κατά τη διεύθυνση $x$ . Γράψτε τις εξισώσεις κίνησης της μάζας.

Άσκηση 2.12.

Αρχή του Fermat
Στη γεωμετρική οπτική η αρχή του Fermat ορίζει ότι ο χρόνος που χρειάζεται μία ακτίνα φωτός για να ταξιδέψει μεταξύ δύο σημείων είναι ελάχιστος μεταξύ όλων των διαδρομών που συνδέουν τα δύο σημεία. Περιοριστείτε στο επίπεδο και θεωρήστε μέσο με δείκτη διάθλασης $n(x,y)$ (δηλαδή, η ταχύτητα στο μέσο είναι $c(x,y)=1/n(x,y)$ ). Βρείτε την καμπύλη $y=y(x)$ την οποία ακολουθεί μία ακτίνα φωτός.

Άσκηση 2.13.

Πρόβλημα βραχυστοχρόνου
Θεωρούμε ένα σωμάτιο μάζας $m$ το οποίο κινείται σε πεδίο σταθερής δύναμης $F$ (έστω με κατεύθυνση προς τον αρνητικό άξονα $x$ ). Το σωμάτιο είναι αρχικά σε ηρεμία στη θέση $(x_{1},y_{1})$ και κινείται έως το σημείο $(x_{2},y_{2})$ . Βρείτε την τροχιά για την οποία η κίνηση θα γίνει στον ελάχιστο χρόνο.

2.4.2 Εργασίες

Εργασία 2.1.

Απλό εκκρεμές
Σχεδιάστε το δυναμικό (2.23). (α) Τι είδους κίνηση κάνει ένα σωμάτιο με ενέργεια $-mg\ell<\mathcal{E}<mg\ell$ ; Είναι η περίοδος της κίνησης μεγαλύτερη ή μικρότερη από $2\pi\sqrt{\ell/g}$ , η οποία βρέθηκε για την αρμονική προσέγγιση; (β) Τι κίνηση κάνει ένα σωμάτιο με ενέργεια $|\mathcal{E}|>mg\ell$ ; (γ) Τι κίνηση κάνει ένα σωμάτιο με ενέργεια $\mathcal{E}=mg\ell$ ; [Υπόδειξη: Δώστε κατ΄ αρχήν ποιοτικές απαντήσεις στα ερωτήματα. Η πλήρης ποσοτική μελέτη του προβλήματος είναι σχετικά εκτενής.]

Εργασία 2.2.

Δυναμικό Lennard-Jones
Θεωρούμε το δυναμικό Lennard-Jones το οποίο περιγράφει χημικούς δεσμούς μεταξύ δύο ατόμων:

V(r)=D\left(\frac{R}{r}\right)^{12}-2\left(\frac{R}{r}\right)^{6},

όπου $r$ είναι η απόσταση μεταξύ των ατόμων τα οποία συμμετέχουν στο χημικό δεσμό και $D, R$ είναι θετικές σταθερές. (α) Μελετήστε το δυναμικό και σχεδιάστε το με υπολογιστή. Περιγράψτε τον ρόλο των σταθερών. (β) Περιγράψτε τις πιθανές κινήσεις του συστήματος. (γ) Βρείτε την περίοδο της ταλάντωσης για μικρές αποκλίσεις από το ελάχιστο του δυναμικού. (δ) Για την περίπτωση περιοδικής κίνησης, βρείτε την περίοδο ταλάντωσης ως συνάρτηση της ενέργειας. Συγκρίνετε με το αποτέλεσμα που δίνει η παραβολική προσέγγιση γύρω από τη θέση ισορροπίας.

Εργασία 2.3.

Πρόβλημα Kepler
Θεωρήστε το κεντρικό δυναμικό $V(r)=-k/r^{2}$ . (α) Γράψτε τις εξισώσεις κίνησης. (β) Λύστε αναλυτικά τις εξισώσεις κίνησης. (γ) Προσδιορίσθε την κίνηση.

Βιβλιογραφία: [8].

Εργασία 2.4.

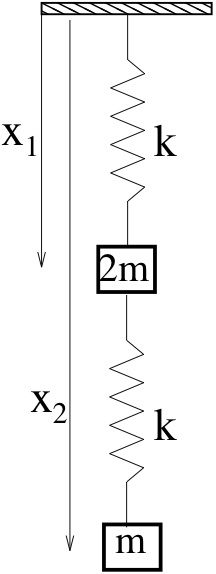
Ταλαντώσεις δύο μαζών
Σώμα μάζας $2m$ κρέμεται από κατακόρυφο ελατήριο σταθεράς $k$ και μήκους ισορροπίας $\ell$ . Από αυτήν τη μάζα κρέμεται δεύτερο ελατήριο της ίδιας σταθεράς (και ίδιου μήκους ισορροπιας) από το οποίο εξαρτάται μια δεύτερη μάζα $m$ . Θεωρήστε μόνο κατακόρυφη κίνηση των μαζών.

(α) Βρείτε τις συχνότητες των κανονικών τρόπων ταλάντωσης του συστήματος.

(β) Η επάνω μάζα $2m$ μετακινείται προς τα κάτω κατά απόσταση $d$ από τη θέση ισορροπίας της, ενώ η δεύτερη μάζα παραμένει στην αρχική θέση ισορροπίας της. Ακολούθως το σύστημα αφήνεται να ταλαντωθεί. Βρείτε την κίνηση των δύο μαζών, δηλαδή τη θέση τους σαν συνάρτηση του χρόνου.