2 Αναλυτική Μηχανική 2 Αναλυτική Μηχανική 2.2 Εξισώσεις Euler-Lagrange και Hamilton

2.1 Νόμοι του Νεύτωνα για σημειακά σωμάτια

2.1.1 Θέση, ταχύτητα και τροχιά σωματίου

Στη Μηχανική [8, 18, 10] υποθέτουμε πολλές φορές ότι τα σωμάτια δεν έχουν μέγεθος και παριστάνουμε τη θέση τους με ένα σημείο. Η θέση λοιπόν ενός σημειακού σωματίου δίνεται από ένα διάνυσμα $\bm{r}$ το οποίο παριστάνεται σε καρτεσιανές συντεταγμένες ως

\bm{r}=x\bm{\hat{\imath}}+y\bm{\hat{\jmath}}+z\bm{\hat{k}},

(2.1)

όπου $\bm{\hat{\imath}},\bm{\hat{\jmath}},\bm{\hat{k}}$ είναι μοναδιαία διανύσματα και $x, y, z$ είναι οι συντεταγμένες του σωματίου σε καρτεσιανές συντεταγμένες. Η θέση του σωματίου είναι γενικά συνάρτηση του χρόνου $\bm{r}=\bm{r}(t)$ . Η παραμετρική μορφή $\bm{r}(t)$ περιγράφει μία καμπύλη στον χώρο την οποία ονομάζουμε τροχιά του σωματίου.

Ταχύτητα λέγεται η χρονική παράγωγος της θέσης, δηλαδή το διάνυσμα

\bm{\upsilon}:=\frac{d\bm{r}}{dt}.

(2.2)

Παράδειγμα 2.1.

Έστω θέση σωματίου επάνω στον οριζόντιο άξονα

\bm{r}(t)=\alpha t\,\bm{\hat{\imath}},

όπου $\alpha$ είναι μία σταθερά. Αν υποτεθεί ότι η μεταβλητή $t$ παριστάνει τον χρόνο, τότε η παραπάνω εξίσωση δίνει τη θέση σημειακού σωματίου το οποίο κινείται ευθύγραμμα με σταθερή ταχύτητα $\bm{\upsilon}=d\bm{r}/dt=\alpha\,\bm{\hat{\imath}}$ επάνω στον άξονα $x$ .

Παράδειγμα 2.2.

Έστω το διάνυσμα θέσης σωματίου

\bm{r}(t)=\alpha t\,\bm{\hat{\imath}}-\frac{1}{2}\,gt^{2}\,\bm{\hat{\jmath}},

ώστε η ταχύτητά του είναι

\bm{\upsilon}(t)=\alpha\,\bm{\hat{\imath}}-gt\,\bm{\hat{\jmath}}.

Παράδειγμα 2.3.

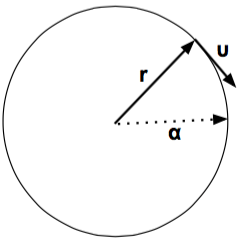
(Κυκλική κίνηση) Έστω το διάνυσμα θέσης σωματίου σε κυκλική κίνηση, όπως στο Σχήμα 2.1,

\bm{r}(t)=\alpha\left[\sin(\omega t)\,\bm{\hat{\imath}}+\cos(\omega t)\,\bm{% \hat{\jmath}}\right].

Πραγματικά το σωμάτιο αυτό βρίσκεται πάντα επάνω σε κύκλο ακτίνας $|\bm{r}|=\sqrt{\alpha^{2}\sin^{2}(\omega t)+\alpha^{2}\cos^{2}(\omega t)}=\alpha$ . Η ταχύτητά του είναι

\bm{\upsilon}(t):=\frac{d\bm{r}}{dt}=\omega\alpha\left[\cos(\omega t)\bm{\hat{% \imath}}-\sin(\omega t)\bm{\hat{\jmath}}\right].

Παρατηρούμε ότι η ταχύτητα έχει μέτρο $|\bm{\upsilon}|=\omega\alpha$ σταθερό στον χρόνο. Επίσης $\bm{\upsilon}\cdot\bm{r}=0$ , δηλαδή το διάνυσμα ταχύτητας είναι κάθετο στο διάνυσμα θέσης.

Σχήμα 2.1: Σωμάτιο σε κυκλική κίνηση ακτίνας $\alpha$ . Σημειώνεται το διάνυσμα θέσης $\bm{r}$ και ταχύτητας $\bm{\upsilon}$ σε μία χρονική στιγμή.

Παράδειγμα 2.4.

(Κυκλοειδής κίνηση) Έστω το διάνυσμα θέσης σωματίου

	$\displaystyle\bm{r}$	$\displaystyle=\bm{r}_{1}+\bm{r}_{2}$
	$\displaystyle\bm{r}_{1}(t)$	$\displaystyle=\alpha\omega t\,\bm{\hat{\imath}}+\alpha\,\bm{\hat{\jmath}}$
	$\displaystyle\bm{r}_{2}(t)$	$\displaystyle=-\left[\alpha\sin(\omega t)\,\bm{\hat{\imath}}+\alpha\cos(\omega t% )\,\bm{\hat{\jmath}}\right].$

Η θέση του σωματίου περιγράφεται από μία ευθύγραμμη ομαλή κίνηση κατά τη διεύθυνση $x$ στην οποία προστίθεται μία κυκλική κίνηση ακτίνας $\alpha$ . Η καμπύλη την οποία διαγράφει το σωμάτιο λέγεται κυκλοειδής και έχει παραμετρική έκφραση:

\bm{r}(t)=\alpha\left[\omega t-\sin(\omega t)\right]\bm{\hat{\imath}}+\alpha% \left[1-\cos(\omega t)\right]\bm{\hat{\jmath}}.

Η ταχύτητά του είναι

\bm{\upsilon}(t)=\frac{d\bm{r}_{1}}{dt}+\frac{d\bm{r}_{2}}{dt}=\omega\alpha[1-% \cos(\omega t)]\,\bm{\hat{\imath}}+\omega\alpha\sin(\omega t)\,\bm{\hat{\jmath% }}.

Παρατηρούμε ότι

•

Για $t=0$ το σωμάτιο έχει θέση και ταχύτητα

$\bm{r}=0,\qquad\bm{\upsilon}=0.$
•

Για $t=\pi/\omega$ (μία ημιπερίοδος της κυκλικής τροχιάς)

$\bm{r}=\alpha\pi\bm{\hat{\imath}}+2\alpha\bm{\hat{\jmath}},\quad\bm{\upsilon}=% 2\omega\alpha.$
•

Για $t=2\pi/\omega$ (μία πλήρης περίοδος της κυκλικής τροχιάς)

$\bm{r}=2\alpha\pi\bm{\hat{\imath}},\qquad\bm{\upsilon}=0.$

Άρα το σωμάτιο έχει $\bm{\upsilon}=0$ κάθε φορά που βρίσκεται επάνω στον άξονα $x$ .

Σύντομο πρόβλημα 2.1.

Σχεδιάστε την κυκλοειδή τροχιά στο επίπεδο κίνησης $x y$ .

2.1.2 Πολικές συντεταγμένες

Είναι πολύ συχνά ευκολότερο να περιγράψουμε τη θέση ή την κίνηση ενός σωματίου σε πολικές συντεταγμένες (παρά στις συνήθεις καρτεσιανές). Θεωρούμε τις πολικές συντεταγμένες $(r,\theta)$ και τα αντίστοιχα μοναδιαία διανύσματα $\bm{\hat{e}}_{r},\bm{\hat{e}}_{\theta}$ τα οποία είναι (δες Σχ. 2.2)

\bm{\hat{e}}_{r}=\cos\theta\,\bm{\hat{\imath}}+\sin\theta\,\bm{\hat{\jmath}},% \qquad\bm{\hat{e}}_{\theta}=-\sin\theta\,\bm{\hat{\imath}}+\cos\theta\,\bm{% \hat{\jmath}}.

(2.3)

Σχήμα 2.2: Οι πολικές συντεταγμένες $(r,\theta)$ ενός σημείου $P$ του επιπέδου. Το διάνυσμα θέσης του είναι $\bm{r}$ . Τα μοναδιαία διανύσματα του συστήματος συντεταγμένων που ορίζονται στο $P$ είναι $\bm{\hat{e}}_{r},\bm{\hat{e}}_{\theta}$ .

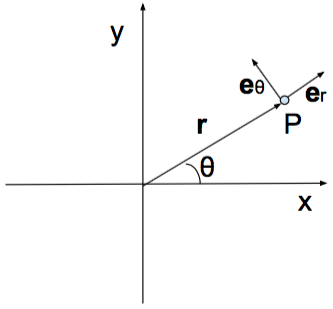
Η θέση σωματίου δίνεται από το διάνυσμα

\bm{r}=r\,\bm{\hat{e}}_{r}.

(2.4)

Η ταχύτητα του σωματίου είναι

\bm{\upsilon}=\frac{d\bm{r}}{dt}=\frac{dr}{dt}\,\bm{\hat{e}}_{r}+r\,\frac{d\bm% {\hat{e}}_{r}}{dt},

(2.5)

όπου έχουμε

\frac{d\bm{\hat{e}}_{r}}{dt}=\frac{d}{dt}(\cos\theta\,\bm{\hat{\imath}}+\sin% \theta\,\bm{\hat{\jmath}})=-\sin\theta\frac{d\theta}{dt}\,\bm{\hat{\imath}}+% \cos\theta\frac{d\theta}{dt}\,\bm{\hat{\jmath}}=\bm{\hat{e}}_{\theta}\frac{d% \theta}{dt}.

(2.6)

Χρησιμοποιούμε τον συμβολισμό $d\theta/dt:=\dot{\theta}$ και $dr/dt:=\dot{r}$ και γράφουμε τελικά

\bm{\upsilon}=\dot{r}\,\bm{\hat{e}}_{r}+r\dot{\theta}\,\bm{\hat{e}}_{\theta}.

(2.7)

Παράδειγμα 2.5.

Αν γράψουμε $\bm{r}=r\,\bm{\hat{e}}_{r}=r\,(\cos\theta\,\bm{\hat{\imath}}+\sin\theta\,\bm{% \hat{\jmath}})$ , παρατηρούμε ότι στο παράδειγμα (2.3), οι πολικές συντεταγμένες είναι $r=\alpha,\,\theta=\omega t$ . Ώστε $\dot{r}=0,\,\dot{\theta}=\omega$ και άρα έχουμε ταχύτητα

\bm{\upsilon}=\dot{r}\,\bm{\hat{e}}_{r}+r\dot{\theta}\,\bm{\hat{e}}_{\theta}=% \alpha\omega\,\bm{\hat{e}}_{\theta}.

2.1.3 Νόμοι του Νεύτωνα

Παρατήρηση 2.1.

(1ος νόμος του Νεύτωνα) Σώμα στο οποίο δεν επιδρούν δυνάμεις κινείται σε ευθύγραμμη κίνηση με σταθερή ταχύτητα.

Ας υποθέσουμε ότι παρατηρούμε ένα σώμα το οποίο βρίσκεται σε ευθύγραμμη κίνηση με σταθερή ταχύτητα. Είναι προφανές ότι ένας περιστρεφόμενος παρατηρητής δεν θα βλέπει το ίδιο σώμα να βρίσκεται σε ευθύγραμμη κίνηση. Άρα με τον 1ο νόμο του Νεύτωνα εισάγεται η έννοια ενός αδρανειακού συστήματος αναφοράς ως προς το οποίο γίνονται οι παρατηρήσεις.

Προχωρούμε τώρα να μελετήσουμε αλληλεπίδραση δύο σωμάτων. Όταν δύο σώματα αλληλεπιδρούν το πείραμα δείχνει ότι έχουμε μεταβολή των ταχυτήτων τους σε αντίθετες κατευθύνσεις:

\frac{d\bm{\upsilon}_{1}}{dt}=-c\,\frac{d\bm{\upsilon}_{2}}{dt},

όπου $c$ είναι μία σταθερά. Γράφουμε αυτή τη σχέση ως

m_{1}\,\frac{d\bm{\upsilon}_{1}}{dt}=-m_{2}\,\frac{d\bm{\upsilon}_{2}}{dt}% \Rightarrow\frac{d(m_{1}\bm{\upsilon}_{1})}{dt}=-\frac{d(m_{2}\bm{\upsilon}_{2% })}{dt}.

Οι $m_{1},m_{2}$ είναι σταθερές, λέγονται μάζες των σωμάτων, χαρακτηρίζουν το κάθε σώμα και δεν εξαρτώνται από το ζευγάρι των σωμάτων που μελετάμε.

Η παραπάνω σχέση δίνει αφορμή να ορίσουμε την γραμμική ορμή

\bm{p}:=m\bm{\upsilon}.

(2.8)

Βλέπουμε λοιπόν ότι μεταβολή της ορμής ενός σώματος προκαλείται από την επίδραση άλλου σώματος. Θα θεωρήσουμε λοιπόν ότι το κάθε σώμα ασκεί στο άλλο μία δύναμη.

Παρατήρηση 2.2.

(2ος νόμος του Νεύτωνα) Λέμε ότι σε σώμα του οποίου αλλάζει η κινητική κατάσταση (δηλαδή, του οποίου αλλάζει η ορμή) ασκείται δύναμη η οποία είναι ίση με τη μεταβολή της ορμής του:

\bm{F}=\frac{d\bm{p}}{dt}=m\,\frac{d\bm{\upsilon}}{dt}.

(2.9)

Δύο σώματα μπορεί να ασκούν δυνάμεις το ένα στο άλλο, είτε εξ επαφής είτε εξ αποστάσεως. Οι δυνάμεις που ασκούνται μεταξύ δύο σωμάτων λέγονται δυνάμεις αλληλεπίδρασης.

Παρατήρηση 2.3.

(3ος νόμος του Νεύτωνα) Οι δυνάμεις που ασκούνται μεταξύ δύο σωμάτων είναι ίσες και αντίθετες:

\bm{F}_{1}=-\bm{F}_{2}

(2.10)

και τις ονομάζουμε δράση και αντίδραση.

Από τα παραπάνω συμπεραίνουμε ότι οι μεταβολές της ορμής για ένα ζευγάρι σωμάτων είναι αντίθετες, ώστε γράφουμε

\frac{d\bm{p}_{1}}{dt}=-\frac{d\bm{p}_{2}}{dt}\Rightarrow\frac{d}{dt}(\bm{p}_{% 1}+\bm{p}_{2})=0\Rightarrow\bm{p}_{1}+\bm{p}_{2}=\hbox{σταθ.}

Η σχέση αυτή είναι βέβαια η ίδια με εκείνη που γράψαμε πριν τον 2ο νόμο, αλλά τώρα για ένα σύστημα δύο σωμάτων.

Με τη μεταβολή της ορμής $d\bm{p}/dt=m\,d\bm{\upsilon}/dt$ έχουμε ουσιαστικά εισάγει μία ακόμα βασική ποσότητα, εκείνη της επιτάχυνσης

\bm{a}:=\frac{d\bm{\upsilon}}{dt}=\frac{d^{2}\bm{r}}{dt^{2}}.

(2.11)

Η δύναμη είναι ανάλογη της επιτάχυνσης με βάση τον 2ο νόμο:

\bm{F}=m\bm{a}.

(2.12)

Παράδειγμα 2.6.

Για το σωμάτιο του παραδείγματος (2.1) βρίσκουμε την επιτάχυνση

\bm{r}=\alpha t\,\bm{\hat{\imath}}\Rightarrow\bm{\upsilon}=\alpha\,\bm{\hat{% \imath}}\Rightarrow\bm{a}=0.

Αυτό το αποτέλεσμα περιγράφει τον 1ο νόμο του Νεύτωνα. Για το παράδειγμα (2.2)

\bm{r}=\alpha t\,\bm{\hat{\imath}}-\frac{1}{2}\,gt^{2}\,\bm{\hat{\jmath}}% \Rightarrow\bm{\upsilon}=\alpha\,\bm{\hat{\imath}}-gt\,\bm{\hat{\jmath}}% \Rightarrow\bm{a}=-g\,\bm{\hat{\jmath}}

έχουμε μία σταθερή επιτάχυνση και άρα, σύμφωνα με τον 2ο νόμο Νεύτωνα, μία σταθερή δύναμη η οποία ασκείται στο σώμα. Για το παράδειγμα (2.3)

\bm{a}=-\omega^{2}\alpha\,[\sin(\omega t)\bm{\hat{\imath}}+\cos(\omega t)\bm{% \hat{\jmath}}]=-\omega^{2}\,\bm{r}

η επιτάχυνση εξαρτάται από τη θέση του σώματος.

2.1.4 Ενέργεια

Θεωρούμε σωμάτιο το οποίο κινείται από μία αρχική θέση $\bm{r}_{0}$ στην οποία βρίσκεται στον χρόνο $t=0$ σε μία τελική θέση $\bm{r}$ σε τυχόντα χρόνο $t$ . Ολοκληρώνουμε την εξίσωση του Νεύτωνα στον χώρο, κατά μήκος της τροχιάς ενός σωματίου από την αρχική στην τελική του θέση

\int_{\bm{r}_{0}}^{\bm{r}}\bm{F}\cdot d\bm{r}=\int_{\bm{r}_{0}}^{\bm{r}}m\,% \frac{d\bm{\upsilon}}{dt}\cdot d\bm{r}.

Στο δεύτερο ολοκλήρωμα αντικαθιστούμε $d\bm{r}=\bm{\upsilon}dt$ και παίρνουμε

\int_{\bm{r}_{0}}^{\bm{r}}m\,\frac{d\bm{\upsilon}}{dt}\cdot d\bm{r}=\int_{t_{0% }}^{t}m\,\frac{d\bm{\upsilon}}{dt}\cdot\bm{\upsilon}\,dt=\int_{t_{0}}^{t}\frac% {d}{dt}\left(\frac{1}{2}m\bm{\upsilon}^{2}\right)\,dt\\ =\frac{1}{2}m\bm{\upsilon}^{2}-\frac{1}{2}m\bm{\upsilon}_{0}^{2}.

Για το παραπάνω αποτέλεσμα θεωρήσαμε ότι το σωμάτιο την αρχική χρονική στιγμή $t=0$ είναι στη θέση $\bm{r}_{0}$ και έχει ταχύτητα $\bm{\upsilon}_{0}$ και τη χρονική στιγμή $t$ είναι στη θέση $\bm{r}$ και έχει ταχύτητα $\bm{\upsilon}$ . Έχουμε τελικά το αποτέλεσμα

\int_{\bm{r}_{0}}^{\bm{r}}\bm{F}\cdot d\bm{r}=T-T_{0},\qquad T:=\frac{1}{2}m% \bm{\upsilon}^{2},

(2.13)

όπου $T$ λέγεται κινητική ενέργεια του σωματίου.

Θα εξετάσουμε την ειδική περίπτωση όπου υπάρχει πραγματική συνάρτηση $V(\bm{r})$ τέτοια ώστε η δύναμη μπορεί να γραφεί ως

\bm{F}=-\bm{\nabla}V(\bm{r}).

(2.14)

Παρατήρηση 2.4.

Τη συνάρτηση $V(\bm{r})$ ονομάζουμε δυναμική ενέργεια και αυτή εξαρτάται από τη θέση του σωματίου. Η δύναμη σε κάθε θέση $\bm{r}$ δίνεται από την κλίση της δυναμικής ενέργειας μέσω της Εξ. (2.14).

Τότε

\int_{\bm{r}_{0}}^{\bm{r}}\bm{F}\cdot d\bm{r}=-\int_{\bm{r}_{0}}^{\bm{r}}\bm{% \nabla}V(\bm{r})\cdot d\bm{r}=V(\bm{r}_{0})-V(\bm{r}).

Από τις παραπάνω σχέσεις προκύπτει

V(\bm{r}_{0})-V(\bm{r})=T-T_{0}\Rightarrow V(\bm{r})+T=V(\bm{r}_{0})+T_{0}.

Ορίζουμε την ποσότητα

\mathcal{E}:=\frac{1}{2}m\bm{\upsilon}^{2}+V(\bm{r}),

(2.15)

η οποία ονομάζεται μηχανική ενέργεια και είναι μία συνάρτηση της θέσης και της ταχύτητας του σωματίου. Έχουμε λοιπόν την εξίσωση $\mathcal{E}=\mathcal{E}_{0}$ όπου $\mathcal{E}_{0}=V(\bm{r}_{0})+T_{0}$ είναι μία σταθερά, δηλαδή η ενέργεια είναι σταθερή (διατηρήσιμη) ποσότητα κατά την κίνηση του σωματίου.

Διατήρηση ενέργειας σε μία διάσταση

Η εξίσωση $T+V=\mathcal{E}_{0}$ για τη διατήρηση της ενέργειας είναι μία διαφορική εξίσωση πρώτης τάξεως για τη θέση $\bm{r}=\bm{r}(t)$ . Στην περίπτωση κίνησης σε μία διάσταση η θέση σωματίου είναι $x=x(t)$ και η εξίσωση αυτή λύνεται ως εξής

\frac{1}{2}m\left(\frac{dx}{dt}\right)^{2}+V(x)=\mathcal{E}_{0}\Rightarrow% \frac{dx}{dt}=\pm\sqrt{\frac{2}{m}\,[\mathcal{E}_{0}-V(x)]}.

(2.16)

Η Εξ. (2.16) προσδιορίζει το μέτρο της ταχύτητας σε κάθε θέση του σωματίου.

Ας θεωρήσουμε ότι το σωμάτιο ξεκινάει την κίνησή του σε χρόνο $t_{0}$ και κινείται από μία αρχική θέση $x(t=t_{0})=x_{0}$ μέχρι την τυχούσα θέση $x(t)=x$ σε χρόνο $t$ . Το χρονικό διάστημα της κίνησης βρίσκεται ολοκληρώνοντας την παραπάνω σχέση:

\int_{t_{0}}^{t}dt=\pm\int_{x_{0}}^{x}\frac{dx}{\sqrt{\frac{2}{m}\,[\mathcal{E% }_{0}-V(x)]}}\Rightarrow t-t_{0}=\pm\int_{x_{0}}^{x}\frac{dx}{\sqrt{\frac{2}{m% }\,[\mathcal{E}_{0}-V(x)]}}.

(2.17)

Αντιστρέφοντας το αποτέλεσμα αυτό μπορούμε, κατ’ αρχήν, να πάρουμε τη θέση του σωματίου ως συνάρτηση του χρόνου $x=x(t)$ .

Παράδειγμα 2.7.

Έστω ένα παραβολικό (αρμονικό) δυναμικό

V(x)=\frac{1}{2}\,kx^{2}.

Η Εξ. (2.16) δίνει

	$\displaystyle t-t_{0}$	$\displaystyle=\pm\int_{x_{0}}^{x}\frac{dx}{\sqrt{\frac{2}{m}\,[\mathcal{E}_{0}% -\frac{1}{2}\,kx^{2}]}}=\pm\int_{x_{0}}^{x}\frac{dx}{\sqrt{\frac{k}{m}}\,\sqrt% {\frac{2\mathcal{E}_{0}}{k}-x^{2}}}\Rightarrow$
	$\displaystyle\sqrt{\frac{k}{m}}$	$\displaystyle(t-t_{0})=\pm\int_{x_{0}}^{x}\frac{dx}{\sqrt{\frac{2\mathcal{E}_{% 0}}{k}-x^{2}}}=\pm\int_{x_{0}}^{x}\frac{\sqrt{\frac{k}{2\mathcal{E}_{0}}}\,dx}% {\sqrt{1-\frac{k}{2\mathcal{E}_{0}}x^{2}}}$

Για την απλοποίηση των υπολογισμών μπορούμε να χρησιμοποιήσουμε τις μεταβλητές

\bar{t}=\sqrt{\frac{k}{m}}\,t,\qquad\bar{x}=\sqrt{\frac{k}{2\mathcal{E}_{0}}}% \,x,

(2.18)

’Ωστε τώρα έχουμε

\displaystyle\bar{t}-\bar{t}_{0}=\pm\int_{\bar{x}_{0}}^{\bar{x}}\frac{d\bar{x}% }{\sqrt{1-\bar{x}^{2}}}=\pm\left[-\arccos(\bar{x})\right]_{\bar{x}_{0}}^{\bar{% x}}=\pm\left[\arccos(\bar{x}_{0})-\arccos(\bar{x})\right],

όπου έχουμε βέβαια θέσει $\bar{t}_{0}=\sqrt{k/m}\,t_{0}\,$ και $\bar{x}_{0}=\sqrt{k/(2\mathcal{E}_{0})}\,x_{0}$ . Θέτουμε τη γωνία $\theta_{0}:=\arccos(\bar{x}_{0})=\arccos(\sqrt{k/(2\mathcal{E}_{0})}\,x_{0})$ και έχουμε

		$\displaystyle\bar{t}-\bar{t}_{0}=\pm\left[\theta_{0}-\arccos(\bar{x})\right]\Rightarrow$
		$\displaystyle\arccos(\bar{x})=\pm(\bar{t}-\bar{t}_{0})+\theta_{0}\Rightarrow$
		$\displaystyle\bar{x}=\cos[\pm(\bar{t}-\bar{t}_{0})+\theta_{0}],$

ή, απλούστερα

\bar{x}(\bar{t})=\cos(\bar{t}+\phi_{0})

όπου $\phi_{0}$ είναι μία σταθερή γωνία. Επιστρέφουμε τελικά στις αρχικές μεταβλητές στις οποίες η λύση έχει την έκφραση

x(t)=\sqrt{\frac{2\mathcal{E}_{0}}{k}}\,\cos\left[\sqrt{\frac{k}{m}}\,t+\phi_{% 0}\right].

Θα μπορούσαμε να ακολουθήσουμε την παραπάνω μέθοδο για τη λύση του προβλήματος φροντίζοντας όμως να απλοποιήσουμε πρώτα τις αρχικές εκφράσεις πριν προχωρήσουμε στην ολοκλήρωση της εξίσωσης. Γράφουμε την ενέργεια

\frac{1}{2}m\left(\frac{dx}{dt}\right)^{2}+\frac{1}{2}\,kx^{2}=\mathcal{E}_{0}.

(2.19)

Θα πρέπει, πριν προχωρήσουμε στην ολοκλήρωση της εξίσωσης, να αναρωτηθούμε ποιές είναι οι πιο κατάλληλες μεταβλητές για αυτό το πρόβλημα, δηλαδή, να βρούμε κατάλληλες αδιάστατες μεταβλητές. Συγκρίνοντας τον πρώτο και δεύτερο όρο (στο αριστερό μέλος) στην εξίσωση της ενέργειας παρατηρούμε ότι η ποσότητα $\sqrt{m/k}$ έχει διαστάσεις χρόνου. Επίσης συγκρίνοντας τον δεύτερο όρο (στο αριστερό μέλος) και το δεξιό μέλος βλέπουμε ότι η ποσότητα $\sqrt{2\mathcal{E}_{0}/k}$ έχει διαστάσεις μήκους. Άρα οι αδιάστατες μεταβλητές για τον χρόνο και τη θέση είναι οι $\bar{t}$ και $\bar{x}$ τις οποίες έχουμε ήδη ορίσει στην Εξ. (2.18). Τις εισάγουμε στην εξίσωση για την ενέργεια και έχουμε

\left(\frac{d\bar{x}}{d\bar{t}}\right)^{2}+\bar{x}^{2}=1\Rightarrow\bar{t}-% \bar{t}_{0}=\pm\int_{\bar{x}_{0}}^{\bar{x}}\frac{d\bar{x}}{\sqrt{1-\bar{x}^{2}}}

(2.20)

η οποία είναι η εξίσωση την οποία ήδη βρήκαμε και στο παραπάνω παράδειγμα.

2.1.5 Δυναμική ενέργεια και δυνάμεις

Παράδειγμα 2.8.

(Σταθερό δυναμικό) Αν θεωρήσουμε τη δυναμική ενέργεια

V(x)=\hbox{σταθ.}

τότε εύκολα υπολογίζουμε τη δύναμη $F=-dV/dx=0$ . Η εξίσωση του Νεύτωνα είναι $m\ddot{x}=0\Rightarrow\dot{x}=\hbox{σταθ.}$ και εκφράζει ουσιαστικά τον 1ο νόμο του Νεύτωνα.

Παράδειγμα 2.9.

(Γραμμικό δυναμικό) Αν θεωρήσουμε τη δυναμική ενέργεια

V(x)=-c\,x,\qquad c:\hbox{σταθ.}

τότε εύκολα υπολογίζουμε τη δύναμη $F=-dV/dx=c$ . Ο νόμος του Νεύτωνα είναι $m\ddot{x}=c$ .

Για το βαρυτικό πεδίο κοντά στην επιφάνεια της Γης έχουμε $c=-mg$ όπου $m$ η μάζα σώματος και $g$ η επιτάχυνση της βαρύτητας. Τότε το δυναμικό $V=mgx$ είναι το βαρυτικό δυναμικό και η εξίσωση σώματος σε βαρυτικό δυναμικό γράφεται και λύνεται ως εξής

m\ddot{x}=-mg\Rightarrow\ddot{x}=-g\Rightarrow\dot{x}=-gt+\alpha\Rightarrow x(% t)=-\frac{1}{2}gt^{2}+\alpha t+\beta,

όπου $\alpha,\beta$ είναι σταθερές.

Παράδειγμα 2.10.

(Αρμονικός ταλαντωτής) Θα μελετήσουμε και πάλι το παραβολικό δυναμικό του παραδείγματος του προηγουμένου κεφαλαίου, ακολουθώντας όμως διαφορετική μέθοδο. Αφού γνωρίζουμε το δυναμικό μπορούμε να υπολογίσουμε τη δύναμη:

V(x)=\frac{1}{2}\,kx^{2}\Rightarrow F=-\frac{dV}{dx}=-kx.

Ώστε η εξίσωση του Νεύτωνα γίνεται

m\ddot{x}+kx=0.

(2.21)

Μας ενδιαφέρει να βρούμε τη γενική λύση της εξίσωσης η οποία δίνει τη θέση του σωματίου $x$ σαν συνάρτηση του χρόνου $t$ . Πρόκειται για μια γραμμική εξίσωση και για να βρούμε λύσεις δοκιμάζουμε τη συνάρτηση

x(t)=C\,e^{i\omega t},

όπου το $C$ είναι μιγαδική σταθερά. Αντικατάσταση στην εξίσωση κίνησης δίνει

-m\omega^{2}x+kx=0\Rightarrow\omega^{2}=\frac{k}{m}.

Ας θεωρήσουμε $\omega=\sqrt{k/m}$ και $C=Ae^{i\phi_{0}}$ όπου $A$ και $\phi_{0}$ είναι πραγματικές σταθερές. Η γενική λύση γράφεται

x(t)=A\,e^{i(\omega t+\phi_{0})}

όπου οι $A$ και $\phi_{0}$ είναι αυθαίρετες σταθερές.

Μία σημαντική παρατήρηση είναι ότι η λύση που βρήκαμε είναι μιγαδική και άρα δεν μπορεί να περιγράφει τη θέση ενός σωματίου. Όμως, επειδή η αρχική διαφορική εξίσωση είναι γραμμική, ξέρουμε ότι και το πραγματικό και το φανταστικό μέρος της λύσης είναι λύσεις της εξίσωσης. Άρα η πραγματική λύση μπορεί να γραφεί, π.χ., ως

x(t)=A\,\cos(\omega t+\phi_{0}).

Η λύση αυτή περιέχει δύο αυθαίρετες σταθερές ( $A,\phi_{0}$ ) και άρα είναι η γενική λύση της εξίσωσης δεύτερης τάξης (2.21).

Η λύση (2.22) περιγράφει μία περιοδική κίνηση η οποία είναι αρμονική ταλάντωση με πλάτος (δηλ., μέγιστη απόκλιση από το κέντρο $x=0$ της ταλάντωσης) ίσο με $A$ και συχνότητα $\omega=\sqrt{k/m}$ . Σημειώνουμε ότι η γενική λύση μπορεί να γραφεί και στη μορφή

x(t)=A\,\sin(\omega t+\phi_{0}).

(2.22)

Απλό εκκρεμές

Υποθέτουμε ότι μία σημειακή μάζα $m$ εξαρτάται από σημείο $O$ μέσω μιας αβαρούς ράβδου με μήκος $\ell$ όπως φαίνεται στο Σχήμα 2.3. Η δυναμική ενέργεια αυτού του συστήματος είναι $V=-mgh$ όπου η απόσταση $h$ μετράται κατά την κατακύρυφο από το $O$ και θεωρείται θετικό όταν η μάζα είναι χαμηλότερα του σημείου $O$ . Το σημείο αναφοράς γι΄ αυτήν τη δυναμική ενέργεια είναι το $O$ , όπου $h=0$ και άρα $V=0$ . Από το σχήμα βλέπουμε ότι $h=\ell\cos\theta$ , όπου $\theta$ είναι η γωνιά σε πολικές συντεταγμένες που μετράται από την κατακόρφο (διακεκομμένη γραμμή στο Σχήμα 2.3). Ώστε βρίσκουμε δυναμική ενέργεια

V(\theta)=-mg\ell\,\cos\theta.

(2.23)

Σχήμα 2.3: Το απλό εκκρεμές. Η μάζα $m$ εξαρτάται από σταθερό σημείο $O$ από ράβδο μήκους $\ell$ .

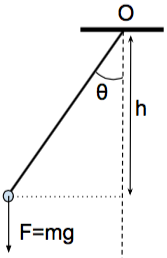
Για να γράψουμε την εξίσωση κίνησης ορίζουμε το μήκος τόξου που διανύει το σωμάτιο $s=\ell\theta$ από την κατακόρυφη θέση ισορροπίας του. Η επιτάχυνσή του είναι $\ddot{s}=\ell\ddot{\theta}$ . Από αυτήν προκύπτει η εξίσωση κίνησης

m\ddot{s}=-\frac{dV}{ds}\Rightarrow m\ell\ddot{\theta}=-\frac{1}{\ell}\,\frac{% dV}{d\theta}\Rightarrow m\ell\ddot{\theta}=-mg\sin\theta\Rightarrow\ddot{% \theta}+\frac{g}{\ell}\sin\theta=0.

(2.24)

Μία απλή λύση που μπορούμε να βρούμε είναι η $\theta(t)=0$ πράγμα που σημαίνει ότι η κατακόρυφη θέση $\theta=0$ είναι μία θέση ισορροπίας του εκκρεμούς. Γενικά, η παραπάνω εξίσωση είναι μη γραμμική και η γενική λύση της είναι περίπλοκη.

Μπορούμε όμως να μελετήσουμε μία προσέγγισή της στην περίπτωση που το εκκρεμές δεν αποκλίνει πολύ από την κατακόρυφη θέση ισορροπίας του, δηλαδή για $\theta\ll 1$ . Η προσέγγιση μπορεί να γίνει με τους ακόλουθους δύο τρόπους.

Ο πρώτος τρόπος είναι να κάνουμε την προσέγγιση στην εξίσωση κίνησης. Χρησιμοποιούμε το ανάπτυγμα Taylor για τη συνάρτηση $\sin\theta$ και θεωρούμε ότι η προσέγγιση είναι επαρκής αν κρατήσουμε μόνο τον πρώτο όρο στο ανάπτυγμα:

\sin\theta\approx\theta,\qquad\theta\ll 1.

Κάνουμε αντικατάσταση στην εξίσωση κίνησης και βρίσκουμε

\ddot{\theta}+\frac{g}{\ell}\,\theta=0.

(2.25)

Εδώ έχουμε τελικά αντικαταστήσει τον μη γραμμικό όρο ( $\sin\theta$ ) στην αρχική Εξ. (2.24) με έναν προσεγγιστικό ( $\theta$ ) ο οποίος είναι γραμμικός. Λέμε ότι έχουμε γραμμικοποιήσει την αρχική διαφορική εξίσωση. Η λύση της γραμμικής εξίσωσης (2.25) είναι

\theta(t)=A\,\cos(\omega t+\phi_{0}),\qquad\omega:=\sqrt{\frac{g}{\ell}}.

(2.26)

Δηλαδή έχουμε περιοδική κίνηση με συχνότητα $\omega$ και περίοδο $T=2\pi/\omega=2\pi\sqrt{\ell/g}$ .

Ο δεύτερος τρόπος είναι να γράψουμε το ανάπτυγμα Taylor για τη συνάρτηση $\cos\theta$ στη δυναμική ενέργεια όπου θα θεωρήσουμε ότι η προσέγγιση είναι επαρκής αν κρατήσουμε όρους μέχρι τον πρώτο μη σταθερό όρο στο ανάπτυγμα. Έχουμε

\cos\theta\approx 1-\frac{\theta^{2}}{2},\qquad\theta\ll 1,

την οποία αντικαθιστούμε στη δυναμική ενέργεια και βρίσκουμε

V(\theta)=\frac{1}{2}\,mg\ell\,\theta^{2}-mg\ell.

(2.27)

Ο σταθερός όρος στη δυναμική ενέργεια $-mg\ell$ δίνει μηδενική δύναμη, όπως έχουμε δει παραπάνω και άρα δεν θα επηρρεαστεί η εξίσωση κίνησης αν τον παραλήψουμε. Γράφουμε τελικά για το προσεγγιστικό δυναμικό

V(\theta)=\frac{1}{2}\,mg\ell\,\theta^{2}.

(2.28)

Η εξίσωση κίνησης προκύπτει τώρα ως εξής

m\ell\ddot{\theta}=-\frac{1}{\ell}\frac{dV}{d\theta}\Rightarrow\ddot{\theta}+% \frac{g}{\ell}\,\theta=0,

(2.29)

και συμπίπτει με αυτήν που βρήκαμε με τον πρώτο τρόπο.

Μπορούμε να έχουμε μία εκτίμηση της συχνότητας της κίνησης πριν καν λύσουμε τις εξισώσεις κίνησης. Παρατηρούμε ότι οι φυσικές σταθερές και οι αντίστοιχες διαστάσεις τους είναι $m :$ [μάζα], $g$ : [μήκος]/[χρόνος] ${}^{2}$ , $\ell$ : [μήκος]. Ο μόνος συνδυασμός τους που δίνει διαστάσεις [χρόνος] είναι ο $\sqrt{\ell/g}$ . Είναι λοιπόν σαφές ότι αυτή η τελευταία σταθερά θα είναι ο χαρακτηριστικός χρόνος του συστήματος (στην προκειμένη περίπτωση σχετίζεται με την περίοδο της ταλάντωσης).

Για να γίνει πιο σαφής η αξία αυτής της παρατήρησης, θα μπορούσε κανείς να ορίσει μια νέα αδιάστατη μεταβλητή $\bar{t}$ για τον χρόνο από τη σχέση

t:=\bar{t}\,\sqrt{\frac{\ell}{g}}.

(2.30)

Με τη βοήθεια αυτής η Εξ. (2.25) γράφεται

\frac{d^{2}\theta}{d\bar{t}^{2}}+\theta=0

(2.31)

όπου δεν εμφανίζεται καμμία φυσική σταθερά.

Δυναμικό χημικού δεσμού

Ο χημικός δεσμός μεταξύ δύο ατόμων προκύπτει από την αλληλεπίδραση μεταξύ τους. Μπορούμε να περιγράψουμε τέτοιες αλληλεπιδράσεις με τη βοήθεια δυναμικών και ένα εμπειρικό τέτοιο δυναμικό είναι το λεγόμενο δυναμικό Lennard-Jones

V(r)=D\left(\frac{R}{r}\right)^{12}-2\left(\frac{R}{r}\right)^{6}.

(2.32)

Αυτή η μορφή δυναμικού (η οποία παριστάνεται στο Σχήμα 2.4 με τη συνεχή γραμμή) περιγράφει δεσμούς Van der Waals μεταξύ των ατόμων, δηλαδή αλληλεπιδράσεις διπόλου-διπόλου. Η απόσταση μεταξύ των ατόμων είναι $r$ , ενώ $D$ και $R$ είναι εμπειρικές σταθερές.

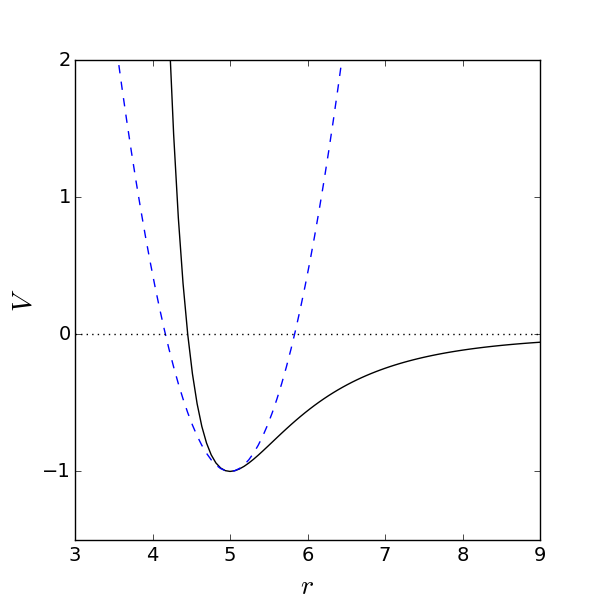
Σχήμα 2.4: Το δυναμικό Lennard Jones (για $D=1,R=5$ ) παριστάνεται με τη συνεχή γραμμή. Ένα παραβολικό δυναμικό παριστάνεται με τη διακεκομμένη γραμμή.

Για να σχεδιάσουμε το γράφημα της $V(r)$ παρατηρούμε κατ΄ αρχήν ότι

		$\displaystyle V(r)\to\infty,\qquad\hbox{όταν}\;\;r\to 0$
		$\displaystyle V(r)\to 0,\qquad\,\,\hbox{όταν}\;\;r\to\infty.$

Για να αποκτήσουμε πληρέστερη εικόνα του γραφήματος της $V$ πρέπει να βρούμε τις παραγώγους της. Η πρώτη παράγωγος είναι

\frac{dV}{dr}=\frac{12}{r}\,\left[\left(\frac{R}{r}\right)^{6}-D\left(\frac{R}% {r}\right)^{12}\right]

(2.33)

και βρίσκουμε ότι το δυναμικό έχει ακρότατο στη θέση $r=r_{0}$ , όπου

\frac{dV}{dr}\Big|_{r=r_{0}}=0\Rightarrow r_{0}=D^{1/6}R,

(2.34)

με τιμή

V(r=r_{0})=-\frac{1}{D}.

(2.35)

Συμπεραίνουμε ότι τα άτομα είναι σε κατάσταση ισορροπίας όταν βρίσκονται σε απόσταση το ένα από το άλλο $r=r_{0}$ , αφού εκεί η δύναμη μεταξύ τους $F=-dV/dr$ μηδενίζεται. Με υπολογισμό της δεύτερης παραγώγου βρίσκουμε ότι

\frac{d^{2}V}{dr^{2}}(r=r_{0})=\frac{72}{R^{2}D^{4/3}}

(2.36)

και άρα (αφού αυτή είναι θετική) έχουμε ελάχιστο.

Η σημασία της παραμέτρου $D$ φαίνεται στην Εξ. (2.35) και δίνει το βάθος του ελαχίστου δυναμικού, δηλαδή καθορίζει πόσο ισχυρός είναι ο χημικός δεσμός. Η παράμετρος $R$ καθορίζει την απόσταση μεταξύ των ατόμων στην κατάσταση ισορροπίας, όπως φαίνεται στην Εξ. (2.34). Για να γράψουμε ένα ρεαλιστικό μοντέλο Lennard-Jones θα πρέπει να χρησιμοποιήσουμε τα σχετικά πειραματικά δεδομένα από τα οποία θα προκύψουν οι δύο αυτές παράμετροι.

Αν και η γενική περιγραφή της δυναμικής των ατόμων είναι συνήθως περίπλοκη, μπορούμε όμως να την περιγράψουμε σχετικά απλά όταν αυτά βρίσκονται κοντά στη θέση ισορροπίας τους. Προσεγγίζουμε το δυναμικό με το ανάπτυγμα Taylor γύρω από το σημείο $r=r_{0}$ :

V\approx V_{0}+\frac{dV}{dr}\Big|_{r=r_{0}}(r-r_{0})+\frac{1}{2}\,\frac{d^{2}V% }{dr^{2}}\Big|_{r=r_{0}}(r-r_{0})^{2}=V_{0}+\frac{1}{2}\,\frac{d^{2}V}{dr^{2}}% \Big|_{r=r_{0}}(r-r_{0})^{2},

όπου οι $V_{0}=V(r=r_{0})$ και $d^{2}V/dr^{2}(r=r_{0})$ είναι σταθερές οι οποίες έχουν δωθεί παραπάνω. Τελικά, για μικρές τιμές της απόκλισης $\xi:=r-r_{0}$ από τη θέση ισορροπίας, το σύστημά μας περιγράφεται προσεγγιστικά από το δυναμικό

V(r)=\frac{1}{2}\,k\xi^{2},

(2.37)

όπου ορίσαμε τη σταθερά

k:=\frac{d^{2}V}{dr^{2}}(r=r_{0})=\frac{72}{R^{2}D^{4/3}}.

Επίσης, παραλείψαμε τη σταθερά $V_{0}$ η οποία δεν θα επηρρεάσει τις εξισώσεις κίνησης. Η παραβολική αυτή προσεγγιστική μορφή του δυναμικού γύρω από το ελάχιστο $r=r_{0}$ παριστάνεται στο Σχήμα 2.4 με τη διακεκομμένη γραμμή. Είναι φανερό ότι η προσέγγιση ισχύει για μικρές αποκλίσεις από τη θέση ισορροπίας, $\xi\ll R$ .

Σύντομο πρόβλημα 2.2.

Τι κίνηση θα κάνει το σύστημα των ατόμων όταν ισχύει η προσέγγιση (2.37);

Επίλυση.

Θα κάνει αρμονική ταλάντωση με συχνότητα

\omega=\sqrt{k/\mu}

όπου $\mu$ είναι η κατάλληλη μάζα. (Ποιά είναι η μάζα $\mu$ την οποία πρέπει να χρησιμοποιήσουμε σε αυτό το σύστημα;)

Δυναμικά γενικότερης μορφής

Ας υποθέσουμε ένα δυναμικό το οποίο έχει ένα τοπικό ελάχιστο όπως φαίνεται στο Σχήμα 2.5. Για να καταλάβουμε ποιοτικά την κίνηση σωματίου γύρω από το ελάχιστο του δυναμικού θα χρησιμοποιήσουμε τη σχέση που προκύπτει από τη διατήρηση της ενέργειας (2.16) και την οποία ήδη συζητήσαμε στο προηγούμενο κεφάλαιο:

\upsilon=\pm\sqrt{\frac{2}{m}\,[\mathcal{E}-V(x)]},

(2.38)

όπου $\mathcal{E}$ είναι η σταθερά που δίνει την ενέργεια του σωματίου.

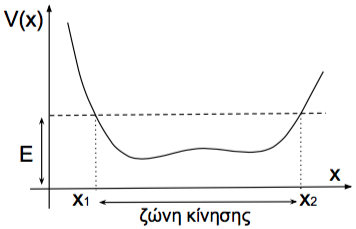
Σχήμα 2.5: Ένα δυναμικό το οποίο παρουσιάζει τοπικά ελάχιστα.

Ας υποθέσουμε ότι η $\mathcal{E}$ είναι μεγαλύτερη από το ελάχιστο του $V(x)$ και ότι έχουμε δύο σημεία $x_{1},x_{2}$ εκατέρωθεν της θέσης του ελαχίστου για τα οποία ισχύει $\mathcal{E}=V(x_{1})$ και $\mathcal{E}=V(x_{2})$ . Πρέπει να είναι σαφές ότι η κίνηση είναι δυνατή μόνο στο διάστημα $x_{1}\leq x\leq x_{2}$ όπου $\mathcal{E}>V(x)$ , δηλαδή στο διάστημα όπου η υπόριζος ποσότητα στην Εξ. (2.38) είναι μη αρνητική. Στα άκρα του διαστήματος η Εξ. (2.38) δίνει $\upsilon(x_{1})=0,\,\upsilon(x_{2})=0$ και, με βάση το Σχήμα 2.5, βλέπουμε ότι η ταχύτητα ενός σωματίου που κινείται μέσα σε αυτό το δυναμικό αλλάζει πρόσημο κάθε φορά που αυτό φθάνει στα σημεία $x_{1}$ ή $x_{2}$ . Από τα παραπάνω συμπεραίνουμε ότι ένα σωμάτιο θα παλινδρομεί μεταξύ των $x_{1}$ και $x_{2}$ .

Παρατηρούμε επίσης ότι η ταχύτητα $\upsilon$ είναι συνάρτηση της θέσης $\upsilon=\upsilon(x)$ και μόνο. Αυτή η παρατήρηση σε συνδυασμό με την Εξ. (2.38) (ή ακριβέστερα την (2.16) δείχνει ότι η χρονική διάρκεια της κίνησης από το $x_{1}$ στο $x_{2}$ και πάλι στο $x_{1}$ είναι σταθερή και άρα μπορεί κανείς τελικά να συμπεράνει ότι η κίνηση ενός σωματίου μέσα σε ένα τυχαίο δυναμικό, σαν αυτό του σχήματος, είναι περιοδική.

Σύντομο πρόβλημα 2.3.

Εφαρμόστε τις ιδέες αυτής της παραγράφου για το δυναμικό Lennard-Jones. Περιγράψτε τις πιθανές κινήσεις του συστήματος. Γράψτε την έκφραση για την περίοδο της κίνησης (όταν αυτή είναι περιοδική). Συγκρίνετε με το αποτέλεσμα που δίνει η παραβολική προσέγγιση γύρω από το $r=r_{0}$ .

Ερώτηση κατανόησης 2.1.

Σε ποιές περιπτώσεις (για ποιές ενέργειες) το σύστημα που περιγράφεται από δυναμικό Lennard-Jones δεν θα κάνει περιοδική κίνηση;

Ερώτηση κατανόησης 2.2.

Στην περίπτωση του απλού εκκρεμούς το οποίο έχει μεγάλος πλάτος ταλάντωσης, η περίοδος ταλάντωσης μικρότερη ή μεγαλύτερη από την περίοδο ταλάντωσης στην αρμονική προσέγγιση;