Σ' αυτό το κεφάλαιο θα θεωρήσουμε διωνυμικά υποδείγματα για τη δυναμική του πρωτογενούς προϊόντος στο διάστημα \([0,T]\), όπου το πλήθος των περιόδων \(N\) είναι πολύ μεγάλο, ενώ η χρονική διάρκεια που αντιστοιχεί σε μια περίοδο είναι \(h=T/N\). Θα δούμε ότι με κατάλληλη επιλογή των παραμέτρων του μοντέλου, στο όριο , καθώς \(N\to\infty\), η στοχαστική διαδικασία που περιγράφει την αξία του πρωτογενούς προϊόντος συγκλίνει σε μια γεωμετρική κίνηση Brown. Αυτή η οριακή διαδικασία συνεχούς χρόνου είναι το μοντέλο που πρότειναν οι Black & Scholes. Θα δούμε επιπλέον ότι η ακολουθία των τιμών που παίρνουμε τιμολογώντας ένα παράγωγο σύμφωνα με όσα μάθαμε στα προηγούμενα κεφάλαια συγκλίνει και αυτή , καθώς το \(N\to\infty\) και το όριό της είναι η αξία του παραγώγου, όπως υπολογίζεται από το μοντέλο των Black & Scholes. Παρόμοιο υλικό θα βρείτε και εδώ.
Ας θεωρήσουμε ένα διωνυμικό υπόδειγμα \(N\) περιόδων για τη δυναμική του πρωτογενούς προιϊόντος στο χρονικό διάστημα \([0,T]\). Η κάθε περίοδος του μοντέλου αντιστοιχεί επομένως σε χρονική διάρκεια \(h=T/N\). Εφόσον όπως είδαμε η παράμετρος \(p\) του διωνυμικού υποδείγματος δεν υπεισέρχεται στην τιμολόγηση παραγώγων, θα θεωρήσουμε ότι \(p=1/2\). Όταν το \(N\) είναι μεγάλο, το \(h\) είναι μικρό, είναι επομένως λογικό να επιλέξουμε τις παραμέτρους \(u,d\) του διωνυμικού υποδείγματος πολύ κοντά στο 1. Επιλέγουμε λοιπόν
\begin{equation} u=u(h)=e^{\mu h+\sigma \sqrt{h}}\qquad\text{και}\qquad d=d(h)=e^{\mu h-\sigma \sqrt{h}}, \end{equation}
όπου \(\mu\) και \(\sigma\) είναι θετικές παράμετροι. Με αυτή την επιλογή, αποκλείονται απότομες μεταβολές της αξίας του πρωτογενούς προϊόντος και δεν μπορούμε να δούμε στο όριο υποδείγματα συνεχούς χρόνου στα οποία η αξία του πρωτογενούς προϊόντος κάνει άλματα, όπως π.χ. οι διαδικασίες Levy. Παρότι αυτά τα υποδείγματα είναι ενδιαφέροντα και είναι πιο γενικά από το υπόδειγμα Black & Scholes, η μελέτη τους ξεφεύγει από τους σκοπούς αυτών των εισαγωγικών σημειώσεων.
Θα υποθέσουμε, όπως συνήθως, ότι στην αγορά μας είναι διαθέσιμο και ένα προϊόν χωρίς κίνδυνο με επιτόκιο \(r\).
Παρατηρήστε ότι, όταν το \(h\) είναι κατάλληλα μικρό, όταν δηλαδή το πλήθος \(N\) των περιόδων του υποδείγματος είναι κατάλληλα μεγάλο, οι περιορισμοί που επιβάλλει η αρχή της μη επιτηδειότητας,
\[ e ^{ \mu h - \sigma \sqrt{h} } < e^{rh} < e^{ \mu h + \sigma \sqrt{h} }, \]
ικανοποιούνται για οποιαδήποτε επιλογή των παραμέτρων \(\mu,\sigma,r\).
Σε αυτό το διωνυμικό υπόδειγμα, η αξία του πρωτογενούς περιγράφεται κατά τις χρονικές στιγμές
\[ 0=t_0,t_1,\ldots,t_N, \qquad \text{με } t_k=kh, \]
και έχουμε ότι
\[ S_{t_k}=S_0\prod_{i=1}^k \xi_k,\qquad k=1,2,\ldots,N, \]
όπου οι \(\{\xi_k\}_{0\le k\le N}\) είναι μια ακολουθία από ανεξάρτητες, ισόνομες, τυχαίες μεταβλητές, οι οποίες παίρνουν είτε την τιμή \(u\), είτε την τιμή \(d\), καθεμία με πιθανότητα 1/2. Μπορούμε να ξαναγράψουμε την προηγούμενη σχέση ως
\begin{equation} E_{t_k}:=\log\left(\frac{S_{t_k}}{S_0}\right)=\sum_{i=1}^k \log \xi_k =\sum_{i=1}^k \mu h+\sigma\sqrt{h} J_i=\mu t_k+\sigma\sqrt{h}\sum_{i=1}^k J_i, \end{equation}
όπου οι τυχαίες μεταβλητές \(\{J_k\}_{1\le k\le N}\) είναι ανεξάρτητες και παίρνουν τις τιμές \(\pm1\) με πιθανότητα 1/2. Επομένως, οι \(\{J_k\}\) έχουν μέση τιμή ίση με μηδέν και διασπορά ίση με 1.
Θέλουμε να περάσουμε στο όριο, καθώς \(N\to\infty\) και να εξετάσουμε την οριακή συμπεριφορά της αξίας του πρωτογενούς προϊόντος.
Έχουμε όμως το πρόβλημα ότι η τιμή του πρωτογενούς προϊόντος είναι ορισμένη για κάποιες μόνο χρονικές στιγμές στο διάστημα \([0,T]\). Για να ξεπεράσουμε αυτό το πρόβλημα, επεκτείνουμε τον ορισμό της για κάθε \(t\in[0,T]\) με γραμμική παρεμβολή των \(\{E_{t_k}\}_k\) της σχέσης (6.2). Συγκεκριμένα,
αν θεωρήσουμε κάποια χρονική στιγμή \(t\in[0,T]\), αυτή θα βρίσκεται ανάμεσα σε δύο διαδοχικές φάσεις \(t_k,t_{k+1}\) του διακριτού διωνυμικού υποδείγματος με \(N\) περιόδους,
\[ t_k \le t < t_{ k + 1 } \Leftrightarrow kh \le t\le (k+1)h, \qquad \text{ για } k = \left[ \frac{tN}{T} \right] = \left[ \frac{t}{h} \right]. \]
Ορίζουμε τότε\[ E_t^{(h)}=E_{t_k}+\frac{t-t_k}{t_{k+1}-t_k} (E_{t_{k+1}}-E_{t_k}) \]
και από την (6.2) έχουμε\begin{equation} E_t^{(h)}=\mu t+\sigma\sqrt{h}\sum_{i=1}^k J_i+\frac{\sigma(t-t_k)}{\sqrt{h}}J_{k+1}, \qquad kh\le t<(k+1)h. \end{equation}
Επεκτείνουμε τέλος την αξία του πρωτογενούς προϊόντος για κάθε \( t \in [0,T] \) ως\[ S_t^{(h)}=S_0e^{E_t^{(h)}}. \]
Προκειμένου να κατανοήσουμε την ασυμπτωτική συμπεριφορά της \(S_t^{(h)}\), καθώς \(N\to\infty\ (h\to 0) \), θα χρειαστούμε τα τρία επόμενα λήμματα από τη Θεωρία Πιθανοτήτων. Tα Λήμματα 6.1 και 6.2 είναι τα Θεωρήματα 4.4.2 και 4.4.6 αντίστοιχα στο [ Chung74 ]. Το Λήμμα 6.3 είναι άμεση συνέπεια του Λήμματος 6.1.
\begin{equation} \EEE{f(X_N)}\to\EEE{f(X)}. \end{equation}
Επιπλέον, αν \(X_N\stackrel{d}{\longrightarrow} X\) και η συνάρτηση \(f\) είναι φραγμένη και συνεχής έξω από ένα σύνολο \(A\), τότε η (6.4) ισχύει με την προϋπόθεση \(\PPP{X\in A}=0\).
Θεωρούμε μια ακολουθία τυχαίων μεταβλητών \(\{X_N\}_{N\in\N}\) τέτοια ώστε \(X_N\stackrel{d}{\longrightarrow} X\), για κάποια τυχαία μεταβλητή \(X\). Αν η \(\{Y_N\}_{N\in\N}\) είναι μια ακολουθία τυχαίων μεταβλητών, τέτοια ώστε για κάποια σταθερά \(\beta\in\R\) έχουμε
\[ \PPP{\, |Y_N-\beta|>\eps}\to 0,\quad\forall \eps>0 \]
και \(\{\alpha_N\}_{N\in\N}\) είναι μια πραγματική ακολουθία με \(\lim\alpha_N=\alpha\), τότε
\[ \alpha_NX_N+Y_N\stackrel{d}{\longrightarrow}\alpha X+\beta. \]
Αν \(\{X_N\}_{N\in\N}\) είναι μια ακολουθία τυχαίων μεταβλητών και \(g\) είναι μια συνεχής συνάρτηση, τότε
\[ X_N\stackrel{d}{\longrightarrow} X\Longrightarrow g(X_N)\stackrel{d}{\longrightarrow} g(X). \]
Ας ξαναγυρίσουμε τώρα στη σχέση (6.3). Εφόσον \(t-t_k\le t_{k+1}-t_k\le h\), έχουμε ότι
\begin{equation} \sup_{0\le t\le T}\big|\frac{\sigma(t-t_k)}{\sqrt{h}}J_{k+1}\big|\le \sigma\sqrt{h}\ \stackrel{N\to\infty}{\longrightarrow}\ 0. \end{equation}
Παρατηρήστε ακόμη ότι από το Κεντρικό Οριακό Θεώρημα, για κάθε \(t>0\) έχουμε
\begin{equation} \frac{1}{\sqrt{k}}\sum_{i=1}^k J_i=\frac{1}{\left[\frac{t}{h}\right]}\sum_{i=1}^{\left[\frac{t}{h}\right]}J_i\stackrel{d}{\longrightarrow} {\cal N}(0,1), \qquad h\to 0. \end{equation}
Για κάθε \(t\in [0,T]\), από τo Λήμμα 6.2 έχουμε ότι
\[ E_t^{(h)}\stackrel{d}{\longrightarrow} \mu t+\sigma\sqrt{t} Z, \quad\text{με } Z\sim{\cal N}(0,1) \]
και από το Λήμμα 6.3 ότι
\[ S_t^{(h)}\stackrel{d}{\longrightarrow} S_0e^{\mu t+\sigma\sqrt{t} Z}. \]
Βλέπουμε λοιπόν ότι κάθε χρονική στιγμή, η ασυμπτωτική κατανομή της αξίας του πρωτογενούς προϊόντος ακολουθεί λογαριθμική κανονική κατανομή. Από το Λήμμα 6.1 έχουμε ότι για κάθε φραγμένη συνάρτηση \(f:\R\to\R\)
\[ \EEE{f\big(S_t^{(h)}\big)}\stackrel{h\downarrow 0}{\longrightarrow} \EEE{f\big(S_0e^{\mu t+\sigma\sqrt{t} Z}\big)}. \]
Μπορούμε να ενισχύσουμε το προηγούμενο αποτέλεσμα, αν, αντί του Κεντρικού Οριακού Θεωρήματος στην (6.6) χρησιμοποιήσουμε ένα βαθύτερο αποτέλεσμα, την αρχή του αναλλοίωτου (invariance principle) του Monroe Donsker. Το Κεντρικό Οριακό Θεώρημα μας δίνει πληροφορία για την κατανομή της \(E_t^{(h)}\) σε μια συγκεκριμένη χρονική στιγμή \(t\). Η αρχή του Donsker περιγράφει την ασυμπτωτική συμπεριφορά ολόκληρης της στοχαστικής διαδικασίας \(\{W_t^{(h)}\}_{0\le t\le T}\), με
\[ W_t^{(h)}={\sqrt{h}}\sum_{i=1}^{\left[\frac{t}{h}\right]}J_i. \]
Το συμπέρασμά της αρχής του Donsker είναι ότι η \(\{W_t^{(h)}\}_{0\le t\le T}\) συμπεριφέρεται ασυμπτωτικά όπως η κίνηση Brown \(\{W_t\}_{0\le t\le T}\). Η κίνηση Brown είναι μια στοχαστική διαδικασία με συνεχή μονοπάτια που χαρακτηρίζεται από το ότι έχει ανεξάρτητες, χρονικά ομοιογενείς και κανονικές προσαυξήσεις. Συγκεκριμένα, { αν } \(0\le s\le t\), { η τυχαία μεταβλητή } \(W_t-W_s\) είναι ανεξάρτητη από τις \(\{W_r\}_{0\le r\le s}\) και ακολουθεί κανονική κατανομή \({\cal N}(0,t-s)\). Ειδικότερα, για κάθε \(t\ge 0\) έχουμε ότι \(W_t\sim{\cal N}(0,t)\). Ένα τυπικό μονοπάτι της κίνησης Brown φαίνεται στο Σχήμα 6.1. Aς εφοδιάσουμε τον χώρο των συνεχών μονοπατιών \(C\big([0,T];\R\big)\) με την τοπολογία που προέρχεται από τη νόρμα
\[ \|x\|=\sup_{0\le t\le T}|x(t)| \]
και ας θεωρήσουμε μια φραγμένη και συνεχή συνάρτηση \(f:C\big([0,T];\R\big)\to \R\). Από τη σχέση (6.5), την αρχή του Donsker και το Λήμμα 6.1 έχουμε ότι
\[ \EEE{f\big(\{S_t^{(h)}\}_{0\le t\le T}\big)}\stackrel{h\downarrow 0}{\longrightarrow} \EEE{f\big(\{S_0e^{\mu t+\sigma W_t}\}_{0\le t\le T}\big)}. \]
Η ασυμπτωτική συμπεριφορά που βρήκαμε για την αξία του πρωτογενούς προϊόντος, στο όριο , καθώς \(h\to 0\), είναι ακριβώς η υπόθεση του μοντέλου των Black & Scholes στο οποίο η αξία \(\{S_t\}_{t\ge 0}\) του πρωτογεννούς προϊόντος περιγράφεται από την
\begin{equation} S_t=S_0e^{\mu t+\sigma W_t}, \end{equation}
όπου η \(\{W_t\}_{t\ge 0}\) είναι κίνηση Brown. Η στοχαστική διαδικασία στο δεξί μέλος της (6.7) αναφέρεται ως γεωμετρική κίνηση Brown (geometric brownian motion). Η παράμετρος \(\mu\) του μοντέλου ονομάζεται τάση (drift), ενώ η παράμετρος \(\sigma\) του μοντέλου ονομάζεται μεταβλητότητα (volatility).

Στην προηγούμενη παράγραφο θεωρήσαμε διωνυμικά υποδείγματα \(N\) περιόδων και, με κατάλληλη επιλογή των παραμέτρων τους, είδαμε ότι μπορούμε να πάρουμε το μοντέλο των Black & Scholes στο όριο, καθώς \(N\to\infty\). Ας θεωρήσουμε τώρα ένα ευρωπαϊκού τύπου παράγωγο με ωρίμανση \(T\) και απόδοση \(f(S_T)\). Μπορούμε να τιμολογήσουμε το παράγωγο σε καθένα από τα παραπάνω διωνυμικά υποδείγματα όπως στα προηγούμενα κεφάλαια. Θα προκύψει έτσι μια αριθμητική ακολουθία \(\{V_N\}_N\)
των αρχικών αξιών του παραγώγου. Σε αυτήν την παράγραφο θα ασχοληθούμε με την ασυμπτωτική συμπεριφορά αυτής της ακολουθίας. Θα δούμε ότι κάθώς \(N\to\infty\) η ακολουθία αυτή συγκλίνει και θα υπολογίσουμε το όριό της.
Είδαμε στο Κεφάλαιο 4 ότι, προκειμένου να τιμολογήσουμε ένα παράγωγο με βάση το διωνυμικό υπόδειγμα, αρκεί να υπολογίσουμε την αναμενόμενή του απόδοση στην ωρίμανση \(Τ\) ως προς το αδιάφορο κινδύνου μέτρο πιθανότητας και να την προεξοφλήσουμε στον χρόνο, πολλαπλασιάζοντας με τον παράγοντα \(e^{-rT}\). Το αδιάφορο κινδύνου μέτρο πιθανότητας \(\QQ_N\) για το διωνυμικό υπόδειγμα με \(N\) περιόδους είδαμε ότι κάνει τις \(\{\xi_k\}_{1\le k\le N}\) ανεξάρτητες, ισόνομες τυχαίες μεταβλητές με κατανομή που δίνεται από τις
\begin{equation} \QQ_N\big[\xi_k=u\big]=q_h=\frac{e^{rh}-d}{u-d}=\frac{e^{rh}-e^{\mu h-\sigma \sqrt{h}}}{e^{\mu h+\sigma \sqrt{h}}-e^{\mu h-\sigma \sqrt{h}}} \end{equation}
και\[ \QQ_N\big[\xi_k=d\big]=1-q_h=\frac{u-e^{rh}}{u-d}=\frac{e^{\mu h+\sigma \sqrt{h}}-e^{rh}}{e^{\mu h+\sigma \sqrt{h}}-e^{\mu h-\sigma \sqrt{h}}} \]
Ακριβώς όπως και στην (6.2) μπορούμε να γράψουμε ότι
\begin{equation} E_{t_k}:=\log\left(\frac{S_{t_k}}{S_0}\right)=\sum_{i=1}^k \log \xi_k =\sum_{i=1}^k \mu h+\sigma\sqrt{h} J_i=\mu t_k+\sigma\sqrt{h}\sum_{i=1}^k J_i. \end{equation}
Οι τυχαίες μεταβλητές \(\{J_k\}_{1\le k\le N}\) συνεχίζουν να είναι ανεξάρτητες ως προς οποιόδηποτε \(\QQ_N\), η κατανομή τους όμως είναι διαφορετική ως προς διαφορετικά \(\QQ_N\). Συγκεκριμένα, έχουμε ότι
\[ \QQ_N\big[J_k=+1\big]=q_h \qquad\text{ και }\qquad \QQ_N\big[J_k=-1\big]=1-q_h. \]
Ειδικότερα, οι \(J_k\) έχουν μέση τιμή \(m_h=\EE^{\QQ_N}\big[J_k\big]=2q_h-1\) και διασπορά
\[ \sigma_h^2=\EE^{\QQ_N}\big[J_k^2\big]-\left(\EE^{\QQ_N}\big[J_k\big]\right)^2=1-(2q_h-1)^2=4q_h(1-q_h). \]
Θα επεκτείνουμε και πάλι τον ορισμό της αξίας του πρωτογενούς προϊόντος σε όλους τους χρόνους \(t\in[0,T]\) παρεμβάλλοντας γραμμικά τις \(\{E_{t_k}\}_{0\le k\le N}\), ακριβώς όπως στην (6.3). Αν εισαγάγουμε τις μεταβλητές
\[ J_k^{(Ν)}=\frac{J_k+1-2q_h}{\sqrt{4q_h(1-q_h)}}, \]
οι οποίες ως προς το μέτρο πιθανότητας \(\QQ_N\) έχουν μέση τιμή ίση με 0 και διασπορά ίση με 1, μπορούμε τώρα να γράψουμε για \(kh\le t\le (k+1)h\)
\begin{align} E_t^{(h)}&=\mu t+\sigma\sqrt{h}\sum_{i=1}^k J_i+\frac{\sigma(t-t_k)}{\sqrt{h}}J_{k+1}\nonumber\\ &=\mu t +\big(\sigma\sqrt{h}k+\frac{\sigma(t-t_k)}{\sqrt{h}}\big)(2q_h-1)+\sigma\sqrt{h}\sum_{i=1}^k (J_i+1-2q_h)+\frac{\sigma(t-t_k)}{\sqrt{h}}(J_{k+1}+1-2q_h)\nonumber\\ &=\big(\mu+\frac{(2q_h-1)\sigma}{\sqrt{h}}\big)t+\sigma\sqrt{4hq_h(1-q_h)}\sum_{i=1}^k J_i^{(N)}+\frac{\sigma(t-t_k)}{\sqrt{h}}(J_{k+1}+1-2q_h). \end{align}
Όπως και στην (6.5) μπορούμε εύκολα να δούμε ότι
\begin{equation} \sup_{0\le t\le T}\big|\frac{\sigma(t-t_k)}{\sqrt{h}}(J_{k+1}+1-2q_h)\big|\le 2\sigma\sqrt{h}\ \stackrel{N\to\infty}{\longrightarrow}\ 0. \end{equation}
Υπάρχουν όμως δύο διαφορές σε σχέση με το επιχείρημα για τη σύγκλιση που αναπτύξαμε στην προηγούμενη παράγραφο. Η πρώτη διαφορά είναι ότι θα πρέπει να κατανοήσουμε την ασυμπτωτική συμπεριφορά του όρου
\[ \frac{2q_h-1}{\sqrt{h}}, \]
καθώς \(h\to 0\), που δεν υπήρχε στην προηγούμενη παράγραφο. Αυτό δεν είναι ιδιαίτερα δύσκολο. Από την (6.8) έχουμε ότι
\begin{align} \frac{2q_h-1}{\sqrt{h}}&=\frac{2e^{(r-\mu)h}-e^{\sigma\sqrt{h}}-e^{-\sigma\sqrt{h}}}{\sqrt{h}\big(e^{\sigma\sqrt{h}}-e^{-\sigma\sqrt{h}}\big)}\nonumber\\ &=\frac{2\big(e^{(r-\mu)h}-1\big)-\big(e^{\sigma\sqrt{h}/2}-e^{-\sigma\sqrt{h}/2}\big)^2}{\sqrt{h}\big(e^{\sigma\sqrt{h}}-e^{-\sigma\sqrt{h}}\big)}\nonumber \end{align}
Διαιρώντας αριθμητή και παρονομαστή του δεξιού μέλους με \(h\) και χρησιμοποιώντας ότι
\[ \lim_{x\to 0}\frac{e^{ax}-e^{-ax}}{x}=2\lim_{x\to 0}\frac{\sinh(ax)}{x}=2a, \]
παίρνουμε ότι\begin{equation} \lim_{h\to 0}\frac{2q_h-1}{\sqrt{h}}=\frac{2(r-\mu)-\sigma^2}{2\sigma}. \end{equation}
Επιπλέον, από το παραπάνω αποτέλεσμα προκύπτει αμέσως ότι\[ 4q_h(1-q_h)=1-(2q_h-1)^2\to 1,\quad h\to 0. \]
Η δεύτερη διαφορά σε σχέση με την προηγούμενη παράγραφο είναι ότι η κατανομή των τυχαίων μεταβλητών \(J_k^{(N)}\) μεταβάλλεται με το \(N\), είναι δηλαδή διαφορετική σε κάθε διωνυμικό δέντρο που χρησιμοποιούμε για την προσέγγιση. Επομένως, στην (6.6) δεν μπορούμε να επικαλεστούμε το κλασικό Κεντρικό Οριακό Θεώρημα. Αυτό που έχουμε εδώ είναι μια τριγωνική διάταξη (triangular array) τυχαίων μεταβλητών.
\begin{align} &J_1^{(1)}\nonumber\\ &J_1^{(2)}, J_2^{(2)}\nonumber\\ &J_1^{(3)}, J_2^{(3)}, J_3^{(3)}\\ &\quad\vdots\qquad\qquad\qquad\ddots\nonumber\\ &J_1^{(N)}, J_2^{(N)}, J_3^{(N)},\cdots, J_N^{(N)}.\nonumber \end{align}
Οι τυχαίες μεταβλητές κάθε γραμμής είναι ανεξάρτητες και ισόνομες, αλλά η κοινή κατανομή κάθε γραμμής μπορεί να είναι διαφορετική. Το Κεντρικό Οριακό Θεώρημα μπορεί να γενικευτεί και για τριγωνικές διατάξεις, όπως αυτή παραπάνω (δείτε π.χ. την Παράγραφο 7.1 στο [ Chung74 ]). Παίρνουμε έτσι ότι για κάθε \(t>0\)
\begin{equation} \frac{1}{\sqrt{k}}\sum_{i=1}^k J_i^{(N)}=\frac{1}{\left[\frac{t}{h}\right]}\sum_{i=1}^{\left[\frac{t}{h}\right]}J_i^{(N)}\stackrel{d}{\longrightarrow} {\cal N}(0,1), \qquad h\to 0. \end{equation}
Από τις σχέσεις 6.9, 6.11, 6.12 και το Λήμμα 6.2 έχουμε τώρα ότι για κάθε \(t\in [0,T]\),
\[ E_t^{(h)}\stackrel{d}{\longrightarrow} \big(r-\frac{\sigma^2}{2}\big) t+\sigma\sqrt{t} Z, \quad\text{με } Z\sim{\cal N}(0,1). \]
Από το Λήμμα 6.3 παίρνουμε ότι
\[ S_t^{(h)}\stackrel{d}{\longrightarrow} S_0e^{\big(r-\frac{\sigma^2}{2}\big) t+\sigma\sqrt{t} Z}. \]
Τέλος, επειδή η κανονική κατανομή είναι συνεχής, από το Λήμμα 6.1 έχουμε ότι για κάθε φραγμένη συνάρτηση \(f:\R\to\R\), η οποία έχει το πολύ αριθμήσιμα σημεία ασυνέχειας,
\begin{equation} \EE^{\QQ_N}\big[{f\big(S_t\big)}\big]\longrightarrow \EEE{f\big(S_0e^{\big(r-\frac{\sigma^2}{2}\big) t+\sigma\sqrt{t} Z}\big)}. \end{equation}
Στο σημείο αυτό είναι απαραίτητο να σχολιάσουμε το αποτέλεσμα στο οποίο καταλήξαμε.
Από το Θεώρημα 4.6 έχουμε ότι, αν τιμολογήσουμε με βάση το διωνυμικό υπόδειγμα \(N\) περιόδων ένα ευρωπαϊκό παράγωγο με απόδοση \(V_T=f(S_T)\), η αρχική αξία του παραγώγου, όπως προσδιορίζεται από την αρχή της μη επιτηδειότητας, είναι ίση με
\[ V_0^{(N)}=e^{-rT}\EE^{\QQ_N}\big[f\big(S_T\big)\big]. \]
Η σχέση (6.15) δίνει ότι, τουλάχιστον στην περίπτωση που η συνάρτηση της απόδοσης του παραγώγου \(f\) είναι φραγμένη και έχει το πολύ αριθμήσιμα σημεία ασυνέχειας, τότε η ακολουθία των αρχικών αξιών του παραγώγου συγκλίνει, καθώς \(N\to\infty\) και το όριό της δίνεται από την
\[ V_0=e^{-rT} \EEE{f\big(S_0e^{\big(r-\frac{\sigma^2}{2}\big) T+\sigma\sqrt{T} Z}\big)}, \]
όπου η τυχαία μεταβλητή \(Z\) ακολουθεί την τυπική κανονική κατανομή. Υπολογίζοντας την παραπάνω αναμενόμενη τιμή με τη βοήθεια της συνάρτησης πυκνότητας πιθανότητας της \(Z\), έχουμε ότι
\begin{equation} V_0=e^{-rT}\int_{-\infty}^{+\infty} f\big(S_0 e^{\big(r-\frac{\sigma^2}{2}\big) T+\sigma\sqrt{T} x}\big)\ e^{-\frac{x^2}{2}}\frac{dx}{\sqrt{2\pi}}. \end{equation}
Αυτός είναι ο διάσημος τύπος των Black & Scholes για την τιμολόγηση παραγώγων ευρωπαϊκού τύπου. Στην επόμενη παράγραφο θα δούμε πώς μπορούμε να τον εφαρμόσουμε για να υπολογίσουμε την παρούσα αξία ευρωπαϊκών δικαιωμάτων αγοράς και πώλησης.
Αξίζει να προσέξουμε ότι το τελικό αποτέλεσμα (6.16) για την αξία ενός παραγώγου στο υπόδειγμα των Black & Scholes δεν εξαρτάται από την τάση \(\mu\) του υποδείγματος που εμφανίζεται στην (6.7). Η τάση εκφράζει τον μέσο ρυθμό μεγέθυνσης της αξίας του πρωτογενούς προϊόντος. Από την (6.7) και το γεγονός ότι \(\EEE{W_t}=0\) έχουμε ότι
\[ \mu=\frac{1}{t}\log\left(\frac{S_t}{S_0}\right). \]
Είναι με άλλα λόγια η τάση για αύξηση που αποδίδει το υπόδειγμα στην αξία του πρωτογενούς προϊόντος. Το ότι η τελική αξία του παραγώγου δεν εξαρτάται από το \(\mu\) είναι σε αντιστοιχία με το ότι η αξία ενός παραγώγου με βάση το διωνυμικό υπόδειγμα δεν εξαρτάται από την υποκειμενική πιθανότητα \(p\), την οποία αποδίδει το υπόδειγμα στο ενδεχόμενο ανόδου της αξίας του πρωτογενούς προϊόντος σε μια περίοδο. Επομένως, δύο επενδυτές, μπορεί ενδεχομένως να έχουν διαφορετικές πεποιθήσεις για την τάση αύξησης της αξίας μιας μετοχής, θα συμφωνήσουν όμως για τη δίκαιη τιμή ενός παραγώγου αυτής της μετοχής.
Είδαμε ότι η (6.15) μας εξασφαλίζει ότι η αξία ενός παραγώγου με απόδοση στην ωρίμανση \(V_T=f(S_T)\), όπως προσδιορίζεται βάσει του διωνυμικού υποδείγματος \(N\) περιόδων, συγκλίνει, καθώς \(N\to\infty\), στην αξία του παραγώγου βάσει του υποδείγματος Black & Scholes, όταν η \(f\) είναι μια φραγμένη συνάρτηση με αριθμήσιμα το πολύ σημεία ασυνέχειας. Αυτό μας καλύπτει π.χ. για την περίπτωση ενός ευρωπαϊκού δικαιώματος πώλησης, για το οποίο
\[ f(x)=(K-x)^+. \]
Στην πράξη, δεν υπάρχουν ενδιαφέροντα παράγωγα, για τα οποία η \(f\) να έχει περισσότερες από πεπερασμένου πλήθους ασυνέχειες. Υπάρχουν όμως παράγωγα για τα οποία η \(f\) δεν είναι φραγμένη, όπως για παράδειγμα το ευρωπαϊκό δικαίωμα αγοράς. Μπορούμε να πούμε κάτι για τη σύγκλιση, στο όριο κλίμακας του διωνυμικού υποδείγματος, της αξίας τέτοιων παραγώγων?
Το ίδιο το πρωτογενές προϊόν είναι ένα παράγωγο του εαυτού του, με συνάρτηση απόδοσης την ταυτοτική συνάρτηση \(f(x)=x\) που δεν είναι φραγμένη. Μπορούμε πάντα να αντισταθμίσουμε αυτό το παράγωγο με ένα χαρτοφυλάκιο που περιέχει μία μονάδα του πρωτογενούς προϊόντος, οπότε η αρχική αξία αυτού του παραγώγου οφείλει, λόγω της αρχής της μη επιτηδειότητας, να είναι \(S_0\), ανεξαρτήτως του υποδείγματος που θα χρησιμοποιούμε.
Συμπεραίνουμε λοιπόν ότι, τουλάχιστον γι' αυτό το παράγωγο που δεν έχει φραγμένη συνάρτηση απόδοσης, η αξία που υπολογίζουμε με βάση το διωνυμικό υπόδειγμα \(N\) περιόδων συγκλίνει, κάθώς \(N\to\infty\), στην αξία του παραγώγου βάσει του υποδείγματος Black & Scholes.
Ας ανακαλέσουμε τώρα την ισοτιμία ευρωπαϊκών δικαιωμάτων αγοράς και πώλησης (1.2). Αποδείξαμε την ισοτιμία
χρησιμοποιώντας μόνο την αρχή της μη επιτηδειότητας, επομένως αυτή είναι σε ισχύ ανεξάρτητα από το μοντέλο που θα υιοθετήσουμε για τη δυναμική του πρωτογενούς προϊόντος. Αν λοιπόν \(c^{(N)}(S_0,T,K)\) και \(p^{(N)}(S_0,T,K)\) είναι οι αξίες των ευρωπαϊκών δικαιωμάτων αγοράς και πώλησης αντίστοιχα, όπως υπολογίζονται με βάση το διωνυμικό υποδειγμα \(N\) περιόδων, έχουμε ότι
\[ c^{(N)}(S_0,T,K)=p^{(N)}(S_0,T,K)+S_0-K\,B(0,T). \]
Εφόσον η \(p^{(N)}(S_0,T,K)\) τείνει, καθώς \(N\to\infty\), στην αξία \(p(S_0,T,K)\), όπως αυτή υπολογίζεται από το υπόδειγμα Black & Scholes, θα έχουμε ότι
\[ c^{(N)}(S_0,T,K)\to p(S_0,T,K)+S_0-K\,B(0,T)=c(S_0,T,K), \]
όπου η τελευταία σχέση ισχύει γιατί και στο υπόδειγμα Black & Scholes η αξία \(c(S_0,T,K)\) ενός ευρωπαϊκού δικαιώματος αγοράς θα πρέπει να σχετίζεται με την αξία του αντίστοιχου δικαιώματος πώλησης, σύμφωνα με τη σχέση ισοτιμίας (1.2). Βλέπουμε λοιπόν ότι και για το ευρωπαϊκό δικαίωμα αγοράς, για το οποίο η συνάρτηση απόδοσης δεν είναι φραγμένη, η ακολουθία των αξιών που υπολογίζουμε με βάση το διωνυμικό υπόδειγμα συγκλίνει στην αξία του διακαιώματος με βάση το υπόδειγμα Black & Scholes.
Μπορεί να αποδειχθεί, χρησιμοποιώντας πιο προχωρημένα εργαλεία από την Θεωρία Πιθανοτήτων, ότι, αν η συνάρτηση απόδοσης ενός ευρωπαϊκού παραγώγου έχει το πολύ αριθμήσιμο πλήθος ασυνεχειών και μεγαλώνει το πολύ πολυωνυμικά, αν δηλαδή υπάρχουν \(p\in\NN\) και σταθερά \(C\), τέτοια ώστε
\[ f(x)\le C(1+x^p),\qquad\text{για κάθε }x>0, \]
τότε η αρχική αξία του παραγώγου \(V_0^{(N)}\), όπως υπολογίζεται με βάση το διωνυμικό υπόδειγμα \(N\) περιόδων, συγκλίνει στην αρχική αξία που δίνει στο παράγωγο το υπόδειγμα Black & Scholes, η οποία υπολογίζεται από την (6.16.
Στην προηγούμενη παράγραφο αναφέραμε ότι, αν αντί για το Κεντρικό Οριακό Θεώρημα, χρησιμοποιήσει κανείς την αρχή του Donsker, μπορεί να αποδείξει τη σύγκλιση κατά κατανομή όχι μόνο της αξίας του πρωτογενούς προϊόντος σε μια δεδομένη χρονική στιγμή, αλλά ολόκληρης της τροχιάς. Κάτι αντίστοιχο μπορεί να αποδείξει κανείς και στην περίπτωση της τριγωνικής διάταξης (6.13). Σε αυτήν την περίπτωση το συμπέρασμα που προκύπτει από τις (6.9), (6.10) και (6.12) είναι ότι η στοχαστική διαδικασία \(\{S_t^{(h)}\}_{0\le t\le T}\) συγκλίνει στη γεωμετρική κίνηση Brown \(\{S_t\}_{0\le t\le T}\), με
\begin{equation} S_t=S_0e^{\big(r-\frac{\sigma^2}{2}\big)t+\sigma W_t}. \end{equation}
Αν θεωρήσουμε τώρα μια φραγμένη και συνεχή συνάρτηση \(f:C\big([0,T];\R\big)\to \R\), έχουμε ότι
\[ e^{-rT}\EEE{f\big(\{S_t^{(h)}\}_{0\le t\le T}\big)}\stackrel{h\downarrow 0}{\longrightarrow}e^{-rT} \EEE{f\big(\{S_0e^{\big(r-\frac{\sigma^2}{2}\big) t+\sigma W_t}\}_{0\le t\le T}\big)}. \]
Βλέπουμε λοιπόν ότι για μια μεγάλη οικογένεια παραγώγων η αρχική αξία που υπολογίζουμε με βάση το διωνυμικό υπόδειγμα \(N\) περίοδων, συγκλίνει, καθώς \(N\to\infty\), ακόμα κι αν η απόδοση του παραγώγου στην ωρίμανση
\[ V_T=f\big(\{S_t\}_{0\le t\le T}\big), \]
εξαρτάται από ολόκληρη την τροχιά του πρωτογενούς προϊόντος. Το όριο το οποίο φαίνεται στο δεξί μέλος της παραπάνω σχέσης είναι η αξία του παραγώγου, όπως αυτή υπολογίζεται στο υπόδειγμα Black & Scholes. Όπως και στην περίπτωση του διωνυμικού υποδείγματος, η σημερινή αξία του παραγώγου είναι η προεξοφλημένη αναμενόμενη απόδοση του παραγώγου, ως προς κάποιο μέτρο πιθανότητας \(\QQ\).
\[ V_0=e^{-rT}\EE^{\QQ}\big[V_T\big]. \]
Κάτω από το μέτρο \(\QQ\), η τιμή του πρωτογενούς προϊόντος συμπεριφέρεται όπως η γεωμετρική κίνηση Brown που περιγράφεται στην (6.17). Βλέπουμε και πάλι ότι το μέτρο \(\QQ\) που πρέπει να χρησιμοποιήσουμε προκειμένου να τιμολογήσουμε ένα παράγωγο σύμφωνα με την παραπάνω σχέση, είναι εν γένει διαφορετικό από το μέτρο \(\PP\), το οποίο αντανακλά τις πεποιθήσεις μας για τη δυναμική του πρωτογενούς προϊόντος. Κάτω από μέτρο \(\PP\) η αξία του πρωτογενούς προϊόντος συμπεριφέρεται όπως η γεωμετρική κίνηση Brown που περιγράφεται στην (6.7).
(κάπως προχωρημένη, μπορεί να παραληφθεί σε μια πρώτη ανάγνωση). Μπορούμε να χρησιμοποιήσουμε την ιδιότητα των ανεξάρτητων προσαυξήσεων της κίνησης Brown για να δείξουμε ότι το μέτρο πιθανότητας \(\QQ\) είναι ένα μέτρο martingales. Πράγματι, αν \(0\le s\le t\) έχουμε
\begin{align*} \EE^{\QQ}\big[e^{-rt}S_t\,\big|\, \F_s\big]&=e^{-rs}\ \EE^{\QQ}\big[S_s e^{\sigma(W_t-W_s)-\frac{\sigma^2}{2}(t-s)}\,\big|\, \F_s\big]\\ &=e^{-rs}S_s\ \EE^{\QQ}\big[e^{\sigma(W_t-W_s)-\frac{\sigma^2}{2}(t-s)}\,\big|\, \F_s\big]\\ &=e^{-rs}S_s\ \EE^{\QQ}\big[e^{\sigma(W_t-W_s)-\frac{\sigma^2}{2}(t-s)}\big]\\ &=e^{-rs}S_s\ e^{-\frac{\sigma^2}{2}(t-s)}\EE^{\QQ}\big[e^{\sigma W_{t-s}}\big]\\ &=e^{-rs}S_s. \end{align*}Η δεύτερη και η τρίτη ισότητα παραπάνω προκύπτουν από τις ιδιότητες 4 και 3 του Θεωρήματος 4.2 αντίστοιχα. Η τέταρτη ισότητα είναι κλασικός υπολογισμός της εκθετικής ροπογεννήτριας μιας κανονικής τυχαίας μεταβλητής.
Σε αυτήν την παράγραφο θα ασχοληθούμε με την τιμολόγηση παραγώγων, σύμφωνα με το υπόδειγμα των Black & Scholes. Ας θεωρήσουμε πρώτα ένα ευρωπαϊκό δικαίωμα αγοράς, με ωρίμανση \(T\) και τιμή άσκησης \(Κ\). Η απόδοση αυτού του δικαιώματος στην ωρίμανση είναι, όπως είδαμε στο Κεφάλαιο 1
\[ V_T=(S_T-K)^+. \]
Η σημερινή αξία αυτού του δικαιώματος δίνεται από τον τύπο των Black & Scholes (6.16). Το ολοκλήρωμα στο δεξί μέλος αυτής της σχέσης μπορεί να υπολογιστεί με τη βοήθεια της συνάρτησης κατανομής πιθανότητας της τυπικής κανονικής κατανομής
\[ \Phi(x)=\int_{-\infty}^x e^{-\frac{y^2}{2}}\frac{dy}{\sqrt{2\pi}}. \]
Αν η τρέχουσα τιμή του πρωτογενούς προϊόντος είναι \(S_0\), τότε η αξία ενός ευρωπαϊκού δικαιώματος αγοράς με ωρίμανση \(T\) και τιμή άσκησης \(Κ\), με βάση το μοντέλο Black & Scholes, δίνεται από την
\begin{equation} c(S_0,T,K)=S_0\Phi(d_+)-Ke^{-rT}\Phi(d_-),\quad\text{όπου } d_\pm=\frac{1}{\sigma\sqrt{T}}\ln\left(\frac{S_0e^{rT}}{K}\right)\pm\frac{1}{2}{\sigma\sqrt{T}}. \end{equation}
Απόδειξη: Από τον τύπο των Black & Scholes έχουμε ότι
\begin{align*} c(S_0,T,K)&=e^{-rT}\int_{-\infty}^{+\infty} \big(S_0 e^{\big(r-\frac{\sigma^2}{2}\big) T+\sigma\sqrt{T} x}-K\big)^+\ e^{-\frac{x^2}{2}}\frac{dx}{\sqrt{2\pi}}. \end{align*}Παρατηρήστε ότι η \(-d_-\) είναι η τιμή του \(x\) για την οποία η παρένθεση στην παραπάνω έκφραση μηδενίζεται. Συμβολίζοντας με
\[ F_0=S_0e^{rT} \]
την προθεσμιακή τιμή του πρωτογενούς προϊόντος, έχουμε
\begin{align*} c(S_0,T,K)&=e^{-rT}\int_{-d_-}^{+\infty} \big(F_0 e^{-\frac{\sigma^2}{2} T+\sigma\sqrt{T} x}-K\big)\ e^{-\frac{x^2}{2}}\frac{dx}{\sqrt{2\pi}}\\ &=e^{-rT}\left(F_0\int_{-d_-}^{+\infty}e^{-\frac{1}{2}(x-\sigma\sqrt{T})^2}\frac{dx}{\sqrt{2\pi}}-K\int_{-d_-}^{+\infty}e^{-\frac{x^2}{2}}\frac{dx}{\sqrt{2\pi}}\right)\\ &=e^{-rT}\left(F_0\int_{-\infty}^{d_+}e^{-\frac{x^2}{2}}\frac{dx}{\sqrt{2\pi}}-K\int_{-\infty}^{d_-}e^{-\frac{x^2}{2}}\frac{dx}{\sqrt{2\pi}}\right)\\ &=S_0\Phi(d_+)-Ke^{-rT}\Phi(d_-), \end{align*}που είναι ακριβώς ο ισχυρισμός του Θεωρήματος.
\(\square\)
\begin{equation} S_0e^{-\frac{1}{2}d_+^2}=Ke^{-rT}e^{-\frac{1}{2}d_-^2}. \end{equation}
Βλέπουμε λοιπόν ότι η αξία ενός ευρωπαϊκού δικαιώματος αγοράς είναι αύξουσα συνάρτηση της αξίας του πρωτογενούς προϊόντος. Αυτό είναι φυσιολογικό, αφού όσο μεγαλύτερη είναι η αρχική αξία του πρωτογενούς προϊόντος, τόσο μεγαλύτερη θα είναι και η αξία του στην ωρίμανση.
Η ευαισθησία ενός παραγώγου ως προς τη μεταβλητότητα του πρωτογενούς προϊόντος ονομάζεται βέγα (vega) και συμβολίζεται με \(\nu\). Είναι και αυτο μια χρήσιμη ποσότητα γιατί η μεταβλητότητα του πρωτογενούς προϊόντος προσδιορίζεται εμπειρικά. Μηδενίζοντας το συνολικό βέγα ενός χαρτοφυλακίου, εξασφαλίζει κανείς ότι η αξία του χαρτοφυλακίου δεν είναι ευαίσθητη σε πρώτης τάξης μεγέθους σφάλματα στον προσδιορισμό της μεταβλητότητας. Θα υπολογίσουμε στη συνέχεια το βέγα ενός ευρωπαϊκού δικαιώματος αγοράς.
\begin{align*} \frac{ \partial c(S_0,T,K) }{ \partial \sigma } &= S_0 \Phi' ( d_+ ) \frac{ \partial d_+ }{ \partial \sigma}-Ke^{-rT}\Phi'(d_-)\frac{\partial d_-}{\partial \sigma} &=S_0\Phi'(d_+) \frac{\partial (d_+-d_-)}{\partial\sigma} \end{align*} λόγω της (6.19) \begin{align*} &=S_0\sqrt{\frac{T}{2\pi}}e^{-\frac{1}{2}d_+^2}. \end{align*}Παρατηρούμε ότι η αξια ενός ευρωπαϊκού δικαιώματος αγοράς είναι αύξουσα συνάρτηση της μεταβλητότητας \(\sigma\) του πρωτογενούς προϊόντος.
Περισσότερα για τους ελληνικούς χαρακτήρες και τη χρήση τους στην αντιστάθμιση μπορείτε να διαβάσετε στο [ Hull11 ].
\begin{equation} p(S_0,T,K)=Ke^{-rT}\Phi(-d_-)-S_0\Phi(-d_+),\quad\text{όπου } d_\pm=\frac{1}{\sigma\sqrt{T}}\ln\left(\frac{S_0e^{rT}}{K}\right)\pm\frac{1}{2}{\sigma\sqrt{T}}. \end{equation}
Απόδειξη: Έχοντας ήδη υπολογίσει την αξία ενός ερωπαϊκού δικαιώματος αγοράς, είναι ευκολότερο να υπολογίσουμε την αξία του αντίστοιχου δικαιώματος πώλησης, χρησιμοποιώντας την ισοτιμία ευρωπαϊκών δικαιωμάτων αγοράς και πώλησης (1.2). Συγκεκριμένα,
\begin{align*} p(S_0,T,K)&=c(S_0,T,K)-S_0+Ke^{-rT}\&= S_0 (\Phi(d_+)-1)+Ke^{-rT}(1-\Phi(d_-))\\ &=Ke^{-rT}\Phi(-d_-)-S_0e^{-rT}\Phi(-d_+). \qquad\qquad\Box \end{align*}\[ c(S_0,T,K)-p(S_0,T,K)=S_0-Ke^{-rT}. \]
Παίρνοντας μερικές παραγώγους ως προς \(S_0\) και ως προς \(\sigma\) στα δύο μέλη της παραπάνω σχέσης, έχουμε ότι\[ \Delta_c-\Delta_p=1\Longrightarrow \Delta_p=-\Phi(-d_+) \]
και\[ \nu_c-\nu_p=0\Longrightarrow \nu_p=S_0\sqrt{\frac{T}{2\pi}}e^{-\frac{1}{2}d_+^2}. \]
Σε αυτήν την παράγραφο θα γνωρίσουμε δύο μεθόδους, με τις οποίες μπορεί κανείς να εκτιμήσει τη μεταβλητότητα \(\sigma\) του πρωτογενούς προϊόντος στο μοντέλο των Black & Scholes. Ο πρώτος βασίζεται σε ιστορικά δεδομένα και ο δεύτερος στις τιμές αγοράς παραγώγων του προϊόντος.
Η πρώτη μέθοδος βασίζεται σε ιστορικά δεδομένα και στις ιδιότητες της κίνησης Brown. Έστω ότι έχουμε διαμερίσει στο διάστημα \([0,T]\) σε \(N\) ίσα χρονικά διαστήματα, διάρκειας \(h=T/N\) το καθένα. Τα αριστερά άκρα αυτών των διαστημάτων είναι τα σημεία \(\{t_k\}_{0\le k\le N-1},\) με \(t_k=kh\).
Ας θεωρήσουμε τώρα την τυχαία μεταβλητή
Χρησιμοποιώντας ότι οι \(W_{t_{k+1}}-W_{t_k}\) είναι ανεξάρτητες και ισόνομες, με κατανομή \({\cal N}(0,h)\), μπορούμε να υπολογίσουμε τη μέση τιμή και τη διασπορά της \(P_h\). Συγκεκριμένα,
\[ \EEE{P_h}=\sigma^2\sum_{k=0}^{N-1}\EEE{(W_{t_{k+1}}-W_{t_k})^2}+\mu^2Th=(\sigma^2+\mu^2h)T \]
και\[ \text{Var}(P_h)=\sigma^2N\text{Var}(W_h^2)+4\mu^2h^2T=2hT(\sigma^2+2\mu^2h) \]
Παρατηρούμε λοιπόν ότι όταν \(h\to 0\) η \(P_h\) συγκεντρώνεται γύρω από την τιμή \(\sigma^2 T\). Επιπλέον
\[ P_h=\sum_{k=0}^{N-1}\left(\log\big(\frac{S_{t_{k+1}}}{S_{t_k}}\big)\right)^2\simeq\sum_{k=0}^{N-1}\left(\frac{S_{t_{k+1}}-S_{t_k}}{S_{t_k}}\right)^2. \]
Με λίγο περισσότερο κόπο μπορεί κανείς να δείξει αυστηρά ότι
\[ \PP\Big[\frac{1}{T}\sum_{k=0}^{N-1}\left(\frac{S_{t_{k+1}}-S_{t_k}}{S_{t_k}}\right)^2\longrightarrow \sigma^2\Big]=1. \]
Μπορούμε επομένως να εκτιμήσουμε τη μεταβλητότητα \(\sigma\) από ιστορικά δεδομένα, χρησιμοποιώντας τη συνεπή εκτιμήτρια
\[ \hat{\sigma}^2=\frac{1}{T}\sum_{k=0}^{N-1}\left(\frac{S_{t_{k+1}}-S_{t_k}}{S_{t_k}}\right)^2. \]
Η δεύτερη μέθοδος βασίζεται στην παρατήρηση των τιμών διαπραγμάτευσης παραγώγων του πρωτογενούς προϊόντος. Η ιδέα είναι απλή. Ας υποθέσουμε ότι μπορούμε να υπολογίσουμε αναλυτικά την τιμή διαπραγμάτευσης ενός παραγώγου, όπως κάναμε π.χ. για τα ευρωπαϊκά δικαιώματα αγοράς και πώλησης. Η θεωρητικά δίκαιη τιμή του παραγώγου με βάση το υπόδειγμα Black & Scholes εξαρτάται από την άγνωστη μεταβλητότητα \(\sigma\) και από ένα σύνολο παραμέτρων του παραγώγου που θα συμβολίζουμε με \(\theta\). Ας συμβολίζουμε με \(V_{BS}(\theta;\sigma)\) τη θεωρητικά δίκαιη τιμή του παραγώγου. Αν υποθέσουμε επιπλέον ότι η αγορά είναι σε ισορροπία, η τιμή διαπραγμάτευσης του παραγώγου \(V_{market}(\theta)\), την οποία μπορούμε φυσικά να παρατηρήσουμε, θα πρέπει να ταυτίζεται με την \(V_{BS}(\theta;\sigma)\). Προκειμένου λοιπόν να εκτιμήσουμε τη μεταβλητότητα, αρκεί να λύσουμε την εξίσωση
\[ V_{BS}(\theta;\sigma)=V_{market}(\theta) \]
ως προς \(\sigma\). Η τιμή που θα βρούμε είναι η μεταβλητότητα που τεκμαίρεται από την τιμή διαπραγμάτευσης του παραγώγου ή, όπως λέμε για συντομία, η τεκμαρτή μεταβλητότητα (implied volatility).
Για παράδειγμα, αν ένα ευρωπαϊκό δικαίωμα αγοράς μιας μετοχής έχει τιμή διαπραγμάτευσης \(c_{market}\), η παραπάνω εξίσωση γίνεται
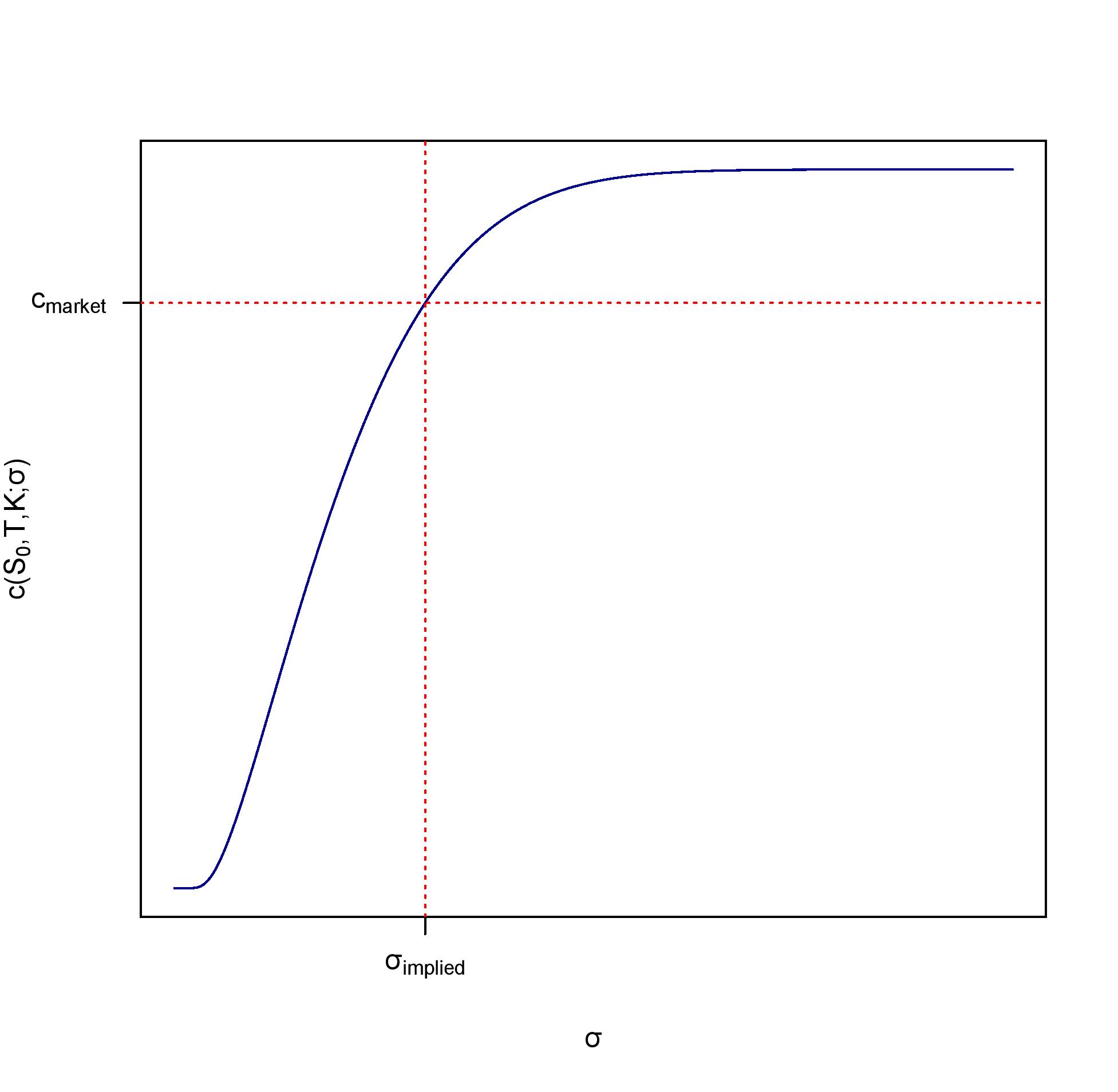
\begin{equation} c(S_0,T,K;\sigma)=S_0\Phi\big(d_+(\sigma)\big)-Ke^{-rT}\Phi\big(d_-(\sigma)\big)=c_{market}. \end{equation}
Η εξίσωση αυτή έχει μοναδική λύση. Πράγματι, από την Παρατήρηση 6.11 το αριστερό μέλος της παραπάνω εξίσωσης είναι συνεχής και γνησίως αύξουσα συνάρτηση του \(\sigma\). Επομένως, αν η εξίσωση έχει λύση, αυτή θα είναι μοναδική.
Ας δούμε όμως τώρα πώς συμπεριφέρεται η αξία του δικαιώματος, όταν \(\sigma\to 0\) ή \(\sigma\to\infty\).
Όταν \(\sigma\to 0\), έχουμε ότι
\[ d_\pm = \frac{1}{ \sigma \sqrt{T} } \ln \left( \frac{ S_0 e^{rT} }{ K } \right) \pm \frac{ 1 }{ 2 }{ \sigma \sqrt{T} } \rightarrow \begin{cases} +\infty, &\text{ αν } S_0 e^{rT} > K\\ 0,&\text{ αν } S_0 e^{rT} = K\\ -\infty, &\text{ αν } S_0 e^{rT} < K .\end{cases} \]
Επομένως, \begin{align*} c(S_0,T,K;\sigma)&=S_0\Phi(d_+)-Ke^{-rT}\Phi(d_-)\rightarrow\begin{cases} S_0-Ke^{-rT},&\text{αν } S_0e^{rT}>K\\ 0, &\text{αν } S_0e^{rT}\le K\end{cases} \&=(S_0-Ke^{-rT})^+. \end{align*}Όταν \(\sigma\to\infty\) έχουμε ότι \(d_\pm\to\pm\infty\), επομένως \(c(S_0,T,K;\sigma)\to S_0\). Συνοψίζοντας όσα είπαμε, η \(c(S_0,T,K)\) ως συνάρτηση της μεταβλητότητας \(\sigma\) αυξάνει από την τιμή \((S_0-Ke^{-rT})^+\), καθώς \(\sigma\to 0\), προς την τιμή \(S_0\), καθώς \(\sigma\to\infty\). Από την Πρόταση 1.3 όμως, προκειμένου να μην υπάρχει ευκαιρία επιτηδειότητας στην αγορά, θα πρέπει η \(c_{market}\) να ικανοποιεί τη διπλή ανισότητα
\[ (S_0-Ke^{-rT})^+< c_{market}< S_0. \]
Θα υπάρχει επομένως μια μοναδική τιμή της μεταβλητότητας \(\sigma_{\text{implied}}\), για την οποία η εξίσωση (6.21) έχει λύση. Αυτή η τιμή είναι η τεκμαρτή μεταβλητότητα και μπορεί εύκολα να προσδιοριστεί αριθμητικά. Το Σχήμα 6.3 δείχνει την ιδέα του υπολογισμού της τεκμαρτής μεταβλητότητας.
Μπορούμε να χρησιμοποιήσουμε την έννοια της τεκμαρτής μεταβλητότητας για να ελέγξουμε κατά πόσον το μοντέλο Black & Scholes είναι ένα καλό υπόδειγμα για τις πραγματικές αγορές. Αν οι τιμές διαπραγμάτευσης των παραγώγων μιας μετοχής ήταν σύμφωνες με το υπόδειγμα Black & Scholes, τότε η μεταβλητότητα που τεκμαίρεται από οποιοδήποτε παράγωγο θα έπρεπε να είναι ίδια και ίση με τη μεταβλητότητα της μετοχής. Μπορεί κανείς να υπολογίσει την τεκμαρτή μεταβλητότητα από δικαιώματα αγοράς με διαφορετικές τιμές άσκησης \(K\) και να παραστήσει γραφικά τα αντίστοιχα σημεία \(\big(K,\sigma_{\text{implied}}(K)\big)\). Αν οι τιμές των δικαιωμάτων στην αγορά ήταν σύμφωνες με το υπόδειγμα Black & Scholes, τα σημεία αυτά θα έπρεπε να βρίσκονται σε μια οριζόνιτα ευθεία, αυτή που αντιστοιχεί στη μεταβλητότητα της μετοχής. Στην πράξη όμως, αν κάνει κανείς αυτήν τη διαδικασία, η γραφική παράσταση της \(\sigma_{\text{implied}}(K)\) φαίνεται να είναι κυρτωμένη. Αυτή η χαρακτηριστική εικόνα ονομάζεται χαμόγελο της μεταβλητότητας (volatility smile) και δείχνει ότι το μοντέλο Black & Scholes δεν περιγράφει ικανοποιητικά τις πραγματικές αγορές. Προκειμένου να εξηγηθεί αυτή η εικόνα έχουν προταθεί περισσότερα πολύπλοκα μοντέλα, όπως για παράδειγμα μοντέλα όπου η μεταβλητότητα είναι μια στοχαστική διαδικασία. Αυτά τα θέματα είναι όμως αντικείμενο του επόμενου βιβλίου που θα μελετήσετε για τη Μαθηματική Χρηματοοικονομία.
\[ f( S_{T} ) =\begin{cases} 1000 \log \left( \frac{ S_{T} }{ K } \right) &, \text{ αν } S_{T} \ge K\\ 0 &, \text{ αν } S_{T} < K, \end{cases} \]
όπου K=50.\[ f(S_{t}) =\begin{cases} 1, &\text{ αν } S_{t}> K\\ 0, &\text{ αν } S_{t}\le K. \end{cases} \]
α) Τιμολογήστε το προϊόν Α χρησιμοποιώντας τον τύπο των Black& Scholes.\[ f(S_{T})=\frac{S_{T}}{K}(K-S_{T})^{+}, \]
όπου \(K=100\).\[ x^{\alpha}=\alpha (\alpha-1)\int_{0}^{\infty}(x-K)^{+}K^{\alpha-2}dK \]
και το θεώρημα Fubini για να εναλλάξουμε την ολοκλήρωση και την αναμενόμενη τιμή, έχουμε\[ \EE[S_{T}^{\alpha}]=\alpha(\alpha-1)\int_{0}^{\infty}\EE[(S_{T}-K)^{+}]K^{\alpha-2}dK. \]
Χρησιμοποιήστε αυτή την παρατήρηση και τον τύπο για την αξία ενός ευρωπαϊκού δικαιώματος αγοράς, προκειμένου να τιμολογήσετε το παράγωγο της προηγούμενης άσκησης.\[ f(S_{T}) =\begin{cases} S_{T}^{2}/S_{0}, &\text{ αν } S_{t}\ge K\\ 0, &\text{ αν } S_{t}< K, \end{cases} \]
όπου \(t\in (0,T)\). Τιμολογήστε αυτό το παράγωγο βάσει του υποδείγματος των Black & Scholes.