
Στο κεφάλαιο αυτό θα παρουσιάσουμε ένα διακριτό αλλά περισσότερο ρεαλιστικό υπόδειγμα αγοράς, το διωνυμικό υπόδειγμα πολλών περιόδων. Θα διαμερίσουμε το χρονικό διάστημα αναφοράς \([0,Τ]\) σε μικρότερα διαστήματα, σε καθένα από τα οποία η δυναμική του πρωτογενούς προϊόντος ακολουθεί την απλή δυναμική του διωνυμικού υποδείγματος μιας περιόδου. Με τον τρόπο αυτό, καθώς η λεπτότητα της διαμέρισης μικραίνει, οι τροχιές της αξίας του πρωτογενούς προϊόντος πλησιάζουν περισσότερο στην ιδέα που έχουμε για το πώς μεταβάλλονται π.χ. οι τιμές των μετοχών, ενώ ταυτόχρονα διατηρούμε τη δυνατότητα να μελετήσουμε αναλυτικά το μοντέλο. Επιπλέον, καθόσον το υπόδειγμα είναι διακριτό, προσφέρεται εύκολα για αριθμητικούς υπολογισμούς. Μια πολύ καλή αναφορά για το περιεχόμενο αυτού του Κεφαλαίου είναι η [ Williams06 ].
Στο υπόδειγμα αυτό η αγορά που θα μελετήσουμε αποτελείται από δύο προϊόντα, το ένα από τα οποία είναι χωρίς κίνδυνο, ενώ
το άλλο είναι ένα προϊόν με κίνδυνο. Επειδή συνήθως θέλουμε να τιμολογήσουμε και να αντισταθμίσουμε παράγωγα του προϊόντος
με κίνδυνο, θα αναφερόμαστε σε αυτό ως πρωτογενές προϊόν και θα θεωρήσουμε ένα χρονικό ορίζοντα \(T\)
ως τον χρόνο ωρίμανσης του παραγώγου που θέλουμε να αναλύσουμε. Το χρονικό διάστημα \([0,T]\) διαμερίζεται
από τους χρόνους \( 0 = t_{0} < t_{1} < \ldots < t_{N-1} < t_{N} = T \) σε \(N\) μικρότερα διαστήματα τα οποία
θα θεωρήσουμε για απλότητα ίσα. Επομένως, κάθε τέτοιο διάστημα έχει εύρος \( h = T / N \) ενώ \(t_{k}=kh,\ k=0,1,\ldots,N\).
Θα υποθέσουμε ότι η σημερινή αξία του άνευ κινδύνου προϊόντος είναι \(B_{0}=1\), ενώ μεταβάλλεται στον χρόνο με ένα
σταθερό ρυθμό, δηλαδή \(B_{t_{k+1}}/B_{t_{k}}=\La\).
Εδώ θα ακολουθήσουμε τη σύμβαση ότι το προϊόν χωρίς κίνδυνο είναι ένας
λογαριασμός με συνεχή ανατοκισμό και σταθερό επιτόκιο \(r\), οπότε \(\La=e^{rh}\).
Η σημερινή αξία του πρωτογενούς προϊόντος είναι \(S_{0}>0\), ενώ η εξέλιξη της στο
χρόνο είναι στοχαστική. Αν τη στιγμή \(t_{k}\) η αξία του πρωτογενούς προϊόντος είναι \(S_{t_{k}}\), τότε
\begin{equation} S_{ t_{ k + 1 } } = S_{ t_{ k } } \xi_{ k + 1 }, \end{equation}
όπου η \(\{\xi_{k}\}_{k\in\{1,2,\ldots,N\}}\) είναι μια ακολουθία από ανεξάρτητες, ισόνομες τυχαίες μεταβλητές. Η κατανομή των \(\xi_{k}\) είναι η ακόλουθη:
\begin{equation} \xi_{k}=\begin{cases} u, &\text{ με πιθανότητα } p\\ d, &\text{ με πιθανότητα } 1-p. \end{cases} \end{equation}
Για παράδειγμα, αν πιστεύουμε ότι σε κάθε διάστημα η τιμή μιας μετοχής είτε θα ανέβει κατά 5% είτε θα πέσει κατά 4% με ίσες πιθανότητες, αυτό αντιστοιχεί στην επιλογή \(u=1,05\), \(d=0,96\) και \(p=\half\) στο μοντέλο μας. Παρατηρήστε ότι σε κάθε διάστημα η δυναμική του πρωτογενούς προϊόντος είναι ίδια με αυτή του διωνυμικού υποδείγματος μιας περιόδου, όπου \(s_{0}=S_{t_{k}}\), \(s_{1}=S_{t_{k}}u\) και \(s_{2}=S_{t_{k}}d\). Όπως είδαμε στο αντίστοιχο υπόδειγμα μιας περιόδου, προκειμένου να μην παρουσιάζονται ευκαιρίες επιτηδειότητας, θα πρέπει τα \(u,d\) να ικανοποιούν τον περιορισμό
\begin{equation} d < e^{rh} < u. \end{equation}
Επιπλέον, θα απαιτήσουμε \(d>0\), ώστε η τιμή του πρωτογενούς προϊόντος να είναι πάντα αυστηρά θετική. Αυτό το μοντέλο για τη δυναμική του πρωτογενούς προϊόντος ονομάζεται διωνυμικό υπόδειγμα πολλών περιόδων (multiperiod binomial model) ή υπόδειγμα των Cox, Ross & Rubinstein (CRR). Η δυναμική του πρωτογενούς προϊόντος στο διωνυμικό υπόδειγμα πολλών περιόδων μπορεί να παρασταθεί διαγραμματικά με το ακόλουθο ανασυνδυασμένο δέντρο.

Σε κάθε κόμβο του δέντρου το ενδεχόμενο να μετακινηθούμε προς τα πάνω έχει πιθανότητα \(p\).
Από την σχέση (4.8) βλέπουμε ότι
\begin{equation} S_{ t_{ k } } = S_{0} \prod_{ j = 1 }^{ k } \xi_j \end{equation}
Οι πιθανές τροχιές της αξίας του πρωτογενούς προϊόντος στο διάστημα \([0,T]\) είναι \(2^{N}\), όσες και
οι συνδυασμοί τιμών που μπορούν να πάρουν οι τυχαίες μεταβλητές \(\{\xi_{k}\}_{k=1,\ldots,N}\).
Η αφετηρία της σύγχρονης θεωρίας της Μαθηματικής Χρηματοοικονομίας είναι να θεωρήσουμε (όπως και στα υποδείγματα μιας περιόδου)
το μοντέλο μας σαν ένα χώρο πιθανότητας \(\Omega\), κάθε σημείο του οποίου αντιστοιχεί σε ένα από τα πιθανά σενάρια εξέλιξης της αγοράς. Επομένως, στο διωνυμικό υπόδειγμα πολλών περιόδων, κάθε σημείο του \(\Omega\) είναι ένα μονοπάτι \(N\) βημάτων στο
παραπάνω δέντρο που ξεκινά από την \(S_{0}\) και καταλήγει σε μια από τις \(N+1\) δυνατές τιμές της \(S_{T}\).
Για παράδειγμα, αν \(N=3\), τότε το μοντέλο μας είναι ένας χώρος πιθανότητας \(\Omega=\{\omega_{1},\ldots,\omega_{8}\}\)
όπου
Οι \(\{\xi_{k}\}\) είναι απεικονίσεις από τον \(\Omega\) (δηλαδή τυχαίες μεταβλητές) στο σύνολο \(\{u,d\}\).
Έτσι στο παραπάνω παράδειγμα έχουμε \(\xi_{1}(\omega_{1})=\cdots\xi_{1}(\omega_{4})=u\) και
\(\xi_{1}(\omega_{5})=\cdots=\xi_{1}(\omega_{8})=d\). Όπως φαίνεται από την (4.8), η αξία \(S_{t_{k}}\)
του προϊόντος με κίνδυνο τη χρονική στιγμή \(t_{k}\) είναι και αυτή μια τυχαία μεταβλητή, επομένως η αξία του
προϊόντος με κίνδυνο είναι μια στοχαστική διαδικασία διακριτού χρόνου ορισμένη στον \(\Omega\).
Το μοντέλο μας καθορίζει επίσης πόσο πιθανή είναι η εμφάνιση καθενός από αυτά τα σενάρια. Μαθηματικά αυτό
σημαίνει ότι εφοδιάζουμε τον \(\Omega\) με ένα μέτρο πιθανότητας \(\PP\). Η πιθανότητα \(\PP\) κάθε ενδεχομένου
αντικατοπτρίζει τις πεποιθήσεις μας για την εξέλιξη της αγοράς. Έτσι στο προηγούμενο παράδειγμα έχουμε
\(\PP(\{\omega_{2}\})=p^{2}(1-p)\).
Αξίζει τον κόπο να ξεκαθαρίσουμε στο σημείο αυτό ένα λεπτό ζήτημα. Μια τυχαία μεταβλητή, καθώς είναι απλά μια
απεικόνιση από τον \(\Omega\) σε κάποιο σύνολο, δεν έχει ανάγκη από κάποιο μέτρο πιθανότητας στον \(\Omega\) για να οριστεί.
Αυτό που καθορίζεται από το μέτρο πιθανότητας είναι το πόσο πιθανή είναι κάθε τιμή της τυχαίας μεταβλητής,
δηλαδή η κατανομή της τυχαίας μεταβλητής. Για παράδειγμα, η από κοινού κατανομή των \(\{\xi_{k}\}\) κάτω
από το \(\PP\) τις καθιστά ανεξάρτητες ισόνομες τυχαίες μεταβλητές με την κοινή τους κατανομή να δίνεται από την (3.2).
Αν στον \(\Omega\) θεωρήσουμε ένα άλλο μέτρο πιθανότητας, οι ίδιες τυχαίες μεταβλητές θα έχουν διαφορετική κατανομή. Π.χ. αν
\(\mu\) είναι ένα μέτρο πιθανότητας στον \(\Omega\) ώστε \(\mu(\{\omega_{1}\})=\mu(\{\omega_{2}\})=\half\), τότε κάτω από το \(\mu\)
οι \(\xi_{1},\xi_{2}\) παίρνουν την τιμή \(u\) με πιθανότητα 1, ενώ η \(\xi_{3}\) παίρνει τις τιμές \(u\) και \(d\) με
πιθανότητα \(\half\) την καθεμία.
Αυτό που λείπει από το μοντέλο μας είναι μια έννοια που να προσδίδει την κατεύθυνση του χρόνου και το ρόλο
αυτό παίζει η έννοια της διήθησης (filtration) που θα εξηγήσουμε παρακάτω. Ας φανταστούμε τον \(\Omega\)
του παραπάνω παραδείγματος σαν ένα σύνολο από τις δυνατές εκβάσεις της αγοράς και ας φανταστούμε την εξέλιξη της αγοράς σαν ένα πείραμα που
πραγματοποιείται και το παρακολουθούμε καθώς αναπτύσσεται. Παρατηρώντας την εξέλιξη της αγοράς, θα επιχειρήσουμε να αποκαλύψουμε
ποιο από αυτά τα σενάρια πραγματοποιείται. Στην αρχή, δεν μπορούμε, όπως είναι φυσικό,
να εκφέρουμε κάποια κρίση. Όλα τα σενάρια είναι δυνατά. Στο τέλος αντίθετα, έχοντας παρατηρήσει την αγορά μέχρι τον χρόνο \(Τ\),
μπορούμε να αποφανθούμε ποιο από τα δυνατά σενάρια πραγματοποιήθηκε.
Τι μπορούμε όμως να πούμε για τους ενδιάμεσους χρόνους? Έχοντας παρατηρήσει την αγορά μέχρι τη στιγμή \(t_{1}\),
η πληροφορία που μπορούμε να συλλέξουμε είναι αν \(S_{t_{1}}=S_{0}u\) ή \(S_{t_{1}}=S_{0}d\). Μπορεί λοιπόν κανείς να αποφανθεί
αν το πείραμα που πραγματοποιείται ανήκει στο ενδεχόμενο
\[ K_{u}=\{\omega_{1},\omega_{2},\omega_{3},\omega_{4}\}\ \text{ ή στο }\ K_{d}=\{\omega_{5},\omega_{6},\omega_{7},\omega_{8}\}. \]
Ομοίως, έχοντας παρατηρήσει την αγορά μέχρι τη στιγμή \(t_{2}\), κανείς μπορεί να αποφανθεί σε ποιο από τα παρακάτω σύνολα ανήκει το σενάριο που εκτυλίσσεται.\[ K_{uu}=\{\omega_{1},\omega_{2}\},\ K_{ud}=\{\omega_{3},\omega_{4}\},\ K_{du}=\{\omega_{5},\omega_{6}\},\ K_{dd}=\{\omega_{7},\omega_{8}\}. \]
Τέλος, όπως είπαμε, έχοντας παρατηρήσει την αγορά μέχρι τη στιγμή \(t_{3}\), κανείς μπορεί να αποφασίσει ακριβώς ποιο σενάριο πραγματοποιήθηκε, δηλαδή σε ποιό από τα μονοσύνολα \(K_{uuu}=\{\omega_{1}\},K_{uud}=\{\omega_{2}\}\) κ.λπ. ανήκει το ενδεχόμενο που πραγματοποιήθηκε. Βλέπουμε λοιπόν ότι καθώς εξελίσσεται η αγορά, η πληροφορία που έχουμε συλλέξει από την \(S_{t}\) διαμερίζει τον χώρο πιθανότητας σε όλο και λεπτότερα ενδεχόμενα. Μπορούμε να παραστήσουμε γραφικά αυτήν την προοδευτικά λεπτότερη διαμέριση του χώρου πιθανότητας ως εξής.

Συμβολίζουμε με \({\cal F}_{k}\) τη διαμέριση του \(\Omega\) που επάγει η συνελεχθείσα από την αξία του πρωτογενούς προϊόντος πληροφορία μέχρι τη στιγμή \(t_{k}\). Έτσι, έχουμε διαδοχικά:
\[ {\cal F}_{0}=\{\Omega\}, \]
\[ {\cal F}_{1}=\{K_{u}, K_{d}\}, \]
\[ {\cal F}_{2}=\{K_{uu},K_{ud},K_{du},K_{dd}\}, \]
κ.τ.λ. Παρατηρήστε ότι κάθε στοιχείο της \({\cal F}_{k}\) αντιστοιχεί σε έναν από τους κόμβους του παραπάνω δέντρου στον χρόνο \(t_{k}\)
και παριστάνει μια δυνατή εξέλιξη της αγοράς μέχρι τη στιγμή \(t_{k}\).
Η απόδοση ενός παραγώγου με ωρίμανση \(T\) είναι μια τυχαία μεταβλητή \(X\) ορισμένη στον \(\Omega\).
Κάθε \(\omega\in\Omega\) αντιστοιχεί σε ένα πιθανό σενάριο εξέλιξης της αγοράς και η \(X(\omega)\) είναι η απόδοση
του παραγώγου σε αυτό το σενάριο. Πολλές φορές θα έχουμε να κάνουμε με παράγωγα ευρωπαϊκού τύπου,
των οποίων η απόδοση εξαρτάται μόνο από την τιμή του πρωτογενούς προϊόντος στην ωρίμανση.
Σε αυτή την περίπτωση θα έχουμε \(X(\omega)=f(S_{T}(\omega))\). Για παράδειγμα, ένα ευρωπαϊκό δικαίωμα αγοράς με τιμή άσκησης
\(K\) έχει απόδοση \(X(\omega)=(S_{T}(\omega)-K)^{+}\). Άλλες φορές πάλι η απόδοση του παραγώγου θα εξαρτάται από όλη την τροχιά
της τιμής του πρωτογενούς προϊόντος. Για παράδειγμα, ένα ευρωπαϊκό δικαίωμα αγοράς με κάτω και εκτός φράγμα αποδίδει
όσο ένα απλό ευρωπαϊκό δικαίωμα αγοράς, μόνο όμως αν η τιμή του πρωτογενούς προϊόντος παραμείνει μέχρι την ωρίμανση
πάνω από ένα φράγμα \(M\). Δηλαδή,
\[ X(\omega)=(S_{T}(\omega)-K)^{+} \times 1\!\!1 \{\min_{t\in[0,T]}S_{t}(\omega)>M\}. \]
Προκειμένου να τιμολογήσουμε ένα παράγωγο, θα θέλαμε να αναπαραγάγουμε την απόδοσή του, χρησιμοποιώντας ένα χαρτοφυλάκιο που αποτελείται από τα δυο προϊόντα της αγοράς μας. Εν γένει, δεν είναι δυνατό να κάνουμε μια στατική αντιστάθμιση, να συνθέσουμε δηλαδή ένα χαρτοφυλάκιο τη χρονική στιγμή \(t=0\) το οποίο να έχει την ίδια απόδοση με το εν λόγω παράγωγο τη στιγμή \(T\). Στο μοντέλο μας όμως έχει νόημα να επιτρέψουμε τις συναλλαγές στους χρόνους \(t_{0},t_{1},\ldots,t_{N-1}\). Μπορούμε να ξεκινήσουμε από ένα χαρτοφυλάκιο \((\phi_{0},\psi_{0})\), να αλλάξουμε τη θέση μας με ένα αυτοχρηματοδοτούμενο τρόπο τη στιγμή \(t_{1}\) σε \((\phi_{1},\psi_{1})\) ανάλογα με την τιμή της \(S_{t_{1}}\), τη στιγμή \(t_{2}\) να αλλάξουμε και πάλι τη θέση μας σε \((\phi_{2},\psi_{2})\) ανάλογα με την πληροφορία που έχουμε διαθέσιμη ως τότε (δηλαδή τις τιμές των \(S_{t_{1}}, S_{t_{2}}\)) κ.λπ. Στην επόμενη παράγραφο θα δούμε πώς, τροποποιώντας το χαρτοφυλάκιο που κατέχουμε ανάλογα με την ως τότε εξέλιξη της αγοράς, μπορούμε να κατασκευάσουμε ένα δυναμικό αυτοχρηματοδοτούμενο χαρτοφυλάκιο που αναπαράγει την απόδοση του παραγώγου στην ωρίμανση και άρα να τιμολογήσουμε οποιοδήποτε παράγωγο με ωρίμανση \(T\).
Θα λέμε ότι μια τυχαία μεταβλητή \(X\) είναι \({\cal F}_{k}\)-μετρήσιμη, όταν η τιμή της εξαρτάται μόνο από τις τιμές του πρωτογενούς προϊόντος μέχρι τη στιγμή \(t_{k}\), δηλαδή
\[ X(\omega)=\Phi(S_{t_{0}}(\omega),S_{t_{1}}(\omega),\ldots,S_{t_{k}}(\omega)), \]
για κάποια συνάρτηση \(\Phi\). Από τον παραπάνω ορισμό, μια \({\cal F}_{0}\)-μετρήσιμη τυχαία μεταβλητή είναι μια σταθερά.
Μια αυτοχρηματοδοτούμενη στρατηγική θα είναι μια ακολουθία χαρτοφυλακίων \(\{(\phi_{k},\psi_{k})\}_k\) τέτοια ώστε για κάθε \(k=0,1,\ldots,N-1\) έχουμε ότι
Η πρώτη από τις δύο παραπάνω συνθήκες σημαίνει ότι η θέση που λαμβάνουμε τη στιγμή \(t_{k}\)
στα προϊόντα της αγοράς εξαρτάται μόνο από τη γνώση που έχουμε για την εξέλιξη της αγοράς μέχρι τότε.
Η δεύτερη συνθήκη σημαίνει ότι η αλλαγή θέσης που κάνουμε τη στιγμή \(t_{k+1}\) είναι αυτοχρηματοδοτούμενη.
Το αριστερό μέλος της σχέσης είναι η αξία του χαρτοφυλακίου (\(\phi_{k},\psi_{k}\))
αμέσως πριν την αλλαγή θέσης,
ενώ το δεξί της μέλος είναι η αξία του χαρτοφυλακίου (\(\phi_{k+1},\psi_{k+1}\))
που θέλουμε να συνθέσουμε τη στιγμή \(t_{k+1}\).
Έστω τώρα ότι θέλουμε να τιμολογήσουμε ένα παράγωγο με δεδομένη απόδοση τη στιγμή \(T\) ίση με
\[ V_{T}=U_{t_{N}}(S_{t_{0}},S_{t_{1}},\ldots,S_{t_{N}}). \]
Προσέξτε ότι επιτρέπουμε στην απόδοση του παραγώγου να εξαρτάται από όλη την τροχιά της τιμής του πρωτογενούς προϊόντος. Θα κατασκευάσουμε μια αυτοχρηματοδοτούμενη στρατηγική που αναπαράγει την παραπάνω απόδοση στη ωρίμανση, δηλαδή
\[ \phi_{N-1}S_{T}+\psi_{N-1}B_{T}=V_{T}. \]
Για να ισχύει η παραπάνω, τόσο στο ενδεχόμενο \(\{\xi_{N}=u\}\) όσο και στο \(\{\xi_{N}=d\}\), θα πρέπει να ικανοποιούνται οι ακόλουθες δύο γραμμικές εξισώσεις:
\[ \begin{cases} \phi_{N-1} S_{t_{N-1}}u + \psi_{N-1}B_{t_{N}}&=U_{t_{N}}(S_{t_{0}},S_{t_{1}},\ldots,S_{t_{N-1}},S_{t_{N-1}}u)\\ \phi_{N-1} S_{t_{N-1}}d + \psi_{N-1}B_{t_{N}}&=U_{t_{N}}(S_{t_{0}},S_{t_{1}},\ldots,S_{t_{N-1}},S_{t_{N-1}}d), \end{cases} \]
από τις οποίες μπορούμε να υπολογίσουμε τις \((\phi_{N-1},\psi_{N-1})\) όπως στο διωνυμικό υπόδειγμα μιας περιόδου. Έτσι, αν ορίσουμε
\[ V_{N}^{\uparrow}=U_{t_{N}}(S_{t_{0}},S_{t_{1}},\ldots,S_{t_{N-1}},S_{t_{N-1}}u),\qquad V_{N}^{\downarrow}=U_{t_{N}}(S_{t_{0}},S_{t_{1}},\ldots,S_{t_{N-1}},S_{t_{N-1}}d), \]
τότε έχουμε
\begin{equation} \phi_{N-1}=\frac{V_{N}^{\uparrow}-V_{N}^{\downarrow}}{S_{t_{N-1}}(u-d)},\qquad \psi_{N-1}=\frac{V_{N}^{\downarrow}\times u-V_{N}^{\uparrow}\times d}{B_{t_{N}}(u-d)}. \end{equation}
Από τις παραπάνω σχέσεις προκύπτει αμέσως ότι οι (\(\phi_{N-1},\psi_{N-1}\)) είναι συναρτήσεις των \(S_{t_{0}},\ldots,S_{t_{N-1}}\), είναι δηλαδή \({\cal F}_{N-1}\)-μετρήσιμες τυχαίες μεταβλητές όπως επιθυμούμε. Πετύχαμε να κατασκευάσουμε, ανάλογα με τη γνώση μας για την εξέλιξη της αγοράς έως τη στιγμή \(t_{N-1}\), ένα χαρτοφυλάκιο (\(\phi_{N-1},\psi_{N-1}\)), η αξία του οποίου τη στιγμή \(t_{N}\) θα ταυτίζεται με αυτήν του παραγώγου. Μπορούμε λοιπόν να ορίσουμε την αξία του παραγώγου τη στιγμή \(t_{N-1}\) ως την αξία του χαρτοφυλακίου (\(\phi_{N-1},\psi_{N-1}\)) που έχει την ίδια αξία με το παράγωγο τη στιγμή \(t_{N}\). Συγκεκριμένα,
\[ V_{t_{N-1}}=U_{t_{N-1}}(S_{t_{0}},S_{t_{1}},\ldots,S_{t_{N-1}}):=\phi_{N-1} S_{t_{N-1}}+\psi_{N-1}B_{t_{N-1}} \]
Αντικαθιστώντας τα \((\phi_{N-1},\psi_{N-1})\) από την (3.5) παίρνουμε
\[ V_{t_{N-1}}=e^{-rh}(qV_{N}^{\uparrow}+(1-q)V_{N}^{\downarrow}), \]
όπου
\[ q=\frac{e^{rh}-d}{u-d}. \]
Μπορούμε τώρα να επαναλάβουμε τα παραπάνω βήματα, οπισθοδρομώντας μέχρι τον χρόνο \(t_{0}\).
Συγκεκριμένα, ο αλγόριθμος έχει ως εξής:
\begin{equation} \phi_{k-1}S_{t_{k}}+\psi_{k-1}B_{t_{k}}= V_{t_{k}}, \end{equation}
\begin{eqnarray} V_{t_{k-1}}=U_{t_{k-1}}(S_{t_{0}},S_{t_{1}},\ldots,S_{t_{k-1}})&:=&\phi_{k-1}S_{t_{k-1}}+\psi_{k-1}B_{t_{k-1}} &=&e^{-rh}\left(qV_{k}^{\uparrow}+(1-q)V_{k}^{\downarrow}\right). \end{eqnarray}
Από την κατασκευή του το χαρτοφυλάκιο (\(\phi_{j-1},\psi_{j-1}\)) έχει τη στιγμή \(t_{j}\) αξία
ίση με αυτού του χαρτοφυλακίου (\(\phi_{j},\psi_{j}\)), όπως φαίνεται από τις (3.7) και (3.6).
Επομένως η αλλαγή θέσης από (\(\phi_{j-1},\psi_{j-1}\)) σε (\(\phi_{j},\psi_{j}\)) που χρειάζεται να κάνουμε τη στιγμή \(t_{j}\)
είναι αυτοχρηματοδοτούμενη. Κατασκευάζουμε λοιπόν έτσι μια αυτοχρηματοδοτούμενη στρατηγική που αναπαράγει την απόδοση
του παραγώγου στην ωρίμανση. Η αρχή της μη επιτηδειότητας επιβάλλει σε αυτή την περίπτωση την αρχική αξία του παραγώγου. Προκειμένου να μην υπάρχει στρατηγική επιτηδειότητας, θα πρέπει
\(V_{t_{0}}=\phi_{0}S_{t_{0}}+\psi_{0}\).
Πράγματι, αν η τιμή διαπραγμάτευσης του παραγώγου είναι \(V\) τότε μπορούμε να κατασκευάσουμε ένα χαρτοφυλάκιο που αρχικά αποτελείται
από:
Το χαρτοφυλάκιο αυτό προφανώς κατασκευάζεται χωρίς κόστος. Αν τις στιγμές \(t_{1},\ldots,t_{N-1}\) κάνουμε τις αυτοχρηματοδοτούμενες αλλαγές θέσεις ώστε τη στιγμή \(t_{k}\) να κατέχουμε το χαρτοφυλάκιο που αποτελείται από:
τότε η αξία της θέσης μας στην ωρίμανση θα είναι:
\[ -V_{T}+\phi_{N-1}S_{T}+\psi_{N-1}B_{T}+(V-V_{t_{0}})B_{T}=(V-V_{t_{0}})e^{rT}. \]
Είναι φανερό λοιπόν ότι, αν \(V\neq V_{t_{0}}\), τότε παίρνοντας θετική ή αρνητική θέση στην προηγούμενη στρατηγική, ανάλογα
με το αν \( V > V_{t_{0}} \) ή \( V < V_{t_{0}} \), μπορούμε να πραγματοποιήσουμε μια στρατηγική επιτηδειότητας.
Ας δούμε τώρα πώς μπορούμε να εφαρμόσουμε την παραπάνω μέθοδο μέσα από δύο παραδείγματα, ένα στο όποιο
η απόδοση του παραγώγου εξαρτάται μόνο από την τελική τιμή \(S_{T}\) του πρωτογενούς προϊόντος και ένα στο οποίο
η απόδοση του παραγώγου εξαρτάται από ολόκληρη την τροχιά \(S_{\cdot}\) της τιμής του προϊόντος.
Έστω λοιπόν ότι η σημερινή τιμή μιας μετοχής είναι \(S_{t_{0}}=54\) και στα επόμενα τρια τρίμηνα (\(h=0,25\) έτη)
η τιμή της ακολουθεί το διωνυμικό υπόδειγμα με \(u=\frac{4}{3},\ d=\frac{2}{3}\) και \(e^{rh}=\frac{16}{15}\).
Η δυναμική της μετοχής μπορεί να παρασταθεί από το ανασυνδυασμένο δυωνυμικό δέντρο
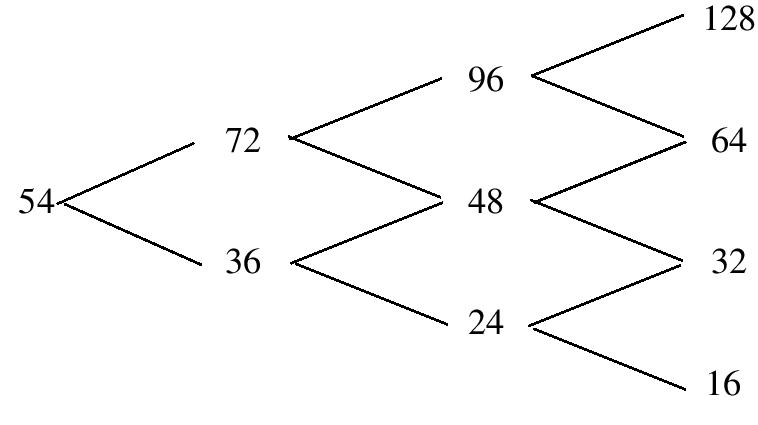
Θα τιμολογήσουμε με βάση το παραπάνω υπόδειγμα ένα δικαίωμα πώλησης της μετοχής με τιμή άσκησης \(K=48\) και ωρίμανση
σε 9 μήνες.
Αξίζει να παρατηρήσουμε ότι, αν η απόδοση του παραγώγου εξαρτάται μόνο από την τελική τιμή του πρωτογενούς προϊόντος, αν δηλαδή
έχουμε \(V_{T}=f(S_{T})\), τότε το χαρτοφυλάκιο (\(\phi_{k},\psi_{k}\)) που πρέπει να κατέχουμε τη στιγμή \(t_{k}\) εξαρτάται μόνο
από την τρέχουσα τιμή του πρωτογενούς προϊόντος \(S_{t_{k}}\). Πράγματι, έχουμε ότι
\[ V_{N}^{\uparrow}=f(S_{t_{N-1}}u),\qquad V_{N}^{\downarrow}=f(S_{t_{N-1}}d). \]
Επομένως, από την (3.5)
\[ \phi_{N-1}=\frac{f(S_{t_{N-1}}u)-f(S_{t_{N-1}}d)}{S_{t_{N-1}}u-S_{t_{N-1}}d},\qquad \psi_{N-1}B_{t_{N}}=\frac{f(S_{t_{N-1}}d)\times u-f(S_{t_{N-1}}u)\times d}{u-d} \]
Βλέπουμε λοιπόν ότι οι \(\phi_{N-1},\psi_{N-1}\) εξαρτώνται μόνο από την \(S_{t_{N-1}}\), άρα και η
\[ V_{t_{N-1}}=\phi_{N-1}S_{t_{N-1}}+\psi_{N-1}B_{t_{N-1}} \]
εξαρτάται μόνο από την \(S_{t_{N-1}}\). Επαναλαμβάνοντας την παραπάνω διαδικασία μέχρι να φτάσουμε στον χρόνο \(t_k\) συμπεραίνουμε ότι οι \(\phi_k\) και \(\psi_k\) εξαρτώνται μόνο από την \(S_{t_k}\).
Στην αναπαράσταση της δυναμικής της αγοράς ως ένα δέντρο, ο κάθε κόμβος του δέντρου αντιστοιχεί σε μια καθορισμένη αξία
για το παράγωγο και ένα καθορισμένο αντισταθμιστικό χαρτοφυλάκιο, αφού αυτά
εξαρτώνται μόνο από την τρέχουσα τιμή του πρωτογενούς προϊόντος (τον κόμβο που βρισκόμαστε)
και όχι από όλη την τροχιά του πρωτογενούς προϊόντος μέχρι εκείνη τη στιγμή (πώς καταλήξαμε
σε αυτόν τον κόμβο). Αρκεί λοιπόν για \(k=N-1,N-2,\ldots,1,0\) να προσδιορίσουμε σε κάθε κόμβο του δέντρου που αντιστοιχεί
στη στιγμή \(t_{k}\) το αντισταθμιστικό χαρτοφυλάκιο και την αξία του παραγώγου στον κόμβο αυτό. Στο παράδειγμά μας έχουμε
\[ V_{T}(\{S_{T}=128\})=V_{T}(\{S_{T}=64\})=0,\ V_{T}(\{S_{T}=32\})=48-32=16,\ V_{T}(\{S_{T}=16\})=48-16=32. \]
Επομένως, στους κόμβους που αντιστοιχούν στον χρόνο \(t_{2}\) έχουμε
\[ \phi_{2}(\{S_{t_{2}}=24\})=\frac{16-32}{32-16}=-1,\qquad \psi_{2}(\{S_{t_{2}}=24\})e^{3rh}=\frac{32\times 4/3 -16\times 2/3}{\frac{4}{3}-\frac{2}{3}}=48 \]
και άρα
\[ V_{t_{2}}(\{S_{t_{2}}=24\})=-1\times 24+48\times(\frac{15}{16})=21. \]
Ομοίως,\[ \phi_{2}(\{S_{t_{2}}=48\})=\frac{0-16}{64-32}=-\half,\qquad \psi_{2}(\{S_{t_{2}}=48\})e^{3rh}=\frac{16\times 4/3 -0\times 2/3}{\frac{4}{3}-\frac{2}{3}}=32 \]
και άρα\[ V_{t_{2}}(\{S_{t_{2}}=48\})=-\half\times 48+32\times(\frac{15}{16})=6. \]
Αντίστοιχα,\[ \phi_{2}(\{S_{t_{2}}=96\})=\psi_{2}(\{S_{t_{2}}=96\})=V_{t_{2}}(\{S_{t_{2}}=96\})=0. \]
Έχοντας προσδιορίσει την \(V_{t_{2}}\) σε κάθε ενδεχόμενο προχωρούμε για να υπολογίσουμε την \(V_{t_{1}}\). Συγκεκριμένα,
\[ \phi_{1}(\{S_{t_{1}}=36\})=\frac{6-21}{48-24}=-\frac{5}{8},\qquad \psi_{1}(\{S_{t_{1}}=36\})e^{2rh}=\frac{21\times 4/3 -6\times 2/3}{\frac{4}{3}-\frac{2}{3}}=36, \]
άρα\[ V_{t_{1}}(\{S_{t_{1}}=36\})=-\frac{5}{8}\times 36+36\times(\frac{15}{16})=\frac{45}{4}. \]
Στο ενδεχόμενο \(\{S_{t_{1}}=72\}\) έχουμε αντίστοιχα,\[ \phi_{1}(\{S_{t_{1}}=72\})=\frac{0-6}{96-48}=-\frac{1}{8},\qquad \psi_{1}(\{S_{t_{1}}=72\})e^{2rh}=\frac{6\times 4/3 -0\times 2/3}{\frac{4}{3}-\frac{2}{3}}=12, \]
άρα\[ V_{t_{1}}(\{S_{t_{1}}=72\})=-\frac{1}{8}\times 72+12\times(\frac{15}{16})=\frac{9}{4}. \]
Τέλος, προσδιορίζουμε το χαρτοφυλάκιο \((\phi_{0},\psi_{0})\).\[ \phi_{0}=\frac{9/4-45/4}{72-36}=-\frac{1}{4},\qquad \psi_{0}e^{rh}=\frac{\frac{45}{4}\times 4/3-\frac{9}{4}\times 2/3}{\frac{4}{3}-\frac{2}{3}}=\frac{81}{4}, \]
συνεπώς\[ V_{t_{0}}=-\frac{1}{4}\times 54+\frac{81}{4}\times(\frac{15}{16})=\frac{351}{64}=5,484375. \]
Μπορούμε να παραστήσουμε γραφικά τη στρατηγική που πρέπει να ακολουθήσουμε για να αναπαραγάγουμε την απόδοση του παραγώγου με το επόμενο ανασυνδυασμένο διωνυμικό δέντρο.
Για να αντισταθμίσουμε λοιπόν το παράγωγο πρέπει να ξεκινήσουμε με αρνητική θέση σε \(1/4\) της μετοχής και \(1215/64\) μετρητά, θέση που αξίζει \(V_{t_{0}}=351/64\). Tη στιγμή \(t_{1}\) το ποσό που είχαμε επενδύσει χωρίς κίνδυνο θα έχει ανέλθει σε \(1215/64\times 16/15=81/4\). Aν τώρα για παράδειγμα η τιμή της μετοχής έχει ανέλθει σε 72, η νέα θέση που πρέπει να πάρουμε στη μετοχή (\(\phi_{1}(\{S_{t_{1}}=72\})\)) είναι αρνητική σε \(1/8\) της μετοχής. Χρειάζεται λοιπόν να αγοράσουμε \(1/8\) της μετοχής προς 72, επομένως στον λογαριασμό χωρίς κίνδυνο θα απομείνουν \(81/4-72\times 1/8=45/4\). Τη στιγμή \(t_{2}\) τα χρήματα αυτά θα έχουν γίνει \(45/4\times 16/15=12\). Αν πάλι για παράδειγμα η τιμή της μετοχής τη στιγμή \(t_{2}\) έχει πέσει σε 48, η νέα θέση που πρέπει να αποκτήσουμε στη μετοχή (\(\phi_{2}(\{S_{t_{2}}=48\})\)) είναι \(-\half\). Θα πρέπει λοιπόν να διαθέσουμε \(3/8\) της μετοχής προς 48 τα οποία θα μας αποφέρουν 18, επομένως στο λογαριασμό χωρίς κίνδυνο θα έχουμε 12+18=30. Στην ωρίμανση του δικαιώματος το ποσό αυτό θα έχει γίνει \(30\times 16/15=32\). Παρατηρήστε ότι, αν στην ωρίμανση η τιμή της μετοχής είναι 64, η αξία του χαρτοφυλακίου μας θα είναι \(-\half\times 64+32=0,\) ενώ αν η τιμή της μετοχής είναι 32, τότε η αξία του χαρτοφυλακίου μας θα είναι \(-\half\times 32+32=16\). Βλέπουμε λοιπόν πώς αναπαράγεται η απόδοση του δικαιώματος πώλησης στο ενδεχόμενο \(\{S_{t_{1}}=72,\ S_{t_{2}}=48\}\). Αξίζει τον κόπο να ελέγξετε μόνοι σας πώς μπορούμε να αναπαραγάγουμε την απόδοση του παραγώγου σε ένα άλλο ενδεχόμενο, π.χ. στο \(\{S_{t_{1}}=36,\ S_{t_{2}}=24\}\).
Θα τιμολογήσουμε τώρα βάσει του ιδίου μοντέλου για τη δυναμική της μετοχής ένα παράγωγο η απόδοση του οποίου
εξαρτάται από όλη την τροχιά της τιμής της μετοχής. Θα χρησιμοποιήσουμε σκοπίμως μια παραλλαγή του προηγούμενου δικαιώματος,
ένα δικαίωμα πώλησης της μετοχής προς 48 με άνω και εκτός φράγμα στην τιμή 60. Το παράγωγο αυτό αποδίδει στην ωρίμανση
\((48-S_{T})^{+}\) με την προϋπόθεση όμως η αξία της μετοχής να μην έχει ξεπεράσει την τιμή 60 πριν την ωρίμανση. Αν κάποια
στιγμή πριν την ωρίμανση η αξία της μετοχής υπερβεί την τιμή 60, τότε το δικαίωμα πώλησης αυτομάτως καταργείται και το παράγωγο έχει μηδενική απόδοση.
Είναι σαφές ότι η τελική τιμή της μετοχής δεν αρκεί για να προσδιορίσουμε την απόδοση αυτού του παραγώγου. Για παράδειγμα, στο ενδεχόμενο
\(\{S_{t_{1}}=36,\ S_{t_{2}}=48,\ S_{t_{3}}=32\}\) η απόδοση του παραγώγου είναι 16 όπως και πριν, όμως στο ενδεχόμενο
\(\{S_{t_{1}}=72,\ S_{t_{2}}=48,\ S_{t_{3}}=32\}\) η απόδοση του παραγώγου είναι μηδέν, αφού το φράγμα των 60 έχει ξεπεραστεί.
Σε αντίθεση λοιπόν με το προηγούμενο παράδειγμα, εδώ η στρατηγική που θα ακολουθήσουμε στον χρόνο \(t_{2}\) για την αντιστάθμιση,
αν \(\{S_{t_{1}}=36,\ S_{t_{2}}=48\}\), θα είναι διαφορετική από αυτήν που θα ακολουθήσουμε, αν \(\{S_{t_{1}}=72,\ S_{t_{2}}=48\}\).
Στην πράξη, για να τιμολογήσουμε με τον αναδρομικό αλγόριθμο παράγωγα η απόδοση των οποίων εξαρτάται από ολόκληρη
την τροχιά της αξίας του πρωτογενούς προϊόντος, θα πρέπει στο δέντρο που θα κατασκευάσουμε για να παραστήσουμε τη στρατηγική
αντιστάθμισης να ΜΗΝ ανασυνδυάζουμε κόμβους που αντιστοιχούν σε διαφορετική απόδοση του παραγώγου. Έτσι σε κάθε χρονική στιγμή
\(t_{k}\) θα έχουμε εν γένει \(2^{k}\) κόμβους - ένα για κάθε δυνατή τροχιά. Με αυτόν τον τρόπο εξασφαλίζουμε ότι η αξία του παραγώγου είναι καλά ορισμένη σε κάθε κόμβο του δέντρου.
Στο παράδειγμά μας έχουμε για τη στιγμή \(t_{2}\) τις ακόλουθες περιπτώσεις:
\[ V_{t_{3}}(\{S_{t_{1}}=72,S_{t_{2}}=96,S_{t_{3}}=128\})=V_{t_{3}}(\{S_{t_{1}}=72,S_{t_{2}}=96,S_{t_{3}}=64\})=0, \]
άρα\[ \phi_{2}(K_{u,u})=\psi_{2}(K_{u,u})=0 \]
και\[ V_{t_{2}}(K_{u,u})=0. \]
\[ V_{t_{3}}(\{S_{t_{1}}=72,S_{t_{2}}=48,S_{t_{3}}=64\})=V_{t_{3}}(\{S_{t_{1}}=72,S_{t_{2}}=48,S_{t_{3}}=32\})=0, \]
άρα\[ \phi_{2}(K_{u,d})=\psi_{2}(K_{u,d})=0 \]
και\[ V_{t_{2}}(K_{u,d})=0. \]
\[ V_{t_{3}}(\{S_{t_{1}}=36,S_{t_{2}}=48,S_{t_{3}}=64\})=0,\ V_{t_{3}}(\{S_{t_{1}}=36,S_{t_{2}}=48,S_{t_{3}}=32\})=16, \]
άρα\[ \phi_{2}(K_{d,u})=\frac{0-16}{64-32}=-\half,\qquad \psi_{2}(K_{d,u})e^{3rh}=\frac{16\times 4/3 -0\times 2/3}{\frac{4}{3}-\frac{2}{3}}=32 \]
και\[ V_{t_{2}}(K_{d,u})=-\half\times 48+32\times(\frac{15}{16})=6. \]
\[ V_{t_{3}}(\{S_{t_{1}}=36,S_{t_{2}}=24,S_{t_{3}}=32\})=16,\ V_{t_{3}}(\{S_{t_{1}}=36,S_{t_{2}}=24,S_{t_{3}}=16\})=32, \]
άρα\[ \phi_{2}(K_{d,d})=\frac{16-32}{32-16}=-1,\qquad \psi_{2}(K_{d,d})e^{3rh}=\frac{32\times 4/3 -16\times 2/3}{\frac{4}{3}-\frac{2}{3}}=48 \]
και\[ V_{t_{2}}(K_{d,d})=-1\times 24+48\times(\frac{15}{16})=21. \]
\[ V_{t_{2}}(\{S_{t_{1}}=72,S_{t_{2}}=96\})= V_{t_{2}}(\{S_{t_{1}}=72,S_{t_{2}}=48\})=0, \]
άρα\[ \phi_{1}(K_{u})=\psi_{1}(K_{u})=0 \]
και\[ V_{t_{1}}(K_{u})=0. \]
\[ V_{t_{2}}(\{S_{t_{1}}=36,S_{t_{2}}=48\})=6,\ V_{t_{2}}(\{S_{t_{1}}=36,S_{t_{2}}=24\})=21, \]
άρα\[ \phi_{1}(K_{d})=\frac{6-21}{48-24}=-\frac{5}{8},\qquad \psi_{1}(K_{d})e^{2rh}=\frac{21\times 4/3 -6\times 2/3}{\frac{4}{3}-\frac{2}{3}}=36 \]
και\[ V_{t_{1}}(K_{d})=-\frac{5}{8}\times 36+36\times(\frac{15}{16})=\frac{45}{4}. \]
\[ \phi_{0}=\frac{0-45/4}{72-36}=-\frac{5}{16},\qquad \psi_{0}e^{rh}=\frac{\frac{45}{4}\times 4/3-0\times 2/3}{\frac{4}{3}-\frac{2}{3}}=\frac{45}{2}, \]
συνεπώς\[ V_{t_{0}}=-\frac{5}{16}\times 54+\frac{45}{2}\times(\frac{15}{16})=\frac{135}{32}=4,21875. \]
Μπορούμε και πάλι να παραστήσουμε με ένα διωνυμικό δέντρο τη στρατηγική που πρέπει να ακολουθήσει κανείς για να αναπαραγάγει την απόδοση του παραγώγου ως εξής:

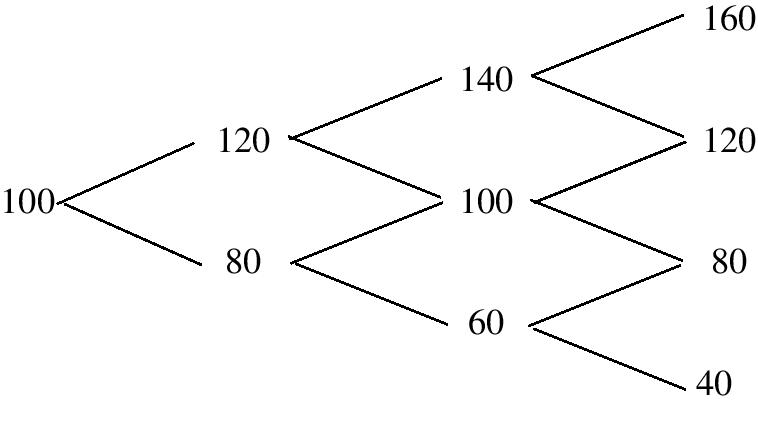
\[ V_{T}(\omega)=\max_{i\in\{0,1,2,3\}}S_{t_{i}}(\omega)-S_{T}(\omega). \]
β) Περιγράψτε ακριβώς τις συναλλαγές που θα έπρεπε να κάνετε τις στιγμές \(t=t_{0},t_{1},t_{2}\) ώστε να αντισταθμίσετε το παράγωγο αυτό στα παρακάτω δύο ενδεχόμενα: