1.1 Μέτρο Lebesgue στο ${\mathbb{R}}$

Αν $E \subseteq {\mathbb{R}}$ το μέτρο (Lebesgue) του $E$, που το συμβολίζουμε με $m(E)$ ή με ${\left\vert{E}\right\vert}$ είναι μια γενίκευση της έννοιας του μήκους. Αν $E = (a,b)$ είναι διάστημα τότε φυσικά το μήκος του είναι ίσο με $b-a$. Εύκολα μπορεί κανείς να ορίσει το μήκος μιας πεπερασμένης ή ακόμη και αριθμήσιμης ένωσης διαστημάτων

$$m(\bigcup_{n} (a_n, b_n)) = \sum_n (b_n-a_n),$$

αν φυσικά τα διαστήματα είναι ανά δύο ξένα. Υπάρχουν όμως πολύ πιο περίπλοκα σύνολα από αυτά.

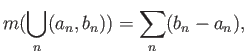
Ο γενικός ορισμός του μέτρου ενός συνόλου δίδεται έμμεσα. Παίρνουμε όλες τις καλύψεις του συνόλου $E$ από αριθμήσιμες οικογένειες από ανοιχτά διαστήματα $I_n = (a_n, b_n)$

$$E \subseteq \bigcup_n I_n$$ (1.1)

και παίρνουμε ως μέτρο $m(E)$ του $E$ το infimum των ποσοτήτων

$$\sum_n (b_n - a_n).$$

Προκύπτει εύκολα ότι με τον ορισμό αυτό δεν αλλάζει το μέτρο των διαστημάτων. Στην κάλυψη (1.1) δεν απαιτούμε να είναι ξένα μεταξύ τους τα διαστήματα $I_n$. Το γεγονός ότι παίρνουμε το infimum των καλύψεων κάπως «αναγκάζει» τα διαστήματα αυτά να μην έχουν επικαλύψεις.

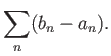
Παραθέτουμε τώρα χωρίς απόδειξη τις κυριότερες ιδιότητες του μέτρου Lebesgue. Όπως μπορεί να δει ο προσεκτικός αναγνώστης οι ιδιότητες αυτές είναι πολύ διαισθητικές (με εξαίρεση ίσως τις 8 και 9) και ανταποκρίνονται σε αυτό που περιμένουμε να ισχύει για το «μήκος» ενός συνόλου. Παρ' όλ' αυτά κάποιες από τις αποδείξεις είναι αρκετά τεχνικές.

Θεώρημα 1.1 (Ιδιότητες του μέτρου Lebesgue)  

1. $0\le m(A) \le \infty$ για καθε $A \subseteq {\mathbb{R}}$.
2. Όλα τα διαστήματα $(a,b)$ (ανεξαρτήτως αν τα άκρα τους είναι μέσα) έχουν μέτρο $b-a$.
3. (Μονοτονία) Αν $A \subseteq B$ τότε $m(A) \le m(B)$.
4. (Προσθετικότητα) Αν $E_1,E_2,\ldots\subseteq{\mathbb{R}}$ είναι ανά δύο ξένα τότε
   $$m(\bigcup_n E_n) = \sum_n m(E_n).$$

5. (Υποπροσθετικότητα) Αν $E_1,E_2,\ldots\subseteq{\mathbb{R}}$ (δε ζητάμε να είναι ανά δύο ξένα) τότε
   $$m(\bigcup_n E_n) \le \sum_n m(E_n).$$

6. (Αύξουσα ένωση συνόλων) Αν $E_n \subseteq E_{n+1}$ τότε
   $$m(\bigcup_n E_n) = \lim_{n\to\infty}m(E_n).$$

7. (Φθίνουσα τομή συνόλων) Αν $E_n \supseteq E_{n+1}$ και για κάποιο $n_0$ ισχύει $m(E_{n_0}) < +\infty$ τότε
   $$m(\bigcap_n E_n) = \lim_{n\to\infty} m(E_n).$$

8. (Προσέγγιση από πάνω με ανοιχτά σύνολα) Αν $E \subseteq {\mathbb{R}}$ και $\epsilon>0$ τότε υπάρχει ανοιχτό σύνολο $G\supseteq E$ τέτοιο ώστε
   $$m(G\setminus E)\le\epsilon.$$

9. (Προσέγγιση από μέσα με κλειστά) Αν $E \subseteq {\mathbb{R}}$ και $\epsilon>0$ τότε υπάρχει κλειστό σύνολο $F \subseteq E$ τέτοιο ώστε
   $$m(E\setminus F)\le\epsilon.$$
   (Δείτε και Σχήμα 1.1 για τα σύνολα $F \subseteq E \subseteq G$.)
   

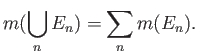
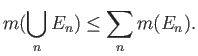
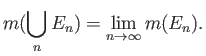
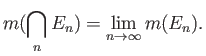
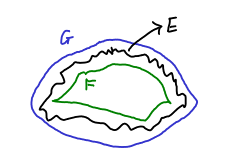
   Σχήμα 1.1: Το μετρήσιμο σύνολο $E$ περιέχει ένα κλειστό $F$ και περιέχεται σε ένα ανοιχτό $G$ τέτοια ώστε τα σύνολα $E\setminus F$ και $G \setminus E$ να έχουν οσοδήποτε μικρό μέτρο θέλουμε.

10. (Αναλλοίωτο ως προς τις μεταφορές) Αν $E \subseteq {\mathbb{R}}$, $t \in {\mathbb{R}}$ και
    $$E+t = {\left\{{x+t: x\in E}\right\}}$$
    είναι η «μεταφορά του $E$ κατά $t$» τότε $m(E+t) = m(E)$.
11. (Ομοιοθεσία) Αν $E \subseteq {\mathbb{R}}$, $\lambda\in{\mathbb{R}}$ και
    $$\lambda E = {\left\{{\lambda x: x\in E}\right\}}$$
    τότε $m(\lambda E) = {\left\vert{\lambda}\right\vert}m(E)$.

Άσκηση 1.1   Αποδείξτε ότι κάθε αριθμήσιμο σύνολο $E={\left\{{x_1,x_2, \ldots}\right\}}\subseteq{\mathbb{R}}$ έχει $m(E)=0$.

Υπόδειξη: Έστω $\epsilon>0$ και θεωρήστε την κάλυψη του $E$ από τα ανοιχτά διαστήματα $I_n = (x_n - \epsilon 2^{-n}, x_n+\epsilon 2^{-n})$. Δείτε το Σχήμα 1.2.

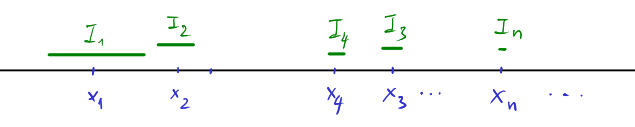
Σχήμα 1.2: Κάλυψη ενός αριθμήσιμου συνόλου από ακολουθία διαστημάτων με μικρό συνολικά μήκος.

Άσκηση 1.2   Δείξτε ότι το σύνολο των αρρήτων του $[0,1]$ έχει μέτρο 1.

Υπόδειξη: Το σύνολο των ρητών είναι αριθμήσιμο. Με βάση την προσθετικότητα έχουμε

$$m([0,1]) = m([0,1]\cap {\mathbb{Q}}) + m([0,1] \cap {\mathbb{Q}}^c).$$

Σχεδόν παντού:
Λέμε ότι μια πρόταση που εξαρτάται από το $x \in {\mathbb{R}}$ ισχύει «σχεδόν για κάθε $x$» αν ισχύει για όλα τα $x$ εκτός από ένα σύνολο εξαιρέσεων με μέτρο 0. Με άλλα λόγια υπάρχει ένα σύνολο $E$ με $m(E)=0$ τέτοιο ώστε η πρότασή μας ισχύει αν $x \notin E$. Αν το $x$ εννοείται τότε λέμε «σχεδόν παντού».

Για παράδειγμα, «η συνάρτηση $\chi_Q$ (η χαρακτηριστική συνάρτηση των ρητών, που είναι 1 για κάθε ρητό και 0 για κάθε άρρητο) είναι σχεδόν παντού ίση με το 0» (αφού $m({\mathbb{Q}})=0$).

Άσκηση 1.3   Δείξτε ότι το τριαδικό σύνολο Cantor έχει μέτρο 0. Το σύνολο αυτό $C$ κατασκευάζεται ως μια φθίνουσα τομή κλειστών υποσυνόλων του $[0,1]$

$$C = \bigcap_{n=0}^{\infty} E_n.$$

Ισχύει κατ' αρχήν $E_0=[0,1]$ και το κάθε $E_n$ φτιάχνεται από το $E_{n-1}$ ως εξής: το $E_{n-1}$ είναι μια πεπερασμένη ένωση κλειστών διαστημάτων. Για να πάρουμε από το $E_{n-1}$ το $E_n$ απλά αφαιρούμε από το κάθε ένα από τα διαστήματά του το μεσαίο ένα τρίτο (χωρίς τα άκρα του) (Δείτε και το Σχήμα 1.3.)

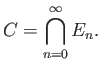
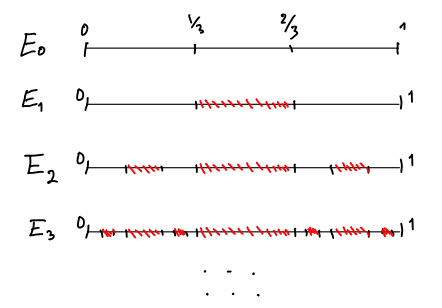
Σχήμα 1.3: Τα στάδια κατασκευής του τριαδικού συνόλου Cantor. Σε κάθε βήμα πετάμε από κάθε διάστημα του συνόλου μας το μεσαίο ένα τρίτο (κόκκινο χρώμα). Ό,τι μένει (μετά από άπειρα βήματα) είναι το σύνολο Cantor.

πετάμε από κάθε διάστημα του συνόλου μας το μεσαίο ένα τρίτο (κόκκινο χρώμα). Για παράδειγμα $E_1 = [0, 1/3] \cup [2/3, 1]$. Προκύπτει ότι το σύνολο $C$ είναι μη κενό, συμπαγές και μάλιστα υπεραριθμήσιμο (δε μπορούμε δηλ. να γράψουμε όλα τα στοιχεία του ως μια ακολουθία).

Δείξτε ότι $m(C)=0$.

Υπόδειξη: Για κάθε $n$ το σύνολο $E_n$ είναι μια κάλυψη του $C$ με διαστήματα. Ποιο το μέτρο του $E_n$;

Άσκηση 1.4   Αποδείξτε ότι στο Θεώρημα 1.1.7 δε μπορούμε να παραλείψουμε την υπόθεση ότι κάποιο από τα $E_n$ έχει πεπερασμένο μέτρο.

Υπόδειξη: Πάρτε την περιπτωση $E_n = (n,+\infty)$.

Άσκηση 1.5   Λέμε ότι ένα σύνολο $S \subseteq {\mathbb{R}}$ είναι τύπου $G_\delta$ αν είναι αριθμήσιμη τομή ανοιχτών, αν υπάρχουν δηλ. ανοιχτά σύνολα $G_n \subseteq {\mathbb{R}}$ τέτοια ώστε $S = \bigcap_n G_n$. Αν $E \subseteq {\mathbb{R}}$ δείξτε ότι υπάρχει $G_\delta$ σύνολο $S \supseteq E$ τέτοιο ώστε $m(S\setminus E)=0$.

Υπόδειξη: Χρησιμοποιήστε το Θεώρημα 1.1.8.